Single-channel properties of glycine receptors of juvenile rat spinal motoneurones in vitro

Abstract

An essential step in understanding fast synaptic transmission is to establish the activation mechanism of synaptic receptors. The purpose of this work was to extend our detailed single-channel kinetic characterization of α1β glycine channels from rat recombinant receptors to native channels from juvenile (postnatal day 12–16) rat spinal cord slices. In cell-attached patches from ventral horn neurones, 1 mm glycine elicited clusters of channel openings to a single conductance level (41 ± 1 pS, n=12). This is similar to that of recombinant heteromers. However, fewer than 1 in 100 cell-attached patches from spinal neurones contained glycine channels. Outside-out patches gave a much higher success rate, but glycine channels recorded in this configuration appeared different, in that clusters opened to three conductance levels (28 ± 2, 38 ± 1 and 46 ± 1 pS, n=7, one level per cluster, all levels being detected in each patch). Furthermore, open period properties were different for the different conductances. As a consequence of this, the only recordings suitable for kinetic analysis were the cell-attached ones. Low channel density precluded recording at glycine concentrations other than 1 mm, but the 1 mm data allowed us to estimate the fully bound gating constants by global model fitting of the ‘flip’ mechanism of Burzomato and co-workers. Our results suggest that glycine receptors on ventral horn neurones in the juvenile rat are heteromers and have fast gating, similar to that of recombinant α1β receptors.

Glycine receptors (GlyRs) are the main mediators of fast synaptic inhibition in the spinal cord and brainstem (Legendre, 2001). In particular, in the ventral area of the lumbar spinal cord, activation of GlyRs is responsible for the control of left–right and flexor–extensor alternation during locomotor rhythms (Kjaerulff & Kiehn, 1997; Beato & Nistri, 1999). Spinal motoneurones, the output cells of the central pattern generator for locomotion, are known to receive rhythmic glycinergic inputs during motor tasks (Rossignol & Dubuc, 1994).

A detailed knowledge of the kinetics of GlyRs at the single-channel level is necessary in order to understand the properties and behaviour of glycine-mediated synaptic transmission. Such knowledge has been recently achieved for recombinant GlyRs, including α1 homomers and α1β heteromeric receptors (Beato et al. 2002, 2004; Burzomato et al. 2004). However, there is little information available on whether the kinetic properties of GlyRs in a native system resemble those of recombinant GlyRs.

The subunit composition of synaptic GlyRs is well known. The α2 homomers of newborn rats are replaced, both at the synapse and on the soma, by α1β heteromeric receptors in juvenile (ca postnatal day 10) animals (Takahashi & Momiyama, 1991). Measurement of RNA expression at different ages (Malosio et al. 1991) confirms the α2 to α1 developmental switch (see, however, Racca et al. 1998). Lamina II neurones are an exception because they mostly express the α3 subunit (Harvey et al. 2004).

In the present work, our aim was to characterize the mechanism of activation of glycine channels on the soma of spinal neurones and to compare it with that of recombinant receptors. Recording from spinal GlyRs in the cell-attached configuration proved to be difficult because very few patches were found to contain channels, possibly owing to a low density of GlyRs on the neuronal soma. Despite that, our data were sufficient to show that native and heteromeric recombinant GlyRs have strong similarities in their gating kinetics.

Methods

Acute spinal cord slices

Acute transverse spinal cord slices (350 μm thickness) were obtained from postnatal day 13–16 rats (Takahashi & Momiyama, 1991). In animals of this age, the developmental switch from the α2 to the α1 subunit of the glycine receptor is already complete (Malosio et al. 1991), as demonstrated by the disappearance of the slowly decaying inhibitory postsynaptic currents (IPSCs) associated with the α2 subunit (Takahashi & Momiyama, 1991; Jonas et al. 1998). Rats were anaesthetized with urethane (1.8 g kg⁻¹, i.p. injection of 10% (w/v) solution, Sigma) and decapitated. All procedures were in accordance with UK Home Office regulations. The spinal cord was rapidly dissected after ventral laminectomy and sliced in ice-cold extracellular solution. Mid-thoracic to lumbar segments were removed and fixed vertically to an agar block with tissue glue (Vetbond™, WPI Scientific Instruments). Ten to 15 lumbar slices were cut from each preparation with a Leica VT1000 vibratome. After 30 min of incubation at 37°C, slices were left at room temperature for another 30 min and then transferred to the recording chamber as needed. The medium was continuously bubbled with 95% O₂−5% CO₂.

The extracellular solution (for dissecting and recording) had the following composition (mm): 124 NaCl, 3 KCl, 25 NaHCO₃, 1 NaH₂PO₄, 0.5 CaCl₂, 3.5 MgCl₂ and 11 d-glucose (pH 7.4). Most recordings were performed from motoneurones, since they probably have a higher density of somatic channels (see Results). Motoneurones were identified as the largest cells in the ventral horn (soma size of at least 20 μm; Takahashi, 1992; Thurbon et al. 1998).

Patch pipettes for cell-attached and outside-out single-channel recording were pulled from thick-walled borosilicate glass (GC150F, Harvard Apparatus) and coated with Sylgard™ (Dow Corning). For cell-attached recordings, the resistance of the electrodes was between 4 and 6 MΩ, while smaller pipettes were used for outside-out patches (8–12 MΩ). Since the reversal potential for chloride ions is close to the resting membrane potential, the driving force in the cell-attached recordings was increased by depolarizing the patch close to 0 mV (assuming a membrane potential of −70 mV, see below). In order to minimize potassium currents, we have used a high-K⁺ pipette solution that matches the intracellular K⁺ concentration (Hamill et al. 1983). The composition of the pipette solution was (mm): 140 KCl, 1 CaCl₂, 1.8 MgCl₂ and 5 Hepes, with 1 mm glycine for cell-attached experiments. In some patches, single-channel potassium currents were observed at depolarized patch potentials. In this case, the pipette potential was adjusted to match the reversal for these single-channel currents (that coincides approximately with the resting membrane potential of the cell, see Verheugen et al. 1999). The estimated resting potential ranged between −73 and −64 mV. When potassium single-channel openings were not detected, the pipette was held at −70 mV.

The same solutions (but without glycine in the pipette) were used for outside-out experiments, to give a reversal potential of 0.3 mV for chloride and −98.5 mV for potassium. Patches were held at −100 mV, thus providing a good driving force for chloride while remaining close to the reversal potential for potassium. Again, this setting was chosen to reduce noise. No correction for junction potential was applied.

Single-channel currents were recorded with an Axopatch 200B amplifier, prefiltered at 10 kHz with the amplifier's four-pole Bessel filter and stored on digital audio tape (Bio-Logic Science Instruments, Claix, France). All outside-out experiments were replayed from the tape, filtered at 3 kHz with an eight-pole Bessel filter and digitized at 30 kHz (Digidata 1322A, Axon Instruments; Clampex software) for off-line analysis. Cell-attached recordings were filtered between 1 and 3 kHz, depending on the noise, and sampled at a rate chosen to be 10 times the filter cut-off frequency.

Analysis of single-channel recordings

Time course fitting (with the program SCAN) was used to idealize recordings. After choosing and imposing the resolution, dwell time distributions and fitted amplitude values were fitted with the appropriate mixture of exponential or Gaussian curves, respectively (program EKDIST). All the programs used in our analysis can be obtained from http://www.ucl.ac.uk/Pharmacology/dc.html.

In the presence of 1 mm glycine, channel openings occurred in clusters separated by long quiescent periods, probably reflecting sojourns in long-lived desensitized states (Takahashi & Momiyama, 1991; Beato et al. 2004; Burzomato et al. 2004). The critical amplitude for separation of high- and low-conductance clusters in outside-out recordings was chosen to minimize the total number of misclassified clusters (Colquhoun & Sigworth, 1995).

Maximum-likelihood fitting for the evaluation of the rates in the kinetic scheme was performed with the HJCfit program (Colquhoun et al. 1996; Hatton et al. 2003). HJCfit calculates a likelihood value for the entire idealized sequence of observed events, given a postulated mechanism, an initial set of guesses for the rate constants and the resolution. This process incorporates full missed-event correction (Hawkes et al. 1992). The rates are then adjusted to maximize the likelihood. The adequateness of the fit was judged by using the optimized rate constants to predict open and shut time distributions and conditional mean open time plots and comparing the predicted distributions with the observed ones.

Since maximum-likelihood fitting was performed on experiments with one saturating concentration of glycine, the only rates that could be reliably estimated were those corresponding to the gating steps of the fully bound states. Binding rates could not be estimated and were fixed to values obtained from previous experiments on recombinant receptors (Burzomato et al. 2004).

Results

Cell-attached recordings

The aim of our experiments was to compare the single-channel kinetic properties of native receptors from ventral horn neurones in postnatal day 12–16 rat spinal cord slices with those of recombinant α1β, which we reported recently (Burzomato et al. 2004). Data from recombinant receptors were obtained in the cell-attached configuration (because of its greater stability) and therefore we started by recording from cell-attached patches. In this recording configuration, only a very small minority of patches contained GlyRs (12 out of about 1400 stable recordings lasting more than 10 min). Even the patches that did contain channels had very few activations, which suggested that the patch contains few channels. Approximately one-quarter of our recordings originated from ventral interneurones, but all the patches with channels were found to come from motoneurones. Because of that, we concentrated on motoneurones for the rest of our work.

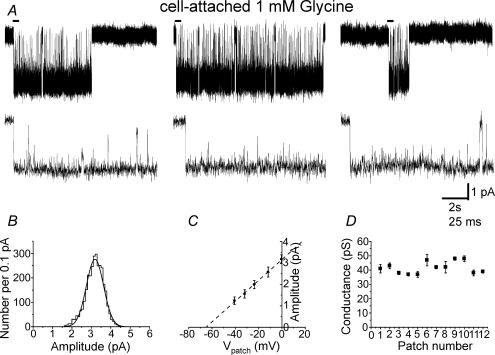
The traces in Fig. 1A show examples of inward currents elicited by 1 mm glycine in a cell-attached patch at a slow (top row) and fast time scale (bottom row). Openings were grouped in long (1–10 s) clusters that were separated by very long shut times (1–20 min, not shown) and had a single amplitude level in each of the 12 patches. For the patch in Fig. 1, this is shown by the distribution of fitted amplitudes, which was well fitted by a single Gaussian curve, with a mean of 3.0 pA and a s.d. of 0.4 pA (Fig. 1B). However, the mean fitted amplitude varied considerably from one patch to the next (range 1.8–3.0 pA). Since these recordings were from cell-attached patches, this could result from variability in the intracellular chloride concentration and in the resting membrane potential of the cell, rather than from true differences in the glycine channel conductance. In order to measure the channel conductance, in each experiment a voltage ramp (1 s duration, from 0 to +90 mV pipette holding potential) was applied during at least one cluster (range 1–4). For the experiment in Fig. 1A, the I–V plot obtained is shown in Fig. 1C (error bars correspond to the s.d. of amplitude measurements at 5 different potentials for 3 separate clusters), where the fitted line gives a slope conductance of 48 pS and a chloride reversal potential of −65 mV (corresponding to an intracellular chloride concentration of 12 mm). From the plot of the conductance measurement for all our cell-attached patches (Fig. 1D), it is clear that the slope conductance was very uniform (41 ± 1 pS, n=12), despite the differences in the individual amplitudes of events between different patches. This value is very similar to the one we reported for recombinant heteromeric α1β receptors (39 pS, Burzomato et al. 2003). The range of observed amplitudes corresponded to a range of intracellular Cl⁻ concentrations between 10 and 40 mm (assuming a resting membrane potential of −70 mV).

Figure 1. Properties of glycine single channels recorded in the cell-attached configuration from rat spinal motoneurones in vitro.

The traces in A show clusters of single-channel openings evoked by 1 mm glycine. The beginning of each cluster (indicated by the bar) is shown on an expanded time scale below each cluster. B shows the distribution of fitted amplitudes obtained in this patch at a transmembrane holding potential of 0 mV. Only openings longer than two filter rise times are included, and the distribution is fitted with a single Gaussian component. Means from such fits, for openings recorded at different transmembrane potentials, give the current–voltage plot shown for this patch in C. Data in the current–voltage plots were fitted to straight lines in order to estimate the (slope) conductance value for each patch. A summary of these results is shown in D.

Thus glycine receptors on the soma of spinal motoneurones are likely to be heteromers, but appear to be present at extremely low density.

Another problem in comparing native and recombinant kinetics is that the time resolution that can be achieved in the analysis of single-channel recordings is different for the two methods. Resolution depends on the signal-to-noise ratio, and we found that cell-attached recordings from neurones were intrinsically noisier than recordings from HEK cells. One reason is that neurones have spontaneous synaptic activity. This was reduced (but not abolished) by perfusing the slices with a low-calcium solution (0.5 mm Ca²⁺, 3.5 mm Mg²⁺) containing 500 nm tetrodotoxin. In addition to that, native patches can contain channels other than GlyRs, especially voltage-activated potassium channels (Hamill et al. 1983). This component of noise was minimized by recording at a transmembrane potential close to the reversal for potassium (see Methods). Despite these precautions, on average the noise was much bigger than what can be achieved in cell-attached recording from HEK cells. In this series of experiments, the typical noise was 400–500 fA at 5 kHz, compared with about 250 fA in recordings from HEK cells (Burzomato et al. 2004).

Resolution also depends on the amplitude of the single-channel currents. In our recording conditions, the amplitude of openings is determined by the resting membrane potential of the cells and by the chloride gradient across the membrane. We found (see above) that the intracellular chloride concentration varied considerably from one recording to the next, and it was only in a minority of patches that intracellular chloride was low enough to give openings as large as those observed in HEK cells (i.e. 3.1 pA, Burzomato et al. 2004).

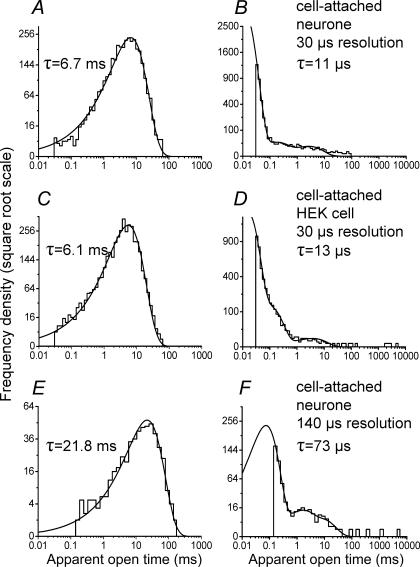
Nevertheless, in a small minority of experiments (n=2), a high signal-to-noise ratio (about 15) was achieved, and in these it was possible to use an imposed resolution of 30 μs, identical to that in recombinant recordings. For such experiments, it was therefore possible to compare directly the open and shut dwell time distributions of native channels (top row of Fig. 2, A and B, respectively) with those from recombinant receptors (second row, Fig. 2C and D, data from Burzomato et al. 2004). The open time distributions for the two high-resolution patches were fitted with a single component with τ=6.7 (Fig. 2A) and 7.2 ms. The shut time distributions were best fitted with three components, and the main component had a τ=11 μs in both patches (98.7% of the area for the patch shown in Fig. 2B and 98.5% for the other one), in close agreement with data from recombinant receptors.

Figure 2. The dwell time distributions of high-resolution recordings from native channels are similar to those obtained from recombinant α1β channels.

The top row of graphs shows the open period (A) and the shut time (B) distributions for native GlyRs for a recording with optimal (30 μs) time resolution. Note the similarity with the data from recombinant α1β receptors expressed in HEK293 cells (C and D, data from Burzomato et al. 2004) recorded at the same resolution. There is good agreement between the values for the time constants for open periods and for the fastest component in the shut time distribution. E and F show distributions from a native patch with a less favourable signal-to-noise ratio, in which only events longer than 140 μs were resolved. Note the differences in the open and shut time distributions (E and F). These differences are only apparent and result from the distortion introduced by a greater number of missed events. Imposition of the same resolution on the patch shown in the top row produces distributions similar to those observed in the low-resolution native patch (details in the text).

In the other 10 out of 12 patches, the time resolution was much worse than 30 μs. The greater distortion introduced in the dwell time distributions by missing more events is clear in the examples in the bottom row of Fig. 2, showing an open period distribution (Fig. 2E) and a shut time distribution (Fig. 2F) for a patch in which the imposed resolution was 140 μs. Here, the open period distribution was fitted by a single exponential with a much longer time constant than that of the high-resolution data (21.8 ms instead of 6–6.7 ms). This increase in the mean apparent open time is a consequence of missing many more short shut times. Thus, imposition of the same, poor resolution (140 μs) on the patch in Fig. 2A and B was found to increase its mean apparent open time to 66 ms.

The low-resolution patch in the bottom row of Fig. 2 had a shut time distribution that was best fitted by a mixture of three exponentials (Fig. 2F). The main component was again the fastest, but had an estimated time constant of 73 μs (area 93%), rather than the 11–12 μs seen in the best native patches and in high-resolution recombinant recordings (Burzomato et al. 2004).

Outside-out recordings

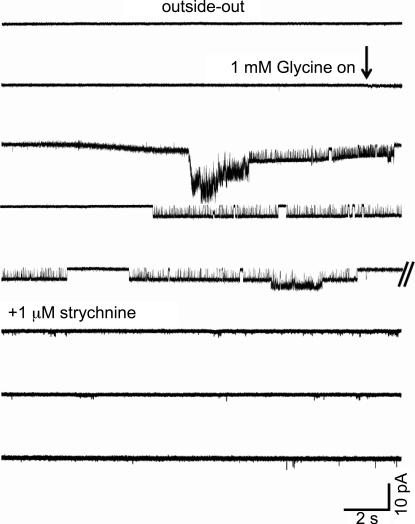
Because of the extremely low rate of success in observing channels in the cell-attached configuration, we switched to outside-out patches, which should stand a better chance of containing a glycine receptor because of their larger surface area. This considerably improved our success rate, as glycine-evoked single-channel currents were observed in 40 out of 59 outside-out patches. Glycine was applied only to patches in which no single-channel activity was detected when held in control solution for at least 2 min. A typical onset of activation is shown in Fig. 3 where, after a long quiescent period, glycine application produced a large inward current caused by the simultaneous activation of more than one channel. Glycine channels quickly desensitized and began to appear in clusters after a few seconds of application. These channel openings disappeared when 1 μm strychnine was added (Fig. 3).

Figure 3. Onset of channel activity during glycine application to an outside-out patch and block by strychnine: no channel openings were detected in this patch before glycine was applied.

The start of glycine superfusion (indicated by the arrow) is accompanied by an increase in noise (agonist is superfused at a faster rate than control medium) and by a baseline drift (because of a change in bath level). Glycine reaches the patch after a short delay because of the distance between the inflow and the patch, which is held as close as possible to the surface in order to reduce noise. At first, several channels open simultaneously (line 3), but the onset of desensitization allows single clusters to be detected (line 4). Here, a low-amplitude cluster occurs on top of a high-amplitude one (double event on line 5, all taken from a continuous trace). Strychnine (1 μm) was applied at the end of the experiment and abolished glycinergic activity within 1 min from the onset of application (not shown). The slight increase in baseline noise results from progressive deterioration of the seal during the recording.

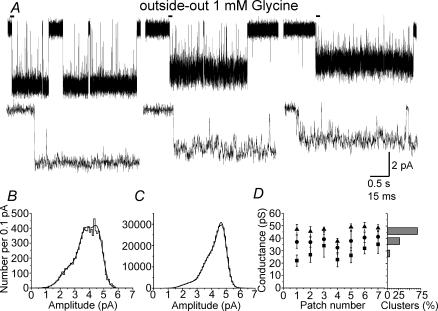
Since the cell-attached data were obtained in the presence of 1 mm glycine, we tried to obtain steady-state outside-out recordings using the same concentration. In most cases, however, patches contained too many channels, and only seven out of 40 patches showed isolated clusters suitable for analysis. Analysis of these experiments showed that the properties of outside-out clusters were different from those observed in the cell-attached configuration. First of all, in all seven experiments, three different amplitude levels were observed, as shown in the example clusters (all from the same patch) of Fig. 4A. The corresponding distribution of fitted amplitudes (Fig. 4B) was fitted with three Gaussian components. These three components were present in all seven patches, with average conductance values of 28 ± 2, 38 ± 1 and 46 ± 1 pS (Fig. 4D). Transitions from one level to the other occurred very rarely and were not further investigated. When the fitted amplitude distributions were analysed, the relative areas of the three conductance levels was found to be 19 ± 3, 56 ± 7 and 25 ± 8%, respectively, showing that most individual opening events were to 38 pS.

Figure 4. Glycine channels open to several conductance levels in outside-out patches.

The traces in A (top row) show clusters of openings elicited by 1 mm glycine in the same patch. Three conductance levels are present but each cluster of openings only visits one level. The traces in the second row are expanded from the beginning of each cluster (bars). Inspection of these traces clearly shows that openings to the two lower levels have higher open channel noise and shorter open times. B and C show the distribution of amplitudes for the openings from the same patch. In B, the fitted amplitudes are shown (each opening is one event), whereas C is an open-point histogram, and effectively weights the contribution of each opening by its duration. The greater predominance of the largest conductance in C is due to the longer duration of its openings. D summarizes our findings across all seven patches. For each patch, the symbols show the values for each conductance obtained from the Gaussian fits to the fitted amplitude distributions (all patches were held at −100 mV). The bar chart on the right displays the overall proportion of clusters (out of the total of 237) that fell in each of the conductance levels.

However, clusters recorded from neurones differed not only in amplitude, but also in their internal structure. It is clear from the example of Fig. 4A that the small-amplitude clusters have a much bigger open channel noise and frequently flicker to the shut state. On the contrary, clusters at the 46 pS level showed much longer open periods (with less open channel noise) and rare short shuttings (see the expanded traces in the second row of Fig. 4A). For this reason, the fitted amplitude distribution is a biased estimate of the relative importance of the three conductance levels and it emphasizes the contribution of the smaller components. When fitting open-point amplitude distributions (Fig. 4C), the relative weight of the bigger third component compared with the other two was reversed, indicating that the majority of charge transfer is carried by clusters at the highest conductance level. The average weight of the three components in the open-point amplitude distributions was (in increasing order of conductance) 8, 37 and 55%, respectively.

When clusters were classified according to their mean amplitude, out of 237 clusters that were analysed, 5% corresponded to the lowest amplitude range, 27% to the intermediate and 67% to the highest conductance level (bar chart in Fig. 4D).

Cell-attached recordings of recombinant α1β glycine receptors open to one conductance only (39 ± 1 pS, Burzomato et al. 2003, 2004), as we have found for native receptors. We performed outside-out recordings from recombinant α1β receptors expressed in HEK cells. In these outside-out experiments, channels exhibited three conductance levels of 27 ± 2, 34 ± 1 and 45 ± 1 pS (n=9, 1 mm glycine, data not shown), in good agreement with the levels observed in native receptors and with values reported by other groups for both native (Takahashi & Momiyama, 1991; Bormann et al. 1987) and recombinant heteromeric receptors (Bormann et al. 1993).

The presence of sublevels made kinetic analysis very difficult. However, some features of clusters at different amplitudes could be identified.

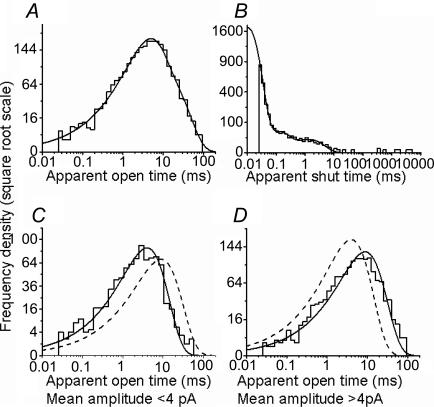
Figure (5A and B) shows example open and shut time distributions for an outside-out patch. When open period distributions were fitted irrespective of their conductance, two exponential components were required, with time constants of 5.0 ± 0.3 (71.4 ± 2.0%) and 18.7 ± 1.6 ms (28.6 ± 2.0%). These corresponded to high- and low-conductance openings, respectively. When these were fitted separately, the resulting two open period distributions could be well described by single exponentials with a time constant of 4.0 ms for openings smaller than 4 pA and 8.8 ms for the highest amplitude clusters in this patch (Fig. 5C and D) and a mean of 5.8 ± 0.6 and 15.1 ± 2.9 ms (n=6). Differences between the two distributions are more evident when they are compared by superimposing the two fits, as in Fig. 5C, where the dashed line in the distribution in Fig. 5C is the fit to the conditional distribution in Fig. 5D; each fit is scaled to the same number of observed events as the continuous line.

Figure 5. In outside-out patches, GlyR openings to the largest conductance are longer than those to lower conductance levels.

A and B show the dwell time distributions for spinal GlyRs recorded in the outside-out configuration and constructed including all conductance levels. C and D show conditional open period distributions, plotted for openings to the largest conductance (greater than 4 pA at −100 mV, D) or to the two smaller conductances (less than 4 pA, C). In D, the dashed line shows for reference the exponential fitted to the distribution in C (and vice versa), scaled to contain the same number of events. The longer duration of the larger openings is very apparent.

Shut time distributions were fitted with three components, the main one being the shortest, with a mean of 14 ± 1 μs (area 96.4 ± 0.4%; resolution 30 μs).

In summary, outside-out patches are not suitable for kinetic analysis because of heterogeneity in conductance and in open period properties, while prolonged efforts at recording in the cell-attached configuration yielded only two patches with an acceptable time resolution. This severely limits the prospects of a kinetic study.

Estimation of the individual rate constants in an activation scheme as complicated as the one used to describe recombinant heteromeric GlyRs (Burzomato et al. 2004) requires the simultaneous fit of experiments at several different agonist concentrations, in order to obtain information on the lower liganded states of the receptor. The recordings must have high resolution, because GlyRs have a very fast (about 10 μs) shut time component that accounts for 95–98% of shut times.

Clearly, our cell-attached data from native receptors, at the saturating concentration of 1 mm, fall short of these requirements. However, the information they contain should allow us to estimate the gating rate constants for the fully bound open state (Fig. 6). Therefore, we proceeded to fit these data with the scheme in Fig. 6D. This is the ‘flip’ mechanism of Burzomato et al. (2004), with all the rate constants corresponding to low liganded states fixed to the values determined for recombinant α1β receptors. Thus, only the values of the gating rate constants to and from the fully bound channel were estimated by maximum likelihood fitting to the two idealized records at 30 μs resolution.

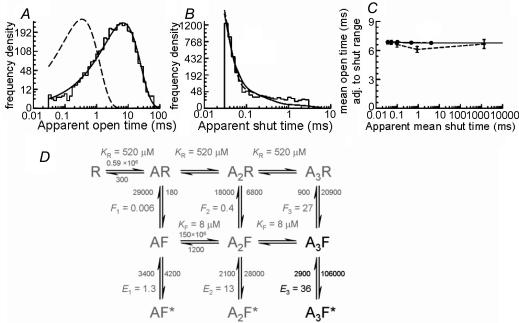
Figure 6. Estimation of the fully liganded gating rates for GlyRs recorded in the cell-attached configuration from spinal neurones in vitro.

Data from the two best high-resolution recordings were fitted by maximum likelihood to the mechanism shown in D (the ‘flip’ mechanism of Burzomato et al. 2004). Since our native data were obtained at a single, saturating glycine concentration, only the fully bound gating rates (black in the mechanism) were estimated in the fit. Rate constants connecting the other states (grey) were constrained to the values estimated for recombinant α1β heteromeric GlyRs by Burzomato et al. (2004). A–C show that the values of rate constants optimized in this process describe the data adequately, in that they predict distributions of apparent open periods (A) and shut times (B) similar to the observed data (shown as histograms; note that the fit is to the actual sequence of openings and shuttings after idealization, not to the distributions shown here). Dashed lines show the distributions predicted for infinite resolution (i.e. no missed events). Note the profound effect of missing the very common short shut times on the apparent open time distribution. In the case of ‘infinite’ resolution, this would have a main exponential component with a time constant of 345 μs and a relative area of 99.3%. The mechanism and its fitted rates also adequately describe the shape of the correlation between mean open periods adjacent to gaps in the specified range (shown in C). Here, observations are shown as diamonds connected by dashed lines and the values calculated from the mechanism as filled circles connected by a solid line.

The calculated dwell time distributions for one of the two patches are shown superimposed to the data histogram in Fig. 6A and B. The fast component in the shut time distribution is well fitted for both patches, giving values of 106 000 and 113 000 s⁻¹ for β₃ (opening rate constant) and 2900 and 3200 s⁻¹ for α₃ (shutting rate constant), in good agreement with the estimates by Burzomato et al. (2004) of 129 000 and 7000 s⁻¹, respectively. The (lack of) correlation between mean open periods and adjacent shut times was also predicted correctly (Fig. 6C). The fitted rate constants predict that, in the presence of 1 mm glycine, the receptor oscillates between A₃F and A₃F* with occupancies of 2.6 and 96.9%, respectively. This is in agreement with the relative occupancies calculated for recombinant receptors (4.8 and 92.8% for the ‘flip’ and open state, respectively, Burzomato et al. 2004) and confirms that data at saturating agonist concentration cannot be used to estimate rates to or from states other than A₃F and A₃F*, because they are barely ever visited.

Discussion

We have recently reported a detailed mechanism for GlyR activation based on the analysis of cell-attached recordings of recombinant channels expressed in HEK cells (Beato et al. 2002, 2004; Burzomato et al. 2004). In principle, the same kind of analysis could be used for studying native glycine channels.

In practice, this task was difficult, for several reasons, the first being the prohibitively low rate of success in obtaining cell-attached recording of native GlyRs. This could be due to an extremely low density of somatic channels on spinal neurones, which in turn may be because GlyRs are clustered both at the soma and at putative postsynaptic sites (see the immunocytochemistry experiments of Nicola et al. 1992 and Kneussel & Betz, 2000). It is possible that, even in the soma, receptor clusters are part of a postsynaptic density and are not easily accessible to patch electrodes. The only other study in which cell-attached recordings were performed on native GlyRs is, to our knowledge, that of Bormann et al. (1987), who report that most patches contained channels. However, this work was carried out on spinal neurones in culture, and it is conceivable that culture conditions alter the distribution of channels on the cell surface, making them more abundant, less clustered and/or more accessible to electrophysiological recording. We decided not to use a culture system because neurones have to be obtained from embryonic animals and cannot be maintained in vitro long enough to ensure a complete α2 to α1 switch (Hoch et al. 1989).

Another problem was the decrease in the signal-to-noise ratio compared with that of recombinant channel recordings. Signals (i.e. channel openings) were smaller, because differences in intracellular chloride concentration reduced the driving force for chloride. Noise was also greater, because of the presence of other channels and because of the spontaneous synaptic activity of the recorded neurones. These factors could be minimized but not eliminated. It was therefore rare to achieve a resolution better than 100 μs (cf. the 30 μs resolution that was standard for our work on recombinant channels). This resolution would be satisfactory for slow channels like GABA, but not for GlyRs, because they have a very fast fully liganded opening rate which produces a fast shut time component with a time constant of approximately 7–8 μs. In the present experiments, we have been able to detect such a fast component only in two out of 12 patches. Reassuringly, the time constants for both the shortest shut times and the open period distribution in these two high-resolution patches are in perfect agreement with those measured from recombinant α1β receptors.

Recording in the outside-out configuration overcame both the problem of channel density and that of the signal-to-noise ratio. Most outside-out patches contained GlyRs, possibly because the patches are bigger. Furthermore, in symmetrical chloride, the amplitude of channels was 4–5 pA, allowing a resolution in the 30 μs range. Nevertheless, another problem became apparent in the outside-out configuration, namely channel behaviour was very different from that observed with cell-attached recordings. Not only did channels open in clusters of different conductance, but differences in conductance were associated with differences in open period distribution. This made data from outside-out recordings unsuitable for kinetic analysis.

It is not clear why subconductance levels are only detected in the excised patch configuration. In neurones, sublevels were reported to be very rare in the only cell-attached study available (Bormann et al. 1987), while in recombinant heteromeric channels, openings to only one conductance were observed (Burzomato et al. 2004). In contrast, the presence of sublevels in the outside-out configuration is well documented for both neurones (Bormann et al. 1987; Takahashi & Momiyama, 1991) and a recombinant system (Bormann et al. 1993). The presence or absence of subconductances depended only on patch configuration, not on whether channels were native or recombinant. Thus it seems likely that subconductances result from intracellular modulatory factors, but that such factors are similar in neurones and in HEK cells. Patch excision was reported to change the kinetic properties of recombinant GlyRs and increase their open probability (Fucile et al. 2000). Although this phenomenon has been shown to be calcium dependent, the identity of the protein responsible for such modulation remains elusive, and it is impossible to relate this to conductance changes.

The main aim of this study was to determine whether recombinant and native receptors share the same kinetic characteristics. In order to do this, we needed to obtain and analyse high-resolution steady-state recordings obtained at many different concentrations, because only this can give enough information on both binding and gating rate constants. This proved impossible, mainly because of the low density of somatic channels. However, in a minority of experiments at saturating agonist concentration, we managed to obtain an estimate of the fully bound gating rates, and found that these values are in excellent agreement with those estimated for recombinant GlyRs.

These values for the fully liganded gating rates were estimated by ‘partial’ fits in which other rates were set to the same values that we observed in recombinant heteromers (Burzomato et al. 2004). We also attempted to fit the data with fewer constraints, e.g. fewer fixed rates. This invariably led to rate constant estimates that were unrealistic, in that binding rates reached values above the theoretical diffusion limit (10⁹m⁻¹ s⁻¹) and gating or ‘flipping’ rates were faster than the standard limit for a conformational change in a protein (10⁶ s⁻¹, Fersht, 1998; Chakrapani & Auerbach, 2005). In general, we found that a fit with more free parameters than the two fully bound gating rates could qualitatively fit the data, but did not converge after the maximum number of iterations. This is not surprising, since the information contained in data at only one (saturating) concentration cannot give a unique solution for all the rate constants in a model as complex as that needed to describe GlyR activation.

Our ultimate aim is to use these data to understand glycinergic synaptic transmission. An obvious limitation is that our recordings come from receptors that are likely to be somatic/extrasynaptic. Despite that, these receptors are likely to have the same subunit composition as synaptic GlyRs, which are, of course, much harder or impossible to access by electrophysiological recording. Evidence that somatic and synaptic glycine receptors are similar comes from observations of synaptic channels in the tail of synaptic currents in electrotonically compact cells, such as small spinal interneurones (Takahashi & Momiyama, 1991), amacrine cells (Gill et al. 2006) or small cerebellar Golgi cells (Dieudonné, 1995). Of course, we cannot exclude subtle differences between somatic and extrasynaptic receptors, because of binding to the cytoskeleton through gephyrin or differences in intracellular modulation, for instance by phosphorylation (reviewed by Moss & Smart, 2001).

In the present work, we provide an estimate for the gating rates of native GlyRs of spinal neurones from cell-attached recordings. Owing to the considerable technical problems we encountered, our analysis falls short of the complete kinetic characterization we planned. However, our data show that native receptors have a gating kinetic similar to that of recombinant heteromeric GlyRs. This reassures us on the validity of using recombinant expression to study GlyRs and confirms that this receptor has very fast gating rates and a high efficacy.