Mutations as trapdoors to two competing native conformations of the Rop-dimer

Abstract

Conformational transitions play a central role in regulating protein function. Structure-based models with multiple basins have been used to understand the mechanisms governing these transitions. A model able to accommodate multiple folding basins is proposed to explore the mutational effects in the folding of the Rop-dimer (Rop). In experiments, Rop mutants show unusually strong increases in folding rates with marginal effects on stability. We investigate the possibility of two competing conformations representing a parallel (P) and the wild-type antiparallel (AP) arrangement of the monomers as possible native conformations. We observe occupation of both distinct states and characterize the transition pathways. An interesting observation from the simulations is that, for equivalent energetic bias, the transition to the P basin (non-wild-type basin) shows a lower free-energy barrier. Thus, the rapid kinetics observed in experiments appear to be the result of two competing states with different kinetic behavior, triggered upon mutation by the opening of a trapdoor arising from Rop's symmetric structure. The general concept of having competing conformations for the native state goes beyond explaining Rop's mutational behaviors and can be applied to other systems. A switch between competing native structures might be triggered by external factors to allow, for example, allosteric control or signaling.

The concept of a funneled energy landscape explains how proteins fold efficiently into a unique native conformation (1–5). A protein can fold by multiple routes in a diffusive process. Within a long evolutionary period, the shape of the energy landscape has been sufficiently smoothened to permit protein function despite environmental changes or mutations. In a funneled landscape, native interactions dominate the folding funnel, making the bias sufficiently large toward the native conformation compared with the roughness that arises from local minima. Going beyond folding, recent work has included multiple folding basins to describe conformational transitions of proteins that regulate molecular processes in biological systems or can explain, for example, the aggregation of prions (6). Approaches include thermodynamic weighting of different potentials (7), coupling of potentials (8), switching of the Hamiltonian (9), and reconstruction of contact maps (10).

This article is focused on the development and application of a dual-funneled energy landscape to understand a protein's mutational behavior.

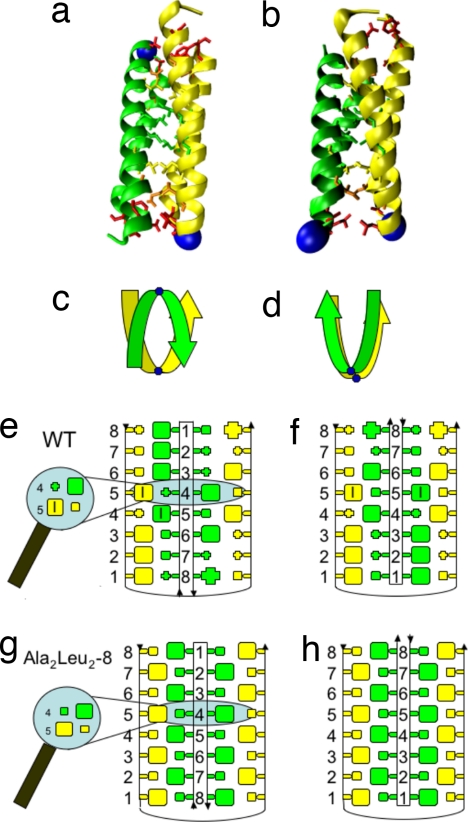
The protein under investigation, the Rop-dimer (repressor of primer, Rop^§), regulates ColE1 plasmid replication in Escherichia coli through RNA binding (11–14). This homodimer shows abnormal mutational behavior, as discussed below. For an interpretation within the framework of a minimally frustrated energy landscape, one must consider the symmetry of the dimer. Each monomer consists of a helix–turn–helix structure (Fig. 1). Wild-type (WT) monomers arrange as antiparallel (AP), coiled-coil, four-helix bundles, with a hydrophobic interface between the monomers. This interface appears to be a key component for Rop's monomer–monomer association (15, 16). In a series of experiments, the hydrophobic core of Rop was systematically mutated to investigate the effect of packing on stability (17). Mutations were performed at the eight layers that constitute the hydrophobic core. The AP arrangement of the WT Rop monomers has layer 1 of monomer A packed against layer 8 of monomer B, layer 2 against layer 7, etc. Stacking these layers in pairs of the hydrophobic Ala and Leu should ensure optimal packing of the protein (Fig. 1). The mutants differ by the position and number of repacked layers. Extreme cases include an “underpacked” core of only Ala or an “overpacked” core of only Leu, which showed strong changes in dimer stability. It is assumed that in these extreme cases mutants lose their similarity to the WT Rop and are unstable. Although the WT contains no disulfide bridges, proline, or cofactors, it folds and unfolds extremely slow with a folding rate k_F ≈ 0.013 s⁻¹, when compared with other quick-folding proteins (18). Upon mutation, the folding/unfolding rates increase by up to four orders of magnitude (for Ala₂Leu₂–8; Fig. 1) (19). Surprisingly, these changes in kinetic behavior were not accompanied by strong changes in thermal and chemical stability (17), as would be expected from energy landscape theory (2).

Fig. 1.

Structures and symmetry of Rop. Experimental structures of the WT protein (a) and Ala₂Ile₂–6 mutant (b) differ by the antiparallel (AP) and parallel (P) arrangement of monomers (colored green and yellow with blue spheres indicating the turn regions). Experimental mutations on Rop concentrate on layers of amino acids in the dimer interface (numbered 1–8). Side chains belonging to the (4, 5) layer (green), (3, 6) layer (yellow), (2, 7) layer (orange), and (1, 8) layer (red) have been mutated as pairs. A simplified presentation of monomer orientation is shown in c and d. Schematic diagrams of the dimer interface for WT Rop (e and f) and the mutant Ala₂Leu₂–8 (g and h) assume that both arrangements AP (e and g) and P (f and h) are possible and suggest a comparable packing in both due to symmetry. Small boxes represent Ala, and big boxes represent Leu (if empty) or isoleucine (with an additional I). All other amino acids are represented as small or large crosses, depending on their size.

These kinetic responses to mutation lead to the question of whether there is a concomitant change in structure. Most of the mutants were assumed to stay in the AP arrangement because they have comparable helical content to the WT (17) and maintain their ability to bind RNA in vitro, even though some others lose it in vivo (20). X-ray and NMR measurements detected, however, three additional structures, a parallel (P, mutant Ala₂Ile₂–6)^¶ arrangement of helices (21), a bisecting U (BU) arrangement for a mutation in the turn region (Ala₃₁Pro; data not shown) (22), and a tetrameric four-helix bundle resulting from a five-residue deletion in the turn region (23). In the cases of P and BU, the tertiary structure of the monomers maintains the WT helix–turn–helix motif.^‖ A synopsis of the experimental data can be found in supporting information (SI) Appendix.

An earlier theoretical study used simulations of a structure-based (Gō-type) model to shed light on the Rop-dimer mystery (24). In the simulations, the folding barrier for the P structure was lower than for the AP structure. Therefore, it was inferred that mutants with increased folding rates could adopt the P structure in addition to the AP structure of WT Rop.

The present study takes this hypothesis as its basis. The system is modeled by a dual-funneled energy landscape with the AP and the P arrangement as basins. The properties of this energy landscape are investigated. Molecular dynamics using all-atom force fields cannot reach the time scales needed for an analysis of a protein of this size and because of their complexity are difficult to interpret. Structure-based C_α-bead models (1, 4, 25) combine low computational demands with a clearly laid out formulation of the force field. These models are typically used to study folding of proteins with a single native structure. This article describes a procedure to include both the P and the AP structure in a mixed system while maintaining a concise formulation of the Hamiltonian.

Results

The multibasin landscape was sampled by using molecular dynamics. One can observe transitions between U, P, and AP, as exemplified in Fig. 2. The corresponding free-energy profile was constructed (Fig. 3a), and the folding temperatures, T_F, corresponding to the folding of P and AP were determined. They are sufficiently similar to consider them equal (Table 1). The barrier heights remain high enough that we do not enter the low-barrier regime <3k_BT (26) and can directly relate barrier heights to (un)folding rates. Below T_F, the system freezes into one of the two competing conformations. Upon further cooling, the lack of traps with nonnative structures indicates that our model is unfrustrated even geometrically. Near T_F, transitions between the U state and the two folded states were observed. These transitions occurred without intermediates. Above T_F, Rop was unfolded. To investigate the role of the hydrophobic interface during structural transitions, it is useful to plot the free energy as a function of interface contacts unique to the P and AP forms (Fig. 3b). The energy landscape has two orthogonal branches originating from the U state. The transition-state ensemble (TSE) between the two forms appears to have only a residual number of native contacts and a partial loss of the secondary structure.

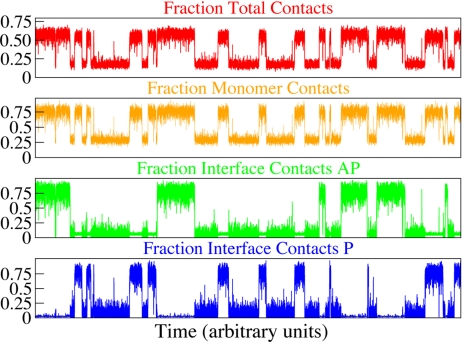
Fig. 2.

Sample trajectory of a dual-funneled simulation at T_F. Each graph displays a specific subset of contacts as fraction of their total number versus time. One observes several transitions between the antiparallel (AP), the parallel (P), and the unfolded (U) ensemble. The top graph (red) shows the sum of all P and AP contacts. It is impossible to form a high fraction (>0.7) of these contacts because the P and AP interface contacts contradict each other (see below). The next (orange) graph shows the number of monomer contacts. They are partially formed in the U state. The last two graphs show the interface contacts of AP (green) and P (blue). It is impossible to form both interfaces at the same time. When one interface is formed, almost no interface contacts of the competing structure are formed. In the unfolded ensemble, only small numbers of interface contacts are formed (<0.25). One can see that there are fewer folding/unfolding events for AP compared with P. In addition, AP, once formed, takes longer to unfold. This can be explained by the different barrier heights for (un)folding of P and AP.

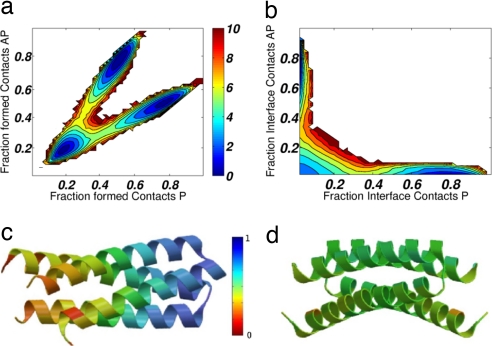
Fig. 3.

Free-energy profiles at T_F. The free energy is shown as a function of the fraction of formed P and AP contacts (a) and P and AP interface contacts (b). Three distinct basins are clearly present, corresponding to the P, AP, and U states. Both profiles indicate a lower energetic barrier for formation of the P conformation compared with the AP conformation. Because the transition-state ensembles TSE-P and TSE-AP are separated, φ-values can be calculated for each barrier individually. The φ-values for TSE-P (c) and TSE-AP (d) are color-coded on their respective folded states. For TSE-P, the φ-values are polarized with larger values in the turn region. φ-values for TSE-AP are homogeneously distributed among the residues. These φ-values indicate that the structures express different folding behaviors: the P structure possesses a folding nucleus polarized around the turn region, whereas the TSE-AP is more diffusive. This folding nucleus indicates a more organized folding behavior for P, consistent with its lower folding barrier.

Table 1.

Thermodynamic quantities for single- and dual-funneled simulations

System	Folding temperature		RatioTFAP/TFP	Barrier in kBT		Ratio barrier AP/P
	TFAP	TFP		AP	P
AP	1.100	—	—	6.9	—	—
P	—	1.060	1.04	—	5.9	1.18
Pmod	—	1.098	1.00	—	5.5	1.27
Dual	1.080	1.080	1.00	5.7	4.6	1.24

The barrier heights obtained from single-funneled simulations differ for P and AP. P_mod possesses an adjusted interface contact strength (as described in the text); i.e., the contribution from P interface contacts matches the contribution from AP interface contacts. To probe differences in the folding of P and AP in the dual system, thermodynamic quantities were calculated twice. All sampled conformations that possessed a higher number of AP(P) contacts were used to obtain quantities for the AP(P) state. The dual-funneled energy landscape produces lower T_F and barrier heights compared with single-funneled simulations. The barriers for the P conformation are lower than for the AP conformation, which suggests quicker kinetics for P.

One can ask the question of whether BU is a high-energy intermediate between the P and AP state (24). The number of formed BU contacts during our simulations was therefore calculated. We could not detect the formation of the BU structural motif of “embracing” helices. This indicates that the BU geometry, at least for our unfrustrated model, is not likely an intermediate in the folding process. This suggests that the BU structure results from the high strain created in the turn region by the mutation Ala₃₁Pro for either P or AP by the removal of one dihedral angle. The BU has a bigger distance between the helices within each monomer. An additional known structure, the tetrameric four-helix bundle, results from a deletion of the amino acids in the loop region of the WT. Although some of the native contacts are shared with the other Rop mutants, the altered sequence length and the tetrameric nature suggest a dissimilar energy landscape and folding mechanism. Therefore, it is outside of the scope of this investigation. All other known mutations have the same sequence length with the WT and are concentrated on the interface region.

The free-energy landscape for this dual-funneled model has reduced folding barriers and folding temperatures when compared with single-funneled folding of Rop (Table 1). Transition-state contact formation can explain these results. While the probability of interface contacts unique to the AP state being formed in the P state is nearly 0, the AP contacts are occasionally formed in the U state (p ≈ 0.01) and in the transition ensemble of state P (p ≈ 0.025). The added stability created by the additional AP contacts formed in the TSE of P and in the U state have the effect of both reducing the barrier and the folding temperature. Formation of P contacts in the TSE of AP has a similar effect. Similar to the effects of nonnative contacts in the folding of SH3 (27), the contacts native to a competing structure reduce the folding barrier and hence increase the folding rate.

Most structure-based simulations tend to underestimate barrier heights because they are governed by additive pairwise interactions. Nonadditive effects, like side chain rearrangements or solvent affects, are not taken into account. Such nonadditive contributions can be added as perturbations. The resulting barriers resemble experimental data more closely (27). The energetic contributions of two- and three-body interactions to the native state are (1 − α)ε₂Q₂N₂ and αε₃Q₃N₃. α is the strength of the three-body perturbation and lies between 0 (full two-body contribution, no three-body contribution) and 1 (no two-body contribution, full three-body contribution), ε_X gives the respective interaction strength [ε₂ = 1 k_BT, ε₃ = ε₂(N₂/N₃) to maintain overall stability of the native state], Q_X are the fraction of formed X-body interactions for the respective conformation and N_X gives the total number of X-body interactions in the Xth structure. For Rop, three-body contributions increase the barrier height for the AP stronger than for the P (data not shown). Although this effect is not very strong, we made the tertiary structures of the monomers equal for P and AP. An even stronger effect would be expected if we had not used the same tertiary structure for both monomers but the original monomers (28).

To characterize the folding transition ensembles, TSE of P and TSE of AP, φ-values were calculated. φ-values measure the contribution of each residue to the TSE relative to the folded state (29) and are used to characterize changes in the TSE upon mutations (30). In structure-based simulations, φ for the residue i is calculated as

where Pⁱ is the probability of formation of contacts involving residue i in the state X, where X is the TSE, unfolded (U), or folded (F) state (28, 31).** Although this definition is not exactly the one used experimentally, it has been shown in earlier work (28, 31–33) that both of these definitions are equivalent. By calculating φ-values, one can construct a structural description of the TSE. The P and AP structures are colored by φ-value for the TSE P and the TSE AP (Fig. 3 c and d). The differences in the TSE P and the TSE AP are quite striking. The φ-values of the P structure are polarized with the highly structured turn-region toward relatively unstructured C- and N-terminal regions. The φ-values of the AP structure are homogeneously distributed. This suggests that the P state possesses a folding nucleus around the turn region. The AP-state has no preferred site for the TSE formation. We observe some nonstandard φ-values outside of the range of 0 and 1. These values result from contact formation of the competing structure. As outlined in the previous paragraph, contacts belonging to the competing native state appear with low probabilities in the U and TSE but not in F. To investigate the effects mutations of Rop have on its folding, we modified the strength of all contacts involving the affected mutation sites for both states. Because the distribution of φ-values for the two states P and AP differs, one might expect changes in the kinetic behavior. One observes modified values of T_F and folding barriers (data not shown), but the kinetic accessibility of the P state remains higher than that of the AP state. It appears that this is a possible key to understanding the folding mechanics of Rop.

Discussion

The Trapdoor Interpretation.

Rop is a homodimer, which suggests that both monomers adopt the same tertiary structure with the monomers arranged symmetrically. Knowing the helix–turn–helix motif of the monomers, one can hypothesize the feasibility of different quaternary structures. P and AP arrangements of the monomers are obvious possibilities. Geometric considerations favor the P conformation. To generate a stable interface, P only needs to localize the turn regions, whereas some flexibility can remain in the termini. In contrast, forming a stable interface in AP requires coordination of the entire interface. Stabilizing the turn region of one monomer requires the forming of an interface with the tails of the other monomer. This imposes an entropic penalty. The entropic cost of stabilization of an interface in the middle of the helices should also be large because this is unlikely without simultaneous localization of the turns. Both possibilities impose an entropic penalty to form the AP structure. These simple arguments agree with the observation that parallelly arranged coiled-coil helices are more common (34). In contrast to our geometric intuition, x-ray and NMR measurements reveal that WT Rop adopts an AP conformation. The structurally resolved Ala₂Ile₂–6 mutant adopts the P conformation and does not bind RNA, neither in vitro nor in vivo. Therefore, the arrangement of monomers as P or AP seems to determine the RNA-binding ability. In addition to these structural data, we know that mutations in the hydrophobic core substantially increase both folding and unfolding rates compared with the WT. The stability varies only slightly and is not correlated with the changes in kinetics. The ability to bind RNA in vitro and in vivo disagrees for some mutants, questioning the early assumption that the mutated forms keep exactly the geometry of the WT. Most of the other mutants have not been structurally resolved, but the assumption that mutants which show in vitro activity and comparable helical content adopt the AP conformation is at least questionable. Why should mutants that do not bind in vivo and show comparable helical content to the Ala₂Ile₂–6 mutant not adopt the P structure? There is also no direct evidence supporting the earlier assumption that the changes in folding rates were due to an effective decrease of the folding barrier.

To generate a more complete description, we modeled Rop as a dual-funneled energy landscape where the two basins represent the P and AP structures. Our in silico simulations show a lower free-energy barrier for the P conformation than for the AP. The φ-values for the P conformation are polarized and ≈0.8 in the turn region with the C and N termini less than 0.3. This suggests a folding nucleus in the turn region. In contrast, the AP conformation has a more homogeneous distribution of φ-values and a higher folding barrier. Guided by the results from the simulations, we formulate a matching interpretation of the experimental and theoretical observations. Simple considerations regarding the structures P and AP let P appear to be preferred. P also appears to be kinetically preferred in our simulations. Random mutations must therefore overcome this bias toward P to generate the WT AP arrangement of monomers. Evolution selects by maximizing function. The P arrangement of the monomers is not active, and evolutionary pressure therefore selects the sequence to favor the AP conformation by lowering its free energy relative to the P state.

This can be achieved by breaking the symmetry in the sequence of the monomers. However, the WT-energy landscape still contains a trapdoor (see Fig. 4) in the free-energy landscape. Because of the high similarity of both conformations and their related hydrophobic core packing, it is impossible to avoid a local energetic minimum for P (Fig. 4c). In contrast to evolutionary pressure for maximal function, the experimentally performed mutations were aimed to optimize the hydrophobic packing. They increase stability by symmetrizing the interface. As described above, this should favor P over AP. Mutants, for which the free energy of P is only slightly higher than that for AP, can none the less possess P as a kinetic trap (Fig. 4d). The folding free-energy barrier for the new state P becomes lower than for the original state AP. Circular dichroism measurements do not allow one to distinguish between the transition from U to P or AP. Therefore, quicker kinetics appear in experiments. Mutations that make P and AP energetically equal lead to a degenerated, nonunique native state (Fig. 4e) with further increased folding/unfolding rates. Both topologies would be expected to be equally populated at equilibrium, resulting in a mixture of both structures. This reduces the mutants RNA-binding ability because the P state is not known to perform this function. Favoring P over AP leads to complete loss of RNA-binding ability. This is observed for the mutant Ala₂Ile₂–6, which adopts the P conformation. Although we cannot address the details of energetics by structure-based simulations, the experimental observations on kinetics and RNA-binding ability are in agreement with our trapdoor explanation.

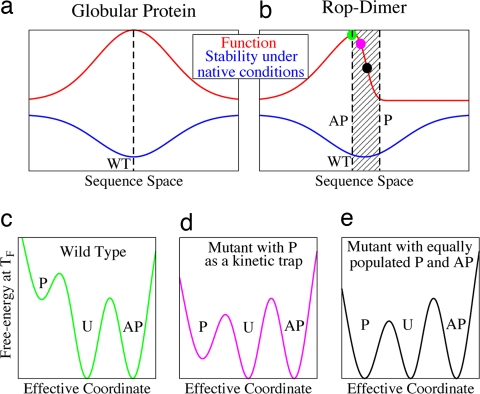
Fig. 4.

Schematic representation of the trapdoor mechanism. For many globular proteins, minor changes in sequence often have small effects on structure and therefore function (a). Evolution can select for stability (i.e., the free-energy difference between U and F under physiological conditions) and function simultaneously (dashed line) by optimizing both, as indicated in the picture. This situation, however, must not be possible in all cases. For Rop (b), because of the symmetry of the interface packing (see Fig. 1), minor mutations can result in large structural transitions. These have significant effects on function (i.e., the ability to bind RNA) while weakly affecting stability. Assuming that the evolutionary pressure on function is stronger than on stability, Rop was selected to have the functional AP structure (green dot). Interactions stabilizing the AP state also affect P; thus, the energy landscape contains a trapdoor to the similar but nonfunctional P. This trapdoor mechanism can be explained as follows. The shaded region between the dashed lines in b indicates a mixing of P and AP in the native ensemble. In c–e, the green, magenta, and black dots in b are illustrated in detail. In general, the native stability of the WT and the mutants differs. To account for these changes, we compare at the respective T_F. c shows the WT free-energy landscape. The AP and U states are equally populated. The P state is not significantly populated and not detected in experiments. Upon mutation, the free-energy balance between AP and P is changed. Once the free-energy barrier between U and P is lower than from U to AP (d), circular dichroism experiments observe quicker kinetics despite AP being energetically favored. Upon further mutations, P and AP become energetically competitive with both states equally populated (e). The native state has become degenerated. This hinders the biological function of Rop because the P structure is not active. The trapdoor that arises from the high symmetry of Rop has been fully opened and functionality decreased. Further mutating Rop to favor the P structure will result in complete loss of functionality (as in Ala₂Ile₂–6; not displayed).

We believe it is possible to create a mutant of Rop for which both states have a comparable free energy. This mutant would have two stable native conformations that are equally populated in equilibrium but express different kinetics. This challenges the common understanding of proteins of having a unique native conformation. Three facts suggest that the mutant Ala₂Leu₂–6 possesses such a degenerated native state. First, it maintains its RNA-binding ability in vitro but not in vivo, indicating that the binding state AP, although present, is not always dominant. Second, this mutant has very high folding/unfolding rates, which suggests that P is a kinetic trap. Third, the sequentially highly similar mutant Ala₂Ile₂–6, which has Ala₂Leu₂–6's Leu in the hydrophobic core mutated to the similar Ile, adopts the P structure. It is likely that both have similar energy landscapes. These three reasons lead us to believe that it actually possesses a mixed native state of both AP and P.

Changing conditions in the cell might also trigger a conformational transition between AP and P by affecting their free-energy balance. The sequential closeness of AP WT and P Ala₂Ile₂–6 might deem this possible. In addition, some mutants have in vitro but no in vivo binding ability, which might result from a conformational rearrangement. A cell could switch Rop's RNA-binding ability on and off without any need of synthesis or degradation. We therefore suggest further theoretical and experimental work on Rop and its mutants. In particular, the question of whether or not some mutants have a degenerated native state and how this affects RNA-binding ability needs to be addressed through experiment.

Conclusion and Perspectives.

The additional complexity introduced to the protein folding problem when the native structure is determined from the competition between two possible conformations explains the strange behavior of Rop folding. In these studies, Rop was simulated by using a dual-funneled energy potential based on two crystal structures, the P and AP (WT motif) conformations. We observe transitions between the unfolded and the two folded states, identify the TSE, and characterize the free-energy landscape. We find nonstandard φ-values outside of the range of 0 and 1 that may result from contacts of competing structures.

If only geometry was solely responsible for determining folding, folding to the P conformation is favored over the AP one. Therefore, our simulations suggest that a trapdoor mechanism may explain Rop's mutational behavior. Because the WT protein needs to be in the AP conformation for binding RNA, this sequence has to energetically favor the AP conformation to overcome the geometrical disadvantage. The experimentally performed mutations, on the other hand, because they are not designed to optimize function, may diminish this energetic favoritism of the AP form and increase the possibility of folding into the P form. Therefore, these mutations can lower the energetic barrier associated with the unstable P relative to the barrier to AP. For some mutations, P becomes more kinetically accessible, yet thermodynamically less stable, than AP. This results in the experimentally observed strong increase of folding/unfolding rates upon mutation without major changes in stability. Specific mutations might even lead to a degenerated native state in which both the P and AP configurations may be present. Further experiments should be conduced to test whether this hypothesis is true.

The developed framework enables structure-based simulations on multiple-basin energy landscapes. In addition to explaining the folding mechanism for Rop, the general concept of competing folding basins will probably have an enormous impact in interconnecting protein folding and function. Switching between the competing structures might not only be triggered by mutations but also by other factors like chemical changes as phosphorylation, ligand and/or ion binding, and pH or temperature changes. Thus, it can regulate the mechanism of allosteric control and signaling, for example. In addition, competing energy basins may be a possible mechanism for describing prion aggregation.

Methods

A variety of approaches are available to model protein folding in silico. Methods include knowledge-based homologue modeling (35), molecular dynamics with empirical biomolecular force fields (36–41), global optimization of free-energy functions (42–44), lattice-based approaches (45), and native structure-based models (2, 4, 24, 31). The latter have the advantage of low computational costs and sufficient characterization of the conformational transition between unfolded and folded states (46, 47).

In previous structure-based simulations, native interactions were determined by a single topology, and the resulting energy landscape is dominated by this structure. Rop and its mutants have multiple crystal structures available. Because we believe that conformational transitions are able to explain the experimental observations on mutants, an extension of the theoretical framework is needed. To describe the multiple-basin dynamics, Rop was reduced to a C_α-bead presentation with two attractive basins belonging to the P and AP structures.

Because the tertiary structure of the monomers for the P and AP forms are very similar (the root mean square deviation of the C_α of the monomers ≈1.3 Å), the distances, angles, and dihedrals of the C_α backbone (r₀, θ₀, and φ₀) were, without loss of generality, assigned to the values found in the AP form. The native contact maps for both structures Q^AP and Q^P were obtained by using CSU (48), and the corresponding distances of native contacts σ_ij^AP and σ_ij^P were calculated. Whereas the intramonomeric contacts for P and AP are the same, the intermonomeric contacts differ. Some contacts in this region appear both in AP and in P with different native distances σ_ij^AP ≠ σ_ij^P. Thus, care must be taken when constructing a contact map that will result in multiple basins. One straightforward approach is simply disregarding such conflicting contacts, which strain the system. This deletion of six contacts common to P and AP allows the construction of a unified contact map. All other contacts are combined into the contact map. Intramonomeric contacts that appear in both structures are only included once. P and AP contribute a different number of interface contacts to the mixed model. Because this would result in an energetic bias toward AP, the interface contacts from P are slightly strengthened in their contribution by a factor of N_{IF − AP}/N_{IF − P} ≈ 1.12 (N_{IF − X} gives the total number of interface contacts for the structure X). An additional weak center-of-mass harmonic constraint allows disassociation of the monomers but prevents the monomers from moving too far apart from each other. This simulates a constant concentration of monomers in the system. A full description of the potential is provided in SI Appendix. We want to point out that this procedure guarantees a mixed model with no energetic bias toward one of the two states. The tertiary structures—i.e., the monomers—are equal. Therefore, the quaternary arrangement of monomers and possible differences in the folding behavior of P and AP are purely determined by different interface contact maps.

Abbreviations

AP

antiparallel

BU

bisecting U

P

parallel

TSE

transition-state ensemble

U

unfolded.