Abstract
Critical fluctuations are investigated in lipid membranes near miscibility critical points in bilayers composed of dioleoylphosphatidylcholine, chain perdeuterated dipalmitoylphosphatidylcholine, and cholesterol. Phase boundaries are mapped over the temperature range from 10°C to 60°C by deuterium NMR. Tie-lines and three-phase triangles are evaluated across two-phase and three-phase regions, respectively. In addition, a line of miscibility critical points is identified. NMR resonances are broadened in the vicinity of critical points, and broadening is attributed to increased transverse relaxation rates arising from modulation of chain order with correlation times on a microsecond time scale. We conclude that spectral broadening arises from composition fluctuations in the membrane plane with dimensions of <50 nm and speculate that similar fluctuations are commonly found in cholesterol-containing membranes.
Keywords: lipid rafts, liquid-immiscibility, NMR relaxation, phase diagram, critical behavior
The first direct observation of immiscible liquid phases in model bilayer membranes was presented only recently, for membranes containing three or more components (1, 2). However, by the early 1970s, it was already clear that lipids in membranes with elevated cholesterol have high chain order yet diffuse as in a liquid (3–6). This liquid-ordered (Lo) phase of lipids (7) is distinguished from the familiar liquid-disordered phase (Lα or Ld) found in bilayers of pure lipids above the chain melting temperature (3–14). Pure lipids below the chain melting temperature are in the solid or “gel” phase (So). Coexisting liquid-ordered and liquid-disordered phases are easily visualized in giant unilamellar vesicles by fluorescence microscopy when membranes contain cholesterol and two types of lipids: one with a high gel–fluid transition temperature and one with a low gel–fluid transition temperature (15–21). Coexisting liquid phases are also easily visualized in membranes of plasma membrane vesicles containing a wide spectrum of lipid and protein components (22).
The research presented here represents a culmination of several years' work in our laboratories on ternary membranes of dioleoylphosphatidylcholine (DOPC), chain perdeuterated dipalmitoylphosphatidylcholine (DPPC-d62), and cholesterol (Chol) (15–18, 23, 24). It has resulted in a straightforward thermodynamic description of micrometer-sized coexisting phases and of submicrometer composition fluctuations in membranes containing cholesterol. Here we use deuterium (2H) NMR to assemble the DOPC/DPPC-d62/Chol phase diagram. NMR allows us to directly measure differences in ordering and partitioning of DPPC-d62 between coexisting phases. In addition, NMR produces results free from artifacts associated with fluorescent probes (24) or oxidation of unsaturated lipid chains (15, 25). We use our NMR data to identify quantitative miscibility phase boundaries and to solve for a large array of tie-lines. Tie-line endpoints yield quantitative compositions of the two liquid phases and provide independent verification of the miscibility phase boundary. Furthermore, we unambiguously determine the extent of a three-phase So-Ld-Lo coexistence region, a task that is difficult to accomplish by other methods (16, 17).
In the theory of critical phenomena, lateral inhomogeneities arise because the energy required to maintain regions of differing composition becomes vanishingly small, and thermal motions lead to composition fluctuations over a wide range of time and distance scales (26, 27). The size of the largest probable fluctuation is described in terms of a correlation length, which diverges as the critical point is approached. We find that broadening of resonance peaks occurs for membranes near known critical points. We attribute broadening to composition fluctuations on length scales of <50 nm in these membranes.
Results and Discussion
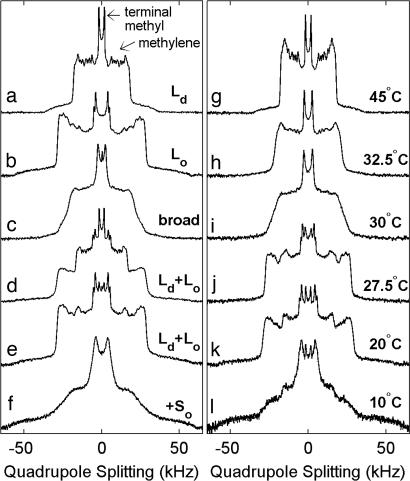
2H NMR spectra from multilamellar vesicles of 31 distinct compositions of DOPC, DPPC-d62, and Chol for temperatures between 5°C and 60°C were acquired, and representative spectra from lipids in uniform liquid phases are shown in Fig. 1 a and b. Each spectrum is composed of superimposed resonances of symmetric 2H quadrupole splittings whose magnitudes reflect the time averaged orientations of 2H–C bonds with respect to the bilayer normal. Here, 2H–C bonds occur within both hydrocarbon chains of perdeuterated DPPC-d62 lipids. The narrowest and most prominent splitting is from the terminal methyl groups, whereas wider splittings arise from superimposed resonances of methylene groups along the chains (23).
Fig. 1.
2H NMR spectra of DPPC-d62 in membranes of DOPC/DPPC-d62/Chol. (a–f) 2H NMR spectra of DPPC-d62 in multilamellar vesicles of various DOPC/DPPC-d62/Chol compositions acquired at 20°C with phase assignments as described in the text. Membrane compositions are in the form DOPC:DPPC-d62 plus % Chol: a, 4:1 plus 15%; b, 4:1 plus 40%; c, 2:1 plus 25%; d, 1:1 plus 15%; e, 1:2 plus 25%; f, 1:4 plus 10%. (g–l) Spectra for membranes of 1:2 DOPC/DPPC-d62 plus 20% Chol at the temperatures indicated.
2H NMR is well suited for resolving whether lipids are in single phases (Ld, Lo, and So), in two coexisting phases (Ld-Lo, Lo-So, or Ld-So), or in all three phases simultaneously (Ld-Lo-So) (18, 23). DPPC-d62 chains in the Ld phase have low chain order parameters and produce a series of narrow and well resolved splittings as in Fig. 1a. In contrast, lipid chains in the Lo phase have significantly higher order and produce wider splittings (Fig. 1b). Ld- and Lo-phase spectra are also distinguished by the number of quadrupolar splittings from terminal methyl groups. A single terminal methyl group splitting is found from DPPC-d62 in the Ld phase, whereas two distinct methyl splittings are found from DPPC-d62 in the Lo phase (13, 23). Spectra from lipids in the So phase are distinguished by their larger quadrupolar splittings and by their poorly resolved resonances. These defining features apply generally to single-phase spectra over a wide range of experimental conditions. The detailed appearance of each Ld, Lo, and So spectrum depends strongly on temperature and composition. For vesicles containing coexisting phases, the relative intensities of the single-phase (Ld, Lo, and/or So) contributions superimposed in each spectrum provide direct measurements of DPPC-d62 partitioning into the different phases (Fig. 1 d and e).
DPPC-d62 spectra like those in Fig. 1 are used to quantitatively calculate tie-lines, with errors, for a wide range of temperatures and compositions as described in Materials and Methods [Fig. 2 a–d and supporting information (SI) Table 1]. Tie-lines span all binary coexistence regions in the DOPC/DPPC-d62/Chol ternary phase diagram. Knowing the location of tie-lines within the Ld-Lo coexistence region is valuable because their endpoints can be read off to give the compositions of the Ld and Lo phases. Tie-line endpoints also provide an independent measurement of the phase boundary. When the compositions of two vesicles lie along the same tie-line, the vesicle membranes contain different ratios of the same two coexisting phases in proportions given by the Lever rule (16). Here, we solve for tie-line slopes by searching the composition space for spectra that superimpose different ratios of the same two endpoint spectra, indicating that they contain the same two coexisting phases. The location of tie-line endpoints is then determined by inserting the measured DPPC-d62 partition coefficients into the Lever rule.
Fig. 2.
Tie-lines, three-phase triangles, and spectral broadening in membranes of DOPC/DPPC-d62/Chol. (a–d) Tie-lines across two-phase regions and endpoints of the three-phase triangles are determined for multilamellar vesicles of DOPC/DPPC-d62/Chol. Errors on tie-lines and three-phase triangles are shown. Transition temperatures and calculated endpoints are shown in SI Tables 1–3. (e–h) Phase data are superimposed on a colored surface indicating a spectral width of 2H NMR methyl resonances as a function of lipid composition, demonstrating that broadening occurs near known miscibility critical points. Small symbols indicate the phase state of acquired spectra.
DPPC-d62 spectra are also used to determine all membrane compositions for which three distinct phases coexist in the membrane. Within a Gibbs phase plot as in Fig. 3a, the three-phase region fills a triangle. Within this triangle, all acquired spectra are a linear superposition of the same three Ld, Lo, and So endpoint spectra. This property is exploited to evaluate the three triangle vertices (values given in SI Table 2). In all cases, calculated tie-line and three-phase endpoints agree with phase boundaries determined through visual inspection of acquired spectra. Miscibility transition temperatures are recorded in SI Table 3. The boundaries of two- and three-phase regions at different temperatures are assembled into the three-dimensional phase diagram shown in Fig. 3b.
Fig. 3.
Phase diagrams of DOPC/DPPC-d62/Chol. (a) A constant temperature cut through the ternary phase diagram at 10°C shows phase assignments. The liquid–liquid (Ld-Lo) coexistence region is shaded blue and terminates in a critical point at the yellow circle. At low cholesterol, the Ld-Lo region is bounded by a three-phase triangle shaded green, in which Ld, Lo, and So phases coexist. The three-phase triangle is connected to two separate regions of solid–liquid coexistence (Lo-So and Ld-So), which are shaded red. (b) Multiple constant-temperature phase diagrams are assembled into a three-dimensional ternary phase diagram spanning 10°C and 37°C, with the dashed yellow line approximating a line of critical points.
Compared with our earlier work (15, 23), the current phase diagram contains the same phases, but the boundaries between phases lie in slightly different positions because here we use exclusively NMR (24). In addition, we have evaluated tie-lines through a large number of compositions using an entirely quantitative method, and the errors in tie-line slopes and endpoints are significantly reduced. Previously, we were not able to determine Ld-So or Lo-So tie-lines, or to unambiguously locate the vertices of the three-phase region. These advances lay the groundwork for our investigation of critical point behavior described below. For example, knowing the location of tie-lines in the Ld-Lo coexistence region makes it possible to identify the compositions of miscibility critical points. One critical point is at the composition with the highest miscibility transition temperature. At lower temperatures, critical points fall near tie-lines located at the high cholesterol edge of the miscibility phase boundary, as illustrated in Fig. 3b.
We observe significant spectral broadening for membrane compositions near known miscibility critical points. This is seen as loss in resolution in the acquired spectra. Examples are shown in Fig. 1 c and i, which show poorly resolved terminal methyl splittings flanked by featureless shoulders that slope gradually to low intensity. This broadening is quantified by fitting the methyl peaks of dePaked spectra (28) with Lorentzian lines to extract peak widths (Fig. 2 e–h). Maximum broadening occurs near known critical points. Fig. 2 g and h shows that broadening is still detectable up to ≈5°C above the highest critical temperature, which lies between 27.5°C and 30.0°C for 1:2 DOPC/DPPC-d62 plus 20% Chol.
To investigate the origin of spectral broadening near miscibility critical points, we conducted a series of relaxation measurements (Fig. 4), focusing on the composition 1:2 DOPC/DPPC-d62 plus 20% Chol because its spectra exhibit maximal broadening (Fig. 1i). Experiments were conducted to measure the longitudinal (R1) and transverse (R2) relaxation rates of 2H nuclei of DPPC-d62 both in the presence and absence of magic angle spinning (MAS), and of 1H nuclei of DOPC with MAS (Fig. 4 a–e). In all cases, R1 smoothly increases as temperature decreases. In contrast, R2 rises sharply as the critical point is approached from higher temperature and then rapidly falls as liposomes enter the two-phase region.
Fig. 4.
Increased transverse relaxation rates (R2) but not longitudinal relaxation rates (R1) are found in membranes of 1:2 DOPC/DPPC-d62 plus 20% Chol in the vicinity of the miscibility critical point (≈30°C). (a and b) Relaxation rates are measured from 2H nuclei. (c and d) Similar trends in relaxation rates occur in the methylene groups of DOPC measured by 1H MAS NMR. (e) 2H MAS NMR relaxation measurements also indicate that line-broadening is dominated by increased R2 values. ( f) Critical features of the acquired static 2H NMR spectrum at 30°C (gray) are reproduced by a simulated spectrum (black) that assumes spectral broadening is dominated by values of R2 from a, as is described in Materials and Methods.
Values of R2 set a lower limit on the width of resonances, Δν1/2, according to Δν1/2 = R2/π, when a Lorentzian shape assumed. The measured peak widths are in excellent agreement with values calculated from R2 relaxation rates (Fig. 4 e and f), indicating that spectra are, to a good approximation, homogeneously broadened. Contributions to broadening due to sample inhomogeneity and exchange effects appear to be insignificant. It is interesting to note that both DOPC and DPPC resonances are broadened. Although it is not often discussed, order parameters of both DOPC and DPPC lipid chains are composition-dependent (29), and our results show that both DOPC and DPPC participate in fluctuations near critical points.
Following the analysis below, we find that transverse relaxation rates, R2, must be enhanced in membranes near critical points as a result of modulations of chain order that occur with correlation times between 0.1 μs and 10 μs. Spin relaxation arises from modification of quadrupolar interactions (2H NMR) or dipolar interactions (1H NMR) by lipid dynamics that are described by spectral density functions J(2ω), J(ω), and J(0), where ω = 2πν, and ν is the NMR resonance frequency. Longitudinal relaxation rates, R1, depend solely on J(2ω) and J(ω). These spectral densities arise from fast motions with correlation times from picoseconds to nanoseconds, such as isomerization of lipid hydrocarbon chains. Transverse relaxation rates, R2, depend on J(2ω), J(ω), and also J(0) (30). Contributions to relaxation from J(0) grow steadily with increasing correlation time. Significant contributions appear at ≈0.1 μs and continue to grow until spectra from different molecular conformations and environments convert from the rapid exchange limit to signal superposition, which occurs at ≈10 μs for 2H NMR and ≈100 μs for 1H NMR. The data in Fig. 4 indicate that transverse relaxation rates (R2) display an anomaly near the critical point, but longitudinal relaxation rates (R1) do not. Changes in J(2ω) or J(ω) would impact both R1 and R2; therefore, only those motions that affect J(0) are responsible for observed increases in R2 near critical points. We conclude that motions that alter lipid order with correlation times from 0.1 to 10 μs are greatly enhanced in the vicinity of critical points.
What might constitute these motions? Time scales can be converted to distances if normal two-dimensional diffusion is assumed, 〈x2〉 = 4Dτ, where D is the lipid lateral diffusion constant [≈10−11 m2/s (31)]. On a time scale of 0.1–10 μs, lipids traverse distances of 2–20 nm. Therefore broadening could arise from lipid diffusion between very small fluctuations with long lifetimes. Radhakrishnan and McConnell (32) have recently shown that the dynamic behavior of complexes near a critical point may enhance R2 rates sufficiently to explain experimental observations (32).
Fluctuations on larger time and distance scales have been described in a similar system investigated by fluorescence microscopy (18). In the current experiments, R2 rates alone explain all spectral broadening; therefore, we observe no evidence of additional inhomogeneous broadening related to large fluctuations. This outcome is not surprising if the length scale of critical fluctuations (ξ) scales as in a two-dimensional Ising model, ξ ≈ f (+)ξoTc/(T − Tc), where Tc is the critical temperature (≈300 K), f (+) is an amplitude factor for T > Tc (≈0.5), and ξo is on the order of a lipid diameter (≈1 nm) (27, 33). In this model, inhomogeneous contributions to broadening are only expected for temperatures and compositions very close to the critical point (e.g., at the critical composition, ξ ∼ 50 nm for T − Tc ∼ 3°C). The amplitude factor is approximately three times smaller for T < Tc compared with T > Tc [f (−) ∼ 0.17] (33), providing a plausible explanation for why R2 values in Fig. 4 decrease faster for T < Tc than for T > Tc.
There is a large body of experimental work suggesting submicrometer organization in model membranes containing cholesterol (9, 13, 34, 35). For example, we (23) and others (13, 36) have previously interpreted broadened 2H NMR spectra as evidence for submicrometer phase-separated domains. Our current results suggest an alternate interpretation, that broadened 2H NMR spectra instead indicate the presence of fluctuations within a single liquid phase in membranes near a miscibility critical point. Similarly, we can imagine that fluctuations provide a mechanism by which lipids and proteins organize on submicrometer dimensions in cholesterol-rich biomembranes in the vicinity of a miscibility critical point.
Materials and Methods
NMR.
All lipids were acquired from Avanti Polar Lipids, stored at −20°C, and used without further purification. Multilamellar vesicles were prepared as described previously with either 2.5 or 5 mg of deuterated lipid (18). NMR experiments were conducted on a Bruker DMX500 spectrometer operating at a 2H resonance frequency of 76.8 MHz. 2H NMR spectra were acquired from 60°C to 5°C at increments of 2.5°C with a quadrupolar echo sequence and processed as described in ref. 23. DePaked spectra were calculated by using the iterative method described in ref. 28. The precise lipid compositions and lipid/cholesterol ratios were determined by dissolving samples in chloroform and conducting high-resolution 1H NMR experiments. 1H MAS NMR experiments were conducted at a 1H resonance frequency of 500.1 MHz and a spinning frequency of 10 kHz. The sample temperature in the spinning rotor was calibrated by monitoring the gel–fluid transition of fully hydrated DPPC-d62 and DMPC-d54 bilayers.
Relaxation experiments were conducted by using multilamellar bilayers composed of 1:2 (mol/mol) DOPC/DPPC-d62 plus 20% Chol over the temperature range from 50°C to 12°C at increments of 2°C. The 2H transverse relaxation rates (R2) without MAS were measured with the quadrupolar spin echo sequence (π/2-τ-π/2-acq) by incrementing τ (37). The reduction of signal intensity in the methylene region of DPPC-d62 corresponding to methylene segments near the lipid glycerol group (the so-called order parameter plateau) was fitted to a single exponential decay with increasing τ. Longitudinal relaxation rates, R1, were measured with an inversion-recovery pulse sequence followed by signal detection with a quadrupolar echo (π-τ-π/2–50 μs-π/2-acq). R2 and R1 of DOPC in 1H MAS NMR were measured by a Hahn echo and an inversion-recovery pulse sequence, respectively. The peak at 2.1 ppm was used for the DOPC relaxation measurements and arises from the methylene groups adjacent to the double bonds of oleic acid.
Tie-Line Determination.
Spectra acquired from membrane compositions along a specific tie-line are a linear superposition of spectra from single-phase membranes with compositions corresponding to tie-line endpoints. For example, if a spectrum S(φ⃗, ν) is acquired at a composition φ⃗ = [%DOPC, %DPPC, %Chol] within the Ld-Lo coexistence region,
where S(φ⃗Ld, ν) and S(φ⃗Lo, ν) are spectra acquired at compositions φ⃗Ld and φ⃗Lo corresponding to the tie-line endpoints, ν is spectral frequency, and A is the fractional partition coefficient of DPPC-d62 into the Ld phase. For this analysis, all spectra were normalized to constant integral intensity. A large number of spectra were acquired from membranes with compositions within the two-phase region. When two acquired spectra have compositions φ⃗1 and φ⃗2 that lie along the same tie-line, endpoint spectra and partition coefficients can be determined by using spectral subtraction according to (13)
where the constants B and C describe the linear combination of the acquired spectra S(φ⃗1, ν) and S(φ⃗2, ν) needed to produce a pure Ld or Lo endpoint spectrum. The constants B and C are algebraically related to partition coefficients and can be used in conjunction with the Lever rule to evaluate the composition of membranes at tie-line endpoints.
This technique has been applied to various two-component lipid mixtures (13, 36, 38), where thermodynamic rules stipulate that all compositions within the two-phase region lie along the same tie-line at constant temperature (16). In these earlier studies, subtraction coefficients were determined through visual inspection of subtracted spectra. Here, the constants B and C are determined quantitatively by performing a least-squares minimization against a single-phase reference spectrum acquired at a composition close to the desired tie-line endpoint. Because reference spectra are not necessarily acquired exactly at the tie-line endpoint compositions, we introduce an additional fitting parameter that stretches or contracts the frequency axis of the reference spectrum to compensate for minor temperature- and composition-dependent changes in these spectra. This operation assumes that order uniformly increases or decreases for all C–2H bonds along the chain and is valid for modest changes in temperature and composition (18, 39).
Evaluating tie-lines in three-component mixtures is complicated by the fact that the tie-line slope is not constrained (16), and it cannot be assumed that any two given compositions will lie along the same tie-line. This is addressed by recognizing that two compositions lie along the same tie-line only if it is possible to completely subtract the Lo-phase spectra without significant distortion to the Ld component. One composition is chosen to lie along a given tie-line, while a second composition along the same tie-line is determined by searching for a second spectrum in the composition space that can be linearly combined with the first spectrum to resemble an Ld-phase reference spectrum. Limitations from the finite sampling of compositions within the two-phase region are overcome by interpolating between spectra acquired from membranes with fixed DOPC:DPPC-d62 ratios. We quantitatively determine tie-line slope and error bounds by performing a least-squares minimization between the calculated Ld endpoint spectra and an acquired Ld reference spectrum using three fitting parameters: the cholesterol composition of the interpolated spectrum, the linear combination of the two spectra needed to obtain the reference spectra, and the factor by which the frequency axis of the Ld reference spectra was scaled.
Once the tie-line slope is known, the standard method of spectral subtraction described above can be used to determine the location of tie-line endpoints. In a second fitting step, we obtain the remaining parameters needed to quantitatively determine the tie-line endpoints, and errors, by performing a least-squares minimization against a single-phase Lo reference spectrum. An example demonstrating the sensitivity of this method is shown in SI Fig. 5.
Three-Phase Triangle.
Within a three-phase region, each acquired spectrum is a linear superposition of three endpoint spectra corresponding to DPPC-d62 in Ld, Lo, and So phases:
formula φ⃗Ld, φ⃗Lo, and φ⃗So are compositions at the triangle vertices and all spectra are normalized to constant integral intensity. Mathematically, this is equivalent to stating that each value of S(φ⃗, νi) at a given frequency νi lies on a plane defined by the points S(φ⃗Ld, νi), S(φ⃗Lo, νi), and S(φ⃗So, νi), and that the position of S(φ⃗, νi) on this plane relative to the endpoints is parameterized by the constants D and E.
Because the endpoint spectra and compositions are unknown, this same plane is defined by using three (or more) experimental spectra acquired from compositions within the three-phase region by solving a system of linear equations:
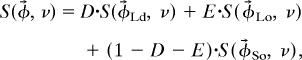 |
where φ⃗j are the compositions of the acquired spectra, and φ⃗DOPC, φ⃗DPPC, and φ⃗Chol are compositions of the three single-component membranes. Spectra for three separate compositions are needed to evaluate three basis spectra S(φ⃗DOPC, νi), S(φ⃗DPPC, νi), and S(φ⃗Chol, νi). When spectra for more than three compositions are available at a given temperature, a best-fit plane is calculated by using least-squares minimization. This procedure defines the linear coefficients and basis spectra that are combined to reproduce spectra acquired within the three-phase region. It is worth noting that the three calculated basis spectra are not themselves physical because they correspond to single-component compositions located outside of the three-phase triangle, in a region where the linear relationship between acquired spectra no longer applies. Each vertex of the three-phase triangle is determined by finding the linear combination of basis spectra needed to produce a pure Ld, Lo, or So endpoint spectrum. As in the tie-line analysis, this is accomplished by performing a least-squares minimization against a reference spectrum acquired at a composition near the suspected triangle vertex. In some cases, calculated endpoint spectra from adjacent binary tie-lines are used as reference spectra instead of raw experimental data. The effectiveness of this method is demonstrated in SI Fig. 6.
The relative intensities of endpoint spectra needed to produce spectra acquired within the triangle (denoted by the constants D and E above) are given by the three-phase Lever rule. In practice, the relative intensities of superimposed spectra can be altered by the quadrupolar echo sequence. This is particularly relevant when evaluating the intensity of So-phase spectra (36). When this attenuation is taken into account, we find that acquired spectra are well represented by weighting the Ld, Lo, and So endpoint spectra within the Lever rule (SI Fig. 6e).
Evaluation of Errors.
In all cases, errors in fitting parameters are determined directly from the covariance matrix at the solution of the least-squares minimization. The diagonal elements of the covariance matrix are the squared standard errors of the fitting parameters, and off-diagonal elements denote the magnitude of cross-covariance between parameters. In the tie-line analysis, a nonlinear least-squares minimization is used, and the covariance matrix (Cov) is evaluated as Cov = r/H, where r is the residual and H is the Hessian at the solution. Errors in fitting parameters are propagated through the tie-line calculation, taking into account cross-covariance between fitting parameters whenever possible. In the three-phase analysis, linear least-squares minimization is used, and the covariance matrix is evaluated as Cov = r/(VV′), where r is the residual and V is the vector of best fit parameters. In the three-phase analysis, the fitting parameters are the desired endpoint compositions, and errors are determined directly from the diagonal elements of the covariance matrix. In practice, errors in tie-line and three-phase endpoints are dominated by the availability of reference spectra. Not surprisingly, the magnitude of errors depends strongly on the choice and availability of nearby reference spectra. When single-phase reference spectra are acquired near the desired tie-line endpoints, errors are significantly reduced (as demonstrated in SI Fig. 5).
Lineshape Fitting of Spectra Near a Critical Point.
MAS converts the intensity of 2H NMR spectra into a spinning centerband and spinning sidebands that appear on both sides from the centerband at multiples of the spinning frequency. Because the differences of chemical shift between resonances of carbon atoms C4-C15 are negligible, most resonances are superposed. At spinning frequencies in the range from 5 to 10 kHz, this signal is dominated by the resonances with the largest quadrupolar splittings, namely the chain methylene segments C2-C8 near the lipid–water interface (40). In Fig. 4e, the measured width at half height of the MAS sideband is compared with the linewidth calculated from the measured R2 rates of this same signal according to Δν1/2 = R2/π.
The broadening of resonances near critical points is also visible in spectra obtained without MAS. The simulated spectrum shown in Fig. 4f was generated by applying the line-broadening arising from R2 rates measured without MAS to an order parameter profile obtained in membranes of the same composition but acquired at a higher temperature where quadrupolar splittings are well resolved (Fig. 7a). The R2 rates were only determined for the largest quadrupolar splittings, corresponding to the so-called order parameter plateau in the spectrum (chain carbon atoms C2-C8). It was assumed in the fit that R2 values at narrower splittings scale as the square of the order parameter, as expected from theory (30). In addition, all acquired 2H NMR spectra show evidence of a slight deviation from randomness of the orientation distribution functions of bilayer normals due to liposome deformation by the strong Bo magnetic field. This was accounted for by fitting a bilayer distribution function to the experimental data (SI Fig. 7b). In addition, the intensity of terminal methyl group resonances was attenuated to account for the experimental attenuation of those signals due to fast data acquisition (23).
Supplementary Material
Acknowledgments
We thank Ben Widom, James Sethna, John Cahn, Jenifer Thewalt, and Harden McConnell for helpful conversations, and Holger Scheidt for use of binary DPPC-d62/Chol spectra. S.L.V. is supported through a postdoctoral fellowship from the Cancer Research Institute. S.L.K. acknowledges a National Science Foundation Career Award (MCB-0133484) and a Cottrell Scholar award from the Research Corporation. O.S. and K.G. are supported by the intramural program of the National Institute on Alcohol Abuse and Alcoholism, National Institutes of Health.
Abbreviations
- Chol
cholesterol
- DOPC
dioleoylphosphatidylcholine
- DPPC-d62
chain perdeuterated dipalmitoylphosphatidylcholine
- Lo
liquid ordered
- Ld
liquid disordered
- MAS
magic angle spinning.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/cgi/content/full/0703513104/DC1.
References
- 1.Dietrich C, Bagatolli LA, Volovyk ZN, Thompson NL, Levi M, Jacobson K, Gratton E. Biophys J. 2001;80:1417–1428. doi: 10.1016/S0006-3495(01)76114-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Samsonov AV, Mihalyov I, Cohen FS. Biophys J. 2001;81:1486–1500. doi: 10.1016/S0006-3495(01)75803-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Chapman D, Penkett SA. Nature. 1966;211:1304–1305. doi: 10.1038/2111304a0. [DOI] [PubMed] [Google Scholar]
- 4.Darke A, Finer EG, Flook AG, Phillips MC. J Mol Biol. 1972;63:265–279. doi: 10.1016/0022-2836(72)90374-9. [DOI] [PubMed] [Google Scholar]
- 5.Oldfield E, Chapman D. FEBS Lett. 1972;23:285–297. doi: 10.1016/0014-5793(72)80300-4. [DOI] [PubMed] [Google Scholar]
- 6.Lentz BR, Barrow DA, Hoechli M. Biochemistry. 1980;19:1943–1954. doi: 10.1021/bi00550a034. [DOI] [PubMed] [Google Scholar]
- 7.Ipsen JH, Karlstrom G, Mouritsen OG, Wennerstrom H, Zuckermann MJ. Biochim Biophys Acta. 1987;905:162–172. doi: 10.1016/0005-2736(87)90020-4. [DOI] [PubMed] [Google Scholar]
- 8.Alecio MR, Golan DE, Veatch WR, Rando RR. Proc Natl Acad Sci USA. 1982;79:5171–5174. doi: 10.1073/pnas.79.17.5171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Almeida PF, Vaz WL, Thompson TE. Biochemistry. 1992;31:6739–6747. doi: 10.1021/bi00144a013. [DOI] [PubMed] [Google Scholar]
- 10.Huang TH, Lee CW, Das Gupta SK, Blume A, Griffin RG. Biochemistry. 1993;32:13277–13287. doi: 10.1021/bi00211a041. [DOI] [PubMed] [Google Scholar]
- 11.McMullen TP, McElhaney RN. Biochim Biophys Acta. 1995;1234:90–98. doi: 10.1016/0005-2736(94)00266-r. [DOI] [PubMed] [Google Scholar]
- 12.Shimshick EJ, McConnell HM. Biochem Biophys Res Commun. 1973;53:446–451. doi: 10.1016/0006-291x(73)90682-7. [DOI] [PubMed] [Google Scholar]
- 13.Vist MR, Davis JH. Biochemistry. 1990;29:451–464. doi: 10.1021/bi00454a021. [DOI] [PubMed] [Google Scholar]
- 14.Jacobs R, Oldfield E. Biochemistry. 1979;18:3280–3285. doi: 10.1021/bi00582a013. [DOI] [PubMed] [Google Scholar]
- 15.Veatch SL, Keller SL. Biophys J. 2003;85:3074–3083. doi: 10.1016/S0006-3495(03)74726-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Veatch SL, Keller SL. Biochim Biophys Acta. 2005;1746:172–185. doi: 10.1016/j.bbamcr.2005.06.010. [DOI] [PubMed] [Google Scholar]
- 17.Veatch SL, Keller SL. Phys Rev Lett. 2005;94:148101. doi: 10.1103/PhysRevLett.94.148101. [DOI] [PubMed] [Google Scholar]
- 18.Veatch SL, Gawrisch K, Keller SL. Biophys J. 2006;90:4428–4436. doi: 10.1529/biophysj.105.080283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Baumgart T, Hess ST, Webb WW. Nature. 2003;425:821–824. doi: 10.1038/nature02013. [DOI] [PubMed] [Google Scholar]
- 20.Scherfeld D, Kahya N, Schwille P. Biophys J. 2003;85:3758–3768. doi: 10.1016/S0006-3495(03)74791-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Zhao J, Wu J, Heberle FA, Mills T, Klawitter P, Huang G, Costanza G, Feigenson GW. Biochim Biophys Acta. 2007 doi: 10.1016/j.bbamem.2007.07.008. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Baumgart T, Hammond AT, Sengupta P, Hess ST, Holowka DA, Baird BA, Webb WW. Proc Natl Acad Sci USA. 2007;104:3165–3170. doi: 10.1073/pnas.0611357104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Veatch SL, Polozov IV, Gawrisch K, Keller SL. Biophys J. 2004;86:2910–2922. doi: 10.1016/S0006-3495(04)74342-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Veatch SL, Leung SS, Hancock RE, Thewalt JL. J Phys Chem B. 2007;111:502–504. doi: 10.1021/jp067636i. [DOI] [PubMed] [Google Scholar]
- 25.Ayuyan AG, Cohen FS. Biophys J. 2006;91:2172–2183. doi: 10.1529/biophysj.106.087387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Sengers JV, Levelt Sengers JMH. Annu Rev Phys Chem. 1986;37:189–222. [Google Scholar]
- 27.Fisher ME. J Math Phys. 1964;5:944–962. [Google Scholar]
- 28.Sternin E, Bloom M, MacKay AL. J Magn Reson. 1983;55:274–282. [Google Scholar]
- 29.Warschawski DE, Devaux PF. Eur Biophys J. 2005;34:987–996. doi: 10.1007/s00249-005-0482-z. [DOI] [PubMed] [Google Scholar]
- 30.Davis JH. Biochim Biophys Acta. 1983;737:117–171. doi: 10.1016/0304-4157(83)90015-1. [DOI] [PubMed] [Google Scholar]
- 31.Scheidt HA, Huster D, Gawrisch K. Biophys J. 2005;89:2504–2512. doi: 10.1529/biophysj.105.062018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Radhakrishnan A, McConnell H. J Chem Phys. 2007;126:185101. doi: 10.1063/1.2730805. [DOI] [PubMed] [Google Scholar]
- 33.Zinn S, Lai S, Fisher ME. Phys Rev E. 1996;54:1176–1182. doi: 10.1103/physreve.54.1176. [DOI] [PubMed] [Google Scholar]
- 34.de Almeida RF, Fedorov A, Prieto M. Biophys J. 2003;85:2406–2416. doi: 10.1016/s0006-3495(03)74664-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Korlach J, Baumgart T, Webb WW, Feigenson GW. Biochim Biophys Acta. 2005;1668:158–163. doi: 10.1016/j.bbamem.2004.11.016. [DOI] [PubMed] [Google Scholar]
- 36.Hsueh YW, Gilbert K, Trandum C, Zuckermann M, Thewalt J. Biophys J. 2005;88:1799–1808. doi: 10.1529/biophysj.104.051375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Davis JH, Jeffrey KR, Bloom M, Valic MI, Higgs TP. Chem Phys Lett. 1976;42:390–394. [Google Scholar]
- 38.Thewalt J, Bloom M. Biophys J. 1992;63:1176–1181. doi: 10.1016/S0006-3495(92)81681-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Barry JA, Gawrisch K. Biochemistry. 1995;34:8852–8860. doi: 10.1021/bi00027a037. [DOI] [PubMed] [Google Scholar]
- 40.Herzfeld J, Berger AE. J Chem Phys. 1980;73:6021–6030. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.