Molecular level stochastic model for competence cycles in Bacillus subtilis

Abstract

The role of stochasticity and noise in controlling genetic circuits is investigated in the context of transitions into and from competence in Bacillus subtilis. Recent experiments have demonstrated that bistability is not necessary for this function, but that the existence of one stable fixed point (vegetation) and an excitable unstable one (competence) is sufficient. Stochasticity therefore plays a crucial role in this excitation. Noise can be generated by discrete events such as RNA and protein synthesis and their degradation. We consider an alternative noise source connected with the protein binding/unbinding to the DNA. A theoretical model that includes this “nonadiabatic” mechanism appears to produce a better agreement with experiments than models where only the adiabatic limit is considered, suggesting that this nonconventional stochasticity source may be important for biological functions.

Bacteria encode in their genetic material many different strategies of responding to environmental stress to ensure their survival. Examples of such strategies are motility, chemotaxis, antibiotic production, and ultimately sporulation (1). Many of these responses occur only in a fraction of an isogenic population: phenotypic variability can be obtained even from identical DNA sequences (2, 3). Thus, a population, without rare genetic mutations, can rapidly regenerate a variety of phenotypes from a single phenotype able to survive a certain condition. This variability most likely arises from fluctuations in the cell network that occur even under favorable conditions. This stresses the biological relevance of stochasticity in cellular processes, allowing functional plasticity by switching between phenotypes (4).

Competence is a differentiated state observed in many bacterial species that is an alternative survival strategy to sporulation. Competence occurs in populations with high cell densities under limited nutrient conditions, when the cells are in stationary growth. When cells become competent, DNA replication stops and cell division ceases. In this state, the cell becomes able to capture DNA from its surroundings. There is no sequence specificity for the subsequent DNA uptake. It has been proposed that the absorbed genetic material can provide templates for DNA repair or be a source of nutrients like phosphates or may simply be incorporated in the cell's genome. Competence is frequently linked to the production of antibiotics that can lyse nearby cells, releasing their genetic material in the medium. Competence is also induced by quorum sensing mechanisms. These observations suggest that competence can have a purpose of exchanging genetic material within the species, functioning as a sexual cycle under limited growth conditions (5).

In B. subtilis, the expression of the DNA-binding, -uptake, and -recombination genes is activated by the transcription factor ComK. Up to five transcription factors have already been identified that bind the comK promoter. These factors are mainly proteins involved in the control of stationary growth and sporulation. Studies where these sites were mutated showed there is a positive feedback loop where ComK activates its own expression. This loop provides the essential regulation of competence control (3, 6–8). The levels of ComK are tightly regulated by the presence of MecA, which recruits ComK for degradation by the ClpC/ClpP protease complex. The concentration of ComK is kept low by MecA/ClpC/ClpP degradation, but when a certain threshold is crossed, self-activation takes place and ComK is brought to high levels. Virtually all cells lacking a functional MecA protein produce ComK and go into competence.

Two different pheromones involved in quorum sensing, ComX and PhrC, induce the srfA promoter. This promoter is linked both to the synthesis of the antibiotic surfactin and also to the synthesis of a small peptide ComS that binds to the MecA/ClpC/ClpP complex. As the expression of mecA and cplC does not change much over stationary growth phase, the production of ComS protects ComK from degradation, allowing ComK levels to reach the threshold for self-activation (5, 9, 10). Experiments have shown that overexpression of ComK is preceded by high levels of ComS. There is also experimental evidence for inhibition of comS by ComK (11) (Fig. 1).

Fig. 1.

Possible dynamical modes for competence control. (Upper Left) Core mechanism of competence control, showing the positive feedback loop of ComK and the competitive degradation of ComK and ComS by the degradation complex MecA/ClpC/ClpP. (Upper Right and Lower) Examples of effective potential surfaces and nullclines for different configurations of fixed points. A system with only one stable fixed point in the vegetative (low ComK) state shows no competence. A system with one stable fixed vegetative point and one unstable competent fixed point shows a predominantly flat region corresponding to the excursions into competence. A system with two stable fixed points, one competent and one not, has the competent and vegetative states relatively stable, and the surface shows two wells. In this case, the system sporadically switches between the two configurations. Parameters were taken from the average parameter set for each behavior, with Γ_k = 100, Γ_s = 50, and ω = ω_d = 10. One stable vegetative fixed point: n_k = 3.5, n_s = 3.5, G₁ = 0.07, G₀ = 0.4, G_s = 0.4, X_k = 0.7, X_s = 0.4. One stable vegetative fixed point, one unstable competent fixed point: standard values (SI Appendix). One stable vegetative fixed point, one stable competent fixed point: n_k = 4, n_s = 3.5, G₁ = 0.06, G₀ = 0.5, G_s = 0.4, X_k = 0.5, X_s = 0.5.

Even in optimal conditions, only ≈10% of the vegetative cells overexpress ComK and become competent, and this percentage is independent of neighboring cells or family history. Interestingly, the overexpression of ComK has a more or less defined duration. Cells that become competent come back to vegetative state and divide after ≈20 h, suggesting that competence is not necessarily a stable state (5). Previous studies have proposed a model where the system shows a stable state and an excitable unstable state (12, 13). The system can be thrown out of the stable state (vegetative) and then make an excursion around the unstable fixed point (competence), only to come back to the stable state after some time. The lack of stability of the competent state would make its duration less variable. These facts strongly suggest that noise plays a crucial role in competence control, exciting the system into the competent state. The noise can have many origins: the synthesis of RNA proteins, the degradation of the proteins through the MecA/ClpC/ClpP complex, and the binding of proteins to the DNA promoter, which are known as intrinsic noise sources (14–16). Noise could also come from extrinsic sources, which are fluctuations in the environment. These extrinsic sources of noise would lead to variations in the rates of the chemical equations that describe the system. Traditionally, an adiabatic approximation is used to temporally average over the neglected dynamics of chemical substeps of the system, such as the degradation complex dynamics and binding and unbinding of proteins to the DNA (17, 18). Such adiabatic approximations usually consider that binding equilibrium is reached rapidly when compared with the other timescales of the system. We argue however that microscopic DNA binding events could be important sources of fluctuations in this system as was discussed earlier in a more abstract context (19). We investigate all these sources of noise, determining their effect in the competence cycle. A stochastic model is developed with the goal of determining the importance of different sources of noise (20–27).

Initially, we examined the deterministic limit to orient our understanding of how different dynamical regimes are obtained for different parameters (12, 13). Once the regimes leading to the excitable mechanism are determined, we could then explore the full stochastic approach, analyzing many possible sources of noise. We express the results of our simulations through sample trajectories plotted over the effective potential surface, obtained from the average of many trajectories. These surfaces, although not denoting a rigorously proper potential field (27), help visualizing the basins of attractions and provide a systematic way of visualizing the probability distribution. To connect our theoretical work to studies in the laboratory, we address two variables that can be measured in in vivo experiments: the competence time T_c and the probability of initiation P_i. The competence time is simply the time that a cell will spend in competence. The probability of initiation is the probability that a vegetative cell will enter competence during its lifetime. Competence itself is defined in this context as ComK expression being above a certain threshold.

The Core Mechanism of Competence Induction

The central part of the mechanism of competence control is the positive feedback loop of ComK. Our model assumes that the main form of regulation of ComK expression is the binding of ComK to its own promoter (20, 28). The unbound promoter (𝒦₁) has a basal rate of expression of g₁ and the bound promoter (𝒦₀) has a fully activated rate of g₀. The binding rate of ComK to its promoter is taken to be h(k) = hk^nk (n_k is a measure of nonlinearity), and the unbinding rate is f. The expression of ComS is repressed by ComK. The molecular mechanism of this repression is not known, so it will be included through a Hill-type function describing the modulation of the synthesis rate of ComS: g_s(k) = g_s/[1 + (k/x_s)^ns], where x_s is the ComK concentration for half-repression and 𝒮 is the comS promoter. It should be noted that using Hill coefficients to model the binding rate of ComK to the promoter h(k) and the ComK-dependent synthesis of ComS g_s leaves potential sources of noise out of the model. The binding rate h(k) could be affected by events such as multimerization of ComK, and the synthesis of ComS could be affected by noise resulting from the unknown mechanism of repression by ComK. The concentration of the degradation complex MecA/ClpC/ClpP is assumed constant in the cell. Free units of the degradation complex can form complexes with ComK or ComS. These, in turn, can lead to the degradation of ComK or ComS and subsequent release of free units of the degradation complex. We denote the total number of degradation complexes as A. Free units of the degradation complex are denoted as A_f, and complexes formed with ComK and ComS are denoted as A_k and A_s, respectively. This model can be expressed by the following chemical reactions

Little is known with certainty about the rates associated with these individual reactions. In this work we will highlight the changes in dynamical behavior that depend on the relative speed of three processes: binding/unbinding events, MecA/ClpC/ClpP dynamics and synthesis/degradation of proteins, and discuss the implication of the relative kinetics in the stochastic context. The first two processes (binding/unbinding and degradation dynamics) are usually assumed to be extremely fast, but in a system where noise plays a decisive role, the fluctuations induced even by fast processes can become important. We will use different stochastic models to explore different sources of stochasticity and observe their effect on the system. We will express our results through trajectories generated over effective potential surfaces. Trajectories are generated from the stochastic reactions using the Gillespie algorithm. In the simulations, the system starts at the vegetative stable state and is followed until a whole competence cycle is completed. The average of many trajectories results in average vegetative times and average competence times, as well as a probability distribution for the states of the system. For better visualization, instead of the probability distributions we plot “effective potential” surfaces, obtained from V_eff = −lnP. These surfaces, although not denoting a “real” potential, help visualize the basins of attraction in the system.

Exploring the Ensemble of Possible Dynamical Behaviors

To characterize when the model shows excitable dynamics, we first simplify our model using the deterministic limit (12, 13). We discuss the kinetic rate equations for k and s under the assumption that the degradation complex binding to ComK and ComS and the binding/unbinding of ComK to DNA are fast compared with synthesis and degradation reactions. Assuming that the time scales for the reactions involving the binding of the degradation complex to ComK and ComS are overwhelmingly faster than the net degradation rate, they can be considered as being in equilibrium. Considering that the total number of degradation complexes is constant (A = A_f + A_k + A_s), we can set dA_f/dt, dA_k/dt, and dA_s/dt equal to zero, yielding A_f = Aφ(k, s), A_k = Aφ(k, s)k/Γ_k, and A_s = Aφ(k, s)s/Γ_s, where Γ_k = (λ_k + λ_0k)/λ_1k and Γ_s = (λ_s + λ_0s)/λ_1s are the concentrations of k and s for half-maximal degradation and φ(k, s) ≡ A_f/A = 1/(1 + k/Γ_k + s/Γ_s) is a measure of the availability of the degradation complex. Assuming that the binding/unbinding rates are also faster than the synthesis/degradation rates, the synthesis rate of k will be obtained from g(k) = g₁ P(𝒦₁) + g₀P(𝒦₀), where P(𝒦₁) = f/(h(k) + f) and P(𝒦₀) = h(k)/(h(k) + f). Introducing the maximal degradation rates Λ_k = Aλ_k//Γ_k and Λ_s = Aλ_s/Γ_s and the equilibrium constant X^eq = f/h = x_k^nk, we find the rate equations:

To study the different kinds of behavior of these equations for different parameters, we can plot nullclines to determine the system's fixed points. We generated 500,000 different sets of random dimentionless parameters and analyzed the fixed points of the system for each set [see supporting information (SI) Appendix]. The sets of parameters were then categorized according to their fixed points. For each of these categories, the nullclines were plotted with the average set of parameters within the category. The excitable system discussed earlier corresponds to the category where there are three fixed points: one stable point, one saddle point, and one unstable point. An unstable fixed point, corresponding to high concentration of ComK, implies that lengthy excursions of the trajectories to that unstable, but slow, region will be observed, but that no true basin of attraction exists in that region. An excitable system can show long competence cycles around the unstable fixed point without having a stable competent state, as pointed out in the pioneering work of Elowitz et al. (12, 13). Histograms of the values of the sets of parameters found to result in an excitable system show wide Gaussian-like distributions. The region in the parameter space corresponding to the excitable system appears to be compact and large enough to be robust to sizeable changes on the parameters. This finding also indicates robustness to extrinsic noise, which can ultimately be translated into variations in the rates of this model of the module. From a biological perspective, it reflects robustness in the variations between phenotypes. We chose from here a standard set of parameters corresponding to the centers of the distributions on the histograms.

Simulating the Full Stochastic Model

Using Eq. 1 as a basis for a stochastic treatment, simulations were performed using the Gillespie algorithm (29), starting in the vegetative state and simulated through many cycles. The Gillespie method accounts for noise by explicitly dealing with the fate of small number of particles actually involved in gene regulation in an individual cell. Simulations were performed for several sets of parameters: some corresponding to the system having one stable fixed point, others for the case having one stable and one unstable fixed points and still others for situations where there are two stable fixed points. Sample trajectories were generated and are displayed over the “effective potential surface.” The effective potential surface is calculated directly from the probability distribution that results from the averaging over many trajectories. The effective surface for a near-equilibrium system is V_eff = −lnP and we use the same construct to orient our thinking in the far-from-equilibrium situation relevant here (Fig. 1).

Excursions into competence usually start with the system having a higher concentration of ComS then the stable vegetative fixed point, due to fluctuations. The ComK concentration then starts to increase and the trajectory begins to drift toward the vicinity of the unstable fixed point. The concentration of ComS then decreases at high levels of ComK because of the repression. Finally, ComK returns to its basal levels and the ComS levels are restored. The effective potential surface exhibits a well that corresponds to the vegetative state and a rather flat region that corresponds to the excursions into competence exploring the neighborhood of the unstable fixed point. To compare our results with the laboratory experiments, we will use the models to compute the probability that a cell under stress (presence of ComS) will go into competence (P_i) and also will compute the time spent in competence cycles (T_c). To compare the results of these calculations with observations, we note that cells in the vegetative state have a life cycle of ≈4 h. However, most vegetative B. subtilis cells in a culture under stationary growth conditions eventually sporulate, providing a limiting time cutoff. Some cells go into competence instead. These cells have cell division arrested until they return to vegetative state, when the cell grows, sceptates, and divides. Considering that each cell division event in the culture leads to a vegetative cell, the total number of competence events observed divided by the total number of cell divisions will give the proportion P_i of vegetative cells that are said to go into competence. Our simulations do not explicitly contain the mechanism of sporulation. The proportion of vegetative cells going into competence corresponds then to the probability of entrance into competence within the average time of a vegetative life cycle. Because cell division is not included in this model, P_i is obtained from the relation of the average time that it takes for the system to go into competence and an average vegetative lifecycle, estimated from a comparison with T_c based in laboratory values. The average life cycle of a vegetative cell in this case was considered to be one-fourth of the average competence time for that set of parameters.

Adiabaticity in Competence Control

To study the effects of different sources of noise on the system, we use the approach of focusing in a specific source while silencing other potential sources of noise. To investigate the importance of considering explicitly the equilibrium of the complex formation between MecA/ClpC/ClpP and ComK/ComS, we silence the noise coming from ComK binding/unbinding to the DNA by using the adiabatic limit of g(k) = g₁P(𝒦₁) + g₀P(𝒦₀). The system then shows stochastic noise coming only from the synthesis and degradation of ComK/ComS and from the degradation complex equilibrium. Simulations performed for different values of a degradation adiabaticity parameter showed that neither the competence times nor the probabilities of initiation were significantly affected by different levels of noise (see SI Appendix). The effective potential surfaces also showed similar qualitative properties. These results suggest that an adiabatic approximation is valid for the degradation complex equilibrium. Making this approximation, simple stochastic reactions referring to the degradation of ComK and ComS would have k- and s-dependent rates φ(k, s)Λ_kk and φ(k, s)Λ_ss.

To study the importance of explicitly considering the binding and unbinding of ComK to the DNA, we silence the noise coming from the degradation complex equilibrium by using the adiabatic approximation discussed above. The sources of noise are now the overall synthesis and degradation of ComK and ComS as well as the binding and unbinding of ComK to the DNA. To indicate the relative speed of these molecularly distinct processes, we introduce the binding/unbinding adiabaticity parameter ω = f/Λ. Simulations were performed for many values of ω and compared with the commonly used adiabatic limit approximation. In the adiabatic limit we use a k-dependent synthesis rate g(k) = (g₁ + (k^nk/X^eq)g₀)/(1 + k^nk/X^eq) in substitution to the explicit binding and unbinding rates.

This approximation corresponds to the case where ω = ∞, meaning the binding/unbinding reactions are much faster than other time scales of the problem and can be averaged. In Fig. 2, we see samples of trajectories plotted over the effective potential surface for some values of ω. The surface is less flat around the unstable fixed point for smaller values of ω. Trajectories do not approach the unstable fixed point and a clear path for entrance and exit from competence emerges. For values of ω smaller than 1, expression of ComK equilibrates to the binding state of the comK promoter, and the system shows a “stable” competent state, which will persist for the lifetime of the ComK–DNA complex (19, 30, 31). In Fig. 3, we see the time evolution of ComK and ComS levels for different values of ω. Smaller values of ω allow a faster transition to competence, as well as a higher expression of ComK and a longer time spent at maximum levels of ComK. When the effects of nonadiabaticity are considered, the probability of initiation of competence is much higher, even for values of ω well above 1 (SI Appendix). Sets of parameters that do not exhibit competence when the adiabatic approximation is made, can show competence when there is nonadiabatic binding/unbinding of the promoter. We see, therefore, that nonadiabaticity can expand the region of the parameter space showing competence, allowing increased the robustness of the system to parameter variation. These results manifest the idea of functional stochasticity, in which fluctuations increase the cell's robustness.

Fig. 2.

Comparison of simulations for different values of the adiabaticity parameter ω with the adiabatic approximation for binding/unbinding events. The surface becomes less flat around the unstable fixed point for smaller values of ω.

Fig. 3.

Time evolution of ComK and ComS levels for competence events for different values of ω. Lower values of the adiabaticity parameter allows higher and more sustainable peaks in the expression of ComK. Parameters are the same as indicated in the SI Appendix.

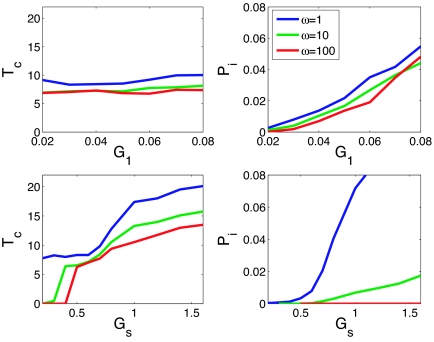
Changing Basal Rates of Expression of ComK and ComS

Laboratory experiments have been performed where the basal rates of expression of ComK and ComS (g₁ and g_s, respectively) were controlled (13). These studies reveal interesting effects on both competence times (T_c) and probabilities of initiation of competence cycles. The basal rate of expression of ComK has been shown to control the probability of initiation of competence events, whereas the basal rate of expression of ComS controls mostly the duration of such events. To see the effects of adiabaticity on this control, simulations were performed for different values of the adiabaticity parameter ω, using the standard set of parameters and changing only the basal rates of expression. These effects are shown in Fig. 4. As observed in the laboratory, increasing the basal ComK expression g₁ does not change the competence time, but does increase the probability of initiation (13). Increasing the basal ComS expression g_s indeed increases the competence times. However, the effect of g_s on the probability of initiation depends on the adiabaticity. In the adiabatic limit or for high values of ω there is no change in P_i. For lower values of ω, there is a slight increase in P_i, whereas for ω ≈ 1, there is a large increase. Laboratory experiments indeed do observe such an increase in P_i as the basal expression of ComS is made larger. This finding suggests the presence of significant nonadiabatic effects in competence control.

Fig. 4.

Effects of changing the basal rates of expression of ComK and ComS on the competence time T_c and probability of initiation P_i. Increasing the basal rate of expression of ComK G₁ will increase P_i, but will not affect T_c. Increasing the basal rate of expression of ComS G_s will increase T_c, and the effect on P_i will depend on the adiabaticity parameter. For high values of ω, there will be a slight increase in P_i, whereas for values as low as 1, there will be a large increase.

To better illustrate these effects, we plot in Fig. 5 the time evolution of ComK and ComS levels obtained from the simulations. Increased g₁ does not change the width of the peaks of ComK expression, but does increase their frequency, eventually leading to oscillatory behavior. This oscillatory behavior corresponds to another region of the parameter space, where there is only one unstable competent fixed point. Increasing g_s causes the width of the peaks to increase. The frequency of the peaks initially stays the same, but increases for higher values of g_s in the case of ω = 10 considered here. For lower values of adiabaticity, there is an increased probability of higher levels of ComS during vegetation (SI Appendix). Higher levels of ComS start competence events, so this change accounts for the increase in the probability of competence initiation observed for nonadiabatic scenarios.

Fig. 5.

Trajectories showing the effects of changes in the basal rates of expression of ComK and ComS. Higher values of the basal rate of expression of ComK G₁ do not alter the width of ComK peaks, but peaks happen more frequently. Higher values of the ComS rate of expression G_s result in wider peaks of expression of ComK. For the adiabaticity parameter ω = 10 considered here, peaks also occur slightly more often.

Entrance into and Exit from Competence

Here, we look more carefully into the events of entering into competence and the exit from competence. We look only at the variations of the ComK level k, considering the level of ComS to be fixed (s is a parameter). We focus the analysis on the behavior of the feedback loop of ComK having a fixed concentration of ComS. This situation arises where ComS levels vary slowly or are determined by other cell processes. The dynamics of the degradation complex are taken to be in the deterministic limit, leaving a stochastic model with noise only from synthesis and degradation of ComK, and binding and unbinding of ComK to the DNA. We then analyze two simplifications of this model, corresponding to the deterministic limits of the synthesis/degradation and the binding/unbinding processes. First, we will consider a model where binding/unbinding processes occur at a deterministic rate and synthesis/degradation are stochastic events. This results in a birth–death process where the rates depend on k. This model corresponds to the case where binding/unbinding events are fast. The more comprehensive model treats the binding/unbinding events explicitly in a stochastic manner and the protein number respond deterministically to the DNA binding state. In this case, the probability of having a binding or unbinding event depends on the number of proteins at that time. This model would correspond to the case where binding/unbinding events are especially slow.

Fast Binding/Unbinding

Considering synthesis/degradation and binding/unbinding deterministically, we write an equation for the probability of having precisely k molecules of ComK:

where g(k) and λ(k) = φ(k)Γ_kk are the k-dependent synthesis and degradation rates discussed in the adiabatic limit. φ(k) is φ(k, s) with s fixed.

The steady-state solution can be obtained iteratively by P(k + 1) = (g(k)/λ(k + 1))P(k). A time-dependent solution can be obtained by expressing the equation through a transition matrix M such that dP/dt = MP, giving the matrix exponential solution P(t) = e^MtP_o (19).

We analyze this approximation by comparing it to simulations performed for different values of the adiabaticity parameter ω (Fig. 6). We consider two scenarios: entrance into competence (s = 100) and exit from competence (s = 20). In both cases, it is clear that nonadiabaticity has a large influence on the stabilization of unfavorable states. Nonadiabaticity allows bistability or excitability in many cases where the adiabatic limit does not allow such behavior, as can be observed from the preservation of the vegetative well in the entrance case and the flat competent region in the exit case. The adiabatic approximation can, however, successfully describe the most stable well in both cases.

Fig. 6.

Fast and slow approximations for binding/unbinding of ComK to DNA. (Upper) Effective potentials for the case of fixed expression of ComS and fast binding/unbinding, considering s = 100 for entrance into competence and s = 20 for exit from competence. The thick red line denotes the adiabatic limit. Nonadiabaticity is a cause of bistability and bimodality, as seen for the efffective potentials in the cases of lower ω. (Lower) Comparison of simulated and calculated competence times and probabilities of initiation for the model with slow binding/unbinding. Using the slow-binding method allows good agreement for low values of the adiabaticity parameter ω.

Slow Binding/Unbinding

We consider now the scenario where switching events between binding states are slow and happen stochastically, whereas synthesis and degradation are modeled in a deterministic fashion. If the system is in a given binding state with synthesis rate g, the ComK level k varies deterministically in time as

This equation is separable, and a solution k(t) can be found. With this solution in hand, given an initial binding state and an initial level of ComK k, we can calculate the probability of switching binding states at any given time based on the time evolution of k. If the system starts with the gene unbound and typical low values of k, we will call t_up the time that it takes for the system to reach the threshold to transition to competence, following a binding event. t_up is then the duration of switches in the binding state necessary for transitions from vegetation to competence to occur. The probability of reaching t_up following a binding event will be called P_up, the probability that the gene will stay bound long enough for the transition to happen. The unbinding rate f is independent of k, so P_up = e^−ftup.

If, instead, the system starts with the gene bound and typical competence values of k, we will call t_down the time that it takes to reach the vegetative state after an unbinding event. The probability of reaching t_down following an unbinding event has to take into consideration the decreasing levels of k when the gene is unbound, since the binding rate h(k) is k-dependent. We have therefore P_down = e^−m(tdown), where m(t) = ∫₀^th(k(t′))dt′.

We know the probabilities that a switch in the binding state will result in a transition between competence/vegetation (P_up and P_down). We can now calculate the average times in the bound and unbound states by t_bound = 1/f and t_unbound = ∫₀^∞th(k(t′))e^−m(t′)dt′. Finally, we can calculate the time that the system will spend between competence cycles as T_b = (t_bound + t_unbound)/P_up and the time that the system spends in competence cycles as T_c = (t_bound + t_unbound)/P_down.

We compare the results of these intuitive approximations with the values of competence times and probabilities of initiation obtained from simulations (Fig. 6). The calculated values start agreeing with the simulations for values of ω as low as 1. Even though such strong nonadiabaticity might not apply to the case of the competence module, the present approximation scheme could be useful for other cellular processes that are extremely nonadiabatic.

Discussion

A stochastic model of the self-activating loop of ComK with competitive degradation of ComS is able to reproduce most of the features observed of this system observed in nature. Our analysis of this model indicates the likelihood that nonadiabaticity accompanying binding/unbinding events is important for this noise-dominated system. Specifically, nonadiabatic noise from binding and unbinding of ComK to the DNA probably plays an important role on determining the region of the parameter space able to exhibit excitable behavior, as well as in robustness to parameter variation. Comparison of our model with laboratory experiments where the basal rates of ComS were varied suggests the presence of nonadiabatic noise in ComK binding/unbinding. Competence in bacteria is a beautiful example of a cell process where noise plays an important constructive role. Understanding the microscopic origins of biochemical noise will be as essential for cell biology in the future as understanding the average behavior of biomolecular subprocesses has been in the past.