Abstract
This study investigates coordination between hand transport and grasp movement components by examining a hypothesis that the hand location, relative to the object, in which aperture closure is initiated remains relatively constant under a wide range of transport speed. Subjects made reach-to-grasp movements to a dowel under four speed conditions: slow, comfortable, fast but comfortable, and maximum (i.e., as fast as possible). The distance traveled by the wrist after aperture reached its maximum (aperture closure distance) increased with an increase of transport speed across the speed conditions. This finding rejected the hypothesis and suggests that the speed of hand transport is taken into account in aperture closure initiation. Within each speed condition, however, the closure distance exhibited relatively small variability across trials, even though the total distance traveled by the wrist during the entire transport movement varied from trial to trial. The observed stability in aperture closure distance across trials implies that the hand distance to the object plays an important role in the control law governing the initiation of aperture closure. Further analysis showed that the aperture closure distance depended on the amplitude of peak aperture as well as hand velocity and acceleration. To clarify the form of the above control law, we analyzed four different mathematical models, in which a decision to initiate grasp closure is made as soon as a specific movement parameter (wrist distance to target or transport time) crosses a threshold that is either a constant value or a function of the above-mentioned other movement-related parameters. Statistical analysis performed across all movement conditions revealed that the control law model (according to which grasp initiation is made when hand distance to target becomes less than a certain linear function of aperture amplitude, hand velocity, and hand acceleration) produced significantly smaller residual errors than the other three models. The findings support the notion that transport–grasp coordination and grasp initiation is based predominantly on spatial characteristics of the arm movement, rather than movement timing.
Keywords: Prehension, Kinematics, Coordination, Aperture opening, Aperture closure
Introduction
Even after numerous studies of prehensile movements, rules and mechanisms governing the coordination between the transport and grasp components are not completely understood. Although in many studies transport duration or speed varied due to modifications of the distance to target or target size, in relatively few studies was the duration of the transport phase manipulated directly over a broad range of speeds (Wallace and Weeks 1988; Wallace et al. 1990; Wing et al. 1986; Wang and Stelmach 2001). A significant modification in the transport speed of reach-to-grasp movements induces changes in the kinematic characteristics of not only the transport component, but also the grasp component. The maximum aperture between the thumb and index finger during the reach becomes wider for faster transport (Wing et al. 1986). Wallace and Weeks (1988) further demonstrated that the maximum aperture is dependent more on the transport duration than the transport speed. Namely, the shorter the transport time, regardless of the movement amplitude, the greater the maximum aperture. Thus, the aperture width appeared to be modified in relation to the temporal characteristics of the transport component. When reach-to-grasp movements were performed under various transport durations or speeds, the maximum aperture occurred at a relatively fixed timing in relation to overall movement duration (Paulignan et al. 1991a; Marteniuk et al. 1990; Rand et al. 2000; Smeets and Brenner 1999; Wallace and Weeks 1988; Wallace et al. 1990). However, some other studies demonstrated that the duration for aperture closure movement was unaffected by different task conditions (Bootsma and van Wieringen 1992; Gentilucci et al. 1992; Paulignan et al. 1991b; Watson and Jakobson 1997; Zaal et al. 1998). These observations led to a hypothesis that grasp formation and kinematics of the arm transport are temporally linked to coordinate the transport and grasp components (Hoff and Arbib 1993; Jeannerod et al. 1995; Jeannerod 1999).
Other studies support the view that the reach-to-grasp movement relies on a spatial coupling between the transport and grasp components (Haggard and Wing 1991, 1995, 1998). More specifically, the grip aperture is modulated based on the distance between the hand and the object. Recent studies from our laboratory support this view by demonstrating an invariant nature of the hand location relative to the object where the aperture begins to close (Alberts et al. 2000, 2002; Rand and Stelmach 2005; Saling et al. 1998; Wang and Stelmach 1998, 2001). It was shown that the distance traveled by the wrist after maximum aperture (aperture closure distance) was relatively invariant, even though the distance traveled by the wrist prior to maximum aperture varied under different task constraints. This was observed in experiments that employed different target sizes and target distances (Alberts et al. 2000; Wang and Stelmach 1998, 2001), different involvements of body segments (Wang and Stelmach 1998, 2001), a forearm rotation during the reach (Rand and Stelmach 2005), different conditions for obstacle avoidance (Alberts et al. 2002; Saling et al. 1998), and with or without mechanical perturbations applied on the reaching arm (Rand et al. 2004). These findings were interpreted as evidence that the onset of aperture closure is controlled by spatial information regarding the hand location relative to the object, and hence the transport and grasp components are coordinated primarily in the spatial domain.
However, such space-based coordination between the transport and grasp has not been examined over a large range of movement speeds. One previous study (Wang and Stelmach 2001) examined the effect of transport speed on the aperture closure distance. Two speed conditions defined as “comfortable” and “as fast as possible” were tested, with the finding that there was little difference in aperture closure distance between these conditions. The aperture closure distance was thus again shown to be rather stable across speed conditions. In the same study, object size and movement distance were varied, producing movements that were executed at different speeds across trials. Despite these manipulations, the range of transport speeds was relatively small. It may be possible that the aperture closure distance could be altered, if a much greater range of transport speed were examined.
Similar to our previous studies (Alberts et al. 2000, 2002; Rand et al. 2004; Saling et al. 1998; Wang and Stelmach 1998, 2001), the current study examines whether transport–grasp coordination is better formulated in terms of spatial or in terms of temporal characteristics of the movement by comparing the extent of invariance in those characteristics with regard to transport speed and distance. For this purpose, in this study we expanded the range of speed manipulations from that previously tested and examined how the aperture closure distance varied across that range. To analyze transport–grasp coordination, we applied a relatively new approach, which is based on a theoretical concept that the initiation of aperture closure is governed by a certain control law, a function defined on certain state parameters of arm-target dynamics, such as the hand distance to target, hand velocity, aperture, etc. This approach was successfully used for modeling neural control of arm movements (Shimansky et al. 2004). In our study, we used it to elucidate the relationship between arm movement parameters and a decision to initiate aperture closure. The existence of such a control law has been shown also in our previous study (Rand et al. 2006).
This study demonstrates that the aperture closure distance significantly increases with faster transport speed across a range of speed conditions. In addition, the trial-to-trial variability of the aperture closure distance can be explained to a significant extent by its dependence on the aperture amplitude, wrist velocity, and acceleration, supporting the above control law hypothesis. Preliminary findings of this study were presented elsewhere (Squire et al. 2004).
Materials and methods
Subjects
Eleven subjects (eight males, three females; mean (SD) age was 22.3 (2.0) years old) participated in this study. All subjects were right-handed. This study was approved by Arizona State University’s Institutional Review Board overseeing the use of human subjects in research. All subjects signed informed consent forms prior to participation.
Procedure
All subjects were seated comfortably in front of a tabletop on which the target object was placed. The start position consisting of a push plate was located approximately 15 cm from the subject’s midline. The target was an opaque cylinder (2.1 cm in diameter, 10 cm height). All subjects performed reach-to-grasp movements with their dominant hand. Subjects were instructed to place the ulnar side of the hand at the start position before each trial and to keep their thumb and index finger together. All trials were preformed in dim lighting. At the beginning of each trial, the target was lit up by a red light emitting diode (LED) for a random period between 1 and 2 s before a “beep”. The “beep” signaled the subject to reach for the target and lift it. The target remained lit for the duration of each trial. The target was placed at 15 or 30 cm along the midline of the trunk from the area at which the index finger and thumb were placed on the start position. Subjects were instructed to reach for and grasp the target using a precision grip (i.e., between the thumb and index fingers), and lift the object a few centimeters from the tabletop. Four speed conditions were tested: slow, comfortable, fast but comfortable, and as fast as possible without knocking the target over. Subjects modified their movement speed based on the examiner’s verbal instruction, which also included an emphasis that each speed should be distinctively different from other speeds. In the rest of the text, these four conditions are referred to as slow, normal, fast, and maximum. Each combination of speed and distance was tested in blocked trials. Twelve trials were performed for each condition, the first two were practice trials to allow the subject to become familiar with the task and the subsequent ten trials were used in the analysis. The order of the speed conditions was randomized across the participants. Half of the subjects started with the 15 cm distance and the other half with the 30 cm distance. Each speed condition was performed at both the 15 and 30 cm distances before moving to the next speed condition.
Arm and finger positions during reach-to-grasp movements were recorded using an Optotrak 3D system (Northern Digital). Infrared light emitting diodes (IREDs) were placed over the wrist, tip of the index finger and the tip of the thumb. An additional IRED was placed on the target in order to record its position and movement. Positions of the IREDs were sampled at a rate of 100 Hz.
Data analysis
Kinematic characteristics related to the grasp component and the transport component were analyzed. The transport component was assessed based on the position of the IRED on the wrist. Wrist velocity during the reach was tangential velocity calculated as the first derivative of wrist position. Derivatives were calculated based on the sliding window technique, where the data points within the window (the window width was 7 points) were approximated with a quadratic polynomial. The polynomial was then used for calculating analytic derivative at the window’s center (or other points, when at the beginning or end of the data array representing the curve). Thus, calculating derivatives using this method also provided data filtering. The grasp component was assessed based on the positions of the IREDs on the index and thumb fingertips. Grip aperture was defined as the resultant distance between these two IREDs. Grip aperture velocity was calculated as the first derivative of grip aperture data. The value of peak velocity during aperture closure was measured as peak aperture closure velocity. Both the temporal changes in grip aperture and maximum grip aperture were determined. Target touch was identified as the onset of any movement of the target, as determined from the movement of the IRED placed on the object. The end of the transport was defined as simultaneous to the target touch. Calculating the onset of transport and aperture was performed by an automated movement parsing algorithm (Teasdale et al. 1993; algorithm B). All of these landmarks were verified by visual inspection by the experimenter; any errors were corrected.
Temporal measurements included: (1) transport time: the duration from movement onset to the target touch, (2) aperture opening time: the duration from movement onset to maximum aperture, (3) aperture closure time: the duration from maximum aperture to the target touch, and (4) normalized aperture opening time expressed as a percentage of transport time. In addition, the following spatial parameters were measured: (1) transport distance: the distance from movement onset to the target touch, (2) aperture opening distance: the distance from movement onset to maximum aperture, and (3) aperture closure distance: the distance from maximum aperture to the target touch. These distances were calculated as a cumulative resultant trajectory length between two positions of the wrist IRED. It should be noted that the end of the arm transport was simultaneous to the target touch in this study, which is slightly earlier than the time defined in many other studies (the end of grasp, Alberts et al. 2002; Castiello et al. 2000; Paulignan et al. 1991a), because the fingers continued to close after the target touch. Forward displacement of the wrist IRED was observed from the target touch to the completion of the grasp, most often for the faster speed conditions. This was because the target was pushed and tilted forward away from subjects. Thus, including the wrist displacement data during this period would distort wrist–target distance information at the time of the aperture closure initiation. Furthermore, since the hand had been transported to the target by the time of the target touch, we chose the target touch to be the end of wrist transport.
For each kinematic measurement, a mean value across all trials for each subject was calculated for each condition. Based on these mean values, a 2 (distance) × 4 (speed) ANOVA with repeated measures, distance and speed as within-subject factors, was performed. When needed, a post hoc comparison was performed by using a paired t-test with Bonferonni correction (α=0.05) to identify significant differences between individual cell means.
Four different models of the control law governing aperture closure initiation (see Introduction) were examined in this study. First, we hypothesized that the aperture closure is initiated at a constant distance D of the hand from the target (Model 1). This control law (formulated in terms of spatial parameters) can be expressed as
| (1) |
where Dthr is a distance-to-target threshold. It is assumed that aperture closure is not initiated, while a state where D > Dthr.
Second, we examined a hypothesis that the aperture closure is initiated at a constant aperture opening time T (Model 2). The initiation is not made while T < Tthr. This control law (formulated in terms of temporal parameters) can be expressed as
| (2) |
where Tthr is an aperture opening time threshold.
Third, we examined a generalization of Model 1 where the distance-to-target threshold depends on certain state parameters (grip aperture (G), wrist velocity (Vw), and wrist acceleration (Aw) (Model 3). Then, the condition for the onset of aperture closure can be presented formally as
| (3) |
Fourth, we examined a generalization of Model 2 where the threshold for aperture opening time depends on the same state parameters as above Model 3 (Model 4):
| (4) |
Note that, as a temporal threshold for the onset of aperture closure in Models 2 and 4, we chose aperture opening time among other possible temporal parameters, such as aperture closure time and normalized aperture opening time. This preference was based on the fact that, while the time expired since movement initiation is observable at any moment in time during the movement, the aperture closure time (or the aperture opening time relative to the total movement time) is not, because the subject has not finished the movement yet.
To test the validity of those control law models, the aperture closure distance, aperture opening time, grip aperture amplitude, wrist velocity and wrist acceleration were measured at the time of maximum aperture (and hence the initiation of the aperture closure). This approach has been successfully used in our previous study (Rand et al. 2006). The coefficients of a particular model of the control law were identified based on the standard method, namely by minimizing the least square deviation of the model’s prediction from the actual, experimentally measured values of the target variable (the aperture closure distance or aperture opening time). Then, the R2 values and the absolute residual errors were calculated for each subject based on all trials across all speed and distance conditions by using a linear regression analysis. The relative residual errors were then calculated as the ratio between the absolute residual error and the average value of the corresponding variable.
Next, the residual errors were statistically compared between different models. A 4 (model) × 11 (subject) ANOVA with repeated measures, model as a within subject factor and subject as a between subject factor, was performed for this purpose. A post hoc comparison was performed by using an dependent t-test with Bonferonni correction (α=0.05).
Results
General characteristics of reach-to-grasp movements
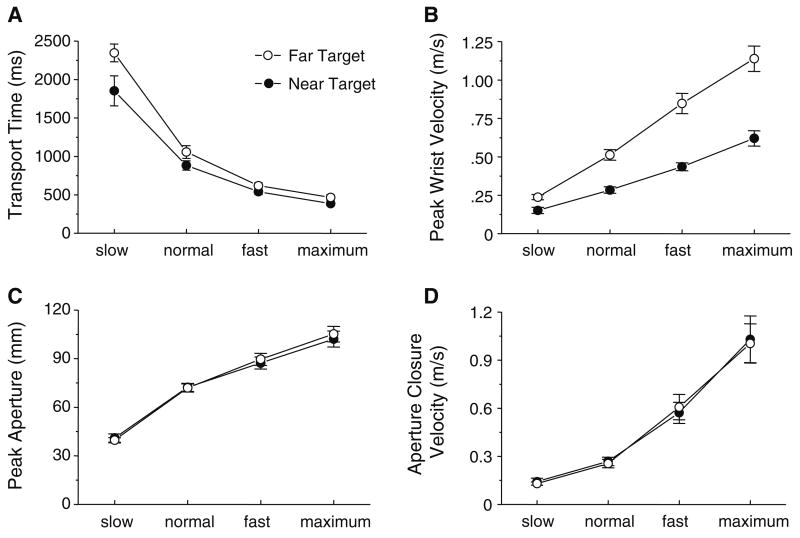
As expected from the four different speed instructions, the subjects altered the speed of wrist transport across the speed conditions. The average transport velocity in the near target condition was 0.08, 0.16, 0.25, and 0.36 m/s for the slow, normal, fast, and the maximum conditions, respectively. The comparable values in the far target condition were 0.12, 0.26, 0.46, and 0.63 m/s. Figure 1 shows the average transport time and peak wrist velocity across subjects. The subjects gradually decreased transport time from the slow speed condition to the maximum speed condition (Fig. 1a). This change was accompanied by the gradual increase in peak velocity of the wrist movement, which was changed with the speed manipulation for both the near and far target conditions (Fig. 1b). An ANOVA revealed that there was a significant speed effect for both parameters (transport time: F(3,30)=86.70, P<0.001; peak velocity: F(3,30)=78.37, P<0.001). However, as can be seen in Plot a, the slope of decrease in the transport time from the slow to the maximum speed condition was steeper for the far-target conditions than that for the near-target condition. Similarly, the slope of increase in the peak wrist velocity was steeper for the far-target condition (Fig. 1b). Accordingly, a distance by speed interaction was significant for both parameters (transport time: F(3,30)=8.66, P<0.001; peak velocity (F(3,30)=34.97, P<0.001). The speed manipulation also changed the grasp component. The maximum aperture amplitude gradually increased as the movement speed increased (F(3,30)=53.38, P<0.001, Fig. 1c). Similarly, the peak velocity of aperture closure movement increased for faster transport movements (F(3,30)=37.56, P<0.001, Fig. 1d). However, the distance to the target did not influence the aperture amplitude or velocity during the reach (Fig. 1c, d).
Fig. 1.
Effect of speed conditions on the average transport time (a), peak wrist velocity (b), amplitude of maximum aperture (c), and peak velocity of aperture closure movement (d) across all subjects. Filled circles refer to the near target condition (15 cm) and open circles refer to the far target condition (30 cm). The error bars indicate the standard errors
Aperture closure distance
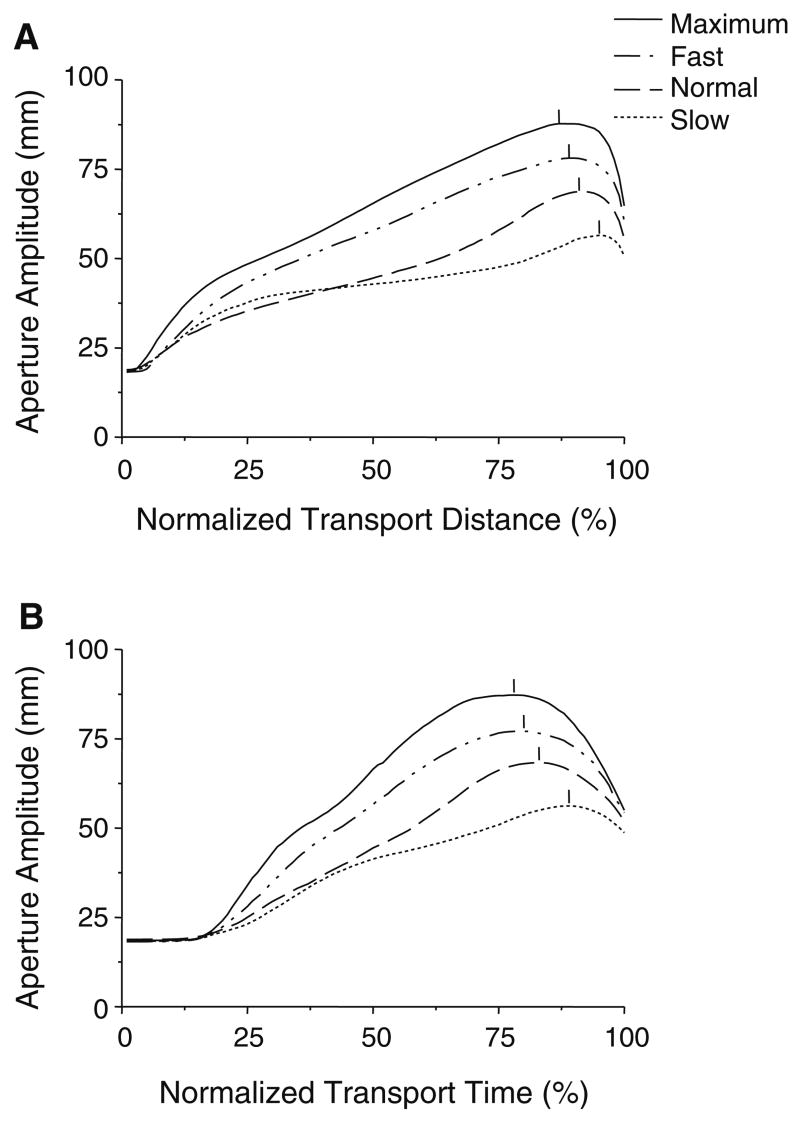
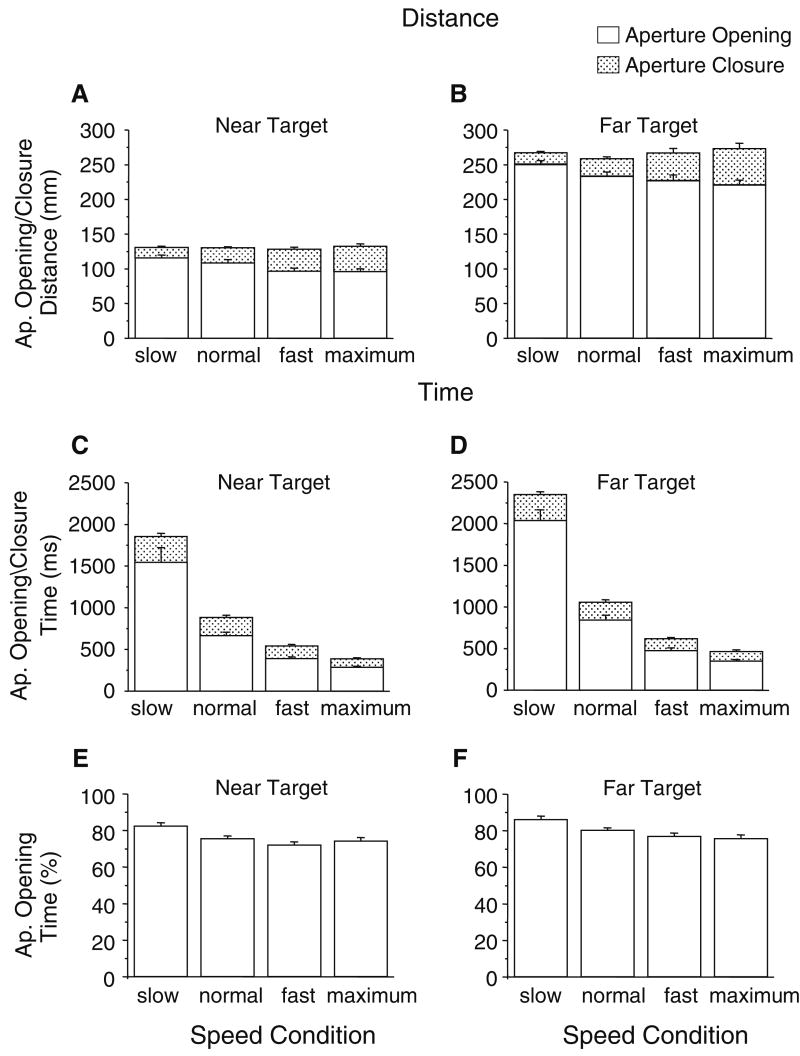
To illustrate aperture formation during the reach, typical aperture profiles for one subject for each of the four speed conditions are shown in Fig. 2a in relation to normalized transport distance. The aperture increased gradually, reached its peak, and closed in the last phase of transport movements. Note that the transport distance during the closure phase of aperture formation was longest in the maximum speed condition and shortest in the slow speed condition, showing that the aperture closure distance changed with speed manipulations. The group data of the total transport distance parsed into the aperture opening distance and closure distance are shown in Fig. 3a, b. The average aperture closure distance across subjects steadily increased from the slow condition to the maximum condition, and there was a significant main effect of the speed condition (F(3,30)=20.02, P<0.001). Since the average total transport distance did not differ across speed conditions (P>0.05), the changes of the aperture closure distance across conditions was accompanied by the changes of the aperture opening distance (F(3,30)=9.56, P<0.001). Furthermore, the closure distance was significantly greater for the far target condition than that for the near target condition (F(1,10)=12.29, P<0.01). These results show that the closure distance changed across speed conditions.
Fig. 2.
Typical examples of aperture profiles for one subject plotted against the normalized transport distance (a) and against the normalized transport time (b) for the four speed conditions. Each trace is an average curve across ten trials of the far target condition. The vertical line for each trace indicates the place (a) or time (b) at which the aperture reached its peak
Fig. 3.
Effect of speed conditions on the average aperture opening distance (open area) and closure distance (dotted area) (a, b), on the average aperture opening time (open area) and closure time (dotted area) (c, d), and on the average normalized aperture opening time (e, f). Panels a, c, and e represent the near target conditions, and b, d, and f represent the far target conditions. The error bars indicate the standard errors
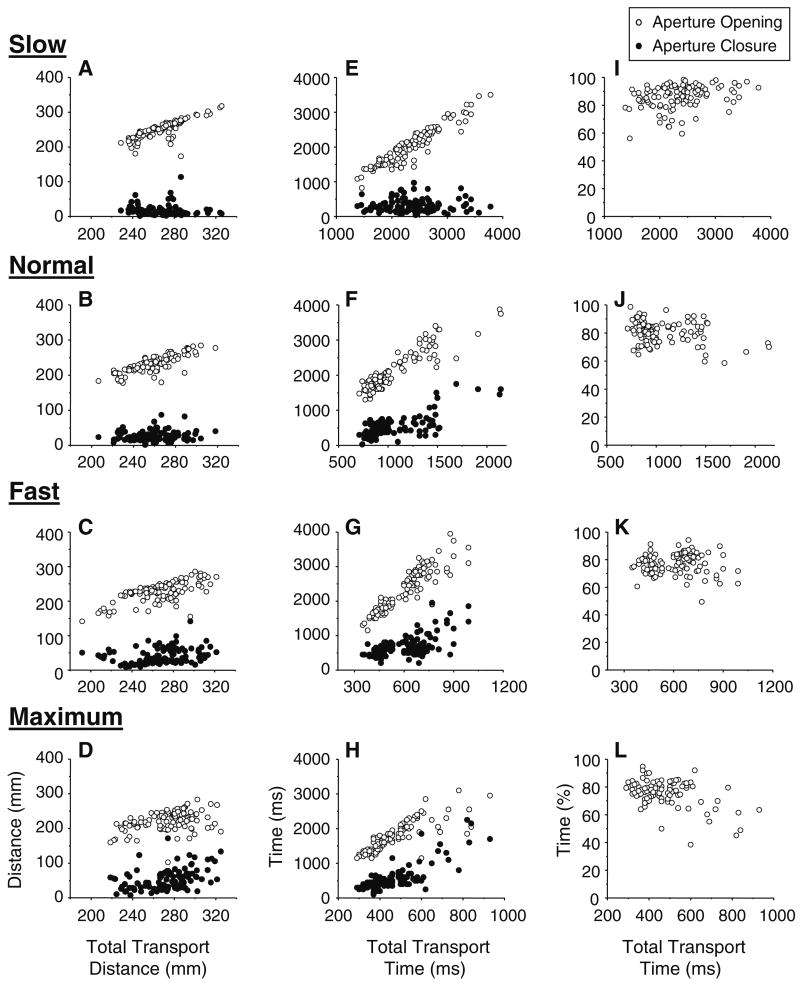
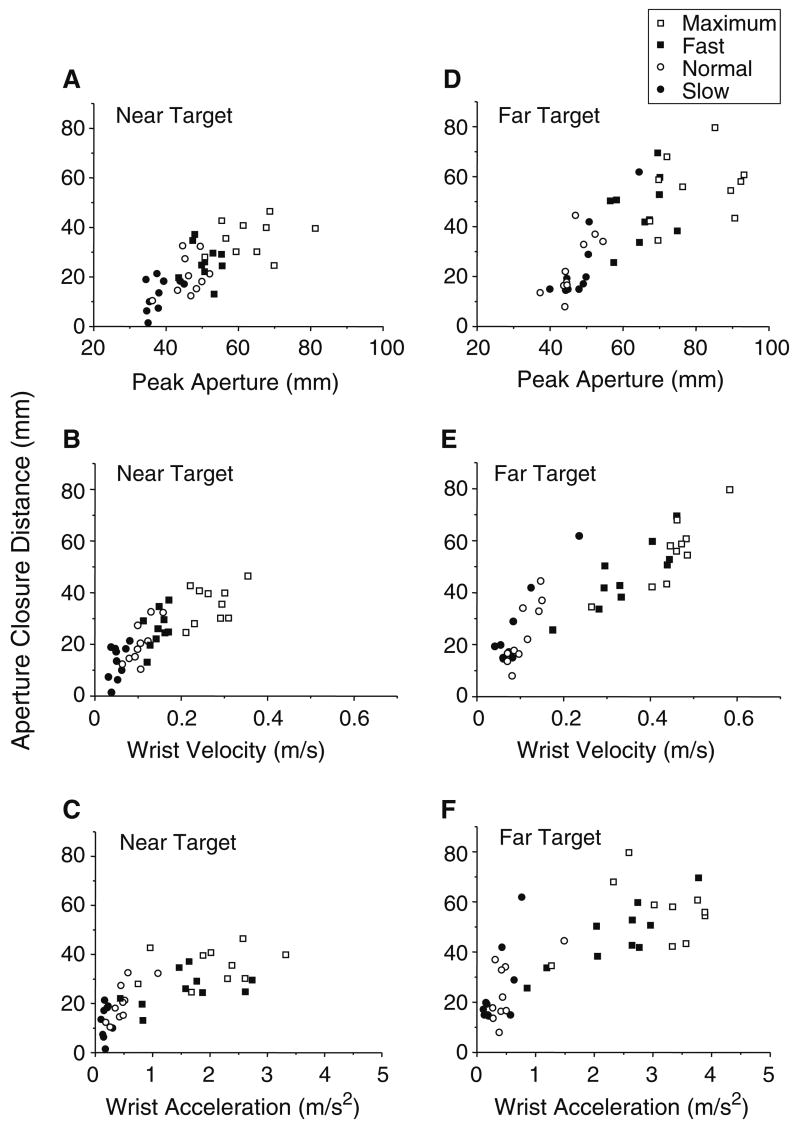
In order to examine if maximum grip aperture (hence the initiation of aperture closure) occurred at a consistent location relative to the hand location at reach onset or object location, the aperture opening distance and aperture closure distance were plotted against the total transport distance for each speed condition (Fig. 4a–d). The near and far target conditions exhibited basically the same results, and the data from the far target condition are shown in Fig. 4. As can be seen in the graph, opening distance varied between trials; namely it increased as the total transport distance increased for all speed conditions. In contrast, the closure distance was consistent across trials with different total transport distances in the slow and normal conditions, and there was no significant correlation between the two parameters (Plots a and b, P>0.05). However, the closure distance slightly increased as the total transport distance increased for the fast and maximum conditions, showing a significant positive correlation between the two parameters (Plot c: slope = 0.263, r=0.309, P<0.01; Plot d: slope = 0.501, r=0.415, P<0.001). When a linear correlation between the two parameters was measured within each subject for each speed condition (Table 1) instead of all trials and subjects together (Fig. 4), a significant condition main effect was found in the slope, but the differences among conditions was not significant in the subsequent post hoc analysis (see statistical results in Table 1). Thus, there was no or only marginal increases in the slope for the fast and maximum conditions. Therefore, each subject produced a relatively constant closure distance across trials in relation to the total transport distance for each speed condition. Such stability in aperture closure distance in comparison to the aperture opening distance was in agreement with other previous studies (Alberts et al. 2000, 2002; Rand and Stelmach 2005; Rand et al. 2004; Wang and Stelmach 1998, 2001). However, across the range of speed conditions the closure distance changed (Fig. 3a, b), suggesting that the initiation of the aperture closure is not determined solely on the distance information from the hand to the target during the reaching.
Fig. 4.
Aperture opening distance (open circles) and closure distance (filled circles) are plotted against the total hand transport distance (a–d) across all trials for all subjects for each condition. Similarly, aperture opening time (open circles) and closure time (filled circles) are plotted against the total hand transport time (e–h), and normalized aperture opening time (open circles) is plotted against the total hand transport time (i–l). Each speed condition is plotted separately (Slow: a, e, i; Normal: b, f, j; Fast: c, g, k; Maximum: d, h, l). The data are from the far target condition
Table 1.
Average slope and correlation coefficient across subjects
| Ap. closure distance vs. total transport distance
|
Ap. closure time vs. total transport time
|
Normalized Ap. opening time vs. total transport time
|
||||
|---|---|---|---|---|---|---|
| Slope | Correlation | Slope | Correlation | Slope | Correlation | |
| Speed condition | ||||||
| Slow | −0.14±0.14 | 0.05±0.10 | 0.14±0.05 | 0.21±0.08 | 0.001±0.002 | 0.06±0.09 |
| Normal | 0.09±0.08 | 0.12±0.07 | 0.19±0.05 | 0.33±0.08 | 0.001±0.004 | −0.03±0.06 |
| Fast | 0.21±0.10 | 0.21±0.09 | 0.39±0.06 | 0.49±0.06 | −0.026±0.010 | −0.20±0.07 |
| Maximum | 0.28±0.14 | 0.30±0.11 | 0.46±0.06 | 0.56±0.08 | −0.049±0.015 | −0.30±0.09 |
| ANOVA results | ||||||
| Condition effect | F=3.70* | NS | F=9.12*** | F=6.40** | F=7.59** | F=4.85** |
| Post hoc test | NS | NS | S–F(*) | S–M* | S–M* | S–M* |
| S–M* | N–M(*) | N–M* | N–M(*) | |||
| N–M* | ||||||
Mean (SE) values across subjects
Slopes and correlation coefficients were calculated for each subject for near and far distances, which were used to calculate the mean value across subjects
NS Not significant, S–F slow–fast comparison, S–M slow–maximum comparison, N–M normal–maximum comparison
df=3,30;
P<0.05;
P<0.01;
P<0.001;
0.1<P<0.05
Aperture closure time
We also examined the effect of speed on the time used for the aperture closure. Typical aperture profiles for one subject (Fig. 2b) show that the subject gradually increased the proportion of transport time that was used for aperture closure from the slow condition to the maximum condition. As group results (Fig. 3c, d), the aperture closure time steadily decreased from the slow condition to the maximum condition. The main effect of speed condition was significant (F(3,30)=31.04, P<0.001). There was no difference between the two distance conditions. The results show that the aperture closure time is influenced substantially by the speed.
To examine whether maximum aperture occurred at a consistent time relative to reach onset or to the grasping of the target object, the aperture opening time and aperture closure time are plotted against the total transport time in Fig. 4e–h). As shown in the plots, the aperture opening time was longer for the trials with longer total transport time for all speed conditions. However, the relation between the aperture closure time and total movement time changed considerably across different speed conditions. The aperture closure time was consistent across trials, regardless of the increase of the total transport times in the slow condition (Fig. 4e, slope = 0.015, r=0.041, P>0.05). This was possibly caused by the fact that the subjects initiated the aperture closure at a short distance from the object (Fig. 3a, b) and under the very slow wrist velocity and acceleration (see Fig. 5b, c). In contrast, aperture closure time increased as the total transport time increased for the maximum condition (Fig. 4h, slope = 0.464, r=0.781, P<0.001). These findings were confirmed in the within-subject data (Table 1). The average slope of the increase of aperture closure time in relation to the total transport time became steeper for faster conditions. The condition main effect was significant (see statistical results in Table 1). These data clearly show that the aperture closure time changed substantially across trials with different total transport times.
Fig. 5.
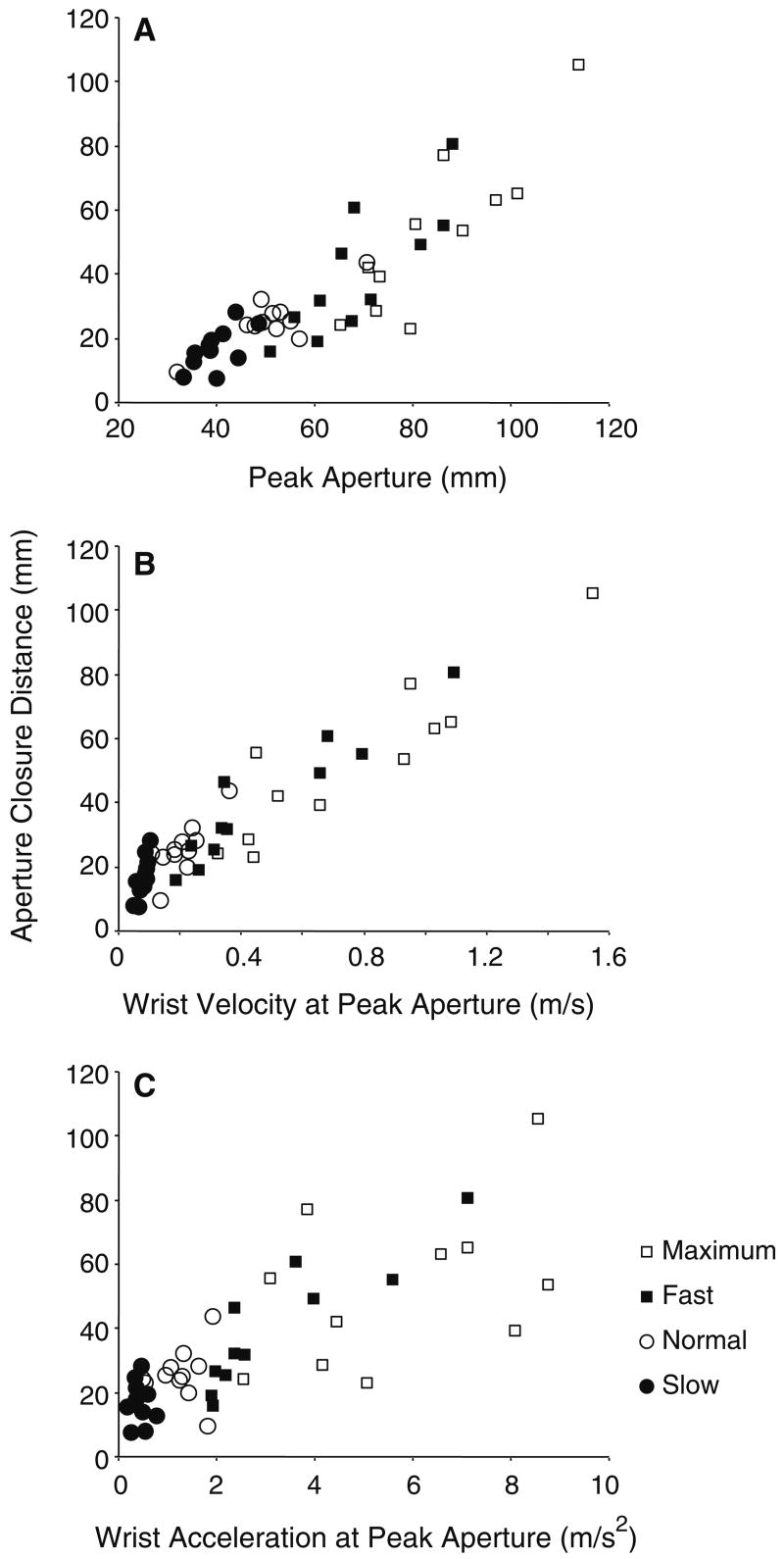
Scatter plots for the aperture closure distance as a function of the amplitude of aperture (a), the wrist velocity (b), and wrist acceleration (c) at the time of maximum aperture. The data from the far target condition are presented. Mean values for each subject are plotted for all speed conditions (slow filled circles; normal open circles; fast filled squares; maximum open squares)
Normalized aperture opening time
Previous studies demonstrated that the maximum aperture occurs at a certain percentage of transport time (Smeets and Brenner 1999). Thus, we further examined the effect of speed on the aperture opening time expressed as a percentage of the transport time (normalized aperture opening time, Fig. 3e, f). The normalized aperture opening time gradually decreased from the slow to the maximum condition. The main effect of speed condition was significant (F(3,30)=15.66, P<0.001). The values of this parameter were significantly greater for the near target condition than those for the far target condition (F(1,10)=36.41, P<0.001). Thus, the maximum aperture occurs at a different percentage of transport time depending on the different speed conditions and the different distance conditions. Furthermore, to assess whether maximum aperture occurred at a fixed time relative to the transport duration, the normalized aperture opening time is plotted against the total transport time in Fig. 4i–l. While the normalized aperture opening time slightly increased for longer total transport time in the slow condition (Fig. 4i, slope = 0.005, r=0.292, P<0.01), it decreased in the maximum condition (Fig. 4l: slope = −0.031, r = −0.439, P<0.001). These features were confirmed in the within-subject data (Table 1). Thus, normalized aperture opening time changed depending on the different total transport times. These findings suggest that the initiation of the aperture closure is not determined primarily based on a fixed percentage of the time spent for the aperture opening in relation to the total movement time.
Additional factors that influence aperture closure initiation
Despite the foregoing analyses, it is still unclear whether the trial-to-trial variance in the aperture closure distance was due to the dependence of this parameter on the speed of transport. One possibility is that the closure distance depended on transport speed within each trial. If the subjects moved slower, they would not initiate aperture closure until the wrist distance to the target was proportionally shorter. This was the case across the range of speed conditions (Figs. 2a, 3a, b).
Based on the control-law hypothesis (see Introduction), we analyzed how aperture closure distance was modulated in relation to other parameters at the time of maximum aperture (and hence the initiation of aperture closure). The relationship between aperture closure distance and maximum aperture amplitude, wrist velocity, and wrist acceleration, was examined. Figure 5a–c depicts the closure distance against each of these parameters for all subjects for all speed conditions to the far target. Data points in the plots are each subject’s mean values. As can be seen in the plots, there is a positive relation between the closure distance and each of these parameters. The aperture closure distance became greater as the maximum aperture amplitude was greater (A), as the wrist velocity at the time of maximum aperture was greater (B), and as the wrist acceleration at the time of maximum aperture was greater (C), which qualitatively supports the above hypothesis. There was also a positive relationship between these three parameters and the aperture closure distance on the trial-to-trial base for each subject, as shown in Figure 6 as an example from one subject.
Fig. 6.
Scatter plots for the aperture closure distance as a function of the amplitude of aperture (a, d), the wrist velocity (b, e), and wrist acceleration (c, f) at the time of maximum aperture. Values from all trials from one subject are plotted for all speed conditions (slow filled circles; normal open circles; fast filled squares; maximum open squares)
The validity of the four models of the law controlling aperture closure initiation across all speed and distance conditions was tested as described in Materials and methods. The corresponding regression analyses were carried out based on all trials across all speed and distance conditions for each subject separately as well as for all subjects taken together. When the analyses were carried out separately for each subject, the average R2 value was similar for Model 3 and Model 4 (Table 2). The average residual error for Model 3 was the smallest among all Models (Table 2). The 4 (model) × 11 (subject) ANOVA revealed that the model main effect was significant (F(3,30)=24.54, P<0.001). The post-hoc analysis confirmed that Model 3 was significantly smaller compared with all other models (P<0.05), indicating that the onset of aperture closure initiation was predicted most precisely in Model 3 which used the distance-to-target threshold depending on other state parameters. This suggests that (1) the control law using a spatial parameter (Model 3) is better than that using a temporal parameter (Model 4), and that (2) the control law using a distance-to-target threshold depending on other state parameters (Model (3) is better than that using a constant distance-to-target threshold.
Table 2.
R2 values and mean (±SE) relative residual errors across subjects for each model
| Based on each subject
|
Based on all subjects
|
|||
|---|---|---|---|---|
| Model | R2 | Residual errors | R2 | Residual errors |
| Model 1: constant ap. closure distance | – | 0.619±0.025 | – | 0.664±0.021 |
| Model 2: constant ap. opening time | – | 0.872±0.023 | – | 0.879±0.022 |
| Model 3: variable ap. closure distance | 0.65 | 0.248±0.008 | 0.74 | 0.289±0.009 |
| Model 4: variable ap. opening time | 0.62 | 0.481±0.014 | 0.50 | 0.584±0.017 |
When the foregoing analyses were carried out based on all subjects, the average R2 value became much higher for Model 3 (0.74) than for Model 4 (0.50). The residual errors obtained based on each subject from Model 3 were compared with those based on all subjects from Model 3 (Table 2) in order to determine whether the same control law can fit all subjects (which one can expect based on the parameter relationships illustrated in Fig. 5). The 2 (calculation method) × 11 (subjects) ANOVA revealed that the average residual error based on each subject was slightly but significantly smaller than those based on all subjects (F(1,858)=44.85, P<0.001). However, as can be seen in Table 2, the magnitude of difference (0.248 vs. 0.289) was much smaller than the differences between Model 3 and each of other models, such as Model 4 (0.481) that used the aperture opening time threshold. This small magnitude of difference indicates that the control law among subjects variability is small, suggesting that Model 3 also works generally across subjects. This result fits well with the results illustrated in Fig. 5. Since the variability of a certain parameters across all subjects is considerably greater than the variability within an individual subject, it is possible that the slight increase in residual errors was due to the violation of relationship linearity assumption within the greater span.
Discussion
The present study was designed to investigate the dependence of the aperture closure initiation on movement parameters across a wide range of speed manipulations. We found that the aperture closure distance increased with the speed of the transport movement across different speed conditions (Fig. 3a, b). The increase of aperture closure distance for faster transport movements apparently was necessary to allow for extra time before touching the object. On the other hand, if the aperture closure movement were carried out fast enough to compensate for the faster transport movement, the aperture closure distance would have been consistent across different speed conditions instead of being gradually lengthened as transport speed was increased. Indeed, the aperture closure becomes faster for the faster speed conditions (Fig. 1d). However, this modulation of the aperture closure speed was apparently not sufficient to keep aperture closure distance invariant across all transport speed conditions.
The observed dependency of aperture closure distance on the speed of transport may seem to contradict with the results of another study (Wang and Stelmach 2001), where no significant change in aperture closure distance with the movement speed was found. This discrepancy possibly stems from the difference in speed manipulation ranges between the two studies. Mean peak wrist velocity ranged from 195 mm/s (slow condition) to 880 mm/s (as fast as possible condition) in the present study, while that of the Wang and Stelmach study ranged from 428 mm/s (comfortable speed condition) to 628 mm/s (as fast as possible condition). Furthermore, even though both studies used the “comfortable” and “as fast as possible” instructions, the difference in peak velocity between the conditions with these instructions was more than two-fold in the current study, whereas it was only about 50% in the previous study. Thus, due to the small range of transport speed manipulations as well as the small difference in transport speed between the conditions of the two instructions, the effect of speed conditions on the aperture closure distance was likely minimized in the previous study. Additionally, the previous study included a condition with strenuous accuracy requirements and a condition with trunk motion involvement during prehensile movements, including these conditions might have reduced the sensitivity of the closure distance measure to speed manipulations.
We found that aperture closure initiation significantly varied with transport speed but did not vary with transport distance. The closure distance was approximately constant across all transport distance variations within a certain transport-speed condition (Fig. 4, Table 1), which is consistent to previous studies (Alberts et al. 2000, 2002; Rand and Stelmach 2005; Rand et al. 2004; Wang and Stelmach 1998, 2001). This suggests that spatial information on the distance from the hand to the object plays a dominant role in triggering the aperture closure. By generalizing this idea, we have formulated a hypothesis that the initiation of aperture closure is controlled based on a specific function arguments of which include observable parameters of the moving arm and its relationship with the target object (see Materials and methods). The behavioral results showed that the aperture closure distance depended on the hand velocity, peak aperture and hand acceleration. This dependence was observed not only across the subjects (for parameter mean values, Fig. 5), but also across trials, for an individual subject (Fig. 6). To verify the above hypothesis, we fit our data into four different linearized models of the control law and statistically compared the corresponding residual errors. From the fact that Model 3 is significantly more accurate than each of the other three models is, two main conclusions can be made. First, aperture closure initiation is based predominantly on spatial parameters of the movement, rather than on hand transport timing. Second, making a decision to start closing the aperture, besides being based on the hand’s distance to the target, significantly involves other state parameters, namely hand velocity, grip aperture, and hand acceleration.
The high R2 values and relatively low residual error values of Model 3 indicate the existence of statistically significant invariance of the corresponding control law with respect to transport speed and overall transport distance to target. Furthermore, it appears that the same model can accurately describe the control law employed by all participating subjects. These results are fully consistent with data from our previous study in which we found that the control law related to grasp initiation is similar even between healthy controls and Parkinson patients (Rand et al. 2006). Thus, the state of arm reach (velocity and acceleration) and state of grasp (aperture amplitude) are likely taken into account by the CNS in order to control the initiation of the aperture closure. To employ this control strategy, subjects likely utilize proprioceptive information regarding arm velocity and acceleration as well as finger grip. Previous studies have demonstrated that proprioceptive information is necessary for the control of reach-to-grasp movements (Gentilucci et al. 1994; Jeannerod 1986).
Movement variability is caused by many factors, such as perception noise, planning noise, movement execution noise, etc. (van Beers et al. 2004). Establishing a model that describes the control of aperture closure initiation and applying it to the current data is desirable to identify the source of variability. The results of the present study provide a constructive approach to identifying the main parameters based on which a decision to initiated aperture closure is made during the movement. However, the functional architecture of the movement control system implementing the corresponding control law remains largely unclear. Several models of reach-to-grasp movements have been developed. For example, the model by Hoff and Arbib (1993) describes the kinematics of hand transport and grasping in a manner that these two components are temporally coordinated, based on an assumption that the aperture closure starts at a moment that corresponds to a consistent aperture closure time (a constant enclosure time model). Our experimental results appear to contradict that assumption.
The existence of a specific control law indicated by the results of this study is generally consistent with modeling movement control as optimal with respect to a specific optimality criterion, an approach that recently has gained much popularity. A digit model proposed by Smeets and Brenner (1999) is based on an idea that the thumb and index finger are independently controlled based on the minimum-jerk model (Flash and Hogan 1985) and move independently to final positions of an object being grasped perpendicularly to its surface. A model by Rosenbaum et al. (2001) that finds an arm-and-hand goal posture, subsequently finds a trajectory in arm–hand posture space so that a collisions with an object being grasped would be avoided. While the Hoff and Arbib model specifies aperture closure initiation, the models by Smeets and Brenner and Rosenbaum et al. achieve the aperture closure through a constraint of minimum jerk or movement cost reduction. Testing whether these and other models can reproduce present experimental data would be useful to better understand what optimality criterion is used by the CNS to develop a control law for the initiation of aperture closure.
Acknowledgments
This research was supported by grants from NINDS NS 39352 and 40266. We are grateful to Dr. Y.P. Shimansky for designing some computer programs and for valuable comments on this study.
References
- Alberts JL, Saling M, Alder CH, Stelmach GE. Disruptions in the reach-to-grasp actions of Parkinson’s patients. Exp Brain Res. 2000;134:353–362. doi: 10.1007/s002210000468. [DOI] [PubMed] [Google Scholar]
- Alberts JL, Saling M, Stelmach GE. Alterations in transport path differentially affect temporal and spatial movement parameters. Exp Brain Res. 2002;143:417–425. doi: 10.1007/s00221-002-1005-0. [DOI] [PubMed] [Google Scholar]
- Bootsma RJ, Van Wieringen PCW. Spatio-temporal organization of natural prehension. Hum Mov Sci. 1992;11:205–215. [Google Scholar]
- Castiello U, Bennett KMB, Bonfiglioli C, Peppard RF. The reach-to-grasp movement in Parkinson’s disease before and after dopaminergic medication. Neuropsychologia. 2000;38:46–59. doi: 10.1016/s0028-3932(99)00049-4. [DOI] [PubMed] [Google Scholar]
- Gentilucci M, Chie S, Scarpa M, Castiello U. Temporal coupling between transport and grasp components during prehension movements. Effects of visual perturbation. Behav Brain Res. 1992;47:71–82. doi: 10.1016/s0166-4328(05)80253-0. [DOI] [PubMed] [Google Scholar]
- Gentilucci M, Toni I, Chie S, Pavesi G. The role of proprioception in the control of prehension movements: a kinematic study in a peripherally deafferented patients and in normal subjects. Exp Brain Res. 1994;99:483–500. doi: 10.1007/BF00228985. [DOI] [PubMed] [Google Scholar]
- Flash T, Hogan N. The coordination of arm movements: an experimentally confirmed mathematical model. J Neurosci. 1985;5:1688–1703. doi: 10.1523/JNEUROSCI.05-07-01688.1985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haggard P, Wing AM. Remote responses to perturbation in human prehension. Neurosci Lett. 1991;122:103–108. doi: 10.1016/0304-3940(91)90204-7. [DOI] [PubMed] [Google Scholar]
- Haggard P, Wing AM. Coordinated responses following mechanical perturbation of the arm during prehension. Exp Brain Res. 1995;102:483–494. doi: 10.1007/BF00230652. [DOI] [PubMed] [Google Scholar]
- Haggard P, Wing A. Coordination of hand aperture with the spatial path of hand transport. Exp Brain Res. 1998;118:286–292. doi: 10.1007/s002210050283. [DOI] [PubMed] [Google Scholar]
- Hoff B, Arbib MA. Models of trajectory formation and temporal interaction of reach and grasp. J Mot Behav. 1993;25:175–192. doi: 10.1080/00222895.1993.9942048. [DOI] [PubMed] [Google Scholar]
- Jeannerod M. The formation of finger grip during prehension: a cortically mediated visuomotor pattern. Behav Brain Res. 1986;19:99–116. doi: 10.1016/0166-4328(86)90008-2. [DOI] [PubMed] [Google Scholar]
- Jeanerrod M. Visuomotor channels: their integration in goal-directed prehension. Hum Mov Sci. 1999;18:201–218. [Google Scholar]
- Jeannerod M, Arbib MA, Rizzolatti G, Sakata H. Grasping objects: the cortical meachisms of visuomotor transformation. Trends Neurosci. 1995;18:314–320. [PubMed] [Google Scholar]
- Marteniuk GG, Leavitt JL, MacKenzie CL, Athenes S. Functional relationships between grasp and transport components in a prehension task. Hum Mov Sci. 1990;9:149–176. [Google Scholar]
- Paulignan Y, Jeannerod M, MacKenzie C, Marteniuk RG. Selective perturbation of visual input during prehension movements. 2. The effects of changing object size. Exp Brain Res. 1991a;87:407–420. doi: 10.1007/BF00231858. [DOI] [PubMed] [Google Scholar]
- Paulignan Y, MacKenzie C, Marteniuk R, Jeannerod M. Selective perturbation of visual input during prehension movements: 1. The effects of changing object position. Exp Brain Res. 1991b;83:502–512. doi: 10.1007/BF00229827. [DOI] [PubMed] [Google Scholar]
- Rand MK, Stelmach GE. Effect of orienting the finger opposition space on the control of reach-to-grasp movements. J Mot Behav. 2005;37:65–78. doi: 10.3200/JMBR.37.1.65-78. [DOI] [PubMed] [Google Scholar]
- Rand MK, Shimansky Y, Stelmach GE, Bracha V, Bloedel JR. Effects of accuracy constraints on reach-to-grasp movements in cerebellar patients. Exp Brain Res. 2000;135:179–188. doi: 10.1007/s002210000528. [DOI] [PubMed] [Google Scholar]
- Rand MK, Shimansky Y, Stelmach GE, Bloedel JR. Adaptation of reach-to-grasp movement in response to force perturbations. Exp Brain Res. 2004;154:50–65. doi: 10.1007/s00221-003-1637-8. [DOI] [PubMed] [Google Scholar]
- Rand MK, Smiley-Oyen AL, Shimansky YP, Bloedel JR, Stelmach GE. Control of aperture closure during reach-to-grasp movements in Parkinson’s disease. Exp Brain Res. 2006;168:131–142. doi: 10.1007/s00221-005-0073-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenbaum DA, Neulenbroek RJ, Vaughan J, Jansen C. Posture-based motion planning: applications to grasping. Psychol Rev. 2001;108:709–734. doi: 10.1037/0033-295x.108.4.709. [DOI] [PubMed] [Google Scholar]
- Saling M, Alberts J, Stelmach GE, Bloedel JR. Reach-to-grasp movements during obstacle avoidance. Exp Brain Res. 1998;118:251–258. doi: 10.1007/s002210050279. [DOI] [PubMed] [Google Scholar]
- Shimansky YP, Kang T, He J. A novel model of motor learning capable of developing an optimal movement trajectory on-line from scratch. Biol Cybern. 2004;90:133–145. doi: 10.1007/s00422-003-0452-4. [DOI] [PubMed] [Google Scholar]
- Smeets JBJ, Brenner E. A new view on grasping. Motor Control. 1999;3:237–271. doi: 10.1123/mcj.3.3.237. [DOI] [PubMed] [Google Scholar]
- Squire LM, Rand MK, Stelmach GE. Effect of speed manipulation in the control of aperture closure during reach-to-grasp movements. Soc Neruosci Abstra. 2004;30:653.3. doi: 10.1007/s00221-006-0423-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Teasdale N, Bard C, Fleury M, Young D, Proteau L. Determining movement onsets from temporal series. J Mot Behav. 1993;25:97–106. doi: 10.1080/00222895.1993.9941644. [DOI] [PubMed] [Google Scholar]
- Van Beers RJ, Haggard P, Wolpert DM. The role of execution noise in movement variability. J Neurophysiol. 2004;91:1050–1063. doi: 10.1152/jn.00652.2003. [DOI] [PubMed] [Google Scholar]
- Wallace SA, Weeks DL. Temporal constraints in the control of prehensile movement. J Mot Behav. 1988;20:81–105. doi: 10.1080/00222895.1988.10735435. [DOI] [PubMed] [Google Scholar]
- Wallace SA, Weeks DL, Kelso JAS. Temporal constraints in reaching and grasping behavior. Hum Mov Sci. 1990;9:69–93. [Google Scholar]
- Wang J, Stelmach GE. Coordination among the body segments during reach-to-grasp action involving the trunk. Exp Brain Res. 1998;123:346–350. doi: 10.1007/s002210050578. [DOI] [PubMed] [Google Scholar]
- Wang J, Stelmach GE. Spatial and temporal control of trunk-assisted prehensile actions. Exp Brain Res. 2001;136:231–240. doi: 10.1007/s002210000572. [DOI] [PubMed] [Google Scholar]
- Watson MK, Jakobson LS. Time to contract and the control of manual prehension. Exp Brain Res. 1997;117:273–280. doi: 10.1007/s002210050222. [DOI] [PubMed] [Google Scholar]
- Wing AM, Turton A, Fraser C. Grasp size and accuracy of approach in reaching. J Mot Behav. 1986;18:245–260. doi: 10.1080/00222895.1986.10735380. [DOI] [PubMed] [Google Scholar]
- Zaal FTJM, Bootsma RJ, Van Wieringen PCW. Coordination in prehension. Information-based coupling of reaching and grasping. Exp Brain Res. 1998;119:427–435. doi: 10.1007/s002210050358. [DOI] [PubMed] [Google Scholar]