The Length of Henle Fibers in the Human Retina and a Model of Ganglion Receptive Field Density in the Visual Field

Abstract

An experimental study of lateral displacement of ganglion cells (GCs) from foveal cones in six human retinas is reported. At 406–675 μm in length, as measured in radially oriented cross-sections, Henle fibers are substantially longer than previously reported. However, a new theoretical model indicates that the discrepancies in these reports are mainly due to meridional differences. The model takes into account the effects of optical degradation and peripheral ON/OFF asymmetry and predicts a central GC:cone ratio of 2.24:1. It provides estimates of cumulative counts and GC receptive field density at 0°–30° along the principal meridians of the visual field.

Introduction

The densities of retinal ganglion cells (GC), their lateral displacements, and functional projection into visual space have been the subject of several contradictory reports (Curcio and Allen, 1990; Sjöstrand, Olsson, Popovic, and Conradi, 1999a; Sjöstrand, Popovic, Conradi and Marshal, 1999b). Early estimates (Drasdo, 1977; Drasdo, 1989) of retinal GC receptive field density per solid degree (D_gcrf) are now considered to be founded on outmoded principles and inadequate data, but following the study of Curcio and Allen (1990) different and more accurate estimates of D_gcrf can be obtained across most of the visual field by means of a suitable wide angle schematic eye. A problem arises, however, within a central part of the visual field, extending to almost 15° from the point of fixation. Here, receptive fields are displaced from the position of their GCs, mainly due to the length of the laterally connecting Henle fibers and to a smaller extent, to the oblique pathway through the bipolar cells (Schein, 1988; Curcio and Allen, 1990). Within this zone of displacement there are many problems in estimating D_gcrf from purely histological data (Schein, 1988; Curcio and Allen, 1990; Azopardi and Cowey, 1996; Sjöstrand, Olsson, Popovic, and Conradi, 1999a), and studies on humans and other primates show a marked variability in findings. Sampling density of foveal cones is known with reasonable certainty (Curcio, Millican, Allen and Kalina, 1993), and the disparity in findings on D_gcrf is therefore evident from the reported ratios of GCs to foveal cones (Table 1).

TABLE 1.

Reported ratios of effective ganglion cells to foveal cones.

Author	ratio
Polyak (1941)	1:1
Missotten (1974)	0.9:1
Curcio and Allen (1990)	(2–3): 1
Sjöstrand, Conradi, & Klaren (1994)	(2.7–3.4): 1
Sjöstrand, Olsen, Popovic, and Conradi, (1999a)	2.93:1
In other primates
Perry & Cowey (1988)a	2:1
Schein (1988)b	2:1
Wässle, Grünert, Röhrenbeck, & Boycott, (1990)b	(3.34–4):1
Klug, Schein, Masarachia, Sterling, & Tsukamoto (1991)c	2.44:1
Wilder, Grünert, Lee, & Martin (1996)d	2.4 – 4.2): 1
Goodchild, Ghosh, & Martin (1996)c,d	>2:1
Ahmad, Klug, Herr, Sterling, & Schein (2003)c	2.6:1

Species Key

^aMacaca mulatto

^bMacaca fascicularis

^cMacaque monkey

^dCallithrix jacchus.

Curcio and Allen (1990) provided comprehensive data on GC density from six human retinas. They considered that GC displacements were probably larger than previously reported and that the peak values for Henle fibers might exceed 600 μm with between two and three GCs per foveal cone. However, after studies mainly on the superior and inferior vertical hemi-meridians of two human eyes and on the inferior hemi-meridian of one eye, Sjöstrand et al (1999a,b) reported substantially higher GC densities than Curcio and Allen along the vertical meridian and measured displacements which were much shorter than predicted, peaking at approximately 370 μm corresponding to a Henle fiber length of 320 μm. They argued that their measurements implied that the GC densities reported by Curcio and Allen (1990) would be too low to be compatible with an acceptable GC:cone ratio at the fovea. These apparently conflicting observations require careful consideration, and we therefore carried out further studies on GC displacements, length of Henle fibers and theoretical modeling of the distribution of D_gcrf in the human visual field. A list of abbreviations used in our study is given in Table 2.

TABLE 2.

Abbreviations and subscript notation.

Abbreviations
Cpd	cycles per degree
DA	displaced amacrine cell
E	angle of eccentricity in degrees
E2	E at which a spatial threshold is twice the foveal value
F	spatial frequency in cpd
GC	ganglion cell
L&M	long and medium wavelength sensitive
MAR	minimum angle of resolution (in degrees)
R	short notation for MAR
D	density per solid degree
Subscripts
gc	relating to ganglion cells
E	relating to an eccentric visual angle
m	relating to midget ganglion cells
n	relating to neural acuity or resolution
o	relating to resolution of the optics of the eye
rf	relating to receptive fields
v	relating to visual resolution
0	relating to foveal vision, when E = 0

Methods

Histology

Lateral displacement of GCs were measured in radially oriented cross-sections of human retina, using methods adapted from those of Schein (1988) and Wässle (1989). Six retinas obtained from Eye Bank donors within 3 hr of death (Table 3) were fixed by immersion in 4% paraformaldehyde and 0.5% glutaraldehyde in 0.1M phosphate buffer following corneal excision. All eyes were fellows of eyes whose distribution of photoreceptors, GCs, or both had been previously mapped (Curcio & Allen, 1990, Curcio & Drucker, 1993, Curcio, Sloan, Kalina & Hendrickson, 1990). A horizontally oriented retinal strip containing the fovea and optic disk and the underlying retinal pigment epithelium/choroid were dissected free of the sclera, dehydrated through ascending alcohols, and embedded in glycol methacrylate (JB-4 kit, Polysciences). Chorioretinal strips were held flat against a glass slide by a tissue paper wrapper during dehydration and infiltration. Tissue volume changes were assessed by comparing tissue area before dehydration and after polymerization. Serial 2 μm sections cut parallel to the horizontal meridian through the foveola were stained with methylene blue - azure II.

TABLE 3.

Eyes studied and displacement lengths (measured and fit).

Age	36	37	68	74	82*	82		Model fit
Gender	M	F	M	M	M	M
	NASAL						Mean	SD	Fit	CI
FH
Maximum	0.613	0.536	0.539	0.675	0.541	0.565	0.578	0.056
Ecc, mm	1.318	1.232	1.020	1.136	0.967	1.345	1.170	0.156
BP+GC
Maximum	0.103	0.070	0.130	0.153	0.110	0.125	0.115	0.028	n.a.
Ecc, mm	1.041	0.862	1.090	0.566	0.380	1.017	0.826	0.290
FH+(BP+GC)
Maximum	0.679	0.577	0.642	0.777	0.587	0.641	0.650	0.073	0.605	0.017
Ecc, mm	1.134	1.160	1.020	1.018	0.967	1.345	1.107	0.138	1.077
	TEMPORAL						Mean	SD	Fit	CI
FH
Maximum	0.632	0.541	0.406	0.664	0.491	0.486	0.537	0.097
Ecc, mm	1.349	1.237	1.032	1.440	0.850	0.995	1.150	0.228
BP+GC
Maximum	0.088	0.077	0.123	0.165	0.111	0.119	0.114	0.031	n.a.
Ecc, mm	0.679	0.644	0.703	0.546	0.292	0.946	0.635	0.214
FH+(BP+GC)
Maximum	0.699	0.570	0.528	0.713	0.502	0.594	0.601	0.088	0.605	0.017
Ecc, mm	1.349	1.648	1.032	1.253	0.850	0.946	1.180	0.296	1.077

Notes

FH, fibers of Henle

BP, bipolar cells

GC, ganglion cells

^*, shown in Figure 1

Ecc, eccentricity in the ganglion cell layer

SD, standard deviation

CI, confidence interval

One section as close as possible to the thinnest part of the foveal center was selected for analysis from each eye (Fig. 1A). Tissue was photographed using a 60×, 1.4 N.A. oil immersion objective on a Nikon Optiphot 2 (Nikon, Melville NY), either an orange or light red filter (Wratten 15 and 23A, respectively), and either Plus-X or Technical Pan film (Kodak). Photomontages from the foveal center to the optic disk and an equivalent distance in the temporal direction were assembled at a magnification of 520x. At regular intervals along the external limiting membrane (ELM), a line was drawn parallel with photoreceptor cell bodies and inner fibers through the outer nuclear layer, into Henle fiber layer, and ending at the layer of cone pedicles (red arrows, Fig. 1B,C). No one fiber was traced in its entirety, but rather a path was inferred through an aggregate of fiber cross-sections that were long and longitudinally oriented when originating in the foveal center and short and oblique in the parafovea (Fig. 1F). The projected length of this line along the ELM constitutes the receptoral component of lateral displacement (right-most yellow arrow pair, Fig. 1B,C). The continuation of this line from the layer of pedicles through the inner nuclear and GC layers (green arrows, Fig. 1D,E) was projected onto the ELM to yield the post-receptoral component of lateral displacement (left-most yellow arrow pair, Fig. 1B,C). Lengths and distances were corrected for shrinkage. Eccentricity from the foveal center was expressed as eccentricity in the GC layer. Total displacement (receptoral and post-receptoral components combined) along the nasal and temporal horizontal meridian for each eye, as well as for data pooled from 6 eyes, were fit piecewise with cubic splines. Data from two additional retinas were not included in this analysis. One lacked a unique maximum for its displacement function. Another had maximal receptoral displacement of 0.392 mm at a GC eccentricity of 1.42 mm and a maximal post-receptoral displacement of 0.066 mm at a GC eccentricity of 0.215 mm. Relative to other eyes (see Results), this pattern was considered anomalous. Fig. 1 was created from images captured using a Nikon Eclipse 80i microscope, a 40X plan apochromat objective, and a Retiga 2000R Fast CCD camera (Q Imaging, Burnaby BC) and assembled with Photoshop CS.

Figure 1.

Histological section, showing the receptoral and post-receptoral components of GC displacement. Glycol methacrylate section, stained methylene blue - azure II, includes the fovea and nasal parafovea from an 82 yr old male (second donor listed in Table 3). A. Low magnification view created by photomontage of multiple higher magnification images. Sites illustrated in panels B,D and C,E are indicated. Bar, located at fovea, 200 μm. B. Site at 1.87 mm eccentricity in the layer of inner segments. Henle fiber length (as traced through zone delimited by red arrowheads) is 0.21 mm. Post-receptoral replacement (as traced through zone delimited by green arrowheads) is zero. The two ends of the displacements were projected onto the external limiting membrane (yellow lines), and lengths were measured along this membrane between the yellow arrows. Bar, 100 μm. C. Site at 0.52 mm eccentricity in the layer of inner segments. Henle fiber is 0.52 mm. Post-receptoral replacement is 0.073 mm, for a total of 0.595 mm. Bar, 100 μm. D, E. Detail of sites shown in B, C, respectively. Contrast in Henle fiber layer is selectively enhanced for illustrative clarity. ONL, outer nuclear layer; HF, Henle fibers; INL, inner nuclear layer; GCL, ganglion cell layer. Inner segment layer is just barely visible at top of panel E. Bars, 20 μm. F. Schematic of Henle fiber layer, viewed from vitreal aspect. The appearance of Henle fibers at section levels pf (parafovea) and f (foveal center) are shown. Fibers at f are mostly long, whereas in parafoveal sections, fibers are shorter. Cross-sectional profiles of those directly superior (or inferior) to the foveal center are circular.

Results

As previously shown, GCs first appear at 150–200 μm from the foveal center (Curcio & Allen, 1990), so total displacement for these close-in cells is 150–200 μm. In eyes sectioned for this study, total displacement declined to zero at the optic nerve head (~3.4 mm nasal to foveal center) but was still detectable up to 4.5 mm temporal to the foveal center. The eccentricity-dependence of lateral displacement and its two components is shown for one representative retina in Fig. 2, and the location of maximal displacements is shown for all 6 retinas in Table 3. In Fig. 2, displacement increases to a maximum of 587 μm for GCs at 0.98 mm nasal to the foveal center and 491 μm for GC at 0.85 mm temporal. Of the receptoral and post-receptoral components of displacement, Henle fiber length is by far the greater contributor. In Fig. 2, maximal post-receptoral displacement is 110 μm at 0.38 mm nasal and 111 μm at 0.292 mm temporal, in both cases ~20% of the total displacement. In general, post-receptoral displacement both peaked and declined closer to the foveal center than receptoral displacement. Considering all retinas, the maximum total displacement of GC was 577–777 μm at 1.02–1.35 mm nasal and 502–713 μm at 0.85–1.65 mm temporal (Table 3). The maximum receptoral displacement was 536–675 μm at 0.97–1.35 mm nasal and 406–632 μm at 0.85–1.349 mm temporal. This variability was unrelated to age, and by inference, macular GC density, which declines ~25% in the elderly (Curcio & Drucker, 1993). Fig. 3 shows the best-fit curve for total lateral displacement for 6 retinas pooled based on parameters listed in Table 4. In this model curve, the maximum total displacement is 650 μm at 1.077 mm nasal and 542 μm at 1.135 mm temporal, very similar to means computed for the 6 eyes (Table 3).

Figure 2.

Lateral displacement of GC along the horizontal meridian, including receptoral (fibers of Henle, FH), post-receptoral (bipolar-GC processes, BP-GC) components, and total displacement (Total). Displacements measured for this 82 yr old male donor (second listed in Table 4) were closest to the curve fit to total displacement for all 6 retinas (Fig. 3). The location of a GC nasal or temporal to the foveal center is shown as eccentricity in the GC layer. The distance to a cone inner segment projected along the external limiting membrane (displacement) is shown as a positive value along the y-axis. The bar denotes the approximate position of the optic disk. Lengths are corrected for shrinkage.

Figure 3.

Total displacement along the horizontal meridian pooled from 6 human retinas. The coefficients of the best fitting cubic splines (solid lines) for nasal (r² = 0.89) and temporal (r² = 0.86) horizontal meridian are given in Table 4. Confidence intervals are shown as dashed lines.

TABLE 4.

Coefficients of piecewise cubic splines fit to pooled total displacements.

Nasal
xi	xi+1	ai	bi	ci	di
0.0000	0.6243	−4.3774	1.1856	0.6898	0.0000
0.6243	2.6231	1.2022	−1.5470	0.5770	0.4841
2.6231	3.9632	0.0000	0.0000	−0.1098	0.1470
Temporal
xi	xi+1	ai	bi	ci	di
0.0000	1.2337	−0.1030	−0.7650	0.9336	0.0000
1.2337	2.5360	1.3537	−0.8921	−0.0885	0.5374
2.5360	5.0000	0.0000	0.0000	−0.0689	0.1639

Lateral displacement at a location in the ganglion cell layer (GCL) is calculated using the coefficients a_i, b_i, c_i, and d_i and a temporary variable T as follows:

For an eccentricity in the ganglion cell layer (ecc_GCL) falling between x_i and x_i+1,

$$\begin{array}{c}\text{T}={\text{ecc}}_{\text{GCL}}-{\text{x}}_{\text{i}}\\ \text{Displacement}=(({\text{a}}_{\text{i}}/6·\text{T}+{\text{b}}_{\text{i}}/2)·\text{T}+{\text{c}}_{\text{i}})·\text{T}+{\text{d}}_{\text{i}}\end{array}$$

Eccentricity in the layer of inner segments (ecc_IS) = ecc_GCL − displacement

Discussion

Displacement and Henle fiber length

Our current mean measurements of 626 μm total displacement and 558 μm Henle fiber length differ substantially from previously available data suggesting that Henle fibers were maximally 280–400 μm in length (Conradi & Sjöstrand, 1993, Sjöstrand, Conradi & Klaren, 1994, Sjöstrand, Olsson, Popovic & Conradi, 1999a, Sjöstrand, Popovic, Conradi & Marshall, 1999b). Some of this difference could be attributable to technical differences in tissue preparation that raise the possibility of Sjöstrand et al missing the foveal center. Whereas we serially sectioned a single large tissue piece, these investigators divided the macula (from rapidly preserved, surgically excised human globes) into small blocks and did not examine serial sections (Conradi & Sjöstrand, 1993, Marshall, Hamilton & Bird, 1975). Indeed, abundant cone nuclei in the outer nuclear layer and/or many short Henle fiber cross-sections (see Fig. 2 B,D and 5B of Marshall et al. (1975) and Fig. 2A, 5A of Conradi & Sjöstrand (1993)) are consistent with this interpretation. These concerns are ameliorated in the most recent report by this group (Popovic & Sjöstrand, 2005), published while our manuscript was written and reviewed. Displacement lengths were determined from serial 1 μm sections through 2.2° × 33.7° fovea-containing strips in newly processed eyes. These fiber lengths, not yet reported, should prove highly informative.

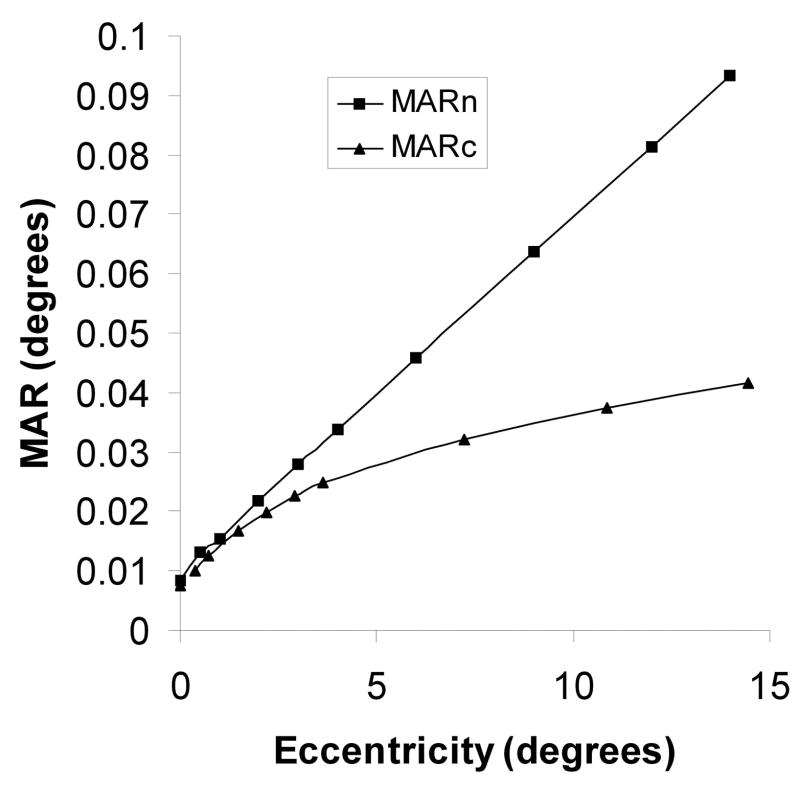
Figure 5.

The neural minimum angle of resolution (MAR_n) in degrees of the eye according to the model. This is assumed to coincide with the MAR of the OFF-midget ganglion cell mosaic. Also shown is the MAR of the cone mosaic (MAR_c), based on the data of Curcio, Sloan, Kalina and Hendrickson (1990). Data are averages of principal meridians.

With regard to the accuracy of our measurements, some plausible sources of error, such as missing the foveal center (see Fig. 1F) or failure to correct for shrinkage would tend to make the measured Henle fiber lengths shorter rather than longer, so it is possible that actual lengths are greater than our current observations. However, we acknowledge that determining Henle fiber length in radial sections offers particular challenges requiring sections with thickness comparable to the fiber diameter, optimum radial orientation, good staining contrast, and localization in the very central foveola. Fiber orientation does not always point to a geometric center or the thinnest part of the foveal center, and the effect of no or negative displacement on effective GC density has been discussed (Wässle, Grünert, Röhrenbeck & Boycott, 1989). We did not see inwardly traveling fibers (Wässle, Grünert, Röhrenbeck & Boycott, 1989), but our power to detect them was limited. We did not account for the displaced amacrine cells via specific markers, either in the eyes used for GC counts (in which we estimated that 5% of macular GCL neurons were amacrine cells by morphological criteria) or in the eyes sectioned for Henle fibers, but such information would not have influenced the fiber lengths. Another limitation is use of an embedding technique that flattened the naturally curved retina, potentially introducing distortions into tissue. Flattening tissue during embedding would not lengthen Henle fibers appreciably, as the difference in the radius of curvature at the inner side of outer nuclear layer and the outer side of the inner nuclear layer is <1%. Folds and kinks, which non-uniformly affect overall tissue geometry and the morphology of individual cells, were eschewed (Fig. 1a). The accuracy of human fiber length measurements could be refined in the future with either whole mounted retinas and markers for Müller cells (e.g., glutamine synthetase (Nishikawa & Tamai, 2001), and GC (e.g., Brn3A (Li, Presley, Zhang, Dashti, Chung, Medeiros, Guidry & Curcio, 2005)) or fixation, histologic, and imaging procedures optimized for quantifying foveal morphology in radially oriented sections (Leung, Sandstrom, Zucker, Neuringer & Snodderly, 2004).

The mean peak displacement reported by Sjöstrand et al (1999b) was 370 μm averaged for the vertical meridian, 41% less than our mean displacement of 626 μm for the horizontal meridian. It is not yet clear if an anatomical meridional difference in displacements contribute to this discrepancy. Studies of the macaque retina do not illuminate this issue, as a difference between the vertical and horizontal meridians was not reported by Schein (1988), but a tendency towards shorter Henle fiber lengths in the vertical meridian was visible in the data of Perry and Cowey (1988). However, in studies on the human retina, Sjöstrand et al (1999a,b) assumed for modeling purposes that data from the vertical meridian were applicable to all meridians. As our displacement study was limited to the horizontal meridian, and the Sjöstrand et al (1999b) data was from the vertical meridian, it was not therefore possible to combine these two datasets to produce a composite model.

Given the incomplete and conflicting data on GC displacement, Henle fiber length, and GC density_, we have employed a theoretical model (see Appendix) to elucidate further the relationships between the different findings. This model of receptive field density in the human central visual field is based on theories of optical degradation, neural sampling, and retinal circuitry combined with histological data. The model takes into account the OFF-dominant nature of the midget system in the periphery (Dacey and Peterson, 1992; Dacey, 1993), provides new estimates of D_gcrf along the major meridians, and estimates of displacements and Henle fiber lengths.

Predictions of the model

The model predicts slightly larger displacements than we measured, but still well within the observed range; some differences are inevitable due to the diverse origins of the consensus data on which it is based. According to the calculation described in the Appendix, the peak displacements averaged for the principal meridians was 637 μm. By repeating this calculation with the appropriate E2 parameters, the displacements for the horizontal and vertical meridians can be estimated separately. These were found to be 715 μm for the horizontal and 545 μm for the vertical meridian (i.e., vertical 24% smaller than horizontal). This difference helps to explain the difference between our mean measured displacement (526 μm) and the 370 μm of Sjöstrand et al (1999a,b), which was 41% smaller than ours. If, as predicted by the model, 24% is the horizontal - vertical meridional difference, then remaining 17% may be due to shrinkage and eye size variation in Sjöstrand et al’s studies. A 17% linear difference is equivalent to about 31% areal difference which, allowing for some variability, could account for the higher GC densities observed by Sjöstrand et al (1999a) in the central retina.

A problem remains beyond 25° in the periphery where Sjöstrand et al (1999a) reported densities more than twice those of Curcio and Allen along the vertical meridian. However, Sjöstrand et al (1999a) found a reducing proportion of displaced amacrine cells at these eccentricities, where an increase would be expected. This possible undercounting of displaced amacrines, in addition to the above-mentioned factors, could explain their high densities of GCs.

The model had densities of 12,469 central foveal cones and 27,930 ganglion cell receptive fields per solid degree. The central foveal GC:cone ratio was therefore 2.24:1. The proportion of L&M midget to all types of GC varied from 89% at the foveal center to 66% at 14.7°. Cumulative counts of receptive fields within a given angle were found to be 37,851 (within 1°); 92,459 (within 2°); 238,148 (within 5°); 414,270 (within 10°); and 540,930 (15°). The predicted values of D_gcrf along the principal meridians are given in Table 5. Several aspects of the model and its predictions require detailed consideration.

TABLE 5.

Ganglion cell receptive field densities in receptive fields/solid degree along the principal meridians of the visual field (0°–15°) according to equation (7) and (15°–30°) from polynomials P₃ – P₆.

Angular Eccentricity (degrees)	NASAL FIELD	TEMPORAL FIELD	SUPERIOR FIELD	INFERIOR FIELD	GENERAL MODEL
0	27930	27930	27930	27930	27930
.25	19238	19438	16514	18528	18608
.5	14368	14614	11273	13518	13613
1	9131	9365	6433	8346	8431
2	4818	4986	3037	4271	4330
5	1561	1633	865	1334	1358
10	549	578	284	460	469
15	279	-	140	232	237
20	146	231	85	136	150
25	93	214	61	102	118
30	59	182	44	77	91

Note: Ganglion cell receptive field densities in receptive fields/solid degree along the principal meridians of the visual field (0°–15°), according to equation (7) and (15°–30°). From polynomials P₃ – P₆

The proportion of midget GCs and the foveal GC: C ratio

The computed GC:cone ratio of 2.24:1 for the center of the fovea was consistent with expectations based on physiological theory. In the central fovea there are no S-cones (Curcio, Allen, Sloan, Leria, Hurley, Klock, and Millam, 1991) or rods (Curcio et al., 1990), and we should expect an absence of small bi-stratified GCs (Blue-ON, Yellow-OFF)(Dacey and Lee, 1994) and S midget GCs (Yellow-ON Blue-OFF)(Klug et al., 2003) and a slightly reduced proportion of parasol GCs (Perry and Cowey 1985; Silveira and Perry, 1991; Grünert, Greferath, Boycott, and Wässle, 1993). We should also expect a reduced proportion of tectally projecting GC at the fovea reported in non-human primates (Perry and Cowey, 1984). A high proportion of foveally projecting GCs must therefore be L&M midget GCs, so the estimate of a 2.24:1 GC:cone ratio for the model appears to be reasonable.

The ratio of 2.24 for the model is significantly lower than the 3–4:1 reported by Wässle, Grünert, Röhrenbeck and Boycott (1990) from studies on a macaque monkey and of approximately 3:1 in the estimates of Sjöstrand et al. (1994, 1999a,b) in humans (Table 1). However, a 3:1 GC:cone ratio is difficult to reconcile with our knowledge of the numbers and types of GC at the fovea. Assuming that there are two midget GCs to each foveal cone, a 3:1 ratio implies that midget GCs would constitute only 67% of ganglion cells projecting to the fovea, a lower percentage than over the retina as a whole. This notion would be counter-intuitive since these cells support high resolution, for which the fovea is specialized. Although high ratios have been reported in some non-human primate studies, it is noteworthy that among the most persuasive studies, Klug et al. (1991) reported a ratio of 2.44:1 without 5% compensation for displaced amacrine cells that would reduce the ratio to 2.32:1. A more detailed report by Ahmad et al. (2003) found a ratio of 2.6:1. Taking all the above factors into account, the estimates from the model reinforced by converging evidence are considered reasonable.

ON/OFF asymmetry

Dacey and Peterson (1992) and Dacey (1993) reported that ON dendritic field sizes were 1.3 times greater in diameter than OFF in midget ganglion cells in the peripheral human retina. Due to close packing of the mosaics, this finding leads to the conclusion that there are only 0.59 ON cells to each OFF cell. Dacey (1993) could not demonstrate ON/OFF asymmetry within 1.5 mm eccentricity (5°), but described structural changes within the retina with dendritic field sizes increasing at about 1.8 mm eccentricity, possibly indicating the beginning of a progressive development of asymmetry. Beyond this point, asymmetry tended to increase, becoming relatively constant beyond 7 mm (25°) eccentricity. Other studies have indicated equal numbers of ON and OFF midget GCs in the parafoveal and foveal retina of human or macaque (Kolb and Dekorver, 1991; Ahmad, et al., 2003). It is difficult to avoid this conclusion if midget GC receptive field centers coincide with those of single cones in and near to the fovea. Interestingly, ON/OFF asymmetry in the parasol (OFF dominated) and S-cone pathway (ON dominated) GCs has been observed both in or near the fovea and in the periphery (Dacey and Peterson, 1992; Ahmad et al. 2003, Klug et al. 2003). In the model, the midget system is presumed to be exceptional in being ON/OFF symmetric (k=2) for central vision within about 5° eccentricity, having marked asymmetry (k= 1.59) for peripheral vision >25° and a progressively increasing asymmetry across the transitional zone. It is useful to consider the functional implications of this arrangement.

Functional significance of ON/OFF asymmetry

Although ON/OFF asymmetry in the periphery may achieve a reduction in neural channels, for a given visual acuity this is evidently not so in central vision. The need for this change in the value of k (see Appendix) in central versus peripheral vision may be related to the low contrast sensitivity of the midget system (Croner and Kaplan, 1995) and the effect of optical degradation in reducing retinal image contrast. At 42 cpd, the limit of resolution at the foveal center, optical degradation reduces the modulation transfer to well below 10%, depending on the pupil size (see Equation 6 of Deeley, Drasdo and Charman, 1991). Within 5° of the foveal center (Fig. 4), resolution improves when retinal image contrast is increased (Green, 1970). Evidently, therefore, this region depends not only on neural sampling but also on neural contrast sensitivity that is demonstrably higher with coupled ON and OFF channels (Schiller, Sandell and Maunsell, 1986). We should not expect ON/OFF asymmetry inside 5°. However, at 25° where R_o in the model is relatively small (Jennings and Charman, 1981, Charman 1991) compared to R_n, in the model, the asymmetry would not be expected to reduce resolution for high contrast gratings which is presumed to depend on the OFF-midget system. According to the logic of this argument, k could not drop precipitously at 5° (because resolution would be compromised), but rather, would change gradually. This arrangement is therefore consistent with both the psychophysical argument and the anatomical findings described above.

Figure 4.

Visual acuity and neural acuity in central vision, according to the model, averaged for principal meridians of the visual field. Experimental studies show inter-individual variation but confirm that the two curves do not differ significantly beyond 5° eccentricity (Green, 1970).

The eccentricity dependent function of the parameter k was designed to take these factors into account. This function provides k=2 for the area affected by optical degradation, but it then declines gradually, reaching maximum rate of change at about 15° eccentricity and the constant value of 1.59 at 25°. This finding is based on the assumption that the ratio between the receptive field diameters of the ON and OFF midget GCs is 1:1 from 0° to 5°, changes roughly linearly between 5° and 25° to a 1.3:1 ratio between 25° and 30°, avoiding any sharp transition by means of a cubic function in Equation 5 (see Appendix).

We conclude that the lateral displacements of GC and the lengths of their Henle fibres along the horizontal meridian of the human retina are quite similar to those estimated by Curcio and Allen (1990) and substantially greater than reported by Sjöstrand et al (1999a,b) for the vertical meridian. The higher GC densities and shorter displacements and Henle fibre lengths reported by Sjöstrand et al (1999a,b) may be partly due to tissue shrinkage and eye size variation. However, the theoretical model indicates that peak displacements in the vertical meridian are 24% shorter than in the horizontal, which largely accounts for the reported differences in GC displacement and Henle fibre length. The model provides a means of obtaining estimates of receptive field density at any point on the principal meridians within an angular eccentricity of 30° from the point of fixation, and, consistent with physiological theory, predicts a central GC:cone ratio of 2.24:1. It provides a first step towards modeling the distribution of specific retinal GC types and useful basic estimates for linking hypotheses in psychophysics, electrophysiology, and clinical perimetry.

Appendix

A model of ganglion cell receptive field density (D_gcrf) in the human visual field

Weymouth (1958) was probably the first to draw attention to the linearity of the increase in the minimum angle of resolution (MAR) for gratings with angular eccentricity from the point of fixation and relate this to the spacing of retinal ganglion cells. Although this principle has been used to obtain estimates of D_gcrf (Drasdo 1977, 1989), it neglects the effect of optical degradation that reduces resolution in the foveal region (Campbell and Gubisch, 1967; Green, 1970). Since the increase in observed MAR with eccentric visual angle is linear, and the effect of optical degradation is non-uniform, the observed MAR must result from a nonlinear increase in neural MAR, which may be related more precisely to receptive field density.

The MAR is conventionally defined as the angular subtense (originally in minutes) of half the spatial cycle (one bar) of the threshold grating (Weymouth 1958). However, to simplify calculations in this report, it will be expressed in degrees. According to reviews of the extensive literature, consensus values for the resolution limit of the optical system of the eye at the fovea for white light, and the neural acuity at the fovea are both accepted as 60 cpd (Wilson, Levi, Maffei, Rovamo, and Devalois 1990; Charman, 1991), whereas the average visual acuity, the result of their combined effect, is given as 42 cpd. (Wilson et al., 1990). This is smaller by a factor of almost exactly 1/√2. For a consensus model, the corresponding optical, neural and visual, MAR values in degrees, R_o, R_n, and R_v for the foveal center are therefore taken as 0.0083333°, 0.0083333° and 0.011785° respectively and may be seen to conform to the following equation:

$${{\text{R}}_{\text{v}}}^2={{\text{R}}_{\text{n}}}^2+{{\text{R}}_{\text{o}}}^2$$ (1)

This simple model of optical degradation resembles one described as an observed rule in the optical industry for dynamically scanned fiber optic images (Kapany, 1967). Theoretically, it may be argued that MARs of image transmission systems are proportional to the width of their Gaussian spread functions, Equation (1) therefore applies because the convolution of two Gaussian functions is another Gaussian which has a standard deviation (SD), which is the root of the sum of squares of the SDs of the original Gaussians.

Since R_v and R_o can both be determined and both change with angular eccentricity (E), we can estimate R_n at any eccentricity from Equation (1). If R_v0 is R_v at 0°, then R_v at any eccentric angle E° is given by the equation, R_vE = R_v0(1+ E/E₂). This notation reflects the linear change in the angle of resolution with increasing peripheral angle (Weymouth 1958) and follows the convention adopted in psychophysics, where E₂ is the positive numerical equivalent of the negative x intercept, and therefore the eccentricity in degrees at which the threshold doubles (Levi Klein and Atsebaomo, 1985; Klein and Levi 1987; Drasdo, 1991). Similarly, due to the smaller, approximately linear change in optical degradation with eccentricity, R_oE = R_o0 (1+E/E₂). To avoid confusion between the two E₂ values, they are identified as E_2v and E_2o. Substituting in (1) we have an equation for the neural MAR, R_nE

$${\text{R}}_{\text{nE}}={({({\text{R}}_{\text{v}0}(1+\text{E}/{\text{E}}_{2\text{v}}))}^2-{({\text{R}}_{\text{o}0}(1+\text{E}/{\text{E}}_{2\text{o}}))}^2)}^{0.5}$$ (2)

While R_v0 is 0.008333, E_2v, in the expression for R_v0 averaged for the principal hemi-meridians from 0 to 15° may be deduced from the data of Wertheim (1894) and is found to be 2°. The much smaller and often neglected change with eccentricity of the optical resolution is considered to be proportional to the standard deviation of the Gaussian spread function for the eye (Charman, 1991), so that E₂ for R_o is taken approximately as E_2o = 20°. The relationship, derived from Equation (2), of neural and visual acuities in the central visual field, is shown in Fig. 4. and in support of the strategy adopted, it is noteworthy that within 5° of the foveal center, the data resemble the experimental findings of Green (1970) and fall roughly midway between those of Green (1970) and Hilz and Cavonius (1974) over a wide range of values. In Fig. 5, the relationship of neural MAR, R_nE, according to Equation (2) is compared with the MAR of the cone mosaic:

Assuming an approximately hexagonal matrix for the central cone mosaic, the cone density may be calculated from the Nyquist limit identified by the finest resolvable grating (Williams, 1988). With such a grating, R_n0 is the visual angle subtended by the row spacing and it may be related to the foveal cone density per solid degree by the expression:

$$\text{Foveal\hspace{0.17em}Cone\hspace{0.17em}Density}=1/(1.155{{\text{R}}_{\text{n}0}}^2)$$ (3)

A neural resolution of 0.0083333 therefore corresponds to a density of 12,469 cones per solid degree. Using the Drasdo and Fowler (1974) eye, this value equates to 164,840 cones/mm², almost exactly midway between the mean (175K) and median (155K) peak cone densities found by Curcio et al. (1993) from 27 human retinas. Resolution is related to cone density only at the fovea by this equation. The divergence of the value of R_nE from the cone MAR with eccentric visual angle (Fig. 5) is thought to reflect the spatial sampling of midget ganglion cell receptive fields that is essential for resolution of high contrast gratings (Merigan, 1989). Their receptive field centers are considered to tile the visual field in two superimposed, but not necessarily coinciding mosaics of ON and OFF units, resembling the arrangement of the dendritic fields of Pβ cells in the cat (Wässle, Peichl and Boycott, 1983) and of midget GCs in the human peripheral retina (Dacey, 1993).

Each of the central foveal L&M cones is assumed to be connected to one ON and one OFF midget bipolar, which in turn, each connect to a corresponding ON and OFF midget ganglion cell (Kolb and Dekorver, 1991; Ahmad et al, 2003), the so- called private wire connection. The peak density of L&M midget GC receptive fields is therefore twice the density of foveal cones. This value would be represented by the factor k, which would therefore be 2 in the following equation for the foveal density of L&M midget GC receptive fields (D_mgcrf).

$${\text{D}}_{\text{mgcrf}}=\text{k}/(1.155{{\text{R}}_{\text{nE}}}^2)$$ (4)

In its simplest form, the model would assume that there are equal numbers of ON and OFF units that could be related to the neural acuity across the whole retina. However, Dacey and Peterson (1992) and Dacey (1993) presented evidence to the effect that, over much of the retina, the density of ON midget ganglion cells appeared to be only about 0.59 times that of the OFF units. It is presumed that the resolution at high contrast would therefore be determined by the OFF mosaic, and the value of k would be 1.59; representing a saving in the number of channels, while achieving the same acuity. The anatomical evidence and functional significance of the changing value of k from the fovea (k=2) to the periphery (k=1.59) is outlined in the discussion. It is modeled by the following equation.

$$\text{k}=1+{(1.004-0.007209\text{E}+0.001694{\text{E}}^2-0.00003765{\text{E}}^3)}^{-2}$$ (5)

By combining the above equations we obtain the following equation for D_mgcrf at any eccentricity (E) in the ganglion cell displacement zone.

$${\text{D}}_{\text{mgcrf}}=\text{k}/(1.155{({({({\text{R}}_{\text{v}0}(1+\text{E}/{\text{E}}_{2\text{v}}))}^2-{({\text{R}}_{\text{o}0}(1+\text{E}/{\text{E}}_{2\text{o}}))}^2)}^{0.5})}^2)$$ (6)

The smallest eccentricity at which ganglion cells are not laterally displaced from their receptive fields varies in different meridians on the retina and has tended to be underestimated in earlier studies. Curcio and Allen (1990) found the average eccentricity of zero lateral displacement for the principal meridians to be 3.7 mm. For the purpose of this model the ganglion cell densities of Curcio and Allen (1990) at an eccentricity of 4.034 mm are considered to be at the margin of the area of displacement. On the nasal half-meridian of the retina, this location falls on the optic nerve head, and the density is estimated by interpolating from a polynomial function fitted to neighboring points. To further develop the model of receptive field densities, it is necessary to determine the proportion of midget GCs at the margin of the area of displacement and the total number of all GCs within the area.

The average of cell densities from Curcio and Allen (1990) for the four principal meridians at 4.034 mm, corrected for projection and eccentricity by means of a wide-angle schematic eye (Drasdo and Fowler 1974) was 245 cells/deg². However, Equation (6) predicts an L&M midget density of 161 cells/deg², indicating that 66% of the ganglion cells are L&M midgets at this eccentricity. Therefore, specifically at 14.7° eccentricity the density from Equation (6) must be increased by about 52% in order to give the density of all types of ganglion cells. However, it is also necessary to consider the effective number of all types of GCs at the fovea and all intermediate points, so that a progressively changing correction factor can be applied across the whole zone. This correction factor is adjusted primarily to satisfy two conditions: (1) It must demonstrate the cumulated number of receptive fields to be equal to the number of ganglion cells within the displacement zone, and (2) it must determine the correct density to match that found by Curcio and Allen (1990) at the margin of the zone. However, if the model is valid it should also satisfy two further conditions: (3) It must result in an acceptable estimate for the effective proportion of midget GCs, to ganglion cells of all types which changes with eccentricity within the zone, and (4) it must determine a foveal GC:cone ratio that is consistent with current theories of retinal circuitry. Confidence in the model will be strengthened if it can satisfy all four of these criteria.

To assess the GCs within the area, two polynomials (P_1, P₂) were fitted to the GC density data of Curcio and Allen (1990) for the average of the densities along major meridians. The coefficients for P₁, for 0 to 1 mm, and P₂ for 1 to 4.034 mm eccentricity, are given in Table 6. By numerical integration, a total cell count of 534,296 was found for the area inside 4.034 mm from the fovea. To equate the receptive field count to that of the GCs, an eccentricity dependent correction factor (1.12+0.0273E) was therefore determined by an iterative process as follows. The parameters were varied until at 14.7° eccentricity, numerical integration of receptive field densities of all GCs closely approximated the cell count of 534,296 and the density of the receptive fields was 245 receptive fields/solid degree. It was noted that the calculation satisfied conditions (1 to 4), outlined above. If either term in the correction factor was increased or decreased significantly, it was no longer possible by adjusting the other term to match the cumulative count of receptive fields and ganglion cells while correctly predicting the density of 245 receptive fields/solid degree. Hence the model provides a unique estimate of the foveal GC:cone ratio of 2 × 1.12, or 2.24:1, and we may conclude that the density of receptive fields of all GCs (D_gcrf) at any eccentricity within the zone is given by

TABLE 6.

Coefficients, a–f, of polynomials of the form: P_n = a + bx + cx² + dx³ + ex⁴ + fx⁵ enable the cell densities described in the text to be calculated. When x is the eccentricity in mm, P₁and P₂ give the GC (in cells/mm²) for the zones 0 to 1 mm and 1 to 4.034 mm respectively. When x is the eccentricity in degrees between 15° and 30°, P₃ – P₆ give the GC receptive field density/solid degree for the nasal, temporal, superior and inferior hemi-meridians in the visual field respectively.

P	a	b	C	d	e	r2
P1 0–1mm	545	−40860	445669	−718300	346448	.9979
P2 1–4mm	12710	50257	−48150	14653	−1475	.9996
P3 nas 15–30°	1678	−167.1	6.036	− 0.07549		.9982
P4 tem 15–30°	1415	−145.9	6.018	− 0.08415		.9986
P5 sup 15–30°	695	−65.42	2.325	− 0.02892		.9989
P6 inf 15–30°	1374	−139.6	5.231	− 0.06728		.9998

$${\text{D}}_{\text{gcrf}}=\text{((1}\text{.12}+\text{0}\text{.0273E)k)}/(1.155{({({({\text{R}}_{\text{v}0}(1+\text{E}/{\text{E}}_{2\text{v}}))}^2-{({\text{R}}_{\text{o}0}(1+\text{E}/{\text{E}}_{2\text{o}}))}^2)}^{0.5})}^2)$$ (7)

The calculation of the correction factor required numerical integration of D_gcrf for narrow concentric annular zones of visual space so that the receptive field counts within the area of displacement (<14.7°) could be determined. This process also provided a means of investigating GC displacement.

The eccentricities enclosing a specific number of GCs and the same number of receptive fields were calculated. To achieve this result, data on receptive field density and eccentricity from Equation (7) were converted to linear measure (Drasdo & Fowler, 1974) and compared with the data from polynomials P₁ and P₂ in Table 6. The difference between the eccentricities containing an identical count provides an estimate of the average lateral displacement of a GC from the corresponding cone inner segment at the given eccentricity. It is therefore possible to generate the function that relates GC displacement to cone inner segment position (Fig. 6), or GC position (Fig. 7). Both are needed for comparison with other studies.

Figure 6.

The computed mean displacement of ganglion cells from the position of their cone inner segments averaged from principal meridians, according to the model.

Figure 7.

The computed mean displacement of ganglion cells from the position of their cone inner segments averaged from principal meridians, as a function of GC soma position.

The functions relating GC displacement to cone inner segment, and GC position (Fig. 6 and 7) showed a peak displacement of 637 μm for a cone inner segment eccentricity of 0.653 mm or a GC eccentricity of 1.29 μm. Applying an 88% correction, based on the data of Perry and Cowey (1988) relating the fibers of Henle in the macaque to the displacement, 637 μm displacement corresponds approximately to a fiber length of 561 μm in the human retina.

The model hitherto described relates to D_gcrf averaged for all meridians, but since D_gcrf at the edge of the region of displacement (4.034 mm) is known for each principal hemi-meridian from the ganglion cell data of Curcio and Allen (1990), E_2v can be adjusted to give the projected densities at 14.7°, thus providing a family of models with the same central density, the correct density at 14.7°, and a best estimate at any intermediate eccentricity. No change is made in E_2o for each meridian, due to lack of available data and the fact that the effects are judged to be negligible. The extension of the general model of receptive field density to the specific principal hemi-meridians of the visual field from 0 to 15°, corresponding to the area of displacement, required the following E_2v parameters; nasal, 2.19; temporal, 2.26; superior, 1.5; and inferior, 1.98. Since the data generated by Equation 7 using these parameters for E < 14.7° are directly continuous with those of Curcio and Allen (1990) when E > 14.7° after conversion by the schematic eye, the model is further extended by the fitted polynomials P_3,4,5,6 in Table 6 to the projected GC density data of Curcio and Allen (1990) between 15° and 30°. The combined data provide receptive field densities to an angular radius of 30° in Table 5.