Abstract
For several years, digitized small radiographs are used to measure Cobb angle in idiopathic scoliosis. The interobserver and intraobserver Cobb angle measurement variability associated with small radiographs were compared with measurement variability associated with the long-cassette radiographs. Twenty adolescent patients with a double major idiopathic scoliosis had erect full-spine p-A radiographs and Cobb angle measurements performed by eight different observers on a 30 × 90 cm plain-film radiograph and a digitized 14 × 42 cm image. Inter-observer and intra-observer reliability using each techniques were assessed using a paired t-test, Spearman rank correlation study and intraclass correlation coefficients. The angle variability between small film and plain-film measurements was assessed using the same methods. Intra-observer and inter-observer study showed good reliability using both techniques. The comparison between small films and plain-films measurements showed very good agreement with an intraclass correlation coefficient of 95% and confidence interval between 0.962 and 0.972. In our study, Cobb angle determination was not found to vary significantly with film size. The small film image used for full-spine radiographs in our institution allows manual Cobb angle measurements to be performed. A study is currently conducted in our institution to determine if a computer-assisted measurement method significantly improves Cobb angle measurements reliability in routine practice compared with manual measurements of Cobb angles on small films.
Keywords: Idiopatic scoliosis, Cobb angle measurement, Digitized radiographs, Reliability
Introduction
Radiographic measurements are used to assess scoliosis curve magnitude, monitor and predict curve progression, and response to treatment. Documented coronal plane deformity progression in scoliosis as reflected by Cobb angle progression beyond defined thresholds directs treatment. Cobb angle is usually measured from erect radiographs and measurement variability associated with this technique has been reported for manual measurement of plain radiographs [6, 10, 11, 14] and computer-based measurement of digitized radiographs [5, 8, 18]. Reduction of digitized image output size could impact image quality. The purpose of this work was to compare the effect of full-spine radiographs on Cobbs’ angle measurement in idiopathic scoliosis with similar measurements on small digitized readiographs.
Materials and methods
This retrospective study reviewed previous full frontal (30 × 90 cm) radiographs of 20 patients with double major (Lenke Type 3) idiopathic scoliotic curves using a standardized imaging protocol, with a constant distance between the patient and image source. The range of curve magnitude was from 20 to 45° in all the cases. From these long-cassette radiographs, a size-reduced conventional radiograph, 14 × 42 cm, was obtained. The thoracic and lumbar Cobb angles of each radiograph were consecutively measured by four pediatric orthopedic fellows, two pediatric orthopaedic surgeons, one pediatric radiology fellow and one pediatric radiologist. Measurements were performed with the same narrow-lead (0.5 mm) mechanical pencil and the same goniometer. The end vertebrae were pre-selected and clearly marked on each radiographs. All identifying information was marked to prevent recognition of the patient’s radiographs by the examiners. Manual measurements of Cobb angles were made in the twenty cases by the eight different observers on two separate occasions in random radiograph sequence order using the same soft lead pencil and goniometer.
Intra-observer and inter-observer reliability of manual technique measurements performed on 30 × 90 cm and small radiographs were assessed. For inter-observer reliability, observers were pooled in “senior” groups (staff pediatric orthopaedic surgeons and radiologist) and “junior” groups (radiologic and pediatric orthopedic fellows). Additional inter-observer reliability was studied between these two sub groups. Agreement between all Cobb angle measurements performed on 30 × 90 cm radiographs and on the small radiographs was assessed.
Reliability for all comparisons between the series of measurements was assessed using Spearman’s rank correlation test, a t-test, intraclass correlation coefficient (ICC) and the limits of agreement by Bland and Altman [2]. The data were analyzed with SPSS® software (SPSS Inc. Chicago, Illinois, USA). A P-value for Spearman’s rank correlation and all t-tests was considered significant if less than 0.05. Intraclass correlation coefficients (ICC) of 1 imply perfect agreement and values less than 1 imply less than perfect agreement [13].
Results
Intra-observer reliability using long-cassette and small radiographs
Using long-cassette (30 × 90 cm) radiographs, the mean angular difference between the two series of measures for the same observer was between 1.55 and 3.07° (Table 1). Paired t-tests showed that the measurement difference was statistically significant with t values between 0.920 and 0.984 with P < 0.0001 (Table 2). Spearman correlation test showed good reliability with R between 0.932 and 0.985 and P < 0.0001 (Table 3). Intraclass correlation coefficients (ICC) showed very good agreement between measurements with ICC values between 0.958 and 0.992 (Table 4).
Table 1.
Intraobserver study of observed Cobbs’ angle differences using 30 × 90 cm radiographs
| N | Minimum | Maximum | Mean | SD deviation | |
|---|---|---|---|---|---|
| Observer 1 | 40 | 0 | 13.00 | 1.7750 | 2.29255 |
| Observer 2 | 40 | 0 | 10.00 | 2.4000 | 2.03558 |
| Observer 3 | 40 | 0 | 15.00 | 2.0250 | 2.55692 |
| Observer 4 | 40 | 0 | 10.00 | 3.0750 | 2.69270 |
| Observer 5 | 40 | 0 | 5.00 | 1.5500 | 1.15359 |
| Observer 6 | 40 | 0 | 14.00 | 2.5500 | 2.92601 |
| Observer 7 | 40 | 0 | 9.00 | 1.9500 | 2.07488 |
| Observer 8 | 40 | 0 | 9.00 | 2.3750 | 2.13262 |
Table 2.
Intraobserver study of Cobbs’ angle values using 30 × 90 cm radiographs (Paired t-test)
| N | T values | Significance | |
|---|---|---|---|
| Observer 1 | 40 | 0.968 | <0.001 |
| Observer 2 | 40 | 0.959 | <0.001 |
| Observer 3 | 40 | 0.961 | <0.001 |
| Observer 4 | 40 | 0.920 | <0.001 |
| Observer 5 | 40 | 0.984 | <0.001 |
| Observer 6 | 40 | 0.937 | <0.001 |
| Observer 7 | 40 | 0.960 | <0.001 |
| Observer 8 | 40 | 0.969 | <0.001 |
Table 3.
Intraobserver study of Cobbs’ angle values using 30 × 90 cm radiographs (Spearman correlation study)
| N | R values | Significance | |
|---|---|---|---|
| Observer 1 | 40 | 0.972 | <0.001 |
| Observer 2 | 40 | 0.954 | <0.001 |
| Observer 3 | 40 | 0.957 | <0.001 |
| Observer 4 | 40 | 0.933 | <0.001 |
| Observer 5 | 40 | 0.985 | <0.001 |
| Observer 6 | 40 | 0.932 | <0.001 |
| Observer 7 | 40 | 0.966 | <0.001 |
| Observer 8 | 40 | 0.963 | <0.001 |
Table 4.
Intraobserver study of Cobbs’ angle values using 30 × 90 cm radiographs (Intraclass correlation coefficients)
| Intraclass correlation coefficient | 95% Confidence interval | ||
|---|---|---|---|
| Lower bound | Upper bound | ||
| Observer 1 | 0.982 | 0.966 | 0.990 |
| Observer 2 | 0.979 | 0.961 | 0.989 |
| Observer 3 | 0.979 | 0.961 | 0.989 |
| Observer 4 | 0.958 | 0.921 | 0.978 |
| Observer 5 | 0.992 | 0.985 | 0.996 |
| Observer 6 | 0.968 | 0.939 | 0.983 |
| Observer 7 | 0.979 | 0.961 | 0.989 |
| Observer 8 | 0.984 | 0.970 | 0.992 |
Using small (14 × 42 cm) radiographs, the mean angular difference between the two series of measures for the same observer was between 2 and 4.25° (Table 5). Paired t-tests showed that the measurement difference was statistically significant with t values between 0.853 and 0.970 with P < 0.0001 (Table 6). Spearman correlation test showed good reliability with R between 0.832 and 0.968 and P < 0.0001 (Table 7). Intraclass correlation coefficients (ICC) showed very good agreement between measurements with ICC values between 0.913 and 0.983 (Table 8).
Table 5.
Intraobserver study of observed Cobbs’ angle differences using small radiographs
| N | Minimum | Maximum | Mean | SD deviation | |
|---|---|---|---|---|---|
| Observer 1 | 40 | 0 | 6.00 | 2.5500 | 1.92087 |
| Observer 2 | 40 | 0 | 8.00 | 2.6000 | 2.18151 |
| Observer 3 | 40 | 0 | 8.00 | 2.3750 | 1.93069 |
| Observer 4 | 40 | 0 | 14.00 | 4.2500 | 3.04454 |
| Observer 5 | 40 | 0 | 12.00 | 2.4500 | 2.73580 |
| Observer 6 | 40 | 0 | 10.00 | 2.0000 | 1.90815 |
| Observer 7 | 40 | 0 | 11.00 | 2.4500 | 2.37454 |
| Observer 8 | 40 | 0 | 10.00 | 2.3500 | 1.81941 |
Table 6.
Intraobserver study of Cobbs’ angle values using small radiographs (Paired t-test)
| N | T values | Significance | |
|---|---|---|---|
| Observer 1 | 40 | 0.970 | <0.001 |
| Observer 2 | 40 | 0.956 | <0.001 |
| Observer 3 | 40 | 0.961 | <0.001 |
| Observer 4 | 40 | 0.853 | <0.001 |
| Observer 5 | 40 | 0.942 | <0.001 |
| Observer 6 | 40 | 0.968 | <0.001 |
| Observer 7 | 40 | 0.963 | <0.001 |
| Observer 8 | 40 | 0.956 | <0.001 |
Table 7.
Intraobserver study of Cobbs’ angle values using small radiographs (Spearman correlation study)
| N | R values | Significance | |
|---|---|---|---|
| Observer 1 | 40 | 0.968 | <0.001 |
| Observer 2 | 40 | 0.947 | <0.001 |
| Observer 3 | 40 | 0.951 | <0.001 |
| Observer 4 | 40 | 0.832 | <0.001 |
| Observer 5 | 40 | 0.955 | <0.001 |
| Observer 6 | 40 | 0.962 | <0.001 |
| Observer 7 | 40 | 0.956 | <0.001 |
| Observer 8 | 40 | 0.961 | <0.001 |
Table 8.
Intraobserver study of Cobbs’ angle values using small radiographs (Intraclass correlation coefficients)
| Intraclass correlation coefficient | 95% Confidence interval | ||
|---|---|---|---|
| Lower bound | Upper bound | ||
| Observer 1 | 0.981 | 0.965 | 0.990 |
| Observer 2 | 0.977 | 0.957 | 0.988 |
| Observer 3 | 0.980 | 0.962 | 0.989 |
| Observer 4 | 0.913 | 0.835 | 0.954 |
| Observer 5 | 0.970 | 0.943 | 0.984 |
| Observer 6 | 0.983 | 0.969 | 0.991 |
| Observer 7 | 0.980 | 0.963 | 0.990 |
| Observer 8 | 0.975 | 0.953 | 0.987 |
Inter-observer reliability using long-cassette and small radiographs
Using long-cassette (30 × 90 cm) radiographs, mean angular difference determinations between junior and senior observers was 3.43° (Table 9). Paired t-tests showed that the measurement difference was statistically significant with t = 0.893 and P < 0.0001 (Table 10). Spearman correlation test showed a good reliability with R = 0.886 and P < 0.0001 (Table 11). Intraclass correlation coefficients (ICC) showed very good agreement between measurements with ICC 95% confidence interval between 0.922 and 0.958 (Table 12).
Table 9.
Cobbs’ angle differences between seniors and fellows using small or 30 × 90 cm radiographs
| N | Minimum | Maximum | Mean | SD deviation | |
|---|---|---|---|---|---|
| 30 × 90 radiographs | 160 | 0 | 20.00 | 3.4313 | 3.41956 |
| Small radiographs | 160 | 0 | 19.00 | 3.5875 | 3.47930 |
Table 10.
Inter-observer study of Cobbs’ angle values using small or 30 × 90 cm radiographs (Paired t-test)
| N | Correlation | Significance | |
|---|---|---|---|
| 30 × 90 radiographs | 160 | 0.893 | <0.001 |
| Small radiographs | 160 | 0.890 | <0.001 |
Table 11.
Inter-observer study of Cobbs’ angle values using small or 30 × 90 cm radiographs (Spearman correlation study)
| N | Correlation | Significance | |
|---|---|---|---|
| 30 × 90 radiographs | 160 | 0.886 | <0.001 |
| Small radiographs | 160 | 0.888 | <0.001 |
Table 12.
Inter-observer study of Cobbs’ angle values using small or 30 × 90 cm radiographs (Intraclass correlation coefficients)
| Intraclass correlation coefficient | 95% Confidence interval | ||
|---|---|---|---|
| Lower bound | Upper bound | ||
| 30 × 90 radiographs | 0.943 | 0.922 | 0.958 |
| Small radiographs | 0.939 | 0.917 | 0.956 |
Using small (14 × 42 cm) radiographs, the mean angular difference measured between junior and senior observers was 3.58° (Table 9). Paired t-tests showed that the measurement difference was statistically significant with t = 0.890 and P < 0.0001 (Table 10). Spearman correlation test showed good reliability with R = 0.888 and P < 0.0001 (Table 11). Intraclass correlation coefficients (ICC) showed very good agreement between measurements with ICC 95% confidence interval between 0.917 and 0.956 (Table 12).
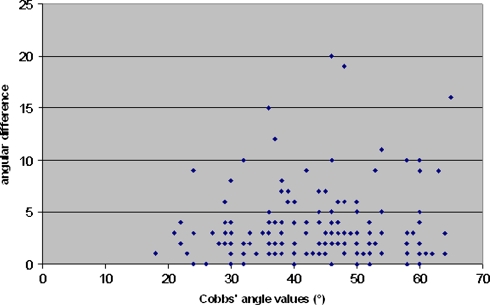
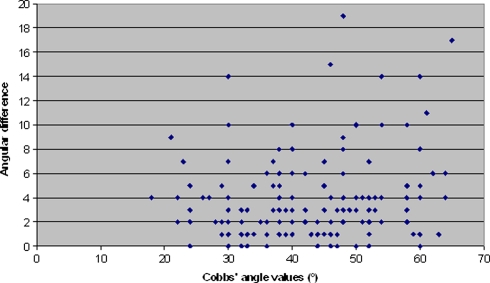
The graphic study of agreement proposed by Altman and Bland showed discordance higher than 10° between seniors and junior Cobb angle measurements for 10 of 160 30 × 90 cm radiographs (Figs. 1, 2). This discordance was noted for 12 of 160 small radiographs. Discordances were especially seen for higher rather than lower angle values (Fig. 3).
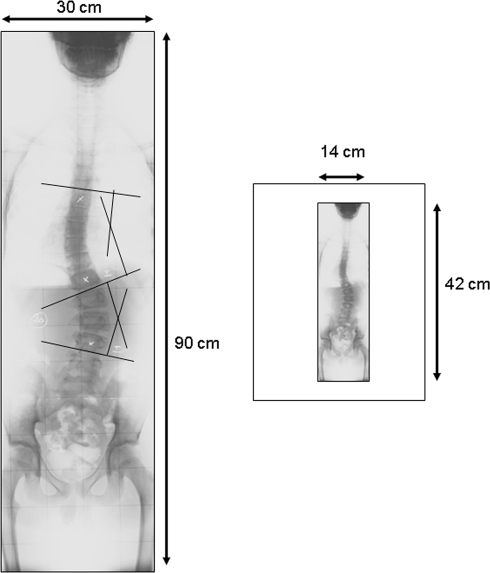
Fig. 1.
Schematic representation of the respective size of 30 × 90 cm plain-films and small (14 × 42 cm) films
Fig. 2.
Graphic representation of the difference between the two series of measures using 30 × 90 cm radiographs
Fig. 3.
Graphic representation of the difference between the two series of measures using small radiographs
Comparison of long-cassette and small radiographs Cobb angle measurements
The mean angular difference between the 30 × 90 cm radiographs and the small radiographs was 2.82° (Table 13). Paired t-tests showed that the measurement difference was statistically significant with t = 0.936 and P < 0.0001 (Table 13). Spearman correlation test showed good reliability with R = 0.935 and P < 0.0001 (Table 13). Intraclass correlation coefficients (ICC) showed very good agreement between measurements with ICC 95% confidence interval between 0.962 and 0.972 (Table 13).
Table 13.
Details of reliability study between Cobbs’ angle measurements performed on 30 × 90 cm radiographs and small radiographs
| Cobbs’ angle difference (degrees) | Paired t-test | Spearman rank correlation | Intraclass correlation coefficient | |
|---|---|---|---|---|
| N | 640 | 640 | 640 | 640 |
| Minimum | 0 | |||
| Maximum | 19.00 | |||
| Mean | 2.8141 | |||
| SD deviation | 2.61537 | |||
| T value | 0.935 | |||
| R value | 0.935 | |||
| Significance | <0.0001 | <0.0001 | ||
| ICC | 0.966 | |||
| 95% Confidence interval | ||||
| Lower bound | 0.961 | |||
| Upper bound | 0.971 | |||
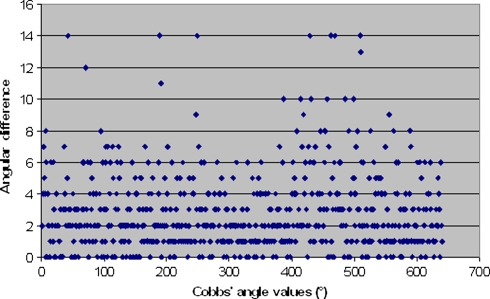
The graphic study of agreement proposed by Altman and Bland showed discordance higher than 10° between 30 × 90 cm radiographs and small radiograph measurements for 16 of 640 measurements (Fig. 4).
Fig. 4.
Graphic representation of the difference between the measures using 30 × 90 cm and 14 × 42 cm radiographs
Discussion
Cobb angle quantifies scoliosis curve magnitude and location. Studies of inter-observer and intra-observer variability in measurement of this angle [3, 7, 9, 15, 16, 20] have revealed that errors in radiographic measurements are typically ±5° and are comparable with thresholds of change that can influence treatment decisions [19]. Recent studies [4, 5, 8, 14, 18] demonstrate computer-assisted methods to reduce technical errors and the need for memorization of measurement and classification procedures. However, the manual technique is routinely used in many surgical teams because of its simplicity and cost [10, 11]. In our institution, imaging technique’s evolution from 30 × 90 cm plain-films to size-reduced digitized films was suspected to affect the clarity of the images and subsequent interpretation of spine radiographs. No relevant literature data were available concerning the effect of image size on Cobb angle measurement reliability. Sources of errors may include incorrect selection of the upper and/or lower vertebral levels, random errors in drawing lines across the endplates, and systematic errors caused by goniometers [1, 15]. Choosing the inappropriate end vertebrae in a scoliotic spine is known to be a major contributor to error [19], so we decided to define the end vertebrae in the current study to really focus solely on angular variations due to films’ size. Because a radiograph only records a patient’s spinal shape at an instant of time, repeated radiographs would introduce additional variability because of possible differing radiographic technique, postural sway, etc. This is why, in the current study, the small and 30 × 90 cm radiographs were different outputs of the same initial radiograph.
Using both radiographs sizes, mean Cobb angle variations in inter-observer and intra-observer determinations were statistically significant between 1.55° ± 1.15° and 3.58° ± 3.47°. The precision of measure was better using 30 × 90 cm films for six out of the eight observers but, nonetheless, such minimal variations (less than 3°) between 30 × 90 cm and small films Cobb measurements could have therapeutic implications [1, 3, 15, 16].
Paired t-test and Spearman rank correlation studies showed excellent intra-observer and inter-observer reliability using both types of radiographs. Intraclass correlation coefficient were higher than 0.9 for all observers. The inter-observer reliability of junior and senior groups showed that experience was not a factor in determining an individual observer’s reliability.
The graphic representation proposed [2] by Altman and Bland showed that the cases of significant discordance were sporadic and not related to the severity of the curve.
The global paired comparison (Table 13) of the data showed very good reliability using both image sets. First, the mean angular difference was 2.81°±2.61°. The reproducibility of the Cobb angle measures obtained here appears equal to or better than previously reported for intra-observer or inter-observer studies using manual or computer-assisted techniques [4, 5, 15, 17, 18, 20]. However, direct comparisons cannot be made with the previously mentioned studies because different radiographs were evaluated and differing statistical methods used in those studies. Paired t-test, Spearman rank correlation test and Intraclass correlation coefficient showed excellent reliability comparing the two techniques. In our study, variability of the Cobb angle determination was not found to vary significantly with the radiograph size. We fully recognize that the precision of Cobb angles’ measurements could be substantially improved because the curves were only moderate double major curves and that end vertebrae were pre-selected [19]. In severe scoliosis, curve magnitude as well as vertebral rotation could influence Cobb angle measurement and decrease the precision of the measurements. However, we think that the gain was the same using both techniques and that we studied only the effect of films’ size on measurement precision.
The small film output currently used for full-spine radiographs in our institution represents a step in the right direction, but clearly not the definitive one. This process can reduce technical errors and allow image processing to improve observer ability to define spinal landmarks [5]. Digitized small films are easier to store in patients’ files and can be stored under secured digital supports [12]. As digital imaging become increasingly available, clinicians can increasingly turn to computerized tools to assist in analyzing and classifying radiographic images used to treat patients with adolescent idiopathic scoliosis. Computerized tools can be helpful in the automated interpretation of data, as well as its storage and display. A study is currently in progress in our institution to determine if a computer-assisted method could significantly improve Cobb angle measurement’s reliability in routine practice compared with use of small radiographs.
Acknowledgments
The authors gratefully acknowledge the assistance provided by Dr Carl Stanitski in the preparation of this manuscript.
References
- 1.Behensky H, Giesinger K, Ogon M, Krismer M, Hannes B, Karlmeinrad G, et al. Multisurgeon assessment of coronal pattern classification systems for adolescent idiopathic scoliosis: reliability and error analysis. Spine. 2002;27:762–767. doi: 10.1097/00007632-200204010-00015. [DOI] [PubMed] [Google Scholar]
- 2.Bland JM, Altman DG. A note on the use of the intraclass correlation coefficient in the evaluation of agreement between two methods of measurement. Comput Biol Med. 1990;20:337–340. doi: 10.1016/0010-4825(90)90013-F. [DOI] [PubMed] [Google Scholar]
- 3.Carman DL, Browne RH, Birch JG. Measurement of scoliosis and kyphosis radiographs. Intraobserver and interobserver variation. J Bone Joint Surg Am. 1990;72:328–333. [PubMed] [Google Scholar]
- 4.Cheung J, Wever DJ, Veldhuizen AG, Klein JP, Verdonck B, Nijlunsing R, et al. The reliability of quantitative analysis on digital images of the scoliotic spine. Eur Spine J. 2002;11:535–542. doi: 10.1007/s00586-001-0381-7. [DOI] [PubMed] [Google Scholar]
- 5.Chockalingam N, Dangerfield PH, Giakas G, Cochrane T, Dorgan JC. Computer-assisted Cobb measurement of scoliosis. Eur Spine J. 2002;11:353–357. doi: 10.1007/s00586-002-0386-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Dang NR, Moreau MJ, Hill DL, Mahood JK, Raso J. Intra-observer reproducibility and inter-observer reliability of the radiographic parameters in the Spinal Deformity Study Group’s AIS Radiographic Measurement Manual. Spine. 2005;30:1064–1069. doi: 10.1097/01.brs.0000160840.51621.6b. [DOI] [PubMed] [Google Scholar]
- 7.Diab KM, Sevastik JA, Hedlund R, Suliman IA. Accuracy and applicability of measurement of the scoliotic angle at the frontal plane by Cobb’s method, by Ferguson’s method and by a new method. Eur Spine J. 1995;4:291–295. doi: 10.1007/BF00301037. [DOI] [PubMed] [Google Scholar]
- 8.Dutton KE, Jones TJ, Slinger BS, Scull ER, O’Connor J. Reliability of the Cobb angle index derived by traditional and computer assisted methods. Australas Phys Eng Sci Med. 1989;12:16–23. [PubMed] [Google Scholar]
- 9.Goldberg MS, Poitras B, Mayo NE, Labelle H, Bourassa R, Cloutier R. Observer variation in assessing spinal curvature and skeletal development in adolescent idiopathic scoliosis. Spine. 1988;13:1371–1377. doi: 10.1097/00007632-198812000-00008. [DOI] [PubMed] [Google Scholar]
- 10.Kuklo TR, Potter BK, O’Brien MF, Schroeder TM, Lenke LG, Polly DW., Jr Reliability analysis for digital adolescent idiopathic scoliosis measurements. J Spinal Disord Tech. 2005;18:152–159. doi: 10.1097/01.bsd.0000148094.75219.b0. [DOI] [PubMed] [Google Scholar]
- 11.Kuklo TR, Potter BK, Polly DW, Jr, O’Brien MF, Schroeder TM, Lenke LG. Reliability analysis for manual adolescent idiopathic scoliosis measurements. Spine. 2005;30:444–454. doi: 10.1097/01.brs.0000153702.99342.9c. [DOI] [PubMed] [Google Scholar]
- 12.Kundel HL, Polansky M, Dalinka MK, Choplin RH, Gefter WB, Kneelend JB, et al. Reliability of soft-copy versus hard-copy interpretation of emergency department radiographs: a prototype study. AJR Am J Roentgenol. 2001;177:525–528. doi: 10.2214/ajr.177.3.1770525. [DOI] [PubMed] [Google Scholar]
- 13.Lin LI. A concordance correlation coefficient to evaluate reproducibility. Biometrics. 1989;45:255–268. doi: 10.2307/2532051. [DOI] [PubMed] [Google Scholar]
- 14.Lyon R, Liu XC, Thometz JG, Nelson ER, Logan B. Reproducibility of spinal back-contour measurements taken with raster stereography in adolescent idiopathic scoliosis. Am J Orthop. 2004;33:67–70. [PubMed] [Google Scholar]
- 15.Morrissy RT, Goldsmith GS, Hall EC, Kehl D, Cowie GH. Measurement of the Cobb angle on radiographs of patients who have scoliosis. Evaluation of intrinsic error. J Bone Joint Surg Am. 1990;72:320–327. [PubMed] [Google Scholar]
- 16.Oda M, Rauh S, Gregory PB, Silverman FN, Bleck EE. The significance of roentgenographic measurement in scoliosis. J Pediatr Orthop. 1982;2:378–382. doi: 10.1097/01241398-198210000-00005. [DOI] [PubMed] [Google Scholar]
- 17.Pruijs JE, Stengs C, Keessen W. Parameter variation in stable scoliosis. Eur Spine J. 1995;4:176–179. doi: 10.1007/BF00298242. [DOI] [PubMed] [Google Scholar]
- 18.Shea KG, Stevens PM, Nelson M, Smith JT, Masters KS, Yandow S. A comparison of manual versus computer-assisted radiographic measurement. Intraobserver measurement variability for Cobb angles. Spine. 1998;23:551–555. doi: 10.1097/00007632-199803010-00007. [DOI] [PubMed] [Google Scholar]
- 19.Stokes IA, Aronsson DD. Computer-assisted algorithms improve reliability of King classification and Cobb angle measurement of scoliosis. Spine. 2006;31:665–670. doi: 10.1097/01.brs.0000203708.49972.ab. [DOI] [PubMed] [Google Scholar]
- 20.Ylikoski M, Tallroth K. Measurement variations in scoliotic angle, vertebral rotation, vertebral body height, and intervertebral disc space height. J Spinal Disord. 1990;3:387–391. [PubMed] [Google Scholar]