A Method for Describing Preschoolers' Activity Preferences

Abstract

We designed a series of analyses to develop a measurement system capable of simultaneously recording the free-play patterns of 20 children in a preschool classroom. Study 1 determined the intermittency with which the location and engagement of each child could be momentarily observed before the accuracy of the measurement was compromised. Results showed that intervals up to 120 s introduced less than 10% measurement error. Study 2 determined the extent of agreement between two observers who simultaneously collected data for 20 children using 30-, 60-, 90-, and 120-s momentary time sampling (MTS) intervals. The three larger intervals resulted in high levels of interobserver agreement (above 90%), whereas the 30-s interval resulted in unacceptably low levels of agreement (less than 80%). By allowing observers to select from among the different MTS intervals via a datasheet array and then collect data with the chosen system, Study 3 determined observers' preferences for the remaining MTS intervals. Both data collectors preferred the 90-s MTS procedure. The sensitivity of the 90-s MTS procedure, which was shown to be accurate, reliable, and preferred, was then demonstrated by its use to describe activity preferences of a classroom of children in Study 4. This system identified high- and low-preference activities for individual children and revealed interesting patterns of response allocation by the group.

Preschools are designed not only to promote early skills (e.g., language development, social and motor skills; Hains, Fowler, Schwartz, Kottwitz, & Rosenkoetter, 1989; Lin, Lawrence, & Gorrell, 2003) but also to foster motivation to learn and acquire more complex skills. A positive disposition to learn may be at least partially developed by engaging in satisfying early classroom experiences; however, the determinants of consistently enjoyable classroom experiences have yet to be identified for preschool children.

Children's enjoyment of learning in the classroom is likely related to the density of preferred events, activities, materials, social interactions, and effective instructional strategies. When preferences are identified systematically (i.e., direct observation; see Fisher et al., 1992), the results are typically used to enhance behavior-management or skill-acquisition programs for children with significant disabilities (Carr, Nicolson, & Higbee, 2000; Vollmer, Marcus, & LeBlanc, 1994). Typically developing children's preferences for classroom events have not yet been systematically evaluated (Ivancic, 2000), but the results of such evaluations could be used to improve the overall early childhood environment as well as to determine preferred events for use in behavior-management and teaching programs.

When preschool children's preferences have been taken into account, they were likely determined indirectly (e.g., by asking caregivers; see Green et al., 1988, for a discussion of the limitations of caregiver report for assessing preferences). This may reflect a lack of technology to measure preferences under increasingly complex conditions. Typical preference assessments involve placing one or a few stimuli in front of an individual and allowing repeated opportunities to observe selections of preferred items (e.g., DeLeon & Iwata, 1996; Fisher et al., 1992). The time and effort required to conduct this type of assessment with all children enrolled in a program are likely prohibitive, particularly when evaluating multiple protracted activities. A more convenient system might be one in which all children's preferences for naturally occurring classroom events are measured simultaneously during typical classroom routines.

The ideal assessment would involve direct and continuous observation of children's location and engagement during periods in which multiple options (activities) are simultaneously available (Bernstein & Ebbesen, 1978; Green & Streifel, 1988; Hanley, Iwata, Roscoe, Thompson, & Lindberg, 2003). Direct and continuous observation strategies are, however, extremely time consuming because one or two observers are required per participant (Kazdin, 1982). A considerably less effortful measurement strategy, known as momentary time sampling (MTS; Powell, Martindale, & Kulp, 1975), involves recording the momentary action of each child intermittently (e.g., a child is observed once every 20 s throughout a 5-min period). This technique is direct (a person directly observes children's behavior) but discontinuous (only a small sample of the child's behavior is observed). MTS is more efficient than continuous measurement in the sense that one or two observers can record the behavior of multiple children simultaneously and, potentially, determine preferences for a large group of children.

Discontinuous measurement strategies like MTS may, however, introduce error into the system (Johnston & Pennypacker, 1992). Researchers have evaluated the extent to which the size of the discontinuous sampling interval influences the degree of error (Mudford, Beale, & Singh, 1990; Powell, Martindale, Kulp, Martindale, & Bauman, 1977; Sanson-Fisher, Poole, & Dunn, 1980). These studies have shown that the accuracy of a discontinuous measure is negatively correlated with the length of the interval between measures, and that this relation is also affected by the overall frequency and stability of the target behaviors as well as bout durations (Powell et al., 1977; Saudargas & Zanolli, 1990). Therefore, analysis of the extent of error introduced by intervals of varying lengths is necessary when developing discontinuous methods to measure activities such as the location and engagement of children in a classroom.

In addition to determining whether the discontinuous measurement system produces accurate data, the extent of agreement between observers should also be determined for intervals of varying lengths. Finally, the social acceptability of a measurement system should also be considered because of the potential impact of this variable on the adoptability of the measurement system. Social acceptability may be best determined by allowing data collectors who have experienced the multiple measurement systems to select and use one or more of the systems for subsequent data collection.

The purpose of the present study was to develop and evaluate a measurement system capable of simultaneously determining the activity preferences of an entire classroom of preschool children during free play. The measurement system was evaluated in terms of its accuracy (i.e., how much error was introduced by discontinuous measurement), interobserver agreement (i.e., the extent to which two observers recorded the same events), and acceptability (i.e., allocation of choices among measurement systems by data collectors). Finally, we used the system to identify location and engagement patterns among a class of preschool children and more and less preferred activities of individual children.

General Method

Participants and Setting

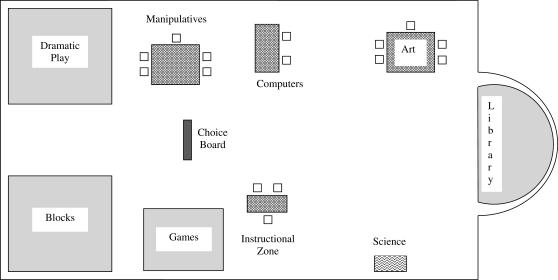
Observations were conducted during free-play periods in a full-day, university-based preschool classroom that served 20 children of typical and atypical development between the ages of 3.5 and 5.5 years. There were 10 boys and 10 girls in the classroom. Four children had been diagnosed with developmental disabilities (Josh with apraxia, Tony with severe mental retardation, and Chris and Ted with nonspecified developmental delays). The classroom was rectangular and measured 12 m by 7 m. Three free-play periods were scheduled throughout the day in which nine activity areas were simultaneously available. Data were collected during the second free-play period each day because the most children were present during this period. To access an activity, children selected a wooden magnetic letter from an easel located in the center of the room and placed the letter on a small magnetic square in the corresponding activity zone. Each zone had a limited number of letters available, such that if no additional letters were available, teachers provided a general prompt for children to select a different letter (e.g., “choose something else”). Different groups of children were scheduled to access the choice board first on different days, and teachers were instructed to allow different children access to the letter board first across free-play periods. In addition, children could switch areas at any time by replacing their letter on the central letter board and selecting a new letter. Descriptions of each activity area and the corresponding number of available letters (i.e., the capacity of the zones) are presented in Table 1. The relative locations of each area are depicted in Figure 1.

Table 1.

Activity Area Descriptions

Activity	Capacity	Description
Dramatic play	4	Pretend play toys (e.g., dress-up clothes, doctor set, flower shop, barber shop) located on a carpeted area.
Computer	2	Two computers with a variety of CD-Rom games (e.g., Clifford's CountingTM, Jumpstart KindergartenTM) located on a desk.
Blocks	4	Toys to occasion large movement (e.g., train sets, large blocks, bowling set) located on a carpeted area.
Manipulatives	4	Smaller toys (e.g., animals, Tinker ToysTM, Lincoln LogsTM) placed atop a table.
Games	3	Age-appropriate board games and large puzzles (e.g., CandylandTM, MemoryTM, dominos) located on a carpeted area.
Art	4	Open-ended art activities (e.g., paint, glue, glitter, crayons) placed atop a table.
Science	3	Open-ended activity for children to explore and use their senses (e.g., digging for dinosaurs in cornmeal; pouring water through sieves in a water table).
Instructional zone	2	One-on-one direct instruction at a table. Each child had individualized skills and relevant materials selected and stored in the area.
Library	3	A variety of age-appropriate books, carpet, and small chairs.
Out of zone	20	Not in the proximity (within 1 m) of any of the nine programmed activities (e.g., selecting a letter, in the bathroom area, or wandering).

Figure 1.

Schematic of the classroom showing the locations of the nine activity zones and the choice board.

Study 1: Error Analysis

Method

Measurement

Ten children were selected for participation in Study 1 based on their attendance regularity. The percentage of observation periods spent in each of the activity zones and the percentage of time the child was engaged with materials in the zones were estimated using a 5-s MTS procedure (intervals were cued via synchronized stopwatches). Observers were undergraduates enrolled in a practicum course in which they learned how to collect, analyze, depict, and interpret behavioral data. In zone was defined as being within 1 m of the play materials in a selected activity. Observers were provided with a schematic that showed the positions of each activity in the classroom (see Figure 1) and recorded a single letter corresponding to one of the 10 activities listed in Table 1 in each 5-s interval. Engagement was defined as touching or orienting towards the material in the selected activities.

Observers circled the previously recorded in-zone letter if the child was engaged with the materials featured in that zone. Each child was observed during a single 18-min session using the 5-s MTS procedure. That is, at the end of each 5-s interval, an observer scored the area in which the child was located and his or her engagement, resulting in 216 scored intervals. When children were in one of the nine activity zones, they were engaged during 97% of the scored intervals. Due to the similarity of these measures, only in-zone data will be reported in subsequent analyses.

Interobserver Agreement

A second observer simultaneously but independently scored in zone and engagement during 30% of sessions. Observers' records were compared on an interval-by-interval basis and scored in agreement if they recorded the same zone during an interval. An agreement for engagement was defined as both observers either circling or not circling the in-zone letter. The sum of the agreements was divided by the total number of intervals and multiplied by 100%, resulting in agreement coefficients of 99% (range, 99% to 100%) for in-zone behavior and 98% (range, 97% to 100%) for engagement.

Procedure

In an attempt to determine an accurate interval length for target behaviors, we measured in zone and engagement using a 5-s MTS as a standard and compared this standard to longer MTS intervals. We chose MTS as opposed to partial-interval recording (PIR) or whole-interval recording (WIR) because MTS has been shown to be superior to both PIR and WIR in estimating the duration of behavior (Ary, 1984; Powell et al., 1975). A 5-s MTS was used as our standard instead of a continuous duration measure for two reasons. First, Mudford et al. (1990), Powell et al. (1977), and Tyler (1979) all showed that the percentage difference between a continuous duration measure and 5-s MTS was near zero (see Figure 4 of Mudford et al. and Figure 1 of Powell et al.). Second, prior to conducting the analyses described in the current study, we repeatedly observed that novice data collectors were able to record a single child's location (in zone) and engagement with high levels of agreement using a 5-s MTS. By contrast, varying levels of agreement (with some measures being quite low) resulted when continuous duration recording was used. We speculated that the time to record location and engagement introduced this unwanted measurement error. This problem was alleviated using the 5-s MTS, which provides a brief recording period between observation samples.

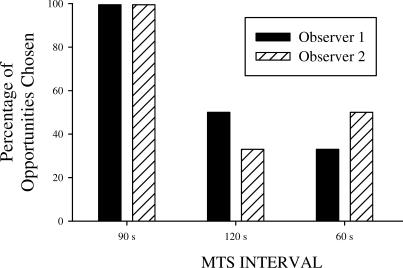
Figure 4.

The percentage of opportunities each of three MTS intervals was chosen by two observers.

From the 5-s MTS data, 10-, 20-, 30-, 60-, 90-, 120-, 180-, 360-, 540-, and 1,080-s MTS intervals were extrapolated and then compared to the results of the 5-s MTS to determine the degree of error introduced by the progressively longer intervals. For example, when evaluating the 30-s MTS, data from every sixth interval were extracted, resulting in 36 observation intervals for an 18-min observation (see Table 2 for descriptions of the extraction rules for each MTS interval).

Table 2.

Momentary Time Sampling

Measurement interval(s)	Number of observations	Percentage of observation	Extraction rule
5	216	100	Each interval
10	108	50	First and every second interval
20	54	25	First and every fourth interval
30	36	16.6	First and every sixth interval
60	18	8.3	First and every 12th interval
90	12	5.6	First and every 18th interval
120	9	4.2	First and every 24th interval
180	6	2.8	First and every 30th interval
360	3	1.4	First and every 60th interval
540	2	0.9	First and 181st interval
1,080	1	0.5	First interval only

In-zone percentages were calculated by summing the number of intervals in which the children were observed in each activity and dividing the sum by the total number of intervals in a session. For example, if art was scored during 108 of a possible 216 intervals, then it was reported as 50% of intervals in the art zone.

Error was determined by calculating the arithmetic difference between in-zone percentages derived from each MTS procedure and the 5-s MTS standard (proportional differences were not calculated). For example, if a child was observed in the art zone during 50% of intervals using the 5-s MTS and 40% of intervals using the 10-s MTS, then the percentage difference (or error) was reported as 10%. The percentage differences for each MTS interval length were then averaged across the 10 observations.

Four separate indices of error were calculated. The first measure was the mean of the obtained error across all activities. However, this measure included activities that were not accessed, which somewhat inflated the level of correspondence (i.e., masked differences between the measurement outcomes). Therefore, the second measure was the mean of the obtained error across only accessed activities. In general, calculating averages may suppress important variability in data, and a large difference in measures for any one activity may be obscured. Therefore, the third measure was the largest mean error for a single activity. Finally, the activity areas were ranked in order of the percentage of intervals allocated to each zone. Mean differences in rank were then calculated between the standard measurement system and the various other MTS-interval systems to determine the degree to which preference rankings shifted as a result of longer MTS intervals.

Results and Discussion

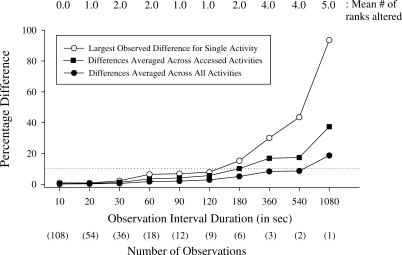
The four indices of error are shown in Figure 2 as a function of each MTS interval. Less than 10% was set as an acceptable amount of error, and is shown by the dotted line. When we averaged the percentage difference across all activities, less than 5% difference was obtained using intervals up to 120 s. When the percentage difference was calculated for only accessed activities, less than 5% difference was obtained using intervals up to 90 s. Error above 5% but below 10% was introduced by the 120-s observation interval, when the largest observed difference for a single activity was analyzed. Two or fewer differences in the rank of the activities were a result of using MTS intervals up to and including 180 s. Larger alterations to the rank (four and above) were observed at intervals of 360 s and above.

Figure 2.

The percentage difference (error) between a 5-s MTS procedure and MTS procedures of increasing duration.

Measurements of children's time allocation showed little difference between intervals of 5 and 30 s. These data show that an 83% decrease in the number of observations (from 216 observations per 18-min period with the 5-s MTS to 36 observations per 18-min period with the 30-s MTS) did not result in an appreciable change in the accuracy of the observation method. Arguably acceptable differences were observed between intervals of 5 and 120 s. This is notable because the 120-s MTS represents a 96% decrease in the number of observations relative to the 5-s MTS. Therefore, based primarily on accuracy, several MTS intervals were considered acceptable for measuring children's free-play behavior.

It is important to note that the selection of these intervals was based on extrapolated data. Therefore, the extent to which data for the entire group of 20 children could be reliably collected using each of these time-sampling intervals required further assessment.

Study 2: Interobserver Agreement Analysis

Procedure

The time allocation (in zone) and engagement of up to 20 children were simultaneously measured during free play using 30-, 60-, 90-, or 120-s MTS intervals within 18-min observations. These intervals were selected because the 120-s interval represents the smallest interval for which there was acceptable error, and the 30-s interval represents the largest interval for which there was negligible error. For each observation, a data sheet was used in which each child's name was listed once down a column in alphabetical order, with a time stamp and a space to record data. This column was repeated, with different time stamps, such that it permitted recording each child's behavior repeatedly and at equal intervals. Therefore, the 30-, 60-, 90-, and 120-s MTS intervals resulted in 36, 18, 12, and 9 scored intervals for each child, respectively, within an 18-min session. Observers used synchronized stopwatches to determine when to record data for each child. Observers learned the relations between the names on the data sheets and the actual children to which the names referred by (a) reviewing the children's cubbies from which hung cards with photographs of the children and their names written in large text, and (b) repeatedly reading different names on the data sheet and simultaneously pointing to the named child. This two-step training took approximately 30 min over the course of 2 days.

An important artifact of the different MTS intervals was how often individual children were observed. With the 30-, 60-, 90-, and 120-s MTS intervals, observations were scheduled every 1.5, 3.0, 4.5, and 6.0 s, respectively. For example, using the 90-s MTS, Pat's in zone and engagement were scored at Second 5 and again at Second 95, Carol's in zone and engagement were scored at Second 10 and again at Second 100, Ted's in zone and engagement were scored at Second 14 and again at Second 104, and so on.

If a child was absent from an observation, his or her intervals were skipped. The number of children present during each observation ranged from 11 to 17 (M  =  14.7, 14.3, 14.0, and 14.0 for the 30-, 60-, 90-, and 120-s MTS, respectively). Two trained undergraduate observers simultaneously but independently scored in zone and engagement using one of the four data-collection procedures during all 18-min sessions. Agreement scores were generated for each procedure by comparing observers' records on a trial-by-trial basis. An agreement was defined as both observers scoring the same zone for each interval. Sessions were conducted in a random and counterbalanced order, conforming to a multielement design, such that any differences in the obtained agreement scores could be attributed to the different measurement systems. Three observations for each of the four systems were arranged, for a total of 12 18-min observations.

Results and Discussion

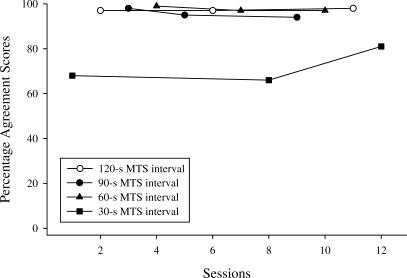
The results of the interobserver agreement assessment for our primary dependent measure, in zone, are shown in Figure 3. Near-equal levels of agreement were obtained when data were collected using the 60-, 90-, and 120-s intervals (Ms  =  97.7%, 95.7%, and 97.3%, respectively). Agreement was substantially lower for the 30-s intervals (M  =  71.7%). These results suggest that although the 30-s MTS was associated with negligible error when extrapolated from 5-s MTS data collected by observing a single child, the 30-s MTS measurement system was unreliable when used to simultaneously measure the time allocation and engagement of multiple children. Therefore, the 60-, 90-, and 120-s MTS intervals were determined to be the only measures both sufficiently accurate and reliable. Given that multiple measurement systems were similarly accurate and reliable, we assessed observers' preferences for the measurement systems.

Figure 3.

The percentage agreement scores as a function of the size of the MTS interval.

Study 3: Observer Preference Assessment

Procedure

Two undergraduate observers, who had experience using each of the measurement systems, were presented with an array of three data sheets used to collect in-zone and engagement data. The data sheets incorporated 60-, 90-, or 120-s MTS intervals. One of the data collectors was then prompted to select a data sheet; both then collected data using the selected data sheet. On the following day, the data sheet array was again presented to the observers, with the previously selected data sheet removed (i.e., multiple stimulus without replacement; DeLeon & Iwata, 1996). After the assessment was completed with Observer 1, the procedure was repeated with Observer 2. Following completion of the preference assessments, the observers were asked in an open-ended survey why they selected each data sheet.

Results and Discussion

The percentage of trials on which each measurement system was selected is shown in Figure 4. The 90-s interval was selected first by both participants. The 120-s interval was selected second by one observer, whereas the 60-s interval was selected second by the other observer. When asked why they selected the 90-s MTS first, the observers responded that the 90-s procedure was the most comfortable and that the others required too much vigilance (e.g., the 60-s MTS) or were boring (e.g., the 120-s MTS).

Observer preference, determined by allowing observers to experience multiple means of collecting behavioral data and then allowing them to select among the procedures, is a factor that should be considered in addition to the reliability and validity of a measurement system. Therefore, the 90-s interval system was selected for simultaneously measuring children's activity preferences because it (a) produced measurement error within acceptable limits, (b) was associated with satisfactory interobserver agreement coefficients, and (c) was preferred by the observers.

Study 4: Description of Response Allocation

Measurement and Procedure

Twenty-five 18-min observations were conducted using the 90-s MTS procedure, such that each child was observed 12 times each session. One session was conducted per day during the second of three regularly scheduled free-play periods. The number of children present during each observation ranged from 10 to 18 (M  =  15), although the data-collection system was arranged to accommodate 20 children. Interobserver agreement data were collected as described above during 44% of sessions, and the mean agreement was 94% (range, 85% to 98%) for in zone. To determine the entire class in-zone percentage for each activity area, the number of intervals scored in each area for all children was divided by the maximum number of intervals, which varied depending on the capacity of the zone. For example, 4 children could attend the dramatic play zone at any given time, and there were 12 instances in which each child could be observed. Therefore, the maximum number of intervals dramatic play could have been scored was 48 per session. If 46 intervals were scored with children in dramatic play, then the time allocation to dramatic play was 96%. Individual children's in-zone percentages were determined by dividing the number of intervals each child was located in each zone by the total number of intervals each child was observed.

Results and Discussion

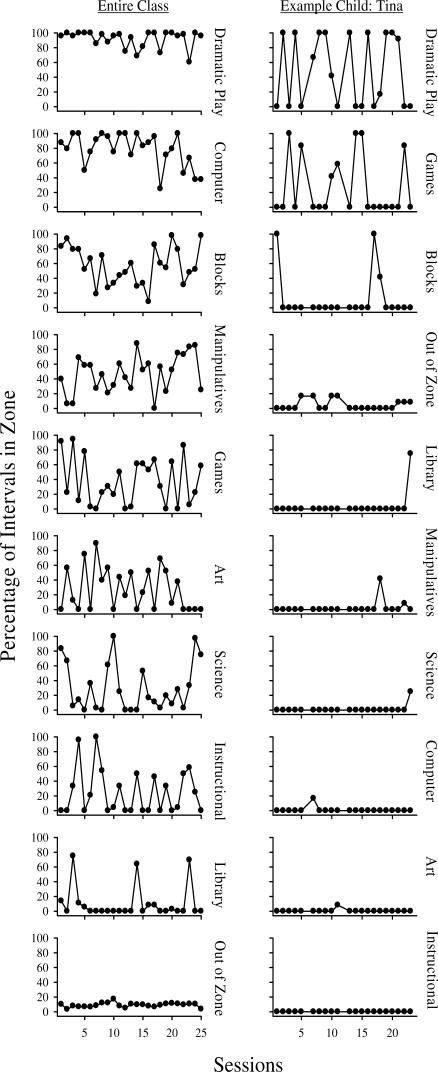
Mean percentages of in-zone allocation, for both the entire class and for a representative child (Tina), are shown for each activity in Figure 5. Both panels are arranged in order from the most to the least preferred activities based on the overall mean percentages of in-zone allocation for each activity. Data for 18 children were averaged, as opposed to 20, because 2 children were consistently absent during the midday observations. The class data show that dramatic play was the most popular activity in the classroom (M  =  92%), and that this area was often full (i.e., there were multiple observations showing the in-zone percentage at or near 100%). The computer zone and blocks zone were the second and third most preferred activities of the group (Ms  =  80% and 58%, respectively). By contrast, there were multiple activities that were rarely full or even attended; these activities were science (M  =  30%), instructional zone (M  =  24%), and library (M  =  10%).

Figure 5.

The mean percentages of in zone, for both the entire class (left) and an individual child (Tina), are shown for each activity. The panels are displayed from the most (top) to the least (bottom) preferred activities.

The data from the entire class have at least two implications for designing effective free-play contexts. The first is that greater access could be made to the dramatic play and computer activities so that more children could partake in these highly preferred activities. The second implication is that the science, instructional, and library zones could be revised to generate greater interest in these presumably important preschool activities.

Tina's data (Figure 5) were selected for display because her patterns were consistent with several children's data patterns and because she was present during most of the 25 observations. Tina's data are consistent with those of the entire class in that dramatic play was her most preferred activity and that the science, instructional, and library zones were among her least preferred. Tina's data differed from those of the entire class in that the computer zone was not highly preferred. Similar to the entire class, Tina's data show a potentially undesirable pattern of time allocation, in that she was regularly observed in only two of the nine activities (dramatic play and games) and rarely attended the other seven zones. Although persistence with activities may be a desirable characteristic of preschool play, not experiencing over 75% of the activities offered during free play seems to warrant some attention.

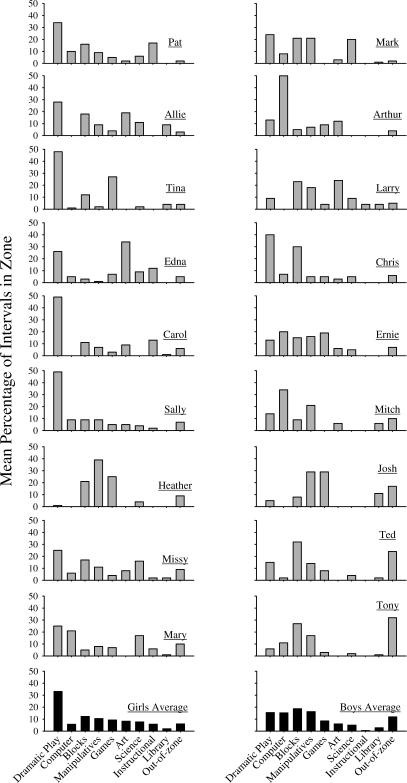
Figure 6 shows the mean percentage of intervals in zone for each individual child across the 10 zones (nine activities and the out-of-zone category). Data for girls are arranged in the left column, and data for boys are located in the right column; the activities are listed from the most to the least preferred based on the entire class mean. The range of bar heights within and across children (from 0% to 50%) shows that the measurement system was sensitive to differences in response allocation. In addition, preference hierarchies are discernible for individual children. From these, the most highly preferred activities are identifiable (e.g., dramatic play for Pat; computer for Arthur) as well as activities that were presumably nonpreferred (e.g., art and library for Mary).

Figure 6.

The mean percentages of in zone across activities are shown for each child. Data for girls are located in the left column, and data for boys are located in the right column. The panels are displayed from the least (top) to the most (bottom) out-of-zone percentages.

Although preferences were fairly idiosyncratic across children, some patterns in the data are worth noting. All children spent some time in the dramatic play zone. This activity was the most preferred for 7 of the 9 girls, yet only 2 of the 9 boys preferred this activity the most. The most preferred activities were not consistent for boys, as evidenced by six of the nine activities being most preferred for one of the boys. It also appears that the boys spent more time out of zone than the girls did; however, this is primarily attributable to high levels of out of zone for Josh, Ted, and Tony. This clustering is important because these were 3 of the 4 children with developmental disabilities.

As important as identifying most preferred activities is identifying least preferred activities. Perhaps most alarming is that 12 of 18 children and 8 of 9 boys never attended the instructional zone, which contained teaching materials for individualized curriculum-based goals. These data suggest either that teaching should be embedded in the other, more preferable activities or that adjustments to the instructional zone should be considered. Other important activities that were often unattended include the library and computer (7 of 18 and 5 of 18 children never attended these activities, respectively).

Several limitations of this measurement system should be considered when evaluating the preference patterns evident for individuals as well as groups. First, because the number of children permitted in each zone was limited, the total array of activities was not available to all children at all times. The variability imposed by this feature, which is necessary if activity preferences are to be determined for 20 children simultaneously, was minimized by providing different children with initial access to the letter board and by allowing children to switch activities any time a letter became available. The variability imposed by limited zone capacities was not, however, altogether avoided. For example, there may have been instances in which the first 4 children selected the dramatic play area and these children did not switch activities throughout the period. Under these conditions, a preference for dramatic play by another child would go undetected. This feature of our evaluative context would be most troublesome if one or a few measures of preference were collected. Because we collected repeated measures of preference for all children, it is unlikely that this feature compromised our interpretation of individual children's preferences.

The fact that children may not have been allowed to select their most preferred activity on all occasions may actually have contributed important, albeit unsystematic, variability to the description of children's preferences in our study. Hanley et al. (2003) found that preference hierarchies among concurrently available activities were determinable only if relatively high-preference activities were restricted from the choice array across observations. Perhaps our unsystematic restriction procedure, which was a result of limited capacities across activities, allowed us to determine preference rankings among multiple activities with all children as opposed to exclusively determining each child's most preferred activity. Future research may evaluate this possibility or develop more systematic means of restricting classroom activities that still allow the detection of preference hierarchies among multiple activities and children simultaneously.

A second limitation is that, because the capacities varied for some zones (e.g., 4 children could attend the art area, whereas only 2 children could attend the computer area at any one time), incorrect conclusions regarding the popularity of activities for the group of children may result. For example, if 3 children attended the art area (capacity of 4) and 2 children attended the computer area (capacity of 2), in-zone percentages would favor computers (100%) relative to art (75%), even though more children attended the art area. Therefore, it is possible that selection percentages for small-capacity activities were inflated relative to large-capacity activities. To determine if this was indeed the case, the percentage of intervals in zone (Figure 5) were recalculated as if each zone only had the capacity of two (i.e., the measure for art would be 100% if 2 children were in art for a given interval). Although the level of some of the data in the 3- and 4-person capacity activities did increase, the relative rankings of the activities were almost identical. The rank order correlation between the two methods of determining group preference percentages, one using varying (true) capacities and the alternative using the same capacity size across all activities, was .98 (the rankings of the blocks and computer activities reversed). Finally, there was a positive correlation, although not large (r  =  .33), between capacity of an activity and its preference value as determined by the group data. In other words, the higher capacity activities showed up as more preferred (not less preferred) in our group data.

A third limitation of our measurement system is that the percentage of intervals in zone for a particular activity can potentially exceed 100% (affecting the data displayed in Figure 5). Overages may occur because data were collected on children's location sequentially within 90-s intervals, as opposed to recording a simultaneous snapshot of children's locations. For example, an overage may occur if a child, who was scored as present in a full activity area, left that area, and another child, whose location had not been scored yet, then entered that area during the same 90-s interval. By contrast, some overages may be a function of an extra child being in an activity area without a letter (i.e., a compromise in the integrity of the letter-board system). Overages occurred in the current study on 6 of 225 occasions. All instances involved the dramatic play and computer activities, and when this occurred, we reported 100% of intervals in zone for that particular activity. Because this phenomenon exclusively discounts the most highly preferred areas, it does not seem to affect the primary functions of the measure—to determine a preference hierarchy among activities for a group of children and to establish repeated measures of a group's preferences over time. Nevertheless, users of this measurement system should be aware that overages may occur. We feel that capping the measures at 100% is the simplest solution, and one that does not affect the utility of the measurement system.

General Discussion

We developed a measurement system that allowed for the simultaneous description of up to 20 preschoolers' free-play activity preferences. We established the accuracy of the measurement system through an error analysis, which involved comparing 10 MTS intervals of varying lengths to a standard using a brief MTS interval. A subsequent analysis of interobserver agreement identified that three of the four MTS intervals with sufficient accuracy were also sufficiently reliable. A preference assessment conducted with observers determined that one of the three remaining MTS intervals was most preferred for collecting data on preschoolers' free-play behavior. This system, which involved the direct observation of child location and engagement using a 90-s MTS interval, was then used to describe individual preferences among nine activities for up to 18 children as well as the whole group's time allocation during free play.

These procedures represent an extension of preference assessment methods to typically developing children and preschool classrooms. Although their utility in clinical conditions is undeniable, more typical procedures of assessing children's preferences (e.g., DeLeon & Iwata, 1996; Fisher et al., 1992) may be limited by (a) the time required to assess all children's preferences, (b) their inability to evaluate typical classroom activities (i.e., those items that are difficult to present during an assessment), and (c) their inability to capitalize on naturally occurring motivating operations (Michael, 1993). For example, dramatic play may be more reinforcing when other children are involved, or books may be more enjoyable while lying on a carpet. These features of the environment are systematically removed during most preference assessments but are retained in the current assessment.

Identifying activities of varying preference may allow teachers to arrange greater access to preferred learning opportunities or contingent access to these activities as reinforcement for other desirable behavior. For example, Baer, Rowbury, and Baer (1973) arranged access to free-play activities as a reinforcer for compliance with teacher-directed instruction. Systematic identification of high- and low-preference activities using the procedures described in the current study may identify the most optimal activities to involve in contingency arrangements.

The identification of low-preference activities may provide valuable information as well. Presumably, the range of activities included in preschool free-play contexts provides opportunities for different types of social and nonsocial skill acquisition and maintenance. The extent to which children routinely avoid particular activities constitutes an applied problem. For example, children were rarely observed in the library, instructional, or science zones in the present study. These patterns may limit the development of early literacy, math, and science skills, among others (Lawhon & Cobb, 2002; Malcom, 1998). A potential solution to the problem of engagement with limited activities is the use of a lag differential reinforcement contingency. For example, Cammilleri and Hanley (2005) described a procedure whereby extra teacher interaction was provided when children selected activities that were different from those they had selected during previous choice opportunities. The children could (and did) select their most preferred activities while also experiencing a range of different activities. An alternative strategy would be to permanently embed more highly reinforcing materials or interactions in the activities that children are not selecting.

In the absence of systematic measurement, problems such as limited engagement in classroom activities may go undetected by teachers. For example, a teacher may notice that the instructional zone was generally attended by children, but fail to notice that a particular student, such as Tina, never attended the area. This suggests that systematic measurement of children's play may be useful to detect critical allocation patterns. The measurement system described herein identifies response-allocation patterns; this provides baselines on which interventions targeting a single child (e.g., idiosyncratic contingencies) or an entire class of children (independent or dependent group contingencies; Litow & Pumroy, 1975) could be evaluated. The number of observations necessary to determine children's preferences will likely vary across children and classrooms. It is worth noting that the in-zone percentages during the first five observations were similar to those of the full 25 observations for both the class and Tina, suggesting that fewer observations than conducted in the current study may be sufficient to establish baselines.

Although the accuracy, reliability, and social acceptability of the measurement system were established with preschool children in free play, this system may have generality beyond the classroom. That is, it may be applicable in any context in which the location and engagement of people are important indicators of a program's success. For instance, ensuring that elders participate in a variety of recreational activities and that staff consistently interact with elders are common goals of many nursing homes (Jenkins, Pienta, & Horgas, 2002). This system could be implemented consistently to determine the likelihood of those outcomes.

The utility of this system as an accurate, reliable, and acceptable means of identifying preferences for groups is dependent on several factors. First, training is required to ensure that observers can associate the names on a data sheet with the relevant members of the group. Second, it must be possible to view all members of the group from a single perspective (playgrounds, recreation rooms, open classrooms, etc.). Third, our data suggest that 4 to 5 s per child was satisfactory to find and record location and engagement reliably and that recording these behaviors every 90 s per child was sufficiently accurate for the types of performance we were measuring. This interval size is likely to have good generality in that is seems to reflect the natural abilities of human transducers. However, the necessary and sufficient size of both intervals for producing usable measures may be affected by the group size, the patterns of performances measured, and the familiarity of the observers with the measurement system and group members. In situations in which these factors may be considerably different than those described in the current study (e.g., the group is considerably larger, the members of the group switch activities much less often, or the observers have more extended histories with members in the group), using the process by which the measurement system was evaluated in the current study may be more beneficial than adopting the specific measurement system that was a context-dependent outcome of our process.

Perhaps the most important indicator of the utility of this measurement system, or one derived using a similar process, is the extent to which the measures are sensitive to functional independent variables. To that end, the measurement system described herein was used to show the influence of satiation and embedded reinforcement on children's preferences during free play (Hanley, Tiger, Ingvarsson, & Cammilleri, unpublished data).

As noted earlier, most preference assessments are geared towards identifying one or a few items or events for use in differential reinforcement programs (Ivancic, 2000); however, as described in the current study, results of preference assessments can also convey how well an environment is supporting desirable behavior. This information can be used to optimize the positive impact of shared environments. Considering the fact that many young children spend a significant proportion of their time in child-care settings (National Institute of Child Health and Human Development, 2003), the early childhood classroom is an ideal context for determining and capitalizing on early preferences. Embedding learning opportunities and active teaching within children's most preferred activities is likely to yield two desirable outcomes. The short-term gain may be that children will be more engaged and less likely to display undesirable behavior. The long-term gain may be that positive dispositions towards learning (i.e., a higher probability of seeking out rather than avoiding challenging learning opportunities) may be developed. Both are speculations that require empirical validation. However, both may be addressed by first adopting measurement systems similar to the one described herein.