Skip to main content
PMC home page
Springer logoLink to Springer
. 2007 Aug 28;184(2):143–156. doi: 10.1007/s00221-007-1085-y

Visual and musculoskeletal underpinnings of anchoring in rhythmic visuo-motor tracking

Melvyn Roerdink 1,✉, Ellen D Ophoff 1, C (Lieke) E Peper 1, Peter J Beek 1
PMCID: PMC2080346  PMID: 17724583

Abstract

Anchoring, that is, a local reduction in kinematic (i.e., spatio-temporal) variability, is commonly observed in cyclical movements, often at or around reversal points. Two kinds of underpinnings of anchoring have been identified—visual and musculoskeletal—yet their relative contributions and interrelations are largely unknown. We conducted an experiment to delineate the effects of visual and musculoskeletal factors on anchoring behavior in visuo-motor tracking. Thirteen participants (reduced to 12 in the analyses) tracked a sinusoidally moving visual target signal by making flexion–extension movements about the wrist, while both visual (i.e., gaze direction) and musculoskeletal (i.e., wrist posture) factors were manipulated in a fully crossed (3 × 3) design. Anchoring was affected by both factors in the absence of any significant interactions, implying that their contributions were independent. When gaze was directed to one of the target turning points, spatial endpoint variability at this point was reduced, but not temporal endpoint variability. With the wrist in a flexed posture, spatial and temporal endpoint variability were both smaller for the flexion endpoint than for the extension endpoint, while the converse was true for tracking with the wrist extended. Differential anchoring effects were absent for a neutral wrist posture and when gaze was fixated in between the two target turning points. Detailed analyses of the tracking trajectories in terms of velocity profiles and Hooke’s portraits showed that the tracking dynamics were affected more by wrist posture than by gaze direction. The discussion focuses on the processes underlying the observed independent effects of gaze direction and wrist posture on anchoring as well as their implications for the notion of anchoring as a generic feature of sensorimotor coordination.

Keywords: Anchoring, Eye–hand coordination, Manual tracking, Coordination dynamics, Visual information, Wrist position, Visuo-motor control, Movement trajectories

Introduction

Although cyclical movements have often been understood and modeled as self-sustained oscillators or limit cycles (Beek et al. 1996; Haken et al. 1985; Kay et al. 1987), their trajectories in phase space (velocity against position) are typically wrinkled and asymmetric, rather than perfectly harmonic and symmetric. A better approximation can be achieved by adding Gaussian white noise to the limit cycle description (Kay 1988), but this is insufficient to account for the observation that cyclical movements are characterized by specific regions of reduced kinematic (i.e., spatio-temporal) variability, which are often, but not solely, located at or around the maximal angular excursions or movement endpoints. Such regions have been dubbed “anchor points”, implying that they serve as ““intentional attractors” or “organizing centers” within, and for” the entire cycle production (Beek 1989; pp 183–184; cf. Beek et al. 1992). Beek (1989) conjectured that at, or around, anchor points critical task-specific information is available for organizing a cyclical act (in his case ball juggling). In line with this conjecture, Kelso and Jeka (1992) concluded from the representation of 4-limb patterns as a single trajectory on a 3-D torus that the essential information for coordination is confined or localized to discrete regions in phase space. In several subsequent studies on rhythmic movement conducted from a dynamical systems perspective, anchor points or anchoring phenomena have been observed, discussed and even modeled. In order to motivate the purpose and design of the present study, it is necessary to highlight the various aspects of anchoring that have been identified so far in the literature.

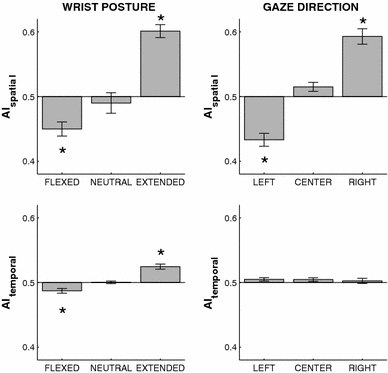
Further evidence for anchoring was obtained in a study by Byblow et al. (1994) in which participants performed bimanual cyclical wrist movements in both in-phase and antiphase coordination, either at a self-paced tempo or to the beat of a metronome that increased in frequency. In both cases, a local reduction of spatial variability was found at maximal angular excursions, which was more pronounced for the dominant than for the non-dominant hand, and more so for pronation than for supination (see also Carson et al. 1994). In a subsequent study, Byblow et al. (1995) reported the same spatial anchoring phenomenon for unimanual rhythmic movements that were synchronized to either a discrete or a continuous visual pacing signal, which led the authors to conclude that anchoring is not dependent on discrete information pulses, but may also occur if the external pacing signal is continuous. Importantly, in this series of studies, anchoring was defined in terms of reduced endpoint variability. The authors assumed that the movement reversal points were also the “regions of the kinematics where information is specified” (p. 124). However, for paced movements, this need not be the case because reduced endpoint variability does not necessarily imply that participants also timed their maximal excursions to the (discrete or continuous) external signal. For this reason, it is important to distinguish between anchoring as reduced spatial variability and as reduced variability in the timing of the movement excursions relative to the beats or the reversal points of the metronome. This difference is illustrated in Fig. 1, which shows the phase plane of a unimanual rhythmic wrist movement that is synchronized to a continuous visual signal with a stationary frequency. As can be readily appreciated from the figure, the reduced variability at one of the endpoints (as indicated by the arrows) does not imply that the temporal locations of the visual signal (as indicated by the circles) coincided with the movement reversal points. Therefore, both aspects should be addressed in a complete analysis of anchoring behavior.

Fig. 1.

Fig. 1

Open in a new tab

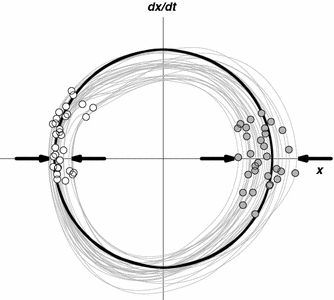
Exemplary phase portrait of rhythmic isofrequency wrist oscillations during an in-phase visuo-motor tracking task. Spatial anchoring, that is points or regions of reduced movement variability, are typically observed at or around movement reversal points (viz. at peak wrist flexion (left) in this example). White and gray circles represent the time indices of left and right target turning points (i.e., the movement reversals of the visual metronome), which were used to determine temporal anchoring

The finding of Byblow et al. (1994) that anchoring depended on whether a pronation or a supination movement was performed was replicated by Byblow et al. (1995) and led to the notion that anchor points are differentiated in terms of their stability due to differences in musculoskeletal properties. Further support for this notion was found by Carson (1996) and Carson and Riek (1998) in an experimental set-up in which participants were instructed to either flex or extend their index finger to an auditory metronome. Performance was found to be more stable in the flex-on-the-beat pattern than in the extend-on-the-beat pattern, especially when the forearm was in a supine position as opposed to a prone or neutral position. With this series of studies, the notion of anchoring became confined to the situation in which a particular point in the movement cycle is synchronized with an auditory metronome, in spite of its more generic original definition. As a result of this narrowing, anchoring was reduced to a purely local effect, which gave Fink et al. (2000) the opportunity to emphasize that anchoring, so defined, also carries global consequences for the overall coordinative pattern, even though this aspect was already inherent to the original formulation of anchoring by Beek (1989). The point was driven home by showing that the bimanual coordination was more stable when both movement reversal points of each finger movement (i.e., peak flexion and peak extension) were paced or ‘anchored’ (so-called double-metronome condition) as opposed to when only one reversal point was ‘anchored’ (single-metronome condition). These effects were explicitly modeled by Jirsa et al. (2000) using a parametric stabilization term which preserves the stability properties of bimanual coordination as captured by the well-known model of Haken et al. (1985) for phase transitions in rhythmic arm and hand movements, while also explaining the varying stability of movement under the two metronome conditions.

Another form of anchoring in the literature on eye–hand coordination is known as “gaze anchoring”, which refers to the phenomenon of an enforced ocular target fixation for the duration of the entire pointing movement (Neggers and Bekkering 2000, 2001, 2002). When pointing to a target the pointing movement is preceded by a saccadic eye movement to the target (Prablanc et al. 1979). This saccadic eye movement is not only correlated to the start of the arm movement, but the coupling between gaze and aiming movements is also observable after pointing initiation, and it appears that the central nervous system demands ocular fixation of the pointing target until pointing is completed (Neggers and Bekkering 2000, 2001, 2002). When participants do not foveate on the homing-in phase of movements, pointing accuracy deteriorates (Neggers and Bekkering 1999; Prablanc et al. 1979; Vercher et al. 1994), which suggests that gaze anchoring serves to facilitate the planning and execution of pointing movements.

The significance of gaze fixations for the dynamical characteristics of cyclical movements became apparent in a recent study on the (de)stabilizing effects of transformed feedback on visuo-motor tracking by Roerdink et al. (2005). When feedback was absent (i.e., during normal tracking), right endpoint variability was smaller than left endpoint variability when participants fixated at the right, whereas the converse was true when participants fixated at the left. Left and right endpoint variability was similar during gaze fixations at the center and when smoothly pursuing the target signal. Those findings may be interpreted to imply that participants actively created visuo-motor anchors by fixating their gaze at one of both endpoints, without being instructed to do so (i.e., gaze direction was not manipulated in the experiment). However, the observation that gaze fixations may promote motor anchoring does not exclude the possibility that musculoskeletal properties played into the observed anchoring phenomena as well. Indeed, Roerdink et al. (2005) also found clear indications that anchoring was affected by musculoskeletal properties. In the conditions with visual feedback gaze fixation at the right resulted in reduced right endpoint variability, as was the case without feedback, but now gaze fixation at the center also resulted in reduced endpoint variability at the right, while no anchoring was observed for gaze fixation at the left. Detailed analyses of the data revealed that, compared to the condition without visual feedback, participants had shifted the center of their hand excursions to the right in the conditions with visual feedback in an apparent effort to align the feedback signal with the target signal. This rightward shift could well have affected the relative contributions of antagonistic muscle groups (i.e., by increasing the active contribution of the wrist extensors and decreasing that of the wrist flexors to the hand excursions that were performed with the right hand), as well as the possibilities for storage and recovery of elastic strain energy in muscles and tendons. Although the viscosity of the wrist joint is negligible, and passive elastic torques are generally small, the latter become sizeable at larger wrist excursions (Lehman and Calhoun 1990), and are known to affect the muscular production of wrist movement (Schieber and Thach 1985). In sum, Roerdink et al. (2005) found firm support for visual underpinnings of anchoring in the form of anchoring promoting effects of gaze fixations, as well as clear indications of musculoskeletal contributions, in line with the existing evidence in the literature that anchoring phenomena are governed by both visual and musculoskeletal factors.

However, as the preceding summary of the pertinent literature illustrates, the effects of visual and musculoskeletal factors of anchoring have not yet been investigated in any systematic fashion, and several theoretically important issues still need to be addressed. For one, the relative contributions of visual and musculoskeletal factors to anchoring are unknown, with researchers placing theoretical emphasis on either type of factor. Furthermore, it is unknown whether the effects of visual and musculoskeletal factors on anchoring are independent (i.e., additive) or dependent (i.e., interactive). To resolve those issues, we conducted an experiment that was specifically designed to systematically delineate the effects of visual and musculoskeletal factors on anchoring behavior in visuo-motor tracking. Our choice for this particular experimental task and set-up was motivated from our previous study on the effects of visual feedback on visuo-motor tracking, which revealed clear instances of visuo-motor anchoring with marked effects of gaze direction and strong hints of wrist posture effects, even though neither of these factors was varied explicitly (Roerdink et al. 2005). Based on those previous results, we expected that systematic manipulations of both factors—with other variables such as tracking frequency and tracking mode being kept constant—would have clearly discernible effects on anchoring, both in terms of its spatial and temporal characteristics. Due to the absence of relevant data, however, we had no specific expectations with respect to their relative contributions to anchoring or the possibility of interaction effects in that regard. In line with the original definition of anchoring, as well as the insights of Fink et al. (2000), we expected both gaze direction and wrist posture to not only influence local features of the dynamics of visuo-motor tracking but also its global organization.

Methods

Participants

Thirteen persons (2 men and 11 women, aged 21–50 years) volunteered to participate in the study. All participants were right-handed, according to their scores on a shortened version of the Edinburgh handedness inventory (Oldfield 1971), and had normal or corrected to normal vision. Participants gave their written informed consent prior to the experiment, which was approved by the ethics committee of the Faculty of Human Movement Sciences at VU University Amsterdam.

Apparatus

Participants were seated on a height-adjustable chair behind a rack on which a vertically oriented manipulandum was mounted (Fig. 2, upper panel). The manipulandum was attached to a rotatable horizontal lever whose axis was aligned with the wrist’s flexion–extension axis. The right hand was strapped to the flat manipulandum (fingers extended and thumbs up), allowing flexion and extension movements about the wrist. Angular position of the wrist was registered by means of a potentiometer (Labmaster, sampling frequency 1,000 Hz), which was positioned underneath the manipulandum. An armrest with two adjustable supports, located on both sides of the forearm just proximal of the wrist joint, was used to prevent forearm movement.

Fig. 2.

Fig. 2

Open in a new tab

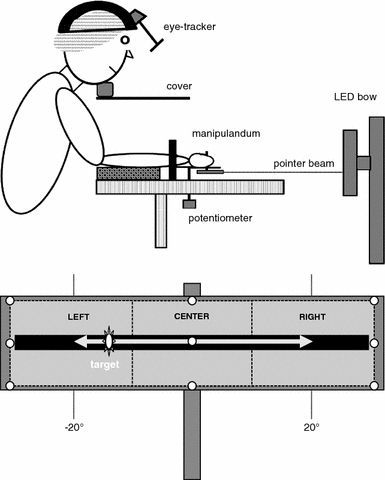
Schematic representation of the experimental set-up. Upper panel Schematic side view of the experimental set-up. Lower panel LED bow from participant’s perspective, with the calibration field superimposed by means of the nine white circles

A semicircular projection bow was positioned in front of the participant at a distance of 113 cm from the rotation axis of the potentiometer, matching the radius of the bow (see Fig. 2, lower panel). The projection bow consisted of a continuous array of 448 light-emitting diodes (LEDs). A harmonically oscillating target signal was projected on the LED bow. Concurrent visual feedback of the angular position of the wrist was provided by means of a laser pointer attached to the manipulandum pointing 22 mm below the trace of the target signal.

The participant’s chin was placed on a height-adjustable chinrest and the head was secured with straps between two vertical supports to prevent head movements. A horizontal cover was attached to the chinrest, which prevented vision of the moving hand (Fig. 2). Left eye orientation was monitored via reflection of pupil–cornea boundaries in near-infrared light (Applied Systems Laboratories, series 5000 Eye Tracker, sampling frequency 50 Hz, spatial error <0.6°). To determine the participant’s point-of-gaze, eye orientation was calibrated using a nine-point calibration field attached to the LED bow (Fig. 2, lower panel). The experimenter received online feedback of the point-of-gaze on a video screen. Eye orientation was recalibrated when necessary (i.e., in case of an apparent mismatch between the actual point-of-gaze and its appearance on the video screen).

The rack with armrest and manipulandum could be positioned in different orientations with respect to the LED bow, allowing manipulation of wrist posture (see below). Each rack orientation was calibrated to the LED bow to facilitate direct comparison of target and feedback signals as well as for offline comparison of target signal and potentiometer data (both expressed in °). Point-of-gaze was expressed in °, allowing for a comparison of point-of-gaze and the target signal. Eye-tracker data were synchronized with potentiometer and LED bow data.

Procedure

In the experimental trials, participants were instructed to follow the oscillating target signal. The amplitude of the target signal was selected to correspond to 20° of hand motion, because Peper and Beek (1998) had established that this was, on average, the preferred amplitude for this kind of experimental task and set-up. The target signal oscillated at 1.8 Hz, that is, with a frequency at which frequency-locked point-of-gaze oscillations were found to be absent for this experimental task and set-up (cf. Roerdink et al. 2005).

Participants tracked the target signal under experimental manipulation of gaze direction and wrist posture. Participants were instructed to direct their gaze to one of three fixation points defined in relation to the oscillating target signal, that is, the left target turning point, the right target turning point, or the center in between the two target turning points (Fig. 3). Wrist posture was manipulated by bringing the wrist in a flexed, neutral, or extended posture (Fig. 3). In the flexed posture the rack with armrest and manipulandum was positioned such that the participant’s forearm was rotated 40° clockwise with respect to the neutral position, whereas in the extended posture the forearm was rotated 40° counterclockwise with respect to the neutral posture. Prior to the experiment the participant’s range of motion was determined: the hand was secured to the manipulandum and the voluntarily achieved maximal wrist flexion and extension positions were measured. The center of this range was considered the neutral wrist posture for the participant in question. In the neutral posture the wrist was on average flexed 12.7° (±3.5°) relative to the position in which the forearm was aligned with the palm of the hand. For all participants, the range of experimental wrist postures fell well within the individually determined maximal range of motion (154.6° ±18.5°), covering on average 77.4% when the additional excursions corresponding to the amplitude of the target signal were taken into account.

Fig. 3.

Fig. 3

Open in a new tab

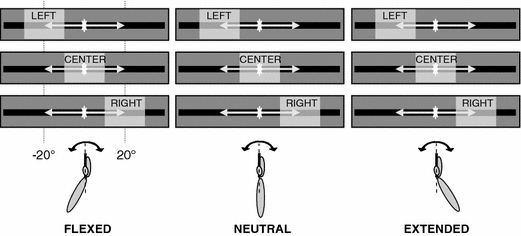
Schematic representation of the experimental design, consisting of all nine combinations of wrist posture (flexed, neutral, extended), induced by altering the orientation of the forearm with respect to the oscillating hand, and gaze direction (left, center, right), schematically represented by transparent rectangles

The three wrist postures (i.e., flexed, neutral, and extended) were crossed with the three gaze directions (i.e., left, center, and right region of the target signal), resulting in nine experimental conditions (see Fig. 3 for a schematic representation). Participants performed all conditions five times, amounting to a total of 45 trials per participant. Trials were presented in blocks with the three wrist postures providing the first level of blocking (3 × 15 trials) and gaze direction (3 × 5 trials) the next. The order of the wrist posture blocks was counterbalanced over participants (with each order being performed by two participants; full counterbalancing was possible because the data of one participant were discarded, see below). The gaze direction blocks within the wrist posture blocks were presented in random order. Prior to each wrist posture block, participants were invited to familiarize themselves with each new wrist posture through making self-paced wrist movements. The laser pointer provided direct feedback of the hand movement during both familiarization and experimental trials. Participants were instructed to move their hand in phase with the oscillating target signal as accurately as possible while directing their gaze to the instructed fixation point (left, center, or right). To facilitate trial initiation, the target signal always started at the attended area. All trials lasted 20 s (i.e., 36 cycles).

Data analysis

The data of one participant were excluded from the analysis because the point-of-gaze data were disturbed (i.e., pupil–cornea boundaries were often undetectable due to ‘squeezing’ of the eyes, i.e., partial eye closures). For the remaining 12 participants point-of-gaze was assessed (in °) for each trial to ensure that they had adhered to the task instructions regarding gaze direction. Specifically, the horizontal point-of-gaze data were classified according to three groups, viz. left, center and right, defined by regions of ±10° centered around −20° (left target turning point), around 0° (center in between the two target turning points) and around +20° (right target turning point), respectively. As is common in eye-tracking, missing or disturbed values occasionally occurred due to blinking or brief eye closures. For a trial to be included in the analyses, at least 80% of the horizontal point-of-gaze samples had to fall within the range from −30° to 30°, while in turn at least 80% of those samples had to fall within the instructed region. Based on this nested criterion, 63 out of the total of 540 trials were discarded. For the 477 included trials gaze was directed to the instructed region (i.e., left, center or right) on average 98.8% of the time. All participants successfully performed the tracking task in that the mean tracking frequency, defined as the inverse of the period between maximal extensions of the wrist, of the included trials was 1.80 Hz with a very small overall standard deviation (±4.0 × 10−5 Hz). One trial was removed because of phase wrapping, which occurred to catch up after a late start.

Pre-processing

Potentiometer data (hand movement) and LED coordinates (target) of the included trials were transformed into ° and low-pass filtered using a bi-directional second-order Butterworth filter (cut-off frequency: 15 Hz). The first five cycles of each trial were excluded from analysis to eliminate possible transient effects. From the remaining 31 cycles several dependent variables were calculated. Those variables related to tracking performance, anchoring, and global kinematics, respectively.

Tracking performance

Tracking accuracy was determined by calculating the root mean square (RMS) of the continuous error between target and hand movement, which was obtained by subtracting the actual position from the required position. In addition, the continuous relative phase (in °) between the target signal and the hand movement was calculated by subtracting the phase of the hand oscillations from that of the target oscillations. Mean relative phase (ϕ) and its transformed circular variance (TCV) were quantified using circular statistics (cf. Burgess-Limerick et al. 1991; Mardia 1972).

Anchoring

In both discretely and continuously paced cyclical movements, as well as in ‘self-paced’ rhythmic movements, anchoring typically occurs at, or around, the movement reversal points (see also Fig. 1), where it may become manifest as a reduction of spatial (e.g., Byblow et al. 1994, 1995; Fink et al. 2000; Roerdink et al. 2005) or temporal (e.g., Roerdink et al. 2007) variability, or both. We therefore determined (a) the spatial variability of maximal wrist flexion and extension excursions by calculating the respective standard deviations (SD in °), and (b) the temporal variability between the time instances of the left and right target turning points and the corresponding time instances of maximal wrist flexion and extension excursions (SD in ms). To quantify the presence or absence of anchor points in the tracking trajectories, variants of the following general anchoring index (AI, dimensionless)

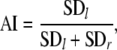graphic file with name M1.gif

were calculated in which SDl and SDr represent the spatial or temporal variability corresponding to the left and right target turning point, respectively. If SDl and SDr are equal, AI = 0.5. AI < 0.5 corresponds to smaller spatial or temporal variability at the left than at the right target turning point (i.e., anchoring at peak flexion), whereas the opposite is true for AI > 0.5 (i.e., anchoring at peak extension). AIspatial and AItemporal denote the anchoring index for spatial and temporal variability, respectively.

The anchoring index captures local effects of wrist posture and gaze direction in predefined regions of the tracking trajectories. In theory, anchor points or regions may be found elsewhere in the movement cycle, but a first inspection of the data indicated that anchoring occurred at or near the endpoints (see also Fig. 1), as indeed was found in the previous studies on anchoring cited in the Introduction. However, to avoid that we would miss important kinematic aspects of the tracking trajectories, we not only focused on the effects of wrist posture and gaze direction around movement reversal points, but also on more global properties of the tracking trajectories.

Global kinematics

The global properties of the tracking trajectories were assessed by means of the velocity profiles (i.e., wrist angular velocity as a function of cycle time) and Hooke’s portraits (i.e., wrist angular acceleration as a function of wrist angular position). To assess those properties, wrist angular position time series were normalized to the amplitude of the target signal (i.e., −1 implies target turning point on the flexion side, +1 implies target turning point on the extension side), after which the normalized position time series were mean centered. Next, velocity and acceleration time series were computed from the position time series by means of a conventional 3-point difference algorithm and normalized to the angular velocity of the target signal (i.e., divided by 3.6π). Based on the minima of the position time series, corresponding to maximal wrist flexion, each cycle was cut from the velocity time series (i.e., from maximal flexion via maximal extension to maximal flexion). The individual velocity profiles were time-normalized to 200 points using a spline interpolation procedure, i.e., a normalization to percentage cycle time, and the average velocity profile was calculated for each participant for each included trial. From this average velocity profile the duration of flexion and extension movements were taken and summarized in the movement duration index (MDI, dimensionless), expressed as:

graphic file with name M2.gif

in which MDflexion (MDextension) is the duration from maximal wrist extension (flexion) to maximal wrist flexion (extension). If MDflexion and MDextension are equal, MDI = 0.5. MDI < 0.5 corresponds to shorter duration of the flexion than the extension half cycle, whereas the opposite is true for MDI > 0.5. Furthermore, peak velocities for the flexion and extension movements were taken (i.e., PVflexion and PVextension, respectively) and represented in the peak velocity index (PVI, dimensionless), expressed as:

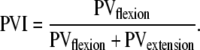graphic file with name M3.gif

If PVflexion and PVextension are equal, PVI = 0.5. PVI < 0.5 indicates that flexion peak velocity is smaller than extension peak velocity, whereas the opposite is true for PVI > 0.5. Note that for harmonic wrist oscillations, PVI and MDI both approach 0.5.

The Hooke’s portraits were constructed as follows. Based on the extrema in the normalized wrist angular position time series, corresponding to peak flexion and extension, each half cycle was cut from the position and acceleration time series (i.e., from peak flexion to peak extension and from peak extension to peak flexion). The position and acceleration half cycles were time-normalized to 100 points using a spline interpolation procedure. Next, the average position and acceleration time series were computed for every half cycle for each trial of each participant. A linear (harmonic) oscillator implies a straight line in the Hooke’s portrait, whereas a deviation from a straight line represents the contribution of nonlinear components. The amount of variance that can be attributed to a harmonic oscillation can be readily quantified by the r2 of the linear regression of position onto acceleration (i.e., r2 = 1 for a purely harmonic oscillation such as the target signal). The explained variance of the summed contribution of nonlinear terms was expressed as NL = 1 − r2 (Mottet and Bootsma 1999; for a similar approach see Beek and Beek 1988).

Statistical analysis

To determine the effects of wrist posture and gaze direction on tracking behavior, each dependent variable was submitted to a repeated measures analysis of variance (ANOVA) with within-subject factors wrist posture (3 levels: flexed, neutral, extended) and gaze direction (3 levels: left, center, right). Individual scores per condition were obtained by averaging the values of the included trials for the condition in question. Significant effects (P < 0.05) are reported, and effect sizes are represented as partial eta squared values 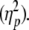Inline graphic Post-hoc analysis was performed using two-tailed paired-samples t tests (with Bonferroni correction). One-sample t tests were conducted to see whether AIspatial and AItemporal differed significantly from 0.5 (the value indicating that spatial or temporal variability corresponding to the left and right target turning point are similar).

Results

Effects of wrist posture

Wrist posture had significant effects on the variability of the relative phase between tracking and the target signal (TCV), the spatial and temporal anchoring indices (AIspatial, AItemporal), the velocity profile characteristics (MDI, PVI) and the harmonicity (NL) of tracking trajectories (see Table 1). Tracking accuracy (RMS; mean ± standard error = 6.0° ±0.3°) and mean relative phase (ϕ; −5.2° ±2.1°, indicating that wrist oscillations were slightly leading the target signal) did not differ significantly over wrist postures. Post-hoc analysis indicated that TCV was significantly larger for the extended wrist posture (21.7° ±1.2°) than for the flexed posture (19.4° ±0.9°), while TCV for the neutral posture (19.9° ±1.4°) was not significantly different from the flexed and extended posture.

Table 1.

Results of the repeated measures ANOVA on dependent variables

Dependent variable Wrist posture Gaze direction Posture × gaze
F(2, 22) P 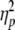Inline graphic F(2, 22) P 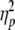Inline graphic F(4, 44) P 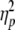Inline graphic
RMS 1.67 NS 0.13 0.60 NS 0.05 1.85 NS 0.14
ϕ 0.49 NS 0.04 9.46 <0.005 0.46 0.84 NS 0.07
TCV 4.38 <0.05 0.28 1.39 NS 0.11 1.20 NS 0.10
AIspatial 36.10 <0.001 0.77 81.60 <0.001 0.88 0.39 NS 0.03
AItemporal 32.55 <0.001 0.75 0.26 NS 0.02 1.39 NS 0.11
PVI 48.25 <0.001 0.81 13.11 <0.001 0.54 1.45 NS 0.12
MDI 41.73 <0.001 0.79 14.79 <0.001 0.57 1.55 NS 0.12
NL 7.09 <0.005 0.39 3.13 NS 0.22 1.73 NS 0.14
Open in a new tab

Main effects of wrist posture and gaze direction and wrist posture × gaze direction interaction effects are presented

RMS root mean square of the continuous error between target and hand movement, ϕ mean relative phase between target and hand movement, TCV transformed circular variance of ϕ, AIspatial spatial anchoring index, AItemporal temporal anchoring index, PVI peak velocity index, MDI movement duration index, NL contribution of nonlinear terms to tracking trajectories

AIspatial for the extended wrist posture differed significantly from that for the neutral and flexed posture, while AItemporal differed significantly between all wrist postures. Importantly, both anchoring indices differed from 0.5 for the flexed and extended postures, but not for the neutral posture (see Fig. 4, left panels). One-sample t tests revealed that AIspatial and AItemporal were significantly smaller (0.450 and 0.487, respectively) than 0.5 in the flexed posture (t(11) = −4.72, P < 0.001 and t(11) = −3.57, P < 0.005, respectively) and significantly greater (0.601 and 0.525, respectively) than 0.5 in the extended posture (t(11) = 10.01, P < 0.001 and t(11) = 6.33, P < 0.001, respectively), indicating that anchoring occurred at maximal flexion and extension, respectively.

Fig. 4.

Fig. 4

Open in a new tab

Spatial and temporal anchoring indices as a function of wrist posture (left panels) and gaze direction (right panels). Asterisks indicate significant differences with AI = 0.5. Error bars represent standard error

These indications of anchoring were accompanied by significant changes in the tracking trajectories, as can be appreciated from the averaged velocity profiles depicted for each wrist posture in Fig. 5 (left column). The cycle duration of the flexion (extension) phase was shorter than 50% for tracking with the wrist in a flexed (extended) posture. Furthermore, flexion peak velocity was higher than extension peak velocity for tracking with a flexed wrist posture, while the opposite was the case for tracking with an extended wrist posture. In a neutral wrist posture, the velocity profile was nearly harmonic, with similar flexion and extension half cycle durations and peak velocities. These observations were all confirmed statistically. Specifically, a significant main effect of wrist posture was observed for PVI and MDI (see Table 1): post-hoc analysis indicated that PVI and MDI differed significantly for all three wrist postures. One-sample t tests revealed that, in the flexed wrist posture, the duration of the flexion phase was significantly shorter than that of the extension phase (i.e., MDI = 0.473; t(11) = −3.47, P < 0.01), while flexion peak velocity was significantly higher than extension peak velocity (i.e., PVI = 0.539; t(11) = 3.92, P < 0.005). In the extended wrist posture, the converse was true (MDI = 0.538; t(11) = 7.52, P < 0.001; PVI = 0.444; t(11) = −6.53, P < 0.001), indicating shorter extension phase duration and higher extension peak velocity. In the neutral wrist posture condition, both PVI (0.510) and MDI (0.494) did not differ significantly from 0.5.

Fig. 5.

Fig. 5

Open in a new tab

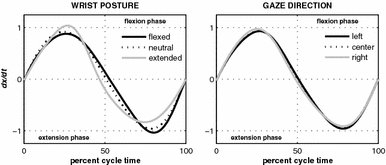
Mean normalized velocity profiles as a function of wrist posture (left panel) and gaze direction (right panel). For a harmonic oscillator extension and flexion peak velocities equal 1 and −1, respectively, while the zero crossing of the velocity profile occurs at the vertical dashed line, indicating that the extension and flexion phase have the same duration

The most striking aspect of the Hooke’s portraits was the general tendency to deviate from a straight line (representing harmonic oscillation) with the wrist flexed or extended. Fig. 6 shows averaged Hooke’s portraits of the flexion and extension half cycles for each combination of wrist posture and gaze direction. The panels in the rows show the Hooke’s portraits for each wrist posture. As is evident from the figure, the harmonicity was reduced in the flexed and extended wrist posture compared to the neutral wrist posture (larger deviations from the line acceleration = −position), especially for tracking with the wrist extended. This was also reflected in the variance that was attributed to nonlinear components as quantified by NL (reflecting the residual of the linear regression of position onto acceleration). In particular, a significant main effect of wrist posture was observed for NL (see Table 1). Post-hoc analysis revealed that the contribution of nonlinear terms was significantly greater in the extended wrist posture compared to the neutral wrist posture (NL = 0.154 ± 0.02 and 0.073 ± 0.01, respectively). NL for tracking with the wrist in a flexed posture (NL = 0.110 ± 0.02) did not differ significantly from the other two wrist postures. Note that the reduced harmonicity of tracking in the extended wrist posture may well have caused the significant increase in TCV in the extended wrist posture relative to that of the flexed posture.

Fig. 6.

Fig. 6

Open in a new tab

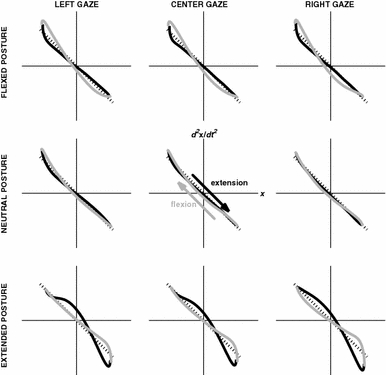
Hooke’s portraits as a function of gaze direction (columns: left, center, right) and wrist posture (rows: flexed, neutral, extended) with flexion and extension half cycles indicated in gray and black, respectively. The dotted black line represents the Hooke’s portrait for the harmonically moving target signal

Effects of gaze direction

Gaze direction had significant effects on mean continuous tracking relative phase (ϕ), the spatial anchoring index (AIspatial) and velocity profile properties (MDI, PVI), but not on tracking accuracy (RMS), relative phase variability (TCV), the temporal anchoring index (AItemporal) and the harmonicity (NL) of tracking trajectories (see Table 1). Post-hoc analysis revealed that ϕ was significantly less negative when gaze was directed to the right (−1.6° ±2.6°) than when gaze was directed to the left (−6.5° ±1.4°) or the center (−7.5° ±1.9°) region.

Post-hoc analysis further revealed that AIspatial differed significantly between all three gaze directions. Moreover, one-sample t tests revealed that AIspatial was significantly smaller than 0.5 when gaze was directed to the left target turning point (0.433; t(11) = −6.73, P < 0.001), indicating smaller left (corresponding to maximal flexion excursions) than right (corresponding to maximal extension excursions) endpoint variability (see Fig. 4, upper right panel). Similarly, AIspatial was significantly larger than 0.5 when gaze was directed to the right target turning point (0.593; t(11) = 7.77, P < 0.001), indicating anchoring at the right (extension) endpoint. AIspatial was not significantly different from 0.5 when gaze was directed at the center region between the two target turning points (AIspatial = 0.515). Whereas gaze direction had a strong effect on the spatial anchoring index 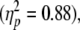Inline graphic the effect of gaze direction on AItemporal was not significant, as can be appreciated from Fig. 4 (lower right panel; see also Table 1).

The right panel in Fig. 5 depicts the averaged velocity profiles as a function of gaze direction. The effect of gaze direction on the velocity profile characteristics PVI and MDI was much smaller than that of wrist posture (i.e., smaller deviations from 0.5; compare also the corresponding effect sizes in Table 1). Nevertheless, the significant main effect of gaze direction entailed that when gaze was directed to the right target turning point PVI and MDI were significantly different from the other two gaze directions (for left, center, and right, respectively: PVI = 0.508, 0.499, and 0.486; MDI = 0.494, 0.500, and 0.511). One-sample t tests indicated that when gaze was directed to the target turning points (left or right), the hand movements in that direction were shorter in duration with a larger peak velocity. As is apparent from a comparison of the Hooke’s portraits depicted in the columns of Fig. 6, gaze direction only had a limited influence on the nonlinear terms in the hand oscillations (particularly if compared to the effect of wrist posture, as presented in the three rows of Fig. 6). The effect of gaze direction on NL was not significant (left 0.115 ± 0.01; center 0.105 ± 0.01; right 0.118 ± 0.01).

Wrist posture × gaze direction interaction effects

None of the dependent variables showed a significant wrist posture × gaze direction interaction effect (see Table 1), implying that the respective effects of the two factors were independent and additive in case both yielded significant main effects. A case in point is the spatial anchoring index AIspatial (see Table 1). Both wrist posture and gaze direction had a significant effect on AIspatial in the absence of a significant wrist posture × gaze direction interaction effect. Fig. 7, presenting AIspatial for all combinations of wrist posture and gaze direction, illustrates the additive manner in which the two factors affected spatial anchoring (cf. the ‘staircase’ pattern in each wrist posture condition).

Fig. 7.

Fig. 7

Open in a new tab

Spatial anchoring index for all combinations of wrist posture (flexed, neutral, extended) and gaze direction (left [L], center [C], right [R]). Asterisks indicate significant differences with AIspatial = 0.5. Error bars represent the standard error

Discussion

In the present experiment we sought to systematically delineate the effects of visual and musculoskeletal factors on anchoring phenomena, that is, local reductions in kinematic variability, which may reflect “organizing centers” for perceptual-motor control. In particular, we investigated the relative contributions of gaze direction and wrist posture on both spatial and temporal anchoring in the performance of a rhythmic, unimanual visuo-motor tracking task. In addition, we examined the velocity profiles and Hooke’s portraits of the full tracking trajectories to gain insight into the relationship between the local anchoring phenomena and the global organization of the tracking movements. In the following, we first outline the main findings of both types of analysis before discussing their broader implications for the theoretical understanding of anchoring.

Effects on spatial and temporal anchoring

As stated in the introduction, previous research revealed that the degree of anchoring is a function of musculoskeletal properties, such as the type of movement performed (i.e., flexion versus extension, pronation vs. supination) and the relative length of flexor and extensor muscles. Besides musculoskeletal influences, Roerdink et al. (2005) also reported evidence for visual underpinnings in that anchoring was found to depend on gaze direction. Based on those findings we expected that systematic manipulations of gaze direction and wrist posture would have clearly discernable effects on anchoring, which was indeed the case.

Both gaze direction and wrist posture significantly affected endpoint variability in the expected direction (see Fig. 4, upper panels). Specifically, when gaze was directed to the left target turning point, left (i.e., flexion) spatial endpoint variability was reduced while the converse was true when gaze was directed to the right target turning point. In contrast, differential anchoring effects were absent when gaze was fixated in between the two target turning points. Furthermore, endpoint variability was smaller for the extension endpoint than for the flexion endpoint when the wrist was in an extended posture, whereas differential anchoring effects were absent when tracking was performed with the wrist in a neutral posture. All of these findings are fully in line with those of Roerdink et al. (2005), even though gaze direction and wrist posture were systematically manipulated only in the present study. Moreover, the current systematic variations of wrist posture also revealed that for the flexed wrist posture flexion endpoint variability was lower than extension endpoint variability.

In addition to spatial anchoring we examined temporal anchoring, that is, local reductions in the variability of the timing of the maximal movement excursions relative to the reversal points of the visual metronome, an aspect that was not addressed in previous studies. This complementary analysis revealed that temporal anchoring was affected by wrist posture but not by gaze direction, suggesting that wrist posture had a different, more pronounced effect on anchoring than gaze direction (see Fig. 4, lower panels). Specifically, with the wrist in a flexed posture the variability in the timing of flexion excursions relative to the target was lower than that of extension excursions while the converse was true with the wrist extended. No differential effect in timing variability was observed for tracking with the wrist in a neutral posture nor for the three different gaze directions. These findings suggest that movements were actively timed or anchored on maximal flexion with the wrist in a flexed posture and on maximal extension with the wrist in an extended posture. In contrast, the absence of an effect of gaze direction on temporal anchoring may imply that gaze direction only affected the spatial accuracy of the tracking movements but not their timing.

For reasons explained in the introduction, we had no specific expectations with respect to the issue whether the effects of visual and musculoskeletal factors on anchoring were independent (i.e., additive) or dependent (i.e., interactive) in nature. The results indicated that gaze direction and wrist posture affected anchoring in an additive rather than interactive fashion (see Fig. 7), because no significant interactions between gaze direction and wrist posture were found for any of the dependent variables (see Table 1). The fact that gaze direction affected only spatial anchoring and not temporal anchoring provided further support for the conclusion that the contributions of gaze direction and wrist posture to anchoring were independent.

Effects on global tracking behavior

The analyses of the velocity profiles and Hooke’s portraits of the full tracking trajectories revealed that wrist posture had a much larger effect than gaze direction on the global tracking behavior. As can be observed in Fig. 5, velocity profiles were asymmetric when tracking was performed with the wrist flexed or extended as opposed to a neutral wrist configuration, which resulted in symmetric, bell-shaped velocity profiles. The three different gaze directions only affected the velocity profiles to a limited yet significant degree. Congruently, wrist posture affected the harmonicity of the wrist movements much more than gaze direction, as can be appreciated from Fig. 6 (viz. greater deviation from the straight line representing harmonic oscillation).

Those qualitative observations were reflected in significant differences in the duration, peak velocity and harmonicity of the flexion and extension phases of the movement as determined from the velocity profiles and Hooke’s portraits. Wrist posture strongly affected the global tracking behavior and led to marked differences between flexion and extension for wrist postures other than neutral. For the flexed (extended) wrist posture, the flexion (extension) phase lasted shorter, had higher peak velocity and was less harmonic than the extension (flexion) phase. Gaze direction also significantly affected movement duration and peak velocity of the flexion and extension half cycles, albeit to a much smaller degree. If gaze was directed to the left (right) target turning point, the duration of the flexion (extension) phase was shorter than that of the extension (flexion) phase, accompanied by higher flexion (extension) peak velocity. When gaze was fixated in between the two target turning points velocity profiles were symmetric. Tracking harmonicity was not significantly affected by gaze direction.

Furthermore, Hooke’s portraits for tracking with the wrist flexed and extended should be rich in information about specific conservative and dissipative nonlinear components giving rise to the observed anharmonicity (Beek and Beek 1988; see also Beek et al. 1992; Buchanan et al. 2003, 2006; Mottet and Bootsma 1999, 2001). As can be appreciated from Fig. 6, local stiffness tended to increase towards the anchored endpoint, indicating a so-called hardening spring corresponding to an additional Duffing term in the equation of motion (Beek and Beek 1988; Mottet and Bootsma 2001). Besides this nonlinear conservative term, also nonlinear dissipative terms appeared to be operative towards the anchored endpoint given the asymmetry in the acceleration and deceleration parts of the half cycle in question. Considering that zero acceleration (i.e., peak velocity) occurred in the first part of the flexion (extension) phase for a flexed (extended) posture, a self-sustaining Rayleigh oscillator is a likely candidate for the dissipative terms contributing to the anharmonic tracking behavior (Beek and Beek 1988; Mottet and Bootsma 2001). Finally, visual inspection of the nine panels of Fig. 6 suggests a graded modulation of those nonlinear conservative and dissipative components as a function of wrist posture and gaze direction, underscoring again that both factors had an additive rather than an interactive effect on the organization of tracking.

Musculoskeletal underpinnings of anchoring

The marked effects of wrist posture on anchoring and the global organization of tracking may be related to a variety of musculoskeletal factors including the possibility of saving mechanical energy from half cycle to half cycle owing to the ability of muscles to store mechanical energy in a potential, elastic form towards the end of each half cycle to facilitate the production of the next half cycle (Guiard 1993). Although this storage and release of elastic strain energy in muscles and tendons is considered to play a limited role in rhythmic wrist movements, passive elastic torques become sizeable at larger wrist excursions (Lehman and Calhoun 1990; Schieber and Thach 1985). Hence, this energy-saving mechanism may well be relevant for tracking with the wrist flexed or extended and underlie the conservative and dissipative terms identified in the Hooke’s portraits, as will be discussed further below.

The temporal anchoring analysis revealed that movements were actively timed or anchored on maximal flexion with the wrist in a flexed posture and on maximal extension with the wrist in an extended posture. In either case, movement durations were shorter (and peak velocities larger) towards the anchored endpoint. Following a similar line of reasoning, the observed deviation from harmonicity in the Hooke’s portraits for a flexed (extended) wrist posture suggests that flexion (extension) movements are actively steered to a specific point in the perceptual-motor workspace (i.e., the movement cycle is anchored on maximal flexion (extension)), while the extension (flexion) half cycle simply serves to bring the hand out again for the next flexion (extension), perhaps in part passively through the release of potential energy stored in the elastic tissues around the wrist. The observed local and global features of tracking are surely consistent with such an interpretation.

In any case, in a flexed (extended) wrist posture, the flexion (extension) reversal point or phase indeed appears to act as an “organizing center” within and for the entire cycle production (Beek 1989; Beek et al. 1992). Thus, by actively timing or controlling the flexion (extension) phase, the movement cycle as a whole is produced to satisfy the imposed synchronization demand of the tracking task. Beek (1989) submitted that anchor points contain critical task-specific information for organizing a cyclical act. The results of the present study suggested that the anchor points may also possess functional task-specific mechanical properties that can be utilized in the organization of the cyclical act (in our case, the possibility to store and release energy). Tracking was controlled in a (partly) discrete manner, with the actively controlled flexion (extension) phase apparently acting as a kind of biological escapement for fueling the potential energy capacity of the extensors (flexors).

Visual underpinnings of anchoring

The absence of interaction effects between gaze direction and wrist posture, in combination with the observations that gaze direction did not affect temporal anchoring and that the global tracking dynamics was more strongly influenced by wrist posture than by gaze direction implied that both factors had different and independent effects on the tracking dynamics. The results strongly suggested that gaze direction predominantly affected the spatial accuracy of the tracking movements and (by and large) not its temporal organization, and is thus associated only with spatial control. Surely, this conclusion is consistent with the results of ample pointing, aiming and reaching studies. For example, pointing accuracy suffers when participants do not foveate at a target during the homing-in phase of aiming movements (e.g., Bekkering et al. 1995; Neggers and Bekkering 1999; Prablanc et al. 1979; Vercher et al. 1994). The tight coupling between gaze and aiming movements is underscored further by the finding that the eyes cannot saccade away from the target until the aiming movement is completed, which has led to the insight that this so-called “gaze anchoring” serves the planning and execution of pointing movements (Neggers and Bekkering 2000, 2001, 2002). Although online concurrent visual feedback of the tracking movements was provided in the present study, the positive effect of gaze direction (or “gaze anchoring” in general) on spatial endpoint accuracy appears independent of the availability of visual information from the pointing or tracking movement itself (either directly or indirectly through extrinsic visual feedback). For example, Neggers and Bekkering (2001) also observed “gaze anchoring” phenomena without vision of the moving arm, while Roerdink et al. (2005) observed reduced endpoint variability in the direction of gaze during tracking in the absence of visual tracking feedback and vision of the moving hand. These findings indicate that the spatial anchoring results mediated by gaze direction observed in the present experiment do not necessarily imply increased accuracy in the foveated direction due to an alignment of visual target and feedback signals, but that also more generic “gaze anchoring” mechanisms (see Neggers and Bekkering 2000, 2001, 2002) are implicated in the observed anchoring phenomena. Future studies should be conducted to reveal the precise contribution of “gaze anchoring” on endpoint variability during rhythmic tracking, for instance by comparing unimanual in-phase and antiphase tracking (without direct or extrinsic visual feedback of the moving hand) under fixed left, center, and right gaze directions.

Theoretical implications with regard to anchoring

Over the years the study, and with it the notion, of anchoring has become confined to synchronization of a particular point in the movement cycle with a discrete or continuous metronome. Against this development we would like to revive the more generic definition of anchoring as originally given by Beek (1989), who described anchor points as “organizing centers within, and for” cyclical movements. Inherent to this description are at least four theoretically and methodologically relevant features. First, anchoring can also occur without an external pacer, as has been reported for juggling (Beek 1989; see also Beek et al. 1992) and self-paced wrist cycling (Byblow et al. 1994). In a similar vein, we expect that the present results regarding wrist posture will be preserved with self-paced rhythmic wrist movements. Second, in the case of paced movements, performing a task at the prescribed frequency does not necessarily imply anchoring (e.g., as a case in point, in the present study AI’s did not differ from 0.5 for a neutral wrist posture when gaze was fixated in between the two target turning points, see Fig. 7). Conversely, it is only useful and possible to examine anchoring to a pacing signal if the task is performed at, or at least very close to, the prescribed frequency. Third, anchoring is not a purely local effect but has implications for the overall coordination (Beek 1989; Fink et al. 2000; Jirsa et al. 2000; Maslovat et al. 2006), as is captured in the statement that anchor points serve as organizing centers within and for the entire cycle production (Beek 1989). By timing the movement to a particular point in the cycle, the movement cycle as a whole is timed and stabilized. Pattern stability may be improved, however, by employing more than one anchor point (Fink et al. 2000; Jirsa et al. 2000; Maslovat et al. 2006). Finally, although in cyclical tasks anchoring is typically observed in the form of a local reduction of kinematic variability at or near the movement endpoints, anchor points may in principle be observed anywhere throughout the cycle (e.g., the point of ball release in juggling; Beek 1989). Moreover, anchor points are not fixed in the perceptual-motor workspace but can be actively created or assembled, for example, by fixating gaze at one of both target turning points (Roerdink et al. 2005).

Coda

In the present study we delineated the effects of gaze direction and wrist posture on anchoring phenomena. A novel methodological feature of the study was that the analysis of spatial endpoint variability was complemented with a temporal counterpart, by quantifying the timing variability between movement reversals and target turning points in an analogous manner. We found that both visual and musculoskeletal factors affected spatial and temporal anchoring phenomena in different ways: the former by making use of task-specific visual information available at the gaze anchored point, the latter by exploiting task-specific mechanical properties. The results are in line with the original definition of anchoring (Beek 1989; see above), which was broadened by suggesting that, besides perceptual information, task-specific mechanical properties may also be available and actively utilized at the anchor point in favor of task performance or task economy.

Finally, we would like to emphasize that anchoring is a generic aspect of coordination dynamics that may have considerable potential for practical applications, such as in learning complex coordination patterns (e.g., Maslovat et al. 2006) or in restoration of pathological gait (e.g., Roerdink et al. 2007). For example, the latter study on the effect of acoustically paced treadmill walking on gait coordination in stroke patients found that the footfalls of the nonparetic limb were anchored to the tones of the metronome (Roerdink et al. 2007). The analysis of temporal anchoring provided insight into the manner in which asymmetric gait patterns are coordinated to symmetric acoustic pacing rhythms. More importantly, the notion of anchoring may also provide an entry point for improving the organization of paced walking in stroke patients in physical therapy (Roerdink et al. 2007), for example, by instructing stroke patients to coordinate or anchor footfalls of the paretic limb to the beat of the metronome.

Acknowledgements

This work was supported, in part, by a grant of the Netherlands Organisation for Health Research and Development (ZonMw grant 1435.0004). The contribution of the third author was facilitated by Aspasia grant 015.001.040 of the Netherlands Organisation for Scientific Research (NWO).

References

  1. Beek PJ (1989) Juggling dynamics. PhD Thesis. Free University Press, Amsterdam
  2. Beek PJ, Beek WJ (1988) Tools for constructing dynamical models of rhythmic movement. Hum Mov Sci 7:301–342 [DOI]
  3. Beek PJ, Turvey MT, Schmidt RC (1992) Autonomous and nonautonomous dynamics of coordinated rhythmic movements. Ecol Psychol 4:65–95 [DOI]
  4. Beek PJ, Rikkert WEI, van Wieringen PCW (1996) Limit cycle properties of rhythmic forearm movements. J Exp Psychol Hum Percept Perform 22:1077–1093 [DOI]
  5. Bekkering H, Adam JJ, van den Aarssen A, Kingma H, Whiting HTA (1995) Interference between saccadic eye and goal-directed hand movements. Exp Brain Res 106:475–484 [DOI] [PubMed]
  6. Buchanan JJ, Park J-H, Ryu YU, Shea CH (2003) Discrete and cyclical units of action in a mixed target pair aiming task. Exp Brain Res 150:473–489 [DOI] [PubMed]
  7. Buchanan JJ, Park J-H, Shea CH (2006) Target width scaling in a repetitive aiming task: switching between cyclical and discrete units of action. Exp Brain Res 175:710–725 [DOI] [PubMed]
  8. Burgess-Limerick R, Abernethy B, Neal RJ (1991) A statistical problem in testing invariance of movement using the phase plane model. J Mot Behav 23:301–303 [DOI] [PubMed]
  9. Byblow WD, Carson RG, Goodman D (1994) Expressions of asymmetries and anchoring in bimanual coordination. Hum Mov Sci 13:3–28 [DOI]
  10. Byblow WD, Chua R, Goodman D (1995) Asymmetries in coupling dynamics of perception and action. J Mot Behav 27:123–137 [DOI] [PubMed]
  11. Carson RG (1996) Neuromuscular-skeletal constraints upon the dynamics of perception-action coupling. Exp Brain Res 110:99–110 [DOI] [PubMed]
  12. Carson RG, Riek S (1998) The influence of joint position on the dynamics of perception-action coupling. Exp Brain Res 121:103–114 [DOI] [PubMed]
  13. Carson RG, Byblow WD, Goodman D (1994) The dynamical substructure of bimanual coordination. In: Swinnen SP, Heuer H, Massion J, Casaer P (eds) Interlimb coordination: neural, dynamical and cognitive constraints. Academic, Orlando, pp 319–337
  14. Fink PW, Foo P, Jirsa VK, Kelso JA (2000) Local and global stabilization of coordination by sensory information. Exp Brain Res 134:9–20 [DOI] [PubMed]
  15. Guiard Y (1993) On Fitts’s and Hooke’s laws: Simple harmonic movement in upper-limb cyclical aiming. Acta Psychol 82:139–159 [DOI] [PubMed]
  16. Haken H, Kelso JA, Bunz H (1985) A theoretical model of phase transitions in human hand movements. Biol Cybern 51:347–256 [DOI] [PubMed]
  17. Jirsa VK, Fink P, Foo P, Kelso JAS (2000) Parametric stabilization of biological coordination: a theoretical model. J Biol Phys 26:85–112 [DOI] [PMC free article] [PubMed]
  18. Kay BA (1988) The dimensionality of movement trajectories and the degrees of freedom problem—a tutorial. Hum Mov Sci 7:343–364 [DOI]
  19. Kay BA, Kelso JA, Saltzman EL, Schöner G (1987) Space-time behavior of single and bimanual rhythmical movements: data and limit cycle model. J Exp Psychol Hum Percept Perform 13:178–192 [DOI] [PubMed]
  20. Kelso JA, Jeka JJ (1992) Symmetry breaking dynamics of human multilimb coordination. J Exp Psychol Hum Percept Perform 18:645–668 [DOI] [PubMed]
  21. Lehman SL, Calhoun BM (1990) An identified model for human wrist movements. Exp Brain Res 81:199–208 [DOI] [PubMed]
  22. Mardia KV (1972) Statistics in directional data. Academic, London
  23. Maslovat D, Chua R, Lee TD, Franks IM (2006) Anchoring strategies for learning a bimanual coordination pattern. J Mot Behav 38:101–117 [DOI] [PubMed]
  24. Mottet D, Bootsma RJ (1999) The dynamics of goal-directed rhythmical aiming. Biol Cybern 80:235–245 [DOI] [PubMed]
  25. Mottet D, Bootsma RJ (2001) The dynamics of rhythmical aiming in 2D task space: relation between geometry and kinematics under examination. Hum Mov Sci 20:213–241 [DOI] [PubMed]
  26. Neggers SF, Bekkering H (1999) Integration of visual and somatosensory target information in goal-directed eye and arm movements. Exp Brain Res 125:97–107 [DOI] [PubMed]
  27. Neggers SF, Bekkering H (2000) Ocular gaze is anchored to the target of an ongoing pointing movement. J Neurophysiol 83:639–651 [DOI] [PubMed]
  28. Neggers SFW, Bekkering H (2001) Gaze anchoring to a pointing target is present during the entire pointing movement and is driven by a non-visual signal. J Neurophysiol 86:961–970 [DOI] [PubMed]
  29. Neggers SFW, Bekkering H (2002) Coordinated control of eye and hand movements in dynamic reaching. Hum Mov Sci 21:349–376 [DOI] [PubMed]
  30. Oldfield RC (1971) The assessment and analysis of handedness: the Edinburgh inventory. Neuropsychologia 9:97–113 [DOI] [PubMed]
  31. Peper CE, Beek PJ (1998) Are frequency-induced transitions in rhythmic coordination mediated by a drop in amplitude? Biol Cybern 79:291–300 [DOI] [PubMed]
  32. Prablanc C, Echallier JF, Komilis E, Jeannerod M (1979) Optimal response of eye and hand motor systems in pointing at a visual target. I. Spatiotemporal characteristics of eye and hand movements and their relationships when varying the amount of visual information. Biol Cybern 35:113–124 [DOI] [PubMed]
  33. Roerdink M, Peper CE, Beek PJ (2005) Effects of correct and transformed visual feedback on rhythmic visuo-motor tracking: tracking performance and visual search behavior. Hum Mov Sci 24:379–402 [DOI] [PubMed]
  34. Roerdink M, Lamoth CJC, Kwakkel G, van Wieringen PCW, Beek PJ (2007) Gait coordination after stroke: benefits of acoustically-paced treadmill walking. Phys Ther 87:1009–1022 [DOI] [PubMed]
  35. Schieber MH, Thach WT (1985). Trained slow tracking. I. Muscular production of wrist movement. J Neurophysiol 54:1213–1227 [DOI] [PubMed]
  36. Vercher JL, Magenes G, Prablanc C, Gauthier GM (1994) Eye-head-hand coordination in pointing at visual targets: spatial and temporal analysis. Exp Brain Res 99:507–523 [DOI] [PubMed]

Articles from Experimental Brain Research. Experimentelle Hirnforschung. Experimentation Cerebrale are provided here courtesy of Springer

RESOURCES