Risk Adjustment and Primary Health Care in Chile

Abstract

Aim

To offer a capitation formula with greater capacity for guiding resource spending on population with poorer health and lower socioeconomic status in the context of financing and equity in primary health care.

Methods

We collected two years of data on a sample of 10 000 individuals from a region in Chile, Valdivia and Temuco and evaluated three models to estimate utilization and expenditures per capita. The first model included age and sex; the second one included age, sex, and the presence of two key diagnoses; and the third model included age, sex, and the presence of seven key diagnoses. Regression results were evaluated by R² and predictive ratios to select the best specifications.

Results

Per-capita expenditures by age and sex confirmed international trends, where children under five, women, and the elderly were the main users of primary health care services. Women sought health advice twice as much as men. Clear differences by socioeconomic status were observed for the indigent population aged ≥65 years who under-utilized primary health care services. From the three models, major improvement in the predictive power occurred from the demographic (adjusted R², 9%) to the demographic plus two diagnoses model (adjusted R², 27%). Improvements were modest when five other diagnoses were added (adjusted R², 28%).

Conclusion

The current formula that uses municipality’s financial power and geographic location of health centers to adjust capitation payments provides little incentive to appropriate care for the indigent and people with chronic conditions. A capitation payment that adjusts for age, sex, and the presence of diabetes and hypertension will better guide resource allocation to those with poorer health and lower socioeconomic status.

Chile scores favorably in terms of health indicators. Life expectancy at birth is 80 years for women and 73 years for men, and the infant mortality rate is 8.6 per 1000 live births (1). This success record largely stems from good socioeconomic living conditions and strong efforts in preventive care. However, the latest epidemiological data reported diverging health outcomes between socioeconomic groups (2). Among the causes is a lack of incentives to provide adequate care for chronic diseases, particularly among people of low socioeconomic status.

Chile is going through an epidemiological and demographic transition. This transition is characterized by a decreasing percentage of the population under the age of 15 and increasing percentage of the elderly population (3). Non-communicable diseases are on the rise in relative and absolute terms (3). Several health risk factors, such as smoking, a high-fat diet, and a sedentary lifestyle, acting alone or in combination are on the rise (2). These risks contribute to the onset of diabetes, coronary disease, and hypertension, which are major causes of morbidity and mortality (4). Since risk factors are synergistic, the relative risk of developing a disease increases when different risks are combined. According to the First National Health Survey, risk behavior has higher prevalence in lower socioeconomic groups (2). Therefore, it may be necessary to align the allocation of health resources with the new challenges posed by the demographic and epidemiological transition.

Health coverage in Chile is largely dominated by the public system. The National Health Fund (FONASA, Fondo Nacional de Salud) manages public health insurance. Individuals covered by FONASA may receive health services from either public facilities or a preferred private provider. The Ministry of Health manages vertical programs, public health interventions, and the health care personnel from public facilities. In 1995, the Ministry of Health introduced capitation at the primary health care level, allocating 60% of total funding from capitation and 13% on a case-by-case basis. The remaining funds are provided by municipalities. The Ministry of Health allocates a prospective capitation rate for all registered beneficiaries. The rate covers the full cost of labor, administration, and a percentage of pharmaceuticals. The base capitation rate was approximately US$20 per year during 1999-2000 and adjusted by two variables, the geographic location of the health centers and the income level of the municipality, where a health center located in a rural area received an upward adjustment of 20% and a poor municipality 18% (5).

All FONASA-insured citizens are entitled to participate in the per-capita program and are required to register with any health center. In 2000, 7.5 million people or 74% of the FONASA-insured persons were enrolled. All enrolled persons (except the indigent) also have access to a private subsidized system that provides primary health care services on a fee-for-service basis.

Health centers provide preventive and curative services, but complex interventions including childbirth are referred to secondary care. Most primary health centers services are clustered under the following programs: (a) Well-baby and Healthy Children, targeting children from 0-9 years, (b) Maternal Health, encompassing family planning and prenatal care, a relatively new program, and (c) Adult Health, preventing and managing risk factors among adults aged 40-64 years and the elderly aged ≥65 years, including two programs dedicated to managing chronic diseases including hypertension and diabetes.

The aim of this study was to evaluate the Chilean primary health care capitation formula for directing health resources toward the greatest health needs by using the risk-adjustment conceptual framework and international evidence.

Subjects and methods

Conceptual framework

Capitation is becoming increasingly prevalent worldwide as a mechanism for funding prospective budgets. Capitation is a fee paid by a financing agency to a health care provider for each of its registered affiliates for the provision of services for a fixed period, usually one year. The objective of most capitation systems is to ensure control of expenditure by sharing the financial risk between the financing agency and the provider, so the increasing number of services delivered by health care providers does not lead directly to increased payments by the financing agency (6,7).

A simple way to design capitation is a uniform flat rate for all clients of a provider and across providers. However, flat capitation rates are likely to overpay or underpay providers for certain patient groups and may lead to disincentives to provide quality care for the chronically ill. The calculation of capitation rates to providers has been the focus of the conceptual and empirical work of the risk-adjustment framework. The principle is that capitation should be adjusted and should reflect beneficiaries’ relative health needs and expenditures, using variables that help to predict these expenditures. These variables are called risk-adjusters and are used to modify the flat rate, so the differences in the mix of health needs among enrollees are reflected in different revenues of these providers (8).

Several types of models – demographic, socioeconomic, and with diagnoses – have been developed and implemented in various health care systems. All models are empirical, but demographic and socioeconomic models have also been used in an approach where adjustments to the capitation rate to subsidize disadvantages are based on informed judgement or under a normative approach (6).

Demographic models are based on age, sex, and ethnicity. Most health care systems started risk-adjustment of capitation payments with age and sex. There are pronounced differences in average per-capita health care expenditures by age groups and sex (8). Expenditures are higher for infants, women, and the elderly. With respect to ethnicity, the rationale is that some ethnic groups are more vulnerable and may underutilize the system, so a higher capitation payment will make them more attractive to providers (8).

Socioeconomic models are based on adjustors such as education, occupation, income, and rural/urban status. Socioeconomic status is a good predictor of health needs. It is well established that mortality and morbidity are higher in low socioeconomic groups (9). However, there are mixed results regarding utilization of health care services. Some studies affirm that socioeconomic indicators are good predictors of utilization of health care, while others were unable to find such a relationship (10). Regional differences in per-capita expenditures can be observed in many countries due to differences in input prices or practice patterns (6).

Epidemiological and health status models include mortality, disability, and diagnoses as risk-adjustors. Crude and standarized mortality rate is used for capitating regional health authorities, such as those in England (6). Mortality has been suggested because of the high health care expenditures before death and because it is a good proxy of the population’s morbidity (11). Standarized mortality rate has a positive but low correlation with utilization and health need (12). Disability and functional health have been shown to be relatively good predictors of future expenditures (13). Regarding health status, models have been developed using diseases diagnosed during or before hospitalization and/or ambulatory consultations, to calculate risk-adjusted capitation payments. The assumption is that certain diagnoses are good predictors of health expenditures. There are pragmatic approaches which identify common diagnoses that are expensive to treat (14). More complex models classifying the whole spectrum of diagnoses exist as well. The two most known classification systems are the Ambulatory Care Group (15) and the Diagnostic Cost Group systems (16,17).

Additionally, various criteria for selecting the best empirical models for capitation payments have been established: statistical performance, administrative feasibility, simplicity, and robustness against manipulation. The measure of the predictive power at the individual level of different risk-adjustment models is the conventional R-square, which measures the proportion of the variance in individuals’ expenditures explained by a model (8). Age and sex can explain about 1-4% of the variance. The percentage of the individual variation that can be predicted by prospective models using diagnoses has been estimated to reach about 20%. The remaining percent is subject to random fluctuation (8). At the group level, “predictive ratios” are used to test the model’s accuracy. Thus, coefficients from regression analysis are used to predict the likelihood of individuals pertaining to different risk groups utilizing health services or to predict their per-capita expenditures. The mean predicted expenditures are divided by the mean actual expenditures, and predictive ratios for different groups are estimated. A ratio of 1.0 indicates accurate prediction, ratio <1.0 under-prediction, and ratio >1.0 indicates over-prediction (18).

From the literature review it is clear that predictive power increases as diagnoses of medical conditions are used in addition to demographic variables. Therefore, our empirical model uses diagnoses in addition to age and sex.

Sampling procedure

The study was carried out in five health centers and 24 subcenters located in south Chile (Valdivia and Temuco). The health centers covered 110  000 individuals in 1999 and 123 000 in 2000. In the selected region, about 65% of the population was affiliated with the public insurer FONASA and about 35% were living in rural areas; both percentages were consistent with FONASA’s national average.

A random sample of health center affiliates registered in the per-capita program of FONASA was drawn. The selected sample consisted of 10 000 affiliates and was the result of a multi-stage stratified sampling design. First, to obtain correct estimates for the overall population, the following sampling weights were used based on the proportion of FONASA affiliates residing in urban/rural areas and in poor and non-poor municipalities as follows: 11% rural poor municipalities, 22% rural non-poor, 25% urban poor municipalities, and 42% urban non-poor. Second, health centers were selected accordingly and their population, age, and sex structure used to estimate sampling weights. Third, a data set of individuals was constructed. The requirements for inclusion of individuals in the database were the following; (a) registered completely or partially from January 1, 1999 and December 31, 2000, and (b) born before December 31, 2000. Finally, the data set was sorted by sex and 5-year interval age-groups. A random sample was drawn from each age and sex group by health center.

From each individual, identified by a unique personal number, medical records were audited and the following information was collected: number of months registered in the health centers between January 1, 1999 and December 31, 2000, date of birth, sex, income level (FONASA classification), number of consultations to the health centers, and the presence of any of the seven selected diagnoses. Number of consultations was chosen to indicate usage of health resources (physicians, nurses, and pharmaceuticals) as data on patient expenditure data was not available. Consultations were grouped as preventive or curative because of variations in costs due to use of drugs and medical vs non-medical personnel. Cost series of the selected preventive and curative consultations were available from the Ministry of Health regional office (19). Preventive consultation included five key interventions, included in the 10th revision of International Statistical Classification of Diseases and Related Health Problems (ICD-10) (20): vaccination (ICD-10 Z27), infant and child examination (ICD-10 Z00.1-Z00.2), sexual education for adolescents and prenatal care (ICD-10 Z-34), general medical examination of adults and the elderly (ICD-10 Z00.0), and other preventive actions. Curative consultations associated with the selected diagnoses or any other diseases were recorded. Health center directors were interviewed and agreed to select diseases based on the following criteria used by the Johns Hopkins Ambulatory Care Group methodology (a) recurrent and chronic diseases, (b) within the chronic conditions, diseases which are stable and likely to require resources on an ongoing basis, (c) diseases with higher likelihood of needing specialized care, and (d) diseases where a diagnostic evaluation is needed. Accordingly, the following diseases were selected: hypertension (ICD-10 I10), diabetes (ICD-10 E11), chronic bronchitis (ICD-10 J41-J42), obstructive bronchitis syndrome (ICD-10 J44), asthma (ICD-10 J45), varicose veins with ulcer (ICD-10 I83), and alcohol abuse (ICD-10 F10). Severe versions of the diagnoses such as diabetes with coma, diabetes with glaucoma, hypertensive heart diseases, and depression were not included because treatment was not available at primary health centers at the time. Consultations were available in electronic format for 3000 people. The remaining information was drawn manually from the medical records and then converted into electronic format.

The model

Regression analysis was performed to estimate how significant the effects were of age and sex on the one hand, and age, sex, and the presence of two or seven diagnoses on the other, on utilization and expenditure of primary health care services, or the extent to which these independent variables accounted for increases in utilization or expenditures of primary health center services. A prospective model was estimated, in which adjustors or individual characteristics from 1999 (year one) seek to predict 2000 (year two) per-capita consultations or expenditures.

The model is represented by the following equations:

CONSULT_i = B₀+B₁ age_i+B₂ sex_i+e_i

EXPEND_i = B₀+B₁ age_i+B₂ sex_i+e_i

CONSULT_i = B₀+B₁ age_i+B₂ sex_i+B₃ chronic diseases_i+e_i

EXPEND_i = B₀+B₁ age_i+B₂ sex_i+B₃ chronic diseases_i+e_i

Two dependent variables were used. CONSULT_i is the sum of preventive and curative primary health care consultations by patient i, whereas EXPEND_i is the sum of primary health expenditures by patient i to general practitioners, specialists, and paramedics in health centers during year two, ie, year 2000. Information was annualized and weighted to adjust for enrollment for one year or a fraction of a year, which happens automatically with births and deaths. The B_i terms are unknown parameters to be estimated, while the e_i terms are error terms.

The independent variables were defined by three sets of dummy variables. Age_i grouped each individual either into 14 age categories (0-4, 5-9, 10-14, 15-19, 20-24, 25-29, 30-34, 35-39, 40-44, 45-49, 50-54, 55-59, 60-65, and ≥65 years) or into two age groups (0-64 and ≥65 years). The variable sex_i was a dummy variable, and it equaled 1 if patient i was female, and 0 if male. Chronic diseases were captured by seven disease_i dummy variables. Each dummy variable – hypertension, diabetes, obstructive bronchitis syndrome, chronic bronchitis, asthma, ulcer varicose, and alcohol abuse – equaled 1 if patient i was diagnosed with that disease in year one, ie, year 1999, otherwise it was zero.

Results

The median age was 29 years. About 53% of the sample were women and 67% were the indigent, compared with 46% of the national population affiliated to the program at the time. Therefore, this subset of the population was poorer than the national average (Table 1).

Table 1.

Annual average primary health consultations and expenditures per capita by age, sex, socioeconomic status, and selected diseases in 2000

		Consultations per capita		Expenditures per capita (CLP)*
Group	Total % (N = 10 000)	preventive	preventive and curative	preventive	preventive and curative
Age (years):
0-4	6.2	0.51	3.41	2217	20 172
5-44	68.2	0.39	1.07	2780	10 097
45-64	16.1	1.27	2.47	11 840	27 706
≥65	9.5	0.62	2.69	13 778	44 515
total	100.0	0.62	1.59	5244	16 817
Sex:
men	47.5	0.32	1.05	2856	11 062
women	52.5	0.90	2.07	7402	22 020
Sex, age, and socioeconomic status:
women aged 0-64:	48.0	0.84	1.98	6547	18 909
indigent	33.0	0.76	1.84	5750	17 134
non-indigent	15.0	1.03	2.29	8303	22 822
women aged ≥65:	5.1	1.48	2.98	15  400	51 131
indigent	2.7	1.18	2.51	12  095	42 549
non-indigent	2.4	1.82	3.52	19 136	60 831
men aged 0-64:	43.0	0.23	0.94	1937	8440
indigent	30.0	0.22	0.96	1784	8433
non-indigent	13.0	0.26	0.89	2287	8458
men aged ≥65:	4.4	1.11	2.12	11 900	36 857
indigent	2.1	0.98	1.77	10 471	30 283
non-indigent	2.3	1.25	2.44	13 228	42 697
Diagnoses:
hypertension	5.4	4.33	6.92	43 836	90 190
diabetes mellitus type 2	1.4	5.55	8.11	56 798	101 778
obstructive bronchitis syndrome (children)	1.5	0.87	4.75	4716	32 189
chronic bronchitis (adults)	0.4	2.30	5.44	22 530	77 257
asthma	0.2	2.25	5.81	17 306	70 578
alcohol abuse	0.2	0.66	2.40	6228	30 429
varicose with ulcer	0.03	2.66	8.66	27 268	124 227

*Chilean pesos (US$1 = CLP540 in 2000).

About 62% of the population affiliated with the per-capita program had zero consultations and expenditures in 2000. The average consultation was 1.59 times and the median was 0. Of these consultations, 0.62 were for preventive care and 0.96 were for curative care (Figure 1). Average per-capita expenditure was CLP16 817 and the median CLP0. At the 75th and 95th percentile, the average consultation was 2.0 and 8.0 and the average per-capita expenditure CLP16 212 and CLP89 591, respectively.

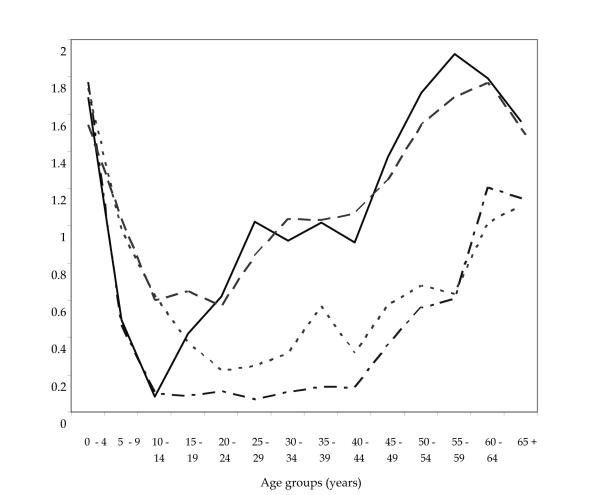
Figure 1.

Preventive and curative primary health care consultations by age and sex in 2000 calculated on a sample of N = 10 000 (curative average = 0.96 consultations). Preventive consultation included 5 key interventions: vaccination (ICD-10 Z27), infant and child examination (ICD-10 Z00.1-Z00.2), sexual education for adolescents and prenatal care (ICD-10 Z-34), general medical examination of adults and the elderly (ICD-10 Z00.0), and other preventive actions. Full line – women, preventive; dashed line – women, curative; dotted line – men, curative; dot-dash line – men, preventive; ICD-10 – International Statistical Classification of Diseases and Related Health Problems, 10th revision (20).

The utilization and expenditures of primary health care services varies systematically by age group and sex (Figures 1 and 2). Per-capita expenditure increased with age. Children aged 0-4 years cost 1.2 times the average, adults aged 45-64 years cost 1.6 times, and people aged ≥65 years cost 2.6 times the average. The principal users of primary health care were children under 5, women, and seniors. Women visited the primary health care centers approximately twice per year, while men in the same age group just once. Women received more preventive care in absolute and relative terms and men sought care for treatment of illness (Figure 1).

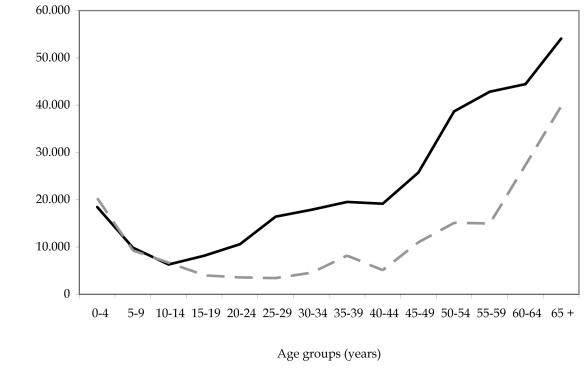
Figure 2.

Per capita primary health care expenditure by age and sex groups in 2000 calculated on a sample of N = 10 000 (average = CLP16 817). CLP – Chilean pesos (US$1 = CLP540 in 2000). Full line – women per capita expenditures; dashed line – men per capita expenditures.

In addition to the significant differences in utilization associated with age and sex, there was a gap in the use of health services associated with socioeconomic status. The socioeconomic gap merged predominantly among those aged ≥65 years, where per-capita expenditure of non-indigents was around 40% higher than that of the indigent, owing to a higher coverage of the non-indigent for the treatment of chronic diseases such hypertension and diabetes (55% vs 33% of the sample).

There were no significant differences by socioeconomic status in the use of services and expenditures among men aged 0-64 years. In contrast, non-indigent women in this age group spent 30% more than non-indigent persons of both sexes. In addition, the non-indigent had access to publicly subsidized private providers as well, so these figures were only partial count of their use of primary health care services. In conclusion, differences of expenditure at the individual level were largely associated with age, sex, and to some extent socioeconomic status among those aged ≥65 years.

The annual distribution of consultations and expenditures was skewed because of the high percentage of non-users, about 62% of total beneficiaries. In 2000, users’ consultations were distributed as follows: 25% visited the health centers 1-4 times per year, 10.3% 5-10 times per year, and just 2.7% more than 11 times. Health expenditures were concentrated. People diagnosed with any of the seven diseases represented 9% of the sample but their per-capita expenditure was 2-7 times above average and their expenditures amounted to 43% of the total. The most common diagnoses, hypertension and diabetes, represented 7% of the sample. Per-capita expenditure was 5-6 times the average, and spending on this group accounted for 38% of the total expenditures (Figure 2).

Regression results

Three regression models by means of ordinary least squares were estimated. The models were assumed to be linear in the coefficients and included an intercept. The dependent variable was the number of primary health care service consultations by each individual in 2000 and independent variables were sex, age, and seven diseases diagnosed in 1999. The demographic model explained 4-9% of variation in individual resource use (Table 2). By adding two-diagnoses, hypertension and diabetes, to the demographic model increased the explanatory power to 20-27% of individual resources use. The demographics plus seven-diagnosis model explained 22-28% of variation in the use of resources (Table 2).

Table 2.

Adjusted R² of three alternative models predicting primary health care consultations and expenditures prospectively in 2000*

	Adjusted R2 (%) (N = 10 000)
Models	consultations	expenditures
age and sex	3.9	8.9
age, sex, and two diagnoses†	20.0	26.7
age, sex, and seven-diagnoses groups‡	22.0	28.1

*Individual variation (%) in use of services explained; P<0.001 for all models.

†The model includes age, sex, and dummies, presence of hypertension and diabetes mellitus.

‡The model includes age, sex and dummies; presence of hypertension, diabetes mellitus, obstructive bronchitis syndrome, chronic bronchitis, asthma, and alcoholism.

Predictive ratios

For the predictive ratios test for four age-sex groups, the models with seven and two diagnoses provided the best and next best prediction (Table 3). In contrast, the use of just age and sex as adjustors underestimated per-capita expenditures of those aged ≥65 years (Table 3).

Table 3.

Predictive ratios for age and sex groups under three models in 2000

	Model’s predictive ratio* (N = 10 000)
		age and sex with
Sex and age groups	age and sex	two-diagnoses†	seven-diagnoses‡
men aged 0-64	1.06	1.03	1.01
men aged ≥65	0.76	0.89	0.95
women aged 0-64	1.02	1.00	1.00
women aged ≥65	0.86	0.99	1.03

*The mean predicted expenditures are divided by the mean actual expenditures; ratio = 1.0 indicates accurate prediction, ratio <1.0 under-prediction, and ratio >1.0 over-prediction;

†The model includes age, sex, and dummies, presence of hypertension and diabetes.

‡The model includes age, sex and dummies, presence of hypertension, diabetes, obstructive bronchitis syndrome, chronic bronchitis, asthma, alcohol abuse, and ulcer with varices.

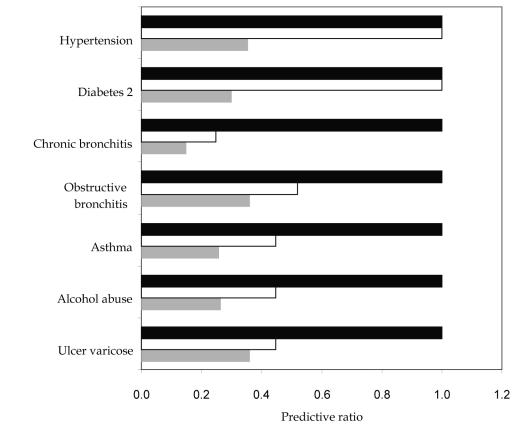
Comparison of the predictive accuracy of three models for the subset of people presenting any of these diagnoses showed that the demographic model underestimated the utilization of health services by beneficiaries with chronic diseases, even for hypertension and diabetes associated with aging (Figure 3). The model that included hypertension and diabetes accurately predicted expenditures when any of these two diagnoses were present. Additionally, it improved the prediction of all other diagnoses, probably because of co-morbidity. The model with the seven diagnoses predicted with perfect accuracy the utilization of services by people with any of these diagnoses (Figure 3).

Figure 3.

Predictive ratios for selected diagnostic groups under three models (sex and age; sex, age, and two diagnoses; and sex, age, and seven diagnoses) calculated on a sample of N = 10 000. A ratio of 1.0 indicates accurate prediction, less than 1.0 under-prediction, and more than 1.0 over- prediction. Closed bars – model including sex, age, hypertension (ICD-10 I10), diabetes mellitus 2 (ICD-10 E11), obstructive bronchitis syndrome (ICD-10 J44), chronic bronchitis (ICD-10 J41-J42), asthma (ICD-10 J45), alcohol abuse (ICD-10 F10), varicose veins with ulcer (ICD-10 I83); open bars – model including sex, age, and two diseases, hypertension and diabetes; gray bars – sex and age model; ICD-10 – International Statistical Classification of Diseases and Related Health Problems, 10th revision (20).

Capitation formula and relative prices

To operationalize the model into a capitation formula for use by the Ministry of Health, weights for two models were estimated as an example. Total expenditure per-capita of primary health care services was used to estimate weights per risk group, where the average per-capita expenditure equaled 1. Weights indicated the relative level of resources considered appropriate for individuals who belonged to that risk group. The first set used age and sex as risk-adjusters, whereas the second set added the presence of hypertension and diabetes (Table 4). Expenditures associated with any diagnoses were implicit in the demographic model, with higher weights for the elderly as chronic diseases tended to cluster in this age group. In contrast, when people with either or both diagnoses were sorted out, weights of the elderly decreased, and weights of individuals with both diagnoses rose to 7.6 times the average. The use of age and sex could identify a 5-fold difference in expected cost prospectively (R² = 8.9%) and the use of the demographic plus two-diagnoses model could distinguish a 19-fold difference in expected cost prospectively (R² = 26.7%).

Table 4.

Primary health care’s weights by age, sex, and diabetes and hypertension as key diagnoses, in 2000 (average = 1)

	Weights (N = 10 000)
Risk adjustors	age and sex	age, sex, hypertension and diabetes*
women aged 0-64	1.2	0.4
women aged ≥65	2.4	0.9
men aged 0-64	0.5	1.0
men aged ≥65	1.8	1.5
presence of hypertension	NA†	5.0
presence of diabetes mellitus 2	NA	3.6
presence of both hypertension and diabetes mellitus 2	NA	7.6

*The model includes age, sex, and dummies, presence of hypertension and diabetes.

†Not applicable.

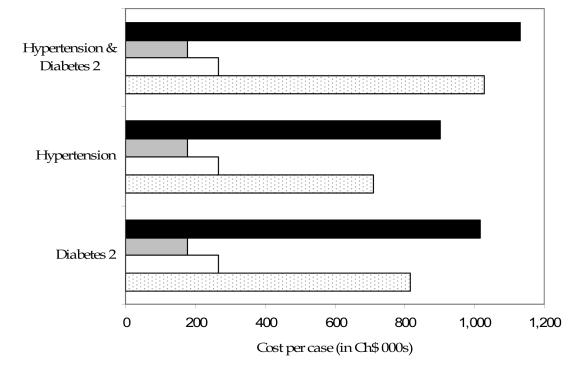
There was a difference between actual per-capita expenditure, predicted payments, and current payments for the subset of patients with hypertension and/or diabetes in a health center that serves the urban poor (Figure 4). Persons with hypertension and diabetes mellitus accounted for 38% of the total health care center’s expenditures. While current per-capita payments grossly underestimate actual per-capita expenditures, new models with either two or seven diagnoses predicted expenditures much more accurately (Figure 4).

Figure 4.

Actual per capita expenditures compared with current per capita payments and predicted model per capita values (CLP) calculated on a sample of N = 10 000. CLP – Chilean pesos (US$1 = CLP540 in 2000). Closed bars – actual expenditures per case; gray bars – current payments per capita by the Ministry of Health; open bars – predicted per capita values from sex and age model; dotted bars – predicted values from sex age and hypertension (ICD-10 I10) and diabetes mellitus type 2 (ICD-10 E11) model; ICD-10 – International Statistical Classification of Diseases and Related Health Problems, 10th revision (20).

Discussion

The present normative formula used by the Ministry of Health at primary health center level is a good principle for allocating funds to municipalities with different financial power, and to compensate health centers located in rural areas where low density and distance increase costs. This formula does not adjust for individual differences in socioeconomic status, as public health centers users were predominantly the poor and people of low socioeconomic status. Our main result is that an age and sex model can identify a 5-fold difference in expected cost prospectively, whereas the model including age, sex, and two diagnoses (hypertension and diabetes mellitus) can identify 5 to 19-fold differences between the high and the low cost, compensating for the higher costs of people with chronic conditions. In contrast to these results, the current payment formula shows only 1/3-fold difference. Therefore, important progress can be achieved if demographic and health information is included.

There are some limitations in the present study that must be taken into account when interpreting the results for policy purposes. First, the sample of two regions is non-representative of the nationwide primary health centers system; however, results at the individual level were consistent with international findings allowing valid comparisons. Second, the per-capita expenditure of the non-indigent group was a partial count of the total expenditures because non-indigents also utilize a private network of care. Third, regarding the demographic model, the predictive ratio shows that the use of four age-sex categories underestimates the utilization of services by the elderly. Therefore, this model requires further refinement. Finally, from a public policy perspective, the financial risk reduction for municipalities and health centers of the proposed formula and the improved incentives to enroll high risk and indigents were not analyzed and should be investigated in further research.

Even in the context of these limitations, the empirical analysis confirmed the results from risk-adjusting studies showing that the inclusion of diagnoses such as hypertension and diabetes as variables significantly improves the predictive power of the demographic model. In contrast, the adjusted R² showed modest improvement when five other diagnoses were added.

In summary, it is recommended to adjust the base capitation rate combining a normative and an empirical approach. A normative approach allows the consideration of a municipality’s financial power and for rural/urban location, whereas an empirical approach includes adjusting for demographic characteristics and the presence of key diagnoses. The formula does not need to include the whole spectrum of diagnoses; rather, implies the selection of the subset that predicts the larger use of resources by the chronically ill. It has a potential for improvement through the incorporation of individual characteristics, such as age, sex, and the presence of selected diagnoses. Therefore, an easy to administer demographic or demographic and two diagnoses model is recommended. An effective capitation formula can be constructed by incrementally adding variables and balancing added statistical power and accuracy against practical concerns such as data availability and administrative burden.

An improved and feasible formula to facilitate a more equitable distribution of resources is recommended to policy makers. The formula with two diagnoses will compensate health centers and create incentives for health centers to provide better care for chronic and indigent patients. In the group of people with chronic diseases, such as hypertension and diabetes, the indigent were underrepresented, likely because of undiagnosed and untreated cases. Providing a special rate for chronic conditions could create incentives to diagnose and to treat indigents and compensate health centers for the extra resource expenditures. A capitation payment that adjusts for age, sex, hypertension, and diabetes will save resources in the long run. Fewer hospital admissions will ensue, as access to care will be inversely associated with hospitalization rates for these chronic medical conditions. This will in turn increase health equity by redirecting resources to those with greater health needs.