Impact of Skin-Subcutaneous Fat Layer Thickness on Electrical Impedance Myography Measurements: An Initial Assessment

Abstract

Objective

To determine the impact of skin-subcutaneous fat layer thickness on electrical impedance myography (EIM) measurements.

Methods

Linear 50 kHz EIM was performed on quadriceps of 62 healthy subjects (mean age 52.2 +/− 20.6 years) with a wide variety of skin-subcutaneous fat layer (SFL) thicknesses, as measured by ultrasound. Correlations were sought between the main EIM outcome parameter phase (θ) and SFL thickness. A multiple regression analysis was also performed for θ with SFL thickness and age as independent variables.

Results

Mean skin fat thickness was significantly different (p <0.01) between men (0.76 ±0.23 cm) and women (1.43 ±0.51 cm). Neither linear nor quadratic fits produced significant correlations between θ and SFL thickness. A significant but weak positive correlation (r² = 0.14, p <0.05) was seen between age and SFL thickness in women, but not in men. A strong negative correlation between age and θ was observed for both men (r²= 0.48, p<0.01) and women (r² = 0.68, p <0.01). In multiple regression analysis, age but not SFL thickness was found to have a significant association with θ.

Conclusions

SFL thickness does not contribute substantially to the phase measured by linear EIM.

Significance

EIM data can be interpreted confidently in individuals with varying SFL thickness.

1. Introduction

Electrical impedance myography (EIM) is a group of non-invasive techniques that is under development for the assessment of neuromuscular disease. Thus far, it has been successfully used to study a variety of disorders, including motor neuron disease, radiculopathy, and myopathy (Rutkove et al., 2002, Rutkove et al., 2005, Tarulli et al., 2005). The most basic form of EIM, linear-EIM, uses high-frequency, low-intensity alternating current applied via adhesive electrodes to the hands or feet with the resulting voltage patterns measured by a second series of surface electrodes placed serially over a muscle or group of muscles of interest. With knowledge of the applied current and the measured voltage, the resistance (R) and reactance (X) can be measured and the phase (θ) calculated via the relationship θ = arctan (X/R). As with all bioimpedance-based methodologies, R is believed to reflect principally the flow of current through intracellular and extracellular fluids, whereas X is due to the capacitive effects of cell membranes and other interfaces (Foster and Lukaski 1996). We have used the parameter θ as our principal outcome measure, as it is less sensitive to the effects of muscle shape and size than R or X (Shiffman et al., 1999).

Unlike needle electromyography (EMG) which directly measures the electrical activity of muscle, EIM provides an indirect assessment of neuromuscular health and disease, since the electrodes are placed on the skin and thus are not in direct contact with the muscle. This has raised the question that measurements obtained by the technique may be adversely influenced in substantial ways by non-muscle tissue and most relevantly by the skin-subcutaneous fat layer (SFL). From a theoretical standpoint, however, we would anticipate that such effects should be relatively minor for two reasons. First, with current injecting electrodes placed at a far distance from the voltage electrodes, relatively little current flows along the SFL itself, since this layer has a substantially higher resistivity and lower cross-sectional area than the underlying muscle (Foster and Lukaski 1996, Faes et al., 1999). Second, linear-EIM measurements are dependent on the voltage-divider effect: namely that minimal current is drawn by the impedance measuring instrument due to its very high internal impedance, thus allowing measurement of voltages along the length of the limb without substantial contributions from the SFL itself (Shiffman and Aaron 2000, Shiffman et al., 1999).

In this study, we assess whether or not these theoretical arguments hold true in practice, by investigating possible relationships between θ and SFL thickness and their association with age in a cohort of normal subjects.

2. Methods

2.1 Subjects

Between September 2004 and August 2005, healthy subjects with no history of neuromuscular disease, normal neurological examinations, and normal needle EMG examinations were recruited for our study. Sixty-two subjects (33 men and 29 women) with a mean age of 52.2 ± 20.6 years participated. All subjects gave informed consent prior to participation, in accordance with the guidelines of the Beth Israel Deaconess Medical Center Institutional Review Board, which approved the study.

2.2 EIM Measurements

The technique of EIM has been described in detail elsewhere (Rutkove et al., 2002, Shiffman et al.,1999) and we outline here the features of the measuring system used in this study. Impedance data were obtained using a modified RJL model 101-A instrument (RJL Electronics, Clinton Township, MI), which supplied a constant 0.8 mA current at a frequency of 50 kHz. Disposable ground plate electrodes with 1.0 m leads (part # 019-768500, VIASYS Healthcare, Neurocare Group, Madison, WI) were used for current injection. These current electrodes were attached over the dorsum of the feet (as shown in Tarulli et al., 2005). Nicolet disposable strip electrodes (part # 019-435500, VIASYS Healthcare) were used for voltage detection, and placed over the quadriceps in a standard array (see Figure 1 and Tarulli et al., 2005) with 2.5 cm between electrodes (marks with an indelible marker were placed along the length of the thigh, starting from 10 cm proximal to the patella to assure consistent electrode placement). Since SFL thickness was being measured only at one point on the limb (between electrodes 4 and 5, see Figure 1) and since SFL thickness will vary along the length of the thigh, rather than utilizing data from the entire array, only data from the pair of electrodes to either side of the point of SFL measurement was included here. R and X values across this pair of voltage electrodes were obtained, and θ was then computed from the formula θ = arctan (X/R).

Figure 1.

The voltage electrode array used for this experiment, with voltage electrodes 4 and 5, from which the impedance measurements were obtained, indicated (arrows).

2.3 SFL Measurements

Ultrasonographic images were obtained with a Terason 2000 Handheld Ultrasound System (Terason, Inc, Burlington, MA) using a 5-MHz probe set at depth 5–7 cm with a focus of 1.3 cm. The ultrasound probe was held perpendicular to the muscle surface with minimal pressure, over the mid-point between the ink marks used for placement of voltage electrodes 4 and 5. The subject was asked to contract the muscle by gently extending the knee to help distinguish the SFL from the muscle and the interface of the SFL and muscle identified. The SFL thickness was then measured to the nearest 0.01 cm using the supplied software.

2.4 Data Analysis

Means and standard deviations of patient age, θ, and SFL thickness were determined for the entire cohort and individually for men and women, and comparisons were made using unpaired, two-tailed t tests. We note that neither raw resistance nor reactance was specifically analyzed since both may be prone to morphometric effects, to which θ is thought to be relatively insensitive (Shiffman et al., 1999). Scatter plots of θ vs. SFL thickness were generated separately for men and women. Both linear and quadratic fits of the data were investigated. From the scatter plots, r² and their associated p values were computed. Similarly, the relationship between age and skin-fat thickness and between age and θ were assessed using linear correlation. Multiple regression analyses were then performed separately for both men and women, using θ as the dependent variable and SFL thickness and patient age as independent variables.

3. Results

3.1 Skin-Fat Thickness and θ Differences Between Men and Women

The mean ± standard deviations for SFL thickness (in cm) were 0.76 ± 0.23 for men and 1.43 ± 0.51 for women. For θ, the mean ± standard deviations (in degrees) were 10.79 ± 2.43 for men, and 8.45 ± 1.78 for women. Both the SFL thickness and θ were significantly different (p <0.01) between men and women.

3.2 Relationship Between θ and SFL Thickness

Scatter plots for θ comparing SFL thickness for men and for women are shown in Figures 2a and 2b. These plots could not be adequately fit by linear (as shown in the figures) or second-degree polynomial (i.e., quadratic) regressions. For linear fits, r² values were 0.02 (p = 0.39) for men, and 0.04 (p = 0.32) for women. For quadratic fits, r² values were 0.13 (p = 0.13) for men and 0.18 (p = 0.08) for women. Other fits (e.g. higher order polynomials, exponential, and logarithmic) proved no better.

Figure 2.

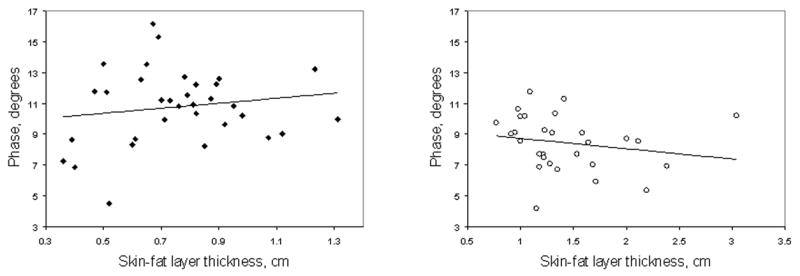
(a) Scatter plot and linear regression of θ vs. SFL thickness in men. No clear correlation was found between θ and SFL thickness (r² = 0.02, p = 0.39). A second-degree polynomial fit (not shown) was also generated, for which the r² value was 0.13 (p = 0.13). (b) Scatter plot and linear regression of θ vs. SFL thickness in women. Similar to the men, no clear correlation was found between θ and SFL thickness using linear or (r² = 0.04, p = 0.32) or quadratic (r² = 0.18, p = 0.08) fits.

3.3 Relationship Between Age and SFL Thickness

No clear linear correlation could be demonstrated between age and SFL thickness for men (r² < 0.01, p = 0.73). For women, however, a weak but significant positive correlation was seen between age and SFL thickness (r² = 0.14, p <0.05).

3.4 Relationship Between Age and θ

As expected from earlier work (Aaron et al., 2006), age and θ showed strong negative correlations for both genders (r² = 0.48, p<0.01 for men and r² = 0.68, p <0.01 for women).

3.5 Multiple Regression Analysis of θ

The multiple regression equation for men was θ = −0.078 × Age + 1.185 × SFL thickness + 13.810. Age (p < 0.01) but not SFL thickness (p = 0.39) was a significant predictor of θ. For women, the multiple regression equation was θ = −0.079 × Age + 0.491 × SFL thickness + 12.047. Similar to the men, age (p < 0.01) but not SFL thickness (p = 0.24) was a significant predictor of θ.

4. Discussion

These results support that linear-EIM can be meaningfully applied to subjects with a wide range of SFL thicknesses. Indeed, we were able to find only very weak relationships between the SFL thickness and the major impedance parameter θ in either gender. We were interested in assessing the effects of the SFL separately in men and women since women, on average, have a thicker SFL (Westerbacka et al., 2004). Indeed, we identified a nearly 0.7 cm mean difference in SFL thickness between men and women. Although θ was lower amongst the women than the men, the lack of any clear relationship between θ and SFL in either group strongly argues that the difference in θ was due to underlying differences in the condition of the muscle itself rather than an effect of the SFL. We also again demonstrated the negative correlation between age and θ seen in our previous study (Aaron et al., 2006), although in that study, data from the entire array was presented. Finally, by performing the multiple regression analyses, we confirmed that this reduction in θ with increasing age was not due to an effect of an age-associated increase in SFL thickness.

Despite the theoretical arguments put forth above against an influence of the SFL on θ, it remains possible that the SFL could make some contribution to EIM measurements, even if only minor. One possible explanation for such a contribution is that increasing depth of the SFL is likely associated with increasing intramuscular fat, which will impact linear EIM measurements. Indeed, earlier studies have found correlations between adiposity as measured by standard bioimpedance analysis (BIA), using computerized tomography (Brown et al., 1987), hydrodensitometry (Organ et al., 1994), and magnetic resonance imaging (MRI) (Fuller et al., 1999). In addition, one prior BIA study made specifically in obese subjects with careful morphometry of different tissue compartments using MRI also showed that subcutaneous fat contributed modestly to the measured resistance (Baumgartner et al., 1998). In especially obese individuals, however, in whom the adipose tissue volume was greater than that of muscle tissue, a stronger relationship between subcutaneous fat volume and resistance was observed. Comparisons between these BIA studies and ours are not straightforward given the very different electrode arrangements for traditional and segmental BIA as compared to linear EIM. Additionally, in this study we focused on θ, which is less dependent on limb cross-sectional area and shape, rather than resistance, the parameter of interest in these studies.

There are several limitations to our study. First, it has focused entirely on normal subjects; in patients with neuromuscular disease producing muscle atrophy, the reduction in muscle bulk will amplify the contributions of the SFL to linear-EIM measurements. In fact, in patients with severe neuromuscular disease and marked muscle atrophy, it is likely that electrical current will be forced to flow through other structures to a greater extent. Determining the role of the SFL in linear EIM measurements in this context will require separate investigation. Second, some inaccuracy in measurements of the SFL thickness with ultrasound is unavoidable, and cannot be discounted as a source of error. Third, this study focused on linear EIM performed at 50 kHz only: it is possible that a greater dependence of impedance measurements on SFL dimensions may be found at higher or lower frequencies and separate study would be required to answer that question. Finally, another variation of EIM, rotational EIM, involves the injection of electrical current in close proximity to the voltage electrodes. In such a situation, current dispersion will be profoundly affected by the size of the SFL, and thus the results obtained here are clearly not relevant to that application.

This work represents only an initial study of the contribution of the SFL to linear-EIM measurements. A logical next step would be to generate multiple regression models to determine the dependences of impedance parameters on muscle, skin, fat, and bone dimensions, using the higher resolution afforded by MRI to more accurately define these dimensions (as has been done for BIA: see Baumgartner et al., 1998). MRI could also permit the study of the actual distribution of the current applied during EIM (Scott et al., 1991). Finally, further work with excised animal tissue (see Tarulli et al., 2006, for example) in which the dimensions of SFL could be readily altered, may also help to elucidate the impact of this layer in all forms of EIM testing.

Nonetheless, the results found here strongly support that linear EIM data is not substantially impacted by the SFL and that the technique can be applied meaningfully to both men and women with a relatively wide range of SFL thicknesses.