Abstract
Total intermolecular interaction energies are determined with a first version of the Gaussian electrostatic model (GEM-0), a force field based on a density fitting approach using s-type Gaussian functions. The total interaction energy is computed in the spirit of the sum of interacting fragment ab initio (SIBFA) force field by separately evaluating each one of its components: electrostatic (Coulomb), exchange repulsion, polarization, and charge transfer intermolecular interaction energies, in order to reproduce reference constrained space orbital variation (CSOV) energy decomposition calculations at the B3LYP/aug-cc-pVTZ level. The use of an auxiliary basis set restricted to spherical Gaussian functions facilitates the rotation of the fitted densities of rigid fragments and enables a fast and accurate density fitting evaluation of Coulomb and exchange-repulsion energy, the latter using the overlap model introduced by Wheatley and Price [Mol. Phys. 69, 50718 (1990)]. The SIBFA energy scheme for polarization and charge transfer has been implemented using the electric fields and electrostatic potentials generated by the fitted densities. GEM-0 has been tested on ten stationary points of the water dimer potential energy surface and on three water clusters (n=16,20,64). The results show very good agreement with density functional theory calculations, reproducing the individual CSOV energy contributions for a given interaction as well as the B3LYP total interaction energies with errors below kBT at room temperature. Preliminary results for Coulomb and exchange-repulsion energies of metal cation complexes and coupled cluster singles doubles electron densities are discussed.
I. INTRODUCTION
Despite significant progress, the field of molecular modeling with its innumerable potential applications, including protein structure prediction and drug design, remains limited by the quality of the available empirical force fields. Conversely, quantum calculations are able to give quantitative results but are limited to relatively small systems. Comparison of quantum and empirical calculations shows the importance of short range effects on intermolecular interaction energies.1 For example, the value of the true intermolecular Coulomb energy (the intermolecular electrostatic contribution) cannot be matched in the bonding area by traditional classical approaches using long range approximations such as fitted point charges2 or even with more advanced distributed multipole representations.3-6
Indeed, short range quantum effects related to the overlap of electron clouds (penetration energy) are missing from current force fields and are a non-negligible source of error. In other words, if the goal is to reach “chemical accuracy” it is not enough for a model energy function to perform well outside the molecular van der Waals envelope; it is also important to be able to reproduce energies even when electronic densities overlap (especially in molecular dynamics simulations where close contacts are frequently generated). In this context, parametric multipolar damping functions7,8 have recently appeared and constituted a notable step towards a better description of electrostatic energies. Nevertheless, short range effects also influence the values of electrostatic potentials and electric fields and consequently modify classical values of induction and dispersion energies. Moreover, overlapping electron clouds directly give rise to the exchange-repulsion energy1 which is a very important contribution to the total intermolecular energy. This contribution is generally misrepresented, diminishing the anisotropy of the interactions.1
van Duijneveldt–van de Rijdt et al.9 recently tested several available molecular mechanics potentials on the difficult ten stationary points of the water dimer potential energy surface as described by Tschumper et al.10 They concluded that in order for a force field to be both accurate and transferable, i.e., useful for a range of similar systems, it must separately reproduce each of the four physical components of the total intermolecular interaction energy, namely, Coulomb, exchange repulsion, induction, and dispersion. In this context, the sum of interacting fragment ab initio (SIBFA) force field,11 initially tested in the paper of van Duijneveldt–van de Rijdt's et al., was recently refined in order to more closely reproduce each of the individual components of the Hartree-Fock intermolecular interaction energy.12,13
Current force fields use potential functions that attempt to mimic the anisotropy of the density. However, a second more natural option would be to model the electron density itself. Two decades ago, Gordon and Kim14 introduced this concept using an analytic expression for frozen atom electron density to calculate intermolecular interactions. This approach offers a solid foundation to reduce empiricism in the parametrization of potential functions and provides a way to more accurately account for short range quantum effects.
The purpose of this paper is to explore this second option and to provide a first insight into the possibility of tailoring such an intermolecular force field. For that purpose, we will use the formalism of the density fitting (DF) method15 usually devoted to the fast evaluation of Coulomb integrals for ab initio codes. We have previously shown that the DF approach can be successfully applied to calculate intermolecular electrostatic (Coulomb) energies as well as the electric field and electrostatic potential.16 In the present contribution we additionally present a density fitting implementation of the overlap model introduced by Wheatley and Price17 to compute exchange-repulsion energies as well as a DF version of the SIBFA force field11 induction scheme computed as the sum of polarization and charge transfer energies.
The SIBFA scheme is based on the use of localized molecular orbitals (LMOs) which can be centered on atoms, bonds, or lone pairs. We have previously shown16 that the use of auxiliary basis elements centered at off-atom sites leads to a more accurate fit of the density. Here we note that using a larger number of fitting sites including LMO positions allows for an accurate fit using only s-type Gaussian auxiliary basis (I=0). To reflect the s-type character of the fitted density, we term the force field Gaussian electrostatic model-0 (GEM-0).
Each of the energetic contributions of the force field total intermolecular interaction energy will be compared to their density functional theory (DFT) counterpart computed with the constrained space orbital variation (CSOV) approach.18 It is important to note that since DFT based CSOV does not include a dispersion term, we have omitted it from our current implementation. The GEM-0 force field obtained by fitting to DFT calculated densities will be denoted GEM-0 (DFT).
We test GEM-0 (DFT) by calculating total intermolecular interaction energies for several water dimer configurations as well as clusters of three different sizes. We also explore the application of GEM-0 (DFT) to water-metal complexes. Some preliminary results are presented for GEM-0 coupled cluster singles and doubles (CCSD) obtained by fitting relaxed CCSD density. These latter results are limited to the Coulomb and exchange-repulsion energies for the ten water dimers and the three water clusters. They are compared to their ab initio counterparts obtained with the symmetry adapted perturbation theory (SAPT).19
II. COMPUTATIONAL DETAILS
A. Methods
1. Density fitting
Following our previous work,16 we have used the formalism of the variational density fitting method.15 This method relies on the use of auxiliary Gaussian basis functions to fit the molecular electron density obtained from a relaxed one-electron density matrix using a linear combination of atomic orbitals (LCAOs),20(a)-20(c)
| (1) |
The central idea of the approach is to minimize the Coulomb self-interaction energy of the error,15,16
| (2) |
The method slightly differs from the one generally used in the quantum similarity community20(d) since the expansion coefficients are not constrained to be positive (no statistical meaning of the density function as a probability distribution being required).
Inserting the right-hand side of Eq. (1) into Eq. (2), we obtain
| (3) |
E2 from Eq. (3) can be minimized with respect to the expansion coefficients x1 and a linear system of equations can be obtained by
| (4) |
Equation (5) is used to determine the coefficients
| (5) |
where and .
The determination of the coefficients requires the use of a modified singular value decomposition procedure in which the inverse of an eigenvalue is set to zero if it is below a certain cutoff. A cutoff value of 10−8 has been previously determined16 to be acceptable for the molecules which will be under study.
2. Fitted densities: Auxiliary basis set and extra points
Since we did not choose to optimize our own auxiliary basis set,20(d) the choice of an auxiliary basis set is important and strongly dependent on its design. Our choice must be compatible with an accurate fit of densities obtained using reference DFT or CCSD calculation with the aug-cc-pVTZ basis set.21 A solution consists of reducing each original higher angular momentum (l>0) function of an available auxiliary basis set to the s-type functions only. This “transformation” results in an immediate reduction in the number of fitting functions, thus the chosen auxiliary basis set must contain a large number of functions.
Several auxiliary basis sets are available such as A1,22 P1,22 g03 (Ref. 23) (tested in our previous work16), and CFIT.24 The Al and P1 auxiliary basis sets are too small when restricted to s components only. On the other hand, the transformation of the g03 and CFIT provides a large number of s functions. The g03 basis set, which is automatically generated from the aug-cc-pVTZ basis set by GAUSSIAN 03,23 includes only one very tight s-type function, while the rest of the basis set is composed of very diffuse functions. For that reason, we chose the CFIT auxiliary basis set which is optimized for the Dunning's correlation consistent basis set family24 and presented the advantage of having a large number of original s functions shared with the original aug-cc-pVTZ basis set which do not require any transformation. A direct consequence of the use of s-type functions is that the atomic positions are no longer sufficient as choices for the expansion sites of the auxiliary basis sets.
We have previously demonstrated16 that additional sites can be employed to improve the fitting results. We also showed that an easy way to estimate the spatial location of the error on the fit of the density is to draw a map of the differences of electrostatic potential values between the original and the fitted densities. It has been shown16 that the errors were mainly located at the lone pair and bond midpoint positions (see Fig. 2 of Ref. 16). Following that idea, we obtained the difference map of electrostatic potential starting with fitted density centered only on atoms. In addition to the expected bond midpoints and lone pair positions, strong deficiencies have been found at points located between the hydrogens and between the positions of the bond midpoints. The origin of these errors is simple and linked to the nature of the s-type Gaussian functions used, which do not have directionality (present in higher angular momentum functions) and require additional sites to mimic the very complex initial density.
FIG. 2.
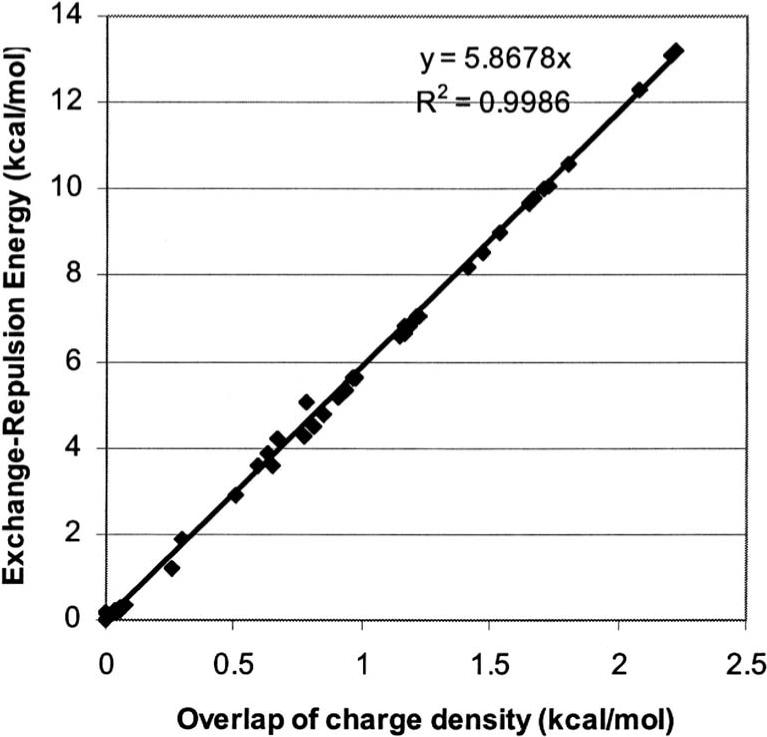
Correlation of the overlap of charge density (kcal/mol) computed with GEM-0 vs exchange-repulsion energy (kcal/mol) obtained at a CSOV/B3LYP/aug-cc-pVTZ level for 200 orientations of the water dimer.
To solve this problem, we chose to place extra points bearing an oxygen auxiliary function16 set at these locations; this gives us a nine point expansion model (as can be seen in Fig. 1) that shows a significant improvement of the least squares fit by adding more degrees of freedom with supplementary s-type Gaussian functions. The lone pair positions were obtained from the corresponding localized molecular orbital (LMO) centroid position (see Fig. 1) obtained with HONDO 95.3 (Ref. 24) using the Foster and Boys procedure.25 This choice also offers the useful possibility to access the positions of the centroids of the localized orbitals required for the computations of the polarization and charge transfer energies in all orientations of the molecules. The SIBFA procedure provided the rotated positions of the lone pairs for each local fragment geometry. The location for the rest of the points is easily deduced based on the hydrogen and midpoint coordinates.
FIG. 1.
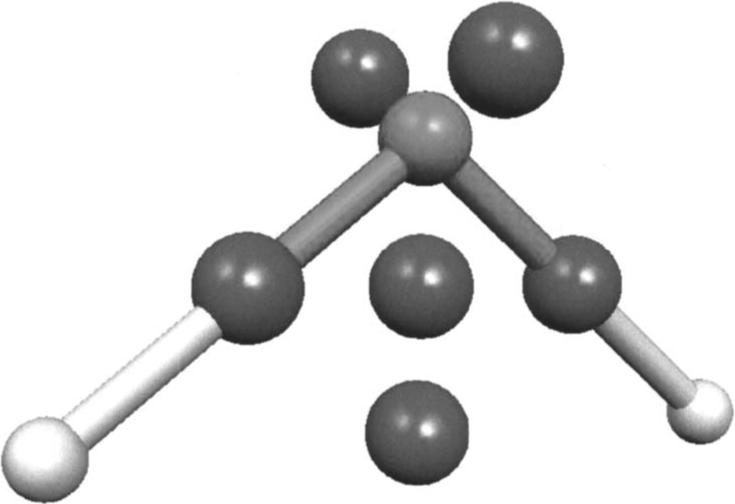
Nine center GEM-0 water model [the coordinates of these centers for an example molecule are given in the supplementary materials (Ref. 30)].
3. Computation of the total intermolecular interaction energy
In our approach, the total interaction is computed as the sum of four intermolecular energetic contributions: electrostatic (Coulomb), exchange repulsion, polarization, and charge transfer. At this point, no long range dispersion contribution26 has been added since this work is focused on the reproduction of DFT intermolecular energies using the B3LYP (Ref. 27-29 functional. The central idea is that each contribution should match its DFT counterpart obtained using the CSOV approach18 (details of the CSOV method can be found in the supplementary materials30),
| (6) |
For all equations, the and fitted densities can be calculated by separately fitting the unperturbed electron density of molecules A and B in order to build a frozen fragment density library (i.e., if A and B are the same molecule, the same density fragment can be employed for the interacting dimer). For that reason, the internal molecular geometry should remain fixed.
a. Coulomb interaction energy.
Using the fitted electronic densities, it has been shown16 that it is possible to accurately compute the intermolecular Coulomb interaction energy from frozen monomer densities,
| (7) |
All the required integrals are computed using the McMurchie-Davidson recursions31 enabling the use of higher angular moment Gaussian functions if required as discussed in Sec. III (no recursions are needed for s-type Gaussian functions). By using DF, both long range multipolar and short range penetration energies are included, if an adequate fit of the density is utilized.
b. Exchange-repulsion energy.
Extending the approach, we followed an idea initially proposed by Wheatley and Price17 and computed a two-body exchange repulsion based on the overlap model. The model relies on the observed proportionality between the overlap of the charge density and the exchange-repulsion energy.32
By using the definition of fitted densities,15,16 the evaluation of the overlap of the charge density is straightforward in the framework of our variational Coulomb fitting approach. Indeed, using s-type Gaussian functions simplifies considerably the computation of an approximate exchange repulsion and requires only the evaluation of overlap integrals between spherical Gaussian functions:
| (8) |
where
The value of the parameter K can be easily determined and corresponded to the slope of a linear regression of the overlap of charge density versus the corresponding ab initio exchange-repulsion energy values.
c. Polarization energy.
The previously considered Coulomb and exchange-repulsion energies have been referred to as frozen core interactions.18,26 They did not involve relaxation of the interacting monomer densities. By contrast, the polarization and charge transfer energies do involve relaxed monomer densities.
As stressed by Böttcher,33 the use of dipole polarizabilities is a very good approximation of the polarization energies when the electric fields generated by the interacting molecules are not too large. We have modeled the polarization energies using monomer properties34 as implemented into the SIBFA molecular mechanics package. In our current implementation, the permanent electric fields are generated by the density fitting procedure and interacted with distributed dipolar polarizabilities computed with the Garmer and Steven's approach35 at the B3LYP/aug-cc-pVTZ level. The polarizabilities denoted α(i)[computed with a modified version of HONDO 95.3 (Refs. 26 and 36)] are 3*3 tensors distributed at the centroids of the Foster and Boys localized orbitals and offer the advantage that the induced dipoles within a molecule do not interact directly:35
| (9) |
where . γ is a parameter used to adjust the field to its reference ab initio value.
Indeed, the advantage of fields generated by density fitting versus multipolar fields relies on their natural reproduction of the ab initio behavior even at short range. Nevertheless, the difficulty of fitting core electrons generates a constant shift in the values of the fitted fields compared to their ab initio counterpart, which requires the scaling of the fields. This is achieved by the use of the parameter γ. Compared to the ab initio value, the density fitting field presents an average systematic error of 6%. We chose 1.06 as a value to correct the field due to the fitted density.
The polarization equation is solved iteratively.37,38 In the first step, an initial guess of induced dipoles (Δμ(i)) is computed, leading to a first estimation of the polarization energy, by interacting each polarizable center i with the permanent field (E0) generated at this point by all the other molecules. In the subsequent iterations, the same procedure occurs but this time each center i of a given molecule will also interact with all the fields due to the induced dipoles generated on the other molecules. Consequently, the value of the center is updated since the applied fields have changed. The procedure is carried out iteratively until self-consistency (a precision of 10−2 kcal on the polarization energy is generally obtained in 6–8 iterations) and should be able to capture an important part of the collective effects, especially since the procedure uses realistic electric fields.
It is important to point out that the use of a classical dipolar polarizability approximation is not always sufficient to match the CSOV polarization value. Indeed, a formalism including some higher moment polarizabilities should be used.34 Moreover, in a CSOV polarization computation, the whole complex is considered and the polarization energy values are strongly influenced by the antisymmetrization of the wave function (i.e., an exchange-polarization contribution is included). In fact, in terms of a classical approximation, these effects can be assimilated to extra intermolecular screening effects due to the overlapping perturbed densities and cannot be recovered using the ground state monomer densities only. For example, in the presence of a metal cation, where high electric fields are generated, these effects are non-negligible and classical approximations lead to a severe overestimation of the true polarization energy. An extension of the formalism will be needed to treat such difficult cases. For these reasons, we have limited our study to water.
d. Charge transfer energy.
For that contribution, we have used the semiempirical formalism implemented in the SIBFA program which differs from the electronegativity equalization approach.39(a),39(b) The energy expression initially derived from an explicit analytic form proposed by Murrel et al.39(c) uses the values of the electrostatic potential generated using the density fitting procedure and has the form40-42
| (10) |
where C is a constant equal to 3.5 calibrated to reproduced the value of Ect (CSOV) at the equilibrium distance of the water dimer. is a function (a) of the overlap between the LMO describing the donor lone pair and the antibonding (virtual) localized orbital of the bond acceptor and (b) the electrostatic potential computed by the density fitting approach exerted on site A by all the other interacting molecules. is a function of the difference between the ionization potential of A and the electron affinity of the electron acceptor.
The ionization potential is increased by the predominantly positive electrostatic potential exerted on A by all the other molecules in the complexes. The electron affinity is reduced by the predominantly negative potential due to its surrounding ligands. In order to include the nonadditive effects of Ect, a coupling between Ect and Epol is introduced, i.e., the potential due to the converged set of induced dipoles is taken into account in the calculation. As for the polarization, the choice of using electrostatic potential generated from the fitted density should enable us to include some short range screening effects. Details can be found in the supplementary materials.30
4. Reference energy calculations
As already introduced, the aug-cc-pVTZ basis set21 has been used for all calculations, except for the ones involving a metal, where the aug-cc-pVTZ basis set is not available and has been replaced by the 6−31G* basis set.43 All CSOV computations have been performed using a modified version of HONDO 95.3 (Refs. 18 and 26) that allows the calculation of intermolecular Coulomb energies,25 two-body exchange repulsion, two-body polarization, and two-body charge transfer energies for molecular clusters.
Since no available ab initio package has the ability to compute many-body correlated polarization interaction energies in complexes encompassing more than two molecules at the DFT level, we have used the restricted variational space44 (RVS) and Kitaura-Morokuma45 (KM) approaches as implemented in the GAMESS software46 at the Hartree-Fock (HF) level. Essentially similar to CSOV at the HF level, RVS has the advantage that it antisymmetrizes the wave function to fulfill the Pauli principle47,48 but is limited to self-consistent field (SCF) optimization of each molecule in the field of the others without taking into account self-consistently the full relaxation due to induced dipoles. On the other hand, the KM decomposition takes all such effects into account but violates the Pauli principle since the total wave function is not antisymmetric (see Ref. 48 for more details). Nevertheless, in our case the molecules do not generate intense electric fields and the errors should be small. For our polarization scheme, the polarization energy of the initial guess of induced dipoles should be close to the RVS energy while our total fully relaxed polarization should be close to the KM energy.
Due to the computational cost related to the aug-cc-pVTZ basis set for large complexes, the RVS and Kitaura-Morokuma energy decomposition computations have been performed at the Hartree-Fock level using the CEP 4−31G (2d) (Ref. 49) basis set augmented with two diffuse 3d polarization functions on heavy atoms (double zeta quality pseudopotential). At the DFT level, the density matrices used for the density fitting have also been derived from HONDO at the same level of theory.
To illustrate our discussion about the extension of the approach to the reproduction of post-Hartree-Fock methodology, reference SAPT (Ref. 20 calculations using the Dalton (Ref. 50) package and the SAPT 96 software51 have been performed for Coulomb energies () and exchange-repulsion energies [] at the coupled cluster level (CCSD). Since the relaxed CCSD density matrices have been extracted from MOLPRO (Ref. 52) for the purpose of the density fitting procedure, we have also computed Coulomb energy using a similar approach proposed by Korona et al.53 with MOLPRO to verify the consistency between the SAPT 96 and MOLPRO values.
Some distributed multipoles were derived from the Vigné-Maeder–Claverie procedure4,54 using the same density matrix as for the density fitting and are distributed up to the quadrupole level on each atoms and bond midpoints. Such a procedure was originally demonstrated to provide a very good approximation of the true multipolar energy.4 The values of the multipolar Coulomb energy were computed using the SIBFA package.
All the B3LYP and post-Hartree-Fock relaxed one-electron density matrices required for the fit have been obtained from a SCF convergence criterion of 10−10 a.u. for the root mean square deviation (RMSD) changes of the density matrix elements. The errors of the DF approach energies compared to the ab initio values (AB) will be discussed as follows:
III. RESULTS
A. Reproduction of density functional theory interaction energies
1. Coulomb and exchange-repulsion interaction energies
a. Water dimers.
We first test our model on the ten minima of the total energy surface of the water dimer.9,10 The expected inclusion of penetration effects in the Coulomb interaction energy values16 is observed and the GEM-0 approach performs notably better than the distributed multipole approach in the reproduction of the true DFT Coulomb energy values obtained with the CSOV approach (see Table I). Using auxiliary coefficients fitted on only one single density matrix, the average absolute error of the ten configurations is 0.095 kcal. Moreover after averaging the fitted coefficients obtained from 20 density matrices obtained from ab initio calculations on random orientations of an isolated water molecule, the error can be reduced to 0.089 kcal/mol (see Table I), close to the best results obtained previously.16
TABLE I.
(a) Intermolecular Coulomb energies (in kcal/mol) for the ten water dimer geometries (Refs. 7 and 8) for the GEO-0 approach fitted on B3LYP (or CCSD)/aug-cc-pVTZ densities. Results in parentheses are interaction energies from a distributed multipole approach (Ref. 4) (up to quadrupoles on bonds and atoms). CSOV/B3LYP and SAPT reference calculations using the aug-cc-pVTZ basis set are provided (for SAPT, ) and compared to SAPT literature results (Ref. 39) using the IOM basis set (Ref. 43). (b) Absolute errors (kcal/mol) for intermolecular Coulomb energies using the GEM-0 approach fitted on B3LYP (or CCSD)/aug-cc-pVTZ densities compared to reference CSOV and SAPT values.
| Water dimer geometry |
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| (a) | Level of theory for ECoulomb | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| CSOV (DFT) | −8.11 | −6.85 | −6.64 | −6.73 | −5.77 | −5.44 | −4.87 | −1.64 | −4.95 | −2.87 | |
| (−6.15) | (−5.08) | (−4.91) | (−4.86) | (−4.17) | (−3.97) | (−3.47) | (−1.09) | (−3.42) | (−2.04) | ||
| GEM-0 (DFT) | −8.14 | −6.89 | −6.55 | −6.77 | −5.77 | −5.48 | −5.05 | −1.77 | −4.76 | −2.74 | |
| SAPT (CCSD) | −7.96 | −6.69 | −6.48 | −6.69 | −5.71 | −5.33 | −4.89 | −1.55 | −4.77 | −2.72 | |
| GEM-0 (CCSD) | −7.92 | −6.76 | −6.35 | −6.76 | −5.86 | −5.56 | −5.01 | −1.44 | −4.63 | −2.72 | |
| SAPT (CCSD) (Ref. 39) | −8.02 | −6.73 | −6.49 | −6.70 | −5.69 | −5.33 | −4.96 | −1.55 | −4.81 | −2.70 | |
| (b) | Water dimer geometry |
||||||||||
| |
Absolute errors for ECoulomb |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| GEM-0 (DFT) | 0.03 | 0.04 | 0.09 | 0.04 | 0.0 | 0.04 | 0.18 | 0.13 | 0.19 | 0.13 | |
| GEM-0 (CCSD) | 0.04 | 0.07 | 0.12 | 0.07 | 0.17 | 0.23 | 0.12 | 0.11 | 0.14 | 0.0 | |
It is important to point out that in comparison, the same procedure limited to a fit using atomic positions only leads to an average error of 1.1 kcal/mol. It is also interesting to point out that the fitted results are a step closer to ab initio results from densities with the aug-cc-pVTZ (−f) basis set [the aug-cc-pVTZ (−f) basis set only differs from the original aug-cc-pVTZ by the removal of diffuse f functions on the oxygen] where the average error is 0.062 kcal/mol. This result shows the general difficulty of the fitting of electron density from diffuse functions as previously noted.55 Nevertheless, the transferability of the auxiliary coefficients is demonstrated and each of the dimers is correctly described.
For the exchange repulsion, the results are encouraging and show the robustness of the overlap model applied to B3LYP [which has a different exchange-repulsion energy behavior than Hartree-Fock or MP2 (Ref. 26). As shown in Table II, the model has an average absolute error of 0.204 kcal/mol (but only 0.053 kcal for the average signed error). The value of 5.8679 for K was determined from initial fits on water dimer computations. As seen in Fig. 2, this value corresponds to the slope of a linear regression of the overlap of charge density versus the true exchange-repulsion values obtained from CSOV (the correlation coefficient is 0.9986, sampled on 190 random orientations).
TABLE II.
Intermolecular exchange-repulsion energies (in kcal/mol) for the ten water diameter geometries (Refs. 7 and 8) for the GEM-0 approach fitted on B3LYP/aug-cc-PVTZ densities CSOV at the B3LYP/aug-cc-pVTZ level. GEM-0 results in parentheses are exchange-repulsion energies obtained with GEM-0 using auxiliary coefficients obtained by averaging fits of the density using a 10−8 cutoff of the eigenvalues with another set obtained using a 10−10 cutoff as discussed in the text.
| Water dimer geometry | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Level of theory for Eeach-rep | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| CSOV (DFT) | 6.84 | 5.63 | 5.37 | 5.08 | 4.22 | 3.85 | 3.59 | 1.18 | 3.59 | 1.89 |
| GEM-0 (DFT) | 6.91 | 5.64 | 5.50 | 4.60 | 3.90 | 3.69 | 3.79 | 1.53 | 3.44 | 1.73 |
| (6.84) | (5.71) | (5.36) | (4.86) | (3.95) | (3.95) | (3.94) | (1.27) | (3.64) | (1.97) | |
At this point, it is important to note that some deviations occur, the worse being observed for dimer 4. It is not surprising since this position which is a transition state obtained at the CCSD(T)/[TZ2P(f ,d)+diff] (Ref. 10) (but not at the B3LYP level, where we found three negative frequencies) already showed the largest deviation between ab initio calculations using different basis sets. The same phenomenon was also observed for electrostatic interactions in our previous work,14 with a difference over 0.5 kcal/mol for this particular interaction between 6−31G* and aug-cc-pVTZ. The structure stability appears to depend on diffuse function interactions and on core correlation8 which are not fully reproduced by our model using the present auxiliary basis set. Moreover, our choice of a unique set of auxiliary coefficients to compute all the energetic contributions is dictated by convenience. In fact, the inherent noise present in the density fitting procedure and reduced by the use of an eigenvalue cutoff (as described in Sec. II A) does not influence each of the contributions in the same way. A slightly different value of this cutoff may improve the agreement of the overlap model with the ab initio results.
b. Water clusters.
In order to test the transferability of the approach to large systems, we also applied the model to water clusters (from 16 to 64 molecules). The tested geometries are all nonequilibrium random geometries extracted from Monte Carlo simulations in ice or in bulk water performed with the SIBFA force field keeping each water fragment rigid. In all cases, the accuracy of the method appears very good, as can be seen in Table III.
TABLE III.
Coulomb and exchange-repulsion intermolecular interaction energies (kcal/mol) for water clusters (n=16,20,64) for the GEM approach fitted on B3LYP (or CCSD)/aug-cc-pVTZ vs ab initio CSOV/B3LYP/aug-cc-pVTZ values. Results in parentheses correspond to the CSOV/B3LYP/aug-cc-pVTZ (−f) level. NC=not computed.
| n | ECoulomb GEM-0 (DFT) | ECoulomb GEM-0 (CCSD) | ECoulomb CSOV (DFT) | Eexch-rep GEM-0 (DFT) | Eexch-rep GEM-0 (CCSD) | Eexch-rep CSOV (DFT) |
|---|---|---|---|---|---|---|
| 16 | −186.84 | −184.80 | −186.38 (−186.84) | 164.95 | 194.96 | 166.54 (166.55) |
| 20 | −309.38 | −305.84 | −307.20 (−309.20) | 292.25 | 341.57 | 292.16 (292.19) |
| 64 | −449.52 | −443.54 | −446.12 (−454.08) | 336.48 | 373.90 | NC |
For the Coulomb interaction energy, the results are −186.84, −309.38, and −449.52 kcal/mol compared to −186.38, −307.20, and −446.12 kcal/mol obtained at the CSOV level for the 16, 20, and 64 water clusters, respectively. Once again, it is interesting to note that the results obtained from the model are always between aug-cc-pVTZ and aug-cc-pVTZ(−f) ab initio results which confirms the difficulty of accurately fitting electronic density from diffuse functions. The approach appears to be very robust even for the 64 molecule clusters where 2016 interaction calculations need to be performed. This emphasizes the importance of considering mean errors which are only 0.001 68 kcal/mol per water-pair Coulomb interaction in the 64 water molecule clusters. For the exchange-repulsion energies, the model is also performing very well with errors below to 1% (see Table III). The results are 164.95 and 292.25 kcal/mol compared to the 166.54 and 292.16 kcal/mol obtained at the CSOV level for the 16 and 20 water clusters, respectively.
2. Beyond the frozen core: Polarization and charge transfer energies
a. Polarization energies.
We found an average absolute error in the polarization energy of 0.096 kcal (see Table IV) in the ten positions of the water dimer. It is interesting to note that the polarization is slightly underestimated which was expected since no induced quadrupoles were taken into account.38
TABLE IV.
Intermolecular polarization interaction energies (kcal/mol) for the ten water dimer geometries Refs. 7 and 8 for the GEM-0 approach fitted on B3LYP/aug-cc-pVTZ densities compared to CSOV B3LYP/aug-cc-pVTZ results.
| Water dimer geometry | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Level of theory for Epol | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| CSOV (DFT) | −1.33 | −1.14 | −1.12 | −0.69 | −0.64 | −0.62 | −0.37 | −0.12 | −0.44 | −0.28 |
| GEM-0 (DFT) | −1.22 | −1.03 | −0.92 | −0.55 | −0.53 | −0.50 | −0.27 | −0.08 | −0.42 | −0.29 |
In order to test the accuracy of the approach on a large number of interactions, we have computed a two-body polarization and compared it to CSOV two-body results. The absolute errors appear to be small and are about 0.28 and 0.48 kcal/mol compared to the CSOV values for the 16 and 20 water cluster geometries, respectively (see Table V). Due to computational time requirement, no CSOV calculation has been performed on the largest 64 molecule clusters. Since the total two-body interaction is only the sum of the polarization pair interactions, the polarization is clearly underestimated. In fact, each molecule should be polarized as well by the electric fields of all the other molecules present in the complex.
TABLE V.
Intermolecular polarization interaction energies (kcal/mol) for water clusters (n = 16, 20, 64) for the GEM-0 approach fitted on B3LYP/aug-cc-pVTZ vs ab initio CSOV/B3LYP/aug-cc-pVTZ values. For the GEM-0 column, results in parentheses correspond to the polarization energy of the first set of induced dipoles. RVS polarization results are given in parentheses in the Morokuma polarization column. Both are computed at the CEP 4−31G (2d) level. NC=not computed.
| n | Epol two-body GEM-0 (DFT) | Epol two-body CSOV | Epol GEM-0 [Epol GEM-0 (DFT) initial guess] | Epol Morokuma/HF (Epol RVS/HF) |
|---|---|---|---|---|
| 16 | −30.75 | −31.03 | −48.53(−36.82) | −45.11(−35.50) |
| 20 | −47.53 | −48.01 | −82.79(−62.60) | −78.6 (NC) |
| 64 | −57.97 | NC | −77.89(−64.78) | NC (NC) |
As discussed in Sec. II A, we performed Hartree-Fock/CEP 4−31G (2d) RVS and Morokuma polarization computations in order to have an ab initio reference on the 16 and on the 20 molecule clusters. As expected, the polarization energy of the initial guess of induced dipoles is close to the RVS energy and the value of fully relaxed polarization should be close to the KM energy. As can be seen in Table V, the results are in excellent qualitative agreement, the HF energy being always less attractive than the DF ones for both levels of polarization. This difference was expected since the polarization energy computed at the CSOV/HF/CEP 4−31G (2d) is already smaller by an average 15% than the one computed at the B3LYP/aug-cc-pVTZ level. The biggest difference was obtained for dimer 1 where the HF/CEP31G (2d) level has a polarization of only 0.99 kcal/mol compared to the 1.33 kcal/mol at the B3LYP/aug-cc-pVTZ level. We have performed the same calculation using multipolar fields (up to quadrupoles as discussed previously) using the same polarization scheme. In the absence of screening of the polarizing fields, a general overestimation of the polarization energies is observed. Compared to the GEM-0 values, a multipole based scheme presents errors on the polarization energies of −12.11, −11.26, and −14.24 kcal/mol for the 16, 20, and 64 molecule clusters, respectively.
These results confirm that GEM-0 inherently embodies some screening effects. In fact, small error compensations probably occur involving a limited gain in polarization due to a missing intermolecular screening which overcomes the fact that no contributions of induced quadrupoles38 are taken into account in the polarization calculation.
b. Charge transfer energies.
Finally, we have computed charge transfer energies on the ten water dimers with the SIBFA procedure using the electrostatic potential generated by density fitting. The results are satisfactory with an average absolute error of GEM-0 of 0.097 kcal/mol (see Table VI) with respect to the CSOV values. It is important to note that the CSOV procedure does not include a correction to the basis set superposition error (BSSE) (the correction is done a posteriori on the total interaction energy). This correction is in general important since a charge transfer energy calculation implies a mixing of the occupied orbitals of a molecule into the virtual of the other (see Ref. 1 for interesting discussion) and includes most of the BSSE. Nevertheless, with the present basis set including diffuse functions, the BSSE is very small and the force field values are generally oriented in the right direction, underestimating the uncorrected CSOV values. We have also calculated the values of the CSOV two-body charge transfer energies. They are about −33.49 and −63.62 kcal compared to the −46.76 and −72.11 kcal/mol GEM-0 values for the 16 and 20 molecule clusters, respectively. These differences indicate that charge transfer interactions are also important in the reproduction of the many-body effects. For this contribution, the two-body CSOV energies are clearly underestimating the true charge transfer energy which is by essence a many-body term. The GEM-0 formalism includes all these effects and should be closer to the right answer.
TABLE VI.
Intermolecular charge transfer interaction energies (kcal/mol) for the ten water dimer geometries (Refs. 7 and 8) for the GEM-0 approach fitted on B3LYP/aug-cc-pVTZ densities compared to CSOV B3LYP/aug-cc-pVTZ results.
| Level of theory for Ect | Water dimer geometry | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| CSOV | −1.77 | −1.48 | −1.42 | −0.96 | −0.80 | −0.68 | −0.53 | −0.20 | −0.54 | −0.26 |
| GEM-0 (DFT) | −1.86 | −1.42 | −1.31 | −0.94 | −0.73 | −0.63 | −0.44 | −0.11 | −0.56 | −0.29 |
3. Total interaction energies
At this point, the final step consists of the comparison of the sum of the energetic components of GEM-0 to the total DFT interaction energies.
For the ten water dimers, we found an average absolute error of 0.16 kcal/mol (see Table VII) (but only 0.038 kcal/mol for the mean error) with respect to the BSSE corrected CSOV total interaction energies. Although the errors are mainly due to a sum of small errors on each of the separate components of the total energy, the results confirm that our methodology is able to reproduce reliably quantum chemical computations.
TABLE VII.
Total intermolecular interaction energies (kcal/mol) for the ten water dimer geometries (Refs. 38 and 39) for the GEM-0 approach fitted on B3LYP/aug-cc-pVTZ densities compared to CSOV B3LYP/aug-cc-pVTZ results corrected from the basis set superposition error.
| Water dimer geometry | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Level of theory for Ect | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| CSOV | −4.39 | −3.82 | −3.80 | −3.38 | −3.00 | −2.91 | −2.36 | −0.78 | −2.30 | −1.56 |
| GEM-0 (DFT) | −4.30 | −3.71 | −3.28 | −3.32 | −3.13 | −2.88 | −1.98 | −0.45 | −2.29 | −1.59 |
In order to test the total accuracy of our model, we have computed the total interaction energy (corrected from BSSE) using JAGUAR 6.0 (Ref. 56) with the same level of theory for the 16 and 20 molecule water clusters. Errors of +3.16 kcal (out of −114.02 kcal/mol) and −3 kcal/mol (out of −168.1 kcal/mol) were found, respectively, confirming the good transferability of the different approximations. At this point, we have also tested another set of auxiliary coefficients that we have “tailored” to try to reduce the noise effects. The new set of coefficients has been obtained averaging the first set of coefficients with a second one obtained with a 10−10 cutoff of the eigenvalues. The improvement on the total interaction energy appeared limited on the ten dimers, with an average error on the total interaction energy reduced to only 0.16 kcal/mol. Furthermore, a slight redistribution of the components occurs, leading to an improvement of the exchange-repulsion results confirming its dependence to cutoffs in the DF procedure. As it can be seen in Fig. 3, the error of the density fitting procedure compared to CSOV is reduced leading to an improved average error of 0.12 kcal/mol. Nevertheless, this extra work does not change drastically the agreement with ab initio, especially on clusters where the errors on the total energy are +1.2 and −5.3 kcal/mol on the 16 and 20 molecule clusters, respectively.
FIG. 3.
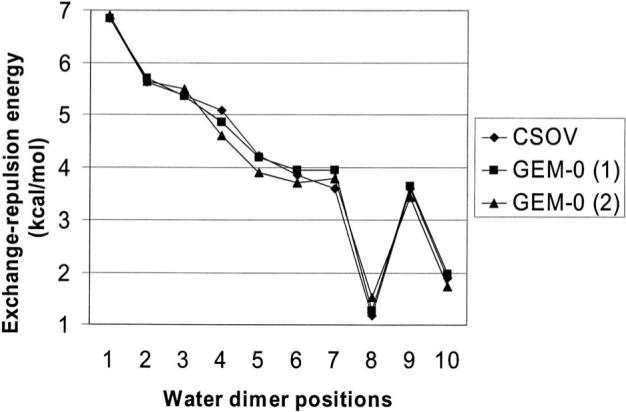
Intermolecular exchange-repulsion energy (in kcal/mol) for the ten orientations of the water dimer (Refs. 38 and 39) for GEM-0 compared to CSOV results at the B3LYP/aug-cc-pVTZ level. (1) GEM-0 results with a cutoff averaged between two sets of coefficients obtained with a cutoff of the eigenvalues at 10−8 and 10−10, respectively (K=6.0220). (2) GEM-0 results with a 10−8 cutoff on the eigenvalues (K=5.8679).
B. Applicability of the procedure to water-metal complexes
We have also tested the approach on metal cation-water complexes. For the reasons detailed in Sec. II A, the results presented here are limited to Coulomb and exchange-repulsion energies.
Ca(II) and Cu(I) were studied using automatically generated g03 basis sets since CFIT auxiliary basis sets were not available for these elements. The s function limitation required the addition of six extra centers placed at ±0.01 Å from the cation in the x, y, and z directions in order to reproduce directionality. In all cases, both Coulomb and exchange repulsion (where the correlation between overlap of charge density and exchange repulsion has correlation factors around 0.999) follow the ab initio behavior [see Fig. 4(a)] even at short range where the maximum error remains below 5% of the ab initio energy [1% at the minimum, see results in Table VIII and Fig. 4(b)] due to an increasing covalent character of the bond. It is important to point out that these errors are really small compared to those obtained with multipoles. Indeed, due to important overlap effects, errors about 100% with respect to the CSOV value are encountered at short range.8 Slightly better results are obtained for Ca(II) than for Cu(I), illustrating the difficulty of the fit of core electron density.
FIG. 4.
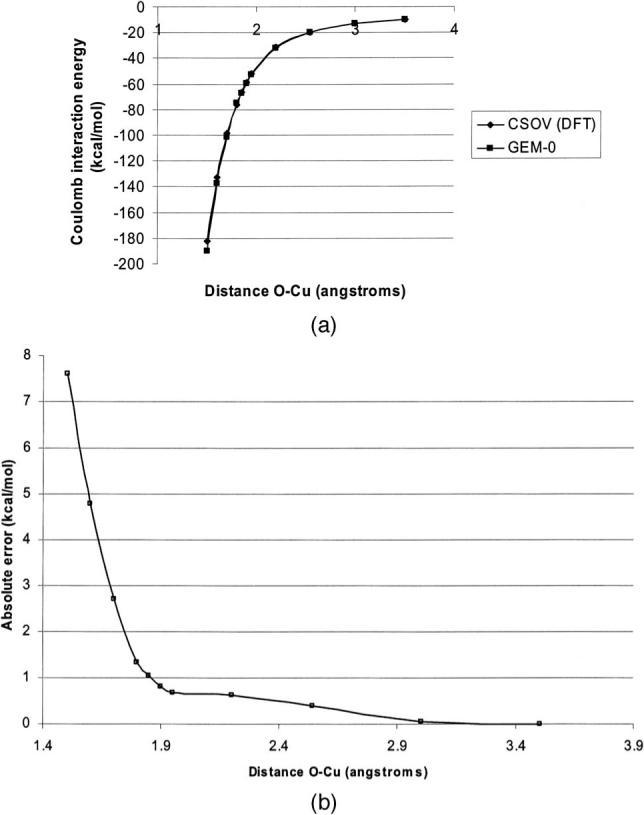
(a) Intermolecular Coulomb energy (kcal/mol) for the water-Cu(I) complex at various distances for GEM-0 and CSOV at the B3LYP/aug-cc-PVTZ level for the water and B3LYP/6−31G* for the cation. The water is immobile at the position of the molecule A of the dimer (Refs. 38 and 39). The K parameter is 2.8942 (R2=0.9991). (b) Absolute errors (kcal/mol) of the GEM-0 approach for the water-Cu(I) complex at various distances compared to CSOV at the B3LYP/aug-cc-PVTZ level for the water and B3LYP/6−31G* for the cation.
TABLE VIII.
Coulomb and exchange-repulsion intermolecular interaction energies (kcal/mol) for water-metal complexes [Ca(II) or Cu(I)] for the GEM-0 approach fitted on B3LYP/aug-cc-pVTZ (6−31G* for the metal) densities compared to CSOV B3LYP/aug-cc-pVTZ (6−31G* for the metal) results. The equilibrium distances found for the cation-water scans of the oxygen-cation distance are 2.31 and 1.83 Å for Ca(II) and Cu(I), respectively.
| Ca(II)-water distances (Å) | Cu(I)-water distances (Å) | |||
|---|---|---|---|---|
| Level of theory for Ect | d=1.5 | Equilibrium | d=1.5 | Equilibrium |
| ECoulomb CSOV | −211.31 | −46.86 | −182.8 | −66.16 |
| ECoulomb | −202.60 | −46.37 | −190.41 | −67.19 |
| GEM-0 (DFT) | ||||
| Erep CSOV | 467.89 | 18.93 | 305.97 | 25.61 |
| Erep | 479.2 | 19.21 | 316.12 | 25.89 |
| GEM-0 (DFT) | ||||
Since the fitting procedure is general, any metal density can be fitted by our model giving realistic interactions. It is important to point out that for the intermolecular Coulomb energy (the case of exchange repulsion is more complex due to Gaussian function directionality17 and has not been treated at this point), it is possible to use higher angular momentum Gaussian functions for the closed shell cation (because of its spherical symmetry). So, in addition to a small increase in accuracy (the changes were below 0.1 kcal/mol at the equilibrium), it was possible to eliminate the extra auxiliary functions expansion points, keeping only the atomic position.
C. Applicability of the procedure to post-Hartree-Fock densities
The approach is not limited to DFT and should be able to fit electron density of any level of theory that provides a relaxed density matrix. Thus in order to complete the tests on the ten water dimers, we have fitted post-Hartree-Fock densities using relaxed density matrices obtained from CCSD computations using MOLPRO.52 We have verified the consistency of using MOLPRO density as a fitting reference in comparison to SAPT 96.51 The differences in Coulomb energy results obtained from SAPT 96 and MOLPRO are below 10−2 kcal/mol.
As discussed previously, we used fitted densities obtained by averaging fits at the 10−8 and 10−10 cutoffs in the eigenvalues in order to limit noise. With respect to our SAPT CCSD reference calculation, an average absolute error of 0.107 kcal/mol is found for our GEM-0 results. Since the reference calculation is performed in the dimer basis set, the model density is seen to perform well, which demonstrates the feasibility of fitting post-Hartree-Fock densities. It is interesting to point out that symmetry adapted perturbation theory results reported in the literature9 for a CCSD level with the smaller IOM basis set57 are very close to our results with an absolute deviation of 0.0316 kcal/mol. These results indicate that the optimization work performed for this IOM basis set (tailored to reproduce aug-cc-pVTZ on water and methanol) allows us to reach high accuracy calculations for electrostatic energies.
The easy access to the CCSD charge density overlap provides us also the possibility to extend our approximate overlap model to post-Hartree-Fock methodology. Based on a 40 water dimer configuration sampling (K=7.927 and correlation=0.997), our GEM-0 (CCSD) results (see Table IX) show a very good agreement with the SAPT results, the average error being 0.12 kcal/mol on the ten water dimers. The maximum deviations are observed for dimers 4 and 7 (see Fig. 3) as for the B3LYP level.
TABLE IX.
Exchange-repulsion intermolecular interaction energies (kcal/mol) for ten water dimers (Refs. 7 and 8) for the GEM-0 approach fitted on CCSD/aug-cc-PVTZ densities compared to SAPT/aug-cc-pVTZ results [].
| Water dimer geometry | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Level of theory for Ect | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| SAPT | 8.01 | 6.62 | 6.31 | 6.12 | 5.06 | 4.64 | 4.26 | 1.28 | 4.35 | 2.22 |
| GEM-0 (DFT) | 8.05 | 6.76 | 6.32 | 5.77 | 5.01 | 4.75 | 4.54 | 1.24 | 4.14 | 2.19 |
It is also important to point out the good performance of the B3LYP functional in the reproduction of the Coulomb interaction energy compared to the high level CCSD (DBS) with an average absolute error of only 0.095 kcal/mol for the ten water dimers.
Nevertheless, at the post-Hartree-Fock level, a better description of the electronic correlation tends not only to decrease the importance of electrostatic interactions in the stabilization but leads also to a higher value of the exchange-repulsion energies compared to Hartree-Fock (Refs. 9 and references therein).
These consequences are not observed in the exchange-repulsion energies obtained with the B3LYP functional which remain always close to the Hartree-Fock values (see Ref. 6 for detailed discussion).
Our CCSD results reflect these general trends, especially for the water clusters (see Table III) where significant differences can be observed when comparing B3LYP and CSSD exchange-repulsion energies. Extension to reproduce second order SAPT energies (i.e., induction and dispersion) has not been performed at this point and requires computations of CCSD polarizabilities and additional dispersion refinements which will be presented in a future paper.
IV. CONCLUSION
This work demonstrates that a force field approach based on density fitting is possible. The GEM-0 energy scheme reproduces intermolecular interaction energies by fitting individual CSOV energetic components separately, rather than relying on error compensation. Absolute errors below 0.2 kcal/mol per interaction have been obtained for each component of the force field as well as for the total intermolecular interaction energies. Accurate intermolecular interaction energies on large clusters were also demonstrated. This is a good indicator of the stability of the energy function which appears particularly suitable for molecular dynamics simulations since its error is below the thermal agitation at room temperature (kBT). We also showed that a density fitting implementation of the Wheatley-Price overlap model can provide very encouraging results for exchange-repulsion energies (even for metals) especially since any level of theory can be chosen for which relaxed one-electron density matrices are available.
This first version of the Gaussian electrostatic model limited to s-type Gaussian functions (GEM-0) is considerably faster than our extended CSOV ab initio approach since no SCF cycles are required. Moreover it can be easily mixed with distributed multipoles in order to gain speed. For example, the calculation on the 64 water molecule clusters takes 160 s on an IBM SP3 for the total interaction energy and stays the same despite the level of theory of the original density (B3LYP or CCSD). In comparison, the same system calculated with HONDO takes 26 h, only for electrostatic energies at the DFT level. For a system of this size, exchange-repulsion energy calculations become prohibitive for a two-body approach (2016 SCF with 210 basis functions) or quasi-impossible for a many-body energy requiring one SCF with 6720 basis functions. Additionally for this cluster, at the B3LYP level, 62% of the interactions show an absence of the overlap of the charge density and can be accurately replaced by distributed multipoles, reducing the time approximately by the same amount. It is obvious that reaching speeds comparable to popular force fields such as AMBER (Ref. 58) or CHARMM (Ref. 59) is impossible due to the calculations of the electrostatic integrals. It is important to note that no optimization of the code was performed at this time and that the density fitting core program was initially designed for energy decomposition and not for force field calculations. For that reason, the speed could be significantly improved and at least the approach should be able to provide accurate energies on large systems or to perform molecular dynamics simulations. Moreover, GEM-0 provides also a straightforward methodology to perform embedded quantum chemistry calculations.
Since the energetic scheme of GEM-0 is fully compatible with the SIBFA approach, a fully integrated implementation of the two approaches is underway60 which will focus on the extension of GEM-0 to a many-body approach able to reproduce high field polarization and charge transfer effects as well as post-Hartree-Fock total interaction energies. This should enable the study of very large water clusters as well as metal complexes where traditional ab initio approaches require impractical amounts of computing time, giving us essential data to improve the parametrization of polarizable force fields such as SIBFA or AMOEBA.61 Finally, a generalization of this model to higher angular momentum auxiliary basis sets is also underway leading to a reduction62 of the number of centers since lone pairs can be handled by atom centered higher moment Gaussian functions, as demonstrated in distributed multipole theory.1,3,4,63
ACKNOWLEDGMENTS
The authors are grateful to Dr. Lalith Perera and Dr. Lee Pedersen for helpful discussions. Support from the National Institute for Environmental Health Sciences and computer time from the Advanced Biomedical Computer Center, NCI-FCRDC, CCR Jussieu (Université Pierre et Marie Curie, France), and CINES (Montpellier, France) is gratefully acknowledged.
References
- 1.Stone AJ. The Theory of Intermolecular Forces. Oxford University Press; Oxford: 1996. [Google Scholar]
- 2.Singh UC, Kollman PA. J. Comput. Chem. 1984;5:129. [Google Scholar]
- 3.Stone AJ. Chem. Phys. Lett. 1981;83:233. [Google Scholar]
- 4.Vigné-Maeder F, Claverie P. J. Chem. Phys. 1988;88:4934. [Google Scholar]
- 5.Chipot C, Angyan JG, Millot C. Mol. Phys. 1998;94:881. [Google Scholar]
- 6.Kosov D, Popelier PLA. J. Chem. Phys. 2000;113:3969. [Google Scholar]
- 7.Freitag MA, Gordon MS, Jensen JH, Stevens WJ. J. Chem. Phys. 2003;112:7300. [Google Scholar]
- 8.Piquemal J-P, Gresh N, Giessner-Prettre C. J. Phys. Chem. A. 2003;107:10353. doi: 10.1021/jp035748t. [DOI] [PubMed] [Google Scholar]
- 9.van Duijneveldt–van de Rijdt JGCM, Mooij WTM, van Duijneveldt FB. Phys. Chem. Chem. Phys. 2003;5:1169. [Google Scholar]
- 10.Tschumper GS, Leininger ML, Hoffman BC, Valeev EF, Quack M, Schaffer HF., III J. Chem. Phys. 2002;116:690. [Google Scholar]
- 11.Gresh N, Claverie P, Pullman A. Theor. Chim. Acta. 1984;66:1. [Google Scholar]
- 12.Gresh N, Piquemal J-P, Krauss M. J. Comput. Chem. 2005;26:1113. doi: 10.1002/jcc.20244. [DOI] [PubMed] [Google Scholar]
- 13.Antony J, Piquemal J-P, Gresh N. J. Comput. Chem. 2005;26:1131. doi: 10.1002/jcc.20245. [DOI] [PubMed] [Google Scholar]
- 14.Gordon RG, Kim YS. J. Chem. Phys. 1972;56:3122. [Google Scholar]
- 15.Dunlap BI, Connoly JWD, Sabin JR. J. Chem. Phys. 1979;71:4993. [Google Scholar]
- 16.Cisneros GA, Piquemal J-P, Darden T. J. Chem. Phys. 2005;123:044109. doi: 10.1063/1.1947192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Wheatley RJ, Price S. Mol. Phys. 1990;69:50718. [Google Scholar]
- 18.Bagus PS, Illas F. J. Chem. Phys. 1992;96:8962. [Google Scholar]
- 19.Jeziorski B, Moszynski R, Szalewicz K. Chem. Rev. Vol. 94. Washington, D.C.: 1994. p. 1887. [Google Scholar]
- 20.a Roothaan CCJ. Rev. Mod. Phys. 1951;23:69. [Google Scholar]; b 1960. p. 179.; c Roothaan CCJ, Bagus PS. Methods Comput. Phys. 1963;2:47. [Google Scholar]; d Constans P, Carco-Dorca R. J. Chem. Inf. Comput. Sci. 1995;35:1046. [Google Scholar]
- 21.Dunning TH., Jr. J. Chem. Phys. 1989;90:1007. [Google Scholar]
- 22.Godbout N, Salahub DR, Andzelm J, Wimmer E. Can. J. Chem. 1992;70:560. [Google Scholar]
- 23.Frisch MJ, Trucks GW, Schlegel HB, et al. GAUSSIAN 03, Revision C.02. Gaussian, Inc.; Wallingford, CT: 2004. [Google Scholar]
- 24.Bernholdt DA, Harrison RJ. J. Chem. Phys. 1998;109:1593. [Google Scholar]
- 25.Foster JM, Boys SF. Rev. Mod. Phys. 1960;32:300. [Google Scholar]
- 26.Piquemal J-P, Marquez A, Parisel O, Giessner-Prettre C. J. Comput. Chem. 2005;26:1052. doi: 10.1002/jcc.20242. [DOI] [PubMed] [Google Scholar]
- 27.Becke AD. Phys. Rev. A. 1988;38:3098. doi: 10.1103/physreva.38.3098. [DOI] [PubMed] [Google Scholar]
- 28.Lee C, Yang W, Parr RG. Phys. Rev. B. 1988;37:785. doi: 10.1103/physrevb.37.785. [DOI] [PubMed] [Google Scholar]
- 29.Becke AD. J. Chem. Phys. 1993;98:5648. [Google Scholar]
- 30. See EPAPS Document No. E-JCPSA6−124−313609 for details on the CSOV method and on the change transfer energy. This document can be reached via a direct link in the online article's HTML reference section or via the EPAPS homepage ( http://www.aip.org/pubservs/epaps.html).
- 31.McMurchie LE, Davidson ER. J. Comput. Phys. 1978;26:21. [Google Scholar]
- 32.Kita S, Noda K, Inouye H. J. Chem. Phys. 1976;64:3446. [Google Scholar]
- 33.Böttcher CFJ. Theory of Electric Polarization. Elsevier; Amsterdam: 1973. [Google Scholar]
- 34.Buckingham AD. In: Intermolecular Interactions: From Diatomics to Biopolymers. Pullman B, editor. Vol. 1. Wiley; New York, NY: 1978. p. 1. [Google Scholar]; Claverie P. In: Intermolecular Interactions: From Diatomics to Biopolymers. Pullman B, editor. Vol. 1. Wiley; New York, NY: 1978. p. 69. [Google Scholar]
- 35.Garmer DR, Stevens WJ. J. Phys. Chem. 1989;93:8263. [Google Scholar]
- 36.Dupuis M, Marquez A, Davidson ER. HONDO 95.3 QCPE. Indiana University; Bloomington, IN: 1995. [Google Scholar]
- 37.Gresh N. J. Phys. Chem. A. 1997;101:46. [Google Scholar]
- 38.Batista ER, Xantheas SS, Jónsson H. J. Chem. Phys. 1999;111:6011. [Google Scholar]
- 39.a Mortier WJ, Ghosh SK, Shankar S. J. Am. Chem. Soc. 1986;108:4315. [Google Scholar]; b Yang W, Mortier WJ. ibid. 1986;108:5708. doi: 10.1021/ja00279a008. [DOI] [PubMed] [Google Scholar]; c Murrel J, Randic M, William D. Proc. R. Soc. London, Ser. A. 1966;284:566. [Google Scholar]
- 40.Gresh N, Claverie P, Pullman A. Int. J. Quantum Chem. 1982;22:199. [Google Scholar]
- 41.Gresh N, Claverie P, Pullman A. Int. J. Quantum Chem. 1986;29:101. [Google Scholar]
- 42.Gresh N. J. Comput. Chem. 1995;16:856. [Google Scholar]
- 43.Rassolov V, Pople JA, Ratner M, Windus TL. J. Chem. Phys. 1998;109:1223. [Google Scholar]
- 44.Stevens WJ, Fink WH. Chem. Phys. Lett. 1987;139:15. [Google Scholar]
- 45.Kitaura K, Morokuma K. Int. J. Quantum Chem. 1976;10:325. [Google Scholar]
- 46.Schmidt MW, Baldridge KK, Boatz JA, et al. J. Comput. Chem. 1993;14:1347. [Google Scholar]
- 47.Ghanty TK, Staroverov VN, Koren PR, Davidson ER. J. Am. Chem. Soc. 2000;122:1210. [Google Scholar]
- 48.Gordon MS, Jensen JH. In: Encyclopedia of Computational Chemistry. Schleyer PVR, editor. Vol. 5. Wiley; Chichester: 1998. [Google Scholar]
- 49.Stevens WJ, Basch H, Krauss M. J. Chem. Phys. 1984;81:6026. [Google Scholar]
- 50.Helgaker T, Jensen H. J. Aa., Joergensen P, et al. DALTON, Release 1.0. p. 1997.
- 51.Bukowski R, Jankowski P, Jeziorski B, et al. SAPT 96. University of Delaware and University of Warsaw; 1996. [Google Scholar]
- 52.Werner H-J, Knowles PJ, Amos RD, et al. MOLPRO, Version 2002.1.
- 53.Korona T, Moszynski R, Jeziorski B. Mol. Phys. 2002;100:1723. [Google Scholar]
- 54.Giessner-Prettre C, Piquemal J-P. unpublished.
- 55.Challacombe M, Schwegler E, Almölf J. In: Computational Chemistry: Review of Current Trends. Leczsynski J, editor. World Scientific; Singapore: 1996. p. 53–107. [Google Scholar]
- 56.JAGUAR, Version 6.0. Schrödinger, LLC; New York, NY: 2005. [Google Scholar]
- 57.Mooij WTM, van Duijneveldt FB, van Duijneveldt–van de Rijdt JGCM, Van Eijck BP. J. Chem. Phys. 1999;103:9872. [Google Scholar]
- 58.Case DA, Darden TA, Cheatham TE, III, et al. AMBER 8.0.
- 59.MacKerell AD, Jr., Brooks B, Brooks CL, III, Nilsson L, Roux B, Won Y, Karplus M. In: The Encyclopedia of Computational Chemistry. Schleyer P. v. R., et al., editors. Wiley; Chichester: 1998. [Google Scholar]
- 60.Piquemal J-P, Cisneros GA, Gresh N, Darden T. unpublished.
- 61.Ren P, Ponder JW. J. Phys. Chem. B. 2003;107:5933. [Google Scholar]
- 62.Cisneros GA, Piquemal J-P, Darden T. unpublished.
- 63.Tsiper EV. Phys. Rev. Lett. 2005;94:013204. doi: 10.1103/PhysRevLett.94.013204. [DOI] [PubMed] [Google Scholar]


