Abstract
The NMR 19F spin-lattice relaxation time constant T1 for CF4 gas is dominated by spin–rotation interaction, which is mediated by the molecular collision frequency. When confined to pores of approximately the same size or smaller than the bulk gas mean free path, additional collisions of molecules with the pore walls should substantially change T1. To develop a method for measuring the surface/volume ratio S/V by measuring how T1 changes with confinement, we prepared samples of known S/V from fumed silica of known mass-specific surface area and compressed to varying degrees into cylinders of known volume. We then measured T1 for CF4 in these samples at varying pressures, and developed mathematical models for the change in T1 to fit the data. Even though CF4 has a critical temperature below room temperature, we found that its density in pores was greater than that of the bulk gas and that it was necessary to take this absorption into account. We modeled adsorption in two ways, by assuming that the gas condenses on the pore walls, and by assuming that gas in a region near the wall is denser than the bulk gas because of a simplified attractive potential. Both models suggested the same two-parameter formula, to which we added a third parameter to successfully fit the data and thus achieved a rapid, precise way to measure S/V from the increase in T1 due to confinement in pores.
Keywords: spin–rotation, T1, collision frequency, surface/volume ratio, perfluorocarbon
1. Introduction
1.1. General
The NMR relaxation of fluorine nuclei in gases such as SF6, SiF4, CF4, and C2F6 is dominated by spin–rotation interaction, which is mediated by the molecular collision frequency [1–8]. When these gases are confined in pores of the order of the bulk gas mean free path, the frequency of collisions with the pore walls should rival that of intermolecular collisions and the NMR relaxation should be strongly affected [9]. By expressing this in numerical terms, we should be able to measure the pore size with quick, easy measurements of the spin-lattice relaxation time constant T1. Inert fluorinated gases are particularly suitable for this application because many porous media do not contain fluorine, so that the only NMR signal is that of the gas. Signal/noise ratios are favorable because these gases achieve nuclear magnetization very quickly, 19F has a high gyromagnetic ratio, and there are multiple 19F atoms per molecule. Furthermore, such gases are inert, inexpensive, and readily available.
It is possible to measure T1 to a high degree of accuracy and precision, e.g., ≤1% in less than 1 min. For small pores, there is promise that the precision will extend to the measurement of the surface/volume ratio S/V. This would provide an improvement over current adsorption isotherm measurements [10], which are so time-consuming that a less precise method is usually chosen. An additional advantage of NMR is the ability to generate images of relaxation parameters, which may provide a non-invasive means of spatially resolving heterogeneous pore distributions, similar to the method of Beyea et al. [11] involving imaging of c-C4F8 absorption isotherms, but in a much shorter time. Of course, if the pores are as small as or smaller than the bulk gas mean free path and they are connected, then gas molecules will diffuse through many pores during the measurement time. Thus, pixels in such images would represent an average S/V value for a local pore system.
1.2. Basic mathematical model
The relationship between spin–rotation interaction and molecular collision frequency is stated for hydrogen in Eq. 4.33 of Bloembergen’s (1948) thesis [12]. Building on the work of Courtney and Armstrong [2], which deals specifically with fluorinated gases, Kuethe et al. [13] presented a method for calculating T1 for bulk gas, T1,b, from pressure and temperature with accuracy known from curve-fitting data at a variety of temperatures and pressures. To calculate the collision frequency of gas molecules in bulk, fg,b, the method uses the Clausius equation of state, Lennard-Jones collision cross-sections, and an expression for the molecular velocity that increases slightly with density. Of the common textbook equations of state, the Clausius equation provided the best fit to the data. Once the molecular collision frequency is calculated, the bulk gas T1,b is:
| (1) |
where a is a coupling constant, ω is the Larmor frequency, T is absolute temperature, and c accounts for thermally mediated intra-molecular relaxation mechanisms in the absence of collisions, i.e., in a near vacuum [13]. The factor bg is approximately the average number of collisions required to effect one spin–rotation exchange. Its slight temperature dependence is 1 modeled by , where s and d are the slope and intercept relating the cross-section for change in molecular angular momentum to the Lennard-Jones cross-section for collisions Ω. A simple extension of this expression to accommodate collisions of gas molecules with pore walls is:
| (2) |
where fw,s is the frequency of collisions with the wall and bw,s is the average number of wall collisions required to cause a spin–rotation event. By restricting the analysis to room temperature, bw,s is a single additional parameter.
From simple gas dynamics, the collision frequency with (or one-directional flux through) a surface area S is ρg,bvg,bS/4, where ρg,b is the number density of gas molecules in the bulk, and vg,b is their average velocity. The number of molecules in a pore is ρg,bV, where V is the pore volume. Thus, the average wall collision frequency for the molecules in a pore is:
| (3) |
and fw,s is proportional to the surface/volume ratio. A graph of T1,s vs. fg,b/bg is shifted to the left by fw,s/bw,s. Pressure P is the parameter most commonly varied to adjust fg,b. There is a similar shift to the left for a graph of T1,s vs. P by an amount proportional to S/V (Fig. 1a).
Figure 1.
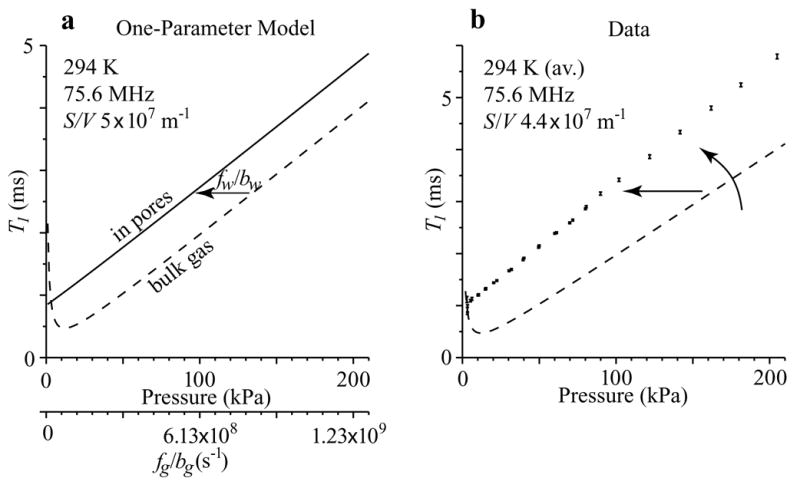
(a) Simple model of how confinement shifts the graph of T1 vs. pressure (or intermolecular collision frequency) for bulk CF4 gas to the left. (b) T1 data, on the other hand, show both a left shift and an increase in slope, or counter–clockwise rotation. The additional axis in (a) is the frequency of intermolecular collisions that cause spin–rotation exchange. The amount of left shift is the frequency of wall collisions that cause spin–rotation exchange. The additional axis is not presented for the graph of data because they were taken at slightly different temperatures.
The prospects for S/V measurement are promising, especially for small pores. We obtain an approximate proportionality by simplifying Eq. (2) using the fact that for typical laboratory conditions the total effective collision frequency is , which implies . As pores become smaller (tens of nm or less) so that fg,b/bg becomes small compared to fw,s/bw,s, we approach the condition at which T1,s∝fw,s/bw,s∝S/V, which would be a suitable feature for using T1,s as a measure of S/V.
Preliminary results indicate that measured curves are not only shifted, but also increase in slope (Fig. 1b). This makes the effect of S/V on T1 even greater, which promises a more sensitive measurement, but additions to the simple model are required.
1.3. Additions to the model to accommodate absorption
Lizak et al. [9] suggested two mechanisms by which confinement to pores may slow relaxation rates: the increase in collision frequency and adsorption. We tried to minimize adsorption by choosing CF4, which has a low critical temperature (228 K). Its critical pressure is 3.7 MPa. For bulk gas, there is no condensed phase at room temperature, especially at pressure substantially lower than 3.7 MPa. However, we observed that the density of gas in the pores is slightly above that of the bulk gas (Section 2.1). Two different models of how absorption (specifically interpreted as an increase in pore gas density above the bulk gas density) affects T1 were evaluated. In one, the “condensation model”, adsorbed molecules are stuck on the walls in a liquid-like state, are in fast exchange with the gas phase, and while condensed show very slow relaxation, as previously suggested [9]. The second “wall-zone model” is a very simplified form of a molecular dynamics model, in which pore walls have simplified attractive potential fields for gas molecules that are not strong enough to make molecules stick to the walls, but still increase the density in a zone near the wall.
A simple assumption for molecules that stick to walls is that their temporary relaxation rate is so slow as to be insignificant. Of course, dipolar relaxation will occur in the liquid-like state. However, this will be approximately two orders of magnitude slower than the spin–rotation relaxation of molecules in fast exchange with the gas phase. Thus, in the first approximation the dipolar relaxation rate is zero and the relaxation rate for the condensation model is:
| (4) |
where ng is the number of molecules in the gas phase, na is the number adsorbed, n is the total, and is the relaxation rate for bulk gas. Then,
| (5) |
where ρp,c is the number density of gas molecules in pores. For sub-monolayer condensation, ρp,c/ρg,b should be greater than one by a multiple of S/V:
| (6) |
where kρg,b is the number of molecules adsorbed per unit surface area. Molecules encounter the wall at a rate proportional to ρg,b S/V and have a short average residence time. The model will predict an increase in number density from measured T1 values, which we can compare with measured values of ρp/ρg,b.
To avoid the assumption that molecules condense on the wall, in the wall zone model the density increases near the pore walls because gas molecules are attracted to the walls. To calculate the increase in density, we first calculate a simple expression for the increase in average impact speed over the average bulk gas speed that arises because molecules accelerate toward the wall. (As they leave the attractive region, they decelerate back to the average bulk gas speed.) Then, to obtain an equation involving density, we use the average impact speed in expressions for pressure from simple gas dynamics, assuming that pressure on the wall is the same as the bulk gas pressure away from the attractive field of the wall.
For simplicity, we assume that molecules within distance δ of the wall experience a force F toward the wall, so that the average impact speed is , where vg,b is the average m speed in the bulk gas and m is the molecular mass. The average speed in the wall zone is then .
The pressure on the wall is the impact force minus the attractive force of molecules in the near-wall region, both per unit area. We know that the numerical value for pressure on the wall has to equal the pressure of the bulk gas, which from elementary gas dynamics is . The force per unit area from impacts is and the attractive force per unit area is ρw,zFδ so:
| (7) |
We can then solve for the density in the wall zone:
| (8) |
where α=F/m. The average velocity in the wall zone is:
| (9) |
Assuming a spherical pore, the fraction of pore volume occupied by the wall zone is:
| (10) |
The gas density in pores, including the bulk gas interior, is then:
| (11) |
The wall collision frequency is:
| (12) |
The gas–gas collision frequency in the wall zone is:
| (13) |
Both the condensation and wall-zone models predict that a graph of T1 vs. P will increase in slope and be left-shifted by confinement to pores. At first glance, the two models seem opposed in concept. The reason why T1 is longer in the condensation model [Eq. (5)] than for the basic model [Eq. (2)] is that molecules adsorbed on the walls are not undergoing spin–rotation exchange. For the wall-zone model, T1 is greater because the collision frequency, and thus the spin–rotation exchange frequency, increases due to a molecular speed and density that are even greater than values already on the high-frequency side of the T1 minimum. However, in more realistic molecular dynamic models, strong wall potentials lead to condensation. In our simplified “wall zone”, it is clear that the density near the wall can increase arbitrarily and approach the density of a liquid as the attractive force gets stronger. With more realistic attractive fields for walls and molecules, a liquid state arises from a high-collision-frequency regime when the temperature and pressure foster substantial cohesive forces between molecules [14]. Then there is a smooth transition between what first appears to be two different reasons for slower relaxation rates.
Both our models show increased density and slow relaxation associated with pore walls, and their underlying functional form is similar. This is easier to comprehend if we consider only pressures at ~100 kPa and above, so that the right-hand term in Eq. (2) is small. We can approximate the condensation model as:
| (14) |
and , to yield:
| (15) |
where and the term is small.
Similarly, for the wall-zone model:
| (16) |
After substituting Eqs. (12) and (13), some algebra and the additional substitution from Eq. (10) leads to the remarkably similar
| (17) |
where and . Reiterating that we are approximating the regime for higher pressures, where T1,b∝P, the k parameters in Eqs. (15) and (17) explain the increase in the slopes of T1,p vs. P curves, and the β parameters explain the shift from T1,b.
For the range of data we examined, the parameters α and δ in the wall-zone model are not independent. The fit is determined by αδ2, so both the condensation and wall zone models are two-parameter models, as borne out by the above analysis. A preliminary result is that neither of the two-parameter models successfully fits the data within the measurement precision, even after restricting the data to higher pressure for Eqs. (15) and (17). With their parameters fixed so that any given T1 datum is used to calculate an S/V value, the above models tend to underestimate low S/V ratios and over-estimate high ones. All tend to increase the slope of T1 vs. P graphs, but not enough, suggesting that for calibration of T1 values for S/V measurements, we need to add another parameter that increases the influence of S/V on T1 in pores (T1,p).
1.4. Three-parameter model for S/V measurement
Preliminary results indicate that higher pressure data are most useful for measuring S/V. Not only does the higher NMR signal at higher pressure allow shorter data acquisition time, but the difference between T1,p in pores and T1,b in the bulk gas also increases with pressure. This remains substantial compared to T1,b, which would not be the case if there were only a shift in the curve as predicted by the simplest, one-parameter model. Therefore, for the purpose of S/V measurement, we can restrict ourselves to data taken at approximately 100 kPa and above. We begin with the simplified versions of the models, Eqs. (15) and (17), that deal with higher-pressure data, and introduce a third parameter γ that allows the increase in T1,p due to confinement to be a stronger function of S/V:
| (18) |
A physical argument for adding the parameter γ is that our models allow only simplified condensation or simplified increases in collision frequency. In a more realistic model there will be a combination of increased collision frequency and cohesive forces, so that T1,p is a stronger function of S/V than in either simple model, and γ should be greater than unity. With the simple functional form of Eq. (18), it is clear that once the three parameters are determined by calibration for a given material, each measurement of T1,p will yield a value for S/V, given the bulk gas T1,b at the same temperature and pressure:
| (19) |
2. Methods
2.1. Experimental
To prepare samples of known S/V, we used CAB-O-SIL M-5 and TS-500 fumed silica particles (Cabot Corp., Billerica, MA, USA) with a surface area per mass of 200±5 and 225±5 m2/g, respectively. M-5 is pure fumed silica, which is hydrophilic, while TS-500 has a hydrophobic surface coating. In the uncompressed state, approximately 98% of their volume is air space. Even when compressed to one-seventh of their bulk volume, they have porosity of 86% and very little particle–particle contact. Thus, upon compression, the surface area remains nearly constant while the pore volume Vp decreases. Samples were compressed in 2.54-cm-diameter polycarbonate cylinders that were closed at one end. The free surface was covered with a piece of filter paper and a polycarbonate disk was glued in the cylinder so that it fit snugly against the filter paper. The end disk had a 6-mm-diameter hole into which a glass tube was glued for connection to a vacuum pump or gas supply. The pore volume was the volume of the container minus the volume of silica and the volume of the shell that is one molecular radius thick around the pores, i.e., the product of surface area and the molecular radius of CF4.
We separated the degree to which we knew S/V for samples into the variation between samples of the same silica product and the accuracy for the true S/V. The inter-sample variation from the precision for measurement of the mass of the fumed silica and its compressed length was ±0.8%. We computed the effect this error had on the variance of measured T1 values and included it in curve-fitting procedures. At this stage of the research, measurements were relative rather than absolute and we relied on the manufacturer’s N2 adsorption isotherm measurements (±2.5%) for the absolute specific surface area. This error did not affect how well the curves fit and only affected the absolute values of the fitted parameters. The error for measurement of the container diameter contributed to a decrease in this accuracy. The sample containers had consistent diameters, i.e., the different pieces of polycarbonate tube were cut from the same stock and fit the same piece of polycarbonate rod consistently. However, the precision for measuring the diameter led to an additional ±1.6% uncertainty for the true S/V. Thus, the accuracy for the “known” S/V values is , and only affected the absolute values of parameters. The inter-sample variation of ±0.8% determined the measurement precision for curve fitting.
Pressure was measured ±0.1 kPa using an Omega PX303-100A5V absolute pressure transducer, calibrated to two pressures, vacuum and local barometric pressure, measured with a mercury manometer. Temperature was measured ±0.25 K using a copper-constantan thermocouple taped to the outside of the sample cylinder, which was in turn jacketed with foam pipe insulation.
To measure the density of CF4 in the pores, we measured the pressure drop, P1 to P2, when a known volume Vk of CF4 was allowed to expand into an evacuated sample and return to room temperature. The density of gas in pores ρ was calculated as [ρ1Vk−ρ2(Vk+Vc)]/Vp, where ρ1 and ρ2 are the bulk gas density at P1 and P2, respectively, and Vc is the volume of the connection between Vk and Vp. As a check, we performed the same experiment with helium and found, as expected, that its density in pores was the same as its bulk gas density.
T1,p data were measured by inversion recovery using at least 60 different delay times between the 180° and 90° rf pulses and recovery times of at least 8×T1. Signal-averaging was from 4- to 512-fold, depending on the signal strength available within the pressure range from 2.5 to 254 kPa. Data collection times ranged from 5 s for the higher pressures to 5 min for the near-vacuum data.
2.2. Data analyses
Inversion-recovery data were fit by the least-squares method to a three-parameter single exponential recovery curve. The error in fitting T1,p was taken as the standard deviation of the T1,p parameter, computed from the covariance matrix. We then calculated the larger errors in T1,p from the model, assuming temperature, pressure, and S/V variations of ±0.25 K, ±0.1 kPa, and ±0.8%, respectively. The square root of the sum of squares of all four error sources σ was then used as the standard deviation for T1,p for curve fitting a model. Because the fit is affected by the errors, which are computed from the model, we iterated the fit and the calculation of σ until there was no change.
The T1,p data, measured at various pressures with accompanying records of ambient temperature, were also fit by the least-squares method. For one index of how well the data fit the model, we calculated a normalized fit statistic (NFS) from the χ2 statistic, where is the sum of squared deviations of T1,p data from the curve values, weighted by the inverse of variance, and nf is the number of degrees of freedom. For approximately 30 data, the NFS approaches a normal distribution with variance of one and expectation of zero. Values of <2 indicate that the model fits the data within the known measurement precision. Values of <−2 indicate a better fit than expected from the measurement precision. A second statistic for goodness of fit was simply the weighted average of the fractional deviation of data from the model.
2.2.1. Physically based two-parameter models
Because α (acceleration toward the wall in the wall zone) and δ (thickness of the wall zone) are not independent parameters, we chose δ so that the bw,z values from the wall zone model matched bw,c for the condensation model when α and bw,z were the free parameters. To set the model parameters, we first let bw,c and k for the condensation model vary to fit the multiple pressure data from 2.5 to 254 kPa for each sample using the known values of S/V. We then chose the average values of these parameters for three samples each of M-5 and TS-500 (bw,c=2.17 and 2.16 collisions/rad, k=5.14×10−9 and 3.27×10−9 m, respectively) as the values for the two materials. We set δ in the wall zone models to a value for each material (1.93×10−8 m for M-5 and 1.38×10−8 m for TS-500) so that when the parameters bw,z and α were allowed to vary, the average bw,z for each material matched that for the condensation model. The average α was 5.53×1011 and 8.04×1011 m s−2 for M-5 and TS-500, respectively.
With the empirical parameters thus fixed, S/V values were measured by curve fitting the multiple pressure data for each sample while treating only S/V as the free parameter. The precision was then the standard deviation for S/V from the covariance matrix. The model predictions for ρp/ρg,b followed from the S/V measurements. The errors reported for ρp/ρg,b are the sum of their standard deviations from the initial curve fit and the change in ρp/ρg,b when the parameters were set to their average value for each material.
Because we used the known S/V values to set the model parameters, the average of the S/V measurements for each material has to be approximately correct. However, systematic bias is apparent when the estimates for high and low values of S/V are incorrect.
2.2.2. Three-parameter model for S/V measurement
Equation (18) was fit by the least-squares method with α, κ, and γ as free parameters using only data from 100 to 254 kPa. For each material, we report the parameters, their standard deviations from the covariance matrix, the normalized fit statistic, and the fractional deviation. We calculated S/V values for each T1,p datum from Eq. (19) and included data from both materials on one graph of the NMR-measured vs. known S/V. The standard deviation for measurement was calculated as the sample standard deviation for all the S/V measurements from the identity curve.
3. Results and discussion
3.1. Physically based two-parameter models
Figure 2 shows graphs of T1,p vs. the full pressure range (2.5–254 kPa) for each of the six samples. Dots with error bars ±σ are the T1,p data. Long-dash lines are the T1,b values for the bulk gas at 294 K calculated from ref. [13] for comparison. (The values used for the model prediction of S/V individually matched the sample temperatures recorded, which varied by 5 K.) Solid and short-dash lines are the curve fits for the wall-zone and condensation two-parameter models. The data and curve fits are indeed shifted to the left and increased in slope from the bulk gas data.
Figure 2.
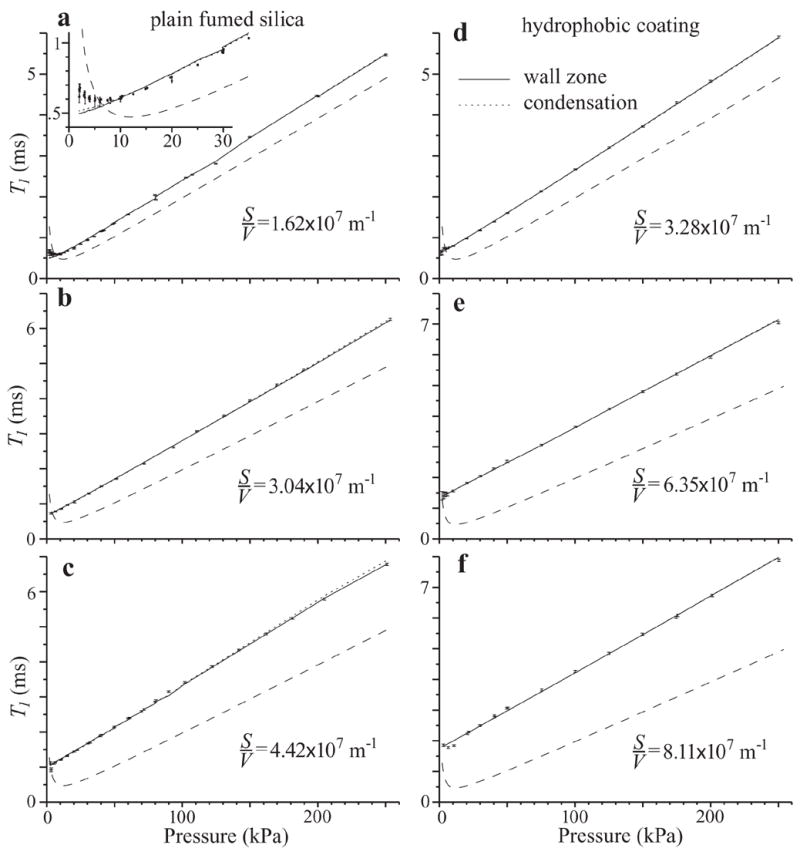
Graphs of T1,p vs. pressure for all six samples. Graphs for M-5, the plain fumed silica, are on the left; those for TS-500, with the hydrophobic coating, are on the right. The surface/volume ratios, as determined from sample preparation, increase from top to bottom and are listed on each graph. Data for T1,p in pores have ±σ error bars. The T1,b of bulk gas at 294 K is shown as long-dash lines for comparison. Solid lines are the wall-zone model, short-dash lines are the condensation model. The curve fit lines are jagged in places because the data were taken at slightly different temperatures and the curves follow suit. The two models fit the data approximately equally well, but neither fits within the precision of T1,p measurement. The model lines depart from too many of the error bars in the top and bottom graphs.
Table 1 lists S/V values known for the samples based on their preparation and ρp/ρg,b values measured for gas expansion into the sample. The results for the two models are also presented, including the NMR-measured S/V, ρp/ρg,b predicted by the models, the normalized fit statistic, and the average fractional departure of data from the curve.
Table 1.
Predicted S/V ratios and pore densities and curve-fitting statistics for the two-parameter models.
| Sample properties | Wall zone model | Condensation model | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| S/V (m−1) | ρp/ρg | T1 data (n) | Model S/V (m−1) | Model ρp,z/ρg | NFS | Fractional deviation | Model S/V (m−1) | Model ρp,z/ρg | NFS | Fractional deviation |
| Plain fumed silica | ||||||||||
| 1.62×107 | 1.083 | 56 | 1.43×107 | 1.045 | 124. | 0.0517 | 1.58×107 | 1.081 | 87.7 | 0.0432 |
| ±3% | ±0.015 | ±6.2×105 | ±0.0092 | ±6.4×104 | ±0.0031 | |||||
| 3.04×107 | 1.128 | 16 | 2.96×107 | 1.086 | 5.46 | 0.0108 | 2.97×107 | 1.153 | 1.16 | 0.00775 |
| ±1.8×105 | ±0.010 | ±1.6×105 | ±0.090 | |||||||
| 4.42×107 | 1.162 | 31 | 5.20×107 | 1.138 | 12.0 | 0.0182 | 4.67×107 | 1.240 | 7.37 | 0.0152 |
| ±1.8×105 | ±0.010 | ±1.5×105 | ±0.011 | |||||||
| Hydrophobic coating | ||||||||||
| 3.28×107 | 1.079 | 21 | 2.56×107 | 1.059 | 5.67 | 0.0184 | 2.94×107 | 1.096 | 3.61 | 0.0163 |
| ±1.4×105 | ±0.0041 | ±1.5×105 | ±0.011 | |||||||
| 6.35×107 | 1.133 | 17 | 7.03×107 | 1.140 | −0.619 | 0.00778 | 6.73×107 | 1.220 | −0.623 | 0.00897 |
| ±3.9×105 | ±0.014 | ±3.4×105 | ±0.026 | |||||||
| 8.11×107 | 1.140 | 18 | 9.69×107 | 1.187 | 15.5 | 0.0217 | 8.55×107 | 1.280 | 7.66 | 0.0221 |
| ±4.0×105 | ±0.0054 | ±3.4×105 | ±0.0087 | |||||||
The two models fit the data approximately equally well, but technically do not fit. Although there is small fractional deviation, there is a systematic departure from the data. The curves fall close to the data, but outside too many of the error bars. This is especially apparent for the high- and low-S/V samples for each material. The normalized fit statistics substantially exceed 2, indicating the data do not fit the models within the measurement precision. A positive interpretation of this result is that T1,p measurements will potentially be useful in future work to refine models for the physics of confinement. T1,p data are of sufficiently high precision to reveal systematic biases in models that would fit less precise data.
Further refinement of such models could lead to an absolute measurement of S/V. It may be possible to predict theoretically how many wall collisions on average are required for a spin–rotation exchange event and how interactions with walls slow relaxation and thus eliminate the need for calibration. Interestingly, the current models indicate that the average number of wall collisions for a spin–rotation exchange is 2.16 collisions/rad, regardless of surface coating, and the models indicate that plain fumed silica is more attractive than the variety with a hydrophobic coating. The higher of the two values of k (5.14×10−9 m for plain fumed silica compared to 3.27×10−9 m for the silica with hydrophobic coating) indicates that at 250 kPa and 294 K, for a number density in bulk CF4 of 6.2×1025 m−3, the surface coverage of CF4 molecules is 3.2×1017 m−2, or only 6/100 of that for hexagonally packed 0.468-nm-diameter spheres. Furthermore, actual measurements of the pore density of CF4 were lower than those calculated from the models, so the assumption of sub-monolayer coverage is probably a safe one.
For one sample, there was an interesting departure from the models at low pressure (Fig. 2a inset). The data show a T1,p minimum, even though S/V and thus fw/bw are too high for such a minimum to exist. We think that this is because the sample is heterogeneous—there are visible voids without fumed silica. At low pressure the diffusion velocity is high enough for molecules to reside in voids and pores during the measurement time. While in a void, the molecules showed slow relaxation, to the left side of the T1,b minimum for the bulk gas. The average pore-void behavior would display a T1 minimum.
One point to bear in mind is that measurement of T1,p represents the average behavior of a large number of collision events. At 101 kPa and 294 K with a S/V of 4.0×107 m−1, the wall and gas collision frequencies are 3.3×109 and 7.1×108 s−1, respectively. Thus, in a time interval as long as T1,p, 3 ms on average, individual molecules experience over 107 collisions and visit approximately 106 pores. In addition, a 1-cm3 sample will contain approximately 2.5×1019 molecules.
3.2. S/V measurement with three-parameter model
Figure 3 graphs only the 39 data taken from 100 to 254 kPa, again with ±σ error bars, along with curve fits of Eq. (18) plotted with the parameters listed in Table 2 for each material. The NFS values in Table 2 indicate that the data fit the model within the measurement precision. This three-parameter model fits the data and serves as a calibrated S/V measurement, which is apparent from Figure 4, which graphs the NMR-measured S/V ratios from Eq. (19) against the known values. The error bar shown is ±1 SD for S/V measurements from the identity function (±7.57×105 m−1 or ±1.7% of the average S/V). This calibrated S/V measurement is precise and without apparent bias.
Figure 3.
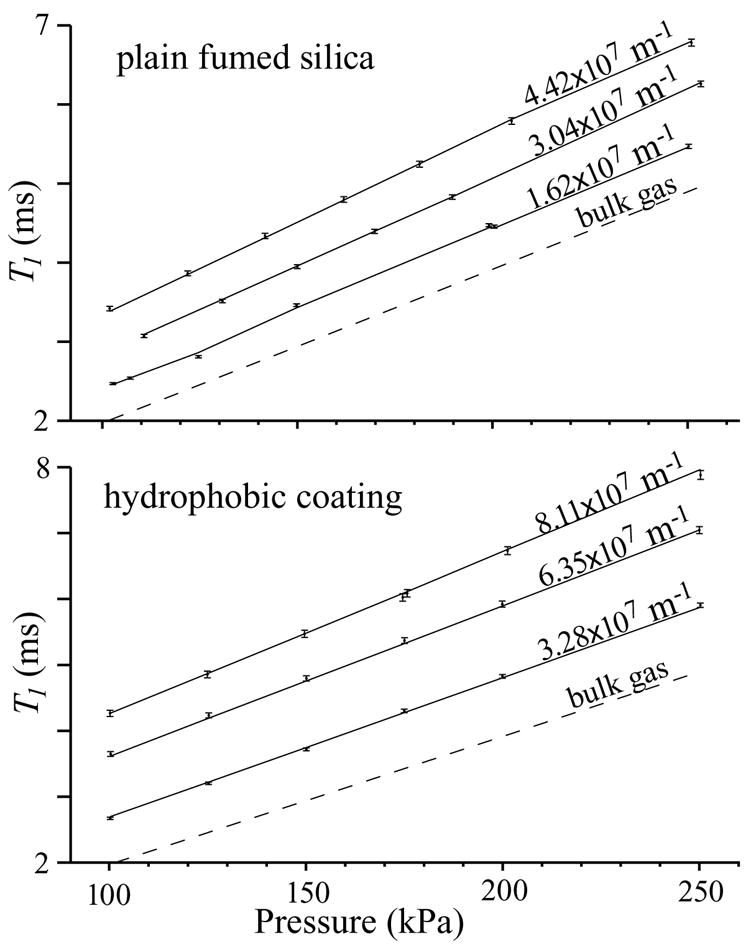
Graphs of T1,p vs. the limited pressure range of 100–254 kPa and the curve fits of Eq. (18) using the parameters in Table 2 for plain fumed silica and silica with a hydrophobic coating. The addition of a third parameter eliminated the systematic bias. The model fits the data.
Table 2.
Calibration parameters and curve fit statistics for the three-parameter formula.
| T1 data (n) | κ (m γ) | β (s m γ) | γ | NFS | Fractional deviation | |
|---|---|---|---|---|---|---|
| Plain fumed silica | 20 | 2.96×10−10±7.06×10−11 | 1.35×10−12±3.04×10−13 | 1.16±0.0131 | 1.69 | 0.00535 |
| Hydrophobic coating | 19 | 2.51×10−11±7.44×10−12 | 1.72×10−13±4.88×10−14 | 1.27±0.0158 | −0.282 | 0.00622 |
Figure 4.
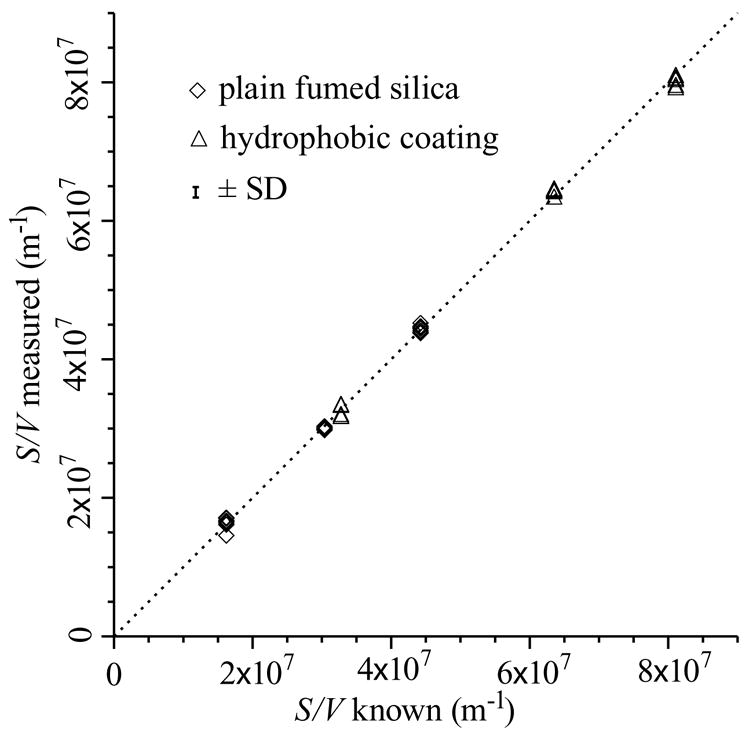
Measured S/V from Eq. (19) vs. that known from sample preparation. The desired identity function is shown as a short-dash line. The error bar is ±1SD of the NMR-measured S/V ratios from the identity function. The measurement is precise and unbiased.
4. Conclusions
Fumed silica, with and without a surface coating, provided good samples with known S/V ratios and different surface chemistry. Physically based two-parameter models captured the essence of how confinement changes the T1,p of CF4 gas. Collisions between gas molecules and the walls increase the rate of spin–rotation exchange compared to pure gas–gas collisions. Interactions with the pore walls support densities greater than the bulk gas density and further slow the relaxation. T1,p data are of sufficient precision to test more complex models. Adding a further parameter allowed us to fit the data within the precision of measurement to calibrate a T1,p-based S/V measurement. The resulting measurement is simple and rapid, makes use of an inexpensive and readily available gas, and has high precision.
Acknowledgments
We thank Andrew McDowell for technical assistance, Arvind Caprihan and Eiichi Fukushima for help with the manuscript, Joe D. Seymour and Larry Werbelow for valuable discussions, NIH grant R01EB002072, and Sandia National Labs PR 522388 for financial support, and Doug Smith, Nanopore Corp., for sample preparation.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Armstrong RL. Nuclear magnetic relaxation effects in polyatomic gases. Magn Reson Rev. 1987;12:91–135. [Google Scholar]
- 2.Courtney JA, Armstrong RL. A nuclear spin relaxation study of the spin-rotation interaction in spherical top molecules. Can J Phys. 1972;50:1252–1261. [Google Scholar]
- 3.Anderson CH, Ramsey NF. Magnetic resonance molecular-beam spectra of methane. Phys Rev. 1966;149:14–24. [Google Scholar]
- 4.Yi PN, Ozier I, Anderson CH. Theory of nuclear hyperfine interactions in spherical top molecules. Phys Rev. 1968;165:92–109. [Google Scholar]
- 5.Bloom M, Bridges F, Hardy WN. Nuclear spin relaxation in gaseous methane and its deuterated modifications. Can J Phys. 1967;45:3533–3553. [Google Scholar]
- 6.Dong RY, Bloom M. Determination of spin-rotation interaction constants in fluorinated methane molecules by means of nuclear spin relaxation measurements. Can J Phys. 1970;48:793–804. [Google Scholar]
- 7.McCourt FR, Hess S. Nuclear magnetic relaxation in a gas of regular molecules. Z Naturforsch. 1970;25a:1169–1177. [Google Scholar]
- 8.McCourt FR, Hess S. On nuclear magnetic relaxation in dilute gases of symmetric and spherical top molecules. Z Naturforsch. 1971;26a:1234–1236. [Google Scholar]
- 9.Lizak MJ, Conradi MS, Fry CG. NMR imaging of gas imbibed into porous ceramic. J Magn Reson. 1991;95:548–557. [Google Scholar]
- 10.Lowell S, Shields JE. Powder Surface Area and Porosity. Chapman & Hall; New York: 1991. [Google Scholar]
- 11.Beyea SD, Glass SJ, DiGiovanni AA, Caprihan A. Non-destructive characterization of nanopore microstructure: Space resolved BET isotherms using NMRI. J Appl Phys. 2003;941:935–994. [Google Scholar]
- 12.Bloembergen N. Nuclear Magnetic Relaxation: A Reprint Volume. W.A. Benjamin; New York: 1961. reprint from N. Bloembergen, Nuclear Magnetic Relaxation, Ph.D. thesis, University of Leiden, 1948. [Google Scholar]
- 13.Kuethe DO, Pietraß T, Behr VC. Inert fluorinated gas T1 calculator. J Magn Reson. 2005;177:212–220. doi: 10.1016/j.jmr.2005.07.022. [DOI] [PubMed] [Google Scholar]
- 14.Gelb LD, Gubbins KE, Radhakrishnan R, Sliwinska-Bartkowiak M. Phase separation in confined systems. Rep Prog Phys. 1999;62:1573–1659. [Google Scholar]


