Estimation of the DNA sequence discriminatory ability of hairpin-linked lexitropsins

Abstract

Three- and four-ring polyamides containing N-methylimidazole and N-methylpyrrole, and their hairpin-linked derivatives, bind side-by-side in the minor groove of DNA in a sequence-specific manner. The sequences recognized by side-by-side molecules are dependent on the pairings of the polyamide rings to the bases. In this study we report a mathematical model for estimating the free energies of binding for γ-aminobutyric acid-linked polyamides to 5- and 6-bp DNA sequences. The model parameters are calibrated by a least-squares fit to 35 experimental binding constants. The model performs well in cross-validation experiments and the parameters are consistent with previously proposed empirical rules of polyamide–DNA binding. We apply the model to the design of targeted polyamides, evaluating the ability of the proposed polyamides to bind to a DNA sequence of interest while minimizing binding to the remaining DNA sequences.

Drugs that bind to nucleic acids, blocking transcription and replication, are important in the treatment of cancer and AIDS-related diseases. Drugs of clinical importance act by several mechanisms: alkylating agents, such as nitrogen mustard and nitrosoureas, and platinum coordination complexes, such as cisplatin, form cross-links in DNA; anthracycline antibiotics, such as daunorubicin and doxorubicin, intercalate in double-stranded DNA; iron-chelating antibiotics, such as bleomycin, fragment DNA; and groove-binding drugs, such as pentamidine, bind in the minor groove of DNA. These drugs show limited sequence specificity and bind to many sites in a typical genome, leading to harmful side effects. Recently, the search for new chemotherapeutic agents has shifted to molecules designed to target a given DNA sequence in a pathogenic organism or neoplastic cell.

Polyamide molecules such as netropsin, distamycin, and their imidazole-containing synthetic derivatives, known as lexitropsins, can bind DNA in a sequence-specific manner in a 2:1 polyamide–DNA stoichiometry (refs. 1–3 and M. L. Kopka, D.S.G., and R.E.D., unpublished work). In this mode, the two molecules bind side-by-side, enabling each molecule to recognize its own strand of DNA. The polyamides are positioned such that each ring makes contact with a single base. The sequence specificity results from the different hydrogen bonding capability of pyrrole and imidazole rings: imidazole binds preferentially to guanine, and pyrrole binds to adenine, thymine, and cytosine, excluding guanine through steric hindrance with the N2 amino group.

Hairpin-linked polyamides, which consist of two covalently linked molecules connected end-to-end via a γ-aminobutyric acid linker residue, exhibit up to an 800-fold enhancement in binding affinity over unlinked molecules (4, 5). Furthermore, the addition of a carboxyl-terminal β-alanine residue further enhances the binding affinity and sequence specificity of hairpin-linked molecules (6). An example of a hairpin-linked polyamide containing a triimidazole lexitropsin and a distamycin is shown in Fig. 1 (7).

Figure 1.

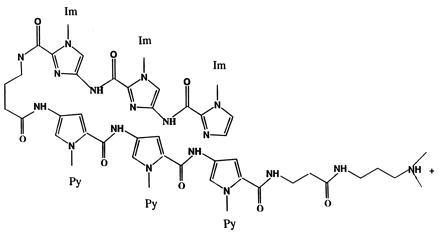
The molecular structure of a hairpin-linked polyamide, ImImIm-γ-PyPyPy-β-Dp, an oligopeptide chain consisting of six ring units. The imidazole group in the upper right hand part of the molecule is the amino-terminal end and the charged group in the bottom right is carboxyl-terminal tail.

In this work, we develop and analyze a linear regression model for predicting the binding free energies of γ-aminobutyric acid hairpin-linked polyamides for 5- and 6-bp DNA sequences. The model then is used to predict the binding free energies of given polyamides for their target DNA sequences as well as for all other possible DNA sequences. The computation of such binding free energies provides a measure of the sequence discriminatory potential of a given polyamide, allowing the design of molecules that bind to the DNA sequence of interest and not the rest of the genome.

EXPERIMENTAL PROCEDURES

Development of Mathematical Models.

We assume that the free energy of binding of any given polyamide for a given DNA sequence is determined by the sum of the free energies of binding of each pyrrole-amide or imidazole-amide unit for the nearest base (and that there are no cross interactions between these units and other bases), the linker (γ-aminobutyric acid in this study) for its corresponding base pair, and the carboxyl-terminal tail for its given base pair. We also make the assumption that the dimensions of the drug and the floor of the minor groove are such that there is no significant difference in binding for linked three-ring polyamides compared with linked four-ring polyamides of the sort observed for longer polyamides (8). The following 12-parameter linear regression model (Model 0) is the ideal representation for the binding-free energy of a polyamide for a specific DNA sequence under these assumptions:

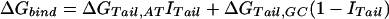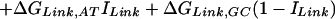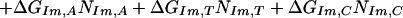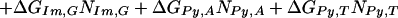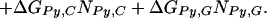ΔG_bind is the dependent variable representing the binding free energy of a given polyamide for a given DNA sequence. ΔG_Link,AT, ΔG_Link,GC, ΔG_Tail,AT, and ΔG_Tail,GC are parameters representing the free energies of binding of the γ-aminobutyric acid linker and the β-alanine tail for AT or TA base pairs and GC or CG base pairs. I_Tail and I_Link are indicator variables whose values are 1 if the tail or linker, respectively, spans an AT/TA base pair and 0 if the tail or linker, respectively, spans a GC/CG base pair. ΔG_Im,A, ΔG_Im,T, ΔG_Im,C, ΔG_Im,G, ΔG_Py,A, ΔG_Py,T, ΔG_Py,C, and ΔG_Py,G are parameters for the binding free energies of imidazole (Im) and pyrrole (Py) rings for A, T, C, and G bases. N_Im,A, N_Im,T, N_Im,C, N_Im,G, N_Py,A, N_Py,T, N_Py,C, and N_Py,G represent the number of times that a pyrrole or imidazole is nearest neighbor to an A, C, G, or T base on the strand that it reads.

The ideal regression analysis for this study would be to fit Model 0 to observed binding free energies for known six-ring and eight-ring polyamide structures with known DNA sequences (7, 9–12). However, it can be shown that this full 12-parameter model is unidentifiable for these types of data. Because each polyamide has precisely one linker and one tail, one can estimate uniquely at most a three-dimensional subset of the four parameters ΔG_Link,AT, ΔG_Link,GC, ΔG_Tail,AT, and ΔG_Tail,GC. In addition to this intrinsic unidentifiability, certain combinations of rings and base pairings are underrepresented in the available data, so that subsets of the remaining eight parameters are poorly identifiable or not identifiable at all. For example, there are very few polyamides in the published data containing imidazoles whose nearest neighbor is an adenine or cytosine.

Therefore, several simplified models were considered with consolidated parameters to predict the binding-free energies. The simplest identifiable model we explored (Model 1) is given as follows:

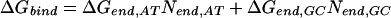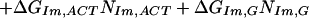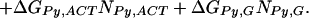ΔG_bind, ΔG_Im,G, ΔG_Py,G, ΔN_Im,G, and ΔN_Py,G are as specified above. ΔG_end,AT and ΔG_end,GC consolidate ΔG_Link,AT, ΔG_Link,GC, ΔG_Tail,AT, and ΔG_Tail,GC parameters assuming that the energetic cost of a GC or CG pairing mismatch is the same for both the hairpin linker and the β-alanine tail. N_end,AT is the number of times that the first and/or the last base pairs in the DNA sequence is AT or TA. That is, N_end,AT = I_Tail + I_Link. Similarly, N_end,GC = (1 − I_Tail) + (1 − I_Link). The polyamide/base interaction parameters were consolidated, taking into account the unique structural role of the guanine N2 amino group. The imidazole parameters were consolidated into two parameters: ΔG_Im,G, identical with the parameter in Model 0, and ΔG_Im,ACT, which consolidates the parameters ΔG_Im,A, ΔG_Im,C and ΔG_Im,T. This parameterization assumes that imidazole interacts similarly with adenine, thymine, and cytosine, but differently with guanine. The pyrrole parameters were consolidated similarly to yield ΔG_Py,G and ΔG_Py,ACT. N_Im,ACT and N_Py,ACT are the number of times that imidazole or pyrrole, respectively, are paired with adenine, cytosine, or guanine.

We found Model 1 to be overly restrictive and developed three additional models that expand the ΔG_Py,ACT match parameter, assuming that differences in the steric interactions between pyrrole rings and these three bases may be significant. The data were not sufficient to identify the three separate parameters used in Model 1, so we tested three intermediate models. Model 2 partially expands ΔG_Py,ACT to ΔG_Py,AC and ΔG_Py,T, and retains the consolidation of the imidazole parameters. Model 2 is defined as:

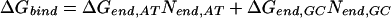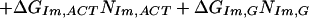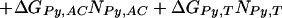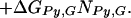Two other expanded models were also considered: Model 3 with ΔG_Py,ACT expanded into ΔG_Py,CT and ΔG_Py,A, and Model 4 with ΔG_Py,ACT expanded into ΔG_Py,AT and ΔG_Py,C parameters.

Analysis of Mathematical Models.

Parameter estimates for Models 1–4 mentioned above were determined based on an unweighted least-squares fit to the 35 free energies of binding of different hairpin-linked polyamides for different DNA sequences (Table 1), using a linear regression program from BMDP statistical analysis software (13). The parameter estimates and quality of model fits for the models are summarized in Table 2. To compare the fits of the models taking into account the number of adjustable parameters for each model we used the Akaike Information Criterion (AIC) (14, 15). Under Gaussian errors, AIC = N⋅ln(RSS) + 2P, where N = 35 is the number of data points, RSS is the residual sum of squares, and P is the number of parameters. Models with smaller values of AIC are favored.

Table 1.

Binding constants used for regression analysis

Ka	DNA	Polyamide	ΔGexpt	ΔGpred (SE)	Residual	Ref.
3.7 e+10	AGTACT	IPPPIPPP	−14.26	−12.42 (0.35)	−1.84	10
4.1 e+08	AGTATT	IPPPIPPP	−11.62	−12.05 (0.60)	0.43	10
3.5 e+09	AGTATT	IPPPPPPP	−12.88	−13.02 (0.41)	0.14	10
5.0 e+08	AGTACT	IPPPPPPP	−11.74	−10.88 (0.47)	−0.86	10
2.9 e+08	TGTTA	IPPPPP	−11.42	−10.68 (0.22)	−0.74	6
4.8 e+06	TGACA	IPPPPP	−9.02	−8.54 (0.38)	−0.48	6
1.0 e+08	TGGTT	IIPPPP	−10.80	−10.09 (0.23)	−0.71	12
1.7 e+06	TGTTA	IIPPPP	−8.41	−8.47 (0.42)	0.06	12
1.0 e+06	GGGTA	IIPPPP	−8.10	−7.90 (0.43)	−0.20	12
1.6 e+07	AACCA	PPPIIP	−9.72	−10.09 (0.23)	0.37	12
1.0 e+05	TAACA	PPPIIP	−6.75	−8.47 (0.42)	1.72	12
1.0 e+05	TACCC	PPPIIP	−6.75	−7.90 (0.43)	1.15	12
2.1 e+08	TGTTT	IPPPPP	−11.23	−10.68 (0.22)	−0.55	9
1.5 e+08	TGTTA	IPPPPP	−11.04	−10.68 (0.22)	−0.35	9
7.3 e+07	TGTAA	IPPPPP	−10.61	−10.68 (0.22)	0.07	9
4.7 e+07	TGTAT	IPPPPP	−10.36	−10.68 (0.22)	0.32	9
3.9 e+07	TGATT	IPPPPP	−10.25	−10.68 (0.22)	0.43	9
2.5 e+07	TGATA	IPPPPP	−9.99	−10.68 (0.22)	0.69	9
2.2 e+07	TGAAA	IPPPPP	−9.91	−10.68 (0.22)	0.77	9
1.8 e+07	TGAAT	IPPPPP	−9.79	−10.68 (0.22)	0.89	9
4.6 e+06	AGGGA	IIIPPP	−8.99	−9.50 (0.39)	0.51	7
7.6 e+06	TGGGT	IIIPPP	−9.29	−9.50 (0.39)	0.21	7
1.3 e+06	TGGGC	IIIPPP	−8.25	−7.31 (0.45)	−0.94	7
8.6 e+05	AGGCA	IIIPPP	−8.01	−6.99 (0.58)	−1.02	7
3.7 e+08	AGGGAA	IIIPPPPP	−11.56	−11.83 (0.42)	0.27	7
1.4 e+07	TGGGTC	IIIPPPPP	−9.65	−9.64 (0.50)	−0.01	7
1.7 e+06	TGGGCT	IIIPPPPP	−8.41	−9.69 (0.50)	1.28	7
2.9 e+06	AGGCAA	IIIPPPPP	−8.72	−9.32 (0.51)	0.60	7
7.6 e+07	TGTTA	IPPPPP	−10.64	−10.68 (0.22)	0.04	11
7.8 e+05	AGAGT	IPPPPP	−7.95	−8.54 (0.38)	0.59	11
2.6 e+06	AGACA	IPPPPP	−8.66	−8.54 (0.38)	−0.12	11
5.2 e+07	AGACA	IPPIPP	−10.41	−10.09 (0.23)	−0.32	5
9.1 e+07	AGACA	IPPIPP	−10.74	−10.09 (0.23)	−0.65	5
8.0 e+06	ATTCA	IPPIPP	−9.32	−8.47 (0.42)	−0.85	5
9.2 e+06	TTACA	IPPIPP	−9.40	−8.47 (0.42)	−0.93	5

The predicted free energies and standard errors of the predictions are based on the fit to Model 2. For all of these experiments the temperature is 295 degrees Kelvin. I refers to an imidazole–amide and P refers to a pyrrole–amide in a γ-aminobutyric acid hairpin-linked molecule with a carboxyl-terminal β-alanine–N, N-dimethylaminopropyl-amide tail. 

Table 2.

Summary of parameter estimates (kcal/mol) and quality of model fit for free energy models

Model	Parameter	Estimates (SE)	Quality of model fit
			RSS	AIC	MSE
1	ΔGend,GC	0.37 (0.77)	21.54	119.45	0.74
	ΔGend,AT	−1.82 (0.57)
	ΔGIm,ACT	0.45 (0.40)
	ΔGIm,G	−0.70 (0.24)
	ΔGPy,ACT	−1.25 (0.19)
	ΔGPy,G	0.67 (0.39)
2	ΔGend,GC	0.05 (0.77)	19.47	117.91	0.70
	ΔGend,AT	−2.14 (0.59)
	ΔGIm,ACT	0.42 (0.39)
	ΔGIm,G	−1.20 (0.37)
	ΔGPy,AC	−0.54 (0.45)
	ΔGPy,T	−1.79 (0.36)
	ΔGPy,G	0.35 (0.42)
3	ΔGend,GC	0.30 (0.81)	21.45	121.30	0.77
	ΔGend,AT	−1.90 (0.62)
	ΔGIm,ACT	0.35 (0.51)
	ΔGIm,G	−0.51 (0.61)
	ΔGPy,A	−1.04 (0.63)
	ΔGPy,CT	−1.39 (0.48)
	ΔGPy,G	0.85 (0.65)
4	ΔGend,GC	0.28 (0.75)	19.45	117.87	0.69
	ΔGend,AT	−1.88 (0.56)
	ΔGIm,ACT	0.86 (0.45)
	ΔGIm,G	−1.20 (0.37)
	ΔGPy,AT	−1.27 (0.18)
	ΔGPy,C	0.21 (0.86)
	ΔGPy,G	−0.44 (0.74)

RSS, residual sum of squares; AIC, Akaike Information Criterion; MSE, mean square error. 

The performance of a model in predicting the binding affinities of various polyamides for various sequences was analyzed by performing seven cross-validation studies. Cross-validation offers a means for testing how well a model is able to predict binding affinities for polyamide/DNA sequence combinations not used in the model fitting. For a given cross-validation study a subset of the binding-free energy data was excluded, and the remaining data points were used to estimate model parameters. These new parameter estimates were then applied to predict the binding-free energies for the data that had been excluded. In addition, each cross-validation study was used to predict binding energies to all nontarget 5-bp sequences contained in the DNA fragment from the footprinting study that had been excluded.

RESULTS AND DISCUSSION

Determination of Parameters.

Model 2 provided the best compromise out of all of the models with regard to having physically meaningful estimates, a good fit to the data, and low standard error estimates (Table 2). The predicted and empirically determined free energy values as well as the residuals (the difference between the experimental and predicted values) for the data set are shown in Table 1 for Model 2. The residual values range from −1.84 kcal/mol to 1.72 kcal/mol with an average magnitude of 0.60 kcal/mol for Model 2. Addition of the extra parameter in Model 2 offers an improvement in the fit of the data relative to Model 1 as judged by the Akaike Information Criterion. While Model 3 predicted physically sensible values for the parameter estimates, it had a worse fit to the data and, in general, slightly larger standard errors of the parameter estimates than did Model 2. Model 4 had the largest standard error estimates out of the four models. Furthermore, we also estimated parameters for a series of more expanded models with the ΔG_Py,ACT and ΔG_Im,ACT parameters expanded. However, for each of these expanded models, the standard error estimates were significantly larger than those for Model 2 (data not shown).

The highly negative value of ΔG_end,AT (−2.14 kcal/mol) and the slightly positive value for ΔG_end,GC (0.05 kcal/mol) for Model 2 suggests that both the γ-aminobutyric acid linker and the β-alanine carboxyl-terminal tail exhibit a strong preference in binding to the match sites of AT and TA base pairs over the mismatch sites of GC and CG base pairs. (Parameter estimates for an expanded version of Model 2 with separate linker and tail parameters differed by only 0.3 kcal/mol and were within 0.3 kcal/mol of −2.0 kcal/mol; data not shown.) The strong binding preference for AT/TA base pairs relative to GC/CG base pairs can be attributed to the unfavorable steric interactions that arise between atoms of the linker or tail and the N2 amino group of guanine. This predicted AT/TA base pair preference to GC/CG base pairs agrees with experimentally observed data (7).

The parameter estimate values yield several physically meaningful interpretations. First of all, the positive value for ΔG_Py,G (0.35 kcal/mol) suggests a free energy penalty for the recognition of a guanine by a pyrrole. This is consistent with a steric clash between the guanine N2 amino group and the pyrrole methyl group. The positive value for ΔG_Im,ACT (0.42 kcal/mol) suggests that the imidazole–ACT mismatch is even more energetically unfavorable than the pyrrole–guanine mismatch. The relatively high free energy value predicted for these imidazole mismatches can be attributed to the burial of hydrogen bond acceptors on both the imidazole and the bases, losing water hydrogen bonds in the complex. The negative value of ΔG_Im,G (−1.20 kcal/mol) indicates the favorable interaction between the imidazole and guanine consistent with the hydrogen bond formation between the imidazole nitrogen and the guanine N2 amino group. Finally the negative values of ΔG_Py,AC (−0.54 kcal/mol) and ΔG_Py,T (−1.79 kcal/mol) indicate favorable interactions of a pyrrole with the A, C, and T bases consistent with their steric complementarity.

Cross-Validation Experiments.

Cross-validation experiments test the predictive ability of the model. The estimated free energies from seven cross-validation studies (Table 3) predict the experimental values to within an root-mean-square deviation of 1.16 kcal/mol for the 27 data points. Thus, Model 2 is successful in predicting binding constants to within an order of magnitude.

Table 3.

Results of seven cross-validation experiments for Model 2

DNA	Polyamide	ΔGexpt	ΔGpred	Residual	Ref.
TGTTA	IPPPPP	−11.42	−10.58	−0.84	6
TGACA	IPPPPP	−9.02	−8.37	−0.65	6
TGGTT	IIPPPP	−10.80	−10.04	−0.76	12 (1)
TGTTA	IIPPPP	−8.41	−8.49	0.08	12 (1)
GGGTA	IIPPPP	−8.10	−7.84	−0.26	12 (1)
AACCA	PPPIIP	−9.72	−10.14	0.42	12 (2)
TAACA	PPPIIP	−6.75	−9.07	2.32	12 (2)
TACCC	PPPIIP	−6.75	−8.35	1.60	12 (2)
TGTTT	IPPPPP	−11.23	−11.08	−0.15	9
TGTTA	IPPPPP	−11.04	−11.08	0.04	9
TGTAA	IPPPPP	−10.61	−11.08	0.47	9
TGTAT	IPPPPP	−10.36	−11.08	0.72	9
TGATT	IPPPPP	−10.25	−11.08	0.83	9
TGATA	IPPPPP	−9.99	−11.08	1.09	9
TGAAA	IPPPPP	−9.91	−11.08	1.17	9
TGAAT	IPPPPP	−9.79	−11.08	1.29	9
AGGGA	IIIPPP	−8.99	−9.25	0.26	7 (1)
TGGGT	IIIPPP	−9.29	−9.25	−0.04	7 (1)
TGGGC	IIIPPP	−8.25	−6.74	−1.51	7 (2)
AGGCA	IIIPPP	−8.01	−5.87	−2.14	7 (1)
AGGGAA	IIIPPPPP	−11.56	−12.92	1.36	7 (2)
TGGGTC	IIIPPPPP	−9.65	−10.49	0.84	7 (2)
TGGGCT	IIIPPPPP	−8.41	−11.24	2.83	7 (2)
AGGCAA	IIIPPPPP	−8.72	−10.34	1.62	7 (2)
TGTTA	IPPPPP	−10.64	−10.72	0.08	11
AGACT	IPPPPP	−7.95	−8.72	0.77	11
AGACA	IPPPPP	−8.66	−8.72	0.06	11

We did not perform cross-validation experiments corresponding to refs. 10 and 5 to avoid removing data points corresponding to mismatched ring base recognition infrequently represented (such as the imidazole–adenine pairing). In refs. 12 and 7, two separate subsets of the data were removed (indicated by 1 and 2) for each cross-validation experiment. I and P defined in Table 1. 

The linear regression model also successfully predicts less favorable free energies of binding for sequences that show little or no binding of polyamide. Results from all seven cross-validation studies are included in Fig. 2, showing the predicted free energy of binding to the 27 target sequences centering around the range of −10 to −11 kcal/mol and nonspecific binding to the remaining plasmid sequences forming a broad Gaussian curve centered around −5 to −6 kcal/mol.

Figure 2.

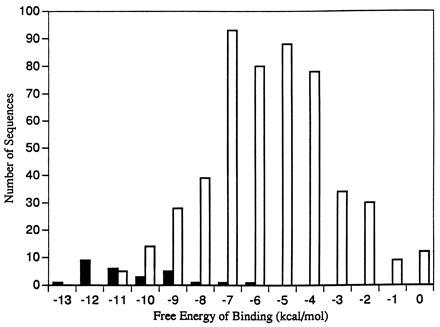
The results of seven cross-validation experiments, omitting the same groups of data as in Table 3, are combined. Solid bars represent the number of times a target sequence is predicted to be bound by its specific polyamide molecule within each energetic range (i.e., the data included in Table 3). Open bars represent the number of times nonspecific binding is predicted to other sequences in the plasmids within each range. Each number on the abscissa is the upper bound of a 1 kcal/mol interval.

Prediction of Polyamide Sequence Discriminatory Ability.

We applied the linear regression model to determine the free energies of binding for the 64 possible polyamides for the 5-bp sequence AGAAA. This sequence is an ideal target site: it is part of the polypurine tract of HIV-1, a sequence that is highly conserved among HIV-1 mutant strains, and is not degraded by RNase H during reverse transcription. However, equally as important as the binding affinity of a drug for its target sequence is its ability to discriminate against other sequences. For instance, one might seek to minimize binding to key sequences found in the host genome, such as transcription factor binding sites, or to minimize nonspecific binding to the entire genome. For each of these 64 compounds, we computed the binding affinities for each of the 5-bp sequences contained in the TATA box consensus sequence TATA(A,T)A(A,T), and the binding affinities for the 4⁵ − 2 = 1,022 possible 5-bp sequences. Table 4 includes results for the eight polyamides that combine the best ring pairings for each base pair: imidazole with guanine and either imidazole or pyrrole with cytosine, and pyrrole with thymine and either imidazole or pyrrole with adenine. The remaining polyamides bound to AGAAA within a similar range of estimated binding constants, but also bound more tightly to many nontarget sequences, resulting in poor sequence discriminatory ability. It is clear in terms of binding-free energies as well as discriminatory abilities that ImPyPyγPyPyImβDp and ImPyPyγPyPyPyβDp are two highly effective polyamides (Im, N-methylimidazole; Py, N-methylpyrrole, γ, γ-aminobutyric acid; β, β-alanine; Dp, N,N-dimethylaminopropylamide). Table 4 clearly indicates that while ImPyPyγPyPyImβDp has a slightly reduced binding-free energy relative to ImPyPyγPyPyPyβDp, it discriminates against the TATA sequences better than does ImPyPyγPyPyPyβDp.

Table 4.

Sequence discrimination ability of six- and eight-ring polyamides

Ring sequence	ΔGbind*	All†			TATA box†			Fraction‡
		A	B	C	A	B	C
IIIPPI	−7.74	935	63	24	10	0	0	0.014
IIPPPI	−8.71	959	47	16	10	0	0	0.018
IPIPPI	−8.71	959	47	16	10	0	0	0.018
IPPPPI	−9.68	991	31	0	10	0	0	0.023
IIIPPP	−8.75	955	51	16	8	2	0	0.018
IIPPPP	−9.72	975	39	8	8	2	0	0.023
IPIPPP	−9.72	975	39	8	6	4	0	0.023
IPPPPP	−10.69	991	31	0	6	4	0	0.029
IIIIPPPI	−9.10	3,863	175	56	10	0	0	0.005
IIIPPPPI	−10.07	3,920	127	48	10	0	0	0.007
IIPIPPPI	−10.07	3,919	127	48	10	0	0	0.007
IIPPPPPI	−11.04	3,967	95	32	10	0	0	0.007
IPIIPPPI	−10.07	3,919	127	48	10	0	0	0.009
IPIPPPPI	−11.04	3,967	95	32	10	0	0	0.009
IPPIPPPI	−11.04	3,967	95	32	10	0	0	0.009
IPPPPPPI	−12.01	4,031	63	0	10	0	0	0.011
IIIIPPPP	−10.11	3,911	139	44	10	0	0	0.007
IIIPPPPP	−11.08	3,959	103	32	10	0	0	0.008
IIPIPPPP	−11.08	3,959	103	32	10	0	0	0.008
IIPPPPPP	−12.05	3,999	79	16	10	0	0	0.011
IPIIPPPP	−11.08	3,959	103	32	9	1	0	0.008
IPIPPPPP	−12.05	3,999	79	16	8	2	0	0.011
IPPIPPPP	−12.05	3,999	79	16	9	1	0	0.011
IPPPPPPP	−13.02	4,031	63	0	8	2	0	0.014

I and P defined in Table 1. 

^*Estimated binding free energy to the target sequence (AGAAA for six-ring polyamides and AGAAAA for eight-ring polyamides) in kcal/mol. 

^†Number of sequences for which the estimated polyamide binding constant is: (A) less than one-tenth of the target sequence; (B) greater than one-tenth that of the target sequence, but less than that of the target sequence; and (C) greater than that of the target sequence. Results are tabulated for all possible 5-bp sequences or all possible 6-bp sequences, excluding the target sequence and its complement, and for the 10 unique 5-bp sequences or for the 10 unique 6-bp sequences from the TATA box consensus sequence TATA(A,T)A(A,T). 

^‡Fraction of bound drug that is bound to the target sequence when this target sequence is 50% saturated. 

Similarly, we computed the sequence discriminatory abilities of the 256 eight-ring polyamides. For each of these compounds, we computed the binding affinities for each of the 6-bp sequences contained in the TATA box consensus sequence TATA(A,T)A(A,T), and the binding affinities for the 4⁶ − 2 = 4,096 possible 6-bp sequences. Table 4 includes the 16 compounds with the best ring pairings, as reported for the six-ring polyamides. A similar result holds for the two compounds ImPyPyPyγPyPyPyβDp and ImPyPyPyγPyPyPyPyβDp. While the former has a slightly worse binding-free energy, once again it discriminates against the TATA box sequences better than does the latter.

With these free energy estimates, one can also estimate the fractional occupancy of a given 5-bp DNA site (i.e., the fraction of those particular sites occupied by a polyamide at a given concentration). This can be approximated mathematically by the following Hill equation (9):

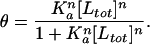where θ is the fractional occupancy, [L_tot], K_a is the equilibrium association constant, and we assume that n is 1 (7). The ratio of polyamide binding to its intended 5-bp target site, relative to all possible 5-bp sequences, may be approximated by:

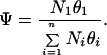θ_i is the fractional occupancy of the i^th site bound by a side-by-side polyamide (i = 1 corresponds to the target site), and N_i is the number of copies of the i^th site in the genome.

For a polyamide concentration corresponding to 99% fractional occupancy of the target sites, using the predicted binding-free energies to the n = 1,024 possible genome sequences for Model 2 and assuming an equal number of copies of each 5-bp sequence in the genome, one can calculate Ψ to be 0.005 for ImPyPyγPyPyImβDp and 0.006 for the polyamide ImPyPyγPyPyPyβDp. For a polyamide concentration corresponding to 50% saturation of the target sites, Ψ is 0.023 for the polyamide ImPyPyγPyPyImβDp and 0.029 for ImPyPyγPyPyPyβDp. The percentages of polyamide reaching the target site for concentrations corresponding to a 50% saturation of the target sites for each of the eight polyamides is summarized in Table 4. The corresponding percentages of polyamide reaching the target site for the 16 eight-ring molecules is summarized in Table 4. These smaller percentages demonstrate the counterintuitive result that the percentage of molecules reaching the target site may decrease as the polyamide length increases. This is because there are approximately four times more 6-bp sequences than 5-bp sequences and the intrinsic discriminatory abilities of the rings are not strong enough to overcome the increase in the number of sequences recognized. As a consequence, more nontarget sequences can be recognized by the longer polyamide than by the shorter polyamide.

In conclusion, these mathematical modeling studies have demonstrated that there are complex trade-offs between the optimal strength of the binding affinity of the polyamide for the target sequence, the number of other sequences recognized with high affinity, as well as which sequences are the ones recognized with high affinity. The mathematical model also predicts the counterintuitive result that because of the limitations of the discriminatory abilities of the pyrrole and imidazole rings, the percentage of polyamide targeting its intended sequence decreases as the polyamide length increases, contrary to the expected enhanced specificity of these longer molecules.

ABBREVIATIONS

Im

N-methylimidazole

Py

N-methylpyrrole

γ

γ-aminobutyric acid

β

β-alanine

Dp

N,N-dimethylaminopropylamide