Axial rotation of sliding actin filaments revealed by single-fluorophore imaging

Abstract

In the actomyosin motor, myosin slides along an actin filament that has a helical structure with a pitch of ≈72 nm. Whether myosin precisely follows this helical track is an unanswered question bearing directly on the motor mechanism. Here, axial rotation of actin filaments sliding over myosin molecules fixed on a glass surface was visualized through fluorescence polarization imaging of individual tetramethylrhodamine fluorophores sparsely bound to the filaments. The filaments underwent one revolution per sliding distance of ≈1 μm, which is much greater than the 72 nm pitch. Thus, myosin does not “walk” on the helical array of actin protomers; rather it “runs,” skipping many protomers. Possible mechanisms involving sequential interaction of myosin with successive actin protomers are ruled out at least for the preparation described here in which the actin filaments ran rather slowly compared with other in vitro systems. The result also indicates that each “kick” of myosin is primarily along the axis of the actin filament. The successful, real-time observation of the changes in the orientation of a single fluorophore opens the possibility of detecting a conformational change(s) of a single protein molecule at the moment it functions.

The actin filament is an array of actin protomers arranged in the form of two-start, right-handed helices with a pitch of ≈72 nm containing ≈13 protomers (1). If myosin tends to interact sequentially with one of the helical strands (the binding site on the other strand being on the opposite side), right-handed rotation of a sliding actin filament around its axis is expected. Indeed, in an in vitro motility assay in which the front end of a sliding filament was fixed on a surface, the middle part formed a left-handed superhelix, indicating right-handed rotation of the sliding rear part (2). However, in another assay where a marker (bead aggregate) was attached at the tail of a freely sliding filament, the filament slid over a long distance without rotating the tail beads (3). Quantitative resolution of this issue is important for the mechanism of motor function, because axial rotation is an indication of (i) sequential interaction of a myosin molecule with successive (or closely apposed) actin protomers, as stated above, and/or (ii) the presence of a genuine torque component in the individual myosin–actin interaction not necessarily related to the helical structure. In the first assay above (2) where the superhelix formation was observed, the number of axial rotations could not be determined in the video images of limited resolution. A complication with the bead-tailed actin (3) was that the beads produced a large rotational, but not translational, friction that may have impeded the axial rotation. Here we show that the amount of rotation is small even in the absence of the external asymmetric load. Neither i nor ii appear to be essential components of the actomyosin motor. Quantitative measurement of the axial rotation without an impeding marker was achieved by continuous, real-time detection of the orientation of individual fluorophores on actin, through fluorescence-polarization imaging on a microscope with extremely low background (4).

MATERIALS AND METHODS

Basic experimental procedures have been described (4). A brief summary and modifications are given below.

Motility Assay.

Actin and heavy meromyosin (HMM) were prepared from rabbit skeletal muscle as described (4). Actin was labeled with pure 5-iodoacetamidotetramethylrhodamine (5) at a final ratio of 1 mol of the dye to 500 mol of actin, and polymerized into filaments (F-actin) in the presence of phalloidin (4). Into an observation chamber made of two quartz coverslips precleaned with KOH and ethanol, 1 mg/ml of poly-l-lysine was infused. After 60 s, the chamber was washed with distilled water and then with buffer A containing 25 mM imidazole/HCl (pH 7.5), 25 mM KCl, and 4 mM MgCl₂. This was followed by a series of 60-s incubations with washes indicated in brackets: (i) 80 μg/ml of HMM in buffer A [buffer A], (ii) 5 μM of unlabeled F-actin in buffer A [buffer A plus 2 mM ATP], and (iii) 5 nM of labeled F-actin in buffer A plus 2 mM ATP [buffer A plus 2 mM ATP]. All solutions were infused from the same side of the chamber. Buffers were degassed under reduced pressure immediately before use. The pretreatment of the chamber with unlabeled F-actin resulted in a smooth (constant speed), linear sliding of labeled F-actin parallel to the direction of infusion. The chamber was placed on a microscope stage such that the sliding direction was at ≈45° in the image plane. Measurements were made at 25 ± 2°C.

Fluorescence Microscopy.

An inverted epifluorescence microscope (Diaphot TMD, Nikon) was modified to reduce its background luminescence by two orders of magnitude (4). Fluorescence was excited at 532 nm with a circularly polarized (by a quarter-wave plate) beam from an Nd/YAG laser (DPY425II, Adlas, Lübeck, Germany). The beam intensity was 8.5 mW over a sample area of 30 μm in diameter. For a fluorophore with a nondegenerate transition moment such as the tetramethylrhodamine used here, the circular excitation is equivalent with unpolarized excitation. That the excitation beam was isotropic in the image plane was confirmed by passing the beam through a polarizer placed on the sample stage; rotation of the polarizer did not change the transmitted intensity. Fluorescence (>565 nm) was collected through a water immersion objective (60×, numerical aperture 1.20, WPlanApo60UV, Olympus, Tokyo), decomposed into vertically and horizontally polarized images in a dual-view apparatus (6), and detected with an image intensifier (KS1381, Video Scope International, Sterling, VA) coupled to an intensified charge-coupled-device camera (C3500, Hamamatsu Photonics, Hamamatsu, Japan). Images were rolling averaged in a digital image processor (C2000, Hamamatsu Photonics) with a half time of 2 frames (67 ms), and recorded on a Hi8 video recorder (EVO-9650, Sony, Tokyo). Recorded images were analyzed frame by frame in the digital image processor.

RESULTS

Fluorescence polarization of the actin filaments labeled with tetramethylrhodamine at high dye/protein ratios showed that the fluorophore was essentially immobile on actin and its transition moment lay at ≈45° to the filament axis. Thus, a suspension of 3% labeled filaments in a cuvette gave a fluorescence anisotropy of 0.32 (λ_ex = 532 nm, λ_em = 575 nm; measured in a Hitachi F-4010 spectrofluorometer), indicating that the wobbling of the fluorophore on actin was confined within a cone of semiangle <25° (7). When individual filaments labeled at 30% were examined on the fluorescence microscope, filaments lying parallel to the polarizer (analyzer) axis gave a polarization of 0.18 ± 0.04 (n = 12). This value, as analyzed in ref. 6 for unpolarized excitation and corrected in ref. 8 for the large numerical aperture of the objective of 1.2 (the effective aperture was much smaller for the excitation), indicates that the absorption and emission moments (assumed parallel) were at ≈45° from the filament axis. (When parallel absorption and emission moments are distributed on the surface of a cone of semiangle 46°, whose axis lies in the image plane, unpolarized or circularly polarized excitation with a beam perpendicular to the image plane will give rise to a fluorescence polarization, with respect to the cone axis, of 0.227. Observation through an objective with a numerical aperture of 1.2 will decrease the polarization value to 0.189.)

The results above allowed us to design an experimental protocol schematized in Fig. 1. Sparsely labeled (molar ratio = 0.2%) filaments were let slide on a glass surface coated with HMM, in the direction at ≈45° in the image plane. Fluorescent spots with an intensity corresponding to a single (or possibly double) fluorophore (4) were seen to move steadily from bottom right to top left, or in the reverse direction. The fluorescence was excited with circularly polarized light, and images of vertically (V) and horizontally (H) polarized fluorescence were acquired simultaneously. In this setup, axial rotation of sliding filaments should show up as alternation of the spot intensity between images V and H (Fig. 1 Right), as was indeed observed (Fig. 2A). Note that the alternating intensity is expected only when the fluorescence from a single (at most a few) fluorophore is resolved; a fully labeled filament in which the fluorophores are arranged with a helical symmetry will give rise to an averaged polarization that is insensitive to the axial rotation. The sudden disappearance (photobleaching) of the spot in Fig. 2 A (at ≈3.1 s) and D (at ≈1.7 s) is an indication (but not proof) that the spot represented a single fluorophore.

Figure 1.

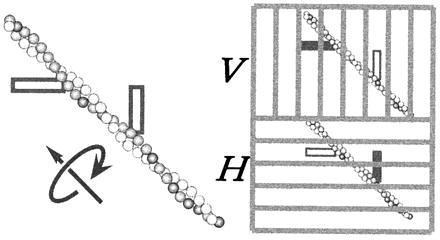
Measurement of axial rotation through fluorescence-polarization imaging. An actin filament was sparsely labeled with fluorophores with their transition moment (shown as a thick bar) at ≈45° from the filament axis. Fluorescence was excited with circularly polarized light. The vertically polarized component of the fluorescence was projected onto the upper half of the detector plane, and the horizontal component onto the lower half, through a dual-view apparatus (6). Filament rotation will result in an alternate appearance of each fluorophore between the V and H images.

Figure 2.

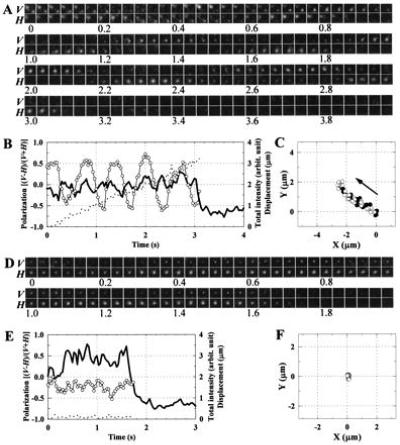
Axial rotation detected in polarized fluorescence images. (A) Snapshots, at 33-ms intervals, of fluorescence from individual fluorophores on an actin filament sliding from bottom right toward top left. V, vertically polarized fluorescence; H, horizontally polarized fluorescence; numbers indicate time in seconds. Each image was spatially averaged over 3 × 3 pixels (0.66 × 0.66 μm²), and corrected for shading (due mainly to inhomogeneous excitation). (B) Time courses of the polarized spot intensities. The peak intensity of the trailing spot in A (starting at bottom right at 0 s) was measured for V and H, from which the total intensity, I = V + H (solid line), and polarization, p = (V − H)/(V + H) (○) were calculated. Because the signal-to-noise ratio was not high, the peak intensities, V and H, were not corrected for the background intensity, which varied to some extent from sample to sample and amounted to, on the average, one-third of the spot intensity; the total intensity beyond 3.1 s (also beyond 1.7 s in E) represents the background intensity. The inclusion of the background intensity resulted in smaller values of p, but our primary concern is its time dependence. Broken line indicates the displacement of the spot peak from the position at time 0. If the absorption and emission moments (assumed parallel) of the dye make an angle θ with the filament axis, and if the filament rotates at an angular velocity of ω around its axis, which lies at 45° with V and H axes, the total intensity and polarization for circularly polarized excitation are given by I = cos²θ + sin²θsin²ωt and p = sin2θsinωt/I (without correction for the large collection angle of the objective). Note that the theoretical I for a single fluorophore takes maximal values at times t when p passes either positive or negative peaks. The drop of the total intensity at ≈3.1 s resulted from photobleaching of the dye. (C) Trace of the trailing spot in A. (•), Spot positions where p > 0; (○), spot positions where p < 0. Arrow indicates the direction of sliding. The frame enclosing the trace represents the same area as each image in A. (D–F) Control experiment in the absence of ATP. The fluctuation of the spot intensity in this sample serves as a measure of the precision in A–C. The dye was photobleached at ≈1.7 s.

In principle, the alternation of spot intensity could also result from snake-like winding of the filament without axial rotation. Traces of the moving spots (Figs. 2C and 3B), however, were linear, and the polarization (= [V − H]/[V + H]) of the spot fluorescence alternated its sign quite regularly over a long distance (Figs. 2B and 3A). Also note, in Fig. 2A at 0–1 s, that two fluorophores, presumably on the same straight filament, flickered out of phase yet with a similar rhythm. In the absence of ATP, where actin binds to myosin tenaciously, the polarization remained relatively constant (Fig. 2 D and E), showing that the alternation of spot intensity did not originate from fluorophore rotation relative to actin nor from instrumental instability.

Figure 3.

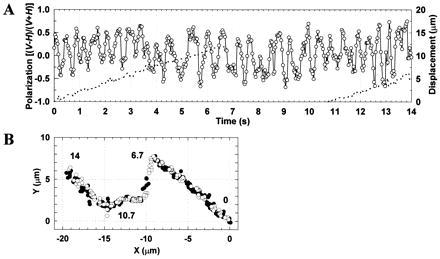
The longest rotation record observed. See Fig. 2 for symbols. Between 6.7 and 10.7 s (−9 and −15 μm in B), the microscope stage was moved manually to keep the moving spot in the field of view.

Fig. 4 summarizes the relation between the speed of axial revolution (estimated in the polarization plot) and sliding velocity. The sliding actin without an external load rotated by one turn per sliding distance of 1 μm, which is much longer than the helical pitch of the actin filament. In the superhelix formation by Nishizaka et al. (2), the end of the supercoil made at least four turns for a sliding distance of 5 μm. If they did not miss rapid rotation, their observation is consistent with ours.

Figure 4.

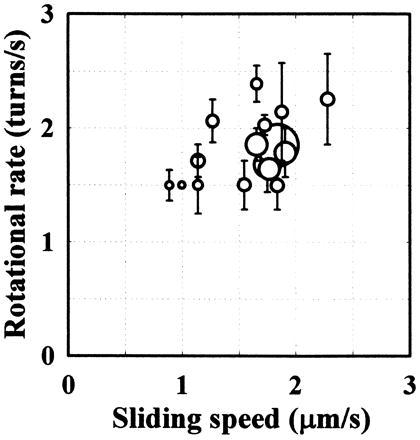
The relationship between axial rotation and forward translocation. The sliding speed (abscissa) was estimated from the slope of the displacement record (broken lines in Figs. 2B and 3A). The rotational rate (ordinate) was calculated as the number of revolutions in a record divided by the total duration determined by photobleaching. The size of the symbols is proportional to the duration of the record. The average of the durations is 5.6 s, which is approximately twice the average lifetime of all single fluorophores (long-lived spots were selected for the analysis of rotation). Vertical bars indicate the uncertainty in the revolution count. In estimating the revolution count, peaks with a small amplitude or short duration (0.1 s or less) were judged as noises and ignored. In Fig. 3A, for example, the revolution count during the 14-s period was estimated to be between 27 and 29.

DISCUSSION

The finding that the rotational pitch was much larger than the helical pitch has two major implications.

First, at least in our system described here, each myosin molecule does not maintain stereospecific interaction with an actin filament while the filament slides past the myosin. The force-generating (strong) interaction, in particular, is most likely to be stereospecific. Thus, the subsequent force-generating interaction of the same myosin molecule must be made on an actin protomer more than ≈36 nm (half pitch of the helix) apart; otherwise, an efficient axial rotation would be expected. Note that, even under “unloaded” conditions, a myosin molecule has to work against the “protein friction” (9) caused by other myosin molecules and thus has to generate force.

The long interval of >36 nm between successive force-generating interactions, longer than twice the physical size of a myosin head of ≈16 nm (10), rules out alternate bindings (“walk”) of the two heads of myosin, a mechanism suggested for kinesin (11). In our system without an external load, myosin “runs” on actin, skipping many actin protomers. That myosin under unloaded conditions interacts with actin strongly only for a small fraction of the ATPase cycle has already been anticipated (see for example ref. 12), on the ground that the sliding velocity (several micrometers per second) divided by ATPase (≈10/s) yields the distance traveled by actin per cycle of >0.1 μm, much greater than the size of a myosin head. Implicit in this argument, however, is the assumption that strong binding of myosin and actin occurs only once in the ATPase cycle, a notion that has been challenged by Yanagida et al. (13), who claim that myosin under a small load undergoes multiple power strokes during one ATPase cycle. If multiple strokes occur in the motility system described here, and if each stroke requires a stereospecific interaction, the successive strokes in one ATPase cycle have to be separated by >36 nm. Although multiple strokes are thus unlikely in our system, the sliding velocity was relatively low (see below). Multiple strokes (leading to efficient rotation) in a faster system cannot be ruled out.

In between the strongly bound states, myosin and actin are considered to interact “weakly,” undergoing rapid cycles of association and dissociation (for a review see ref. 14). The nature of this weak interaction is not yet clear, but our results indicate that this interaction, too, cannot keep a myosin molecule on one strand of a sliding actin helix. Either the weak interaction also occupies only a small fraction of the ATPase cycle, or else the interaction is really weak and nonspecific, occurring indiscriminately over any part of the actin surface.

The other implication of our finding is that the individual myosin–actin interaction does not produce a significant rotational torque, compared with the sliding force parallel to the actin filament. If the interaction force is oblique to the filament axis and the perpendicular component contributes to the torque, the latter is likely to be <10% (72 nm/1 μm) of the parallel, sliding force. The experiment using bead-tailed actin also indicated that the torque component was much smaller than the sliding force (3).

The above estimate of torque rests on the assumption that the movement of myosin relative to actin was parallel to the oblique force. If the axial rotation was somehow hindered in our motility system, the torque component may be underestimated. The sliding velocity on the polylysine-coated glass (Fig. 4) was indeed low, compared with 3.5–4 μm/s at 25°C on nitrocellulose surfaces (3, 15) or 7.8 μm/s at 22°C on Sigma-coat (16), suggesting the presence of an impeding factor(s) in our system, probably myosin damaged on the surface. Normal myosin, too, exerts protein friction (9), which impedes the filament motion. Let us consider the impeding mechanism in detail. When a myosin molecule pulls the actin filament, it stretches the holding linkages of other myosin molecules, normal or damaged. A next myosin molecule may bind and pull, but it only increases strain of existing linkages. It is the release of holding myosin molecules that allows the filament to slide and rotate continuously. It is primarily the release rate that determines the extent of resistance. In this scheme, the impeding mechanism will affect the rotation and linear sliding more or less equally, unless the spring in the linkage is highly anisotropic. A decrease in the release rate (an increase in the number of holding molecules) will slow down rotation and sliding equally. A myosin molecule with internal flexible joints (17) is unlikely to be rigid only in the particular direction opposing the axial rotation. Denatured myosin is less likely to be rigid. Hindrance by possible binding of actin to polylysine is also unlikely to be anisotropic. Thus, our contention that the torque component of individual myosin–actin interaction is small appears to be basically valid.

The small torque component in the actomyosin motor is contrasted to the case of Tetrahymena 14S (but not 22S) dynein, which caused axial rotation of a microtubule with a rotational pitch shorter than the helical pitch of the protofilaments of the microtubule (18). The 14S dynein produced a genuine torque component. The ncd motor on a microtubule also appears to produce a genuine torque (19). Among myosins, brush border myosin I may produce a genuine torque because the head of this myosin has been shown to swing around an actin filament upon release of ADP (20). In the skeletal myosin studied here, such a lateral swing is absent or, if it occurs, it does not generate enough torque to produce efficient axial rotation. The torsional stiffness of an actin filament has suggested that, in an intact skeletal muscle where actin filaments are bound at one end to the Z-disk, the actin filament of length 1 μm is twisted by only one turn even if 10% of the isometric contractile force contributes to the torque component (21). In a shortening muscle producing a much smaller force, myosin will not be able to follow the helical track of the fixed actin filament. A skeletal muscle is an asymmetric system, where the z-disk hinders rotation without impeding shortening.

Although the rotational pitch in our motility system was long, the sliding actin filament did rotate axially with a relatively constant pitch. This slow rotation may have been caused by a small torque generated in the myosin–actin interaction. Or, the rotation may have resulted from the right-handed helical structure of the actin filament: if the steps of running myosin are distributed such that the probability of landing within 36 nm is slightly greater than on further sites, a slow, right-handed rotation is expected. In this latter case, the genuine torque could be totally absent or could even be left-handed (the magnitude being small).

In conclusion, we note that the polarization imaging of single fluorophores as described here should be useful in detecting a conformational change(s) in a single protein molecule during function. Once a fluorophore is firmly attached to a particular site on the protein, reorientation of the fluorophore as a result of the conformational change will be detected as a change in the fluorescence polarization. Because individual protein molecules (molecular machines) always operate stochastically and cannot be synchronized in the rigorous sense, single-molecule observation is vital to the understanding of their mechanisms. Chemical reaction (ATPase) in a single molecule has already been imaged (22). A future challenge is the simultaneous observation of chemistry and conformational changes in a single protein molecule.

ABBREVIATION

HMM

heavy meromyosin