Femtosecond time resolution in x-ray diffraction experiments

Abstract

This paper presents the theoretical background for a synthesis of femtosecond spectroscopy and x-ray diffraction. When a diffraction quality crystal with 0.1–0.3 mm overall dimensions is photoactivated by a femtosecond laser pulse (physical length = 0.3 μm), the evolution of molecules at separated points in the crystal will not be simultaneous because a finite time is required for the laser pulse to propagate through the body of the crystal. Utilizing this lack of global crystal synchronization, topographic x-ray diffraction may enable femtosecond temporal resolution to be achieved from reflection profiles in the diffraction pattern with x-ray exposures of picosecond or longer duration. Such x-ray pulses are currently available, and could be used to study femtosecond reaction dynamics at atomic resolution on crystals of both small- and macromolecules. A general treatment of excitation and diffraction geometries in relation to spatial and temporal resolution is presented.

Diffraction exposures are limited by the pulse length of the x-ray sources (1–4) containing sufficient x-ray photons for interpretable diffraction patterns to be collected (around 10¹¹–10¹³ for macromolecules; refs. 5 and 6). Laser plasma sources (7–9) can deliver this number of x-ray photons in a pulse of a picosecond duration, two orders of magnitude faster than that achievable with existing synchrotron sources (2, 4, 10–12). Future free electron lasers may provide even shorter pulses of coherent radiation. Laue data sets with a temporal resolution of nanoseconds have already been reported (1, 4, 10–18), and interpretable, near-picosecond macromolecular x-ray diffraction data have been collected (11, 12).

Although picosecond Laue exposures are of considerable importance, basic chemical steps, such as the breaking of bonds, are usually over within a few hundred femtoseconds. With the advent of the femtosecond pulsed laser, several beautiful ultra-fast spectroscopy experiments have been performed on small molecules (19–21) as well as on biologically important macromolecules (22–26). These experiments have opened a window through which the behavior of chemical and biological systems can be studied at time scales characteristic of transition-state life times.

Given the wealth of fundamental chemical and biological phenomena that can be studied through femtosecond photoexcitation of atoms, ions, molecules, and macromolecules, and the definitive structural information that is accessible only through x-ray crystallography, it is natural to anticipate that technological advances will witness the merger of these two fields. It is therefore highly pertinent to consider the potentials and limitations of such a merger.

Crossed-Beam Topography

The standard procedure in time-resolved x-ray crystallography is to record a series of short-pulsed diffraction data sets at known times, τ, following reaction initiation. Structure factors F_hkl(τ) are then calculated by treating each temporally distinct data set as an instantaneous “photograph” of an average static electron density, ρ(x, y, z, τ), from which a “movie” of its evolution is constructed through discrete Fourier transformation. If one wishes to obtain better than picosecond temporal resolution, however, it must be appreciated that any light-initiated reaction requires a finite time for the light pulse to propagate through the crystal and excite separated molecules, excited in turn like a “Mexican wave” propagating across a football stadium. Thus, the time evolution of the reaction at separated lattice points within the crystal is not synchronized but is out of phase by a position-dependent quantity.

Consider an experimental configuration, crossed-beam topography (CBT), illustrated in Fig. 1, which utilizes the noninstantaneous nature of photoexcitation in a macroscopic crystal. This arrangement has the potential to achieve near-femtosecond time resolution in x-ray diffraction experiments using available x-ray pulses of picosecond or longer duration. Onto an idealized 0.3-mm-long crystal laminar (typical crystal length for x-ray diffraction experiments) lying in the x − y plane, falls a homogeneous, collimated picosecond x-ray pulse propagating at velocity c parallel to the z-axis, with the entire crystal exposed to the beam. The pulse intensity, P(u), is characterized by a single parameter u ≡ z − ct. Diffraction from the Miller plane (hkl) produces a two-dimensional topographic image of the crystal with intensity I_hkl(x′), where the image coordinates x′ ≡ x′_hkl ≡ (x′, y′)_hkl are defined by the projection, parallel to the scattered x-rays, of (x, y, 0) onto the image plate. A simulated diffraction image, which contains topographical crystal images from Bragg reflections off several Miller planes, is illustrated in Fig. 2. If the crystal were homogeneous over the duration of its exposure to P(u), as would be the case for its native state, the recorded intensity across any crystal image would be independent of x′_hkl.

Figure 1.

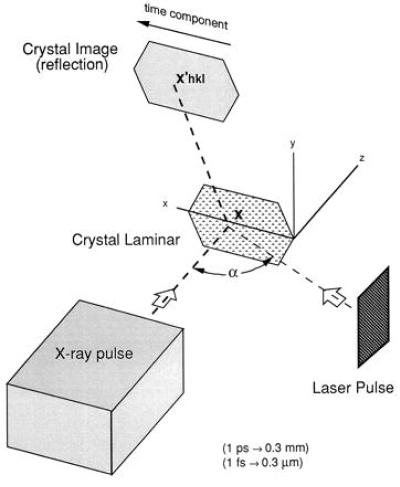
Schematic illustration of a CBT experimental arrangement. X-ray photons incident upon the crystal laminar at x are Bragg scattered and recorded at x′_hkl. During a picosecond x-ray exposure a femtosecond laser pulse sweeps across the crystal laminar, exciting separated lattice points in turn. Because the crystal excitation is not instantaneous, the recorded images contain intensity gradients, Eq. 5, from which electron density maps for structural intermediates can be determined with near-femtosecond temporal resolution.

Figure 2.

A simulated diffraction image from a CBT exposure using white x-radiation. Correlated intensity variations across all crystal images yield information on the temporal evolution of the photoactivated crystal.

Initially suppose the crystal achieves 100% excitation when exposed to a femtosecond laser pulse oriented at an angle α relative to the x-ray pulse, with both pulses lying in the x − z plane and crossing at the crystal site. This laser pulse sweeps across the 0.3-mm-long crystal laminar in sin α ps, a time interval by which the opposite edges of the crystal are out of synchronization. Furthermore, at any moment x-rays scattered from spatially separated molecules will scatter from distinct molecular electron densities with different time delays following (or preceding) their excitation. Therefore, at each instant (or each value of u) we may define an instantaneous structure factor,* F_hkl(τ[x, u]), describing the scattering of P(u) at x, which depends only on the time interval τ[x, u] between the photoactivation of the crystal at x and the arrival of P(u) at x. If τ[x, u] ≤ 0, then F_hkl(τ[x, u]) = F_hkl⁰, the structure factors for the native state of the crystal, because the laser pulse had not reached x when scattering occurred.

An algebraic expression for τ[x, u] follows from geometrical arguments. At any moment F_hkl(τ[x, u]) is retarded by Δτ = x sin α/c relative to F_hkl(τ[0, u]) because of the time delay between the arrival of the laser pulse at the origin 0 and its arrival at x. Furthermore, τ[x, u] is smaller than τ[x, 0] by u/c because, if u > 0, P(u) arrives at x before P(0). If τ₀ denotes the time interval between the arrival of the laser pulse and P(0) at 0 we find

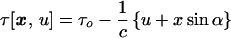1

The observed intensity I_hkl(x′), to within a constant scaling factor, consists of the sum of all x-ray scattering contributions from structures present throughout the pulse duration weighted by the x-ray pulse intensity†

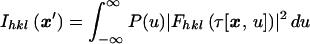2

In summing intensity contributions as the square of the structure factor amplitudes we considered only single scattering events within the sample. All crystals of macromolecules and most small molecule crystals satisfy this condition with x-rays (ideally imperfect crystals).

If the x-ray pulse is a step function of duration ΔT,

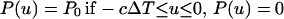3

otherwise, Eq. 2 becomes

4

Differentiating with respect to x′ (because the map x → x′ is one-to-one onto) produces

5

Unlike in the native crystal state, a lack of global homogeneity arising from noninstantaneous excitation of the crystal produces gradients in the observed intensity. These gradients are proportional to the difference between the squared magnitudes of the molecular structure factors at the beginning and the end of the x-ray pulse, scaled by sin α. Structural transitions on this time scale include the formation of excited states, changes in resonance frequencies, bond breaking, isomerizations, and motions of atoms and groups in the order of a few Ångströms. Coherent reaction dynamics have been observed up to a few picoseconds following femtosecond photoexcitation (e.g., see ref. 23). Changes in magnitude of observed intensities across a single topogram depend on the size of the molecule and on the degree of the structural rearrangement. In recent diffraction studies on carbonmonoxy-myoglobin (11, 12), intensity changes of ≈5% were recorded in Laue diffraction spots immediately following partial photoexcitation by a nanosecond laser pulse. In CBT experiments, intensity gradients across a topogram are maximized when the x-ray pulse length is the order of the crystal diameter. Longer exposures dilute observable intensity gradients, and repeated exposures may be required to build up sufficient statistics to observe small changes in structure factor amplitudes.

Eq. 5 has an intuitive interpretation, which is illustrated in Fig. 3. With τ₀ = 0‡ the magnitude of F_hkl(ΔT − x/c sin α) relative to F_hkl⁰ may be determined experimentally by measuring correlated intensity gradients across all crystal images. If F_hkl⁰ is known, the phase factors for F_hkl(τ) may be calculated (e.g., by using difference Fourier techniques). An exciting feature of this technique is that, in principle, the temporal resolution is limited only by the spatial resolution of the detector. For instance, by using a bare charge-coupled device for x-ray detection, a spatial resolution ∼3 μm can be achieved, with a corresponding potential temporal resolution ∼10 fs.

Figure 3.

Schematic illustration of the temporal information contained within a scattered x-ray pulse when τ₀ = 0 and α = 90°. Different photons within the x-ray pulse scatter from the crystal at different time delays following (or preceding) reaction initiation. As such, the intensities recorded at x′₁ and x′₂ (given by integration over the dashed vertical lines) consist of scattering contributions from several temporally distinct species. Taking the difference between I(x′₂) and I(x′₁) in the limit as x′₂ → x′₁, we observe that gradients in the recorded intensities are proportional to the difference between the native crystal scattering intensity and the scattering intensity of the species present at τ = ΔT − x/c, Eq. 5.

Physical Crystal

The above model has value in so far as it provides an intuitive illustration of how near-femtosecond time resolution may be achieved using x-ray pulses of picosecond or longer duration. A physical crystal, however, does not have negligible thickness, 100% excitation of a crystal by a femtosecond laser pulse is problematic, and any picosecond x-ray pulse will not be a spatially homogeneous step function. We therefore reconsidered the above experimental situation from the perspective of a physical crystal of thickness Δz and an inhomogeneous x-ray pulse propagating through the crystal at velocity v_P parallel to e_z, where |v_P| = c/n_p and n_P is the x-ray refractive index of the crystal.

When focusing extremely intense laser pulses onto a physical crystal, one risks stimulating unwanted reaction pathways (multiphoton processes) or creating a plasma on the crystal surface.§ For optimum crystal excitation the laser pulse should be tuned to overlap the molecular absorption peak of interest. Due to absorption this will result in inhomogeneous concentrations of excited species that may be modeled by an instantaneous effective structure factor:

6

a linear sum of the structure factors for the excited and unexcited species weighted by η(x), the average density of the excited molecules at x. Inhomogeneous absorption of electromagnetic energy will cause thermal shock waves to propagate through the crystal at the speed of sound, thereby increasing crystal mosaicity. An increase in mosaicity has been observed through streaking out Laue diffraction spots on a time scale of microseconds (12) to seconds (30), but can be neglected in this analysis as observable distortion of the crystal lattice does not occur during the picosecond time domain during which all data are collected. By the same reasoning the radiation limit (31), which restricts the x-ray exposure intensity any crystal can withstand under usual circumstances, may be overstepped on an ultra-short time scale.

In the vicinity of an optical resonance the refractive index of the crystal is strongly frequency-dependent, causing a femtosecond light pulse (not monochromatic through the Heisenberg uncertainty principle) to broaden as it propagates through the crystal, a phenomenon encountered in near-femtosecond spectroscopy experiments (19–26) that is compensated for optically by focusing the minimum pulse duration at the center of the sample. Hence, dispersion of the laser pulse should not significantly limit the potential temporal resolution in x-ray diffraction experiments. We therefore treat the laser pulse as if it were propagating with constant velocity v_l, with |v_l| = c/n_l, n_l being the refractive index of the crystal at maximum absorption. The orientation of v_l relative to the incident beam is obtained by applying Snell’s law at the crystal boundary.

As previously, τ(x, u) is calculated geometrically. At x the evolution of excited species is retarded by Δτ= x ⋅ v_l/|v_l|² relative to excited species at the origin because this time is required for the laser pulse to propagate from 0 to x. Similarly, it takes an interval Δt = x ⋅ v_p/|v_P|² for the x-ray planes of constant u to reach x following their arrival at 0. Thus we find

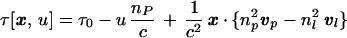7

which recovers Eq. 1 in the limit of both n_P and n_l → 1 and x → x₀ ≡ (x, y, 0).

Image coordinates, illustrated in Fig. 4, are now defined by the projection of x₀ through the crystal parallel to x-rays scattered from each Miller plane (hkl), then refracted at the second crystal boundary and eventually intercepting the image plate at x′_hkl ≡ (x′, y′)_hkl. Therefore, I_hkl(x′) is composed of partial scatterings from all points lying within the crystal along the line

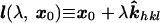8

where k̂_hkl is the unit normal parallel to the x-rays scattered from the Miller plane (hkl) of the native crystal. This expression represents an idealization of any experimental situation, because divergence of the x-ray beam and mosaicity inherent within the crystal itself will lead to partial blurring of the recorded topograms. Laue diffraction studies will be particularly sensitive to these considerations. Nevertheless, because photoexcitation does not produce additional mosaicity on a picosecond time scale, one will proceed by recording a topogram of the crystal native state prior to initiating time-resolved diffraction studies. Topographic images of protein crystals have been recorded (32), providing experimental proof that beam divergence and mosaicity do not fundamentally limit this method even with these crystals. Generalizing Eq. 2 to include a spatial integration over l(λ, x₀) we obtain

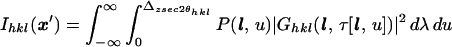9

where the end points λ = 0, Δz sec 2θ_hkl correspond to where l ≡ l(λ, x₀) enters and leaves the crystal.

Figure 4.

X-rays scattered from a three-dimensional crystal are projected onto a two-dimensional image. As such, one must integrate over the line l(λ) (in bold) when calculating the intensity recorded at x′_hkl, Eq. 9.

In recovering the desired temporal information from the recorded intensities (|F_hkl(τ)| over 0 ≤ τ ≤ sin α ps) spatial variations in P(x, u) pose no problem in principle. The average concentration of excited species, η(x), could initially be calculated from the known laser intensity and cross-section (33). From this starting point |F_hkl(τ)| could be recovered by deconvolution of Eq. 9. Structural refinement would proceed by treating each electron density ρ(x, τ) as a distribution in its own right, with appropriate physical constraints demanded by its position in the temporal evolution of the photoactivated molecule. In cases where multiple exposures are needed to collect a complete data set (34), a new crystal may be required for each exposure.

Future Light Sources

It is anticipated that future developments in accelerator technology will produce extremely intense hard x-ray sources with a pulse duration ∼100 fs, which will be achievable by using linear accelerators operating in sase mode (35–36). Our above analysis, however, demonstrates that images scattered from Miller planes for which

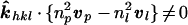10

will necessarily record scattering contributions from several time-distinct excited species because, from Eq. 7, τ[x, u] is not constant along the integration over the crystal thickness. Even when v_P is parallel to ∥v_l, Eq. 10 does not vanish because n_p ≠ n_l, and consequently, there is little advantage in generating x-ray pulses shorter than (n_l − n_P) × (crystal thickness)/c (∼200 fs for samples ∼100 μm thick). This condition sets a temporal resolution barrier on standard parallel beam techniques with crystals, whereas CBT does not suffer this limitation.

Slower Reaction Initiation Techniques

Significantly, slower diffusion-triggered x-ray studies on enzyme reactions in macromolecular crystals (37), which constitute the overwhelming majority of time-resolved diffraction experiments with macromolecules at present (most do not utilize photons in their biological function), may also apply the principle of CBT. If the diffusion wave is orientated perpendicular to the x-ray pulse, structural information on several reaction intermediates will be contained within a single x-ray topography exposure. Because this technique relaxes the requirement that an overall homogeneous state be obtained throughout the crystal, currently the limiting factor in diffusion-initiated studies, we anticipate that certain improvements in temporal resolution may be possible this way.

ABBREVIATION

CBT

crossed-beam topography. E-mail: neutze@xray.bmc.uu.se and janos@xray.bmc.uu.se