Radiation dose reconstruction from L-band in vivo EPR spectroscopy of intact teeth: Comparison of methods

Abstract

In vivo EPR tooth dosimetry is a more challenging problem than in vitro EPR dosimetry because of several potential additional sources of variation associated with measurements that are made in the mouth of a living subject. For in vivo measurement a lower RF frequency is used and, unlike in the in vitro studies, the tooth cannot be processed to optimize the amount and configuration of the enamel that is measured. Additional factors involved with in vivo measurements include the reproducibility of positioning the resonator on the surface of the tooth in the mouth, irregular tooth geometry, and the possible influence of environmental noise. Consequently, in addition to using the theoretical and empirical models developed for analyzing data from measurements of teeth in vitro, other unconventional and more robust methods of dose reconstruction may be needed. The experimental parameter of interest is the peak-to-peak amplitude of the spectrum, which is correlated to the radiation dose through a calibration curve to derive the reconstructed dose. In this study we describe and compare the results from seven types of computations to measure the peak-to-peak amplitude for estimation of the radiation induced signal. The data utilized were from three sets of in vivo measurements of irradiated teeth. Six different teeth with different doses were placed in the mouth of a volunteer in situ and measurements of each tooth were carried out on three different days. The standard error of dose prediction (SEP) is used as a figure of merit for quantifying precision of the reconstruction. We found that many of the methods gave fairly similar results, with the best error of prediction resulting from a computation based on a Lorentzian line model whose center field corresponds to the known parameter of the radiation-induced EPR spectra of teeth, with corrections from a standard sample that was measured as part of the data acquisition scheme. When the results from the three days of measurement were pooled, the SEP decreased dramatically, which suggests that one of the principal sources of variation in the data is the ability to precisely standardize the measurements conditions within the mouth. There are very plausible ways to accomplish improvements in the existing procedures.

1 Introduction

Electron paramagnetic resonance (EPR) tooth dosimetry is a very promising method for after-the-fact determination of radiation dose. Initially such measurements were done with isolated teeth, usually obtained after natural loss of teeth, but in at least one case the teeth were actively extracted (Rossi, et al. 2000). Most of the work has been done using X-band (∼9 GHz) EPR in vitro with a technique that involves mechanical isolation of the enamel of the tooth (enamel is the site of most of the radiation-induced EPR signals in irradiated teeth). Recent references are by Tieliwuhan, et al. (2006), Wieser et al. (2006), and Skvortsov et al. (2006). In vitro measurements using lower frequency (1.2 GHz, or L-Band) EPR also have been reported using intact teeth (Zdravkova et al. 2003).

The ability to make measurements in the mouth without the need to extract teeth is very attractive (in vivo tooth dosimetry), but this is a more challenging task. There are many factors that can affect measurements that are made in the mouth of a patient and it is necessary to use less sensitive lower frequency EPR spectrometers (typically 1.2 GHz). In addition to the background/native signal that also must be considered with measurements in vitro, several other sources of variation emerge: the challenge of exact positioning the resonator in the mouth; the effects of adjacent tissues that non-resonantly attenuate the microwave frequencies used for the measurement; differences in the size of teeth; irregular geometry of the tooth surface; and the constraints on shielding from unwanted microwave sources when a subject needs to be positioned within the magnet. These complications require that we modify our approaches to dose reconstruction and need to apply spectral models that are sufficient for fitting the radiation-induced EPR spectra for in vivo data. The goal of the present communication is to compare several methods of the dose reconstruction that we are exploring for analyzing data obtained in vivo. We use the standard error of prediction as the figure of merit to compare the methods. This research is ongoing and the methods are under continuous attempts to improve them, but the results that already are obtained provide some very useful insights and indicate that the challenges are likely to be overcome.

2 Materials and methods

Six previously extracted teeth were irradiated with 0, 2, 5, 10, 15, and 30 Gy. These teeth we placed in a gap in the dentition in the mouth of a volunteer and sets of EPR spectra were acquired on three days. All measurements were done with a clinical 1.2 GHz spectrometer at the EPR center at Dartmouth (Swartz et al, 2006) with 1024 points recorded for each EPR spectrum. On each day, spectra for all six teeth were acquired using the same acquisition parameters. Typically these were: scan range 25 Gauss (10G = 1 mT), scan time 3 s, 30 to 90 scans that were averaged (more scans were used for low dose spectra), modulation amplitude 4 Gauss, modulation frequency 24.5 kHz, incident radio frequency (RF) power 100 mW. The N = 6 × 3 = 18 EPR spectra are shown in Fig. 1. The spectra were adjusted for tooth-size, by measurements of the surface of the teeth in two orthogonal directions (D₁ and D₂) and each original signal was divided by (D₁D₂)/100. This provides the amplitude of the EPR signal per 100 square millimeters of the surface of the tooth.

Figure 1.

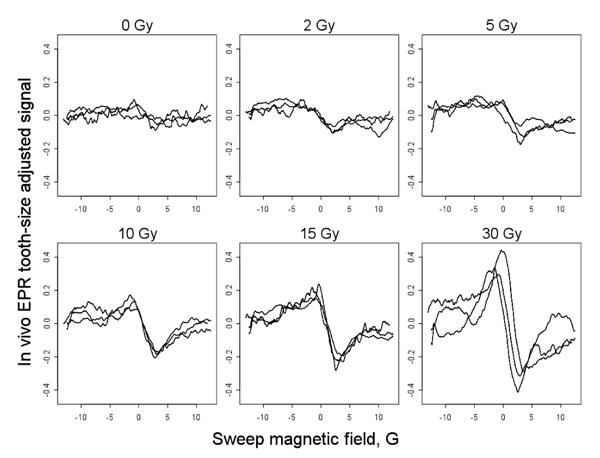
Eighteen tooth-size adjusted EPR spectra in vivo with six teeth that received 0, 2, 5, 10, 15 and 30 Gy radiation. The irradiated teeth were inserted into a gap in the dentition of a volunteer. Measurements were repeated on three days with identical instrumental settings, as described in the text.

The reconstructed dose is derived from a calibration curve that is traditionally obtained as a linear regression of the peak-to-peak amplitude (P2P) on the radiation dose given. The method of abscissa prediction using regression analysis is called an inverse regression (Draper and Smith, 1998). To compare various methods of the dose reconstruction a precision measure should be used. We used an intuitively appealing standard error of prediction (SEP) as the measure of precision computed as

$$\text{SEP}=\sqrt{\frac{1}{N}\sum _{i=1}^N{({\widehat{D}}_i-D_i)}^2},$$

where N is the number of spectra, D_i is the dose given and ${\widehat{D}}_i$ is the predicted dose in the ith measurement. This parameter of merit for dose reconstruction has been useful for linear and nonlinear calibration curves and corresponds to the formula of the standard error widely accepted in statistics (Snedecor and Cochran, 1989). Geometrically, the standard error of the dose prediction is an average of horizontal distances of the data points to the calibrations curve. SEP gives rise to a quick computation of the confidence interval: the probability that dose is within interval $\left({\widehat{D}}_i-2\times \text{SEP},{\widehat{D}}_i+2\times \text{SEP}\right)$ is 0.95 (the rule of two sigmas). If $\widehat{\sigma }$ is an estimated standard error of the linear regression in amplitude on dose given (the error of the amplitude), SEP is approximately equal to $\widehat{\sigma }$ divided by the slope of the regression. In other words, $\widehat{\sigma }$ is an error on the y-axis and SEP is the error on the x-axis computed from the former by scaling with respect to the slope of the calibration curve. Consequently, with the same error of the amplitude, SEP is smaller for a steeper calibration curve.

We employed seven different computational methods and obtained the figure of merit for each method using all eighteen spectra from Fig. 1. The nomenclature of the methods considered in the present paper are shown in Table 1. Most of the methods have a modification parameter, such as the magnetic field range over which the fitting is carried out, and/or the value of the fixed linewidth. These parameters are noted in the abbreviations and the parameters are separated by the character “/”.

Table 1.

Methods nomenclature for in vivo EPR radiation dose prediction

#	Abbreviation	Full Name/Description	Parameters
1	EMP2P/F	Empirical peak-to-peak, Max–Min	Field range (F)
2	SMP2P/F/W	Peak-to-peak after smoothing	Smoothing window range (W)
3	L/F	Lorentzian fit with independently variable linewidth and centers	Field range (F)
4	L/F/LWC	Lorentzian with fixed LW and variable center	Field range (F)
5	G3	Three Gaussian components with fixed linewidth and centers
6	LLiPc	Lorentzian fit with independently variable linewidth and fixed center determined using LiPc standard
7	LLiPc/LW	Lorentzian fit with fixed linewidth and fixed center determined using LiPc standard	Fixed linewidth (LW)

With the empirical peak-to-peak method (EMP2P), the amplitude of the EPR signal is computed as the difference between the maximum and minimum value of the spectrum. For a small dose, this amplitude may be overwhelmed by noise at the ends of the spectra, so it can be useful to restrict the field interval that is utilized in the spectral fitting calculation. We specify the value of the modification parameter after the name. For example, the abbreviation EMP2P/F5 means that the empirical amplitude is computed for the 2×5 = 10 gauss interval corresponding to ±5 gauss of the expected position of the center of the radiation-induced spectrum.

The SMP2P method is the same as EMP2P/F but the amplitude estimation was performed after the signal was smoothed. We use a simple running-window smoothing technique (also known as moving average) with the width W. Precisely, if W is an even integer and y_i is the original spectrum, the smoothed signal is computed as ${\widehat{y}}_i={\sum }_{j=-W/2}^{W/2}{y}_{i+j}/\left(W+1\right)$.

In the next family of methods, a Lorentzian curve is used to fit the spectrum and estimate the amplitude of a radiation induced signal. As above, to eliminate noisy ends we may use the signal in the range ±F. To a reasonable approximation, the linewidth (LW) of the Lorentzian curve should be the same for all spectra and equal to that of highly irradiated teeth in which the radiation-induced signal dominates the spectrum. L/F/LWC method fits Lorentzian curve to all spectra with a common linewidth. We optimize fitting for fixed LW value and field range to obtain the minimal SEP.

The three Gaussian component model is similar to models used in in vitro studies mentioned in the Introduction. One component reflects the native signal and two components describe the radiation induced signals (RIS); the maximal amplitude of the RIS is correlated with the radiation dose through the calibration curve. This model also contains a linear slope to account for a possible baseline shift.

Finally, to improve the reconstruction at low doses one may carry out additional measurements with a strong standard signal and use these measurements in fitting tooth data. We used a lithium phthalocyanine (LiPc) crystal, sealed under vacuum, that was reproducibly placed in the resonator and measured its spectrum prior to the measurement of each tooth with the same instrumental settings. Under these conditions the modulation amplitude will affect the observed linewidth of the LiPc, so a spectral model that incorporates these effects was applied (Robinson et al., 1999). Several parameters from the LiPc spectrum may be used for fitting the tooth data. In the present work, we use the center field parameter, so the tooth spectra were fitted with a fixed center, as determined using the LiPc. Two versions were tested: with LW varying from tooth to tooth (LLiPc) and the LW fixed (LLiPc/LW).

3 Results

The results for various methods of the dose reconstruction are presented in Table 2. While these results are quite instructive, it should be noted that with the improvements in techniques that are expected in the near future, the magnitude of the observed SEPs and the differences among techniques are likely to change. The acquisition parameters, especially the length of acquisition were selected to reflect times that would be desired when the measurements would be made in the field—in retrospect at this state of development of the in vivo techniques these times may have been suboptimal for obtaining data to evaluate the different methods.

Table 2.

Standard error of prediction (SEP) for different methods with optimized parameters

Method	Standard error of the dose prediction
Empirical amplitude	EMP2P/F9=2.65 Gy	SMP2P/F12/W110=2.13 Gy
Lorentzian fit	L/F8=2.08 Gy	L/F6/W2.2=1.94 Gy
Three-component model	G3=3.24 Gy
Combination with LiPc data	LLiPc=1.84 Gy	LLiPc/LW1.9=2.19 Gy

We have optimized methods using modification parameters, so only the minimal standard error with optimized parameters is shown. For example, if 110 points on the EPR spectrum are smoothed there is no need to cut the ends (optimal F is 12 G, almost the entire field range), which results in SEP=213 (method SMP2P/F12/W110). Obtaining the peak-to-peak amplitude from fitting the data to a Lorentzian curve improved the precision. In particular, the minimum SEP was achieved when data were restricted to abscissa values within the interval ±6 Gauss and the linewidth for the tooth was fixed at LW = 2.2 Gauss.

The three Gaussian component model, similar to models used for in vitro data, did not give satisfactory results. We attribute this to the additional sources of variation with EPR measurements in vivo resulting in noise that makes discrimination of the relatively small native signal not feasible, under specified acquisition conditions. Also note that the splitting between the centers of the various components, which reflect different g-values, collapse when a lower RF frequency is used.

The dose-response relationship with the LiPc fit is shown in Fig. 2. Different symbols indicate the EPR measurements on different days. SE P2P is the standard error of variation of P2P estimates around the calibration line. From ANOVA theory (Demidenko, 2004), the total P2P variance can be decomposed as the sum of the regression model variance and the set-to-set variance (in our case the day-to-day variance since each set of measurements was done on one particular day). We conclude that the most variation comes from a set-to-set variation, not a variation from the Lorentzian fit. The SE P2P on the y-axis translates into a standard error of the dose prediction 1.84 Gy, the variation on the x-axis.

Figure 2.

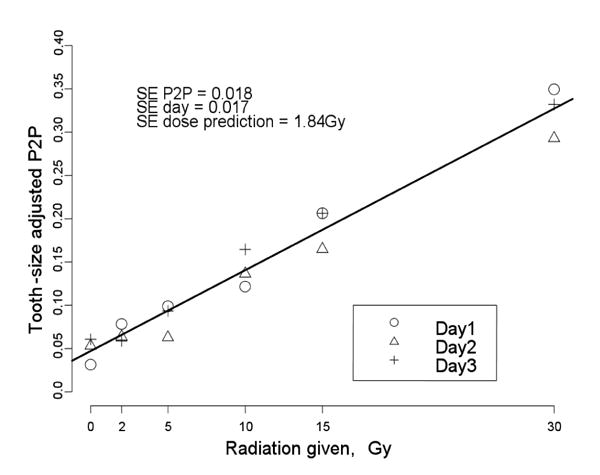
The dose-response relationship for eighteen in situ EPR measurements using the tooth-size adjusted peak-to-peak amplitude in combination with LiPc data fitting (method LLiPc, Table 1).

Since the major variation comes from the variation among the three sets of measurements, it is beneficial to combine the data from all of the measurements for each dose point and plot the data P2P as shown in Fig. 3.

Figure 3.

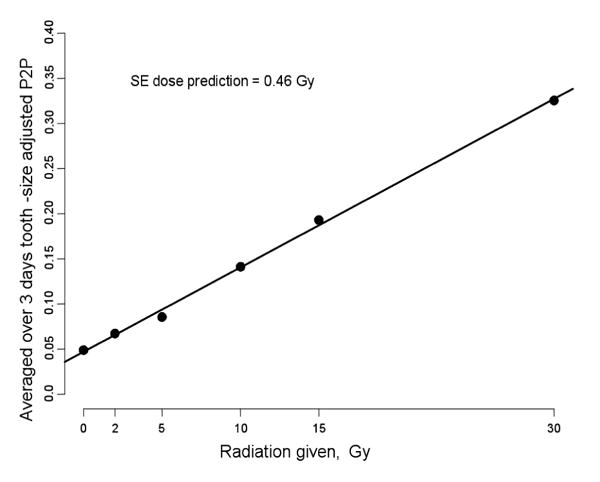
The averaged over three days peak-to-peak amplitude as a function of the radiation dose.

This is a very interesting and important result. It suggests that even with the present state of the technique, with repeated measurements the SEP could come into a range that would be quite sufficient for the desired use of the technique. Part of the observed improvement from combining the results should be due simply by increasing the number of measurements that were averaged (which would, of course, require that the time of acquisition be increased by a factor of three). The improvement from this source should be $\sqrt{n}$. The error from irreproducibility of positioning, on the other hand, could be addressed by repositioning the resonator within one series of measurements. Additional sources of error that are likely to have been compensated for by combining the three sets of measurements may be related to variations in the technique—especially the fitting of the resonator on the tooth (both the relationship of the loop to the depth of the tooth and its angle with respect to the tooth and the principal magnetic field. There also may have been important variations from the position of lossy tissues (which are constrained by pads in the mouth) and the position with respect to the modulation coils (which could be determined by the measurement of the line width of the LiPc standard). The results summarized in Fig. 3 are insufficient to conclude that we could make measurements with this precision by using 3 independent measurements, but they do indicate the potential for some near term improvements that may be achievable by improvements in the ability to position the resonator accurately and by extending the acquisition time (e.g. to 15 minutes).

4 Conclusions

In summary, in vivo EPR tooth dosimetry requires new methods of dose prediction and modeling. These results provide very useful insights into ways to improve the technique for in vivo after-the-fact measurements of radiation dose. One way to restrict variation is to carry out additional spectral measurements, such as those with LiPc. Another is to either improve the reproducibility of the placement of the resonator on the teeth or to average out variations by obtaining data with several placements. Although these approaches increase the time of data acquisition and adds some complexity to the measurement it clearly offers benefits for short term improvement until more fundamental improvements eliminate the need for these measures.