Oscillations in multi-stable monotone systems with slowly varying feedback

Abstract

The study of dynamics of gene regulatory networks is of increasing interest in systems biology. A useful approach to the study of these complex systems is to view them as decomposed into feedback loops around open loop monotone systems. Key features of the dynamics of the original system are then deduced from the input-output characteristics of the open loop system and the sign of the feedback. This paper extends these results, showing how to use the same framework of input-output systems in order to prove existence of oscillations, if the slowly varying strength of the feedback depends on the state of the system.

1 Introduction

One of the most important challenges facing biologists and mathematicians in the postgenomic era is to understand how the behaviors of the cells arise from properties of complex signalling networks of proteins.

Networks that support bistable ([27, 29, 18, 6, 7, 30, 28]) and periodic ([14]) behaviors have attracted much attention in recent years. Bistable systems are thought to be involved in the generation of a switch-like biochemical responses ([18, 6]) as well as establishment of cell cycle oscillations and mutually exclusive cell cycle phases ([30, 28]).

In the recent work [2], Angeli and the second author developed a method that allows the detection of bistability in certain networks with feedback by studying the properties of the open loop system. The theory applies to systems that can be represented as a positive feedback loop around a monotone system with well-defined steady-state responses to constant inputs. The follow-up paper [5] described how this approach can be fruitfully applied in interesting biological situations, and [15] developed extensions of the basic framework. In principle, this approach applies to networks of arbitrary complexity. See [33] for a survey-level discussion of the topic.

Biologically, relaxation oscillators appear to underlie many important cell processes, such as the early embryonic cell cycle in frog eggs (Xenopus oocytes), cf. [30, 28]. Mathematically, a typical way in which relaxation (or “hysteresis-driven”) oscillators arise is through the interplay of a slowly acting parameter adaptation law and the dynamics of a bistable system. Let us briefly review the (well-known) intuitive picture.

Suppose that a certain one-dimensional system ẋ = f_λ(x) has a bifurcation diagram that looks like the curve shown in Figure 1, where the horizontal axis indicates the parameter λ, with solid arrows showing, for each value of the parameter, in which direction the state x will move. Note the bistable region in the middle range of parameter space, where two stable (and one unstable) states x exist for each parameter value, such as for instance for λ = q.

Figure 1.

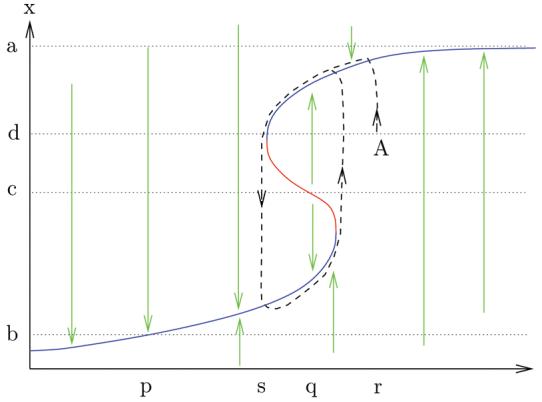
Relaxation from bistability

For example, still referring to Figure 1, if the parameter value is λ = p, the point x = a will converge towards x = b as the time t → ∞; when the parameter is λ = q, the point x = c is unstable; and so forth. Now suppose that the parameter itself is a function of the state x, with the “negative feedback” rule that the parameter will slowly decrease when x is larger than x = c but will slowly increase when x < c. Let's now analyze, for this feedback situation, what happens when the initial state is x = d and the initial parameter is λ = r (point labelled “A” in the (λ, x) plane). The state x will move toward the positive direction, approaching an equilibrium (dashed curve). However, the parameter will slowly decrease, so that the equilibrium being approached keeps decreasing. In effect, the trajectory in the (λ, x) plane will tend to follow the bifurcation curve, until a point at which there are no stable equilibria nearby (parameter value “s”), A fast transition will occur towards the bottom branch. Now the state is less than c, so the feedback rule forces the parameter to increase, rather than decrease. There results an oscillation as shown by the dashed curve. For systems in dimension 1, a rigorous proof that a periodic orbit indeed exists for the joint (λ, x) dynamics can be based upon phase-plane techniques via the Poincaré-Bendixon Theorem, or using singular perturbation tools.

In essence, the techniques from [2] allow one to analyze the dynamics of ẋ = f_λ(x), for states x of arbitrary dimension, using phase-plane-like techniques, where instead of the (λ, x) plane of Figure 1 one uses the (λ, u) space, and u is an “input” associated to the full system. In the case when u is scalar, the (λ, u) space is a plane and the the analysis required is as simple as for Figure 1. Bifurcation diagrams such as the one shown in Figure 1 are used to predict the behavior of the whole system.

This suggests that a slow feedback adaptation, acting entirely analogously to the description for one-dimensional systems, should again result in periodic orbits in this far more general situation. This fact would represent another instance of the principle that monotone input/output systems, as components of larger systems, behave in some sense like one-dimensional subsystems. The purpose of this paper is to provide a proof of this fact. Our proof is based upon a combination of i/o monotone systems theory and Conley Index theory. We also illustrate our results with the analysis of a model of the mitogen-activated protein kinase (MAPK) cascade in eukaryotic cells [18, 6, 7, 5]. We show that if the strength of the feedback from p42 MAPK to Mos depends on the state of the system, then the cascade is able to exhibit periodic behavior.

We observe that a totally different mechanism for the emergence of oscillations in feedback loops around monotone systems arises from negative feedback. There is by now a rich set of results characterizing conditions for non-oscillation in such negative feedback loops, see e.g. [1, 16, 13, 17]. When these conditions fail, there often result oscillations, at least if delays are inserted in the feedback loop ([3]). This other mechanism is closely related to Hopf bifurcations, in contrast to the relaxation oscillation framework studied in the present paper.

2 Preliminaries

We consider a finite-dimensional controlled system

$$\stackrel{.}{x}=f(x,u),y=h\left(x\right)$$ (1)

where u(t) ∈ U ⊆ R^m is the input, y(t) ∈ Y ⊆ R^m is the output, f, h are at least C², and the state space variable x(t) ∈ X ⊆ Rⁿ. We assume that U, Y, X lie in the closure of their interiors. We assume that the input space and the output space have the same dimension, because we will investigate also a closed loop system, where, in addition to (1), we set

$$u=\lambda y.$$ (2)

. Here λ is a scalar parameter, where in case n > 1, λ is understood to be a matrix λI. In order for (2) to be well defined we assume that λ ∈ L a real interval and that ⋃_λ∈L λY ⊂ U.

Our main motivation is the study of gene regulatory networks [5, 8], where often systems of the form (1),(2) have an additional structure of monotone systems. We now recall necessary definitions and for more background we refer the reader to [1, 31].

A cone is a closed, convex set with nonempty interior and with αK ⊂ K for α ∈ R⁺ and K ∩ (−K) = {0}. If a space Z is endowed with a cone K_z we will write

$$x\underset{-}{\succ }y\text{if},\text{and only if},x-y\in K_z\text{and}x\succ y\text{if},\text{and only if},x-y\in \mathrm{int}{K}_z.$$

We assume that the input space U, the state space X and the output space Y each has a distinguished cone K_u ∈ U, K_x ∈ X and K_y ∈ Y.

We say the controlled dynamical system (1) is a monotone system with outputs if the following two implications hold

$$\begin{array}{cc}\hfill u_1\left(t\right)\underset{-}{\succ }{u}_2\left(t\right)\forall t,x_1\underset{-}{\succ }{x}_2& \Rightarrow \phi (t,x_1,u_1)\underset{-}{\succ }\phi (t,x_2,u_2)\hfill \\ \hfill x_1\underset{-}{\succ }{x}_2& \Rightarrow h\left(x_1\right)\underset{-}{\succ }h\left(x_2\right)\hfill \end{array}$$

where φ is the flow generated by (1), and the ≽ is with respect to appropriate cones. We say that the controlled dynamical system is strongly monotone if it is monotone and

$$u_1\left(t\right)\underset{-}{\succ }{u}_2\left(t\right)\forall t,x_1\underset{-}{\succ }{x}_2\Rightarrow \phi (t,x_1,u_1)\succ \phi (t,x_2,u_2)$$

Infinitesimal characterizations of monotonicity, which are more suitable for verification, can be found in [1] and [31]. We say that two points x, y ∈ Z are order related if either x ≻ y or y ≻ x with respect to cone K_z.

The most important set of questions in this context concerns the predictability of the closed loop dynamics

$$\stackrel{.}{x}=f(x,\lambda h\left(x\right))$$

based on the properties of the open loop system (1),(2).

Definition 2.1

We say that the controlled dynamical system (1) is endowed with input-state characteristic k_x(u) : U → X if for each constant input u(t) ≡ ū there exists a (necessary unique) globally asymptotically stable equilibrium k_x(ū) of system (1). We also define the input-output characteristic as

$$k\left(u\right)≔h\left(k_x\left(u\right)\right),k:U\to U.$$

.

Lemma 2.2

[1, Proposition V.5] The input-state characteristic k_x(u) is a continuous function, which is monotone i.e u ≽K_u v implies k_x(u) ≽K_x k_x(v).

3 Statement of the main result

The goal of this paper is to prove the existence of a periodic orbit in a closed loop system with a variable feedback strength

$$\begin{array}{cc}\hfill \stackrel{.}{x}& =f(x,\lambda h\left(x\right)),\hfill \\ \hfill \stackrel{.}{\lambda }& =-∊q(x,\lambda )\hfill \end{array}$$ (3)

where q(x, λ) : Rⁿ × R → R is a suitable function that will be specified later. The function q(x, λ) can always be constructed so that q(x, 0) = 0 which implies λ(t) ≥ 0 for all t > 0 if λ(0) ≥ 0. This is often desirable in biological applications.

The system (3) has two time scales. Setting ∊ = 0 we obtain a fast subsystem

$$\stackrel{.}{x}=f(x,\lambda h\left(x\right))$$ (4)

where λ is a parameter. We will explore the correspondence between dynamics of the parameterized system (4) and the parameterized system

$$\stackrel{.}{u}=k\left(u\right)-\frac{1}{\lambda }u.$$ (5)

We are ready to state our main Theorem. Our approach is especially useful when m < < n and thus the dimension of the input and the output space are much smaller then that of the state space X. Thus the dimensionality of the system (5) is much smaller then that of (4). Therefore we impose all technical assumptions of the next Theorem 3.1 on system (5), but the conclusions are drawn about the system (3). In the applications to gene regulation, the input-output function k(u), as well as the strength λ of the feedback, are often experimentally accessible and controllable.

Theorem 3.1

Assume that the system (1) is monotone and is endowed with an input-state characteristic k_x(u). Further assume that

• for all λ the system (4) is strongly monotone and its solutions are bounded;

• there are values 0 < λ_min < λ₁ < λ₂ < λ_max in L such that (5) has one stable equilibrium for λ = λ_min, two stable and one unstable equilibrium for λ ∈ (λ₁, λ₂) and one stable equilibrium for λ = λ_max;

• for each λ ∈ [λ_min, λ_max] these equilibria are order-related with respect to the cone K_u;

• the set of equilibria is connected.

Then, for a generic function f, there is a function q(x, λ) with q(x, 0) = 0, and an ∊₀, such that for all ε with 0 < ∊ ≤ ∊₀ there is a periodic orbit of the system (3).

If, in addition, the control is scalar (m = 1) then the function q(x, λ) can be constructed as

$$q(x,\lambda )=\lambda (h\left(x\right)-h\left(x_0\right))=u-u_0.$$

where (λ₀, u₀) an unstable equilibrium of (5) and x₀ = k_x(u₀).

Remark 3.2

Notice that the Theorem is not necessarily true for all nonlinearities f, but only for an open and dense subset of C² functions R^n+m → Rⁿ in the compact-open topology. In fact, we need the following generic properties in the proof:

1. the input-state characteristic k_x is not constant on any open set in R^m;

2. the limit-point bifurcations of equilibria in the fast subsystem (4) with the bifurcation parameter λ are generic;

3. homoclinic orbits, if they exist, are isolated;

4. solutions of (4) with λ = λ₁ and λ = λ₂ on the unstable manifold of the semi-stable equilibrium at the limit-point bifurcation converge to the set of equilibria. Recall that by [31, Theorem 4.3] in a strongly monotone system for a generic x ∈ Rⁿ, ω(x) is contained in the set of equilibria. Therefore this assumption is generic in the class of functions satisfying assumption 1 of Theorem 3.1.

Remark 3.3

We will show below that the assumptions of Theorem 3.1 imply that there is an S-shaped set of equilibria of (5) in U × R. We will call the two branches that contain stable equilibria upper V_top and lower branch V_bot. The assumption that the equilibria are order related is used to show that there are corresponding disjoint equilibria branches of (4) in X × R. Since the branches are disjoint, we construct the function q(x, λ) : X × R in such a way that the upper branch of equilibria belongs to the set where q(x, λ) > 0 and the lower branch of equilibria to the set where q(x, λ) < 0.

We now outline the proof of the main result. In section 4 we describe what the assumptions of Theorem 3.1 imposed on the system (5) imply for the system (4). In section 5 we formulate a simple two dimensional model which exhibits bistability and an S-shaped curve of equilibria. Using geometrical techniques we show that such system admits a positively invariant set in the shape of an annulus. Existence of such set together with a Poincaré section implies existence of a periodic orbit in the model problem in R². There is generalization of this result to higher dimensional spaces, based on the Conley index theory, due to McCord et. al. [26]. We verify the assumption of this result in a couple of steps. As the first step we identify a local 2-dimensional manifold in the neighborhood of the equilibria of the system (4) which can be mapped diffeomorphically to a neighborhood of the set of equilibria of the model problem. This map respects the direction of the flow.

The inverse image by this map takes the annular neighborhood of the equilibria of the model problem to a set, which can be extended to a neighborhood of the equilibria of (4). We show that, for all ∊ small enough, this neighborhood is an isolating neighborhood for system (3) and compute its Conley index. After verifying that the neighborhood admits a Poincaré section, we conclude that there is a periodic orbit in the neighborhood for all sufficiently small ∊.

4 Correspondence between (5) and (4)

Definition 4.1

A vector field u̇ = ϕ(λ, u), where ϕ : R × R → R, undergoes a generic limit point bifurcation at (λ*, u*) when

$$\varphi ({\lambda }^{\ast },u^{\ast })=0,\frac{d\varphi }{\mathit{du}}({\lambda }^{\ast },u^{\ast })=0,{\varphi }_{\mathit{uu}}\ne 0\text{and}{\varphi }_{\lambda }\ne 0.$$

Definition 4.2

A limit point bifurcation of vector fields in Rⁿ, generated by u̇ = g(λ, u), is generic, if the Lyapunov-Schmidt reduction ϕ(λ, u) to the one-dimensional kernel of dg_u(λ*, u*) satisfies Definition 4.1.

Lemma 4.3

Assume all assumptions of Theorem 3.1.

1. If the pair (λ*, u*) ∈ Λ × R^m is an equilibrium of (5) then (λ*, k_x(u*)) ∈ Λ × Rⁿ is an equilibrium (4). On the other hand, if (λ*, x*) ∈ Λ × Rⁿ is an equilibrium (4) then there exists u* such that x* = k_x(u*) and (λ*, u*) is an equilibrium of (5).

2. The system (5) undergoes a limit point bifurcation at λ = λ*, if and only if, (4) undergoes a limit point bifurcation at the same value of λ = λ*.

Proof.

1. The equilibria of (4) satisfy the equation f(x*, λ*h(x*)) = 0. This means that if we apply the constant input

   $$u^{\ast }≔{\lambda }^{\ast }h\left(x^{\ast }\right),$$ (6)

   , then the system (1) converges to the equilibrium x*. By the definition of the function k_x this means that x* = k_x(u*). Inserting the last expression into (6) we get u* = λh(k_x(u*)) = λk(u*), which implies that u* is an equilibrium of (5). This shows that if (λ*, x*) is an equilibrium of (4) then there exists u* with x* = k_x(u*) and (λ*, u*) is an equilibrium of (5).

   Now we assume that (λ*, u*) is an equilibrium of (5). Then u* = λh(k_x(u*)) by the definition of the function k. Set x* := k_x(u*). By definition of the I/S function k_x we have f(k_x(u), u) ≡ 0 and so f(k_x(u*), u*) = 0. Taking into account the definition of x*, this equation can be rewritten as f(x*, λh(x*)) = 0. This shows that (λ*, k_x(u*)) is an equilibrium of (4).

2. The normal form of the limit point bifurcation [19, Proposition 9.1] that we can parameterize the equilibrium set f(x*, λ*h(x*)) = 0 of (4) in a neighborhood of a limit point bifurcation by a C² function (0, 1) → Λ × R^n+m, t → (λ*(t), x*(t)). Since k_x is continuous by Lemma 2.2, it follows from 1. of this Lemma that there is a corresponding parameterization t → (λ*(t), u*(t)) of equilibria of (5) such that the equilibria of (4) are then parameterized by the induced parametrization t → (λ*(t), k_x(u*(t))). The limit point bifurcation happens at a parameter value t* that satisfies $\frac{d{\lambda }^{\ast }\left(t^{\ast }\right)}{\mathit{dt}}=0$. Since this condition holds at the same value t* for both parameterizations, the limit point bifurcations of (4) happens at the same values λ₁, λ₂ as limit point bifurcations of (5). Set

   $$g(\lambda ,u)≔k\left(u\right)-\frac{1}{\lambda }u.$$ (7)

   It follows from the assumptions of Theorem 3.1 that g undergoes a limit point bifurcation at λ₁ and at λ₂.

If (λ, u) is a regular zero of g, that is, g(λ, u) = 0 and dg_u(λ, u) is nonsingular, then by the Implicit Function Theorem there is a C² function u : (λ − ∊, λ + ∊) → R^m such that g(λ, u(λ)) = 0. It follows from the assumptions on genericity of f that the limit point bifurcation in the system (4) is generic at λ₁. Therefore the equilibria of (4), and, as a consequence of Lemma 4.3.2, the zero set of g(λ, u) = 0 as well, can be parameterized by a C² function (0, 1) → [λ₁, λ₁ + ∊) × R^m, t → (λ(t), u(t)). A similar function exists in the neighborhood (λ₂−∊, λ₂]×R^m of the limit point bifurcation at λ₂. Since the set of equilibria is connected we paste all local functions together to obtain a parameterization of the set of equilibria of (5) by a C² embedding

$$z:[0,1]\to \Lambda \times {\mathbf{R}}^m$$ (8)

which maps t → (λ(t), u(t)). There are two values t₂ < t₁ ∈ [0, 1] that correspond to limit point bifurcations at λ₂ and λ₁, respectively. That is, the lambda coordinate of z(t₂) is λ₂ and of z(t₁) is λ₁. Let V := z([0, 1]), V_bot := z([0, t₂]), V_mid := z([t₂, t₁]) and V_top := z([t₁, 1]) be the equilibria branches of (5) in Λ × R^m.

Definition 4.4

We define sets

$$M_{\ast }≔\{(\lambda ,k_x\left(u\right))\mid (\lambda ,u)\in V_{\ast }\}$$

where * = mid, top, bot. Observe that M_* ⊂ Λ × Rⁿ.

It follows from Lemma 4.3.1 that the set M consists of equilibria of the system (4). Next, we address the stability of these equilibria.

Lemma 4.5

Assume all assumptions of Theorem 3.1

1. If v ∈ R^m spans the kernel of Dg_u(λ*, u*) then Dk_xv ∈ Rⁿ spans the kernel of Df_x at (λ*, k_x(u*)).

2. (λ*, u*) is a stable equilibrium of (5) if, and only if, (λ*, k_x(u*)) is a stable equilibrium (4).

3. If for every λ ∈ Λ the equilibria of (5) are order related, then M_bot ∩ M_top = ∅.

Proof.

1. Along the curve z(t) of equilibria of (5) we have

   $$h\left(k_x\left(u\left(t\right)\right)\right)-\frac{1}{\lambda \left(t\right)}u\left(t\right)\equiv 0$$

   for all t ∈ [0, 1] and by the chain rule

   $$\mathit{Dh}(k_x\left(u\left(t\right)\right)\circ {\mathit{Dk}}_x\frac{\mathit{du}}{\mathit{dt}}+\frac{1}{{\lambda }^2\left(t\right)}\frac{d\lambda }{\mathit{dt}}u\left(t\right)-\frac{1}{\lambda \left(t\right)}\frac{\mathit{du}}{\mathit{dt}}\equiv 0.$$ (9)

   At the limit point bifurcation (λ*, u*) we have $\frac{d\lambda }{\mathit{dt}}({\lambda }^{\ast },u^{\ast })=0$, from which we obtain

   $$(\mathit{Dh}(k_x\left(u^{\ast }\right)\circ {\mathit{Dk}}_x\left(u^{\ast }\right)-\frac{1}{\lambda \left(t\right)}I)\frac{\mathit{du}}{\mathit{dt}}=0.$$ (10)

   Since (compare (7))

   $${\mathit{Dg}}_u({\lambda }^{\ast },u^{\ast })=\mathit{Dh}\left(k_x\left(u^{\ast }\right)\right)\circ {\mathit{Dk}}_x\left(u^{\ast }\right)-\frac{1}{\lambda \left(t\right)}I$$

   we see that the vector

   $$v≔\frac{\mathit{du}}{\mathit{dt}}$$

   is a zero eigenvector of Dg_u(λ*, u*). By assumption this is the unique zero eigenvector of Dg_u(λ*, u*).
   Now we analyze the system (4). The equilibria of (4) satisfy the identity

   $$f(x\left(t\right),\lambda h\left(x\left(t\right)\right))\equiv 0.$$

   We differentiate to obtain

   $${\mathit{Df}}_x\frac{\mathit{dx}}{\mathit{dt}}={\mathit{Df}}_1\frac{\mathit{dx}}{\mathit{dt}}+\left({\mathit{Df}}_2\right)\left(\frac{d\lambda }{\mathit{dt}}h\left(x\left(t\right)\right)+\lambda \frac{\mathit{dh}}{\mathit{dx}}\frac{\mathit{dx}}{\mathit{dt}}\right)\equiv 0,$$ (11)

   where Df_i, i = 1, 2 denotes the derivative of f with respect to the i-th argument. At the bifurcation point $\frac{d\lambda }{\mathit{dt}}=0$ and we get

   $${\mathit{Df}}_x\frac{\mathit{dx}}{\mathit{dt}}=[{\mathit{Df}}_1+{\mathit{Df}}_2\lambda \frac{\mathit{dh}}{\mathit{dx}}]\frac{\mathit{dx}}{\mathit{dt}}=0.$$

   Since x(t) = k_x(u(t)) along the set of equilibria, the null vector at the bifurcation is

   $$\frac{\mathit{dx}}{\mathit{dt}}={\mathit{Dk}}_x\frac{\mathit{du}}{\mathit{dt}}={\mathit{Dk}}_{x}v.$$

   Therefore Dk_xv spans the kernel of Df_x at (λ*, k_x(u*)).

2. This is the result [15, Theorem 2].

3. Assume that M_top ∩ M_bot ≠ ∅. By the definition of branches M_bot and M_top this means there are equilibria (λ₁, u₁) ∈ U_bot and (λ₂, u₂) ∈ U_top of (5) such that (λ₁, k_x(u₁)) = (λ₂, k_x(u₂)). This implies λ₁ = λ₂ and k_x(u₁) = k_x(u₂). Since k_x is monotone by Lemma 2.2, we must have k_x(u₁) = k_x(u) = k_x(u₂) for any constant input u satisfying u₁ ≻ u ≻ u₂. By the assumption the equilibria u₁ and u₂ at the parameter value λ are order related, let us say u₁ ≻ u₂ and u₁ ≠ u₂. Therefore the set of such u contains an open set in R^m. This is a contradiction with the assumption that k_x is not constant on open sets, see Remark 3.2. □

We summarize the results of this section in a Proposition.

Proposition 4.6

Assume all assumptions of Theorem 3.1. Then there is an S-shaped curve of equilibria M = M_bot ∪ M_mid ∪ M_top in Λ × Rⁿ and a function q(x, λ) : Rⁿ × Λ → R such that

1. at λ₁, λ₂ ∈ Λ a generic limit point bifurcations take place;

2. the relative interior of M_top and M_bot consist of stable equilibria of (4);

3. q(x, λ) > 0 on M_top, q(x, λ) < 0 on M_bot and the set

   $$\mathcal{𝒢}≔\{(x,\lambda )\in {\mathbf{R}}^n\times \Lambda \mid q(x,\lambda )=0\}$$

   has a distance from M_bot ∪ M_top bounded away from 0;

4. q(x, 0) = 0.

Proof. By the discussion after Lemma 4.3 there is an S-shaped curve of equilibria of the system (5) in Λ × R^m and the bifurcations at λ₁, λ₂ are generic limit point bifurcations. By the definition of the set M and Lemma 4.3.1, M consists of equilibria of (4) and by Lemma 4.3.2 and 4.5.1 there are generic limit point bifurcations at λ₁, λ₂. By Lemma 4.5.2 the relative interior of M_top and M_bot consists of stable equilibria of (4) since by assumption the relative interior of V_top and V_bot consists of stable equilibria of (5).

Since by Lemma 4.5.3 M_bot ∩ M_top = ∅ there exists a separating n dimensional manifold 𝒢 ⊂ Rⁿ × Λ that is given by q(x, λ) = 0 for some real-valued function q. Without loss of generality we may assume that q(x, λ) > 0 on M_top and q(x, λ) < 0 on M_bot. Since 𝒢 is closed, the distance from 𝒢 to either M_top or M_bot is bounded below by a nonzero constant. Finally, we may select function q with additional property that q(x, 0) = 0 in order for λ in the equation (3) to remain positive. Since all the equilibria satisfy λ > 0, we can guarantee such property by modifying the function q locally in the neighborhood of λ = 0.

5 Planar problem

Define a model planar problem

$$\begin{array}{cc}\hfill \stackrel{.}{y}& =\zeta -y(y^2-1)\hfill \\ \hfill \stackrel{.}{\zeta }& =-∊y.\hfill \end{array}$$ (12)

The fast subsystem is obtained by setting ∊ = 0 in (12)

$$\begin{array}{cc}\hfill \stackrel{.}{y}& =\zeta -y(y^2-1)≕\zeta -G\left(y\right)\hfill \\ \hfill \stackrel{.}{\zeta }& =0\hfill \end{array}$$ (13)

with ζ ∈ [−1, 1]. Let S := {(ζ, y) ∈ R²|ζ = G(y)}. The set S has three branches S_bot, S_mid and S_top defined by $y<-1∕\sqrt{3}$, by $1∕\sqrt{3}>y>-1∕\sqrt{3}$ and by $y>1∕\sqrt{3}$, respectively. We denote by Z a curve in R² depicted in Figure 2.A, that consists of S_bot ∪ S_top and the two vertical connecting pieces.

Figure 2.

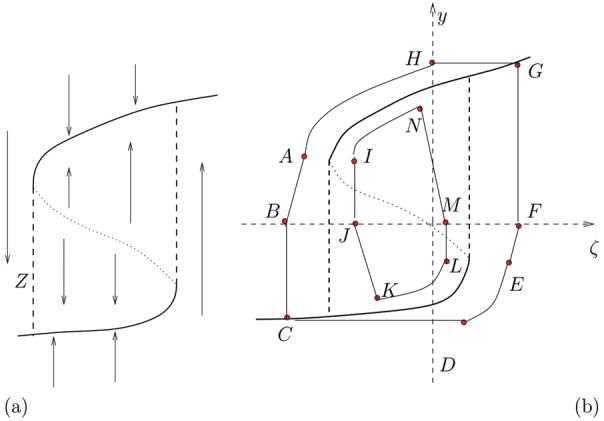
(a) The Z curve, (b) The set N in the neighborhood of the Z curve, that is positively invariant under the flow of (12)

We now recall a classical construction, where we follow Jones [22]. Similar constructions also appear in Lefschetz [23] and Hale [20].

Lemma 5.1

For any δ > 0 there exists an ∊₀ > 0 and an open set N, lying entirely within a distance δ of Z, that is positively invariant for (12).

Proof. The construction is seen most easily with the aid of a picture, see Figure 2.B. We construct the boundary of the set N. Draw graphs of ζ = G(y) ± h; take a point A on the graph of ζ = g(y) − h just above (in y-coordinate) the left turning point of ζ = g(y) − h, draw a line with positive slope to a point B on the horizontal axis, and then draw a vertical line to a graph ζ = G(y) at point C. This is followed by a horizontal line to a point D on graph of ζ = G(y) + h and then piece of graph of ζ = G(y) + h to a point E just below of the right turning point of ζ = G(y) + h. This point is symmetric to the point A and we finish the construction in a symmetric way by constructing points F, G and H. This finishes the outer boundary of N. The inner boundary consists of 2 pieces of graphs ζ = G(y) ± h, two vertical pieces and two pieces with negative slope, see Figure 2.B.

Now we show that the flow of (12) is pointing inward on the outer boundary of N. As a guidance we will use the vector field generated by (13); if it points inward on the boundary of N, so does the vector field of (12) for small ∊. On the segment AB the slope is positive and vector field of (13) is vertical and pointing down so it points in on AB. Analogous reasoning applies for segments CD and DE, using the fact that the slope is positive on DE, since E is below the right turning point of ζ = G(y) + h. By symmetry, the vector field points in on EF, GH and HA. The argument for BC and FG cannot be made using (13), since these lines are vertical. However, the second equation in (12) causes the vector field to point right along BC and left along FG, as desired.

Analogous arguments can be used for the inner boundary and by choosing h sufficiently small, we can make N to be in a δ neighborhood of Z for any δ > 0.

6 Correspondence between (13) and (4)

The essential step in description of the correspondence between (13) and (4) is to define special coordinates in the neighborhood of the set of equilibria M. We start by using the Lyapunov-Schmidt reduction ([19]) at the limit point bifurcation (λ₁, x₁). Since the limit point bifurcation at λ₁ is generic, by [19, Proposition 9.1] in the neighborhood U₁ of the point (λ₁, x₁) there are local coordinates (λ₁, v₁, v₂) ∈ R × R × Rⁿ⁻¹ in which the flow of (4) has the form

$$\begin{array}{cc}\hfill {\stackrel{.}{v}}_1& =(\lambda -{\lambda }_1)-v_1^2\hfill \\ \hfill {\stackrel{.}{v}}_2& =A_1\left(\lambda \right){(v_1,v_2)}^T+h_1(\lambda ,v_1,v_2)\hfill \end{array}$$

where h₁(λ, v) = O(∥v∥²) as ∥v∥ → 0. Since we assume that M_bot consists of stable points, all eigenvalues of A₁(λ) are negative and bounded away from zero.

Similarly, near (λ₂, x₂) there are local coordinates (λ, w₁, w₂) ∈ R × R × Rⁿ⁻¹ in a neighborhood U₂ of (λ₂, x₂) in which the flow of (4) has the form

$$\begin{array}{cc}\hfill {\stackrel{.}{w}}_1& =({\lambda }_2-\lambda )-w_1^2\hfill \\ \hfill {\stackrel{.}{w}}_2& =A_2\left(\lambda \right){(w_1,w_2)}^T+h_2(\lambda ,w_1,w_2),\hfill \end{array}$$ (14)

with h₂ and A₂ having the same properties as h₁ and A₁ respectively. By taking U₁ and U₂ smaller, if necessary, we can assure that U_i ∩ 𝒢 = ∅ for i = 1, 2.

Now we prove a global result which uses in an essential way the fact that for each fixed λ the system (4) is monotone.

Lemma 6.1

Assume all assumptions of Theorem 3.1. Take x in the branch of the unstable manifold of a point w ∈ M_mid∩U₂ that leaves U₂ in finite time. Then ω(x) ⊂ M_top. Similarly, for x in the branch of the unstable manifold of a point w ∈ M_mid ∩ U₁ that leaves U₁ in finite time, we have ω(x) ⊂ M_bot.

Proof. We prove only the first part, since the proof of the second part is analogous. Let

$$\pi :{\mathbf{R}}^n\times \Lambda \to \Lambda$$

be the coordinate projection. The system (4) generates a parameterized flow ψ, that is, for each λ fixed, the flow preserves the λ-slice of the phase space. We denote the induced flow by ψ^λ. Let (μ, λ₂] be the set of all values of λ in (U₂) smaller then λ₂.

Take arbitrary λ ∈ (μ, λ₂]. Then by (14) there are two equilibria $w_{\mathit{mid}}^{\lambda }$ and $w_{\mathit{bot}}^{\lambda }$ in U₂; the second being stable and the first one with one-dimensional unstable manifold. Further, one branch of the unstable manifold of $w_{\mathit{mid}}^{\lambda }$ connects to $w_{\mathit{bot}}^{\lambda }$. We denote by Ξ^λ the other branch of $W^u\left(w_{\mathit{mid}}^{\lambda }\right)$. By the assumptions of Theorem 3.1 there exist three equilibria of ψ^λ; the third one lies on M_top and we denote it by $w_{\mathit{top}}^{\lambda }$.

We now show that there is an interval (ν, λ₂] ⊂ (μ, λ₂] such that for all λ, ∈ (ν, λ₂] and all x^λ ∈ Ξ^λ, $\omega \left(x^{\lambda }\right)=w_{\mathit{top}}^{\lambda }$.

First, for a generic f (see Remark 3.2.4) and all $x^{{\lambda }_2}\in W^u\left(w_{\mathit{mid}}^{{\lambda }_2}\right)={\Xi }^{{\lambda }_2}$ the omega-limit set ω(x^λ₂) is contained in the set of equilibria. Further, by assumption the flow ψ^λ is strongly monotone. It follows from [31, Theorem 4.3] that for a generic x ∈ Rⁿ, ω(x) is contained in the set of equilibria. Therefore there is μ₁ < λ₂ such that for all λ ∈ (μ₁, λ₂] and all x^λ ∈ Ξ^λ, ω(x^λ) is contained in the set of equilibria.

Since the bifurcation at λ = λ₂ is generic (see Remark 3.2.2), there is no homoclinic orbit to $w_{\mathit{mid}}^{{\lambda }_2}$. Further, for a generic f, (see Remark 3.2.3) the homoclinic orbits are isolated. Therefore there is an μ₂ with μ₁ ≤ μ₂ < λ₂ such that for all λ ∈ (μ₂, λ₂] and any x^λ ∈ Ξ^λ, the omega-limit set $\omega \left(x^{\lambda }\right)\ne w_{\mathit{mid}}^{\lambda }$.

Finally, since by assumption all solutions of (4) are bounded, for all λ ∈ (μ₂, λ₂] and all x^λ ∈ Ξ^λ either $\omega \left(x^{\lambda }\right)=w_{\mathit{top}}^{\lambda }$ or $\omega \left(x^{\lambda }\right)=w_{\mathit{bot}}^{\lambda }$. We first note that these conditions are open, that is, if $\omega \left(x^{{\lambda }_0}\right)=w_{\mathit{top}}^{{\lambda }_0}$, then for all λ with |λ − λ₀| sufficiently small we have $\omega \left(x^{\lambda }\right)=w_{\mathit{top}}^{\lambda }$ for all x ∈ Ξ^λ. Therefore there is either a ν with μ₂ ≤ ν < λ₂ such that for all λ ∈ (ν, λ₂] and all x^λ ∈ Ξ^λ we have $\omega \left(x^{\lambda }\right)=w_{\mathit{top}}^{\lambda }$, or there is a sequence $\{{\zeta }_n{\}}_{n=1}^{\infty }\subset ({\mu }_2,{\lambda }_2]$ such that lim_n→∞ ζ_n = λ₂ such that for all x^ζ_n ∈ Ξ^ζ_n, $\omega \left(x^{{\zeta }_n}\right)=w_{\mathit{bot}}^{{\zeta }_n}$.

We assume the second case and show that this leads to a contradiction. Observe that in the second case all solutions on both branches of $W^u\left(w_{\mathit{mid}}^{{\zeta }_n}\right)$ converge to the point $w_{\mathit{bot}}^{{\zeta }_n}$, and this is true for all n. By continuity and by the fact that the bifurcation at λ₂ is generic, there exists a periodic orbit for λ > λ₂, with λ − λ₂ << 1. See Figure 3.

Figure 3.

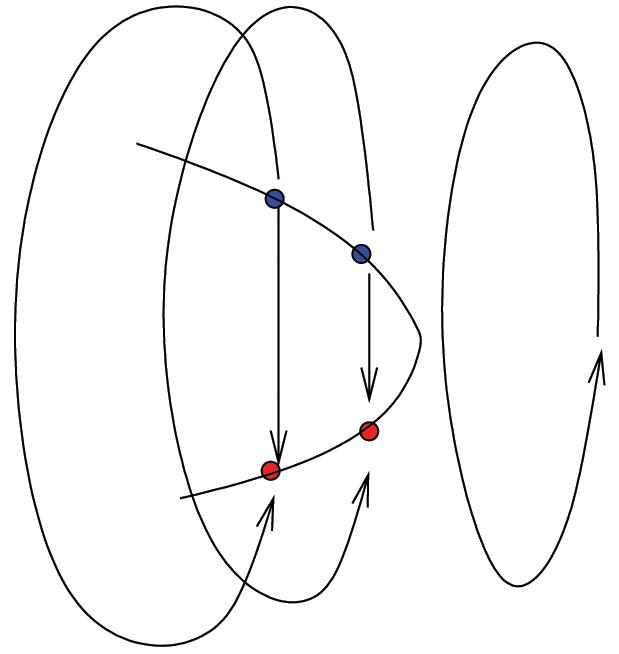
Limit point bifurcation gives rise to a stable periodic orbit

Again, since the bifurcation at λ₂ is generic limit point bifurcation and since the branch M_bot consists of stable equilibria, this periodic orbit must be stable for λ > λ₂, with λ − λ₂ << 1. This contradicts the fact that the stable periodic orbits do not exist in monotone dynamical systems [31, Theorem 4.3]. Therefore there is an interval (ν, λ₂] such that for all λ ∈ (ν, λ₂] and all $x^{\lambda }\in {\Xi }^{\lambda }\omega \left(x^{\lambda }\right)=w_{\mathit{top}}^{\lambda }$. The result now follows if we choose U₂ satisfying π(U₂) ⊂ (ν, ∞). Let

$$\mathcal{ℳ}≔M_{\mathit{top}}\cup M_{\mathit{bot}}\cup (M_{\mathit{mid}}\cap (U_1\cup U_2)).$$

We extend the local coordinates defined around the bifurcation points to a neighborhood of ℳ.

Lemma 6.2

There is a neighborhood U of ℳ with U₁ ∪ U₂ ⊂ U and coordinates (λ, u, v) ∈ R × R × Rⁿ⁻¹ in U in which the flow has the form

$$\begin{array}{cc}\hfill \stackrel{.}{u}& =h(\lambda ,u)\hfill \\ \hfill \stackrel{.}{v}& =A\left(\lambda \right){(u,v)}^T+H(\lambda ,u,v)\hfill \end{array}$$

such that

1. u = v₁ and v = v₂ in U₁;

2. u = w₁ and v = w₂ in U₂;

3. H(λ, u, v,) = O(∥(u, v)∥²) as ∥(u, v)∥ → 0.

Proof. We first review the information about the set of equilibria M. By Proposition 4.6 there are generic limit-point bifurcations at λ_i, i = 1, 2, the equilibria in the relative interior of M_bot ∪ M_top are stable. Since limit point bifurcations in U₁ and U₂ are generic, each equilibrium w ∈ M_mid ∩ (U₁ ∪ U₂) has one-dimensional unstable manifold.

Now we extend coordinates (w₁, w₂) ∈ U₂ to a neighborhood of M_bot. Let A_w be the linearization of (4) at w = M_bot ∩ π⁻¹(λ). Then the map x → A_wx is monotone with respect to K_X ([2, Lemma 6.4]) and the matrix A_w admits a Perron-Frobenius eigenpair (μ_w, e_w). Since the equilibrium w is stable, the eigenvalue μ_w ≤ 0. We would like to select a one dimensional stable manifold that is tangent to the eigenvector e_w which changes continuously with the base point w. Unfortunately, such manifold is not unique, as one can see from the following example in the plane. Consider the vector field

$${\stackrel{.}{x}}_1=-x_1,{\stackrel{.}{x}}_2=-2x_2.$$

In this example, the choice of two points, one in the left and one in the right half-plane determines unique manifold, that is tangent to x₁ axis in the origin. A result of Brunovsky [9] generalizes this observation. Let Σ₁ = {μ_w} and let Σ₂ contains the rest of the spectra of A_w. Assume for the moment that there is β, γ, μ such that λ < β < γ < μ_w < μ < 0 for all λ ∈ Σ₂. Let P_i be spectral projection corresponding to Σ_i, let X_i = P_iX and A_i = P_iA_w. By the standard theory, there are local coordinates x₁, x₂ in the neighborhood of w such that

$$\gamma \mid x_1{\mid }^2<\langle x_1,A_1{x}_1\rangle <\mu \mid x_1{\mid }^2,\langle x_2,A_2{x}_2\rangle <\beta \mid x_2{\mid }^2.$$

For given η let Γ_η := {x₁ : |x₁| = η} which in our case is a two point set, since x₁ ∈ R. Then a result of Brunovsky [9] states, that for sufficiently small η and any function σ : Γ_η → X₂, there is a unique manifold O_w, tangent to e_w, such that graph(σ) ⊂ O_w. In our case, the function σ has only two values, one for x₁ = η and one for x₁ = −η.

An important observation is that the manifold changes continuously with the point w ∈ M_bot, if the function σ changes continuously.

We assumed in the above argument that μ_w is an isolated point of the spectra. If μ_w has higher multiplicity k, the set Σ₁ would have dimension k. Non-uniqueness is still present, but once we select a particular k-dimensional manifold tangent to the eigenspace corresponding to Σ₁, this manifold is foliated by one dimensional sub-manifolds, since all eigenvalues in Σ₁ are identical. Thus we specify a continuous function σ to select a continuous set of k dimensional manifolds parameterized by the base point w, and then select one dimensional sub-manifolds in such a way that they change continuously as a function of w ∈ M_bot.

We will now select a particular one dimensional manifold for each w ∈ M_bot. By Lemma 6.1, if λ ∈ U₁ and λ₁ < λ then one branch of the unstable manifold of w_mid at this λ has to connect to w_bot. By continuity, all points (x,λ) on such a branch of $W_{\mathit{mid}}^u$, with λ < λ₁ and ∥x−x*∥ < ∊ converge to M_bot and we can assume without loss that this is true for all (x,λ) ∈ U₁. We select the one dimensional manifolds along M_bot in such a way that they coincide with the unstable manifold W^u(w_mid) for all w_mid ∈ M_mid ∩ U₁ and extend this choice continuously for λ < λ₁. We select variables u along these sub-manifolds and select v to be the complementary variables.

A similar construction allows the extension of the local coordinates v₁, v₂ from U₂ to a neighborhood of M_top. The result now follows.

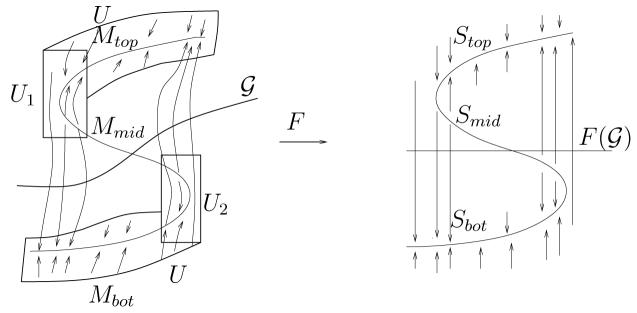
Definition 6.3

Using the coordinates of Lemma 6.2, define a 2-dimensional manifold in the neighborhood U of ℳ (see Figure 4),

$$\mathcal{𝓤}≔\{(\lambda ,u,v)\in U\mid v=0\}.$$

.

Figure 4.

Map F maps the 2-dimensional manifold in the neighborhood of the set M to its image in R². The flow ψ (left figure), generated by (4), is orbit equivalent to the flow φ (right figure), generated by (13). The neighborhoods U₁ and U₂ of the turning points on M are also indicated.

Having defined local coordinates in neighborhood U of ℳ we relate them to local coordinates in the neighborhood of S. Recall that ψ denotes the parameterized flow of (4) and let φ denotes the parameterized flow of (13).

Define a mapping F : 𝒰 → R² in two stages. First, since (13) undergoes a generic limit point bifurcation at $\zeta =\pm 1∕\sqrt{3}$ and the parameterization e of M is continuous, there exists a diffeomorphism F taking M to S in such a way that M_top, M_bot and M_mid map to S_top, S_bot and S_mid, respectively and F(𝒢 ∩ M_mid) = (0,0). Take an arbitrary $w_{\mathit{top}}^{{\lambda }_0}\in M_{\mathit{top}}$. Take B a neigborhood of λ₀ in (λ,∞) and let 𝒰_B := {(λ, u, v) ∈ U | λ ∈ B, v = 0} be a 2-dimensional manifold, that is foliated by one-dimensional stable sub-manifolds $W^s\left(w_{\mathit{top}}^{\lambda }\right)$, λ ∈ B. There is also a neighborhood $\stackrel{-}{\mathcal{𝓤}}\in {\mathbf{R}}^2$ of $F\left(w_{\mathit{top}}^{{\lambda }_0}\right)$ that is foliated by the stable manifolds of points $F\left(w_{\mathit{top}}^{\lambda }\right)$, λ ∈ B. We extend F to 𝒰_B in such a way that it maps flow lines of ψ on 𝒰_B to flow lines of φ on $\stackrel{-}{\mathcal{𝓤}}$ and preserves the direction of the flow. By a similar argument we can define the map F on a neigborhood 𝒰_B of an arbitrary point $w_{\mathit{bot}}^{{\lambda }_0}$.

If $w_{\mathit{mid}}^{{\lambda }_0}\in M_{\mathit{mid}}\cap U_1$ or $w_{\mathit{mid}}^{{\lambda }_0}\in M_{\mathit{mid}}\cap U_2$, then there is a 2-dimensional manifold 𝒰_B, given by v = 0, such that B := ∏(𝒰) is a neigborhood of λ₀. The manifold 𝒰_B is foliated by unstable manifolds $W^u\left(w_{\mathit{mid}}^{\lambda }\right)$ with λ ∈ B. There is a also a neighborhood of $\stackrel{-}{\mathcal{𝓤}}\in {\mathbf{R}}^2$ of $F\left(w_{\mathit{mid}}^{{\lambda }_0}\right)$ that is foliated by unstable manifolds of points $F\left(w_{\mathit{mid}}^{\lambda }\right)$ with λ ∈ ∏(B). We can again extend F to 𝒰_B in such a way that it maps flow lines of ψ on 𝒰_B to flow lines of φ in $\stackrel{-}{\mathcal{𝓤}}$ and preserves direction of the flow.

Finally, since both systems undergo generic limit point bifurcations, the map F can be defined in the union U₁ ∪ U₂.

Definition 6.4 ([24])

Two C^r flows φ on M and ψ on N are C^m orbit equivalent (m ≤ r) if there is a C^m diffeomorphism h : M → N such that χ(t) = h ∘ ψ (t) ∘ h⁻¹ is a time re-parameterization of the flow φ.

We summarize our construction in the following Lemma.

Lemma 6.5

The flow ψ restricted to the 𝒰, is orbit equivalent to the flow φ in the neighborhood of S, via the map F.

By Lemma 6.1 the omega limit set of x ∈ 𝒰 ∩ U₁ lies in M_bot and the omega limit set of x ∈ 𝒰 ∩ U₂ lies in M_top.

We now show that the map F can be extended the set

$$\bigcup _{x\in U_2\cup U_1}\bigcup _{t\ge 0}\psi (t,x).$$

. By Lemma 6.5 there is a flow χ(t) on R² defined by χ(t) = F ∘ φ(t) ∘ F⁻¹ and an increasing function τ(t) such that

$$\phi \left(\tau \left(t\right)\right)=\chi \left(t\right).$$

. Fix λ ∈ π(U₁), λ > λ₁. For such λ the flow ψ^λ has equilibria $w_{\mathit{mid}}^{\lambda }\in M_{\mathit{mid}}$, $w_{\mathit{bot}}^{\lambda }\in M_{\mathit{bot}}$ and one branch of the unstable manifold connects $w_{\mathit{mid}}^{\lambda }$ to $w_{\mathit{bot}}^{\lambda }$. We denote this branch by ${\stackrel{-}{W}}^u\left(w_{\mathit{mid}}^{\lambda }\right)$. Fix a point $x^{\lambda }\in {\stackrel{-}{W}}^u\left(w_{\mathit{mid}}^{\lambda }\right)\cap U_1$ and observe that there are intervals (−∞, a^λ) and (b^λ, ∞) such that ψ(t, x^λ) ∈ U for t ∈ (−∞, a^λ) ∪ (b^λ, ∞). It is on these intervals that the function τ(t) is defined.

By the construction of the neighborhood U₁ we have 𝒢 ∩ U₁ = ∅. Since q(α(x^λ), λ) < 0 and q(ω(x^λ), λ) > 0 for α– and ω– limit sets of x^λ, there is a at least one time T^λ ∈ [a^λ, b^λ] such that ψ(T^λ, x^λ) ∈ 𝒢. By the flow box theorem the flow emanating from all such $x^{\lambda }\in {\stackrel{-}{W}}^u\left(w_{\mathit{mid}}^{\lambda }\right)$ is parallelizable. Therefore, by changing the function q if necessary, we can assure that this time T^λ is in fact unique for every $x^{\lambda }\in {\stackrel{-}{W}}^u\left(w_{\mathit{mid}}^{\lambda }\right)$, where $w_{\mathit{mid}}^{\lambda }\in M_{\mathit{mid}}\cap U_1$. Now we extend the function τ(t) = τ(λ, t) continuously and monotonically to

$$(\pi \left(\Lambda \right)\cap \{\lambda >{\lambda }_1\})\times [a^{\lambda },b^{\lambda }]$$

in such a way that

$$F(\lambda ,\psi (T^{\lambda },x^{\lambda }))=(\lambda ,0).$$ (15)

Finally, for a pair (λ, y) where λ > λ₁, λ ∈ π(Λ) and y = ψ^λ (t, x^λ) for some t ∈ [a^λ, b^λ] we define

$$F(\lambda ,y)≔\phi (\tau \left(t\right),F(\lambda ,{\psi }^{\lambda }(-t,y))).$$

. Since we renormalized the time in the interval [a^λ, b^λ], this map is well defined. A similar extension can be done for λ ∈ π(U₂), λ < λ₂ and x^λ ∈ W^u(M_mid). The choice (15) implies that the map F maps points lying on 𝒢 into the line y = 0 in R².

Now we consider λ ∈ π(U₁), λ < λ₁. By making the neighborhood U₁ smaller, if necessary, we can assure that for (λ, x^λ) such that x^λ ∈ 𝒰 ∩ U₁ and λ < λ₁, ω(x^λ) ∈ M_bot. This follows by continuity on initial conditions and the fact that M_bot consists of stable equilibria. The analogous construction to the one above allows an extension of F to all trajectories starting at such pairs (λ, x^λ); this obviously also holds in the neighborhood U₂ of the other turning point.

We call the resulting map, defined on

$$\mathcal{𝓗}≔\mathcal{𝓤}\cup \bigcup _{x\in U_2\cup U_1}\bigcup _{t\ge 0}\psi (t,x),$$

, again F. Observe that the range F contains a neighborhood of the curve Z in Figure 2.

6.1 Lifting of the planar problem.

Let ψ∈ denotes the flow of (3) and let φ∈ denotes the flow of (12).

A set 𝓝 is an isolating neighborhood if Inv 𝓝 ⊂ int 𝓝 that is, if the maximal invariant set S in N lies in the interior of 𝓝.

An isolating neighborhood N is an isolating block if ∂N = N⁺ ∪ N⁻, where N⁻ is the immediate exit set and N⁺ is the immediate entrance set

$$\begin{array}{cc}\hfill N^{-}≔& \{x\in N\mid \phi ([0,t],x)\not\subset N\text{for all}t>0\}\hfill \\ \hfill N^{+}≔& \{x\in N\mid \phi ([t,0],x)\not\subset N\text{for all}t<0\};\hfill \end{array}$$

and both N⁺ and N⁻ are subsets of local sections of the flow.

Lemma 6.6

Let N′ := F⁻¹(N) ⊂ 𝓗, where N ⊂ R² is the neighborhood of the Z-curve constructed in Lemma 5.1.

Then there is an neighborhood 𝓝 of N′ in Λ × Rⁿ and ∈₀, such that 𝓝 is positively invariant under ψ_∈, for all ∈ < ∈₀ and ∈₀ sufficiently small. In particular, 𝓝 is an isolating block under ψ_∈.

Proof. We will extend the set N′ ⊂ 𝓗 to its neighborhood 𝓝 ∈ Λ × Rⁿ, i.e. a set with a nonempty interior, in such a way that the flow ψ_∈ on the boundary is transversal inward. This will imply that 𝓝 is an isolating block.

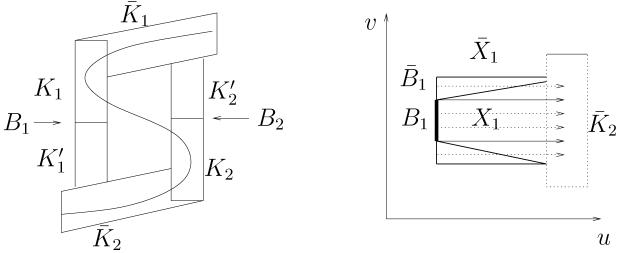
We start with the neighborhood U₁ and use the local coordinates of Lemma 6.2. Since the matrix A₁ has spectrum bounded away from zero, there is η > 0 and the set

$$K_1≔\{(u,v)\in U_1\mid u\in N^{\prime }\cap U_1,\mid v\mid \le {\eta }_1\},$$

such that ψ_∈ points inward on the part of the boundary ∂K₁ given by

$$\{(u,v)\in U_1\mid u\in N^{\prime }\cap U_1,\mid v\mid ={\eta }_1\}.$$

. Now we need to check the other parts of the boundary. Lemma 6.5 and continuity implies that for sufficiently small η the flow ψ points inward on ∂K₁ ∩ F⁻¹ (AB), where AB is the segment of the boundary of N in R², see Figure 2. Therefore ψ_∊ for small ∊ points also inward on ∂K₁ ∩ F⁻¹ (AB). On ∂K₁ ∩ F⁻¹ (IJ), which is by construction a λ = const hyperplane, the flow ψ_∊ points inward since the map F maps 𝒢 to y = 0 line and thus $\stackrel{.}{\lambda }<0$ on ∂K₁ ∩ F⁻¹ (IJ). Observe now that W^u(M_mid) ∩ ∂K₁ ≠ ∅ and therefore there is a neighborhood B₁ of W^u(M_mid) ∩ ∂K₁ such that the vector field of (3) points outward in B₁. The last part of the boundary ∂K₁ is the part where M_top ∩ ∂K₁ ≠ ∅. We now extend K₁ along M_top so that this will not be part of $\partial \mathcal{𝓝}$. Along the branch M_top the equilibria are stable and there is a neighborhood of M_top ∩ N′ of the form

$${\stackrel{-}{K}}_1≔\{(u,v)\in U\mid u\in N^{\prime },\mid v\mid \le {\eta }_1^{\prime }\},$$

which coincides with K₁ in U₁. Again we choose ${\eta }_1^{\prime }$ small enough so that ψ_∊ on the subset of ∂K̄₁ of the form

$$\{(u,v)\in U\mid u\in N^{\prime },\mid v\mid ={\eta }_1^{\prime }\}$$

points inward. Similar observations as above show that ψ_∊ points inward on $\partial (K_1\cup K_1^{\prime })$ except for the set B₁ ⊂ ∂K₁.

A similar construction can be done in the neighborhood U₂ of the other bifurcation point to construct K₂ and then extend K₂ to a neighborhood K̄₂ of M_bot ∩ N′. Then flow ψ_∊ points inward along the boundary $\partial (K_2\cup K_2^{\prime })$ except a neighborhood B₂ ⊂ ∂K₂ of W^u(M_mid)∩∂K₂.

The last step in the construction of the set 𝓝 is to extend N′ along the pre-images by F of the vertical connections from the turning points to the other branch of S.

Take the set B₁ ⊂ K₁ and flow it forward by the flow ψ. Observe that B₁ is a neighborhood of a collection of orbits for which the omega-limit set lies in M_top and M_top ⊂ K̄₂. By choosing η smaller, if necessary, we can assure that ψ(x, t(x)) ∈ intK̄₂ for all x ∈ B₁ and some t(x), which depends on x. The flow ψ between B₁ and the arrival in K̄₂ is a parallelizable flow. Take B̄₁ a neighborhood of the set B₁ and set

$$\stackrel{-}{X}≔\bigcup _{x\in {\stackrel{-}{B}}_1,t\in [0,t\left(x\right)]}\psi (t,x),X≔\bigcup _{x\in B_1,t\in [0,t\left(x\right)]}\psi (t,x).$$

We shave the set X̄ in the way indicated in Figure 5 (b) in such a way that the flow ψ points inward along its boundary. The same property then holds for ψ_∊ for small ∊.

Figure 5.

(a) A projection of various sets into 2-dimensional manifold ū. (b) Shaving between flow boxes X and X̄. The picture on the right is in complementary directions to the picture on the left.

We call this set $K_1^{\prime }$ and construct an analogous set $K_2^{\prime }$ by flowing the exit set B₂ of K₂ until it enters K̄₁. Set

$$\mathcal{𝓝}≔K_1\cup K_1^{\prime }\cup {\stackrel{-}{K}}_1\cup K_2\cup K_2^{\prime }\cup {\stackrel{-}{K}}_2.$$

By construction the flow ψ_∊ points inward along the boundary $\partial \mathcal{𝓝}$.

7 The Conley Index theory

We recall basic definitions of the Conley index theory. Recall that a set 𝓝 is an isolating neighborhood if $\mathrm{Inv}\mathcal{𝓝}\subset \mathrm{int}\mathcal{𝓝}$; that is, if the maximal invariant set S in N lies in the interior of 𝓝. Such set S is an isolated invariant set.

The pair of compact sets L ⊂ N is an index pair for an isolated invariant set S if

1. S = Inv(cl(N\L)) and N\L is a neighborhood of S;

2. L is positively invariant in N, i.e. given x ∈ L and φ([0, t], x) ⊂ N then φ([0, t], x) ⊂ L;

3. L is an exit set for N, i.e. given N and T > 0 such that φ(T, x) ∉ N, there is t [0, T] such that φ([0, t], x) ⊂ N and φ(t, x) ∈ L.

4. Observe that if N is an isolating block then (N, N⁻) is an index pair.

The cohomological Conley index $\mathit{CH}\left(\mathcal{𝓝}\right)$ of an isolating neighborhood 𝓝 is defined as a cohomology

$$\mathit{CH}\left(\mathcal{𝓝}\right)≔H^{\ast }(N,L).$$

It can be shown [10], that the index is independent on the choice of the index pair and on the choice of the isolating neighborhood. In fact, it only depends on the maximal invariant set $S≔\mathrm{Inv}\mathcal{𝓝}$ and so we use notation CH(S) and talk about the Conley index of an isolated invariant set S.

Given isolating neighborhood 𝓝 and the flow φ, we say that Σ is a Poincaré section for φ in 𝓝 if Σ ∩ N is closed and for every x ∈ N

$$\phi (x,(0,\infty ))\cap \Sigma \ne \varnothing .$$

Now we are ready to recall a theorem relating Conley index of 𝓝 to the existence of a periodic orbit in 𝓝.

Theorem 7.1

[26, Theorem 1.3] Assume X is an absolute neighborhood retract and Ψ : X × [0, ∞) → X is a semi-flow with compact attraction. If N is an isolating neighborhood for ψ which admits a Poincaré section Σ and either

$$\dim {\mathit{CH}}^{2n}(N,\Psi )=\dim {\mathit{CH}}^{2n+1}(N,\Psi )\mathit{for}n\in Z$$

or

$$\dim {\mathit{CH}}^{2n}(N,\Psi )=\dim {\mathit{CH}}^{2n-1}(N,\Psi )\mathit{for}n\in Z$$

where not all the above dimensions are zero, then Ψ has a periodic trajectory in N.

8 Proof of Theorem 3.1

We apply the Theorem 7.1 to the neighborhood $\mathcal{𝓝}\in \Lambda \times {\mathbf{R}}^n$ and the flow Ψ := ψ_∊ for sufficiently small ∊. First we observe that Λ × Rⁿ is an absolute neighborhood retract and all flows ψ_∊ are trivially semi-flows with compact attraction.

Next we verify that 𝓝 admits a Poincaré section. We start with the set B₁ defined in Lemma 6.6. All trajectories starting at B₁ must enter the set K̄₂ in finite time. Since $\stackrel{.}{\lambda }>0$ in K̄₂ and the flow on the boundary of 𝓝 points inward, these solutions have to enter K₂ in finite time. In K₂ we still have $\stackrel{.}{\lambda }>0$, so there are is no invariant set in K₂. Since B₂ is the exit set of K₂, all the trajectories entering K₂ have to leave through B₂ in finite time. Therefore all trajectories starting at B₁ arrive at B₂ in finite time. A symmetric argument starting at B₂ finishes the proof that B₁ is a Poincaré section of 𝓝.

We can make a cohomology calculation for the flow (12). Since N is an annulus in the plane

$$H^{\ast }\left(N\right)=\{\begin{array}{cc}Z\hfill & \text{for}\ast =0,1\hfill \\ 0\hfill & \text{otherwise}.\hfill \end{array}\phantom{\}}$$

Now we compute the Conley index of 𝓝. By Lemma 6.6 𝓝 is an isolating block and the flow on the boundary is inward. It follows that $(\mathcal{𝓝},\varnothing )$, is an index pair. Therefore

$${\mathit{CH}}^{\ast }\left(\mathcal{𝓝}\right)=H^{\ast }(\mathcal{𝓝},\varnothing ).$$

By construction of 𝓝 this is set is a topological product of the set N′ and a small n − 1 dimensional disc Dⁿ⁻¹ in the v-directions. Therefore

$$H^{\ast }(\mathcal{𝓝},\varnothing )=H^{\ast }\left(\mathcal{𝓝}\right)=H^{\ast }(N^{\prime }\times D^{n-1})=H^{\ast }\left(N^{\prime }\right)=H^{\ast }\left(F^{-1}\left(N\right)\right).$$

Finally, since F is a homeomorphism we have

$$H^{\ast }\left(F^{-1}\left(N\right)\right)=H^{\ast }\left(N\right).$$

Therefore ${\mathit{CH}}^{\ast }\left(\mathcal{𝓝}\right)=H^{\ast }\left(N\right)$ and the Conley index satisfies the index assumptions of Theorem 7.1. Since 𝓝 admits a Poincaré section, Theorem 7.1 implies existence of a periodic orbit in 𝓝 for all sufficiently small ∊.

9 An application

In this section we apply Theorem 3.1 to a well-known model of mitogen-activated protein kinase (MAPK) cascades in eukaryotic cells ([18, 6, 7, 5]), and specifically in Xenopus oocytes. All enzymatic reactions are considered fast, and hence a quasi-steady state approximation allows them to be modelled by Michaelis-Menten expressions for reaction rates, as functions of protein substrate concentrations. (For a similar model, but using negative feedback rather than positive feedback, see [25].) MEK is assumed to activate p42 MAPK by a nonprocessive, dual phosphorylation mechanism, so (see for instance [5]) we suppose there are three main MAPK species: unphosphorylated MAPK (z₁), MAPK-YP (z₂), and MAPK-YP/TP (z₃). Dephosphorylations are assumed to occur in separate steps, as indicated from experiments in Xenopus oocytes and extracts ([32]). Similarly, there are three forms of MEK (y₁, y₂, y₃). Activation of Mos (concentration of active Mos is indicated by x) is known to be a function of many regulatory processes. As in [5], we assume that the amount of active Mos is directly stimulated by active MAPK (z₃). Such a positive feedback loop from MAPK (or from some species downstream from MAPK) into Mos is known to operate in intact oocytes ([18]).

With parameters as in [5], we obtain the following model, after eliminating y₂ and z₂ by use of stoichiometry conservation laws (total MAPK = 300, total MEK = 1200). It is five-variable system of differential equations that describes the dynamics of the cascade:

$$\begin{array}{cc}\hfill \stackrel{.}{x}& =-\frac{V_{2}x}{K_2+x}+V_0{z}_3+V_1\hfill \\ \hfill {\stackrel{.}{y}}_1& =\frac{V_6(1200-y_1-y_3)}{K_6+(1200-y_1-y_3)}-\frac{V_3{\mathit{xy}}_1}{K_3+y_1}\hfill \\ \hfill {\stackrel{.}{y}}_3& =\frac{V_{4}x(1200-y_1-y_3)}{K_4+(1200-y_1-y_3)}-\frac{V_5{y}_3}{K_5+y_3}\hfill \\ \hfill {\stackrel{.}{z}}_1& =\frac{V_{10}(300-z_1-z_3)}{K_{10}+(300-z_1-z_3)}-\frac{V_7{y}_3{z}_1}{K_7+z_1}\hfill \\ \hfill {\stackrel{.}{z}}_3& =\frac{V_8{y}_3(300-z_1-z_3)}{K_8+(300-z_1-z_3)}-\frac{V_9{z}_3}{K_9+z_3},\hfill \end{array}$$

where V₀ = 0.0015, V₁ = 0.09, V₂ = 1.2, V₃ = V₄ = 0.64, V₅ = V₆ = 5, V₇ = V₈ = 0.06 V₉ = V₁₀ = 5, K₂ = 200, K₃ = K₄ = K₅ = K₆ = 1200, K₇ = K₈ = K₉ = K₁₀ = 300. We set the control u := z₃ in the first equation and let the output function h(x, y₁, y₃, z₁, z₃) = z₃. Therefore the variable feedback will be applied in the first equation which will change to

$$\stackrel{.}{x}=-\frac{V_{2}x}{K_2+x}+\lambda V_{0}u+V_1.$$

The monotonicity and boundedness assumptions of Theorem 3.1 have been verified in ([5]). The input-output function k(u) : R → R has been computed numerically in Figure 5.C of the same paper. We will reproduce it here together with lines $z_3=\frac{1}{\lambda }u$ for different value of the feedback parameter λ, see Figure 6.a.

Figure 6.

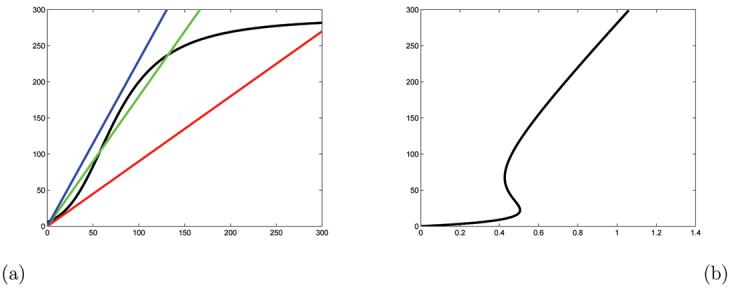
(a) The graph of the function k(u) and lines with slopes 0.9, 1.8 and 2.3; (b) The set of equilibria of the system 5 as a function of λ. These are the intersections of the graph of k(u) and the lines $\frac{1}{\lambda }u$.

The intersections of these lines with the graph of the input-output function k(u) are the equilibria of (5) in Figure 6.b. These equilibria satisfy the rest of the assumptions of Theorem 3.1, except genericity. Since the function k(u) is computed numerically and thus represents an approximation of the true input-output function, we can justifiably assume genericity of k. To construct the function q in (3) we choose u₀ = 150. By Theorem 3.1 the function q then has the form

$$q(x,y_1,y_3,z_1,z_3,\lambda )=\lambda (z_3-150).$$

We do not have biological justification for this adaptation law. We pick it in order to illustrate our theorem. However, the rate of synthesis of Mos could well be regulated by yet undiscovered feedback loops.

With such q and ∊ = 0.000005, the projections of solutions starting at four different initial conditions into the λ, z₃ plane is in the Figure 7.a. The time evolution of the variable y₃ for the same four initial conditions are shown in Figure 7.b. The matching colors in these two figures correspond to the same initial condition. These solutions converge to a periodic orbit predicted by Theorem 3.1.

Figure 7.

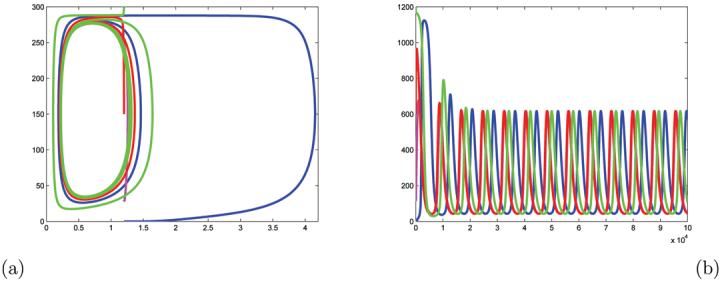
(a) Projections of solutions into λ, z₃ plane and (b) the y₃ as a function of time, for four different initial conditions. The matching colors in these two figures correspond to the same initial condition.