Sensory adaptation

Abstract

Adaptation occurs in a variety of forms in all sensory systems, motivating the question: what is its purpose? A productive approach has been to hypothesize that adaptation helps neural systems to efficiently encode stimuli whose statistics vary in time. To encode efficiently, a neural system must change its coding strategy, or computation, as the distribution of stimuli change. Information theoretic methods allow this efficient coding hypothesis to be tested quantitatively. Empirically, adaptive processes occur over a wide range of timescales. On short timescales, underlying mechanisms include the contribution of intrinsic nonlinearities. Over longer timescales, adaptation is often power-law-like, implying the coexistence of multiple timescales in a single adaptive process. Models demonstrate that this can result from mechanisms within a single neuron.

Adaptation as efficient coding

Barlow’s efficient coding hypothesis suggests that, given a finite capacity to transmit information, neural systems employ an optimally efficient coding strategy to represent the inputs that they typically process [1-3, Box 1]. However, when collected over relatively short time or length scales, the local statistics of many natural stimuli differ greatly from their global distribution. For example, luminance and contrast in natural visual environments vary over orders of magnitude across time in a day or across space in a complex scene. A sensory system that matched its distribution of outputs to the global distribution of stimuli would then be inefficient in transmitting the stimulus’ local distribution. Under these circumstances, one might expect the system’s coding strategy to adapt to local characteristics of the stimulus statistics.

Efficient coding (Box 1).

Maximizing efficiency with a fixed dynamic range requires that the system maps its inputs to its outputs such that all outputs are equally likely [figure 1,25,64]. The optimal coding strategy thus depends on the statistics of the stimulus that the system represents.

Recent experimental designs have begun to test the efficient coding hypothesis in the context of adaptation. In these experiments, the distribution of a random time-varying stimulus, rather than a single stimulus parameter, is varied. This design allows one to examine the coding strategy that the neural system uses to represent an entire stimulus distribution, and to relate changes in coding strategy to changes in stimulus distribution. The framework underlying these experiments presents the task of adaptation as essentially an inference problem: the timescale for the change in coding strategy cannot be shorter than the time required for the system to “learn” the new distribution.

In order to analyze experiments of this type, one must describe the coding strategy of the system during changes in the stimulus distribution. To do so, it is necessary to reduce the system’s entire input-output mapping to a simpler characterization. Linear-nonlinear (LN) models have often been successful in capturing changes in the computation of an adapting system (Box 2).

Capturing adaptive computation (Box 2).

To effectively characterize adaptation, one must begin with a characterization of computation. A powerful method for characterizing neural computation is to approximate the neural system as first linearly filtering the stimulus by an identified relevant feature or set of features, and then to generate spikes according to a nonlinear function of the stimulus’ similarity to the feature(s) (figure 2). Models of this simple type are known as linear/nonlinear (LN) models, and have had considerable success in capturing some aspects of neural processing [26].

In this simplified framework, adaptation to stimulus statistics might affect the features that linearly filter the stimulus, or the nonlinear function that determines the probability to fire (figure 2B). A change in response gain (without a change in the feature) can be manifested as either a vertical scaling of the linear feature or a horizontal scaling of the nonlinearity. Changes in the feature for different stimulus conditions occur, for example, in the retina; in low light levels, the receptive fields of retinal ganglion cells show increased temporal integration and decreased inhibitory surround [25].

One can sample these potentially time-dependent components using reverse correlation either with spikes conditioned on the phase of their arrival time with respect to the stimulus cycle if the stimulus is changing periodically, or with an adaptive filter [65].

Systems adapt to a variety of stimulus statistics

The simplest instantiation of a stimulus probability distribution is one in which the stimulus takes one of two possible values. If one of these values is presented more frequently than the other, a system may adapt to give a stronger response to the rarer stimulus. This effect was observed in cat auditory cortex A1 in response to two tones presented with different probabilities [4,5]. A potential substrate for this effect was demonstrated in a cultured network by Eytan et al. [6], who varied the relative frequency of current injection inputs applied at different locations. Such stimulus-specific adaptation may implement a kind of novelty detection, in which the strength of the response is adjusted according to the information it carries.

More generally, the efficient coding hypothesis might be taken to suggest that stimulus encoding is sensitive to the variations in stimulus statistics seen in natural stimuli. The properties of natural visual scenes, in particular, have been extensively studied [7]. A simple model for natural stimuli is of local Gaussian fluctuations with a long-tailed mean and variance modulated on longer time or length scales [8].

Inspired by this description of natural stimuli, a class of experiments has examined adaptation to a change in the mean or variance of a Gaussian white noise stimulus. Using a switching paradigm in which a random stimulus is chosen from a distribution whose parameters change periodically between two values (figure 2A), Smirnakis et al. [9] showed that retinal ganglion cells exhibit an adaptive change in firing rate when the variance of a flickering light stimulus changes. In the fly motion sensitive neuron H1, Brenner et al. [10] computed an LN model for different variances of a randomly varying velocity stimulus. They showed that the nonlinear gain function adapted such that the scaling of the stimulus axis was normalized by the stimulus standard deviation, and that this serves to maximize information transmission about the stimulus. Further, this gain change occurs in ~100 ms, rapidly maximizing information transmission during continuous changes in stimulus variance [11]. A separate slower adaptive process modulates the overall firing rate on much longer timescales. Analogously, retinal ganglion cells display contrast gain control [12-16], which occurs on a much faster timescale than rate changes due to contrast adaptation [9,14].

Figure 2. Neuronal computation modeled using a linear/nonlinear (LN) model.

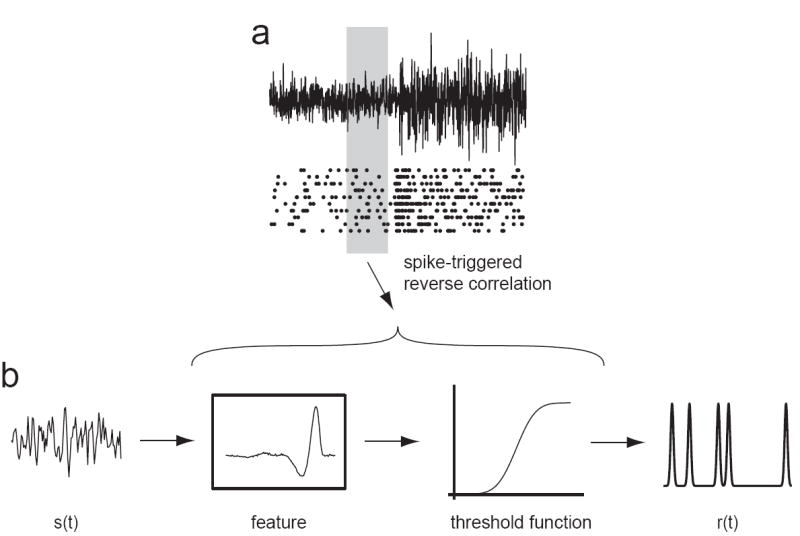
The linear filter(s) and nonlinear threshold function of the model are estimated by using reverse correlation between spikes and stimuli. (a) The spike times of a neuron are recorded in response to some stimulus. In this example, a filtered Gaussian white noise stimulus is presented, where the variance of the stimulus changes periodically between two values, but the white noise is generated anew in each variance cycle. A raster plot of spike times produced in response to several different instantiations of the white noise process are shown below. The stimulus preceding each spike is used to find the feature(s) and threshold function of the LN model by reverse correlation. (b) Computation is then modeled by linearly filtering incoming stimuli with the previously determined feature(s). Filtered stimuli are then passed through the threshold function, which gives the probability of firing an action potential as a function of time. To examine how the LN model changes with the variance context, spikes are sampled from a particular time bin with respect to the changes in the variance (shaded box) to compute time-dependent features and threshold functions.

Adaptation to stimulus variance has also been observed in several higher brain regions. In rat barrel cortex, when the variance of a white noise motion of the whiskers was changed, the relevant features remained approximately unchanged, but the gain curves showed a change in scaling by the stimulus standard deviation [17]. In field L, the avian analog of primary auditory cortex, Nagel and Doupe [18] observed rapid changes in filters and gain curves as well as a slower modulation of the overall firing rate, similar to observations in H1 and RGCs, as the distribution of sound intensity was varied. While individual neurons in inferior colliculus responding to sound amplitudes showed a variety of response changes during adaptation, Dean et al. [19] used Fisher information to demonstrate that the population as a whole shifted responses to best encode the high probability sounds, even when the distributions were relatively complex, such as bimodal. Neural responses in macaque inferior temporal cortex adapted to the width of the distribution of image stimuli along arbitrarily chosen stimulus directions [20].

Beyond white noise

In the LGN, Mante et al. [21] examined the interaction between adaptation to the mean and the variance (mean luminance and contrast) of drifting grating stimuli and found that the changes in filters due to luminance and contrast adaptation are independent. Suggestively, their analysis of natural images also showed independence of luminance and contrast. The same group found no adaptation to higher order statistics—the skewness and kurtosis—of a random checkboard stimulus in LGN [22]. However, Hosoya et al. [23] generalized a previous finding of rate adaptation to the spatial scale of a flickering checkerboard [9] to demonstrate adaptation to a variety of arbitrary spatiotemporal correlations in visual stimuli in RGCs, and showed that the new filters that evolve after exposure to these correlations act to remove the correlations and so perform predictive coding [24,25].

Determining the effect of complex changes in stimulus distribution is difficult to address due to the biases introduced into white noise analysis by non-Gaussian stimuli [26], which are difficult to separate from observed dependences of sampled receptive fields on the stimulus ensemble [27-30]. Sharpee et al. [31] introduced an information theoretic reverse correlation method which finds the stimulus dimensions that maximize mutual information between spiking responses and the stimulus. This method was used to find significant differences between the features encoded by V1 neurons in a white noise ensemble and a natural stimulus ensemble [32].

Multiple timescales

How might the goal of maintaining efficient information transmission constrain the dynamics of adaptation? In tracking changing stimulus statistics, there are two relevant timescales for any system: the characteristic timescale of changes in the stimulus distribution, and the minimum time required by an ideal observer to estimate the parameters of the new distribution. The first timescale is established by the environment, while the second is determined by statistics and sets a lower bound on how quickly any adapting system could estimate parameters of the new distribution. Given these constraining timescales, an adapting system should choose an appropriate estimation timescale for computing local stimulus statistics. For example, consider a system that adapts to the local stimulus mean. If this system estimates the local mean by averaging over only a few samples, the system would amplify noise and transmit little information about its stimulus [33]. Conversely, a system that averages over a timescale much longer than the timescale of changes in stimulus mean will not be optimally adapted to the local stimulus ensemble.

This argument assumes that the neural system can choose an adaptation timescale to match the dynamics of stimulus statistics. Experimentally, it appears that two separable phenomena describe the dynamics of adaptation to variance or contrast, at least in early visual and auditory systems. As discussed above, the first of these components rapidly rescales the system’s input-output gain following a change in stimulus statistics [11-16,18,34]. The second component of adaptation dynamics is a slow change in the system’s mean firing rate [9,11,13,15,18,35,36]. It is not yet clear what, if any, relationship exists between these two phenomena. In the fly H1 neuron, these effects appear to be independent [11], but such a result does not appear necessary a priori. At least in some cases, the adaptive rescaling of input-output functions in rat barrel cortex appears to follow the slow timescale rate adaptation [17]. Perhaps consistent with this, Webber and Stanley found that transient and steady-state adaptation in this area could be modeled with a single state variable [37].

The timescale of the fast gain change is often on the order of the timescale of the system’s relevant feature, and does not appear to depend on the timescale of switches in stimulus ensemble. In at least some cases, fast gain changes in response to changes in stimulus variance or correlation time are a consequence of the system’s static nonlinearity with no change in system parameters [38-44]. Whether such effects should rightly be called adaptation is something of a philosophical question. There is no doubt that finite dimensional stimulus/response characterizations such as LN models are limited and adaptation may appear to change model parameters. On the other hand, these models may, in some cases, capture all stimulus dependence if appropriately extended.

Slower changes in overall excitability have variable dynamics and may be subserved by a wide variety of mechanisms. Spike frequency adaptation (SFA) occurs over many timescales in cortical neurons [45], and has been analytically described for simple model neurons [46,47]. By specifying only the initial and steady-state firing rate-input (f-I) curve as well as the effective time constant, SFA can be described without knowledge of particular neuronal dynamics [48,49]. Slow currents have been implicated in altering the gain of f-I curves, allowing neurons to remain sensitive to input fluctuations at high mean currents [50-52].

Power law adaptation

In some cases, the dynamics of slow changes in excitability might be matched to the dynamics of stimulus changes. Many researchers using a switching paradigm with a single switching timescale have reported the dynamics of this slow gain change as an exponential process with a fixed time scale [5,9,13-15,35]. However, in the fly visual neuron H1, when the time between stimulus changes was varied, the apparent adaptation timescale scaled proportionally [figure 3A, 11,53] . Thus, the dynamics of slow gain changes in fly H1 are consistent with a power-law rather than an exponential process [36,54]. Power law dynamics are significant because there is no privileged timescale: dynamics are invariant with respect to changes in temporal scale, and such a system could therefore adjust its effective adaptation timescale to the environment.

Figure 3. The apparent timescale of adaptation depends on the dynamics of changes in the stimulus ensemble.

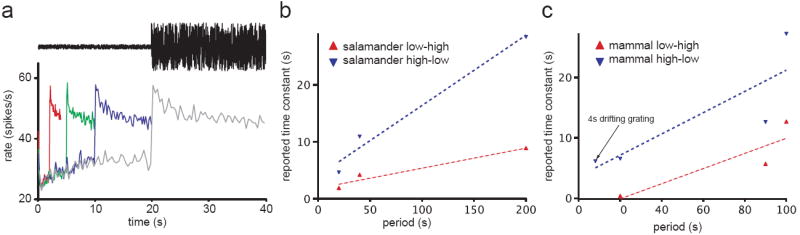
(a) In this example of a switching experiment, the variance of a Gaussian white noise stimulus is changed periodically between two values (top). Following an increase in stimulus variance, the average firing rate of a motion sensitive H1 cell in the fly visual system (bottom) increased transiently and then relaxed towards a baseline (gray trace). As the period of switches in stimulus variance was increased, the time constant of the slow relaxation in firing rate increased proportionally from 5s period (red trace) to 40s period (gray trace). (b) The reported time constant of slow relaxation in firing rate [9] or input currents [13] of RGCs or input currents to bipolar cells [60] following an increase (red) or decrease (blue) in contrast of a full field flickering stimulus increases with increasing switching period. Where Rieke [60] reports a sum of exponentials, we have plotted the time constant of the best fitting single exponential. In this and (c), dashed lines are linear regression fits. (c) The reported time constant of slow relaxation in firing rate of rabbit RGCs [9,34] or the firing rate [16] or input currents [35] of guinea pig RGCs following an increase (red) or decrease (blue) in contrast of a full field flickering stimulus increases with increasing switching period. An arrow identifies the exceptional stimulus [35] in which a non-periodic 4s sinusoid grating was presented instead of a flickering field. Where Brown et al. [34] report time to 66% recovery, we plot the time constant of an exponential with equal time to 66% recovery. The results of (b-c) are expected if the observed systems modify their rate of gain change according to stimulus history, and are consistent with power law, not exponential, dynamics.

Although studies in other systems have not explicitly tested for multiple time scales, results from studies of temporal contrast adaptation in salamander and mammalian (rabbit and guinea pig) retina suggest that the apparent time constant of the slow gain change indeed varies as a function of the period between stimulus switches (figure 3B-C).

Few studies provide direct evidence for the biophysical mechanisms underlying multiple timescale dynamics. Power law dynamics can be approximated by a cascade of many exponential processes [36,54,55]. Thus, a leading hypothesis is that multiple timescale dynamics are the result of a cascade of exponential processes in a cell or network. Multiple timescales exist in the multiplicity of channel dynamics present in single neurons [45]. Even in single channels, power-law recovery from inactivation has been shown in isolated NaII and NaIIa channels [56]. This behavior is captured by a stochastic sodium channel model that includes a Markov chain of multiple inactivation states [55].

Intrinsic properties or circuit mechanisms?

A leading candidate for a mechanism of contrast gain control in V1 is divisive normalization, in which the output of a given neuron is modulated by feedback from the responses of neurons with similar receptive fields [57,58]. However, many of the mechanisms we have discussed here may operate at the level of single neurons [59]. Recent work has made considerable progress in elucidating where in particular circuits adaptation occurs. In salamander retinal ganglion cells, rapid contrast adaptation is partially inherited from the adaptation of synaptic inputs [13,60] while a second component is contributed by intrinsic mechanisms [61]. Manookin et al. [35] also find that recovery from high contrast stimulation in guinea pig RGCs, characterized by a slow “afterhyperpolarization,” is mediated in large part by inherited changes in synaptic inputs with an additional intrinsic component. In mouse retina, adaptation to dim mean background luminance occurs in rod photoreceptors and at the rod bipolar-to-AII amacrine cell synapse [62]. In this case, the dominant site of adaptation was predicted by the likely site of saturation in response due to convergence of signals in the retinal circuitry. In rat barrel cortex, Katz et al. [63] showed that a subthreshold component of adaptation is whisker-specific, while responses in barrel cortex are multi-whisker, implying that the adaptation occurs in intracortical or thalamocortical connections as opposed to intrinsic mechanisms in the barrel cortical neurons.

Conclusion

A growing body of evidence suggests that representations at all levels throughout sensory processing pathways are plastic, depending on the recent history of the stimulus, on a range of timescales varying from virtually instantaneous to timescales more typically associated with synaptic changes. This plasticity can increase the information transmission rate of the signal. One would thus like to determine whether constraints on timescales are imposed by the time required to learn dynamic efficient representations. It is becoming clear that some components of what we think of as advanced processing may be occurring at low levels. Furthermore, some types of sophisticated apparent learning effects may be a result of intrinsic nonlinearities. A view of sensory systems as a simple feed-forward relay of filtered sensory information from transducers to cortex is no longer appropriate. Instead, we must consider the statistics of the natural world, plasticity at multiple levels of sensory processing, and the consequences for encoding of sensory information at each stage.

Figure 1. An example of efficient coding.

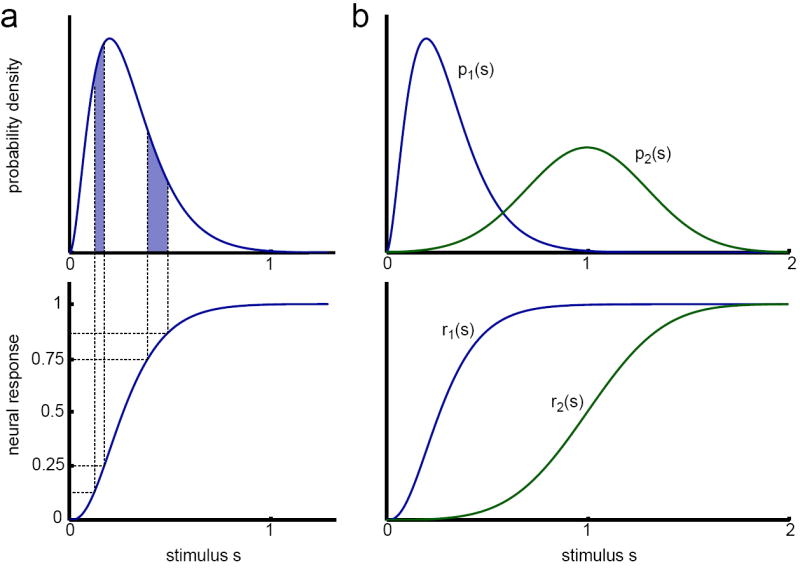
(a) Given a stimulus distribution (top), and a fixed output range, the maximally efficient mapping from stimulus to response is the integral of the stimulus distribution (bottom), known as the cumulative distribution. This mapping transforms equal probability in the stimulus distribution (shaded areas) to equal response ranges, making all responses equally likely. (b) When the stimulus distribution changes, for example from p₁ to p₂ (top), the maximally efficient mapping also changes. The new mapping, r₂(s), is the cumulative distribution of p₂(s). In this case, both the mean and the variance of the stimulus distribution change, leading to a shift in the half-maximum and a decrease in gain (slope) of r₂(s) compared to r₁(s), respectively.