Abstract
To maintain normal physiology, cells must properly process diverse signals arising from changes in temperature, pH, nutrient concentrations, and other factors. Many physiological processes are controlled by temporal aspects of oscillating signals; that is, these signals can encode information in the frequency domain. By modeling simple gene circuits, we analyze the impact of cellular noise on the fidelity and speed of frequency-signal transmission. We find that transmission of frequency signals is “all-or-none”, limited by a critical frequency (fc). Signals with frequencies <fc are transmitted with high fidelity, whereas those with frequencies >fc are severely corrupted or completely lost in transmission. We argue that fc is an intrinsic property of a gene circuit and it varies with circuit parameters and additional feedback or feedforward regulation. Our results may have implications for understanding signal processing in natural biological networks and for engineering synthetic gene circuits.
INTRODUCTION
To maintain their normal physiology, cells must process diverse signals such as temperature, pH, and nutrient concentrations. This process can be conceptualized as consisting of three steps: encoding, transmission, and decoding. One strategy employed to encode information is using the amplitude domain of a signal. Such amplitude signals are predominantly based on concentrations of signaling molecules.
Alternatively, information may be encoded in the frequency domain of an oscillatory signal. Oscillatory signals have been observed in diverse cellular processes, such as circadian clocks (1), segmentation clocks (2), Ca2+ signaling pathways (3,4), p53 DNA repair pathways (5), NF-κB pathways (6), and cell cycles (7–9). These signals can directly control the spatiotemporal dynamics of downstream cellular processes, and are likely to be the prevalent mechanism for regulating cellular processes where oscillations are involved. For example, the frequency of Notch protein oscillations in the posterior presomitic mesoderm (PSM) of mice controls cyclic expression of downstream genes such as HES1 (10) and Lfng (11), which in turn modulates periodic patterning in somite development (12–14). Loss of these oscillations, through perturbation of either the Notch protein or the downstream genes, will cause chaotic segmental organization (15–18). In mammalian circadian clocks, the mCLK/BMAL1 protein oscillations control cyclic expression of an albumin-D-binding protein containing a basic leucine zipper. The albumin-D-binding protein regulates critical cellular processes, such as circadian sleep consolidation and rhythmic EEG activity (19). Disruption of the oscillation frequency may be detrimental to the circadian rhythm and ultimately to human physiology (20).
In other cases, frequencies of oscillatory signals are correlated with activities of specific cellular processes that further suggest frequency encoding. During inflammatory response of T-lymphocytes, [Ca2+] oscillation frequencies of ∼0.01/s were found to maximize expression of interleukin-2 and interleukin-8 cytokines (21). During growth and differentiation of HeLa cells, [Ca2+] oscillation frequencies of ∼0.008/s significantly increased the activity of Ras proteins (22). Similarly, the frequency of NF-κB oscillations was proposed to regulate the activity of downstream genes involved in cell division, apoptosis, and inflammation response (6). In addition, chemical networks with specific architectures may function as frequency decoders (23). Table S1 lists many biological systems where frequency signal encoding is potentially adopted.
Regardless of encoding strategies, cellular signals are processed in the presence of noise, which arises from reactions between small number of molecules and perturbations inside a cell or from the environment (24–32). The presence of noise presents an important challenge for cellular signal processing. To understand the effects of noise on biological systems, considerable research has been performed to study noise generation and propagation (33,34), noise frequency modulation by negative feedback (35,36), and noise filtering in bacterial chemotaxis pathway (37). However, little is understood about how cellular noise impacts transmission of frequency signals. There is evidence for small amplitude oscillations in genome wide transcription of yeast respiratory cycles (38,39), which could be affected by cellular noise. Therefore, if cells do use frequency encoding, what are the basic characteristics of frequency-signal processing, in terms of processing speed and fidelity? How do these characteristics depend on the biochemical parameters and the architecture of underlying cellular networks? More generally, have cells evolved to take advantage of different strategies to properly control the transmission?
We address these questions by analyzing the impact of cellular noise on frequency-signal transmission in simple gene circuits. By using both analytical and numerical methods, we define a metric—critical frequency—that quantifies the speed limit of frequency-signal transmission. We argue that the critical frequency is an intrinsic property of a cellular network. Strategies to vary the critical frequency will introduce a tradeoff between speed and metabolic cost of signal transmission: an increase in transmission speed will come with an increase in metabolic cost. Our results further indicate that the critical frequency is dependent on network architectures. Our findings suggest a classification scheme for gene regulatory motifs, such as feedback regulations, based on their performance in transmitting frequency signals. Furthermore, insights into fundamental fidelity and speed limits may guide gene circuit designs for cellular computing in the long term (40). Finally, this work presents a general framework for analysis of frequency signal transmission in other types of cellular networks, such as signaling networks and metabolic networks.
METHODS
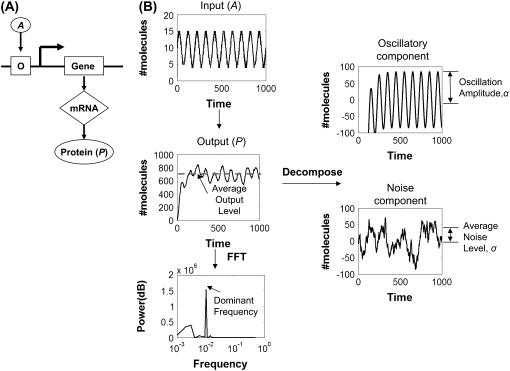
To elucidate the questions raised above, we analyzed transmission of frequency signals in simple gene circuits by mathematical modeling. To start, we consider a one-stage gene circuit where an output protein (P) is driven by an oscillatory input signal (A) (Fig. 1 A). In the cellular context, the input oscillations may be directly derived from environmental conditions (e.g., day-night cycles) or endogenous cellular oscillators (e.g., circadian clocks). Without loss of generality, we assume that the oscillation in Fig. 1 A is characterized by a sinusoid function (Fig. 1 B):
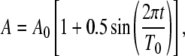 |
(1) |
where A0 defines both the average signal strength (A0 = 10 in the base model) and the corresponding oscillation amplitude, and T0 is the oscillation period. The choice of A0 does not affect the general conclusions of the following studies (results not shown).
FIGURE 1.
Analysis of frequency signals with noise. (A) A one-stage gene circuit where the output protein P is controlled by a transcription activator, A. (B) An oscillatory input signal can generate an output signal with oscillations compounded with noise. The mean and standard deviation of the output signal of the linearized model can be analytically computed. Here, we define the mean value as the oscillatory component and the standard deviation as the noise component. Alternatively, the stochastic simulations of the output signal for the nonlinear system can be analyzed by the FFT method to obtain its dominant frequency (see Methods for more details).
Fig. 1 B illustrates the two approaches we took to analyze transmission of the frequency signal. The first approach was to decompose the output P time course into its mean and standard deviation, which is an application of a linear genetic network method (41,42). The output signal P would oscillate when the gene circuit was driven by the oscillatory input signal A (Eq. 1). We define the mean as the oscillatory component and the standard deviation as the noise component, which tends to obscure or mask the oscillatory component (see Supplementary Materials). We anticipate that the frequency signal is transmitted accurately if the oscillation amplitude (α) exceeds the noise level (σ). For simplicity in terminology, we call α and σ the amplitude and noise level, respectively, of the output signal.
To complement the analytical method, we analyzed the P time course for its dominant frequency using numerical methods. If the signal transmission was accurate, this dominant frequency would be the same (within numerical errors) as the input frequency. The dominant frequency of the P time course was calculated by using the fast Fourier transform (FFT) method. Methods of numerical simulation and data analysis are detailed in Supplementary Materials. Briefly, the steady-state portion of the P time course for each simulation was analyzed using the FFT method (see Supplementary Materials, Fig. S1). Results from the FFT analysis were then used to extract the dominant output frequency. This output frequency would correspond to the signal frequency “perceived” by downstream processes.
RESULTS
The critical frequency
By linearizing the mathematical model of the gene circuit and then decomposing the output using established methods (41–43) (also see Supplementary Materials), we could obtain the average output level (b):
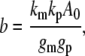 |
(2) |
where km is the transcription rate constant, kp is the translation rate constant, gm is the mRNA decay rate constant, and gp is the protein decay rate constant.
When changing a circuit parameter, we maintained the average output level at a constant (500 molecules) by adjusting the kp. For instance, if gm is increased 10-fold, b can be kept constant by increasing kp 10-fold. By doing so, we ensured that different circuit configurations or parameter settings would on average elicit the same average level of downstream gene expression (whether or not the input frequency was maintained through transmission).
The amplitude of the output oscillations (α) follows:
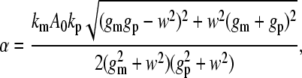 |
(3) |
where w=2πfin and fin is the frequency of input signal. The corresponding average noise level (σ) is
 |
(4) |
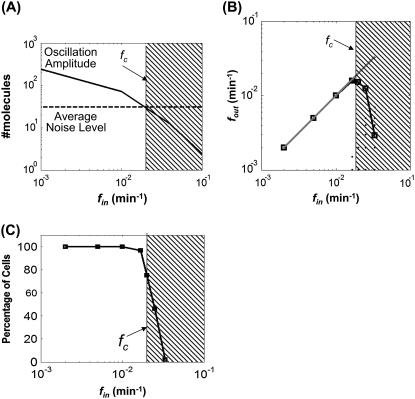
Eq. 3 defines a decreasing function of α with increasing input frequency (fin). This dependency reflects the low-pass filter characteristic of linear gene circuits (44). In contrast, σ is independent of fin (Eq. 4). Although the noise level oscillated in response to an oscillatory input (see Supplementary Material), we only used σ for analysis because the amplitude of noise oscillations was negligible (Fig. S2). Therefore, α would decrease below σ for sufficiently high fin (Fig. 2 A). In this region, frequency signals will be masked by the noise. The intersection between the σ curve and the α curve thus defines a critical frequency (fc), beyond which the circuit will fail to transmit the input signals. For the given circuit configuration, fc was ∼0.02/min.
FIGURE 2.
Critical frequency for the one-stage gene circuit. (A) The amplitude of output oscillations decreased with fin. fc was calculated as the intersection between the “average noise level” curve and the “oscillation amplitude” curve. (B) Calculations of fout for varying fin using stochastic simulations. (C) Fraction of stochastic simulations that generated correct fout (i.e., where fout = fin).
The results of the decomposition method were consistent with those from stochastic simulations. Specifically, we varied fin from 0.002/min to 0.033/min. For each fin, we carried out 200 stochastic simulations using the Gillespie algorithm (45). We then determined the dominant frequency for each output time course (fout) using FFT (Fig. 1). Fig. 2 B shows a parity plot between fin (x axis) and corresponding fout (y axis). The estimated fc (0.02/min) using the decomposition method corresponds to a transition region in the parity plot. In most simulations, when fin was <0.02/min, fout was equal to the corresponding fin. We consider these signals to be accurately transmitted despite cellular noise. Beyond 0.02/min, however, the average fout started to deviate from the corresponding fin and the deviation increased drastically with further increase of fin (Fig. 2 B, shaded region).
The drastic deviation was due to the fact that most output time courses gave incorrect fout. To gain better insight, we analyzed the percentage of the outputs that oscillated at the correct fout for each fin. This analysis can be considered as quantifying the fraction of a cell population that could correctly transmit the frequency signal, where behavior of each cell was represented by one stochastic simulation. It provided a quantitative measure of signal transmission fidelity for each fin (Fig. 2 C). Again, the estimated fc defines a transition point that corresponds to a drastic reduction of cells that generated the correct fout. When fin was <0.02/min, nearly 100% of the cells produced the correct fout, indicating high fidelity in signal transmission. However, for fin > fc, the percentage decreased drastically, indicating that the majority of cells failed to transmit the frequency signal accurately.
We also calculated signal/noise ratio (SNR) of each cell to assess the fidelity of frequency-signal transmission (Fig. S3). The SNR was calculated by dividing the power spectrum density (PSD) at fin by the maximum PSD of output signals. We assumed that a SNR of 1.0 would ensure accurate transmission of a signal. Again, the fc calculated from the analytical method corresponds to a sharp transition point where SNR dropped drastically due to the decreasing PSD at fin and the increasing PSD at noise frequencies. In this region (Fig. S3, shaded region), downstream processes may have a lower probability of reading the frequency signals due to the dominant PSD of the noise frequencies.
Therefore, both the analytical method and the “brute-force” method by stochastic simulation revealed an intrinsic property of frequency-signal transmission in the simple gene circuit: it is “all or none”, with the transmission fidelity limited by fc (Fig. 2, A–C). The analytical method also suggests how the fc emerges as the interplay between the amplitude and the noise level of each output oscillation. For subsequent analyses, we present results from the analytical method, unless noted otherwise.
Frequency multiplexing
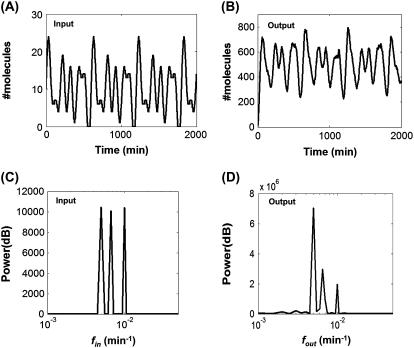
Frequency multiplexing is a mechanism where multiple frequencies are encoded in one signal. For example, frequency of [Ca2+] oscillations regulate several cellular processes, such as exocytosis (46), gene expression (21,47), cell growth, and differentiation (22), suggesting the possibility that multiple frequencies are multiplexed in [Ca2+] signals (48). To analyze the impact of noise on frequency multiplexing, we modeled transmission of a composite signal carrying three distinct fin that are <fc (Fig. 3 A), which generated a corresponding multiplexed output (Fig. 3 B). Frequency-domain analysis indicated that this composite signal was transmitted with absolute fidelity, where the three input frequencies (Fig. 3 C) were reproduced by the output (Fig. 3 D). The PSD of the three frequencies were at least 10-fold higher than the PSD of noise frequencies. These findings suggest an advantage of frequency encoding whereby multiple frequencies can be encoded in a composite signal and transmitted to downstream target genes or proteins with high fidelity. In addition, frequency signals may also be more cost-effective than amplitude signals. It has been shown that an oscillatory [Ca2+] signal is more effective than a constant [Ca2+] signal in inducing translocation of the nuclear factor NF-AT (49). In light of these observations, our results suggest that encoding multiple frequencies in cellular signals may be an efficient yet accurate signaling strategy.
FIGURE 3.
Transmission of a multiplexed signal. (A) A multiplexed input signal. (B) The corresponding output signal computed by stochastic simulation. (C) Power spectra of the input signal. (D) Power spectra of the output signal. Power spectra of the output signal indicate that all three frequencies were transmitted with complete fidelity. Even though power spectra decreased when the input frequency increased, they were still at least 10-fold higher than the power spectra of background noise. Three frequencies (0.005/min, 0.0067/min, and 0.01/min) were multiplexed in a composite signal with an amplitude of five molecules for each input frequency.
Nevertheless, processing of a multiplex signal requires an efficient frequency decoder that can respond to a specific range of frequencies. Although frequency decoders have been suggested both theoretically (23,50) and experimentally (21), the underlying mechanisms of frequency decoding in nature have not been well established experimentally. In this study, we have assumed that a SNR <1.0 (Fig. S3) would likely impact processing of the corresponding frequency signal by a downstream frequency decoder.
Modulation of fc by circuit parameters
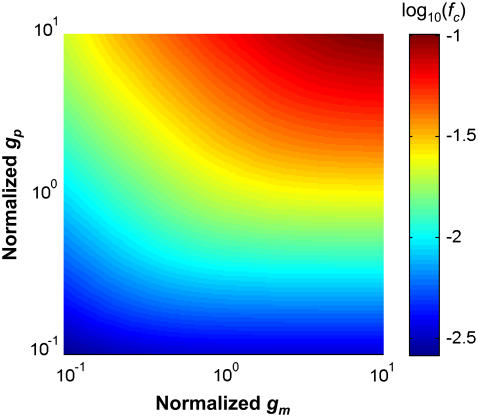
Circuit parameters such as transcription (km) and translation (kp) rate constants, as well as mRNA (gm) and protein (gp) decay rate constants, can affect the dynamics of gene circuits. Increasing decay rate constants can speed up enzymatic kinetics (51) and increase noise frequencies in simple gene circuits (36). Based on these studies, we hypothesized that increasing mRNA and protein decay rate constants can increase fc of a gene circuit. Indeed, Fig. 4 shows that increasing gm, gp, or both, led to a significant increase in fc, thus permitting faster signal transmission. Fig. S4, A and B, highlights the interplay between the oscillation amplitude and the noise level that gave rise to the fc curve. In all cases, increasing gm or gp, as well as kp, increased the oscillation amplitude more significantly than the noise level, which led to an increase in fc.
FIGURE 4.
Effects of mRNA or protein dynamics on fc demonstrate the dependence of fc on the speed of mRNA dynamics and the speed of protein dynamics. The speed of mRNA or protein dynamics was modulated by proportionally changing the translation rate constant, kp, and the mRNA or protein decay rate constant (gm or gp), keeping other parameters constant. It was normalized with respect to the base case (gm = 0.2/min, gp = 0.02/min). The color bar represents log10(fc).
Effects of feedback regulations
Regulatory mechanisms, such as negative feedback, positive feedback, and feedforward, are prevalent in cellular networks. They have been shown to impact generation, propagation, and control of cellular noise (24,26). For instance, negative feedback can reduce the noise in gene expression and improve response speed to a steady-state input (43,52–54). Here, we examined how regulatory mechanisms might impact frequency-signal transmission by simultaneous modulation of the oscillatory and noise components of the signal. Negative feedback was established by a protein that represses its own transcription; positive feedback was established by a protein that enhances its own transcription. We first analyzed feedback with an OR gate in regulating gene expression. In these models, the protein and the activator were assumed to bind to separate, independent binding sites (Fig. S5, A and B). These models were linearized (Eqs. S2–S4 and S6–S8) to allow decomposition of output signals. To study the effects of network architectures, we perturbed the dissociation constant (Kd) of the binding reaction between the output protein and its operator site. The strength of feedback regulation increases with an increase in 1/Kd. While varying feedback strength, we also changed the translation rate constant accordingly to maintain the same average protein output level. Qualitative aspects of our conclusions remained true for low to intermediate feedback strength (1/Kd < 10−3 nM−1) if other parameters (e.g., decay rate constants of the protein or mRNA) were changed to balance the average output level.
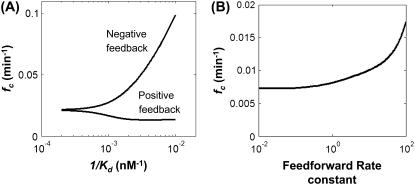
Fig. 5 A shows that negative feedback increased fc. This is because the negative feedback increased the oscillation amplitude but modulated the noise level in a biphasic manner (Fig. S6 A). The noise level decreased with increasing feedback strength (1/Kd) when the latter was small. However, when the feedback strength was sufficiently large (1/Kd > 10−3 nM−1), its further increase would increase the noise. The noise increased with strong negative feedback because of the constraint to maintain the same average output level. In particular, very strong negative feedback would lead to a very small number of mRNA molecules. To maintain the average output level, cells would have to amplify protein production from the small number of mRNA molecules. Yet, fast translation coupled with slow transcription has been shown to amplify noise in the protein level (55,56). If we introduced negative feedback without “balancing” it by increasing the translation rate, negative feedback would reduce noise, as reported previously (43). Although increased fc can be accounted for by the interplay between modulations of the noise amplitude and the oscillation amplitude (Fig. S6 A), a frequency shift of noise due to negative feedback (36) might also have contributed to this fc increment. Previous study using an oscillatory input signal has also shown that noise fluctuations resonate at a specific frequency due to negative feedback (41). This resonance, however, would not affect our conclusions here, because it occurred at a frequency much higher than fc (results not shown).
FIGURE 5.
Effects of circuit architectures on fc. (A) Dependence of fc on negative feedback and positive feedback. A high 1/Kd value corresponds to stronger feedback regulation. Cooperativity of feedback regulation (n) was fixed at 2. (B) Dependence of fc on feedforward rate constant (normalized with respect to the base value of 0.1/min). See Supplementary Material for description of models.
In contrast, positive feedback reduced fc (Fig. 5 A). In particular, it reduced the oscillation amplitude while modulating the noise level in a biphasic manner (Fig. S6 B). The noise level increased with increasing positive feedback strength when the latter was weak (small 1/Kd); it would decrease with the latter if it was sufficiently large (1/Kd >10−3 nM−1). This noise reduction at high positive feedback strength was due to the balancing reduction in the translation rate constant (results not shown) to maintain the same average output protein level. However, increasing positive feedback strength (balanced by reducing translation rate constant) also led to a decrease in the oscillation amplitude and this decrease was always greater than the noise reduction. As a consequence, overall positive feedback would always result in a decrease in fc. Further increase of the positive feedback strength led to a decrease in the noise level and a similar decrease in the oscillation amplitude. This would result in a plateau for fc.
To verify results from the linearized models of feedback regulations, we simulated the corresponding full nonlinear models by using the Gillespie algorithm (see Supplementary Materials). Similar to the case of the unregulated circuit, we calculated fout for a range of fin (5-min intervals) by using FFT to determine a critical point where the mean fout deviated significantly from the corresponding fin (Fig. 2 B). This “brute-force” method generated results qualitatively consistent with those of the linearized models (Figs. 5 A and S7, A and B). Generally, negative feedback increased fc but positive feedback reduced it. Hence, the linear models were accurate and they were useful to decipher the underlying mechanisms that limit the speed of signal transmission.
In addition to feedback regulation with OR gates, we analyzed feedback regulation with AND gates. In a negative-feedback loop with an AND gate (see Supplementary Materials, Eq. S5), the protein competes with the activator for the same binding site, hence represses its own transcription activation. In a positive-feedback loop with an AND gate (Eq. S9), the protein binds to the activator and enhances its own transcription. In either case, the model could not be solved analytically; thus, we resorted to numerical simulations. Interestingly, we found that feedback regulation with AND gates showed results qualitatively different from those of feedback regulation with OR gates. In particular, negative feedback with an AND gate had biphasic effects on fc: it only increased fc if the feedback strength was small (1/Kd < 0.0025 nM−1); further increase in 1/Kd, however, would lead to a decrease in fc. Similar to the positive feedback with an OR gate, the positive feedback with an AND gate also reduced fc. However, when 1/Kd increased to 0.01 nM−1, fc was increased by the positive feedback. In the feedback regulation with AND gates, the noise curves changed in a pattern similar to that of their counterparts with OR gates. For negative feedback, noise first decreased and then increased with increasing feedback strength (Fig. S7 C). For positive feedback, noise first increased and then decreased with increasing feedback strength (Fig. S7 D). In either case, however, amplitude of output oscillations did not change significantly with feedback strength, due to competition between the protein and the activator (for negative feedback) or their nonlinear interaction (for positive feedback). As a consequence, fc depended solely on the inverse of the noise curve: fc increased when noise decreased, and vice versa.
Effects of feedforward regulations
We further investigated signal transmission in a two-stage circuit (Fig. S5 C). Without regulation, the two-stage circuit fc (0.007/min) was lower than that of the one-stage circuit (0.02/min). In general, fc decreased progressively with increasing cascade length (results not shown). This finding is consistent with low-pass property of long-cascade circuits (33,57). However, the fc of the two-stage cascades can be increased by incorporating a feedforward regulation. To illustrate this point, we here considered a coherent Type 1 feedforward regulation with an OR gate (58). In this circuit, either the activator molecule or the protein generated from the first stage can activate the second stage (Fig. S5 C). Our results indicated that increasing feedforward rate constants increased fc (Fig. 5 B). At small feedforward rate constants (<0.1/min), fc did not change significantly due to negligible changes in the oscillation amplitude and noise level (Fig. S8). In this region, the contribution of feedforward regulation toward the expression level and the noise level of the second stage were masked by the signal and noise from the first stage. At higher feedforward rate constants, fc increased drastically because the oscillation amplitude increased significantly faster with respect to the noise level. Essentially, strong feedforward regulation (with an OR gate) creates a “short cut” between the input signal and the output. However, more detailed analysis is required to elucidate the effects of other types of feedforward motifs (58) on frequency signal transmission.
DISCUSSION
Our work builds upon previous studies on characteristics of noise generation, propagation, and modulation (33,34). In addition to analysis in the amplitude domain, recent work has shown that noise frequency structures are affected by autoregulation in gene circuits driven by a constant input (35,36). Along another line, it has been suggested that noise characteristics of a circuit in response to an oscillatory input may help infer the underlying network properties (41). Here, we have extended and applied these concepts to analyze the impact of cellular noise on the transmission of frequency signals, introducing the concept of critical frequency (fc).
The critical frequency defines the fundamental speed limit of signal transmission in a gene circuit: a higher fc will allow faster response. Only signals with frequencies below fc can be transmitted with high fidelity (Fig. 2, B and C). We further note that signals with different frequencies can be multiplexed as long as all these frequencies are <fc. Thus, fc also defines the capacity or the bandwidth of a circuit in processing frequency signals. This fundamental speed limit for signal transmission may be a general, intrinsic property of diverse cellular networks, including signaling cascades and metabolic pathways. Simulations indicate that a critical frequency also exists for a MAPK signaling pathway (Fig. S9) or in a gene circuit consisting of repressors (results not shown). However, aspects of our predictions may differ when considering some nonlinear gene circuits. For example, negative feedback will introduce instability and amplify noise if the time delay is considerably long (59). Stochastic resonance can occur in nonlinear circuits driven by noise (60).
The speed of reliable signal transmission can be constrained by the associated metabolic cost. In the unregulated gene circuit, for instance, increasing fc always requires an increase in the oscillation amplitude (Fig. S4). This increase will require faster protein or mRNA production and turnover and, as such, will incur faster consumption of energy and resources. In this scenario, cells may need to properly balance the speed of signal transmission and the corresponding metabolic cost to maximize their fitness. It has been suggested that energy consumption can constrain evolution of proteins (61) and organization of viral genomes (62,63). It will be interesting to explore whether evolution of the cellular networks involved in frequency-signal transmission has been constrained by the available energy and resources.
In nature, the speed of signal transmission will be further influenced by extrinsic noise, which arises from other cellular processes or from the extracellular environment (25,64). The extrinsic noise will increase the total noise level and further decrease the fc (Fig. S10). In general, signals with low frequencies can be transmitted in noisier environments. For example, transmission of a signal with fin of 0.001/min in the linear gene circuit (Fig. 1 A) will not be affected even if the noise level increases appreciably. However, the full picture may be more complex: the frequency of extrinsic noise may also affect the fidelity of frequency signals. It has been suggested that extrinsic noise contains low-frequency signals (31,65). Perhaps these slow fluctuations and the intrinsic noise together define an optimal frequency bandwidth for frequency-signal transmission. Further analysis will be needed to elucidate these questions.
We have illustrated the high fidelity in the transmission of frequency signals if their frequencies are below the critical frequency of a given gene circuit. In natural systems, applicability of this signal-transmission strategy depends on the complexity and adaptability of the available cellular infrastructure. We expect frequency signals to be more likely adopted by higher organisms that can provide sufficiently complex infrastructure, including encoders, decoders, and metabolic capacities to transmit frequency signals. Consistent with this notion, we have found many examples where frequency signals may play an important role in regulating physiological functions in higher organisms, including immune response, metabolism, and sleep cycle (Table S1). In contrast, frequency-signal transmission will likely be less common in prokaryotes, as they lack long regulatory gene cascades to provide the adequate infrastructure and energy needed to transmit diverse frequency signals (66). Yet, for critical processes, frequency signals appear to be adopted even in bacteria. In cell-division regulation, for example, the oscillatory dynamics of MinD and MinE proteins at particular frequencies determine the formation of septum in the middle of cells (67,68). Consistent with our findings, it has been suggested that this complex process is highly noise-resistant (69). Nevertheless, this signal transmission strategy will require higher metabolic costs due to its complex cellular architecture. After this study, it will be interesting to examine the tradeoff between energy requirements and signaling fidelity of frequency decoders in biological systems.
Finally, we note that our modeling predictions can be tested experimentally by implementing and measuring the responses of synthetic gene circuits in model organisms such as bacteria and yeast. To obtain fc, the gene circuits can be modulated by using oscillatory concentrations of small inducer molecules, such as isopropyl-ß-D-thiogalactopyranoside. In the long term, the high fidelity of frequency signals and the ability to multiplex frequency signals suggests a promising means of programming reliable cellular computation using synthetic gene circuits (40).
SUPPLEMENTARY MATERIAL
To view all of the supplemental files associated with this article, visit www.biophysj.org.
Supplementary Material
Acknowledgments
We thank Mike West, Ron Weiss, Eric Haseltine, Hao Song, and Yu Tanouchi for helpful discussions.
This work was partially supported by a David and Lucile Packard Fellowship (to L.Y.), a Whitaker Foundation graduate assistantship (to C.T.), and the Duke University Computational Biology and Bioinformatics Program (to F.R.). Further support was provided by a Biotechnology Predoctoral Training Fellowship to F.R. from National Institutes of Health grant GM08555.
The authors declare no competing interests.
Editor: Alexander van Oudenaarden.
References
- 1.Harmer, S. L., S. Panda, and S. A. Kay. 2001. Molecular bases of circadian rhythms. Annu. Rev. Cell Dev. Biol. 17:215–253. [DOI] [PubMed] [Google Scholar]
- 2.Pourquie, O. 2003. The segmentation clock: converting embryonic time into spatial pattern. Science. 301:328–330. [DOI] [PubMed] [Google Scholar]
- 3.Berridge, M. J., M. D. Bootman, and H. L. Roderick. 2003. Calcium signalling: dynamics, homeostasis and remodelling. Nat. Rev. Mol. Cell Biol. 4:517–529. [DOI] [PubMed] [Google Scholar]
- 4.Berridge, M. J. 1997. The AM and FM of calcium signalling. Nature. 386:759–760. [DOI] [PubMed] [Google Scholar]
- 5.Lahav, G., N. Rosenfeld, A. Sigal, N. Geva-Zatorsky, A. J. Levine, M. B. Elowitz, and U. Alon. 2004. Dynamics of the p53-Mdm2 feedback loop in individual cells. Nat. Genet. 36:147–150. [DOI] [PubMed] [Google Scholar]
- 6.Nelson, D. E., A. E. Ihekwaba, M. Elliott, J. R. Johnson, C. A. Gibney, B. E. Foreman, G. Nelson, V. See, C. A. Horton, D. G. Spiller, S. W. Edwards, H. P. McDowell, J. F. Unitt, E. Sullivan, R. Grimley, N. Benson, D. Broomhead, D. B. Kell, and M. R. White. 2004. Oscillations in NF-kappaB signaling control the dynamics of gene expression. Science. 306:704–708. [DOI] [PubMed] [Google Scholar]
- 7.Holtzendorff, J., D. Hung, P. Brende, A. Reisenauer, P. H. Viollier, H. H. McAdams, and L. Shapiro. 2004. Oscillating global regulators control the genetic circuit driving a bacterial cell cycle. Science. 304:983–987. [DOI] [PubMed] [Google Scholar]
- 8.Klevecz, R. R., and D. B. Murray. 2001. Genome wide oscillations in expression. Wavelet analysis of time series data from yeast expression arrays uncovers the dynamic architecture of phenotype. Mol. Biol. Rep. 28:73–82. [DOI] [PubMed] [Google Scholar]
- 9.Klevecz, R. R., J. Bolen, G. Forrest, and D. B. Murray. 2004. A genomewide oscillation in transcription gates DNA replication and cell cycle. Proc. Natl. Acad. Sci. USA. 101:1200–1205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Jouve, C., I. Palmeirim, D. Henrique, J. Beckers, A. Gossler, D. Ish-Horowicz, and O. Pourquie. 2000. Notch signalling is required for cyclic expression of the hairy-like gene HES1 in the presomitic mesoderm. Development. 127:1421–1429. [DOI] [PubMed] [Google Scholar]
- 11.Morales, A. V., Y. Yasuda, and D. Ish-Horowicz. 2002. Periodic Lunatic fringe expression is controlled during segmentation by a cyclic transcriptional enhancer responsive to notch signaling. Dev. Cell. 3:63–74. [DOI] [PubMed] [Google Scholar]
- 12.Palmeirim, I., D. Henrique, D. Ish-Horowicz, and O. Pourquie. 1997. Avian hairy gene expression identifies a molecular clock linked to vertebrate segmentation and somitogenesis. Cell. 91:639–648. [DOI] [PubMed] [Google Scholar]
- 13.Forsberg, H., F. Crozet, and N. A. Brown. 1998. Waves of mouse Lunatic fringe expression, in four-hour cycles at two-hour intervals, precede somite boundary formation. Curr. Biol. 8:1027–1030. [DOI] [PubMed] [Google Scholar]
- 14.Jiang, Y. J., B. L. Aerne, L. Smithers, C. Haddon, D. Ish-Horowicz, and J. Lewis. 2000. Notch signalling and the synchronization of the somite segmentation clock. Nature. 408:475–479. [DOI] [PubMed] [Google Scholar]
- 15.Conlon, R. A., A. G. Reaume, and J. Rossant. 1995. Notch1 is required for the coordinate segmentation of somites. Development. 121:1533–1545. [DOI] [PubMed] [Google Scholar]
- 16.Oka, C., T. Nakano, A. Wakeham, J. L. de la Pompa, C. Mori, T. Sakai, S. Okazaki, M. Kawaichi, K. Shiota, T. W. Mak, and T. Honjo. 1995. Disruption of the mouse RBP-J κ gene results in early embryonic death. Development. 121:3291–3301. [DOI] [PubMed] [Google Scholar]
- 17.Jen, W. C., D. Wettstein, D. Turner, A. Chitnis, and C. Kintner. 1997. The Notch ligand, X-Δ-2, mediates segmentation of the paraxial mesoderm in Xenopus embryos. Development. 124:1169–1178. [DOI] [PubMed] [Google Scholar]
- 18.Pourquie, O., and K. Kusumi. 2001. When body segmentation goes wrong. Clin. Genet. 60:409–416. [DOI] [PubMed] [Google Scholar]
- 19.Franken, P., L. Lopez-Molina, L. Marcacci, U. Schibler, and M. Tafti. 2000. The transcription factor DBP affects circadian sleep consolidation and rhythmic EEG activity. J. Neurosci. 20:617–625. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Richardson, G. S. 2005. The human circadian system in normal and disordered sleep. J. Clin. Psychiatry. 66(Suppl. 9):3–9. [PubMed] [Google Scholar]
- 21.Dolmetsch, R. E., K. Xu, and R. S. Lewis. 1998. Calcium oscillations increase the efficiency and specificity of gene expression. Nature. 392:933–936. [DOI] [PubMed] [Google Scholar]
- 22.Kupzig, S., S. A. Walker, and P. J. Cullen. 2005. The frequencies of calcium oscillations are optimized for efficient calcium-mediated activation of Ras and the ERK/MAPK cascade. Proc. Natl. Acad. Sci. USA. 102:7577–7582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Samoilov, M., A. Arkin, and J. Ross. 2002. Signal processing by simple chemical systems. J. Phys. Chem. A. 106:10205–10221. [Google Scholar]
- 24.Kaern, M., T. C. Elston, W. J. Blake, and J. J. Collins. 2005. Stochasticity in gene expression: from theories to phenotypes. Nat. Rev. Genet. 6:451–464. [DOI] [PubMed] [Google Scholar]
- 25.Raser, J. M., and E. K. O'Shea. 2005. Noise in gene expression: origins, consequences, and control. Science. 309:2010–2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Rao, C. V., D. M. Wolf, and A. P. Arkin. 2002. Control, exploitation and tolerance of intracellular noise. Nature. 420:231–237. [DOI] [PubMed] [Google Scholar]
- 27.Paulsson, J. 2004. Summing up the noise in gene networks. Nature. 427:415–418. [DOI] [PubMed] [Google Scholar]
- 28.Bahar, R., C. H. Hartmann, K. A. Rodriguez, A. D. Denny, R. A. Busuttil, M. E. Dolle, R. B. Calder, G. B. Chisholm, B. H. Pollock, C. A. Klein, and J. Vijg. 2006. Increased cell-to-cell variation in gene expression in ageing mouse heart. Nature. 441:1011–1014. [DOI] [PubMed] [Google Scholar]
- 29.Bialek, W., and S. Setayeshgar. 2005. Physical limits to biochemical signaling. Proc. Natl. Acad. Sci. USA. 102:10040–10045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Colman-Lerner, A., A. Gordon, E. Serra, T. Chin, O. Resnekov, D. Endy, C. G. Pesce, and R. Brent. 2005. Regulated cell-to-cell variation in a cell-fate decision system. Nature. 437:699–706. [DOI] [PubMed] [Google Scholar]
- 31.Rosenfeld, N., J. W. Young, U. Alon, P. S. Swain, and M. B. Elowitz. 2005. Gene regulation at the single-cell level. Science. 307:1962–1965. [DOI] [PubMed] [Google Scholar]
- 32.Barkai, N., and S. Leibler. 2000. Circadian clocks limited by noise. Nature. 403:267–268. [DOI] [PubMed] [Google Scholar]
- 33.Hooshangi, S., S. Thiberge, and R. Weiss. 2005. Ultrasensitivity and noise propagation in a synthetic transcriptional cascade. Proc. Natl. Acad. Sci. USA. 102:3581–3586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Pedraza, J. M., and A. van Oudenaarden. 2005. Noise propagation in gene networks. Science. 307:1965–1969. [DOI] [PubMed] [Google Scholar]
- 35.Simpson, M. L., C. D. Cox, and G. S. Sayler. 2003. Frequency domain analysis of noise in autoregulated gene circuits. Proc. Natl. Acad. Sci. USA. 100:4551–4556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Austin, D. W., M. S. Allen, J. M. McCollum, R. D. Dar, J. R. Wilgus, G. S. Sayler, N. F. Samatova, C. D. Cox, and M. L. Simpson. 2006. Gene network shaping of inherent noise spectra. Nature. 439:608–611. [DOI] [PubMed] [Google Scholar]
- 37.Andrews, B. W., T. M. Yi, and P. A. Iglesias. 2006. Optimal noise filtering in the chemotactic response of Escherichia coli. PLoS Comput. Biol. 2:e154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Alter, O., P. O. Brown, and D. Botstein. 2000. Singular value decomposition for genome-wide expression data processing and modeling. Proc. Natl. Acad. Sci. USA. 97:10101–10106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Klevecz, R. R. 2000. Dynamic architecture of the yeast cell cycle uncovered by wavelet decomposition of expression microarray data. Funct. Integr. Genomics. 1:186–192. [DOI] [PubMed] [Google Scholar]
- 40.Tan, C., H. Song, J. Niemi, and L. You. 2007. A synthetic biology challenge: making cells compute. Mol. Biosyst. 3:343–353. [DOI] [PubMed] [Google Scholar]
- 41.Lipan, O., and W. H. Wong. 2005. The use of oscillatory signals in the study of genetic networks. Proc. Natl. Acad. Sci. USA. 102:7063–7068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Gadgil, C., C. H. Lee, and H. G. Othmer. 2005. A stochastic analysis of first-order reaction networks. Bull. Math. Biol. 67:901–946. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Thattai, M., and A. van Oudenaarden. 2001. Intrinsic noise in gene regulatory networks. Proc. Natl. Acad. Sci. USA. 98:8614–8619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Walleczek, J. 2000. Self-Organized Biological Dynamics and Nonlinear Control. Cambridge University Press, Cambridge, UK.
- 45.Gillespie, D. T. 1977. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 81:2340–2361. [Google Scholar]
- 46.Tse, A., F. W. Tse, W. Almers, and B. Hille. 1993. Rhythmic exocytosis stimulated by GnRH-induced calcium oscillations in rat gonadotropes. Science. 260:82–84. [DOI] [PubMed] [Google Scholar]
- 47.Li, W. H., J. Llopis, M. Whitney, G. Zlokarnik, and R. Y. Tsien. 1998. Cell-permeant caged InsP3 ester shows that Ca2+ spike frequency can optimize gene expression. Nature. 392:936–941. [DOI] [PubMed] [Google Scholar]
- 48.Berridge, M. J. 2005. Unlocking the secrets of cell signaling. Annu. Rev. Physiol. 67:1–21. [DOI] [PubMed] [Google Scholar]
- 49.Tomida, T., K. Hirose, A. Takizawa, F. Shibasaki, and M. Iino. 2003. NFAT functions as a working memory of Ca2+ signals in decoding Ca2+ oscillation. EMBO J. 22:3825–3832. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Hasty, J., M. Dolnik, V. Rottschafer, and J. J. Collins. 2002. Synthetic gene network for entraining and amplifying cellular oscillations. Phys. Rev. Lett. 88:148101. [DOI] [PubMed] [Google Scholar]
- 51.Schimke, R. T. 1969. On the roles of synthesis and degradation in regulation of enzyme levels in mammalian tissues. Curr. Top. Cell. Regul. 1:77–124. [Google Scholar]
- 52.Becskei, A., and L. Serrano. 2000. Engineering stability in gene networks by autoregulation. Nature. 405:590–593. [DOI] [PubMed] [Google Scholar]
- 53.Rosenfeld, N., M. B. Elowitz, and U. Alon. 2002. Negative autoregulation speeds the response times of transcription networks. J. Mol. Biol. 323:785–793. [DOI] [PubMed] [Google Scholar]
- 54.Savageau, M. A. 1974. Comparison of classical and autogenous systems of regulation in inducible operons. Nature. 252:546–549. [DOI] [PubMed] [Google Scholar]
- 55.Blake, W. J., M. Kaern, C. R. Cantor, and J. J. Collins. 2003. Noise in eukaryotic gene expression. Nature. 422:633–637. [DOI] [PubMed] [Google Scholar]
- 56.Ozbudak, E. M., M. Thattai, I. Kurtser, A. D. Grossman, and A. van Oudenaarden. 2002. Regulation of noise in the expression of a single gene. Nat. Genet. 31:69–73. [DOI] [PubMed] [Google Scholar]
- 57.Becskei, A., M. G. Boselli, and A. van Oudenaarden. 2004. Amplitude control of cell-cycle waves by nuclear import. Nat. Cell Biol. 6:451–457. [DOI] [PubMed] [Google Scholar]
- 58.Mangan, S., and U. Alon. 2003. Structure and function of the feed-forward loop network motif. Proc. Natl. Acad. Sci. USA. 100:11980–11985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Elowitz, M. B., and S. Leibler. 2000. A synthetic oscillatory network of transcriptional regulators. Nature. 403:335–338. [DOI] [PubMed] [Google Scholar]
- 60.Wiesenfeld, K., and F. Moss. 1995. Stochastic resonance and the benefits of noise: from ice ages to crayfish and SQUIDs. Nature. 373:33–36. [DOI] [PubMed] [Google Scholar]
- 61.Drummond, D. A., J. D. Bloom, C. Adami, C. O. Wilke, and F. H. Arnold. 2005. Why highly expressed proteins evolve slowly. Proc. Natl. Acad. Sci. USA. 102:14338–14343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.You, L., and J. Yin. 2006. Evolutionary design on budget: robustness and optimality of bacteriophage T7. IEE Proc. Syst. Biol. 153:46–52. [DOI] [PubMed] [Google Scholar]
- 63.Lim, K. I., T. Lang, V. Lam, and J. Yin. 2006. Model-based design of growth-attenuated viruses. PLoS Comput. Biol. 2:e116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Volfson, D., J. Marciniak, W. J. Blake, N. Ostroff, L. S. Tsimring, and J. Hasty. 2006. Origins of extrinsic variability in eukaryotic gene expression. Nature. 439:861–864. [DOI] [PubMed] [Google Scholar]
- 65.Spudich, J. L., and D. E. Koshland, Jr. 1976. Non-genetic individuality: chance in the single cell. Nature. 262:467–471. [DOI] [PubMed] [Google Scholar]
- 66.Rosenfeld, N., and U. Alon. 2003. Response delays and the structure of transcription networks. J. Mol. Biol. 329:645–654. [DOI] [PubMed] [Google Scholar]
- 67.Raskin, D. M., and P. A. de Boer. 1999. Rapid pole-to-pole oscillation of a protein required for directing division to the middle of Escherichia coli. Proc. Natl. Acad. Sci. USA. 96:4971–4976. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Howard, M., and K. Kruse. 2005. Cellular organization by self-organization: mechanisms and models for Min protein dynamics. J. Cell Biol. 168:533–536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Kerr, R. A., H. Levine, T. J. Sejnowski, and W. J. Rappel. 2006. Division accuracy in a stochastic model of Min oscillations in Escherichia coli. Proc. Natl. Acad. Sci. USA. 103:347–352. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.