Coarse-Grained Free Energy Functions for Studying Protein Conformational Changes: A Double-Well Network Model

Abstract

In this work, a double-well network model (DWNM) is presented for generating a coarse-grained free energy function that can be used to study the transition between reference conformational states of a protein molecule. Compared to earlier work that uses a single, multidimensional double-well potential to connect two conformational states, the DWNM uses a set of interconnected double-well potentials for this purpose. The DWNM free energy function has multiple intermediate states and saddle points, and is hence a “rough” free energy landscape. In this implementation of the DWNM, the free energy function is reduced to an elastic-network model representation near the two reference states. The effects of free energy function roughness on the reaction pathways of protein conformational change is demonstrated by applying the DWNM to the conformational changes of two protein systems: the coil-to-helix transition of the DB-loop in G-actin and the open-to-closed transition of adenylate kinase. In both systems, the rough free energy function of the DWNM leads to the identification of distinct minimum free energy paths connecting two conformational states. These results indicate that while the elastic-network model captures the low-frequency vibrational motions of a protein, the roughness in the free energy function introduced by the DWNM can be used to characterize the transition mechanism between protein conformations.

INTRODUCTION

Transitions between different conformational states are essential for the function of many proteins (1–3). Understanding the molecular mechanism of protein conformational changes: how they are induced, how they proceed, and how they are regulated, is thus one of the fundamental challenges in biology and biophysics. This understanding of protein structural transitions has mainly been developed by determining the x-ray structures of proteins at different states; for example, before and after binding to ligand molecule(s) (4–7). Although static information does not provide a clear mechanistic picture, x-ray structures often reveal invaluable insight into the structural transitions and the key interactions that may be involved (4–7). However, a molecular-level understanding of conformational changes requires sequential measurements of protein structure during a transition event. This challenge has motivated the development and use of cryo-electron microscopy (8–11), time-resolved x-ray (12–15), nuclear magnetic resonance (16,17), atomistic force spectroscopy (18,19), and single-molecule spectroscopy such as florescence energy transfer (20,21) to probe the dynamics of protein conformational changes. However, the spatial and temporal resolution of these measurements is still limited for describing protein conformational changes.

Molecular dynamics (MD) simulations (2,22), on the other hand, can be used to trace the dynamics of protein molecules at the atomistic scale. However, the accessible timescale (∼100 ns) is still too short compared to that of most protein conformational changes (μs-s). Even though significant advances have been made in computational methods for studying rare events (23–26), the complicated and rough potential energy surface of proteins still makes it very difficult to study structural transitions at the atomistic scale. Therefore, coarse-grained (CG) models, with the reduction of degrees of freedom and the consequent extension of accessible timescales, may be very useful for studying protein conformational changes (27–35). CG models of polypeptides often involve only one site or two sites (one for backbone and the other for side chain) for each amino-acid residue (33), and the resulting CG potential energy function is effectively a free energy function in a reduced dimensional space. Since the molecular mechanics of a protein involves the interplay of different specific interactions such as dihedral angles, hydrogen bonds, electrostatic interactions, van der Waals interactions, and hydrophobic interactions, etc., the fewer degrees of freedom at the CG scale can make it very difficult to accurately describe the structural properties and the relative free energies between the different conformational states of a protein molecule.

One strategy to overcome this difficulty is to incorporate the information of native structures in CG force fields to ensure that the native fold of a protein is the global minimum of a free energy function. A typical example of this kind is the Gō model in which only native contacts have attractive interactions (36,37). Since Gō-like models have a funnel-like energy landscape, they have been applied to study the kinetics and mechanism of protein folding (38–45). Another example of utilizing native structures is the elastic network model (ENM) (46–48). In the typical implementation of the ENM, only the C_α atoms are usually kept to represent a protein molecule (33,46,49). Based on a reference structure (typically an x-ray structure) of the protein, harmonic interactions are placed between C_α atoms that are within a cutoff distance, and a universal force constant is then used for these harmonic interactions. Normal mode analysis (49,50) can be performed with ENM to calculate the mean-square displacements of each C_α from its position in the reference structure. Mean-squared displacements are commonly used, for example, to characterize the structural flexibility of protein by x-ray crystallography (B factors) (49,50). Despite its simplicity and the use of a universal force constant, the ENM describes the distribution of the mean-squared displacement quite well for many proteins when compared to x-ray data (2,22,46,47,49). It should be noted that these comparisons are based on the shape of mean-squared displacements, i.e., their relative magnitudes, but not their absolute values.

The fact that a universal value of the force constant in the ENM can reasonably capture the structural flexibility of a protein suggests that the shape of the native structure is a determining factor for its structural flexibility (45–47,49,51–58). It has also been shown that the mean-squared displacement of each residue in a protein is inversely proportional to its local packing density (52). This result is also consistent with the ENM in that if a C_α is more closely packed, it is harmonically connected to more sites and thus more restrained, and its mean-squared displacement will thus be smaller compared to a less packed site. Since mean-squared displacements are dominated by low frequency vibrational modes that depend strongly on the shape of a macromolecule, applying normal mode analysis to the ENM also allows the visualization of the low frequency modes that may likely be related to protein function.

If a protein molecule has two distinct x-ray structures for two different conformational states, e.g., before and after binding to a ligand, each structure can be used as the reference state in an ENM representation of the protein in that state. If each ENM can be used to describe the structural flexibility around its reference structure, an interpolation between these two ENMs may be a good starting point to study the conformational change between these two states. Toward this end, several very insightful schemes have been proposed to study protein conformational changes by bridging two CG free energy functions (59–64). For example, Kim et al. (59) and Miyashita et al. (60) defined cost functions to limit the deviation of the intermediates along a path from the reference structures, and the intermediate structures along a path are estimated by minimizing these cost functions. In the work of Maragakis and Karplus (62), a novel empirical valence bondlike (65,66) approach was applied to interpolate two multidimensional harmonic potentials, each corresponding to the ENM associated with a particular conformation, structure, and the resulting model was referred to as the plastic network model (PNM) (62). A similar interpolation scheme has also been applied to Gō-like models (64). An alternative interpolation scheme with exponential Boltzmann weighting between two Gō models has further been proposed (61); this approach may also be applied to the ENM.

Since a multidimensional reference free energy function is mixed with another one in all of the aforementioned schemes (59–64), a single reaction channel is generated to connect the two states. However, the true free energy function for the protein conformational space is not only highly dimensional but also rough and complicated (22,38,41) so that multiple reaction channels connecting two conformational states may exist. With only knowledge of reference state structures, the development of an efficient and accurate CG method to interpolate two effective free energy functions, which effectively includes the roughness in the underlying potential energy surface, is an ongoing challenge in modeling protein conformational change. To use fewer degrees of freedom to represent the complicated behavior of an underlying fine-grained system such as a protein, the need to interpolate between different free energy functions will be an important future aspect of CG model development, so that such models are not overly restricted to a conformational space related to their native structures. In this spirit, Tozzini et al. have used a quartic double-well potential to interpolate the backbone dihedral angle potentials corresponding to different regions of the Ramachandran plot in their CG model for peptide and protein systems (67–69).

In this work, we propose a new scheme to interpolate two ENM free energy functions, each of which is based on one of the x-ray structures of a protein. Instead of generating a single, multidimensional reactive potential, our scheme uses a set of interconnected, one-dimensional double-well potentials to connect the two ENM free energy functions, and is thus referred to a double-well network model (DWNM). Consequently, many local minima and saddle points can be formed in the effective free energy function and multiple reaction channels can be found to connect one protein conformation to another.

It is important to note that this DWNM represents a physically distinct picture for describing protein conformation compared to the ENM. The latter is similar to the venerable Debye elastic model for homogeneous solids, with the important distinction that protein shape is imposed on the interconnected elastic network and hence imparts a unique character to the resulting vibrational modes of the system related to the protein native structure. On the other hand, the DWNM, while retaining the ENM character in its stable states, is more similar to the physical model of a glass, which is very different from an elastic medium. The DWNM is therefore an attempt to step back from the many molecular-scale details of protein structure and conformational change. It is, in some sense, a minimalist construction that hopefully captures certain general coarse-grained (though still complicated) features of protein conformation change.

The reminder of this article is organized as follows: The formulation and particular choice for the numerical implementation of the DWNM is described in the next section. The DWNM is then applied to the conformational change of two protein systems: the coil-to-helix transition of the DB-loop in the protein actin (G-actin) induced by ATP hydrolysis and the open-to-closed transition of adenylate kinase due to the binding of ATP and AMP substrates. The minimum free energy paths obtained via the DWNM are compared with the result of the PNM to highlight the effect of free energy function roughness on protein conformational change at the CG level. Finally, concluding remarks will be given.

THEORY

Double-well network model (DWNM)

The CG free energy function of the ENM can be written as

(1)

where R_ij is the distance between CG sites i and j, 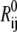is the distance between i and j in the reference structure, R_c is the cutoff distance within which a harmonic potential, 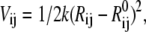is assigned between two sites, and k is the universal ENM force constant. Note that in coarse-grained modeling, the molecular degrees of freedom that are not included in the model are effectively integrated-out from the partition function, so that a resulting many-dimensional potential of mean force (configurational free energy distribution function) effectively describes the interactions between the remaining degrees of freedom. Although the connection of this coarse-graining concept to the elastic or double-well network models is not completely straightforward, in this article such a connection will be asserted and thus particular functional forms are assumed for the resulting free energy functions for each model in Eqs. 1–5. An alternative view is that these functions are potential-energy functions, but the connection of these network models to the actual molecular potential-energy functions of proteins seems much less clear.

With two reference states of a protein molecule, for example, two x-ray structures for the with-ENM force constants A and B states, two ENMs can be constructed:

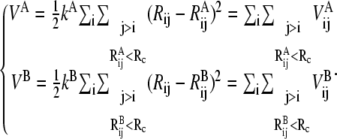(2)

In Eq. 2, V^A and V^B are the ENMs for states A and B, respectively; 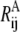and 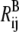are the distances between sites i and j in the reference structure of A and B states, respectively; 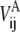and 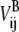are the harmonic potential for the ij pair in the A and B state, respectively, and k^A and k^B are the effective force constants used in the ENMs for states A and B, respectively.

First we will describe an approach similar to the PNM, and then we will introduce the DWNM. By using an empirical valence bondlike approach (65,66), these two free energy functions can be combined as

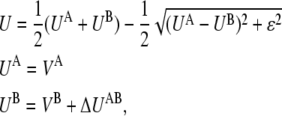(3)

and a single first-order saddle point is defined connecting A and B. In Eq. 3, ΔU^AB is the free energy difference between the A and B states. The coupling parameter ɛ is a nonzero number to ensure the continuity of the derivative of U; for a specified value of ɛ, the location, curvature, and the value of U (hence the barrier) at the saddle point are also determined. For example, in the implementation of the PNM (62), ɛ is chosen to be small (compared to U_A and U_B), and the saddle point is thus located around the position where U_A ≈ U_B with a resulting cusped barrier (62).

As a general way of interpolating between two potentials, the term ɛ in Eq. 3 can be a function of all R_i values, i.e., ɛ(R_i) values provide additional flexibility as to how the A and B state free energy functions are coupled. If information on the barrier, curvature, and location of the saddle point are available, a function ɛ(R_i) may be developed to reproduce these parameters (66).

The value of ΔU^AB in Eq. 3, if known from experimental measurements or other means, may also be implemented. The effects of ΔU^AB, though, may be examined empirically by using different values of ΔU^AB in pathway calculations.

In the DWNM, instead of generating a single, multidimensional double-well potential, U_A and U_B can be viewed as a network of one-dimensional double-well potentials:

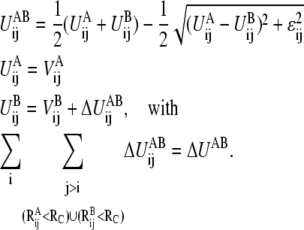(4)

Importantly, each 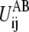in Eq. 4 is a one-dimensional double-well potential as a function of R_ij i.e., with one well located at 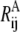and the other at The term 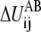is the contribution to ΔU^AB from the ij pair and the summation of 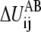thus equals ΔU^AB. There could be many ways to distribute ΔU^AB into 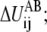for example, by an even distribution. In such a case, if there is a total of N^TOT distinct harmonic interactions in the model, then 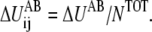When more information about the underlying free energy function is available through methods such as all-atom MD simulations, this flexibility of distributing ΔU^AB into of the DWNM may be very useful to systematically refine the CG model for better quantitative agreement with all-atom simulations. Since our focus is the effect of free energy function roughness on the pathway of structural transition, such a procedure will not be discussed in this work and a value of zero will be used for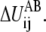

In the DWNM, the combined potential energy function is thus

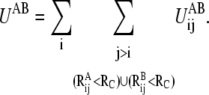(5)

At each reference state of the protein molecule, the DWNM reduces to the corresponding ENMs defined in Eq. 2.

For each 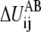in Eq. 4, ɛ_ij also specifies the location, barrier, and curvature at the saddle point of 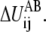If a general form, ɛ_ij(R_ij), is used, the information of the saddle point location, barrier, and curvature can be employed to specify the 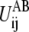double-well. In some applications, two minima may not be necessary for each ij pair to characterize the conformational change. In such cases, ɛ_ij(R_ij) can be adjusted so there is no saddle point between 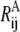and 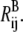Information to help determine ɛ_ij(R_ij) may be obtained from all-atom simulation. In cases where no such information is available, the following approximate procedure may be used to represent ɛ_ij(R_ij):

1. In the case ΔU^AB = 0, the maximum of 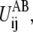R*_ij, is the crossing point between the two reference potentials, i.e.,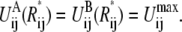

2. The Hessian of 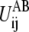at R*_ij is estimated to be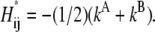

3. The barrier height of 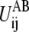is assigned a value that increases with the difference in R_ij between the two reference structures, i.e., 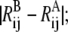for example, by multiplying 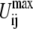defined in step 1 by a factor α, where α < 1. In this implementation, the same value of α is applied to all ij pairs.

4. Following Chang and Miller (66), ɛ_ij(R_ij) is written as

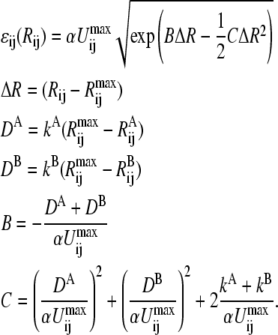(6)

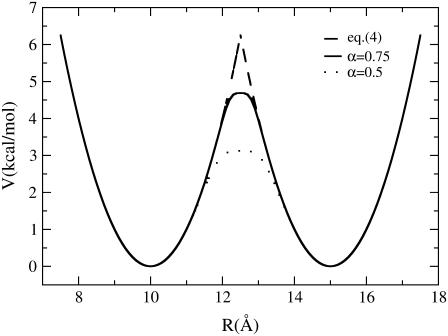
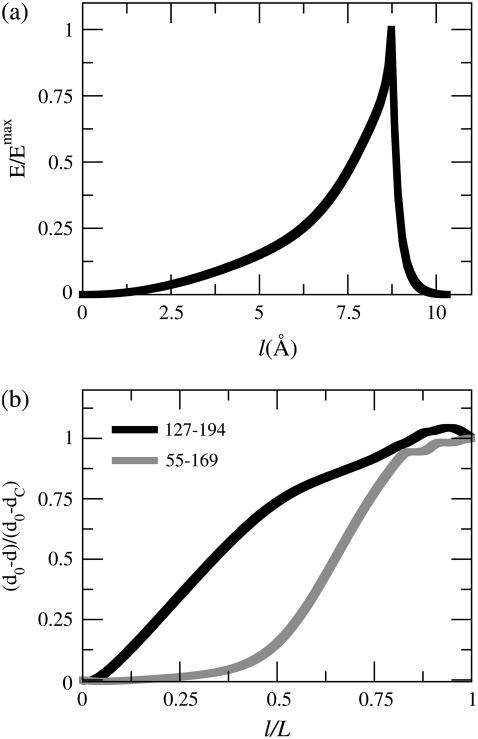
The resulting free energy functions for several different values of α are shown in Fig. 1.

FIGURE 1.

The combined energy profile in kcal/mol/Å of interpolating two one-dimensional harmonic potentials by using the PNM and DWNM approaches. The equilibrium positions for the two potentials are located at 10 and 15 Å, respectively. Both potentials have a force constant of 1 kcal/mol/Å. The solid curve was obtained by PNM (Eq. 4), the dashed curve was obtained by DWNM (Eq. 6), with α = 0.75, and the dotted curve was obtained by DWNM (Eq. 6), with α = 0.5.

The above procedure is certainly not unique, and is employed here for a simple representation of ɛ_ij(R_ij) as a function of R*_ij, H*_ij, and barrier height. Alternatively, one could directly use the mathematical formula in Eq. 4 if an estimate of the required information was available, e.g., from MD simulations or other means. Our focus here is to analyze the effects of the rugged topology of the free energy function on the mechanism of protein conformational changes (as compared, for example, to the free energy function of the plastic network model), so steps 1–4 listed above suffice for this purpose. Testing a different choice of parameters such as the values of α in step 3 results in a similar mechanism of conformational changes, indicating that the observed effects of free energy function roughness described later are insensitive to the details of the free energy function. The results presented in this work were obtained by setting α = 0.5.

Minimum free energy path (MFEP) optimization

To characterize the effects of free energy function topology on the mechanism of protein conformational changes, minimum free energy paths (MFEPs) were computed for both the PNM (Eq. 3) and the DWNM (Eqs. 5 and 6). First, the replica path method (70) was used to optimize a path connecting two stable structures of a protein molecule. Second, geometries of the replicas were then used as the input for conjugated peak refinement (71) to locate the first-order saddle points along the path with a tolerance of 10⁻⁷ kcal/mol/Å for the root mean-squared gradient of a saddle point. The MFEP connecting two states and the saddle points in between was then obtained by the synchronized chain minimization method. All calculations were conducted using the CHARMM program (72).

RESULTS AND DISCUSSION

In this section, the conformational changes of two protein systems, the coil-to-helix transition of the DB-loop in G-actin induced by ATP hydrolysis (73,74) and the open-to-close transition of adenylate kinase induced by binding to an inhibitor (75,76), were analyzed by combining two ENMs by using the PNM (Eq. 3) and the DWNM (Eqs. 5 and 6). Both methods reduce to the original ENM potential at each reference structure. To elucidate the effects of free energy function topology on the mechanism of conformational change, the MFEPs obtained by using different interpolation schemes were compared. In the PNM (Eq. 3), a single, multi-dimensional double-well potential is used to connect two ENMs, whereas in the DWNM (Eqs. 5 and 6), a network of one-dimensional double-well potentials is used. These are physically distinct representations of the protein conformation problem, as discussed earlier.

Coil-to-helix transition of the DB-loop in G-actin

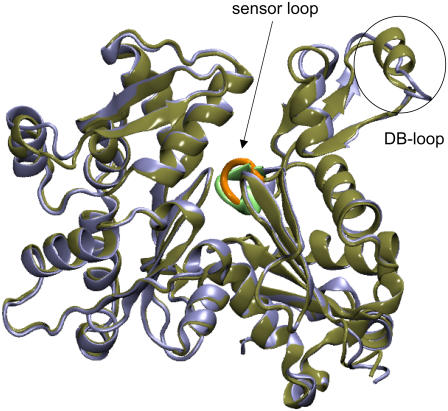
G-actin is the building block of the actin filament (F-actin), the most abundant component of the cytoskeleton in eukaryotic cells (77–79). G-actin has 375 residues and monomers in the cytosol that are primarily bound with ATP before polymerization. Upon polymerization, the ATPase activity of G-actin increases significantly and ATP is hydrolyzed into ADP in F-actin (79). The ATP bound G-actin is denoted as G-ATP, and the ADP bound G-actin is refereed to as G-ADP. The x-ray structures of G-ATP (73) and G-ADP (74) are shown in Fig. 2 and it can be seen that the two states of G-actin have essentially the same conformation except the DB-loop and to a lesser extent the sensor-loop. As highlighted in Fig. 2, the DB-loop may assume a coil structure in G-ATP but fold into an α-helix in G-ADP. The structure of the sensor-loop around the ATP binding cleft (see Fig. 2) is slightly perturbed when compared to that of G-ATP due to the loss of a phosphate group; this local structural perturbation then augments and leads to the folding of the DB-loop into an α-helix in G-ADP.

FIGURE 2.

The x-ray structures of ATP-bound (G-ATP, blue, PDB code No. 1NWK) and ADP-bound (G-ADP, green, PDB code No. 1J6Z) G-actin. The sensor-loop and the DB-loop are highlighted. The sensor-loop is colored orange for G-ATP and light green for G-ADP. The DB-loop assumes a coiled structure in G-ATP while folding into an α-helix in G-ADP.

ATP hydrolysis and DB-loop conformation have been shown to play a critical role in regulating F-actin properties for its proper functioning (79–87); elucidating how ATP hydrolysis induces conformational change in the DB-loop is thus important in understanding the behavior of F-actin and its network. In this work, our analysis is based on the Otterbein structure of G-ADP (74), although different G-ADP structures have been observed under various conditions and also when actin interacts with other actin-associated proteins (78,80–82). The influence of ATP hydrolysis on the properties of actin may thus be complicated and multifaceted. In addition to the pathways of the coil-to-helix transition of the DB-loop, the DWNM can also be employed to systematically investigate the mechanisms of how ATP hydrolysis induces conformational changes of actin by utilizing different structural information.

As a first step toward the goal of understanding how ATP hydrolysis induced actin conformational change, the ENM can be used to describe the structural flexibility of G-actin at the ATP- and ADP-bound states based on their x-ray structures (PDB code No. 1NWK for G-ATP (73) and No. 1J6Z for G-ADP (74)). The ENM model has been applied to G-ATP and shown to give good agreement in predicting the mean-squared displacements of G-actin as compared to the measured x-ray B-factors (47). Here, only the C_α atoms have been kept in the ENMs of G-ATP and G-ADP. The cutoff radius for truncating pairwise harmonic interactions was 13 Å: This value was optimized to best reproduce the mean-squared displacements observed in all-atom MD simulations (88). A force constant of 1 kcal/mol/Ų was used for all elastic bonds; note that the shape of low-frequency vibration modes is insensitive to the values of force constants.

The ENMs of G-ATP and G-ADP were then interpolated both via Eq. 3 (PNM) (62) and Eqs. 5 and 6 (DWNM) to analyze the effects of free energy function roughness on the structural transition. To obtain a mechanistic view of these pathways, the strain energy (E_S), i.e., the sum of all harmonic interactions associated with a particular C_α site for certain residues, will be presented. In particular, the strain energy of Met⁴⁴ and mHis⁷³ (methylated His⁷³) will be shown for different MFEPs. Met⁴⁴ is in the middle of the DB-loop and the evolution of its E_S corresponds to the progress of DB-loop folding. MHis⁷³, on the other hand, is in the sensor-loop, and the evolution of its E_S corresponds to the progress of sensor-loop reorganization around the ATP binding cleft. By employing a CG representation, our focus is to examine the order by which sensor-loop reorganization and DB-loop folding occurs during the conformational change.

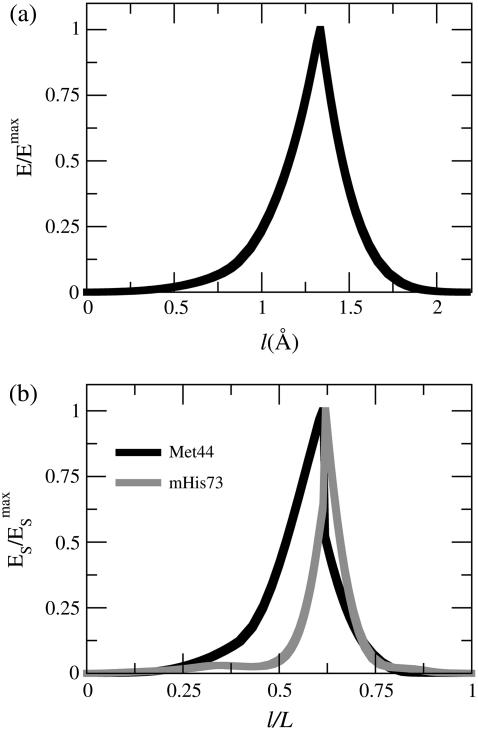
Fig. 3 a shows the free energy profile of the MFEP obtained by using the PNM (Eq. 3). Because the value of force constant is arbitrary, the energies shown in Fig. 3 a are normalized by the largest value along the path. The x axis of Fig. 3 a is the path length (accumulated root mean-squared deviation between neighboring structures along the path) in the units of Å. The total path length of this MFEP is only 2.5 Å, indicating the similarity between the structures of G-ATP and G-ADP. Movie 1 in the Supplementary Material of this article displays this path in a continuous series. Since the ENM of each reference structure is interpolated as a single state in the PNM, the MFEP exhibits a single saddle point and a cusplike profile in Fig. 3 a.

FIGURE 3.

Properties along the minimum free energy path (MFEP) connecting G-ATP and G-ADP structures by applying the PNM. (a) The normalized free energy as a function of path length. The energies are normalized by the maximum value along the path. (b) The normalized strain energy of Met⁴⁴ in the DB-loop and mHis⁷³ in the sensor-loop as a function of the normalized path length.

The strain energies of Met⁴⁴ and mHis⁷³ along the MFEP in the PNM are shown in Fig. 3 b. The strain energies are also normalized by their maximum values to indicate its progression along the path (zero for the G-ATP state and unity for the G-ADP state). To compare different MFEPs, the normalized path length (by the total path length of a MEP) is shown as the x axis in Fig. 3 b. It can be seen that the transition of sensor-loop reorganization (the maximum strain energy location of mHis⁷³) and DB-loop folding (the maximum strain energy location of Met⁴⁴) occur at the same location along the path and it is also the location of the saddle point. However, it can still be seen in Fig. 3 b that DB-loop folding starts before sensor-loop reorganization along the MEP. To the left of the saddle point, the PNM free energy function corresponds to the ENM of G-ATP, and the flexibility of the DB-loop makes its motion the major component of the low-frequency vibrational modes. As such, DB-loop folding precedes sensor-loop reorganization in the PNM. However, this order is not consistent with the known biochemistry data of G-actin in which ATP hydrolysis induces conformational changes of G-actin (79).

By contrast, when using the DWNM (Eqs. 5 and 6) to interpolate the ENMs of G-ATP and G-ADP, the combined free energy function is a network of interconnected one-dimensional double-well potentials. The transition from one conformation to another thus involves the breaking and the reforming of different effective bonds from one CG ENM structure to another. Since these events of effective bond breaking and bond forming can occur in different sequential orders, many intermediate states and saddle points and hence, MFEPs, may be identified.

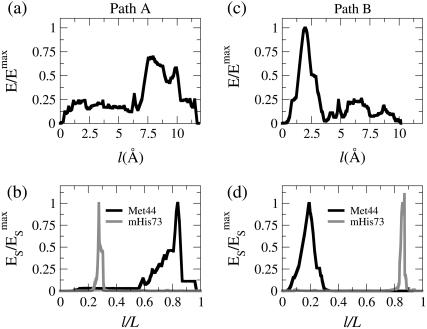
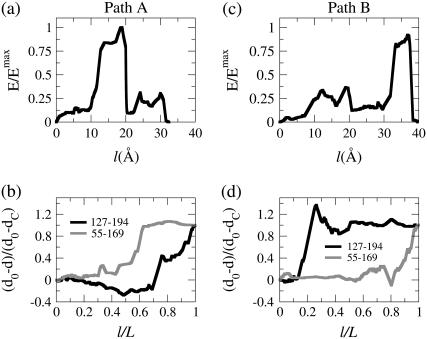
Indeed, for the transition from G-ATP to G-ADP, MFEPs in which sensor-loop reorganization and DB-loop folding occur in distinct orders can both be identified by using the DWNM. Fig. 4, a and b, illustrate the free energy profile and the strain energies of Met⁴⁴ and mHis⁷³ of Path A, while Fig. 4, c and d, presents that information for a different path, Path B. Path A was found by using a linearly interpolated initial guess for MFEP optimization and Path B was obtained by using the PNM MFEP (Fig. 3) as the initial structure.

FIGURE 4.

Properties along the MFEP connecting G-ATP and G-ADP structures by applying the DWNM. Path A was obtained by a linearly interpolated initial structure and Path B was obtained by using the PNM MFEP as the initial structure for MEP optimization. (a) The normalized energy as a function of the path length of Path A. The energies are normalized by the maximum value of energy of Path B. (b) The normalized strain energy of Met⁴⁴ in the DB-loop and mHis⁷³ in the sensor-loop as a function of the normalized path length of Path A. (c) The normalized energy as a function of the path length of Path B. The energies are normalized by the maximum value of energy of Path B. (d) The normalized strain energy of Met⁴⁴ in the DB-loop and mHis⁷³ in the sensor-loop as a function of the normalized path length of Path B.

The free energy profile of Path A shown in Fig. 4 a is more rugged compared to that of the PNM MFEP (Fig. 3 a) and has several intermediate states and saddle points. From Fig. 4 b, it can be seen that sensor-loop reorganization occurs before DB-loop folding in Path A, opposite to the case of the PNM MFEP (Fig. 3 b). Path A is demonstrated in Movie 2 in the Supplementary Material of this article. The free energy cost for sensor-loop reorganization is small since the variation of bond lengths in this region is also small in the DWNM, and the major contribution of the free energy barrier is still DB-loop folding even if it occurs after sensor-loop reorganization (79).

Starting with the PNM MFEP for path optimization, the resulting MFEP, Path B, still maintains the same mechanistic feature that sensor-loop reorganization occurs after DB-loop folding as indicated by the strain energy of Met⁴⁴ and mHis⁷³ shown in Fig. 4 d. Movie 3 in the Supplementary Material of this article shows the MFEP of Path B resulting from the DWNM in a continuous format. The free energy barrier of Path B, however, is 30% higher than that of Path A. To compare the free energy barriers of Path A and B, the free energies shown in Fig. 4, a and c, have been scaled by the maximum free energy value of Path B. Since DB-loop folding is induced by ATP hydrolysis around the region of the sensor-loop, the MFEP of the DWNM is consistent with G-actin biochemistry (79).

Both panels a and c of Fig. 4 show that the DWNM introduces roughness in the combined free energy function as compared to the PNM, and multiple intermediates and saddle points exist during the structural transition of G-actin. Even though DB-loop folding can proceed without sensor-loop reorganization in Path B, the DWNM predicts that it would be energetically more favorable for it to proceed after sensor-loop reorganization due to the underlying structural connectivity given by the native fold of G-actin. Moreover, in the PNM, the transition of different molecular events occurs simultaneously around the saddle point when the system goes from one ENM free energy function to another (see Fig. 3). In the rough free energy function of the DWNM, however, these molecular events are much more distant from each other as seen by comparing Fig. 4, c and d, with Fig. 3 b, in that the intervals between sensor-loop reorganization and DB-loop folding are much larger in the DWNM than in the PNM. The total lengths of MFEPs are also much longer in the paths of the DWNM than that in the PNM, as seen in Fig. 3 a and Fig. 4, a and c. These results suggest that there exists a significant difference in time (much longer than the timescale of molecular relaxation, ∼10 ps) between the molecular events occurring at the ATP-binding cleft and the DB-loop. Indeed, our atomistic MD study indicated that the transition of the DB-loop to helix did not occur within 50 ns after the reorganization of the ATP-binding cleft (results not shown), even though our earlier studies (89) and a recent work of Zheng et al. (90) indicated that both G-ATP and G-ADP structures are stable in an aqueous environment. Many groups, including ours, are currently developing computational methods that can be used to characterize the minimum free energy paths of protein conformational changes at the atomistic scale. DWNM pathways will be compared with the results of such atomistic simulations as they become available in the future.

The major difference between the x-ray structures of G-ATP and G-ADP is the secondary structure of the DB-loop. The tertiary structure of G-actin, on the other hand, does not show a dramatic difference between the two states. Since the ENM has been shown to be robust in capturing large amplitude motions of protein molecules, comparing the PNM and DWNM in transitions involving tertiary structural changes would elucidate how free energy function roughness may affect the mechanism of large-scale protein conformational changes. The open-to-closed transition of adenylate kinase (AKE) is an example of protein conformational changes involving significant variation in tertiary structure, and it will be analyzed in the next section.

Open-to-closed transition of adenylate kinase (AKE)

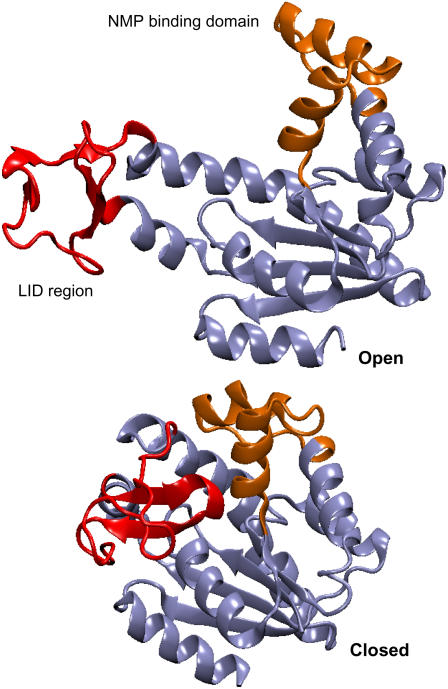
AKE is a 214-residue enzyme that catalyzes the transfer of a phosphate group from ATP to AMP, and is a well-studied example of nucleoside monophosphase kinases (62,75,76). As shown in Fig. 5, the x-ray structures of AKE indicate that its LID region and NMP-binding domain assume an open structure in the ligand-free form (75) but assumes a closed structure in the presence of an inhibitor (76). Therefore, the open-to-closed transition of AKE is dictated by the relative position of its LID region and NMP-binding domain with respect to the CORE domain (the major portion of AKE). An order parameter, (d_o − d)/(d_o − d_c), where d is the distance between two C_α values in AKE, d_o is the distance in the open-state structure, and d_c is the distance in the closed-state structure, can be thus used to describe the progression of the open-to-closed transition, with (d_o − d)/(d_o − d_c) = 0 corresponding to the open state and (d_o − d)/(d_o − d_c) = 1 corresponding to the closed state. In particular, the distance between residue 127 in the LID region and residue 197 in the CORE domain is used to represent its closing, and the distance between residue 55 in the NMP-binding domain and residue 169 in the CORE domain is used to represent the closing of the NMP-binding domain. These residues are chosen because they have also been labeled in single-molecule and bulk florescence resonance energy transfer experiments to study the conformational changes of AKE (91).

FIGURE 5.

The x-ray structures of the open-state conformation (PDB code No. 4AKE) and the closed-state conformation (PDB code No. 1AKE) of adenylate kinase. The LID region is colored in red and the NMP-binding region is colored in orange.

The ENMs of AKE are constructed based on its x-ray structures in the open state (PDB code No. 4AKE, (88)) and in the closed state (PDB code No. 1AKE, (76)). Only C_α atoms were kept in the ENM and a cutoff radius of 8 Å was used for truncating the pairwise harmonic interactions (62). A force constant of 1 kcal/mol/Ų was used for the harmonic interactions.

Although the PNM has already been applied to study the open-to-closed transition of AKE and these results are very similar to the earlier work (62), these results are still presented here for completeness and for comparison with the DWNM. The free energy profile along the MFEP of the PNM (see Movie 4 in Supplementary Material) is shown in Fig. 6 a, with the energies scaled by the maximum value along the path. The profile also shows a cusped barrier. The saddle point is located very close to the closed state and the majority of the MFEP is spent in the well of the open state because the vibrational frequencies of the open state are smaller than those of the closed state due its more extended conformation. The progression of (d_o − d)/(d_o − d_c) between residues 127 (LID region) and 194 (CORE domain) and between residues 55 (NMP-binding domain) and 169 (CORE domain) in Fig. 6 b) clearly shows that the LID region closes before the NMP-binding region.

FIGURE 6.

Properties along the MFEP connecting the open- and closed-state conformations of AKE by using the PNM. (a) The normalized energy as a function of path length. The energies are normalized by the maximum value of the path. (b) The values of (d_o − d)/(d_o − d_c) between residues 127 (LID region) and 194 (CORE domain) and between residues 55 (NMP-binding domain) and 169 (CORE domain) as a function of the normalized path length.

By using the DWNM and introducing roughness in the free energy function via Eqs. 5 and 6, two distinct MFEPs have been identified for the open-to-closed transition of AKE. Path A (Movie 5 in Supplementary Material) was obtained by using a linearly interpolated initial structure and Path B (Movie 6 in Supplementary Material) was obtained by using the PNM MFEP as the initial structure for path optimization. The energy profile of Path A shown in Fig. 7 a indicates that the highest energy saddle point occurs in the middle of the MFEP, and the progression of (d_o − d)/(d_o − d_c) between residues 127 and 194 and between residues 55 and 169 shown in Fig. 7 b indicates that NMP-binding domain closes before the LID region in Path A. These features of Path A are very different from the PNM MFEP. The rough free energy function of the DWNM allows the NMP-binding domain to close before the LID region in a MEFP, even though the LID region has a higher contribution to the low-frequency modes in the open state than the contribution of the NMP-binding domain. The higher contribution of the LID region to the slow modes of the open state is also the reason why it closes before the NMP-binding domain in the PNM. The highest saddle point of Path A also shifts toward the middle of the path instead of locating at the end of the MFEP as in the PNM.

FIGURE 7.

Properties along the MFEP connecting the open- and closed-state conformations of AKE by using the DWNM. Path A was obtained by a linearly interpolated initial structure and Path B was obtained by using the MFEP obtained by the PNM. (a) The normalized energy as a function of the path length of Path A. The energies are normalized by the maximum value of energy of Path A. (b) The values of (d_o − d)/(d_o − d_c) between residues 127 (LID region) and 194 (CORE domain) and between residues 55 (NMP-binding domain) and 169 (CORE domain) as a function of the normalized path length of Path A. (c) The normalized energy as a function of the path length of Path B. The energies are normalized by the maximum value of energy of Path A. (d) The values of (d_o − d)/(d_o − d_c) between residues 127 (LID region) and 194 (CORE domain) and between residues 55 (NMP-binding domain) and 169 (CORE domain) as a function of the normalized path length of Path B.

Starting from the PNM MFEP in the path optimization of the DWNM results in Path B, such that the LID region closes before the NMP-binding domain (see Movie 6 in Supplementary Material), opposite to the case of Path A. Although this sequential order of the LID region and the NMP-binding domain closing is similar to the result of the PNM, the energy profile is quite different. The energy profile of Path B is more rugged and has several intermediates and saddle points (see Fig. 7 c). It can also be seen by comparing the progression of (d_o − d)/(d_o − d_c) between different pairs of residues in Fig. 7 d and Fig. 6 b that the closing of the LID region and the NMB-binding domain is further separated in the DWNM MFEP than in the PNM MFEP. These trends are similar to those observed in the coil-to-helix transition of G-actin.

Comparing Path A and Path B obtained via the DWNM, it can be seen that both paths have similar barriers with Path B having a slightly lower value than that of Path A (the energies shown in Fig. 7, a and c, have been scaled by the maximum energy value of Path A). However, the total length of Path B is longer (40 Å) than that of Path A (33 Å) even though Path B has a slightly lower barrier. For diffusive processes such as large-scale protein conformational changes, a longer path length may also correspond to a lower rate of reaction. The DWNM thus predicts that both reaction channels described by Path A and Path B are likely to coexist in the open-to-closed transition of AKE. Free energy simulations using atomistic force fields and simple order parameters also suggest that both of these two pathways may coexist (92). Starting from the closed conformation without ligand, we indeed observed the opening of AKE following path A in an all-atom MD simulation with explicit solvent (J. B. Brokaw and J.-W. Chu, unpublished results). The agreement of the DWNM pathways with all-atom simulations indicates the robustness of the method in describing protein conformational change. However, determining the relative ratio between different pathways will require future experimental measurements at the single molecule level and detailed, very large-scale free energy and/or kinetics calculations of transition pathways from atomistic MD simulations (23–26).

CONCLUDING REMARKS

In this work, a new method is presented for interpolating two ENMs to characterize coarse-grained protein conformational changes. This method differs from the plastic network model proposed by Maragakis and Karplus (62) in that instead of generating a single, multidimensional double-well potential, a set of networked, one-dimensional double-well potentials (Eqs. 5 and 6) are used to connect two protein structures. This scheme has thus been referred to as the double-well network model (DWNM). Unlike the PNM, the interpolated potential by this latter method has many intermediate states and saddle points. While both the PNM and DWNM reduce to the original ENMs at the reference protein structures, the DWNM scheme systematically introduces roughness into the combined free energy function.

The DWNM was applied to study the conformational changes of two protein systems: the coil-to-helix transition of the DB-loop in G-actin and the open-to-closed transition of adenylate kinase. For each system, the rough free energy function of the DWNM resulted in the identification of distinct minimum free energy paths connecting two x-ray structures. In G-actin, sensor-loop reorganization was found to occur before DB-loop folding in the energetically more favorable MFEP. The PNM, however, predicted the opposite order of events. Since DB-loop folding is induced by ATP hydrolysis in a region near the sensor-loop, the DWNM predicts a path that is consistent with the biochemistry of G-actin. For the open-to-closed transition of adenylate kinase, the DWNM suggests that AKE can go through two different pathways where the LID region closes before or after the closing of the NMP-binding domain, while the PNM predicts only the former.

In a general sense, the DWNM is a reductionist computational method that can be used to gain insight into the intermediate structures connecting two protein conformations at a CG level. First, it can be used to suggest mechanisms of protein conformational change that may be tested experimentally; for example, the sequential order of the closing of the LID region and NMP-binding domain during the open-to-closed transition of AKE upon the binding of substrates. Second, the DWNM can be used to guide more detailed, fined-grained studies, such as atomistic MD simulations, to examine the mechanisms and to compute the free energy profiles of protein conformational changes in greater detail. The DWNM specifies possible rugged pathways of conformational change by interpolating between the native structures of the protein. Using multiscale methods to extract model parameters from atomistic MD simulations may improve the energetics predicted by the DWNM, but the CG level of resolution and the simplified form of free energy function in the DWNM may still limit the accuracy of the energetics so that atomistic details may be necessary for the calculation of highly accurate free energy profiles. On the other hand, studying protein conformational change directly at the atomistic scale is very difficult, even with accelerated sampling methods (23,24). Reaction path optimization and sampling techniques require the knowledge of initial pathways, which is not trivial and can be a substantial bottleneck (23,24). Methods based on steering may bias the transition mechanism in a way that depends on the nature of the steering forces and how fast they are applied. Therefore, the resulting pathways from these methods may not be directly relevant to the actual protein conformational change. The fact that protein conformational change may involve multiple mechanisms and multiple barrier crossing events provides many challenges to atomistic-scale studies. One possible approach is to use CG models such as the DWNM to quickly examine the possible mechanisms and the barrier crossing events in each mechanism, and then use this information to guide more detailed atomistic-scale studies. The DWNM developed in this work introduces essential ruggedness into the effective free energy function, allowing different possible mechanisms of protein structural transitions to be identified. The pathways predicted by the DWNM can then be used to construct the initial configurations for reaction path optimization and sampling methods to further validate and distinguish the different mechanisms of the transition between protein conformations and to calculate accurate free energy profiles.

These results indicate that even though the ENM may capture the low-frequency (function-related) vibrational motions of a protein near one of its reference structures, roughness of the free energy function is expected to play an important role in determining the mechanism by which the protein evolves from one conformation to another. By comparing the DWNM and PNM approaches, the effects of free energy function roughness on the mechanism of protein conformational changes were investigated. Since the DWNM interpolation is formulated in a general manner (Eqs. 5 and 6), it can be readily applied to ENMs in which the force constant for each harmonic interaction is different (29).

In the most general (and perhaps most important) sense, the rough free energy function in the DWNM is also consistent with the observation that protein free energy surfaces have a similar character to disordered media such as glasses (93–96), and a network of interconnected double-well potentials is a physically correct way to represent the rugged free energy surface in such systems.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.