Abstract
PcrA helicase from Bacillus stearothermophilus is one of the smallest motor proteins structurally known in full atomic detail. It translocates progressively from the 3′ end to the 5′ end of single-stranded DNA utilizing the free energy from ATP hydrolysis. The similarities in structure and reaction pathway between PcrA helicase and F1-ATPase suggest a similar mechanochemical mechanism at work in both systems. Previous studies of PcrA translocation demonstrated a domain stepping mechanism in which, during one ATP hydrolysis cycle, the pulling together and pushing apart of two translocation domains is synchronized with alternating mobilities of the individual domains such that PcrA moves unidirectionally along single-stranded DNA. To substantiate this translocation mechanism, this study applies molecular dynamics simulations, elastic network theory, and multiple sequence alignment to analyze the system. The analysis provides further evidence that directional translocation of PcrA is regulated allosterically through synchronization of ATP hydrolysis and domain mobilities. We identify a set of essential residues coevolutionarily coupled in related helicases that should be involved in the allosteric regulation of these motor proteins.
INTRODUCTION
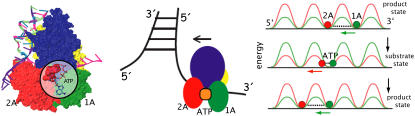
DNA helicases are nucleoside triphosphate (NTP)-driven molecular motors involved in many aspects of DNA function, such as replication, transcription, and recombination. They induce the separation of double-stranded DNA (dsDNA) into its constituent single-stranded DNA (ssDNA) components by moving along ssDNA and consuming energy from NTP hydrolysis (1–6). In their functional forms, helicases exist as oligomers (such as hexamers, trimers, or dimers) or monomers (1,3,4,7). An example of a helicase that has been proposed to work in monomeric form (8) is PcrA, a member of the helicase superfamily I (SF1) (9). PcrA from Bacillus stearothermophilus (BACST) is one of the smallest molecular motors known to date with its complete atomic-level structure available in two key states, one with ATP (actually an ATP analog) bound and one with neither ATP nor ADP bound (8); the two states captured in the structure will be referred to, respectively, as the “substrate” and “product” states. It should be noted that PcrA is crystallized in its bound form to its molecular track, the ssDNA; this advantage is not afforded to cytoskeleton motors myosin, dynesin, and kinesin. PcrA is presented in its subdomain structure in Fig. 1. The translocation of PcrA proceeds unidirectionally from the 3′ end to the 5′ end of ssDNA at a rate of ∼50 nucleotides/s, presumably consuming one ATP for each nucleotide step (10).
FIGURE 1.
Sketch of PcrA helicase translocating 3′ to 5′ along ssDNA. Shown on the left is a PcrA-DNA complex with PcrA shown in surface representation and DNA in cartoon representation. The ATP binding site (ATP shown enlarged) is highlighted. PcrA domains 1A, 2A, 1B, and 2B are colored green, red, yellow, and blue, respectively. Shown in the middle is a sketch of the helicase on the ssDNA near a junction formed by dsDNA and ssDNA. The directed translocation is powered by ATP hydrolysis. Shown on the right is a rudimentary physical model explaining the directed translocation (11,13): PcrA is represented through two of its domains, 1A and 2A (green and red), in the state without ATP/ADP bound (product state (top and bottom)) and with ATP bound (substrate state (middle)). As suggested in (8,11), unidirectional translocation comes about through alternating domain mobilities along ssDNA controlled by energy barriers.
In view of its structure, it was suggested (8) that PcrA translocates in an inchworm fashion mainly involving domains 1A and 2A depicted in Fig. 1; domain 1A always faces the 3′ end of the ssDNA strand and domain 2A faces the 5′ end, with the ATP binding site located between the two domains, as shown. The resolved x-ray structures reveal that the two domains move closer together when ATP is bound and move apart when ADP is released. The directionality arises through ATP binding and ADP + Pi (γ-phosphate) release, altering the mobilities of domains 1A and 2A with respect to ssDNA (11). As illustrated in Fig. 1, domain 1A (green) is more mobile (low potential energy barrier for translation relative to ssDNA) than domain 2A in the product state, such that upon ATP binding, the attraction between 1A and 2A induces 1A to move 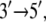 whereas 2A “sticks” to the ssDNA (high-energy barrier). In the substrate state, the domains reverse their roles, so that 2A, being more mobile (low-energy barrier), moves away from domain 1A in the
whereas 2A “sticks” to the ssDNA (high-energy barrier). In the substrate state, the domains reverse their roles, so that 2A, being more mobile (low-energy barrier), moves away from domain 1A in the 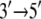 direction upon release of ADP + Pi, whereas domain 1A remains “stuck” on the ssDNA. The behavior can also be described as domains 1A and 2A alternating their mobilities to ssDNA during the ATP hydrolysis cycle such that, combined with the attraction and repulsion of the two domains upon ATP binding and ADP + Pi release, a
direction upon release of ADP + Pi, whereas domain 1A remains “stuck” on the ssDNA. The behavior can also be described as domains 1A and 2A alternating their mobilities to ssDNA during the ATP hydrolysis cycle such that, combined with the attraction and repulsion of the two domains upon ATP binding and ADP + Pi release, a 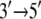 motion results. The physical mechanism of PcrA translocation accordingly involves alternating increase and decrease of domain mobilities along ssDNA, as well as alternating attraction and repulsion between the domains, during the ATP hydrolysis cycle. Of these two properties, the regulation of alternating mobilities is the more “mysterious” one as it involves action at a distance, i.e., allosterism.
motion results. The physical mechanism of PcrA translocation accordingly involves alternating increase and decrease of domain mobilities along ssDNA, as well as alternating attraction and repulsion between the domains, during the ATP hydrolysis cycle. Of these two properties, the regulation of alternating mobilities is the more “mysterious” one as it involves action at a distance, i.e., allosterism.
The translocation mechanism of PcrA has been probed through a combination of quantum chemistry, molecular dynamics, and stochastic modeling calculations at the electronic, atomic, and domain level of resolution (11–13). Using quantum chemistry calculations, we investigated the coupling of ATP hydrolysis to interactions with ssDNA, revealing a close structural homology between PcrA and F1-ATP synthase in regard to their ATP binding sites, suggesting that insights from PcrA are relevant for a broad class of motor proteins (12). Equilibrium molecular dynamics (MD) simulations determined the domain mobilities in terms of the energy barriers of domains 1A and 2A along ssDNA in the substrate and product states, demonstrating the behavior depicted in Fig. 1 (11). The study (11) also showed, through so-called steered molecular dynamics (SMD) simulations (14), that ssDNA can be pulled past domain 2A more easily than past 1A in the substrate state, whereas the situation is reversed in the product state.
Although MD simulations describe the dynamic properties of proteins on the nanosecond timescale, the function of PcrA is realized on the millisecond timescale; in fact, movement from nucleotide to nucleotide of PcrA requires about tens of milliseconds. Using a stochastic model, Yu and co-workers provided a description linking the two disparate timescales for the millisecond motion of domains 1A and 2A as a whole, basing the model, however, on properties determined from nanosecond MD simulations (11). The stochastic model accounted well for the 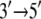 directed motion of PcrA. The calculations in (11–13) also identified amino acid side groups of PcrA that are the most essential for its function and likely determine the
directed motion of PcrA. The calculations in (11–13) also identified amino acid side groups of PcrA that are the most essential for its function and likely determine the 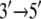 translocation direction of this helicase.
translocation direction of this helicase.
The mechanism for PcrA translocation suggested in (8,11–13) might answer a fundamental question regarding any molecular motor function: how is NTP hydrolysis coupled to the generation of force? The mechanism of alternating domain mobilities offers a fascinating hypothesis related to the general idea of motors being driven by a ratchet mechanism (15–17), yet it is more specific than the respective earlier suggestions. In particular, the suggestions in (8,11–13) definitely deserve much further scrutiny, since the reliance on nanosecond simulations for a millisecond process is error-prone. In addition, the stochastic model describes the translocation of PcrA as movements of featureless beads (domains 1A and 2A), but how amino acids interact inside or between the domains, and how the amino acids interact with the ssDNA nucleotides upon ATP binding or ADP + Pi release, is still ambiguous. Furthermore, even though the energy barriers estimated from the MD simulations revealed some detailed information about PcrA at the individual residue level (11), the conceptual understanding of what specific type of interactions regulate the domain mobilities along ssDNA, as well as how the localized movements of residue/nucleotides are coordinated with the alternating domain mobilities, still needs to be clarified. Finally, it would be desirable to collect more evidence about the overall control of the mobilities of domains 1A and 2A on ssDNA during the ATP hydrolysis cycle.
In this article, the suggestion of alternating domain mobilities in PcrA translocation will be substantiated through further computational investigations. For this purpose, we will still use atomic-scale MD simulations first to demonstrate dynamical correlation patterns of amino acid residues and nucleotides in the PcrA-DNA complex that are in concert with the alternating mobilities of domains 1A and 2A. We will then inspect specific interactions, such as interfacial hydrogen bonding inside the atomic-scale structures, to illustrate how they contribute to the alternating domain mobilities. On a coarser level, we employ a residue network of the PcrA-DNA complex, examining the packing densities of the complex and, based on an elastic network model, further exploring the dynamical coupling between ssDNA and the ATP binding pocket. The coupling turned out to be abolished, along with the alternating domain mobilities, in a modified system with DNA 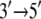 polarity switched, but was preserved along with the alternating domain mobilities in another modified system with ssDNA sequences altered. Finally, to obtain further information on structurally and functionally essential residues from an evolutionary point of view, we apply conservation and coevolutionary analyses of PcrA and related helicases based on multiple sequence alignments. In particular, we suggest residues the mutation of which might affect the polarity preference of PcrA translocation. Altogether, the studies are aimed at enhancing our understanding of the fundamental molecular mechanism underlying directional movement of a prototype motor.
polarity switched, but was preserved along with the alternating domain mobilities in another modified system with ssDNA sequences altered. Finally, to obtain further information on structurally and functionally essential residues from an evolutionary point of view, we apply conservation and coevolutionary analyses of PcrA and related helicases based on multiple sequence alignments. In particular, we suggest residues the mutation of which might affect the polarity preference of PcrA translocation. Altogether, the studies are aimed at enhancing our understanding of the fundamental molecular mechanism underlying directional movement of a prototype motor.
METHODS
To investigate the regulation mechanisms of alternating domain mobilities of PcrA from various perspectives, we employed nanosecond MD simulations to investigate both structural and dynamical features of the PcrA-DNA complex, an elastic network model to probe the topological and slow-mode motional characteristics of the complex, and multiple sequence alignment to identify the amino acids most essential for PcrA helicase.
Equilibrium molecular dynamics simulations
Starting from the crystal structures (8) of PcrA helicase at a resolution of ∼3 Å in the substrate (PDB code 3PJR) and product (PDB code 2PJR) states, we added missing residues in the protein and elongated both duplex DNA and ssDNA (polythymine), as detailed in (11). The structures of the PcrA-DNA complex were solvated in a box of explicit water, with sodium, magnesium and chloride ions added in similar proportions to account for physiological ionic strength (0.1 M) and to neutralize the net negative charge of the PcrA-DNA complex. The simulated system, including protein, DNA, water, and ions, contained ∼110,000 atoms.
MD simulations of the original PcrA-DNA complex in the substrate and product states were conducted after 5000 steps of energy minimization for ∼3 ns. Starting from the equilibrated structures, systems with the DNA polarity switched (by keeping the positions of bases fixed while switching the sequences of backbone atoms) and with poly-T ssDNA changed to poly-C ssDNA (by holding the position of backbone atoms fixed while replacing the bases) were constructed in both substrate and product states. MD simulations on these modified systems were performed for ∼6 ns, each after 5000 steps of energy minimization.
All simulations used the program NAMD2 (18) with the CHARMM27 force field (19) and assumed an integration time step of 1 fs, as well as periodic boundary conditions. Van der Waals (vdW) energies were calculated using a smooth (10–12 Å) cutoff and the particle mesh Ewald method (20) was employed for full electrostatics. The simulations were performed in the NPT ensemble, using the Nośe-Hoover Langevin piston method (21,22) for pressure control (1 atm); Langevin forces (23) were applied to heavy atoms for temperature control (310 K).
Calculating the cross-correlation in MD simulation
To investigate dynamical correlation between ssDNA and PcrA domains, we calculated the cross-correlation matrix of the system based on MD simulations (24). For our special purpose of separately examining the correlation arising from motions along different directions, we decomposed each element of the correlation matrix into two parts, one for the motions in the yz plane, approximately parallel to the surface of the 1A and 2A domain where ssDNA is bound, and one for the motions along the x-direction, perpendicular to the surface, written as
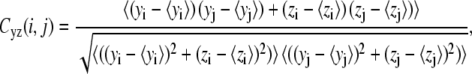 |
(1) |
and
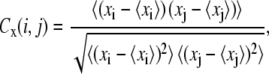 |
(2) |
where xi, yi, and zi are the Cartesian coordinates of atom i (Cα atoms of protein and phosphorus atoms of DNA) obtained from an MD simulation and where 〈···〉 denotes the time average over the MD simulation. Accordingly, Cyz(i, j) describes how the direction and the phase of the in-plane (the plane in which the ssDNA translocation occurs) motions of two atoms are coupled, whereas Cx(i, j) describes how the phase of the perpendicular motions of two atoms are coupled. The values of Cyz(i, j) and Cx(i, j) range from −1 to +1, but only absolute values are given in Results.
Dynamical coupling analysis based on an elastic network model
The dynamical coupling analysis based on an elastic network model (25,26) was carried out as developed in (27) and is summarized here.
Given the coordinates of Cα and phosphorus (P) atoms in the protein-DNA complex, one builds an elastic network model by using harmonic potentials with a single force constant kf to account for pairwise interactions between the atoms within a cutoff distance Rc (15 Å for Cα-Cα, 20 Å for P-P, and 17.5 Å for Cα-P). The energy in the elastic network representation of the system is
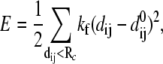 |
(3) |
where dij is the distance between the dynamical coordinates of atoms (Cα or P) i and j, and 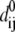 is the equilibrium value of dij defined through the average structure.
is the equilibrium value of dij defined through the average structure.
Based on normal mode analysis of the elastic network model, one can compute the mean-square fluctuation at position i (Cα or P atom position of residue i) using
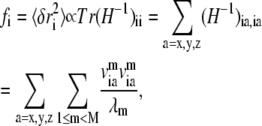 |
(4) |
where H−1 is the inverse of the Hessian matrix of the elastic network; λm and 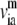 are the eigenvalue and eigenvector of mode m. A cutoff mode M at 10% of the total number of normal modes (3N for N atoms; N = 687 for the PcrA-DNA complex) was used to compute H−1, whereas the six zero-frequency modes corresponding to overall rotations and translations of the system were excluded (the nonzero modes start from m = 1; a factor T/kf is omitted in Eq. 4 for simplicity, where T is the temperature and kf is the force constant).
are the eigenvalue and eigenvector of mode m. A cutoff mode M at 10% of the total number of normal modes (3N for N atoms; N = 687 for the PcrA-DNA complex) was used to compute H−1, whereas the six zero-frequency modes corresponding to overall rotations and translations of the system were excluded (the nonzero modes start from m = 1; a factor T/kf is omitted in Eq. 4 for simplicity, where T is the temperature and kf is the force constant).
By introducing a translationally and rotationally invariant perturbation at position j, i.e., perturbing by δkf the force constant kf of the springs connecting atom j to its neighbors within a cutoff distance, the correspondingly perturbed Hessian matrix elements can be calculated as
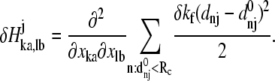 |
(5) |
Then the change of fi in response to δHj is
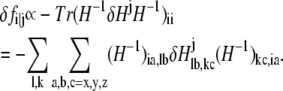 |
(6) |
One can show that
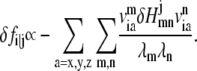 |
(7) |
Accordingly, the pairwise dynamical coupling between i (site of fluctuation) and j (site of perturbation) is defined as
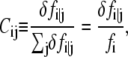 |
(8) |
and the dynamical coupling between a set of atoms I (i ∈ I) and atom j (site of perturbation) is
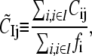 |
(9) |
where fi is the mean-square fluctuation (nonzero) at position i, as defined in Eq. 4.
Multiple sequence alignments
To apply conservation analysis and coevolutionary statistical coupling analysis (SCA) (28,29), a multiple sequence alignment is needed as input. We employed three multiple sequence alignments involving different groups of helicases related to PcrA, illustrating the conservation and coevolution character of these proteins.
To examine conserved regions in PcrA-Rep-UvrD helicases, 500 sequences most similar to that of PcrA–BACST (entry name in Swiss-Prot) were collected using PSI-BLAST (30,31) and were aligned (alignment 1) using ClustalW (32). For a focus on the conserved regions in PcrA helicases, 106 sequences of PcrA from different species were collected using BLAST and aligned (alignment 2) using ClustalW. Since SCA is based on a mutational perturbation strategy within a multiple sequence alignment, analyses of alignments 1 and 2 cannot reveal the coevolutionary couplings among the conserved residues in these alignments.
To examine the coevolutionary couplings among the residues in PcrA-Rep-UvrD helicases, one needs to include further helicase sequences as a “perturbation” set into the PcrA-Rep-UvrD alignment so that there are no conserved residues in the expanded sequence alignment. For this purpose, 829 sequences of helicases, which share structural similarity in domains 1A and 2A (33), were collected using BLAST. Among them, the majority are composed of 422 PcrA-Rep-UvrD sequences most similar to PcrA–BACST, whereas the remainder are the “perturbational” set, including 87 sequences most similar to UvrB–BACCA, 152 sequences most similar to RecQ–ECOLI, 120 sequences most similar to Rad54–CHICK, and 48 sequences most similar to POLG–HCVBK. These sequences were prealigned in five separate groups using ClustalW sequence alignment. Then, based on STAMP structural alignment (34) of the five structures for PcrA–BACST, UvrB–BACCA, RecQ–ECOLI, Rad54–CHICK, and POLG–HCVBK, a profile alignment of the five prealigned groups of helicases was conducted. In this way, the 829 sequences are aligned together (alignment 3). The necessary procedures were implemented through the MultiSeq (35) plugin embedded in VMD (36). The three sequence alignments are provided in Supplementary Material.
Evolutionary statistical coupling analysis
Here, we briefly summarize for the convenience of the reader the SCA developed by Ranganathan et al. (28,29). Basically, this analysis measures the change in the amino acid distribution at one position j in a multiple sequence alignment given a perturbation at another position i as a statistical coupling energy 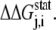 By finding the individual amino acid frequencies at position j in the alignment, a vector of statistical energies
By finding the individual amino acid frequencies at position j in the alignment, a vector of statistical energies 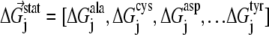 is defined, with individual terms given by
is defined, with individual terms given by
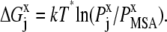 |
(10) |
Here, kT* is an arbitrary energy unit and 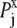 is the probability of observing amino acid x at site j,
is the probability of observing amino acid x at site j, 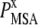 is the probability of observing amino acid x overall in the multiple sequence alignment and serves as a common reference state for all sites. An overall empirical evolutionary conservation parameter is given by the magnitude of vector
is the probability of observing amino acid x overall in the multiple sequence alignment and serves as a common reference state for all sites. An overall empirical evolutionary conservation parameter is given by the magnitude of vector 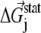 for site j as
for site j as
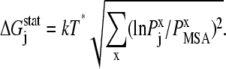 |
(11) |
The coupling between a perturbation at site i and any site j is measured by a difference energy vector
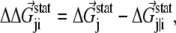 |
(12) |
where 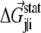 is the statistical energy vector of site j in the subalignment derived from the perturbation at i (with a fixed amino acid at site i). The scalar coupling energy
is the statistical energy vector of site j in the subalignment derived from the perturbation at i (with a fixed amino acid at site i). The scalar coupling energy 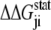 thus reports the combined effect of perturbation on all amino acids at position j: a zero value indicates that sites i and j are evolutionarily independent, whereas a nonzero
thus reports the combined effect of perturbation on all amino acids at position j: a zero value indicates that sites i and j are evolutionarily independent, whereas a nonzero 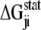 measures the interaction extent of the two sites. Details implementing the algorithm are provided in (37) and recent applications of SCA in protein design are discussed in (38,39).
measures the interaction extent of the two sites. Details implementing the algorithm are provided in (37) and recent applications of SCA in protein design are discussed in (38,39).
RESULTS AND DISCUSSION
We first present results of MD simulations that identified correlation and hydrogen-bonding patterns, which are in harmony with earlier suggested alternating domain mobilities. We then show that an elastic network model reveals a dynamical coupling pattern that also supports the mobility pattern suggested earlier. Finally, we extract information from multiple sequence alignments regarding conserved and mutationally coupled residues and suggest which key residues differentiate the polarity preference of PcrA translocation.
Dynamical correlations from MD simulations
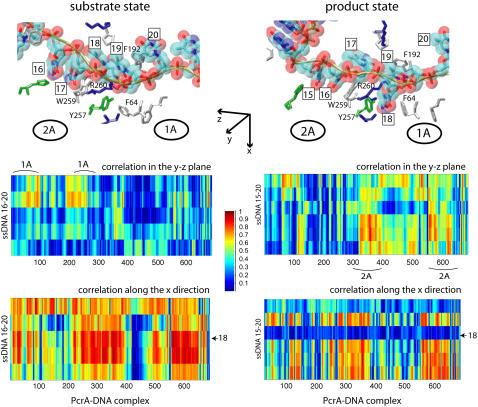
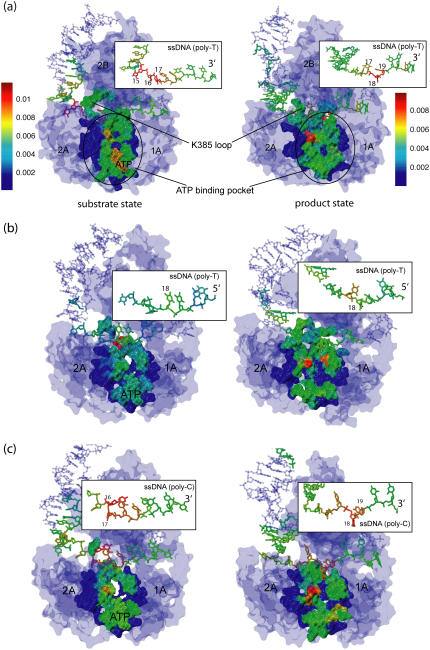
To examine how ssDNA nucleotides are coupled with the protein residues to coordinate the domain mobility, we performed a cross-correlation analysis using the dynamical coordinates of Cα and P atoms of the PcrA-DNA complex recorded from 3-ns MD simulations for both substrate and product states. Since the translocation of ssDNA happens on top of a domain “surface” of 1A and 2A, to separate the correlation effect due to the motions within the surface from the effect due to the motions perpendicular to the surface, we decomposed each element of the correlation matrix into two components, Cyz(i, j) and Cx(i, j), defined respectively in Eqs. 1 and 2. Cyz(i, j) is based on motion in the yz plane, approximately parallel to the top surfaces of 1A and 2A, and is related to ssDNA translocation; Cx(i, j) is based on motion along the x-direction, perpendicular to the mentioned surfaces, and should not be related to ssDNA translocation. The resulting maps of the correlation between ssDNA and the full complex are shown in Fig. 2. Since there are only small amounts of slightly negative values of the correlation, Fig. 2 shows only absolute values to differentiate correlated motions (value → 1) from noncorrelated ones (value → 0).
FIGURE 2.
Cross-correlation analysis of the PcrA-DNA complex based on MD simulations. The analysis was carried out for complexes in the substrate (ATP bound (left)) and product state (no ATP/ADP bound (right)). (Top) Detailed views of the bound ssDNA, as well as nearby key amino acids. The DNA is shown in both licorice and (transparent) vdW (hydrogens not shown for clarity) presentation, color-coded (red, oxygen; cyan, carbon; blue, nitrogen; tan, phosphorus; white, hydrogen), with each nucleotide labeled by a number (15 or 16–20); the amino acids are shown in licorice presentation, also color-coded (green, polar; white, nonpolar; blue, positively charged; red, negatively charged). (Bottom) MD cross-correlation maps, displaying the correlation (decomposed into two components, one in the yz plane and one along the x-direction; see text) between the ssDNA and the full complex. In the substrate state (left), movement (in the yz plane) of the right segment of the ssDNA (nucleotides 19 and 20) is strongly correlated with that of domain 1A; in the product state (right), movement (in the yz plane) of the left segment of the ssDNA (nucleotides 15–17) is strongly correlated with that of domain 2A; nucleotide 18, with its base trapped inside a pocket formed by F64 and Y257 in the product state, is relatively decoupled (along the x-direction) from the protein.
From Cyz(i, j) in Fig. 2, one can recognize an asymmetrical correlation pattern between the domains (1A and 2A) and ssDNA: in the substrate state (with ATP bound), domain 1A is strongly correlated to its ssDNA segment (nucleotides 19 and 20), suggesting a lower mobility of this domain along ssDNA; in the product state (without ATP/ADP bound), domain 2A is particularly strongly correlated to its ssDNA segment (nucleotide 15–17), again suggesting a lower domain mobility along ssDNA. The correspondence between the correlations and the domain mobilities (the domain mobilities are illustrated in Fig. 1 and suggested in (11)) indicates that on a nanosecond timescale, the fluctuating motions of domains and ssDNA are coordinated accordingly to the alternating domain mobilities needed for 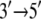 translocation. No such pattern is seen for the correlation along the x-direction (Cx(i, j)).
translocation. No such pattern is seen for the correlation along the x-direction (Cx(i, j)).
Interestingly, Cx(i, j) in Fig. 2 shows that ssDNA nucleotides 18 and 20 fluctuate perpendicularly out of phase with the rest of the protein-DNA complex in the state without ATP/ADP, but are well correlated with the rest in the state with ATP bound. Nucleotide 18 is of particular interest since its base is trapped downward inside a pocket formed by side chains of F64 and Y257 in the state without ATP/ADP, whereas in the ATP-bound state, the pocket is closed and the base flipped upward.
Hydrogen-bonding interactions in the PcrA-DNA complex
To probe which interactions specifically regulate the alternating domain mobilities, we examined hydrogen bonding, as well as salt-bridge interactions, between domains 1A and 2A and ssDNA. Hydrogen bonding was determined from the equilibrated structures (last frame of the 3-ns MD simulation) of the complex in its substrate and product states using the FIRST software (40) and assuming an energy cutoff of −1.0 kcal/mol. A salt bridge was considered to be formed if it was observed within a cutoff distance of 3.2 Å in at least one frame of the MD trajectory.
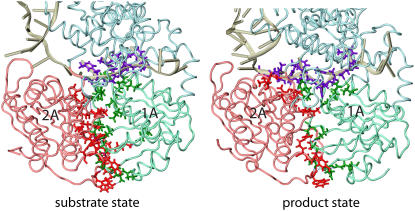
The calculations show, as seen in Fig. 3 and Table 1, that there are more hydrogen bonds formed between domains 1A and 2A in the ATP-bound (substrate) state, when the two domains are close to each other, than in the product state (without ATP/ADP bound), when the two domains are relatively separated. On the other hand, hydrogen bonds formed between protein and ssDNA in the product state outnumbered those formed in the substrate state. Hence, in general, the two domains are attached to ssDNA through hydrogen-bonding interactions; ATP binding weakens the attachment of the domains to ssDNA and makes them more engaged with each other, also through hydrogen-bonding interactions.
FIGURE 3.
Interfacial hydrogen bonding in the PcrA-DNA complex between domains 1A and 2A, and between protein and ssDNA. Hydrogen bonding was determined from the equilibrated (3 ns) structures for the complex in its substrate (ATP bound) and product (no ATP/ADP bound) state using the FIRST software (40), assuming an energy cutoff of −1.0 kcal/mol. The protein-DNA complexes for the two states are shown in tube format; nucleotides on the ssDNA involved in hydrogen bonding with either domain 1A or 2A are shown in purple licorice format; amino acids from domain 1A (2A) involved in hydrogen bonding with the ssDNA or domain 2A (1A) are shown as green (red) licorice. Numbers and energies of hydrogen bonds formed between domains 1A and 2A and ssDNA are provided in Table 1.
TABLE 1.
Number and total energy of interfacial hydrogen bonds formed between domains 1A and 2A and ssDNA in the PcrA-DNA complex
| Interfacial hydrogen bonds | Substrate state (with ATP) | Product state (no ATP/ADP) |
|---|---|---|
| Between 1A and 2A | 18 bonds | 13 bonds |
| Between protein and ssDNA | 8 bonds | 14 bonds |
| Between 1A and ssDNA | 6 bonds | 5 bonds |
| Between 2A and ssDNA | 1 bond | 5 bonds |
| Total energy between 1A and ssDNA | −22.5 kcal/mol | −15.1 kcal/mol |
| Total energy between 2A and ssDNA | −5.8 kcal/mol | −24.6 kcal/mol |
The comparison of hydrogen bonds formed between individual domains and ssDNA in Fig. 3 and Table 1 shows that in the substrate state, there are more hydrogen bonds formed between domain 1A and ssDNA than between 2A and ssDNA, whereas in the product state, although there are equal numbers of hydrogen bonds formed between individual domains and ssDNA, the hydrogen bonds formed between domain 2A and ssDNA are stronger (with lower energies) than those between domain 1A and ssDNA. One can see that the asymmetrical hydrogen bonding between individual domains and ssDNA alternates in concert with domain mobilities: when there are stronger hydrogen-bonding interactions established between a domain and ssDNA, the domain exhibits a lower mobility along ssDNA.
We note that hydrogen bonds between individual domains (1A and 2A) and ssDNA involve, as acceptor atoms (oxygen), the backbone of ssDNA, i.e., the O3′, O5′, or phosphate oxygen atoms, whereas the respective donor atoms (nitrogen) are located on protein residues N66, T91, R260, Y257, and T563 (in the substrate state) or N66, T91, T360, N361, and T563 (in the product state). An exception is a hydrogen bond formed between the oxygen atom (ON2) of D227 and the nitrogen atom (N3) of the base (thymine) of nucleotide 18 in the product state (this base is trapped in a pocket formed between the side chains of F64 and Y257, as seen in Fig. 2; it is also nucleotide 18, using its phosphate oxygen atom, that forms the single hydrogen bond with domain 2A through T563 in the substrate state (Fig. 3 and Table 1)). Hence, the hydrogen-bonding interactions, in concert with the domain mobilities of PcrA, originate mainly from interactions with the backbone of ssDNA, which explains why helicases usually don't recognize sequences along ssDNA. The base stacking interaction of nucleotide 18 with the side rings of amino acid residues (F64 and Y257) might regulate the step size of PcrA along ssDNA.
A comparison of salt bridges formed between domains 1A and 2A in substrate and product states does not show obvious differences except that the salt bridges formed between residue D223 and E224 and the γ- or β-phosphate of ATP in the substrate state are replaced by salt bridges formed between D223, E224, and K37 in the product state. It has been noticed that there are three arginine residues residing along the ssDNA track from left to right (5′→3′), namely, R142, R260, and R98, which can form salt-bridge interactions with DNA phosphates in both substrate and product states. The only residue that acts quite differently in the two states is K385: the side chain of K385 points directly toward ssDNA in the product state, forming a salt-bridge interaction with every phosphate passing by (as seen in a test SMD simulation pulling ssDNA across PcrA, not shown here), whereas the side chain turns ∼180° away from ssDNA in the substrate state. K385 has been identified as an important residue affecting the translocation energetics of PcrA (11).
Packing densities of the PcrA-DNA complex
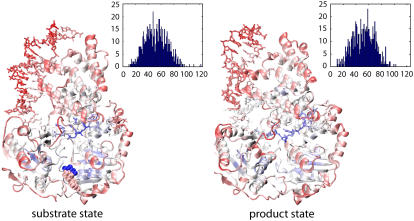
To investigate the structural properties of the PcrA-DNA complex at intermediate resolution, we built a residue network of the complex using the coordinates of Cα (from each amino acid) and phosphorus (P) atoms (from each nucleotide) from the equilibrated structures in the substrate and product states. The residue network was constructed with its nodes composed of the Cα and P atoms; a connection was assumed between two nodes within a distance of 15 Å for Cα-Cα, 20 Å for P-P, and 17.5 Å for Cα-P (the qualitative characters described below are insensitive to these cutoff distances). We examined the packing densities of the complex through the so-called connection degrees of residues, the connection degree measuring the number of neighbors within the cutoff distance. The results are shown in Fig. 4.
FIGURE 4.
Connection degree in the PcrA-DNA complex. The connection degree measures the number of neighbors within a cut-off distance for all residues and prosthetic groups in a protein. For the PcrA-DNA complex in its substrate (ATP bound) and its product (no ATP/ADP bound) state, a residue network was constructed with its nodes composed of Cα atoms from amino acids, as well as phosphorus (P) atoms from nucleotides, as explained in the text. PcrA-DNA complexes are shown in cartoon (protein) and licorice (DNA) format, colored according to the connection degree: blue represents a high degree whereas red represents a low degree. It can be recognized that the highest connection degree (123 connection degree), corresponding to the most densely connected region, occurs at the site of ATP-γ phosphate in the substrate state. Histograms displaying the distribution of the connection degrees for the PcrA-DNA complexes in both substrate and product state are also shown.
The packing densities of the PcrA-DNA complex look similar in both substrate and product states. The most highly packed regions are found at the ssDNA binding interface and in the cores of domains 1A and 2A. The packing densities of domain 1A are not significantly different from those of domain 2A, the average connection degree in domain 1A (∼60) being slightly higher than that in domain 2A (∼54) in both states. Therefore, there seems no obvious correspondence between packing densities and domain mobilities, since the latter alternate between the two states. The distribution of the connection degrees, displayed through histograms in Fig. 4, turns out to be Gaussian-like for both states. This character indicates that the residue network is not a power-law-distributed scale-free network (41), which is composed of a few highly connected nodes (hubs) along with a majority of lowly connected nodes; rather, the residue network is randomly wired around an average scale, ∼53 connection degrees (with a standard deviation of ∼17) for both states.
Interestingly, in the substrate state (ATP bound), the P atom of the ATP-γ phosphate becomes the highest connected node, connecting to 123 neighbors in the residue network (we took the P atom in γ-phosphate and one of the carbon atoms in adenine as two nodes representing the ATP molecule). Accordingly, in the substrate state, the PcrA-DNA complex should be very sensitive to ATP hydrolysis, since to lose the γ-phosphate in ATP is to lose the central hub of the residue network, directly affecting ∼20% of residues. The γ-phosphate may act similarly as a central hub in other motor systems and explain the particular role of ATP hydrolysis in motor systems.
Dynamical couplings in the framework of the elastic network model
PcrA translocation along ssDNA is an ATP-hydrolysis-powered process in which a close coupling between the ssDNA binding region and the ATP binding pocket is expected. The binding pocket includes, altogether, 80 residues on the seven conserved motifs (5,9) located between domains 1A and 2A. Inspection of the structure of the PcrA-DNA complex, however, shows a distance of >20 Å separating the tightly bound ssDNA region from the ATP binding pocket. Thus, how the “action at a distance” coordinates with the alternating domain mobilities of PcrA poses a key question in understanding the translocation mechanism.
To investigate the coupling between two sites, i.e., the ssDNA bound region and the ATP binding pocket, one imposes a perturbation at one site and monitors the response at the other site. In our previous study (11), we conducted dynamical coupling analysis (27) based on an elastic network model (25,26), perturbing a residue's spring constant and monitoring, through a low-pass filter (i.e., accounting only for low-frequency normal modes), the ensuing effect on the vibrational fluctuation 〈δr2〉 of the ATP binding pocket. From that analysis, we identified an interesting dynamical coupling pattern between the ssDNA nucleotides and the ATP binding pocket. Since it appeared vague how exactly the coupling was achieved, we sought, in this study, to examine whether the coupling pattern is accidental or not. For this purpose, we conducted the same analysis on the PcrA-DNA complex under modified conditions, with the polarity of the DNA reversed in one case, and with the ssDNA sequences altered in another case, to see whether the pattern persisted or not. Fig. 5 a shows the results of our previous study (11), for comparison with the results of this study, shown in Fig. 5, b and c.
FIGURE 5.
Dynamical coupling analysis based on an elastic network model (25,26) for the PcrA-DNA complex. In this analysis, dynamic coupling is probed (27) through perturbation of a residue's spring constant and monitoring through a low-pass filter (i.e., accounting only for low-frequency modes) the ensuing effect on the vibrational fluctuation 〈δr2〉 of the ATP binding site. The analysis was carried out for complexes in the substrate (ATP bound) and product (no ATP/ADP bound) state of the original system (a) (from (11)), the system with the DNA polarity reversed (b), and the system with poly-T ssDNA changed to poly-C (c). The PcrA-DNA complexes are colored according to the magnitude of dynamical coupling of residues to the fluctuations of the ATP binding pocket in both states. The protein, DNA, and ATP are shown in surface, licorice, and vdW representations, respectively. The inserts zoom into the ssDNA region showing the dynamical coupling of the ssDNA segment to the ATP binding pocket for each complex. In the original system (a) with a 3′ poly-T ssDNA bound to the PcrA, it can be recognized that the coupling is higher in the left region (nucleotides 15–17) of the ssDNA segment in the substrate state, whereas the coupling is higher in the right region (nucleotides 18 and 19) of the ssDNA segment in the product state; the pattern disappears in the system with a 5′ poly-T ssDNA bound to the PcrA (b), whereas the pattern is retained in the system with a 3′ poly-C ssDNA bound (c).
One can see from Fig. 5 a (taken from our previous study (11)) that in the substrate state of the original system, with a piece of 3′ poly-T ssDNA bound to the PcrA, nucleotides 15–17 are more strongly coupled to vibrational fluctuations of the ATP binding pocket, whereas in the product state, nucleotides 17–19 are more strongly coupled to these fluctuations. We note that nucleotides 15–17 bind to domain 2A and shift relative to the protein as domain 2A, upon ATP hydrolysis (or product release), moves forward toward the 5′ end of ssDNA, whereas nucleotides 17–19 bind to domain 1A and shift relative to the protein as domain 1A, upon ATP binding, moves forward. The dynamical coupling patterns closely support the picture of alternating domain mobilities.
When DNA polarity is reversed, i.e., when PcrA is bound to 5′ ssDNA, as shown in Fig. 5 b, the alternating asymmetrical patterns of dynamical coupling between the ssDNA segment and the ATP binding pocket disappear. The only difference between this system and the original one is that the sequential positions of backbone atoms, which determine the polarity of the DNA strand, were switched (the system was subsequently energy-minimized and equilibrated through MD simulations (see Methods)). It is known that PcrA from BACST is a 3′→5′ helicase and does not translocate 5′→3′. A likely reason is that PcrA does not associate well with 5′ ssDNA, so that the alternating domain mobilities cannot be maintained. The disappearance of the coupling patterns seems to suggest a loss of alternating mobilities, however, enforcing again the motor mechanism suggested in (11).
When 3′ poly-T ssDNA is replaced by 3′ poly-C ssDNA, as shown in Fig. 5 c, the alternating asymmetrical patterns of dynamical coupling between ssDNA and the ATP binding pocket are maintained. Since helicases usually do not recognize sequences as they travel along DNA, the alternating domain mobilities are expected to be maintained such that PcrA can still translocate from 3′ to 5′ on ssDNA.
From the above observations, one can conclude that the correspondence between dynamical coupling and domain mobilities is not accidental in the PcrA-DNA system. It is likely that the domain mobilities are regulated through dynamical coupling between the ssDNA and the ATP binding pocket. The strong coupling of nucleotides 15–17 to the ATP binding pocket (in the original system (Fig. 5 a)) renders the ssDNA segment in contact with domain 2A sensitive to the ATP hydrolysis event. As a result, ATP hydrolysis (or product release) contributes to a movement of the ssDNA segment past domain 2A. We recall that in the MD cross-correlation analysis, domain 1A of the substrate state is strongly coupled to nucleotides 19 and 20 (Fig. 2), implying a low mobility of 1A. The combined effect of domain 1A adhering to its ssDNA segment while the ssDNA segment of domain 2A is agitated through hydrolysis leads to preferential movement of domain 2A past DNA. Similarly, in the product state, nucleotides 17–19, in contact with domain 1A, are coupled to the ATP binding event while domain 2A adheres to nucleotides 15–17, maintaining low mobility; as a result, ATP binding agitates ssDNA segment 17–19 and domain 1A moves past the ssDNA. Altogether, the alternating domain movements lead to directional (3′→5′) translocation.
We note that dynamical coupling is calculated based on low-frequency normal modes (including the 200 modes of lowest frequencies (see Methods)) of the residue network connected by elastic springs. Such networks of N amino acid residues capture long-time behavior beyond the reach of typical all-atom MD simulations (42–44), as estimated by the following analysis (I. Bahar, personal communication). The Hessian associated with the network can be brought to a diagonal form 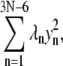 where λ1 ≤ … ≤ λ3N–6. The highest frequency,
where λ1 ≤ … ≤ λ3N–6. The highest frequency,  corresponds to a mode with a vibrational period of ∼100 ps. In our case, the ratio
corresponds to a mode with a vibrational period of ∼100 ps. In our case, the ratio 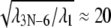 suggests that λ1 corresponds to a mode with a period in vacuum of 2 ns, that extends by a factor of ∼N1/3 in solution, i.e., to ∼20 ns in this case, which indeed is longer than the MD simulations carried out. From this, we conclude that the low-pass filtered elastic network analysis offers a better glimpse of the long-time control of alternating domain mobilities in PcrA than conventional molecular dynamics.
suggests that λ1 corresponds to a mode with a period in vacuum of 2 ns, that extends by a factor of ∼N1/3 in solution, i.e., to ∼20 ns in this case, which indeed is longer than the MD simulations carried out. From this, we conclude that the low-pass filtered elastic network analysis offers a better glimpse of the long-time control of alternating domain mobilities in PcrA than conventional molecular dynamics.
Conservation analysis
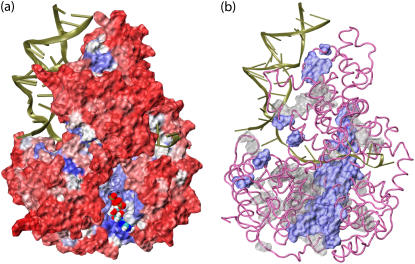
Insight into the structure-function relationship of PcrA can be gained also from an evolutionary point of view by aligning the sequences of PcrA from different species and identifying conserved residues that are likely to be important in function. Belonging to the same superfamily, SF1, Rep and UvrD helicases are natural candidates to be included in such an examination, since both are structurally homologous to PcrA in their monomeric forms, and also share ∼40% sequence identity; all three helicases translocate progressively from 3′ to 5′ on ssDNA (10,45–47). We determined conserved residues in the alignment of 500 sequences of PcrA-Rep-UvrD helicases that are most similar to the sequence of PcrA from BACST (alignment 1 (see Methods)). We also determined conserved residues in the alignment of 106 sequences of PcrA-only helicases from different species (alignment 2 (see Methods)). The degree of conservation is calculated through conservation scores defined in Eq. 11 (see Methods), using the SCA software package (29). The results are presented in Fig. 6.
FIGURE 6.
Conserved residues in the PcrA family. Conservation of residues was determined through sequence alignment of a family of proteins; for smaller families more residues are conserved than for larger families. We based our analysis on two families, a large family including 500 sequences of PcrA, Rep, and UvrD helicases (alignment 1), and a small family including 106 sequences of PcrA helicases (from different species; alignment 2). The proteins in the two families were selected through PSI-BLAST (30,31); the alignment was obtained through ClustalW (32). Shown in a is the degree of conservation for PcrA-Rep-UvrD helicases from alignment 1. The PcrA-DNA complex (from BACST) is colored according to the calculated score of conservation using the SCA software package (29): red represents nonconserved residues while blue represents conserved ones; DNA is shown in cartoon presentation, the protein in surface presentation, and the bound-ATP in vdW presentation. One can recognize that the protein region around ATP and DNA exhibits preferentially conserved residues (blue). Shown in b is a comparison of conserved residues for the families of PcrA-Rep-UvrD helicases (blue) and PcrA-only helicases (gray) from alignment 2. It can be noticed that there are many conserved residues near dsDNA in PcrA-only helicases.
Shown in Fig. 6 a is the degree of conservation for residues in the alignment of PcrA-Rep-UvrD helicases, with the PcrA-DNA complex (from BACST) colored according to the conservation score. Conserved regions in PcrA-Rep-UvrD helicases indeed seem to be functionally important, since they are located mostly around the ATP binding pocket and the DNA binding region, including both the ssDNA binding “tunnel” and the dsDNA binding interface. The ATP binding pocket resides between domains 1A and 2A, including seven conserved “helicase motifs” (5,9) that were proposed to be critical for helicase function. The ssDNA binding tunnel runs through PcrA “on top” (in the views shown in all figures) of domains 1A and 2A, interacting directly with DNA nucleotides during PcrA translocation. The dsDNA binding interface is located on the left side of PcrA (in Fig. 6) near domains 2B and 2A, yet it is not well determined structurally in PcrA due to likely artifacts in crystallization (8). Nevertheless, the dsDNA binding region plays an important role in PcrA, for example, actively distorting dsDNA to facilitate unwinding (8,48). In particular, there exists a dsDNA binding motif on the top left part of domain 2B (GIG residues 421–423) (49) and a DNA-binding initiation region on domain 2A (SRF residues 635–637). The conserved regions can be inspected in a movie rotating the PcrA-DNA complex (provided in Supplementary Material). A comparison in Fig. 6 b of conserved regions in PcrA-Rep-UvrD helicases (alignment 1) and in PcrA-only helicases (alignment 2) shows that conserved regions in PcrA are found preferentially in the 2A and 2B domains, surrounding the dsDNA binding interface. These conserved residues may play special roles in the helicase function of PcrA. In summary, the results indicate that the conserved regions in PcrA-like helicases are closely related to pivotal functions of PcrA.
Coevolutionary analysis
Regulation of the alternating mobilities of PcrA domains 1A and 2A through ATP hydrolysis cycles requires allosteric control and must involve the pairwise functional coupling of spatially separated amino acids. Such amino acids can also be identified through a coevolutionary analysis that examines to what extent pairs of amino acids experienced joint, i.e., correlated, replacement. For the purpose of such coevolutionary analysis, carried out using SCA (28,29) (introduced in Methods), one needs to involve large enough protein families, since in small families there exist strictly conserved residues that exhibit zero correlation with other residues due to their conservation. Hence, we introduced a large family of helicases, including PcrA, Rep, UvrD, UvrB, RecQ, Rad54, and NS3, which share domain structures in 1A and 2A similar to those of the PcrA helicase (33). The alignment of the stated helicases involved 829 protein sequences (alignment 3 (see Methods)) and contains no strictly conserved residues.
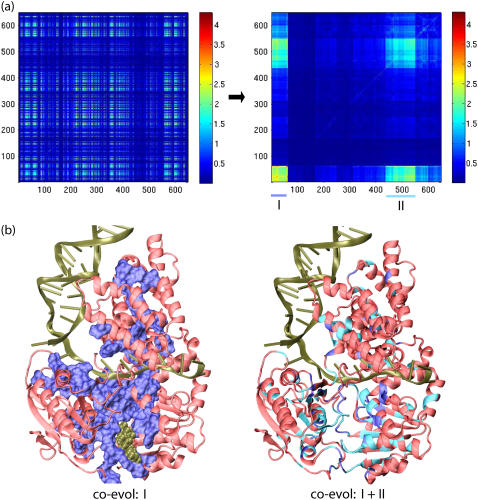
Shown in Fig. 7 a is a correlation map colored according to the SCA correlation matrix elements that describe the mutational coupling strength between residues in the protein sequence alignment (Eq. 12). The correlation map is rearranged through a procedure that clusters highly correlated residues (29). Two such clustered regions arise in this case (Fig. 7 b, I and II), which can also be recognized in the PcrA-DNA complex in Fig. 7. The two regions, I and II, contain ∼30% residues altogether in the reference sequence PcrA–BACST. The residues are spatially connected in PcrA (Fig. 7 b, left), suggesting that functional communication among these residues involves allosteric interactions. Since the residues in regions I and II are highly correlated in mutational events during evolution, they are defining a coevolutionary core region of PcrA-related helicases, enclosing the most essential residues and representing a “minimal” PcrA helicase. Below, we will relate the “minimum set” of residues to the translocation function of PcrA.
FIGURE 7.
Coevolution analysis of essential residues in helicases related to PcrA. Coevolutionary SCA studies pairwise mutational correlation in protein sequences; results indicate the essential amino acids of proteins (28,29). For the purpose of coevolutionary analysis, one needs to involve large enough protein families, as strictly conserved amino acids (in small families) obviously do not exhibit coevolution. Accordingly, SCA was based on alignment of over 800 sequences of helicases (alignment 3, including PcrA, Rep, UvrD, UvrB, RecQ, Rad54, and NS3, i.e., helicases that share structurally similar domains 1A and 2A). (a) Shown on the left is the correlation map colored according to the SCA correlation matrix elements that describe the mutational coupling strength between two residues in the protein sequence alignment. This correlation map is rearranged on the right, employing a procedure that clusters highly correlated residues (29); two such clustered regions arise and are labeled I and II. (b) Regions I and II are illustrated in the PcrA-DNA complex, shown in cartoon presentation, with the bound ATP in vdW presentation. On the left, coevolutionary region I, the highest autocorrelated region, is displayed in blue surface representation, with red showing the rest of the regions; on the right, both coevolutionary regions, I (blue) and II (light blue), are highlighted. Coevolutionary regions I and II represent the functional core of PcrA-related helicases.
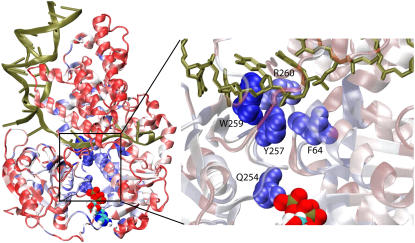
By means of SCA, we determined, in particular, those residues that are seen to have mutated jointly with residues Q254, K385, and R260, which had been identified earlier as prime candidates for regulating PcrA function (11,12,50). The coevolutionary residues of Q254 are shown in Fig. 8. Remaining in close contact with the γ-phosphate of ATP in the substrate state, Q254 was proposed to be a Pi sensor coupling ATP hydrolysis to ssDNA binding (12,50). The blue regions shown in Fig. 8 exhibit high correlation with Q254, whereas the red regions exhibit low correlation. A loop region connecting Q254 in the ATP binding pocket to the ssDNA binding interface near R260 is shown in an enlarged view; the key residues involved in ssDNA binding—Y257, W259, R260, and F64—are all highly correlated with Q254 according to SCA; we note that Y257 and F64 form the key pocket discussed above, which accommodates a DNA base in the product state (no ATP/ADP) (see nucleotide 18 in Fig. 2 b), and which closes in the substrate (ATP-bound) state when the base flips up. The coevolutionary correlations demonstrated between Q254 and the ssDNA binding sites confirm the suggestion that the event of ATP hydrolysis is closely coupled to the event of pocket closing and base flipping (12,50).
FIGURE 8.
Residues that coevolved with Q254. By means of coevolutionary SCA, we determined residues that mutated jointly with Q254, implying that they are functionally (or structurally) related to this residue. Q254 was singled out for this analysis since it is in close contact with the γ-phosphate of ATP in the substrate state and has been proposed as a Pi sensor coupling the ATP hydrolysis to ssDNA binding (12,50). Shown on the left is the PcrA-DNA complex in cartoon presentation with bound ATP in a vdW presentation. The protein is colored according to the degree of correlation of its residues with respect to coevolution with Q254; this correlation is determined through the SCA correlation matrix (Fig. 7); red regions exhibit low correlation with Q254, whereas blue regions exhibit high correlation. On the right is an enlarged view of the boxed loop region in a, connecting Q254 in the ATP binding pocket to the ssDNA binding interface near R260, with the ssDNA nucleotides in licorice format and key amino acids in vdW format. Note that residues Y257, W259, R260, and F64, which are highly correlated with Q254 in “coevolution”, play important roles in ssDNA binding (8,11,50,53); in particular, the side chains of Y257 and F64, in the product state (no ATP/ADP), form a pocket that accommodates a base from the ssDNA (see nucleotide 18 in Fig. 2 b).
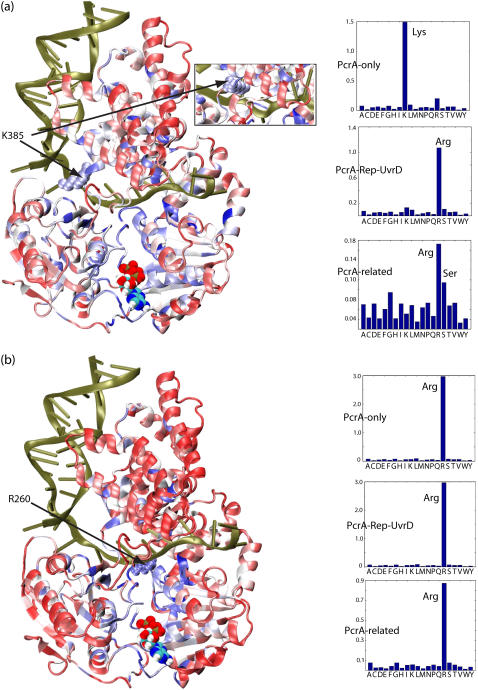
We have carried out the coevolutionary analysis also for R260 and K385, which were identified in our previous studies (11) as two residues possibly affecting unidirectional translocation of PcrA through their prominent electrostatic interactions. The SCA results for these residues are shown in Fig. 9. It can be seen that among the PcrA-only helicases, residue 385 is relatively conserved as lysine; among the PcrA-Rep-UvrD helicases, residue 385 is mainly conserved as arginine; among the largest family, including a variety of PcrA-related helicases, residue 385 has a broader distribution, being mainly conserved as arginine and serine (note the corresponding residue is serine in Rep helicase and arginine in UvrD helicase). At the same time, residue 260 is mainly conserved as arginine in all three alignments. The amino acid distributions of these two residues suggest that, most likely, R260 plays an important role in the translocation of all those helicases that share structural similarity in the 1A and 2A domains; on the other hand, since K385 is specific to PcrA, K385 may play an important, but very specific, role in PcrA helicases, such as controlling the step size.
FIGURE 9.
Residues that coevolved with K385 and R260 and their evolutionary substitutions. We have carried out the same evolutionary analysis for K385 and R260 in PcrA–BACST as for Q254 in Fig. 8. We also determined, through sequence alignment, which amino acids are found to replace K385 and R260. Residues K385 and R260 were singled out, since they were identified in our previous study (11) as residues important for the translocation of PcrA. (a) At left is the PcrA-DNA complex in cartoon format with bound ATP in vdW format. The protein is colored according to the degree of correlation of its residues with respect to coevolution with K385: red regions exhibit low correlation with K385, whereas blue regions exhibit high correlation. (Inset) The conformation of K385 in the product state, which differs from that in the substrate state by a 180° rotation toward the ssDNA. At right are the distributions of amino acids found to replace residue 385 in the multiple sequence alignment of PcrA-only helicases (top); PcrA-Rep-UvrD helicases (middle); and PcrA-related helicases (bottom), including not only PcrA, Rep, and UvrD, but also UvrB, RecQ, Rad54, and NS3. Note that K385 is substituted by serine in Rep helicase and arginine in UvrD helicase. (b) Shown on the left is the PcrA-DNA complex with the protein colored according to the degree of correlation of its residues with respect to coevolution with R260. Shown on the right are the distributions of amino acids found to replace residue 260 in the three multiple sequence alignments, as in a. Note that R260 is always relatively conserved as arginine.
What differentiates translocation polarity?
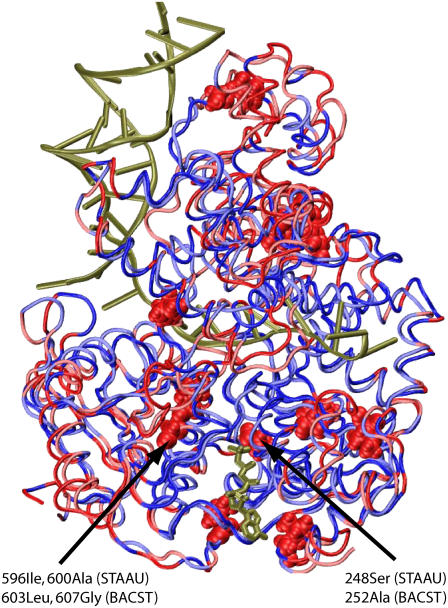
PcrA helicases are present in almost all Gram-positive bacteria. It is known that PcrA from BACST translocates 3′→5′ (10) and unwinds dsDNA through a ssDNA with a 3′ end, but not one with a 5′ end. However, a PcrA from Staphylococcus aureus (STAAU) can unwind dsDNA through either a 3′ or a 5′ ssDNA (51). This, along with some preliminary measurements, suggests that PcrA–STAAU exhibits bipolar translocation. It is natural to assume that the functional divergence of these two PcrA helicases originated from sequence divergence. Comparison of the sequences of the two PcrA helicases may then identify regions of sequences critical for the control of polarity, i.e., red and light red regions in the aligned structures of the two PcrAs shown in Fig. 10 (the structure of PcrA–STAAU was built through homology modeling using MODELLER (52)). Among the residues of these regions, there are 12 belonging to the coevolutionary core regions of PcrA according to our SCA (Fig. 7). Since the coevolutionary core residues are closely coupled during mutational events and are proposed to govern the function of a protein, one may then assume that only those 12 core residues differentiate the helicase functions of the two PcrAs. Focusing on the translocation function, only seven of the residues are located in translocase domains 1A and 2A. These residues are L12, I59, I222, A252, I311, L603, and G607 in PcrA–BACST, and M8, V55, V218, S248, L307, I596, and A600 in PcrA–STAAU. Among these seven residues, three reside on helicase motifs VI and III, as indicated by the arrows in Fig. 10. Among these three residues, the motif VI residues, I596 and A600 in STAAU, or L603 and G607 in BACST, are more likely important for differentiating translocation polarity. These two residues are showing up as LEU and GLY, not only in PcrA–BACST, but also in Rep and UvrD, which are unidirectional 3′→5′ helicases. Therefore, one may connect the unipolarity of these helicases to the LEU and GLY residues, at the same time assuming that the bipolarity of PcrA–STAAU stems from mutations of the amino acids at the corresponding positions. In contrast, the motif III residue, S248 in PcrA–STAAU or A252 in PcrA–BACST, changes to aspartic acid in Rep and UvrD helicases. Therefore, we suggest that by mutating the two amino acids ILE and ALA at positions 596 and 600 in PcrA–STAAU to LEU and GLY, respectively, one may change the bipolar translocation of PcrA–STAAU to 3′→5′ polarity; likewise, by mutating LEU and GLY at positions 603 and 607 in PcrA–BACST to ILE and ALA, respectively, one may change the unidirectional translocation of PcrA–BACST to a bipolar one.
FIGURE 10.
Comparison of sequences of a PcrA helicase from B. stearothermophilus (BACST) and from S. aureus (STAAU). PcrA from BACST translocates 3′→5′ (10), whereas PcrA from STAAU exhibits bipolar character (51). The two structures are shown aligned in tube format with the bound ATP in licorice format. PcrA from BACST is colored red and blue, whereas PcrA from STAAU is colored light red and light blue. Blue and light blue represent regions with identical sequences, whereas red and light red represent regions of variant sequences. In the regions of variant sequences (red and light red), there are 12 residues that also belong to the coevolutionarily determined core regions shown in Fig. 7, seven of which are located in domains 1A and 2A; in particular, three residues reside on helicase motifs VI and III, as indicated by arrows. The two residues located on motif VI are suggested here to be a dominant factor differentiating the translocation polarities of the two PcrA helicases.
CONCLUSION
In previous studies (11,13), we suggested an alternating-domain-mobilities mechanism of PcrA translocation by combining MD simulation and stochastic dynamics modeling. To substantiate the proposed mechanism, we employed here a variety of computational techniques, analyzing the internal interactions and correlations among individual amino acids and nucleotides based on both atomic-scale and residue-network level structures, as well as on sequences of related helicases. The new analyses support the earlier suggestion, revealing a correspondence between dynamical correlation patterns and domain mobilities that alternate between states and control the directional translocation of PcrA along ssDNA. The analyses also suggest a set of nonobvious residues that likely play a role in allosterically regulating 3′→5′ translocation in some PcrA helicases.
On an atomic resolution level, correlation analyses from MD simulations suggest that higher (lower) motional correlations between a domain and an ssDNA segment correspond to a lower (higher) mobility of that domain along ssDNA. Calculations of interfacial hydrogen bonding also show evidence that stronger (weaker) hydrogen-bonding interactions between a domain and an ssDNA segment correspond to a lower (higher) mobility of that domain along ssDNA.
At an intermediate resolution level, examination of packing densities of the PcrA-DNA complex with ATP bound shows that the complex has an extremely high density around the ATP-γ phosphate such that ATP hydrolysis can affect directly a large portion of the protein's amino acid residues. Dynamical coupling analysis based on an elastic network model suggests that ATP binding and ATP hydrolysis (or product release) alternatively influence the ssDNA nucleotides bound to domains 1A and 2A allosterically, regulating the alternating domain mobilities. The regulation seems to be abolished with DNA polarity switched, but preserved with DNA sequences altered.
Sequence analysis revealed the conserved regions in PcrA-like helicases to be located around ATP and DNA binding sites. Coevolutionary statistical coupling analysis identified a set of core residues with high mutational coupling strength that are likely involved in functions such as sensing ATP hydrolysis and propagating the signal from the ATP binding pocket to the ssDNA region to coordinate translocation. The analysis also reveals functional divergences in closely related PcrA helicases that are unipolar and bipolar, suggesting which amino acids control the polarity of PcrA translocation.
SUPPLEMENTARY MATERIAL
To view all of the supplemental files associated with this article, visit www.biophysj.org. Molecular images in this article were generated with VMD (36).
Supplementary Material
Acknowledgments
This work was supported by grants from the National Institutes of Health (P41-RR05969 and GM065367). The authors also acknowledge computer time provided through grant LRAC MCA93S028.
Editor: Kathleen B. Hall.
References
- 1.Lohman, T., and K. Bjornson. 1996. Mechanisms of helicase-catalyzed DNA unwinding. Annu. Rev. Biochem. 65:169–214. [DOI] [PubMed] [Google Scholar]
- 2.Bird, L., S. Subramanya, and D. Wigley. 1998. Helicases: a unifying structural theme. Curr. Opin. Struct. Biol. 8:14–18. [DOI] [PubMed] [Google Scholar]
- 3.Waksman, G., E. Lanka, and J. Carazo. 2000. Helicases as nucleic acid unwinding machines. Nat. Struct. Biol. 7:20–22. [DOI] [PubMed] [Google Scholar]
- 4.Marians, K. 2001. Crawling and wiggling on DNA: structural insights to the mechanism of DNA unwinding by helicases. Structure. 8:R227–R235. [DOI] [PubMed] [Google Scholar]
- 5.Caruthers, J., and D. McKay. 2002. Helicase structure and mechanism. Curr. Opin. Struct. Biol. 12:123–133. [DOI] [PubMed] [Google Scholar]
- 6.Spies, M., M. Dillingham, and S. Kowalczykowski. 2005. DNA helicase. In McGraw-Hill Encyclopedia of Science and Technology. McGraw-Hill, New York.
- 7.Singleton, M., M. Dillingham, M. Gaudier, S. Kowalczykowski, and D. Wigley. 2004. Crystal structure of RecBCD reveals a machine for processing DNA breaks. Nature. 432:187–193. [DOI] [PubMed] [Google Scholar]
- 8.Velankar, S., P. Soultanas, M. Dillingham, H. Subramanya, and D. Wigley. 1999. Crystal structures of complexes of PcrA DNA helicase with a DNA substrate indicate an inchworm mechanism. Cell. 97:75–84. [DOI] [PubMed] [Google Scholar]
- 9.Hall, M., and S. Matson. 1999. Helicase motifs: the engine that powers DNA unwinding. Mol. Microbiol. 34:867–877. [DOI] [PubMed] [Google Scholar]
- 10.Dillingham, M., D. Wigley, and M. Webb. 2000. Demonstration of unidirectional single-stranded DNA translocatin by PcrA helicase: measurement of step size and translocation speed. Biochemistry. 39:205–212. [DOI] [PubMed] [Google Scholar]
- 11.Yu, J., T. Ha, and K. Schulten. 2006. Structure-based model of the stepping motor of PcrA helicase. Biophys. J. 91:2097–2114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Dittrich, M., and K. Schulten. 2006. PcrA helicase, a prototype ATP-driven molecular motor. Structure. 14:1345–1353. [DOI] [PubMed] [Google Scholar]
- 13.Dittrich, M., J. Yu, and K. Schulten. 2006. PcrA helicase, a molecular motor studied from the electronic to the functional level. Top. Curr. Chem. 268:319–347. [Google Scholar]
- 14.Isralewitz, B., M. Gao, and K. Schulten. 2001. Steered molecular dynamics and mechanical functions of proteins. Curr. Opin. Struct. Biol. 11:224–230. [DOI] [PubMed] [Google Scholar]
- 15.Feynman, R., R. Leighton, and M. Sands. 1963. The Feynman lectures on physics. Addison-Wesley, Reading, MA.
- 16.Astumian, R. 1997. Thermodynamics and kinetics of a Brownian motor. Science. 276:917–922. [DOI] [PubMed] [Google Scholar]
- 17.Wang, H., and G. Oster. 2002. Ratchets, power strokes, and molecular motors. App. Phys. A. 75:315–323. [Google Scholar]
- 18.Phillips, J., R. Braun, W. Wang, J. Gumbart, E. Tajkhorshid, E. Villa, C. Chipote, R. Skeel, L. Kale, and K. Schulten. 2005. Scalable molecular dynamics with NAMD. J. Comput. Chem. 26:1781–1802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.MacKerell, A. D., Jr., C. L. Brooks III, L. Nilsson, B. Roux, Y. Won, and M. Karplus. 1998. CHARMM: the energy function and its parameterization with an overview of the program. In The Encyclopedia of Computational Chemistry, Vol. 1. N. L. Allinger, T. Clark, J. Gasteiger, P. Kollman, and H. F. Schaefer III, editors, John Wiley & Sons, Chichester, UK. 271–277.
- 20.Batcho, P. F., D. A. Case, and T. Schlick. 2001. Optimized particle-mesh Ewald/multiple-time step integration for molecular dynamics simulations. J. Chem. Phys. 115:4003–4018. [Google Scholar]
- 21.Martyna, G. J., D. J. Tobias, and M. L. Klein. 1992. Constant pressure molecular dynamics algorithms. J. Chem. Phys. 2:4177–4189. [Google Scholar]
- 22.Feller, S. E., Y. Zhang, R. W. Pastor, and B. R. Brooks. 1995. Constant pressure molecular dynamics simulation—the Langevin piston method. J. Chem. Phys. 103:4613–4621. [Google Scholar]
- 23.Brunger, A. T. 1992. X-PLOR, Version 3.1. A System for X-ray Crystallography and NMR. Yale University Press, New Haven, CT.
- 24.Hünenberger, P. H., A. E. Mark, and W. F. van Gunsteren. 1995. Fluctuation and cross-correlation analysis of protein motions observed in nanosecond molecular dynamics simulations. J. Mol. Biol. 252:492–503. [DOI] [PubMed] [Google Scholar]
- 25.Tirion, M. 1996. Large amplitude elastic motions in proteins from a single-parameter atomic analysis. Phys. Rev. Lett. 77:1905–1908. [DOI] [PubMed] [Google Scholar]
- 26.Hinsen, K. 1998. Analysis of domain motions in large proteins. Proteins. 33:417–429. [DOI] [PubMed] [Google Scholar]
- 27.Zheng, W., and B. Brooks. 2005. Identification of dynamical correlations within the myosin motor domain by the normal mode analysis of an elastic network model. J. Mol. Biol. 346:745–759. [DOI] [PubMed] [Google Scholar]
- 28.Lockless, S., and R. Ranganathan. 1999. Evolutionarily conserved pathways of energetic connectivity in protein families. Science. 286:295–299. [DOI] [PubMed] [Google Scholar]
- 29.Suel, G., S. Lockless, M. Wall, and R. Ranganathan. 2003. Evolutionarily conserved networks of residues mediate allosteric communication in proteins. Nat. Struct. Biol. 10:59–69. [DOI] [PubMed] [Google Scholar]
- 30.Altschul, S., W. Gish, W. Miller, E. Myers, and D. Lipman. 1990. Basic local alignment search tool. J. Mol. Biol. 215:403–410. [DOI] [PubMed] [Google Scholar]
- 31.Altschul, S., T. Madden, A. Schäffer, J. Zhang, Z. Zhang, W. Miller, and D. Lipman. 1997. Gapped BLAST and PSI-BLAST: a new generation of protein database search programs. Nucleic Acids Res. 25:3389–3402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Thompson, J., D. Higgins, and T. Gibson. 1994. CLUSTAL W: improving the sensitivity of progressive multiple sequence alignment through sequence weighting, position-specific gap penalties and weight matrix choice. Nucleic Acids Res. 22:4673–4680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Singleton, M., and D. Wigley. 2002. Modularity and specialization in superfamily 1 and 2 helicases. J. Bacteriol. 184:1819–1826. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Russell, R., and G. Barton. 1992. Multiple protein sequence alignment from tertiary structure comparison: assignment of global and residue confidence levels. Proteins. 14:309–323. [DOI] [PubMed] [Google Scholar]
- 35.O'Donoghue, P., and Z. Luthey-Schulten. 2003. Evolution of structure in aminoacyl-tRNA synthetases. Microbiol. Mol. Biol. Rev. 67:550–573. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Humphrey, W., A. Dalke, and K. Schulten. 1996. VMD visual molecular dynamics. J. Mol. Graph. 14:33–38. [DOI] [PubMed] [Google Scholar]
- 37.Web, S. C. A. http://www.hhmi.swmed.edu/Labs/rr/SCA.html.
- 38.Socolich, M., S. Lockless, W. P. Russ, H. Lee, K. Gardner, and R. Ranganathan. 2005. Evolutionary information for specifying a protein fold. Nature. 437:512–518. [DOI] [PubMed] [Google Scholar]
- 39.Russ, W. P., D. M. Lowery, P. Mishra, M. B. Yaffe, and R. Ranganathan. 2005. Natural-like function in artificial WW domains. Nature. 437:579–583. [DOI] [PubMed] [Google Scholar]
- 40.Jacobs, D., A. Rader, M. Thorpe, and L. Kuhn. 2001. Protein flexibilty predictions using graph theory. Proteins Struct. Funct. Genet. 44:150–165. [DOI] [PubMed] [Google Scholar]
- 41.Barabási, A.-L., and R. Albert. 1999. Emergence of scaling in random networks. Science. 286:509–512. [DOI] [PubMed] [Google Scholar]
- 42.Bahar, I., and A. J. Rader. 2005. Coarse-grained normal modes in structural biology. Curr. Opin. Struct. Biol. 15:1–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Nicolay, S., and Y.-H. Sanejouand. 2006. Functional modes of proteins are among the most robust. Phys. Rev. Lett. 96:078104. [DOI] [PubMed] [Google Scholar]
- 44.Cui, Q., and I. Bahar, editors. 2006. Normal Mode Analysis. Theory and Applications to Biological and Chemical Systems. Chapman and Hall/CRC. Boca Raton, FL.
- 45.Brendza, K., W. Cheng, C. Fischer, M. Chesnik, A. Niedziela-Majka, and T. Lohman. 2005. Autoinhibition of Escherichia coli Rep monomer helicase activity by its 2B subdomain. Proc. Natl. Acad. Sci. USA. 102:10076–10081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Myong, S., I. Rasnik, C. Joo, T. Lohman, and T. Ha. 2005. Repetitive shuttling of a motor protein on DNA. Nature. 322:1321–1325. [DOI] [PubMed] [Google Scholar]
- 47.Fischer, C., N. Maluf, and T. Lohman. 2004. Mechanism of ATP-dependent translocation of E. coli UvrD monomers along single-stranded DNA. J. Mol. Biol. 344:1287–1309. [DOI] [PubMed] [Google Scholar]
- 48.Soultanas, P., M. Dillingham, P. Wiley, M. Webb, and D. Wigley. 2000. Uncoupling DNA translocation and helicase activity in PcrA: direct evidence for an active mechanism. EMBO J. 19:3799–3810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Lee, J., and W. Yang. 2006. UvrD helicase unwinds DNA one base pair at a time by a two-part power stroke. Cell. 127:1349–1360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Dillingham, M., P. Soultanas, and D. Wigley. 1999. Site-directed mutagenesis of motif II in PcrA helicase reveals a role in coupling ATP hydrolysis to strand separation. Nucleic Acids Res. 27:3310–3317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Anand, S., and S. Khan. 2004. Structure-specific DNA binding and bipolar helicase activities of PcrA. Nucleic Acids Res. 32:3190–3197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Sali, A., and T. Blundell. 1993. Comparative protein modelling by satisfaction of spatial restraints. J. Mol. Biol. 234:779–815. [DOI] [PubMed] [Google Scholar]
- 53.Dillingham, M. S., P. Soultanas, P. Wiley, M. R. Webb, and D. B. Wigley. 2001. Defining the roles of individual residues in the single-stranded DNA binding site of PcrA helicase. Proc. Natl. Acad. Sci. USA. 98:8381–8387. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.