Structural Change and Nucleotide Dissociation of Myosin Motor Domain: Dual Gō Model Simulation

Abstract

We investigated the structural relaxation of myosin motor domain from the pre-power stroke state to the near-rigor state using molecular dynamics simulation of a coarse-grained protein model. To describe the spontaneous structural change, we propose a dual Gō-model—a variant of the Gō-like model that has two reference structures. The nucleotide dissociation process is also studied by introducing a coarse-grained nucleotide in the simulation. We found that the myosin structural relaxation toward the near-rigor conformation cannot be completed before the nucleotide dissociation. Moreover, the relaxation and the dissociation occurred cooperatively when the nucleotide was tightly bound to the myosin head. The result suggested that the primary role of the nucleotide is to suppress the structural relaxation.

INTRODUCTION

The mechanism of biomolecular motors is one of the major topics in biophysics. Among a number of such systems that have been found so far, the actomyosin motor is of particular interest, because it is responsible for muscle contraction and cellular movements in eukaryotic cells. Myosin moves unidirectionally along the actin filament using chemical energy released by ATP hydrolysis (1–5). In contrast to macroscopic artificial machine, biomolecular motors work under a noisy environment in the cell. In fact, the free energy released during each ATP hydrolysis is only ∼20 k_BT; therefore the thermal fluctuation should be appreciable. Although recent progress in imaging and of nanomanipulation has enabled the observation of single molecules, the movement mechanism of the actomyosin motor is still not understood.

There has been a long-standing controversy between the tight-coupling (lever-arm) model and the loose-coupling model. X-ray crystallographic studies have revealed that the angle of the neck domain changes relative to the motor domain, depending on the nucleotide state. The lever-arm model was proposed based on these observations, in which the structural change of myosin is tightly coupled with the ATP hydrolysis cycle and directly causes a stepwise sliding motion. It was shown, however, that the sliding distance of the myosin along the actin filament per ATP at the muscle contraction can be much longer than the displacement predicted by the lever-arm-like structural change of a single myosin molecule (6). Moreover, it is questionable whether a material as soft as proteins can accurately switch its conformation in the same way as a macroscopic machine under thermal fluctuation.

In the loose-coupling model, in contrast, the structural change does not always correspond to a step in a one-to-one correspondence; the motion is intrinsically stochastic and thermal fluctuation is an essential ingredient for its mechanism (7). The simplest class of models that produce the loose-coupling mechanism is based on a thermal ratchet, in which a myosin molecule is treated as a Brownian particle that moves along a periodic and asymmetric potential under both thermal noise and nonthermal perturbations (8,9). Although ratchet systems can, in fact, exhibit unidirectional flow in a noisy environment, a high efficiency comparable to that of the actomyosin system is found difficult to achieve using only a simple ratchet system. Even if the ratchet models do express some essence of the mechanism of the biomolecular motor, they are too much simplified and we should say that the connection with the real actomyosin system is rather vague. In particular, since the myosin is expressed as a particle, the effect of its conformational change is, at best, only implicitly taken into account. A somewhat more realistic modeling is desirable, which can reflect the chain conformation.

Recently, it was revealed by single molecule experiments that the chemomechanical cycle of the myosin head is controlled by a load on the actomyosin cross bridge (10–12). The observation suggested that the rate of ADP release from the myosin head depends on the force acting on myosin; namely, the chemical reaction rate varies with the deformation of the myosin. If the myosin head indeed acts as such a strain sensor, this would be reminiscent of a classical model by A. Huxley (13); in this model, the myosin head is supposed to undergo Brownian motion and change into a tightly bound state to the actin filament triggered by a structure dependent chemical reaction.

The relationship between structure and function of proteins has long been investigated. Thus far, mainly the static aspects of proteins have been considered; for example, the classical lock-and-key model of an enzyme. Recently, the role of structural fluctuations, or that of a more drastic structural change including partial unfolding on protein functions, has become a subject of growing interest. Although there have been many experimental studies to clarify the dynamical processes of protein at a functional level, it is still difficult to observe the structural changes with high resolution in both space and time. Computer simulations serve as possible alternatives. Typical computational studies treated equilibrium fluctuations near a crystal structure using the all-atom model (14–16) or the elastic network model (17–20); although these types of simulations are not suitable to study large-scale structural change, the low-frequency fluctuation modes were found to be consistent with the direction of motion of the structural change associated with the function.

Some attempts have been made to simulate a larger structural change beyond the elastic regime using a class of models called the Gō-like model (21). According to the recently developed theory of spontaneous protein folding, the protein energy landscape has a funnel-like global shape toward the native structure. The Gō-like model is certainly the simplest class of model that can realize a funnel-like landscape (22,23) and has successfully described the folding process of small proteins. It is, however, not suitable for the study of a change between two conformations, because only the interaction between the pairs of residues that contact each other in the native state are taken into account; the conformation other than the native state becomes too unstable as a result. Here, we introduce a dual Gō model in which two conformations can be embedded as a variant of the coarse-grained Gō-like model.

In this article, we investigate the dynamics of the spontaneous myosin conformational change from the pre-power stroke state to the near-rigor state by molecular dynamics simulations of dual Gō model. This process is called power-stroke because the angle of the lever-arm changes remarkably, and it is considered in the lever-arm model that this structural change directly causes the force generation. The spontaneous dissociation process of the nucleotide that accompanies the conformational change is also involved in the simulation by introducing a coarse-grained nucleotide as a short chain. To our knowledge, the ligand at the binding site has not been considered explicitly in coarse-grained protein simulations, possibly because the primary role of ATP is considered to be the release of chemical energy through hydrolysis, and the excluded volume effect of the molecule has not been investigated. We, however, consider that the presence or absence of nucleotides in the binding site would profoundly affect the structural fluctuation, which may play a key role in the protein function. Therefore, it is important to perform simulations including the nucleotide.

MODELS AND METHODS

Dual Gō model

We introduce the dual Gō model, a variant of the C_α Gō-like model (24,25). In this model, a protein chain consists of spherical beads that represent C_α atoms of amino-acid residues connected by virtual bonds. While only the native structure is taken as a reference structure for the potential energy function in the conventional Gō-like models, the dual Gō model takes two reference structures, structure 1 and structure 2, in the effective potential.

The effective protein energy U_p at a conformation Γ is given as

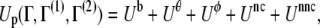(1)

where Γ⁽¹⁾ and Γ⁽²⁾ stand for the conformations of the two reference structures. The terms in Eq. 1 are defined as

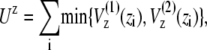(2)

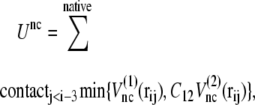(3)

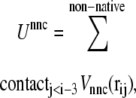(4)

where z stands for b, θ, or φ, and superscripts (1) and (2) again indicate the reference conformations. The vector r_ij = r_i – r_j is the distance between the i^th and j^th C_α, where r_i is the position of the i^th C_α, and b_i = |b_i| = |r_{i i+1}| is the virtual bond length between two adjacent C_α. The value θ_i is the angle between two adjacent virtual bonds, where cos θ_i = b_i–1 · b_i/b_i–1b_i, and φ_i is the i^th dihedral angle around b_i. The first three terms of Eq. 1 provide local interactions, while the last two terms are interactions between nonlocal pairs that are distant along the chain.

For potential functions, 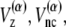and V_nnc, we use the same functions as Clementi et al. (24),

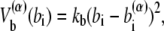(5)

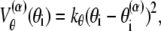(6)

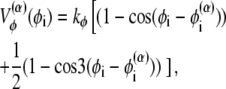(7)

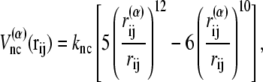(8)

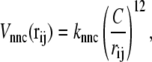(9)

where the superscript α is 1 or 2 and represents the appropriate reference structure. Parameters with superscripts 1 or 2 are constants taken from the corresponding values in structure 1 or 2, respectively. For the local interaction terms (bond length, bond angle, and dihedral angle), the potential energy for each set of beads takes the smaller of V⁽¹⁾ and V⁽²⁾. For example, the length of the i^th bond is 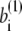in structure 1 and is 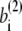in structure 2; therefore, the potential energy for this bond is k_b min 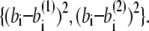We define that the i^th and j^th amino acids are in the native-contact pair of structure 1 (or structure 2) if one of the nonhydrogen atoms in the j^th amino acid is within 6.5 Å of one of the nonhydrogen atoms in the i^th amino acid at structure 1 (or structure 2). 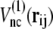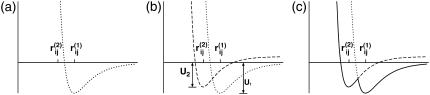The interaction potential for each native-contact pair, ij, takes the smaller of and 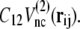C₁₂ is the ratio of the potential depth of structure 2 to that of structure 1 (Fig. 1). Here, since we intend to perform simulations of the structural change from structure 2 to structure 1, that is, we set structure 1 as the final stable structure, we assign a value smaller than unity to C₁₂ (C₁₂ = 0.8). Although each potential function has a cusp, which results in discontinuity of force, in practical terms it causes no trouble in numerical simulations of equation of motion.

FIGURE 1.

Gō-potential: the solid line is dual Gō-potential energy profile for the ij pair. C₁₂ = U₂/U₁.

If a residue pair ij is a native-contact pair in structure 1(2) but not in structure 2(1), the interaction potential between the i^th and j^th residues is a Lennard-Jones potential, 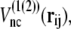with a single minimum. Other relevant parameters are k_b = 100.0, k_θ = 20.0, k_φ = 1.0, k_nc = k_nnc = 0.25, and C = 4.0. The cutoff length for calculating 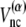is taken to be 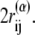If a residue is included in the gap region of one of the reference structures, a potential energy function that has only a single minimum corresponding to the other reference structure is assigned. That is, a potential function for such a residue is the same as that of the standard Gō-like model.

Initial and final structure

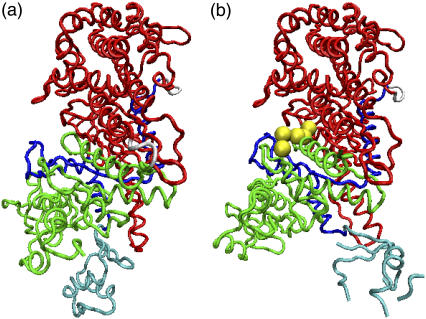
To understand the mechanism of the actomyosin motor, it is desirable to study the conformational change to the rigor state. However, no x-ray crystal structure is currently available for a true rigor complex with actin; therefore, we study the structural relaxation from the pre-power stroke state to the near-rigor state. Structures 1 and 2 thus correspond to the near-rigor and pre-power stroke structures, respectively. We use 1Q5G (26), which is the nucleotide-free structure of Dictyostelium discoideum myosin II, as the near-rigor state. Although a few nucleotide-free structures of myosin II have been determined, only 1Q5G is regarded to be the near-rigor state, because both switch I and switch II are in the open position. We choose 1VOM (27) for the pre-power stroke structure. It includes an ADP·P_i analog (ADP·VO₄) in the nucleotide binding site. While 1Q5G consists of residues 2–765 without a gap region, 1VOM includes only residues 2–747 and has gap regions where the structure has not been determined by x-ray crystallography. Therefore, we use the structures of residues 2–747 for simulations. The residues in the gap regions of 1VOM are set randomly in the initial conformation and with self-avoiding conditions being satisfied under the condition that the bond length is 3.8 Å. (See Fig. 2.)

FIGURE 2.

We chose (a) near-rigor structure, 1Q5G, and (b) pre-power stroke structure, 1VOM for structure 1 and 2, respectively. 1VOM contains the ADP·P_i analog, ADP·VO₄ (yellow). Also shown are the N-terminal (green), 50-kDa subdomain (red) and the converter (cyan) included in C-terminal subdomain (blue) that is connected to the lever arm.

Nucleotide molecule

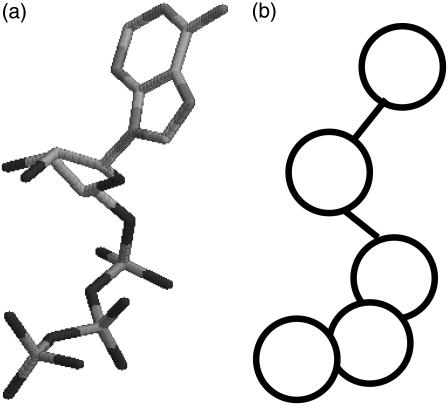
The nucleotide molecule is also included in the simulation explicitly as a coarse-grained chain (Fig. 3). The coarse-grained nucleotide is represented as a short linear chain of five beads, corresponding to a purine base, a sugar (ribose), two phosphates, and VO₄ (a phosphate analog), respectively. Explicit treatment of nucleotide molecule as a short chain makes it possible for us to investigate the relation between nucleotide dissociation and structural change of the myosin motor domain.

FIGURE 3.

(a) ATP and (b) coarse-grained ATP.

The intranucleotide interaction is defined as

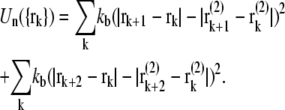(10)

The interaction potential between the protein and the nucleotide is similar to that between the nonlocal residues in the protein. Here, we assume that only structure 2 includes the nucleotide: therefore, the potential function has only a single well (the standard Lennard-Jones potential). We specify that the i^th residue of the protein and the k^th bead in the nucleotide chain should be in native-contact in the pre-power-stroke conformation when one of the nonhydrogen atoms in the k^th bead (base or sugar of P_i) is within 4.5 Å of one of the nonhydrogen atoms in the i^th amino acid. The residues that form native-contacts with the nucleotide are called nucleotide-contact residues,

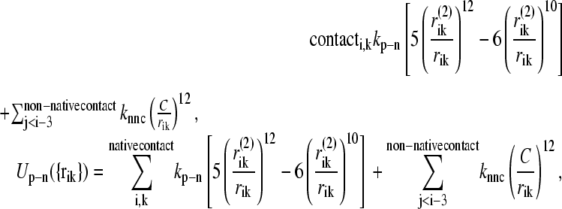(11)

where i stands for the i^th residue and k stands for the k^th bead in the nucleotide chain, and k_p-n is the strength parameter of the protein-nucleotide interaction. We perform simulations under conditions k_p-n = 0.55, 0.6, 0.65, 0.7, 0.75.

We introduce an index to characterize the state of the nucleotide binding, Q_nucl(Γ); we count how many of the nucleotide contacts formed in structure 2 (the pre-power stroke) remain in a given conformation, Γ. Then, Q_nucl(Γ) is defined as this number divided by the number of nucleotide contacts in structure 2. Q_nucl ∼ 1 when a nucleotide is bound, and Q_nucl = 0 if the nucleotide-binding site is empty.

Dynamics

The total energy of the system, U_tot is the sum of three terms:

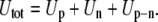(12)

The dynamics of the proteins are simulated using the Langevin equation at a constant temperature T,

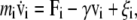(13)

where v is the velocity of the i^th bead and a dot represents the derivative with respect to time t (thus, 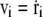), and F_i and ξ_i are systematic and random forces acting on the i^th bead, respectively. The systematic force F_i is derived from the effective potential energy U_tot and can be defined as F_i = – ∂U_tot/∂r_i. The value ξ_i is a Gaussian white random force, which satisfies 〈ξ_i〉 = 0 and 〈ξ_i(t)ξ_j(t′)〉 = 2γTδ_ijδ(t – t′)1, where the bracket denotes the ensemble average and 1 is a 3 × 3 unit matrix. We use an algorithm by Honeycutt and Thirumalai (28) for a numerical integration of the Langevin equation. We use γ = 0.25, m_i = 1.0, and the finite time step Δt = 0.02.

For a given protein conformation, Γ, we note that the native contact of structure 1 (or 2) between i and j is formed if the C_α distance r_ij = |r_ij| satisfies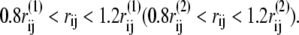

Simulations are started from the pre-power-stroke structure. The initial velocities of each bead is given to satisfy the Maxwell distribution. The temperature is set lower than the folding temperature for structure 1.

Implicit nucleotide simulation

We also run an implicit nucleotide simulation, in which the nucleotide is not explicitly included. Instead, the relative distance of nucleotide-contact residues are constrained by virtual bonds in all-to-all connection to keep the pre-power-stroke form. The natural length of the virtual bonds i-j, 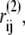is the C_α distance between the i^th and j^th residues in the pre-power stroke conformation (structure 2). The total effective potential energy, U_tot is U_p + U_con, and

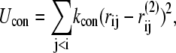(14)

where i and j run the nucleotide-contact residues, and k_con = 1.0.

Distance root-mean-square deviation (dRMSD)

The dRMSD from the near-rigor structure is defined as

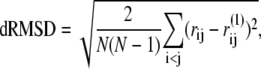(15)

in which r_ij = |r_ij| = |r_i – r_j| is the distance between C_α carbons of the i^th and j^th residues in the given conformation, and 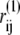indicates their distance in the near-rigor structure.

RESULTS

Relaxation process

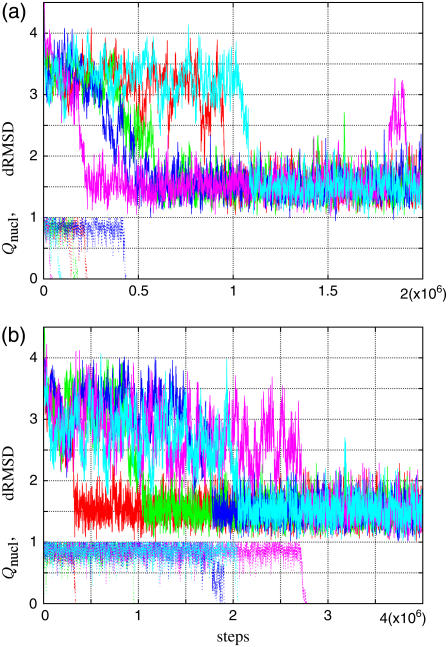
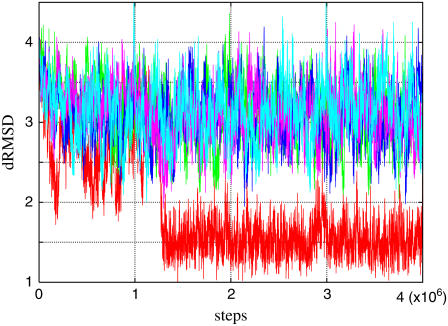
Typical time courses of dRMSD are shown in Fig. 4 for (a) k_p-n = 0.6 and (b) 0.7. At the initial conformation, the dRMSD is ∼3.9 Å, and decreases rapidly to ∼3 Å, and stays there for a while. After that, the conformation abruptly relaxes into the final state, dRMSD ∼1.5 Å. This final state is actually the near-rigor state, judging from its average structure; in fact, the dRMSD of the average structure is ∼1 Å. In short, the myosin motor domain in the pre-power stroke conformation relaxes at first into the intermediate state and then to the near-rigor conformation. The time courses of Q_nucl are also shown in Fig. 4. The structural relaxation occurs after, or at the earliest, at the same time, as the nucleotide dissociation. Furthermore, the relaxation tends to synchronize with the dissociation as k_p-n increases.

FIGURE 4.

Relaxation time courses of dRMSD (from 1Q5G) (solid line) and Q_nucl. (dotted line) for five trajectories are shown. Different colors distinguish different runs. (a) k_p-n = 0.6; (b) k_p-n = 0.7.

The largest difference between the intermediate state and the initial (pre-power stroke) conformation is the position of the converter domain with respect to the other subdomains; the relative positions among other subdomains (for example, the N-terminal and the 50-kDa subdomain) are similar to those in the pre-power stroke conformation (see Supplementary Material Figs. 1 and 2). The average dRMSD of the intermediate state varies slightly with the parameter k_p-n (Fig. 5), reflecting little difference in the position of the converter relative to the other subdomains.

FIGURE 5.

Time sequence of dRMSD. The red line is the trajectory of the no-constraint simulation, and the other lines are trajectories of simulations in which nucleotide-binding site are constrained.

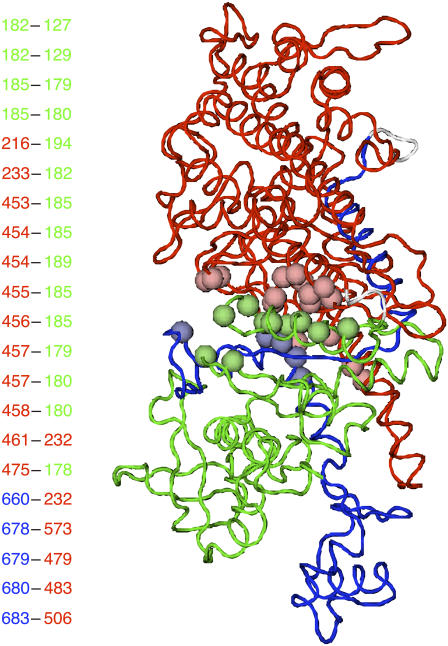
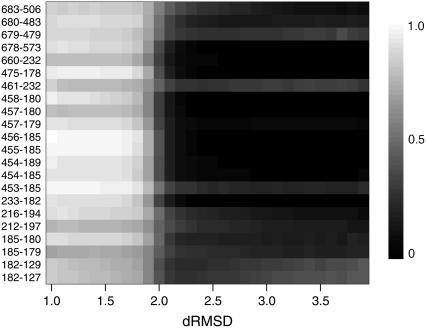
To discuss cooperativity of the final relaxation, we defined the contact formation rate, P^ij(d_L, d_H), as a probability that the native-contact in structure 1 between i and j residues is formed for d_L < dRMSD < d_H. Fig. 6 shows location of the native pairs that make contacts at the final relaxation. The residues involved in pairs that the contact is not formed in the intermediate state, P^ij(2 Å, 3 Å) < 0.3, and is formed in the final state, P^ij(0 Å, 2 Å) > 0.7, at k_p-n = 0.7, as indicated by beads. The figure shows that these relaxation-associated pairs are concentrated at the boundary between N-terminal and 50-kDa subdomain, that is, the region around the nucleotide binding site. Thus, the final relaxation process consists of a rearrangement of the N-terminal subdomain against the other part. For the relaxation-associated contacts, we calculated the dRMSD dependence of the contact formation rate at intervals of 0.1 Å( P^ij(d, d + Δd) with 1 < d < 4(Å) and Δd = 0.1(Å)). The result is shown in Fig. 7. In this resolution, virtually all these contacts form at the same dRMSD, and thus simultaneously in time. We found that the native-contact formation takes place cooperatively at the final relaxation irrespective of k_p-n (see also Supplementary Material Fig. 3).

FIGURE 6.

The relaxation-associated contacts satisfying the conditions P^ij(2 Å, 3 Å) < 0.3 and P^ij(0 Å, 2 Å) > 0.7 are shown. Residues included in the contacts are represented by spheres; residue numbers are indicated at the left. Green, red, and blue correspond to N-terminal, 50-kDa, and C-terminal subdomain, respectively.

FIGURE 7.

dRMSD dependence of the contact formation rate of the relaxation-associated contacts at k_p-n = 0.7. Residue numbers of the contacts are indicated at the left.

Dwell-time distributions

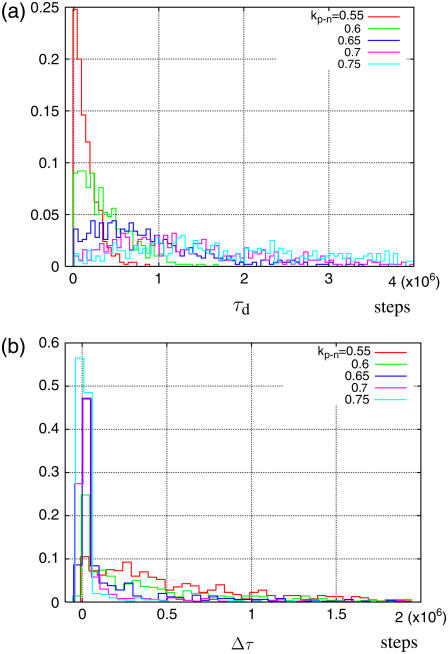
To clarify the k_p-n dependency of the synchronization, we plot the histograms of τ_d and of Δτ = τ_d – τ_r from 500 independent runs for each value of k_p-n, where τ_d is the number of steps taken before the nucleotide dissociates, τ_r is the number of steps taken before the conformation relaxes to the near-rigor state, and Δτ is the delay in the relaxation after the dissociation takes place (Fig. 8). For small k_p-n, both the histograms of τ_d and of Δτ show exponential decay; thus, the nucleotide dissociation and the relaxation of the myosin conformation are considered to be decoupled. For larger k_p-n, on the other hand, the histogram of τ_d cannot be fitted to an exponential decay. In addition, the average of τ_d is shifted to the right and the delays Δτ become shorter; in other words, the nucleotide stays longer at the binding site and the conformational relaxation tends to occur immediately after the nucleotide dissociation. For k_p-n = 0.7, dissociation and relaxation occur nearly simultaneously in >70% of 500 trajectories. Note that apparent Δτ < 0 cases are caused simply from the numerical ambiguity of τ_d and τ_r and actually correspond to coincidental dissociation-relaxation.

FIGURE 8.

Histogram of (a) the number of steps before dissociation and (b) the delay of the relaxation after the dissociation from 500 independent runs for each k_p-n.

Implicit nucleotide simulation

As already mentioned, the myosin motor domain relaxes to the near-rigor conformation only after the dissociation of the nucleotide and not before. Thus, it seems that the nucleotide must be unbound for the final relaxation to occur. This observation leads to a speculation that the nucleotide blocks the deformation of myosin around the nucleotide-binding site by its volume. To investigate the case of when the nucleotide cannot dissociate, we attempt an implicit nucleotide simulation. In this simulation, instead of treating the nucleotide molecule explicitly, we connect the residues that would contact with the nucleotide by virtual bonds, to force the nucleotide-binding site to keep the pre-power stroke form. Fig. 5 shows the time courses obtained by the simulations. We find that the conformation remains at the intermediate state and that the relaxation toward the near-rigor state is not completed.

DISCUSSION

We have shown that the myosin motor domain does not relax to the near-rigor conformation before the nucleotide dissociates. Ishijima et al. (29) showed by simultaneous observation of ADP release and mechanical events that force is generated at the same time as or several hundreds of milliseconds after the dissociation of ADP. Our results are consistent with their experimental findings if force generation is preceded by structural relaxation. Moreover, the results from the simulations in which the conformation of the nucleotide-binding site is constrained also indicate that the relaxation is indeed prevented if the nucleotide cannot dissociate.

Based on these observations, we now suggest that the primary role of the nucleotide in the power stroke process is to suppress relaxation through blocking deformation around the nucleotide-binding site by its volume. In this scenario, hydrolysis is required to alter the affinity of the nucleotide to the binding site.

Our simulations have also shown that the structural relaxation is synchronous with nucleotide dissociation when the nucleotide is tightly bound to the myosin head. In other words, the nucleotide dissociates cooperatively with the motion of the subdomain. This strong coupling of deformation and dissociation seems to be relevant to the function of the strain sensor, in which nucleotide dissociation is controlled by the strain induced by an external force. The correlation depends on the binding strength, k_p-n; the relaxation is only loosely coupled with the dissociation for weak binding conditions. A large kinetic diversity among myosins observed by experiment (4,30) may be attributed to this binding strength dependence.

The intermediate state observed in the relaxation process should also be discussed. Although several intermediate states have been revealed by kinetic experiments (4), their structural aspects, except for ADP·P_i state, are little known. Shih et al. (31) reported, from their FRET study, that there are two pre-power stroke conformations; while one conformation corresponds to the crystal structure of the complex with the ADP·P_i analog, the other conformation has not yet been observed using crystallography. We found that the average structure of the intermediate state observed in this study is consistent with the latter conformation.

Recently, another process in a reaction cycle, the recovery stroke, which is the process from ATP-bound structure to pre-power stroke structure, was studied using the conjugate peak refinement method of all-atom model (32). In this method, structural change is described as an adiabatic process. Although it is suitable to investigate the detail of the side-chain interaction, it cannot treat dynamics of spontaneous nucleotide dissociation (our main interest) or distribution of dwell time.

In this work, actin filament was not included in the simulation. It is in fact known that the rate of the nucleotide release and of the structural change are affected by actin. But it is also known that the myosin motor domain alone undergoes structural changes depending on status of the nucleotide binding site. Thus, we regard that the relation between the nucleotide release and the structural change can, at least, be captured qualitatively without actin. Detailed study on effect of actin will be left for a future study.

We did not treat the releases of ADP and P_i separately. Although it is believed that a powerstroke is associated with the P_i release, as far as we are aware there is no direct observation that the P_i release is tightly linked to the myosin structural change or the force-generation. Since the P_i release is known as the rate-limiting step for myosin II, and ADP dissociates immediately after P_i is released (4,33), we suppose that the releases of ADP and P_i can be treated as a single nucleotide-release event in our coarse-grained model.

Some attempts to extend the Gō-like model to treat the structural change have been made. In the model of Hyeon et al. (34), the energy potential is gradually switched from that of the initial state to that of the final state. During the switching process, the potential function has a minimum at an intermediate structure of the initial and the final structure. The approach of Zuckerman (35) is similar to our model in the sense that each interaction potential function contains information on two structures. He introduced a double-square-well potential for the native-contact pairs into a lattice protein model. Okazaki et al. (36) proposed another type of model in which total effective energy has a double-basin. These types of models, in which two conformations are embedded in an energy potential function, will be useful in understanding the dynamics of protein conformational change.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.