Model of Polarization and Bistability of Cell Fragments

Abstract

Directed cell motility is preceded by cell polarization—development of a front-rear asymmetry of the cytoskeleton and the cell shape. Extensive studies implicated complex spatial-temporal feedbacks between multiple signaling pathways in establishing cell polarity, yet physical mechanisms of this phenomenon remain elusive. Based on observations of lamellipodial fragments of fish keratocyte cells, we suggest a purely thermodynamic (not involving signaling) quantitative model of the cell polarization and bistability. The model is based on the interplay between pushing force exerted by F-actin polymerization on the cell edges, contractile force powered by myosin II across the cell, and elastic tension in the cell membrane. We calculate the thermodynamic work produced by these intracellular forces, and show that on the short timescale, the cell mechanics can be characterized by an effective energy profile with two minima that describe two stable states separated by an energy barrier and corresponding to the nonpolarized and polarized cells. Cell dynamics implied by this energy profile is bistable—the cell is either disk-shaped and stationary, or crescent-shaped and motile—with a possible transition between them upon a finite external stimulus able to drive the system over the macroscopic energy barrier. The model accounts for the observations of the keratocyte fragments' behavior and generates quantitative predictions about relations between the intracellular forces' magnitudes and the cell geometry and motility.

INTRODUCTION

Directed cell motility—a fundamental phenomenon underlying morphogenesis, wound healing, and cancer—results from a complex combination of protrusion, adhesion, and contraction activity of the cell (1–3) based on treadmilling of the actin-myosin arrays (2,4). A nonmotile cell is spread on a substrate and has a roughly circular morphology. Its transition into the motile state is preceded by cell polarization—a symmetry breaking between two opposite edges of the cell and establishing a front-rear structural and functional asymmetry of the actin-myosin arrays (5) and the cell shape. This transition establishes the cell front where there is almost no myosin, and the growing barbed ends of actin filaments face the direction of the upcoming crawling. The opposite, myosin-rich, edge becomes the cell rear at which the cell body is dragged forward (6).

Cell polarization may result from external cues such as gradients of chemoattractants (1,5) or mechanical stimuli (7), but in some cases a cell self-polarizes spontaneously and maintains the polar motile state for a long time (8,9). Extensive studies implicated complex and redundant spatial-temporal feedbacks between multiple signaling pathways and the actin-microtubule cytoskeleton in the cell polarization (3,5,10,11). Most studies focused on polarization as a result of signaling reaction-diffusion processes, with the single exception of a qualitative mechanical-restriction idea assuming that an extension at the front of the cell is physically coupled to a retraction at the rear (reviewed in (5)). However, cell is a mechanical system (2,12), and here we suggest and examine quantitatively a physical mechanism of the cell symmetry breaking (in cells with lamellipodia on flat surfaces) (2) based solely on intracellular mechanical interactions and independent of the extracellular signals or biochemical signaling. This mechanism is applicable directly to the much studied motile cells on flat surfaces.

We base our model on observations of fragments of epithelial keratocyte cells, the migration of which is crucial in wound healing (13). These cells are streamlined for locomotion. They glide individually remarkably fast (∼0.05–0.25 μm/s (4,6,14,15) and steadily. The cell's motile appendage is the lamellipod, a broad, flat sheetlike structure enveloped by the cell membrane and consisting of a branched polarized treadmilling array of actin filaments with myosin at the rear (6). Keratocytes can crawl without microtubules (16), indicating that at least one, and maybe more than one, signaling pathway implicated in polarity maintenance (10) is absent in these cells.

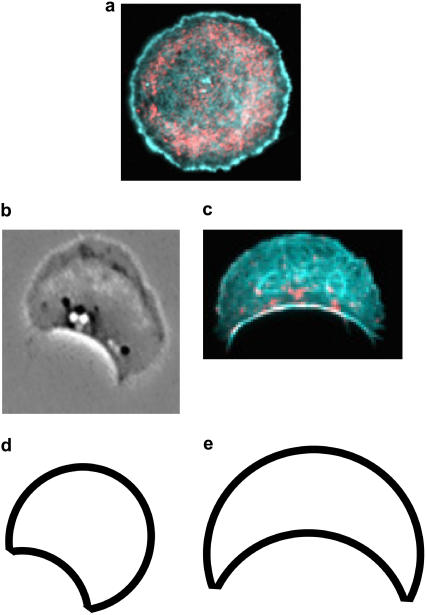
Strikingly, keratocyte fragments separated from the cell lamellipodium and lacking the major cell organelles and microtubules retain the ability to establish the front-rear polarity and to crawl directionally with speed and characteristic crescentlike shape similar to that of the intact keratocyte (7). Though signaling-based polarization cannot be definitively ruled out in these fragments, it is less likely than that in the whole cells, and mechanics-based polarization is a strong possibility. The fragments are either stationary, symmetric, and discoid (Fig. 1 a); or motile, polarized, and crescent-shaped (Fig. 1, b and c) (7). The stationary fragments can be deformed by a weak transient hydrodynamic load, after which the fragment remains stationary and recovers its discoid shape (7). However, if the load is strong, the fragment deforms to an almost half-disk shape, and then, even when the load is removed, the symmetry is broken; the crescent-shaped motile fragment evolves and crawls steadily for hours (7). On a rare occasion, when a motile fragment encounters an obstacle, it stalls and resumes the discoid nonmotile shape, which remains steady without further perturbation. These observations indicate that the keratocyte fragment representing a relatively simple actin-myosin-membrane system is bistable: both stationary disk and motile crescent are locally stable, while global perturbations can switch the fragment between these two states.

FIGURE 1.

Shapes of keratocyte lamellipodial fragments. (a) Nonpolarized circular state. (b and c) Polarized state characterized by crescentlike shapes (reproduced from (7)). (d and e) Theoretically predicted shapes corresponding to the parameter values σ_B/f = 0.15, and σ_B/f = 0.25, respectively.

In the discoid stationary state, fragment's actin network is isotropic. The filaments' barbed ends polymerize along the edge very slowly (∼0.02 μm/s (5, 7)); this polymerization is balanced by slow F-actin centripetal flow (7). Myosin II molecules form large (∼0.4 μm) clusters that have multiple heads (6) developing local contractile stresses (18), which, in the stationary fragments, are distributed evenly across the fragments and are stationary relative to the actin network (7). In contrast, the actin-myosin distribution in the crescent-shaped motile fragments is highly anisotropic (7). The polarized actin network density decreases from the front to the rear. At the rear, the network is disintegrated; the filaments are reoriented in parallel with each other and form an arc-shaped bundle underlying the rear edge. The myosin distribution is shifted toward the rear, colocalizing with the actin bundle.

A qualitative scenario for creation and stabilization of the fragment polarized state was proposed based on a hypothetical rearrangement of the actin-myosin system upon an asymmetrical mechanical stimulus of the cell (7). At the same time, the physical mechanism underlying the existence of the stable nonpolarized and polarized states of a keratocyte fragment separated by a kinetic barrier controlling the transition between them is unknown. Here we propose such a mechanism based on the interplay between the forces of the actin polymerization, myosin-driven contraction, and membrane tension. In addition to explaining the cell bistability and the related symmetry breaking, the model describes quantitatively the crescentlike motile shape of a keratocyte fragment and makes predictions about the relationships between the intracellular forces' magnitudes and the motile cell geometry.

Model

We consider a keratocyte lamellipodial fragment on a flat substrate as a two-dimensional (2D) object since the linear dimension of its projection on the substrate plane is close, ∼10 μm exceeding by orders of magnitude its thickness h ∼ 0.1–0.2 μm (7,14) (Fig. 2 a). Mechanically, the fragment interior consists of the actin-myosin network and is enveloped by the cell membrane (Fig. 2 a). For simplicity, we will refer to the fragment as the cell. We limit this study to the transition between the symmetric (Fig. 2 a) and polarized (Fig. 2 b) states of the cell and do not address the downstream motile stage, therefore, the cell center will be assumed not to move relative to the substrate. We first present the model for the nonpolarized state and discuss the cell shape, the cytoskeleton distribution, and the physical forces (Fig. 2 b). Then, we describe how shape, distribution, and forces change in the transition to the polarized state. Finally, we analyze the thermodynamic work associated with these changes, the stability of the two states and the transition between them. After we solve the model equations, we discuss the model assumptions and results.

FIGURE 2.

Model of keratocyte fragment. (a) Three-dimensional view. (b) Two-dimensional model of the nonpolarized state. The red arrows illustrate the actin normal force at the edge, the purple arrows represent the membrane tension. The gray area corresponds to the actin-myosin network. (c) Two-dimensional model of the polarized state. The bold line at the rear denotes the actin-myosin bundle forming in the course of polarization; other notations are the same as in panel b.

Nonpolarized state

In the nonpolarized state, the fragment is a disk of radius R₀ with area 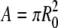(Fig. 2 b), which remains constant, A = const, in the course of polarization. This is based on previous observations of other cells (17), and on data on the whole keratocyte cells and their fragments (44). Though more complex interpretations are possible, we interpret this condition as follows: given the way the keratocyte fragments are formed (they are torn out of the lamellipodium), the total plasma membrane area in fragments is conserved and the membrane is pulled taut around the flat actin network. Membrane folds and intracellular membrane pools observed in many motile cells are probably either absent in the fragments, or exchange with the plasma membrane on the timescales, much more slowly than those relevant for the polarization. (In the whole cells, the membrane dynamics is likely more complex (18).) The membrane is unstretchable and uncompressible. As the thickness h of the keratocyte fragment (Fig. 2 a) is very small, the total fragment area is simply equal to the constant plasma membrane area divided by 2 (ventral and dorsal surfaces).

Based on the observations (7), we assume that in the nonpolarized state the F-actin and myosin are distributed approximately uniformly and homogeneously across the ringlike area of width D near the fragment edge (Fig. 2 b). For simplicity, we assume that the ring of the actin-myosin network in the nonpolarized state reaches the cell half radius, so D = R₀/2. Three major cell structures—actin, myosin, and membrane—are the sources of the three principal forces.

First, the uncapped barbed ends of the actin filaments abutting the cell edge generate pushing force at the cell boundary (20) (Fig. 2 b). The source of this force is most likely the polymerization ratchet mechanism (21); other mechanisms (22) lead to the same mathematical model. This force can be quantified by the 2D pressure Π applied to the membrane at the fragment boundary and equal to the normal force per unit length of the circumference, or by the total normal force f given by the integral of the pressure over the fragment perimeter, f = ∮ΠdL. In the symmetric state, f = 2πR₀Π.

Second, the actin pushing generates lateral tension γ_mem in the cell membrane (Fig. 2, b and c). Since the membrane has properties of a 2D fluid, the tension γ_mem is isotropic and constant in the membrane plane. Finally, myosin generates an average contractile stress γ_net in the actin network (18) (Fig. 2, b and c), which will be assumed constant. (Distributions of actin and myosin in the fragments are not completely homogeneous and isotropic, but away from the edges anisotropies and inhomogeneities are weak (15).) Its units, same as those of membrane tension or actin pressure, are force per unit length.

Polarized state

In short, we hypothesize that when a mechanical load significantly deforms one side of the discoid fragment, the following events take place within a few seconds: First, at the deformed side, the isotropic actin network is collapsed into the bundle underlying the boundary at that side referred to as the rear edge. Quantitative mechanism of the bundle formation is beyond our model's framework; we only analyze contribution of the bundle to the cell energy. However, qualitative microscopic and mechanistic explanation of the bundle formation exists (23): compression of the fragment boundary both induces breaks in the actin network, and aligns many broken-off actin filaments parallel to the boundary and each other, and increases concentration of both such filaments and myosin clusters at the boundary. Then, myosin clusters further align the filaments into the bipolar bundle, which is contractile, because most of the actin filaments within the bundle are not cross linked (3). All myosin molecules that were distributed evenly throughout the lamellipodial network at the rear edge also collapse into the bundle making it contractile—we assume, following the literature (24–26), that a line tension, σ_B, is developed along this bundle by the myosin contractile stress. At the opposite side, referred to as the front edge, actin filaments keep polymerizing and, hence, pushing on the membrane.

We consider the deformed fragment to be crescent-shaped and characterized by the convex front edge arc of radius R, by the concave rear edge arc of radius ρ, and by the angle ϕ that determines the degree of the shape asymmetry, and which we refer to as the polarization angle (Fig. 2 c). The symmetric nonpolarized shape is characterized by ϕ = 0, whereas progressing cell polarization is described by the growing value of ϕ. The area conservation assumption provides a relation between the radii R and ρ and the polarization angle ϕ.

When the fragment is deformed, its shape momentarily changes in such a way that the membrane tension is relieved, and then actin rapidly, within seconds, polymerizes freely in the radial direction into the ring of the expanding front edge until the membrane is stretched again (15) (Fig. 2 c) (characteristic distances are the μm-range, while the polymerization rate at protruding leading edge is ∼0.1 μm/s (5,27)). We assume that all growing actin filaments rapidly redistribute to the front edge and disappear from the rear (F-actin network adjusts to activations/inhibitions within seconds (4)), so the total actin normal force acting on the front edge remains equal to f, same as in the symmetric state, and independent of ϕ. Meanwhile, tens of seconds are needed for the myosin redistribution (7), so we assume that the myosin does not spread into the ring of the expanding front edge (Fig. 2 c), resulting in formation next to the cell front of the arc-shaped area filled by the newly polymerized actin but free of myosin. Nor does the inner boundary of the ring filled with myosin shifts, conserving its initial radius R₀/2 (Fig. 2 c) (10).

We assume that the linear actin-myosin bundle grows or shrinks in length together with evolution of the cell rear edge, hence, supporting the rear edge membrane at all stages of polarization. Formation of such bundle with two ends anchored in the large adhesions at the corners between the front and rear edges is supported by multiple observations (2,6,7,28,29). Since we assume that all myosin molecules from the section of the actin-myosin ring above the emerging rear edge condense into the actin-myosin bundle, the number of myosin molecules per unit length of the bundle equals the density of myosin in the actin-myosin ring integrated from the outer to the inner radii of the ring. This leads us to the simple assumption that the line tension (force) in the rear bundle σ_B, resulting from the additive action of the condensed myosin molecules, is equal to the contractile stress in the 2D actin-myosin ring γ_net multiplied by the width of the ring R₀/2: σ_B = γ_netR₀/2, or γ_net = 2σ_B/R₀.

Energy of cell polarization

Intracellular forces do thermodynamic work changing the free energy of the system in the course of transition between the nonpolarized and polarized states. Below we discuss subtleties of this nontrivial statement. The 2D pressure Π or, equivalently, the total actin normal force f, performs a positive thermodynamic work when each element of the front edge of the cell moves in the normal direction by dR. This is accompanied by decrease of the free energy of the polymerizing actin system F_polym,

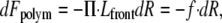(1)

where the pressure Π is assumed to be constant along the front edge following the constant density of the actin filaments, and L_front is the length of this edge. The work done by the contractile myosin tension γ_net is related to the change of the lamellipodial area A_net containing myosin. The corresponding change of the free energy of the actin-myosin system is

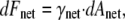(2)

implying that the energy decreases with contraction (area decrease) of the actin-myosin network.

The work of the contractile line tension σ_B generated within the actin-myosin bundle at the cell rear is proportional to variation of the bundle length L_B, and the corresponding change of the free energy of the bundle is

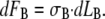(3)

The potential thermodynamic work performed by the fourth force factor, the isotropic membrane tension γ_mem, is proportional to the change of the cell membrane area. We assume conservation of the latter, so the membrane tension does not directly contribute to the energy of the cell polarization, but, as shown below, it influences the energy indirectly by coupling the pushing at the front and the shape of the rear edge.

The total change of the free energy is the sum of all three contributions (Eqs. 1–3). Since we assume that the force parameters f, γ_net, and σ_B remain constant in the course of the cell polarization, the total free energy, which is a first-order homogeneous function of the extensive thermodynamic variables including R, A_net, and L_B (30), can be written in the integrated form,

(4)

where F₀ is part of the free energy independent of R, A_net, and L_B.

Model equations

To analyze the system free energy (Eq. 4) as a function of the polarization angle ϕ and find the conditions for the bistable cell behavior, the variables R, A_net, and L_B have to be expressed in terms of the angle ϕ. Conditions of mechanical equilibrium at the fragment boundary and conservation of total area of the fragment A_mem lead to the geometrical connections between R, ρ, L_B, and ϕ.

To address the equilibrium of the front edge, we consider an infinitesimal element of the edge, which has a shape of a convex circular arc of radius R and the arc angle dχ so that the element length is dl = R · dχ. There are three forces acting on the edge element in the normal direction. First, the force generated by the 2D pressure Π of the pushing actin filaments, which is equal to Π · R · dχ. Second, the force coming from the membrane tension and equal to −γ_mem · R · dχ, where the minus sign indicates that the membrane tension γ_mem, which is generated as a result of the actin pressure pushing the cell edge, is directed oppositely to the pressure Π (Fig. 2, b and c). Finally, the edge can be, generally, characterized by line tension σ_front accounting for an excess of the membrane free energy at the edge compared to the flat part of the cell membrane. This excess energy includes contributions of the energy of the membrane tension, ∼γ_memh, and of the membrane bending at the edge, ∼κ/h, where h is the lamellipodium thickness and κ is the membrane bending modulus (31). Since, on one hand, the line tension is tangential to the front profile, and, on the other hand, the profile has a circular convex shape, the contribution of σ_front to the normal force acting on the edge element is −σ_front · dχ. Mechanical equilibrium of the edge element corresponds to vanishing sum of these three forces. This leads to the equation which is a two-dimensional analog of the Laplace equilibrium equation of interfaces. An estimate taking into account the relevant values of the pressure Π ≈ 100 pN/μN (20,22) and the value of the membrane bending modulus κ ≈ 10⁻¹⁹ J (31) shows that the contribution to the edge line tension σ_front of the membrane bending energy ∼κ/h is negligible in comparison with that of the membrane tension γ_mem generated by the actin pushing. Furthermore, inserting into the equilibrium equation above the contribution of γ_mem to σ_front renders σ_front/R ≈ γ_memh/R ≪ γ_mem, meaning also that this contribution can be neglected and the mechanical equilibrium at the front edge is expressed by the simple equation γ_mem = Π. Taking into account the relationships Π · L_front = f and L_front = (2π − ϕ) · R, we obtain:

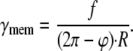(5)

The rear edge is subjected to action of the membrane tension γ_mem and the line tension of the actin-myosin bundle σ_B (Fig. 2 c), which, is considerable and cannot be neglected. Direction of γ_mem with respect to the rear edge requires a concave shape of the latter (Fig. 2 c). Consideration analogous to the above one renders the equation of equilibrium at the rear edge:

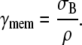(6)

Simple, yet tedious, geometric-algebraic calculation, using Eqs. 5 and 6 and area conservation, results in the formulas

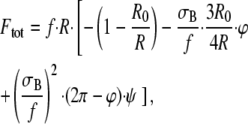(7)

where

(8)

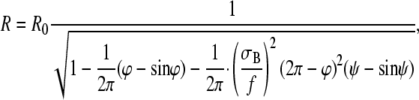(9)

and the terms independent of the polarization angle ϕ such as F₀ are omitted.

Equations 7–9 determine the system free energy as a function of the degree of the cell polarization described by the polarization angle ϕ. Remarkably, this function depends on the single dimensionless factor, σ_B/f—the ratio between the myosin powered tension in the rear bundle and the pushing force produced by the actin polymerization.

RESULTS

The first and second terms in the right-hand side of Eq. 7 describe, respectively, the negative contributions of the actin pushing and network contractile forces into the fragment's free energy. These factors favor the cell polarization causing the energy decrease with growing polarization angle ϕ: allowing actin polymerization to move forward the front edge lowers free energy of the actin system, while decreasing the area of the actin-myosin ring effectively contracts the actin-myosin network and lowers its energy. The third term in the right-hand side of Eq. 7 is positive and accounts for the resistance to the cell polarization coming from the expanding rear edge due to the increase of the energy when the contractile bundle is elongated.

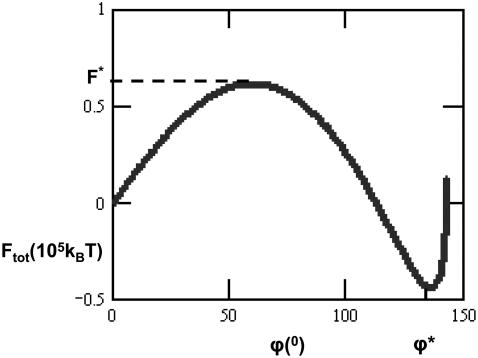
Asymptotic analysis of Eqs. 7–9 reveals that when polarization is weak, ϕ ≪ 1, the actin polymerization energy is proportional to ϕ³ and is negligibly small compared to the two myosin contributions, which are proportional to ϕ. The effect of the expanding rear contractile bundle turns out to be stronger than that of the shrinking actin-myosin network, and as a result, the total free energy increases with the angle: F ≈ σ_B · R₀ · ϕ/4. For greater values of the polarization angle, ϕ ≥ 1, a sufficiently large total normal force f ≥ 1.5 σ_B overcomes the resistance of the rear bundle and results in decrease of the free energy. The resulting nonmonotonic energy profile is illustrated in Fig. 3 for the ratio between the bundle tension and the total normal force σ_B/f = 1/4.

FIGURE 3.

Dependence of the free energy of the cell F_tot measured in unit of thermal energy, k_BT, on the polarization angle ϕ measured in degrees. The parameter values are R₀ = 10 μm, f = 6 nN, and σ_B/f = 0.25.

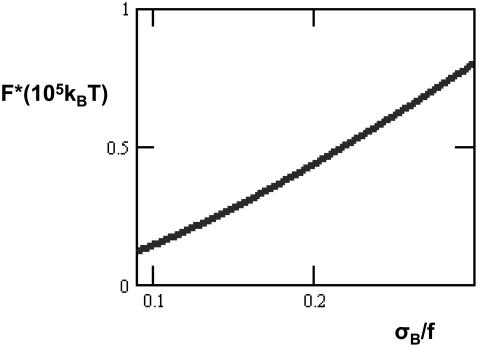
According to the energy dependence on the polarization angle F(ϕ) (Fig. 3), the cell has two distinct states of minimal free energy. The first corresponds to ϕ = 0 and, hence, represents the nonpolarized discoid state. The second is characterized by a nonvanishing polarization angle ϕ* and describes the polarized state. The two states are separated by an energy barrier F* (Fig. 3) that guarantees stability of the two states and a need of finite energy input for transition between them. The height of the energy barrier decreases with the ratio σ_B/f, as illustrated in Fig. 4 showing the energy barrier F* between the nonpolarized and polarized states. This means that the stronger is the total normal force compared to the rear bundle tension, the easier is the transition from the nonpolarized to the polarized state of the cell. Altogether, the system properties predicted based on the energy profile (Fig. 3) correspond to the bistable behavior of the cell observed experimentally.

FIGURE 4.

Dependence of the polarization angle ϕ* in the stable polarized state on the ratio between the intracellular forces σ_B/f. The parameter values are as in Fig. 3.

The value of the polarization angle ϕ* determines the cell shape in the stable polarized state and depends on the ratio σ_B/f, as illustrated in Fig. 5. The smaller the bundle tension σ_B compared to the total normal force f, the smaller the polarization angle ϕ* of the crescentlike shape that stabilizes the cell in the polarized state. To estimate the relevant values of the ratio σ_B/f, we found its values corresponding to the polarization angles ϕ* that describe the characteristic shapes of the keratocyte fragments observed experimentally in Verkhovsky et al. (7). The comparison of the real and modeled cell shapes is presented in Fig. 1, b–e, for σ_B/f = 0.25 and σ_B/f = 0.15. Hence, the suggested model is able to predict the realistic shapes of the cells in the polarized states by reasonably small variations of the single parameter σ_B/f.

FIGURE 5.

Dependence of the energy barrier F* corresponding to transition from the nonpolarized to the polarized state on the ratio between the intracellular forces σ_B/f. The parameter values are as in Fig. 3.

Model assumptions

There are several assumptions underlying the model, but the most fundamental issue is the use of the notions of free energy and thermodynamic work for description of the cell behavior. A cell has features of both mechanical system generating and balancing elastic stresses of its cytoskeletal and membrane components, and of a thermodynamically nonequilibrium structure (3,10) in which chemical energy is constantly released and dissipated through viscoelastic macroscopic flows of polymer networks (29) and cytoplasm (3,10). We propose that the event of polarization of a cell fragment is determined by the mechanical behavior of the cell components, and is, therefore, treatable thermodynamically, whereas the irreversible processes of ATP hydrolysis by actin and myosin generate constant forces and tensions within the three actin subsystems considered by our model. In other words, and analogously to the general thermodynamic approach to treatment of systems in contact with external reservoirs, the steady-state ATP hydrolysis and related dissipative processes are assumed to ensure existence of thermodynamic reservoirs of constant tensions imposed on the intracellular actin subsystems. For each subsystem, the specific mechanism of functioning of such an effective thermodynamic reservoir may be different. For example, for the polymerizing actin filaments pushing the cell edge, the total normal force f, and, hence, the tensions within the actin network and the membrane, are determined, ultimately, by maintaining a G-actin concentration near the filament barbed ends. Constancy of this concentration and the related steadiness of the stresses are guaranteed by a regulated depolymerization of the filament pointed ends, which is controlled by the rate of hydrolysis of the filamentous ATP-actin into the ADP-actin. Similarly, hydrolysis maintains the ability of actin-myosin complexes to turn over and generate constant contractile stresses. The respective energy flows are complex, but from the macroscopic mechanical point of view, both growing actin filaments and myosin clusters perform mechanical work (1). Detailed consideration of physics of these effective reservoirs and analysis of the conditions where their capacities are sufficient to maintain constant tensions in the course of cell polarization are outside the scope of this simple model. Thermodynamic analysis does not predict actual movements or the rate at which energy is transferred to work, but it does predicts tendencies: as long as a transition is associated with a decrease in free energy, this transition will proceed spontaneously. This is the only law of thermodynamics that we use.

Our calculation of the free energy is based on the following essential assumptions (other than those listed in the model description): The mechanical rigidity of the lamellipodial F-actin network and adhesions is sufficiently high to guarantee negligible deformations of these structures upon the stresses developed within the system. Otherwise, the elastic deformation energy would have to be considered as a part of the total free energy. This assumption is justified: keratocyte's lamellipodial Young modulus Y ∼ 5 · 10⁴ pN/μm² (32). The total traction force in the keratocyte, presumably generated by the myosin contraction, is ∼10⁴ pN (33). At least half of this force is generated by the tangential contraction of the actomyosin bundle at the lamellipodial rear, so it is fair to assume that <T ∼ 5 · 10³ pN is applied to the lamellipodial network. The order of magnitude of the deformation, ɛ, of the actin lamellipodial network can be estimated as the ratio of this myosin-generated force to the network's Young modulus multiplied by the cross-section area of the lamellipod to which this force is applied, ɛ ∼ T/(Yhl), where h is the height of the lamellipod, and l is its width. Substituting h ∼ 0.1 μm, l ∼ 10 μm, we estimate ɛ ∼ 0.1, so the elastic deformation is insignificant. Also, adhesion complexes have to adjust very fast to the cell shape changes. There are no quantitative data on adhesion turnover, but keratocyte adhesions are known to be very dynamic (29).

We assumed that the intracellular forces, namely, the total actin normal force f and the contractile stresses γ_net and σ_B generated by myosin remain constant in the course of the cell polarization. Steadiness of f can simply mean that the total number of growing filaments at the cell edge is constant. Constancy of γ_net and σ_B implies that the numbers of the actin-myosin force generating elements per unit length of the bundle and per unit area of the network remain constant in the course of polarization. Though there is no relevant data, these assumptions are plausible. Variations in the force parameters would change the quantitative but not the qualitative character of the model predictions. For example, constancy of the actin polymerization-induced pressure Π instead of the total normal force f would impede to some extent the cell polarization. The same effect would follow from increase of the rear bundle tension σ_B.

We assumed the width of the actin-myosin network to be equal to the half radius of the nonpolarized cell shape, D = R₀/2. While the exact location of the inner boundary of the actin-myosin network cannot be exactly determined from the experimental data, our assumption corresponds, approximately, to the observations (7). Change of the value of D, as well as possible anisotropy and inhomogeneities of myosin and actin distributions and stresses, would not change the qualitative character of the model results. Similarly, deviations from the relation σ_B = γ_net · D do not change the model predictions qualitatively. This assumption is plausible if the contractile stresses are determined by the numbers of myosin molecules per cross section of the actin-myosin bundle and the actin-myosin network, respectively, and if, in the course of cell polarization, the myosin molecules do not move relative to F-actin.

DISCUSSION

We suggest a physical mechanism for the phenomenon of cell polarization—a key stage at the onset of the cell directional motility (5). The model is based on the observations of the lamellipodial fish keratocyte fragments (7), probably the simplest system exhibiting polarization and directional crawling. The essence of the proposed mechanism is in the thermodynamic work and the related free energy changes of the system, generated by the following intracellular forces: the pushing force produced by polymerizing actin at the cell edge, the membrane tension generated by this force, and the myosin contractile stress throughout the cell and in the rear actin-myosin bundle. Direct and indirect measurements of these forces, stresses, and tensions (18,20,33) and other data (34) indicate that all of them are crucial for cell migration and spreading.

We calculated the dependence of this free energy on the degree of polarization, and discovered that it is nonmonotonic and characterized by two minima corresponding to symmetric nonmotile and polarized motile cell states. The two states are locally stable and separated by a finite energy barrier, which explains the observed property of bistability of keratocyte fragments (7). First, the model predicts that the cell can reside practically indefinitely in distinct nonpolarized and polarized states. Second, it predicts that these states are interconvertible upon an external stimulus that drives the system over the energy barrier. Since the barrier constitutes a macroscopic amount of energy of the order of 10⁴ k_BT (where k_BT, the product of the Boltzmann constant and the absolute temperature, is the molecular thermal energy), the transition between the states requires a strong external stimulus, i.e., a direct mechanical force coming from fluid stream or microneedle (7). Such force can also come from the cell-cell collisions that were observed to trigger transitions between the nonpolarized and motile states (7). Further, the model reproduces the observed crescentlike shapes of the polarized keratocyte fragments (7). In the model, the shapes are determined by the single parameter—the ratio of the myosin-powered tension in the rear actin-myosin bundle to the total normal force generated by the actin polymerization, σ_B/f. The model predicts that the observed shapes correspond to the values of this ratio ∼0.15–0.25. No direct measurements of these forces were made, but the data (20,33) indicates that both f and σ_B have similar magnitudes ∼10 nN, so this prediction is feasible. The model also predicts that as this ratio increases, the push needed to polarize the discoid fragment has to become stronger, while the motile fragment would be less circular and more crescentlike. This prediction can, in principle, be tested in the future and used to assess the model.

The model only explains the cell polarization and does not address the upcoming cell movement, which likely involves additional mechanical and transport mechanisms. Thus, Verkhovsky et al. (7) proposed an elegant qualitative scenario explaining the polarization maintenance during the cell motion as a result of the following positive feedback loop: F-actin barbed ends grow at the front advancing the leading edge and keeping the network polarized, while myosin contraction at the rear constantly relieves the membrane tension allowing protrusion of the front and retraction of the rear. Myosin concentrates at the rear because its clusters detach from the actin network slowly, and so they end up at the rear of the rapidly crawling cell. Meanwhile, actin assembles at the front and disassembles everywhere else maintaining rigid network at the front rendered stationary by adhesion (28,29) and weak contracting network at the rear. It is likely that the resulting spatially graded distributions of protrusion and retraction along the cell boundary (8,26) explain the observed bent-rectangle-like shapes of mature motile cell fragments. Detailed model of this process is still pending.

Another essential factor determining the cell shape and polarity maintenance is the dynamic adhesions (28,29) that transmit the forces developed by the actin-myosin system to extracellular substrates. The adhesion complexes are influenced by the myosin stresses (35) and, at the same time, affect the myosin-powered centripetal flow of actin (36). In the nonpolarized state, the symmetrically distributed cytoskeleton elements apply to the cell adhesions isotropic forces directed to the cell center. Hence, there is no resultant force tending to move the cell in a certain direction. In the polarized state, the tension in the actin-myosin bundle at the rear is likely to facilitate development of the observed strong adhesions concentrated in the sharp corners between the front and rear edge (2,6,7,28,29). The myosin tension is applied to these adhesion and results in strong traction forces transverse to the direction of locomotion (33), as well as in weak traction in the direction of locomotion (33). These forces and their influence on the cytoskeleton distribution and cell shape have to be considered to understand the motile cells dynamics.

The model we propose is applicable directly to the much studied cells with lamellipodia on flat surfaces. In cells much larger than the specialized, fast-moving keratocytes, or in important amoeboid motility (e.g., during development or cancer cell migration), the same principles as those described in this article should hold, but additional levels of redundant spatial and temporal regulation (specifically, signaling cascades and more complex, not dendritic, actin arrays) are likely required to initiate and maintain the cell treadmill (2,10). Interestingly, polarized morphology in whole keratocyte cells arise spontaneously (15) with greater frequency than that in fragments. This is possibly related with complex ρGTPase-dependent pathways (44). Also, complex membrane dynamics in motile keratocytes (37) could be involved.

It is tempting to speculate that simple mechanical systems are robustly bistable, while additional mechanochemical pathways vary cell sensitivity to external cues. Further research is needed to address this idea, as well as to find generality and differences between symmetry-breaking phenomena of varying complexity, including the simplest biomimetic actin-no myosin-no membrane (38,39) and actin-myosin-membrane (40,41) assays. Relation between the proposed physical mechanism and other models of actin network polarization based on simple autocatalytic F-actin branching (42) and more complex reaction-diffusion-drift processes (43) has to be examined. Our model is but one of the first steps in this important direction.