One-Dimensional Elastic Continuum Model of Enterocyte Layer Migration

Abstract

Necrotizing enterocolitis is the leading cause of death from gastrointestinal disease in preterm infants. It results from an injury to the mucosal lining of the intestine, leading to translocation of bacteria and endotoxin into the circulation. Intestinal mucosal defects are repaired by the process of intestinal restitution, during which enterocytes migrate from healthy areas to sites of injury. In this article, we develop a mathematical model of migration of enterocytes during experimental necrotizing enterocolitis. The model is based on a novel assumption of elastic deformation of the cell layer and incorporates the following effects: i), mobility promoting force due to lamellipod formation, ii), mobility impeding adhesion to the cell matrix, and iii), enterocyte proliferation. Our model successfully reproduces the behavior observed for enterocyte migration on glass coverslips, namely the dependence of migration speed on the distance from the wound edge, and the finite propagation distance in the absence of proliferation that results in an occasional failure to close the wound. It also qualitatively reproduces the dependence of migration speed on integrin concentration. The model is applicable to the closure of a wound with a linear edge and, after calibration with experimental data, could be used to predict the effect of chemical agents on mobility, adhesion, and proliferation of enterocytes.

INTRODUCTION

The ability of the cells that line the surface of the intestine to move plays a critical role in the ability of the body to heal any injury to the intestinal lining. The process by which such cells—called enterocytes—move is of great scientific interest. For example, there are certain conditions in which enterocyte migration is inhibited, therefore rendering the body susceptible to further injury and illness. One such condition is termed necrotizing enterocolitis (NEC), a disease that affects young babies and is characterized by impairment in the ability of enterocytes to move effectively, resulting in impaired healing (1–5). Mucosal healing also requires the generation of new enterocytes from precursors that are located deep within crypts of the mucosal lining, a process termed enterocyte proliferation (6). Enterocyte proliferation takes days before new cells are generated, as compared to enterocyte migration that may be completed within hours. Accordingly, it has become apparent that mucosal healing is largely determined by enterocyte migration (7), at least during the early phases. An understanding of the mechanisms that govern enterocyte migration is therefore of vital importance to gain insights into the regulation of intestinal physiology during conditions of both health and disease. Importantly, little information exists to characterize the factors that regulate enterocyte migration under conditions that are associated with intestinal inflammation such as occurs in NEC.

Although many molecules may act in concert to inhibit enterocyte migration in the development of NEC, bacterial endotoxin (lipopolysaccharide (LPS)) is likely to act as one of the earliest. LPS, which is found on the outer wall of gram negative bacteria, is a potent immunostimulant that exerts a large effect on the ability of enterocytes to migrate, given the large concentrations present within the lumen of the intestine. Mathematical modeling is emerging as an approach by which to address the complexity of inflammation in general (8) and of NEC in particular (9). To design experimental and mathematical models to predict the development of NEC, we therefore turned to an in vitro system in which small intestinal enterocytes (IEC-6 cells) were exposed to LPS at concentrations known to be present in the lumen of animals with experimental NEC (100 ng/ml to 50 μg/ml). The exposure of enterocytes to LPS in this concentration range leads to a profound, dose-dependent inhibition of enterocyte migration (10). Studies directed at elucidating the mechanisms that could mediate this migration inhibitory effect showed that LPS increases the adhesion of cells to the underlying matrix. This increased adhesion occurred due to a profound increase in the number of attachment sites—termed focal adhesions (10)—as well as an increase in the expression of binding receptors, called integrins, on the surface of the cell (11), in response to LPS.

The primary motivation for development of the model described herein is that the ability to predict the effect(s) of LPS and integrins on migration of enterocytes could have tremendous significance in understanding, and perhaps correcting, the factors leading to the defect in mucosal healing that characterizes NEC. We give a mathematical description of the moving enterocyte layer and describe its properties by three constants related to the adhesion of cells to substrate, the elasticity of the layer, and the force exerted by lamellipodia, which are foot-like projections from the cell surface that allow the cell to move forward. We calibrate our model with real-time observations of cell migration and obtain estimates of these parameters. Finally, we find that with natural assumptions regarding the dependence of adhesion and lamellipod force on integrin concentration, the model yields results that are in qualitative agreement with experimental observations of the effect of adhesion on cell migration speed (12,13).

THEORY AND METHODS

Existing mathematical models of wound healing are generally based on reaction-diffusion formalism in which moving edge of the cell layer is represented as a traveling wave of cell concentration. For adult epidermal wound healing, Sherratt and Murray (14) proposed a two-component model in which the epithelial layer is described by giving cell density per unit area and the time-dependence of this density is related to the concentration of the mitosis-regulating chemical. For embryonic epidermal wound healing Sherratt (15) developed a model involving actin filament network formation, based on a mechanochemical model for the deformation of epithelial sheets proposed by Murray and Oster (16). Recently Walker et al. (17,18) used an agent-based model to simulate the wounded epithelial cell monolayers and suggested that simple rules are sufficient to qualitatively predict the calcium-dependent pattern of wound closure observed in vitro. In dermal wound healing, the mathematical model derived by Tranquillo and Murray (19) includes the mechanism of dermal wound contraction. More complicated models including multiple cell types and multiple types or phases of the viscoelastic extracellular matrix (ECM) have been developed, some including additional equations for chemicals (such as growth factors) that modulate cell proliferative, motile, and contractile behavior (20,21). A detailed model of the dependence of cell speed on adhesion-receptor/ligand binding was proposed by DiMilla et al. (22). Most recently, we have used an agent-based model to describe the interactions between inflammation and healing in the setting of chronic, nonhealing diabetic foot ulcers (23).

In this article, we focus on modeling the natural, unimpeded, cell migration during healing of the damaged intestinal mucosa. To design experimental and mathematical models to predict the development of the migration defect that characterizes NEC, we utilized a system in which small intestinal enterocytes (IEC-6 cells) are cultured on a glass coverslip, grown to confluence, and then scraped with a pipette or cell scraper to create a gap that represents the wound. The cells undergo motion, deformation, and proliferation. We have observed that the enterocyte cell layer is only one cell deep, and that during migration cells do not separate from the edge and no holes are formed in the interior of the layer. In addition, during migration cells at the edge and in the interior of the layer move generally toward the wound and never away from it (see Fig. 4). Therefore, instead of a collection of diffusing cells, the cell layer can be described as an elastic continuum in which cells are connected, albeit loosely, to each other. The cells appear to move in accord with the so-called “sliding mechanism”, in which cells in the interior respond passively to the pull of the cells at the edge (24–26).

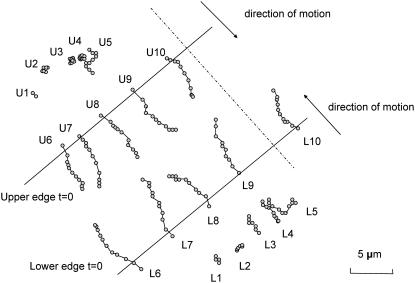
FIGURE 4.

The observed paths of cells U1…U10 and L1…L10 of Fig. 3. The positions of edges at t = 0 are indicated by solid lines. The direction of motion, along which traveled distances were measured, is shown as dash-dotted line.

Mathematical formulation

The motion of cells is assumed to be driven by the cells at the edge of the wound through the formation of lamellipodia, which produce the driving force (27). The cells in the interior do not form lamellipodia and hence are not directly actuating the motion. However, they are tightly connected to the cells at the boundary. Tight junctions between the cells prevent separation (28) and hence the edge cells pull with them the cells in the interior of the layer. The cell layer stretches because of the tension applied by the edge cells, and the motion of the cells is slowed down by the adhesion between cells and the substrate.

The cell layer is represented by a one-dimensional elastic continuum capable of deformation, motion, and material growth (see Fig. 1). Initially, the continuum is uniform and free from internal stresses. After part of the layer is scraped, a net external force F acting on the layer will develop at the resulting boundary as a result of lamellipod formation. This force, which will cause the layer to move and deform, will be opposed by the tension in the continuum resulting from stretching of the cells in the layer, and also by the adhesion between the continuum and the substrate during the motion.

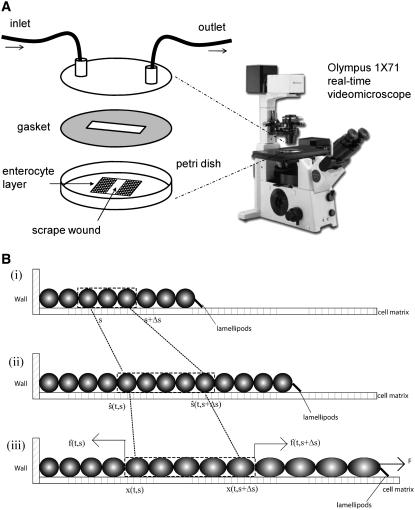
FIGURE 1.

(A) Sketch of the experimental setup for monitoring in vitro mobility. Confluent IEC-6 cells were plated on glass coverslips, scraped with a cell scraper, and then mounted on the stage of an Olympus 1X71 (Tokyo, Japan) inverted microscope warmed to 37°C. Fresh medium was continuously perfused across the cells. Differential interference contrast images were obtained every 5 min. (B) Schematic representation of the cell layer as one-dimensional continuum (only one side of the wound is shown): i), initial state; ii), hypothetical state at time t accounting for growth but not deformation; iii), true configuration of the layer at time t.

Our model differs from published viscoelastic continuum models of epithelial sheets (19) in that we ascribe elasticity to the cell layer itself, but not to the substrate matrix. The forces considered in Tranquillo and Murray (19) are elastic forces and traction forces arising from the actin filament network between the cells and substrate that attaches to the cells. In our model, because we are concerned with in vitro experiments in which IEC-6 cells are planted on glass coverslips, we can safely ignore the elasticity of the substratum and only consider the forces coming from the lamellipod of the cells at edge and interaction between cells.

We employ the variable s to describe the position of a cell in the original layer. A proliferating cell generates two “offsprings”. We adhere to the convention that the offspring that is closer to the moving edge of the layer carries the s-value of the original cell and we employ the variable 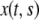to denote the position of cell s in the layer at time t. In other words, 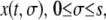is the position at time t of the offsprings of cells originally located between 0 and s. In addition, we introduce the variable 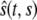that describes the hypothetical position of cell s at time t if all deformation in the layer was instantaneously removed. Thus, 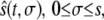would be the position at t of the offsprings of cells originally located between 0 and s if we accounted for growth but not deformation (see Fig. 1).

Let us now consider a segment of cells that are the offsprings of cells between s and 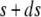of the original layer with ds assumed small. At time t, such a segment extends between 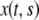and 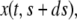its velocity is 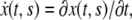and acceleration 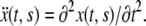Balance of momentum implies that

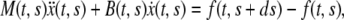(1)

where 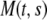is the time-dependent mass of the segment, 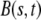is the coefficient describing the sliding resistance due to adhesion of the cells to the substrate, and f the resultant force on a cross section of the layer.

It is reasonable to assume that the coefficient 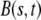is proportional to the extent of contact of the segment with the substrate (10,11) and hence

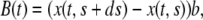(2)

where b is the adhesion constant, which has the units of force times time divided by length squared. In addition, for slow motions one may neglect the acceleration term in Eq. 1 and hence, in view of Eq. 2, one obtains

(3)

which, in the limit 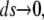becomes,

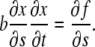(4)

The strain (deformation gradient) in the cell layer can be described by the quantity 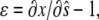with 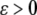corresponding to stretch and 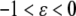corresponding to compression. The model must be completed by an appropriate choice of the constitutive relation describing the dependence of f on ɛ. When ɛ is small, one could assume that the resultant force is a linear function of the strain (Hooke's law):

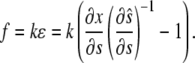(5)

Here the stretching modulus of the layer k has the unit of force as the cell-layer thickness is assumed constant. The drawback of Eq. 5 is that the resultant force (and hence the strain) remains finite if the material is compressed to infinitesimal volume. A more appropriate choice, which we make here, yields infinite magnitude of the resultant force for both 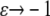and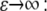

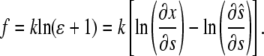(6)

(The difference between Eqs. 5 and 6 is exhibited only when the cell layer is subjected to extreme deformation. We have verified that the choice of Eq. 5 instead of Eq. 6 would yield results essentially indistinguishable from those presented in this article.)

Any deformation of a cell is accompanied by an active remodeling of the cytoskeleton, which generally results in a viscoelastic stress-strain response (29). In Eqs. 5 and 6 it is implicitly assumed that the stretching modulus k of the cell layer is time independent and hence the cell layer responds instantaneously and passively to the forces generated on it. This assumption is made due to the fact that the timescale of the motion of the layer (order of hours) is slow compared to the relaxation time of single-cell deformation, which is of the order of tens of seconds (30). Therefore, one should think of k as the residual stretching modulus of the layer after cytoskeleton relaxation.

Material growth and decay of the layer can be described using the growth gradient 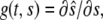which obeys

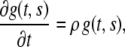(7)

where the growth rate ρ may generally depend on s, t, but also ɛ or g itself. If one assumes that the growth rate is time and strain independent, the solution of Eq. 7 with initial condition 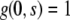is easily obtained as

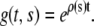(8)

From Eqs. 4, 6, and 8 we obtain resulting equation:

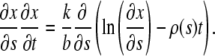(9)

We assume that the location of the left boundary of the cell layer (at 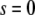) is fixed whereas the right boundary (at 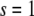in dimensionless units) is free to move, and that the force applied at the right boundary is constant and equal to F. Thus, the initial and boundary conditions are, in view of Eq. 5,

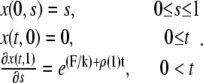(10)

Note that the constants b, k, and F appear in the problem only as the ratios 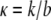(units of length squared divided by time) and 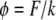(dimensionless). The differential equation Eq. 9 with boundary and initial conditions Eq. 10 can be solved numerically using finite difference methods (see Appendix).

Constant growth rate

If the growth rate ρ is spatially independent, the problem of Eqs. 9 and 10 further simplifies as

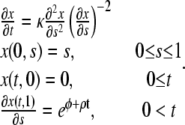(11)

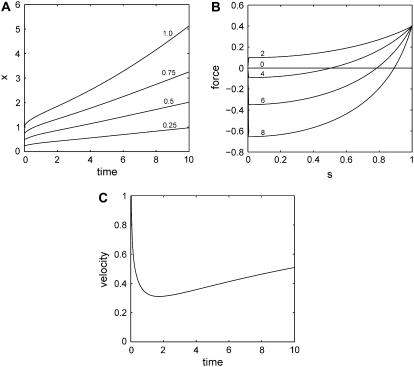
Fig. 2 gives an example of the typical features of solutions of Eqs. 11 with a constant, positive growth rate. The initial motion is dominated by the force applied by the lamellipodia on the edge of the layer. The velocity of the edge is decreasing as a result of increasing tension and increasing adhesion in the extended layer. The cells in the interior of the layer remain static for a time period proportional to their distance from the edge. At later times the motion of the layer becomes dominated by cell proliferation and the velocity of the edge increases again. The tensile strain decreases and eventually becomes positive. At this stage, the proliferation of new material, which pushes the old cells out of the way, is the driving force behind the motion of the layer.

FIGURE 2.

Generic behavior at constant proliferation rate. Here 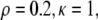and 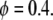(A) Graphs of the position x of cells with s = 0.25, 0.5, 0.75, 1 as a function of time (in hours). (B) Resultant force f in the layer versus position s for t = 0, 2, 4, 6, 8 h. (C) Velocity of the edge as a function of time (in hours).

Calibration in the absence of proliferation

In the case of migration of enterocytes on glass coverslips considered in this article, we have observed that the proliferation rate is very low. In this case, ρ can be neglected and the problem Eq. 11 becomes

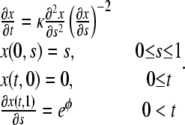(12)

The differential equation in Eq. 12 has an equilibrium (i.e., time-independent) solution 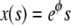that obeys the prescribed boundary conditions (but not the initial condition). This solution is a limiting case of the time-dependent solution and it implies that the maximum distance the right edge of the layer can reach is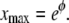

RESULTS

The parameters κ and φ of the model in Eq. 12 can be determined by calibration with experimental data obtained in vitro. In the experiment described in Cetin et al. (5), IEC-6 cells were grown on glass coverslips to 100% confluence, serum-starved for 12 h, scraped with a cell scraper, and then transferred to the stage. Pictures were taken every five minutes for 17 h to record the migration profiles of the cells. Fig. 3 shows examples of such pictures. We used the recorded pictures of migrating cells to track the motion of selected 10 cells located near the edges and in the interior of the layer. The cells are marked L1-L10 (in the lower right layer) and U1-U10 (in the upper left layer) (see Fig. 4). The distance traveled by the cells was measured in the direction perpendicular to the axis of the wound.

FIGURE 3.

Snapshots of IEC-6 cells migrating on a glass coverslip at (A) t = 0, (B) t = 5 h, and (C) t = 10 h. The tracked cells are labeled as U1…U10 and L1…L10.

From these measurements, we fit the average position of the group of cells L1-L5 in the interior of the lower right layer and the group of cells L6-L10 near the edge. The model parameters were estimated using numerical solution of Eq. 12 and a routine nonlinear unconstrained minimization of the least square error. The distance of the wound edge from the fixed edge of the cell layer was assumed to be very large compared to the gap size and cell diameter. In our optimization code, we observed that the results are insensitive to this value (data not shown). The following values were obtained for the motion of the lower edge:

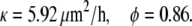We repeated the data fitting for the upper left layer where we averaged the position of cells U1-U5 located in the interior of the layer and the position of cells U6-U10 located near the edge. We obtain the following values:

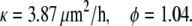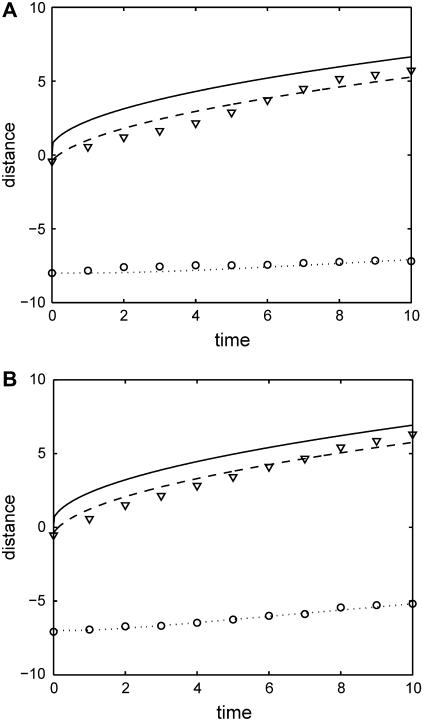
The averages over both layers are κ = 4.9 μm²/h and φ = 0.9. As shown in Fig. 5, the velocity of the cells at the edge is gradually decreasing whereas the velocity of cells in the interior of the layer is initially zero and then slowly increasing.

FIGURE 5.

Dependence of traveled distance (μm) on time (h) for cells in (A) the upper left layer and (B) the lower right layer. Average distance traveled by cells in the direction perpendicular to the wound edge is shown as hollow circles (U1-U5 or L1-L5) and triangles (U6-U10 or L6-L10). Computed predictions are shown as solid (edge), dashed, and dotted curves.

Dependence of migration on integrin concentration

The adhesion of cells to the substrate and the force exerted by lamellipodia are modulated by adhesion receptors, such as integrins, that connect the cell to the extracellular matrix. Integrin concentration and integrin-ligand affinity have been found to affect the speed of migrating cells (12).

This model allows us to investigate the effect of integrins on migration speed by examining the dependence of the constants b, k, and F on integrin concentration I. At this time this dependence is not known, however, the following assumptions appear reasonable: i), the adhesion constant b should be proportional to I, ii), the lamellipod force F should be proportional to 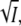and iii), the stretching modulus k of the layer should be independent of I. The difference in scaling between b and F stems from the fact that adhesion is generated on the entire cell-matrix contact surface, whereas the force of the lamellipod is only exerted at the cell edge. Since our one-dimensional model represents a two-dimensional layer of cells, b is proportional to the area of contact between the cell and the substrate whereas F is proportional to length of the cell edge. Remarkably, under these simple assumptions the graph of migration velocity versus integrin concentration in Fig. 6 shows the characteristic bell-shaped curve with low velocity corresponding to low or high integrin concentration and maximum velocity corresponding to intermediate integrin concentration (12,13). This observation is not meant to replace the detailed and quantitatively accurate model of the dependence of cell speed on adhesion (22), but rather to give some insight into the possible causes of observed velocity variability, such as may occur during inflammatory states.

FIGURE 6.

Dependence of edge migration velocity (μm/h) on integrin concentration for three different time instants: t = 2 h (○), t = 4 h (×), t = 6 h (▵). Here 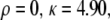and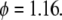

DISCUSSION

The model developed in this article accounts for the three effects influencing cell migration, i.e., the driving force of lamellipodia, the motion impeding adhesion between cells and the substrate, and the elasticity of the cell layer. In the case of constant proliferation, the model predicts increasing velocity of the wound edge. In the case of negligible proliferation the model predicts that the velocity of cells at the edge is initially greater and decreases with time, as is seen experimentally (31). This prediction differs dramatically from predictions of models based on reaction-diffusion equations in which the motion of the edge has constant or gradually increasing velocity. The velocity of cells in the interior of the layer is initially zero and then slowly increases, again in accord with observations. In contrast, none of the existing reaction-diffusion models makes predictions about the migration speed of cells in the interior of the layer.

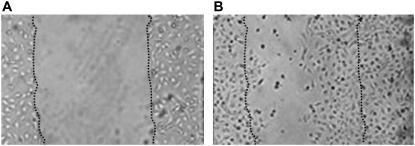
One important consequence of the model is that in the absence of proliferation the maximum distance traveled by any edge is finite. It follows that if the gap of the wound is sufficiently large, the remaining enterocyte layer may not be able to close the wound. This phenomenon was observed experimentally in studies of enterocytes cultured on glass coverslips (see Fig. 7) and is not easily explained by a model based on reaction-diffusion equations.

FIGURE 7.

Enterocyte migration is incomplete under conditions of excessive wound formation. IEC-6 cells were plated on glass coverslips, scraped to induce a wound, then allowed to undergo wound closure over the ensuing 24 h. The position of the wound edge (A) at the beginning of the experiment and (B) 24 h later is indicated by the dotted line. In panel B the dark cells in the wound have undergone apoptosis.

At its present form the model yields ratios of the quantities of interest (κ characterizes the ratio of the stretching modulus k of the layer to the adhesion coefficient b, and φ is the ratio of the force F exerted by lamellipodia to the stretching modulus k) and hence the model enables us to make relative comparisons between these effects. To obtain true magnitudes of F, b, or k, one would need to perform an independent measurement of at least one of the three quantities. Prass et al. (32) have measured the cell stall force for keratinocytes using atomic force microscopy catilever and obtained a value ∼40 nN. If enterocytes migrating on glass coverslips exert similar force, then the corresponding value of the cell-layer stretching modulus k would be ∼44 nN and adhesion/friction constant b would be ∼0.11 h nN/μm².

Two different fits were performed to determine the coefficients κ and φ, one for the lower and one for the upper edge of the wound, yielding two different sets of parameters. There are several possibilities as to likely sources of this difference. One possibility is that the coverslip was locally inhomogeneous in adhesion properties, which would have affected both κ and φ constants. Other sources of discrepancy could be local inhomogeneities in initial cell density or cell maturity.

The model described herein is sufficiently general in that it allows for more general growth rate laws to be incorporated. One extension would be to implement spatially variable growth rate There are indications that the proliferation is increased in the area near the edge shortly after creation of the wound. Another possibility is to make growth rate dependent on the stretch in the layer—stretched layer may be more likely to reproduce than compressed, crowded one.

In summary, we have developed a simple model that accurately describes the migration of the enterocyte cell layer (both at the edge and in the interior) in terms of three characteristics: the adhesion of cells to substrate, the elasticity of the layer, and the force exerted by lamellipodia. Fitting of the model to measured data enables one to determine the magnitude of each of these characteristics as a function of the treatment conditions (such as the concentration of LPS).

It is important to point out that although this model is clearly applicable to the situation of scrape wounding of enterocyte monolayers on glass coverslips in vitro, it also provides for useful—albeit partial—information regarding the applicability to in vivo wound healing. For instance, although wound healing in vitro occurs in three dimensions and may be influenced by the presence of inflammatory cells that could serve to modify the rate and extent of healing that occurs, we have recently demonstrated that the fundamental forces that drive wound healing within the intestine in vivo bear striking similarity to the in vitro situation described in this study. The similarities between in vitro migration of enterocytes and in vivo healing as occurs in NEC include a dependence on intact gap junction mediated cell-cell contacts for migration to occur (33), the inhibition of migration by inflammatory cytokines (e.g., IFN-γ) (33), and nitric oxide (34), and marked inhibition by proinflammatory macrophages that may be present within the subepithelial lamina propria (R. Anand, C. Leaphart, C. Rippel, and D. Hackam, unpublished data). Moreover, although proliferation of enterocytes must occur to replace cells that are lost due to damage, the role of enterocyte proliferation in the modulation of mucosal healing is significantly more important during chronic inflammatory states as opposed to the acute inhibition of healing as occurs during exposure to LPS (C. Leaphart, R. Anand, and D. Hackam, unpublished data). Taken in aggregate, we submit that the current model provides important insights into enterocyte migration in vitro with useful correlates for the in vivo situation, both under basal conditions and during conditions of intestinal inflammation such as NEC.

APPENDIX

We present the numerical method used to solve Eq. 9. Let 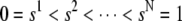be a subdivision of (0,1), such that 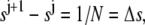the mesh size. Let 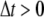be a given step size and 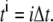let Let 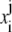denote the numerical approximation of 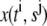Equation 9 is rewritten as:

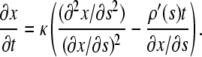(A.1)

Using the finite difference approximations of the partial derivatives of x, we obtain the following combined implicit/explicit scheme that is second order in space and first order in time (note that explicit difference has been used in the denominator and implicit difference in the numerator):

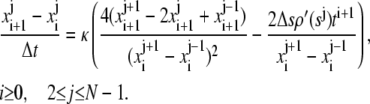(A.2)

After rearranging the terms, we obtain:

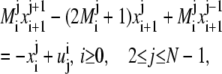(A.3)

with 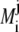and 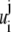are as defined below:

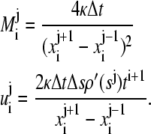(A.4)

The initial condition is simply 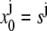and the boundary conditions yield:

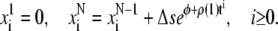(A.5)

The solution 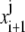at the time step i + 1 can be found by solving the linear system

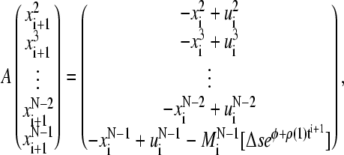(A.6)

where

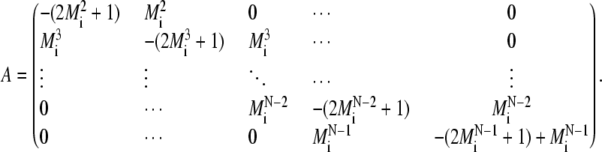(A.7)