Direct Observation of Active Protein Folding Using Lock-in Force Spectroscopy

Abstract

Direct observation of the folding of a single polypeptide chain can provide important information about the thermodynamic states populated along its folding pathway. In this study, we present a lock-in force-spectroscopy technique that improves resolution of atomic-force microscopy force spectroscopy to 400 fN. Using this technique we show that immunoglobulin domain 4 from Dictyostelium discoideum filamin (ddFLN4) refolds against forces of ∼4 pN. Our data show folding of this domain proceeds directly from an extended state and no thermodynamically distinct collapsed state of the polypeptide before folding is populated. Folding of ddFLN4 under load proceeds via an intermediate state. Three-state folding allows ddFLN4 to fold against significantly larger forces than would be possible for a mere two-state folder. We present a general model for protein folding kinetics under load that can predict refolding forces based on chain-length and zero force refolding rate.

INTRODUCTION

In the recent years, the development of novel single molecule techniques has provided new insight into the folding and dynamics of proteins. Force spectroscopy has proven especially useful for studying protein unfolding. However, examples of direct measurement of protein refolding forces are rare. Those examples include thermodynamically extremely stable proteins like membrane proteins, ankyrin, ubiquitin, or leucine zippers (1–5). Active refolding of a topologically more complex protein has only recently been reported for RNase H using optical tweezers (6). Attempts to measure the active contraction force of a folding polypeptide using atomic force microscopy (AFM) force spectroscopy have so far been severely hampered by the limited force resolution (∼10 pN) as well as detector drift producing force artifacts that are often difficult to distinguish from true folding events. In this study, we introduce a lock-in-detection scheme that has been inspired by earlier studies employing AC-modulated force spectroscopy (7–10). In contrast to the earlier studies, we use this approach to separate instrumental drift from the data and therefore improve force resolution into the sub-pN regime. We apply this method to study the active folding forces of an immunoglobulin domain from Dictyostelium discoideum filamin (11).

MATERIALS AND METHODS

Protein expression

The ddFLN1-5 construct, containing five immunoglobulin rod domains, was expressed and purified as described before (11).

Ni²⁺-NTA glass slides

Glass slides were prepared as described in Sakaki et al. (12).

Force spectroscopy of single proteins

All single-molecule force measurements were performed with a custom-built atomic force microscope at room temperature. Calibration of cantilevers was done in solution by using the equipartition theorem (13). For all experiments we used type-B biolevers (Olympus Optical, Tokyo, Japan) with spring constants between k_lever = 4.8 and 6.9 pN nm⁻¹. For data acquisition and analysis we used a DT3016 board (DataTranslation, Marlborough, MA) and a modified software (Asylum Research, Santa Barbara, CA) with Igor PRO 4.09A (WaveMetrics, Lake Oswego, OR). Data was either taken at a sampling rate f_S = 5 kHz for lock-in measurements or at a sampling rate f_S = 20 kHz for high amplitude measurements. A drop of 1 mg/ml protein solution in PBS (10 mM Na-phosphate, 137 mM NaCl, 2.7 mM KCl, pH 7.4) was placed on the Ni²⁺-NTA glass slide and incubated for 10 min. The regular piezo-movement signal was superimposed by a sinusoidal signal at f_FG = 20 Hz or 52 Hz for lock-in or high-amplitude measurements, respectively, resulting in a piezo oscillation amplitude A = 5 or 20/25 nm, respectively (see Fig. 1 b).

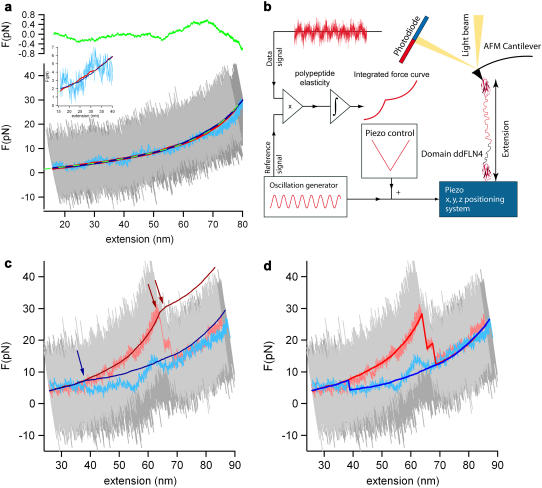
FIGURE 1.

High resolution lock-in force spectroscopy reveals discrete refolding events. (a) A polypeptide force-extension curve of a relax-stretch cycle at v_p = 5 nm/s at full bandwidth of f_S = 5kHz (light and dark gray) and a low-pass filtered relax trace (light blue) are shown. A lock-in trace of the same relax-stretch cycle is shown in dark red and dark blue. The inset shows a zoom into the low forces low extension regime. The lock-in signal is free from detector drift and the noise level is reduced by one or two orders of magnitude. The green-dashed line is a WLC fit to the relaxing lock-in signal returning a persistence length of p = 5 Å ± 0.2 Å. The green line in the top graph shows the deviations of the WLC fit and gives us an estimate of the improved force resolution of ∼400 fN. (b) A schematic illustration of the modified AFM setup is shown. The oscillating signal is superimposed to the regular surface movement signal. Both, the oscillation reference and the full deflection signal are recorded and in-phase multiplied, the result is then integrated to obtain the lock-in force-curve. (c) A typical folding force extension curve at full bandwidth (dark and light gray), low-pass filtered (light blue and light red), and the corresponding integrated lock-in signals (blue and red). The relaxation trace (light blue) shows typical erratic detector drift, which can lead to wrong refolding force interpretations. The refolding extension, however, can be precisely measured, where the two lock-in signals join each other (blue arrow). (d) The same force-extension trace as in panel c. The lock-in signals have been reconstructed such that they exhibit the familiar appearance of a typical force extension trace.

Reconstruction of lock-in curves at nonequilibrium transitions

The integrated lock-in curves show a kink at extensions where an un- or refolding event happened, indicated in Fig. 1 c with red or blue arrows, respectively. For clarity, these integrated traces can be reconstructed to appear as usual force-extension traces (Fig. 1 d). A first-order assumption is that force drift in the deflection signal is small over the timescale of a folding/unfolding event. Therefore the regular deflection traces were averaged over ∼200 ms before and after the event to recover the force difference. This force difference value was then added to the integrated lock-in curve at the respective kink extension.

Determination of refolding forces

The lock-in signal of the refolding trace and of the unfolding trace superimposed very well in the low force regime. The refolding event can be identified by the kink in the refolding trace at small extension. Only traces showing both the kink in the integrated signal and a force shift in the box-filtered force trace at similar extension were counted as observable refolding events. Refolding forces were calculated from the extension of the unfolded wormlike chain (WLC) curve. Since for this calculation it is important to know the zero extension position as exactly as possible, after several folding/unfolding cycles the molecule was fully relaxed until the cantilever was pushed in the surface ∼20–60 pN. If one still assumes an error of ∼10–15 nm in zero position determination, this would yield a maximum force error of 0.5 pN and a Gaussian widening of the histogram. To account for this effect, all theoretical force distributions were therefore convolved with a Gaussian distribution (width σ = 0.5 pN).

Automatic kink detection

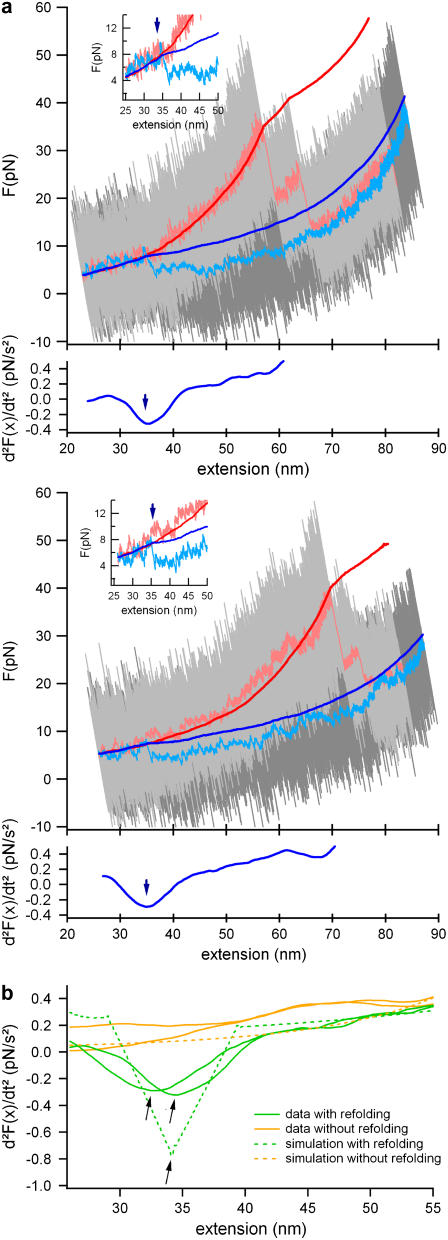
To detect refolding events as objective as possible, we developed an automatic detection algorithm. The second derivative (d²F(t)/dt²) of the lock-in force trace is calculated and box-filtered with a time constant of ∼500 ms. Lock-in force traces with a kink exhibit their global minimum of the second derivative before the turning point of the folding-unfolding cycle (see green traces and arrows in Fig. 2 b), while traces without a refolding event show their global minimum right at the end of the folding cycle (orange traces in Fig. 2 b). Fig. 2 b also shows second derivatives of simulated lock-in force-extension traces with and without a refolding event. Clearly, these simulated curves coincide very well with the data. In Fig. 3 a, we show, for comparison, next to the refolding force histogram of the automatically determined kink positions (blue bars), the histogram of the manually determined kink positions (red line). Both histograms are nearly identical.

FIGURE 2.

Refolding traces and refolding event detection. (a) A set of two typical refolding traces. For color scheme, see previous figure. The automated kink finder detects the minimum of the second derivative of the lock-in trace (bottom corresponding graphs). The refolding forces were calculated from the automatically detected extensions. (b) Comparison of the second derivative of lock-in force extension traces with refolding events (green) and without refolding events (orange). The dashed lines are the second derivatives of simulated lock-in force extension traces. In those traces, also the refolding events exhibit a global minimum.

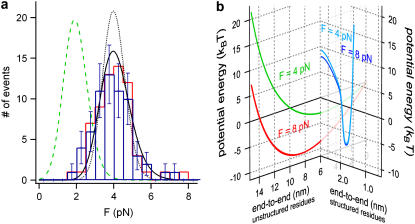
FIGURE 3.

Refolding force distribution and an energy landscape. For comparison, the folding force distribution obtained from the automatic kink detector and the manual kink detection are shown as blue bars and red cityscape, respectively. (a) The obtained refolding force distribution of ddFLN4 (blue bars) can be fitted by a minimal model for protein folding under force. A zero-force refolding rate of k₀₁ = 55 s⁻¹ and a partial contraction of ΔL_C = 19.5 nm fit the data best (black line). A full contraction using the same value for k₀₁ would result in a distribution at much lower forces (green dashed line). A full contraction at ∼4 pN requires a drastically k₀₁ = 3500 s⁻¹ (black dotted line). (b) Schematic illustration of an energy landscape of an unstructured polypeptide spacer of 19.5 nm contour length at a constant load of 4 and 8 pN (green and red line, respectively). The energy landscape of the folded protein (blue line) is illustrated on a different reaction coordinate since it has the boundary condition that the residues between the N- and C-terminus are structured.

Modeling of refolding force distributions

In Fig. 3 a, the refolding force values are compiled into a histogram. To extract the refolding kinetics, the force distributions were fitted with a two-state model including the WLC-elasticity of the polypeptide spacers as introduced by Evans et al. (14). The probability distribution dP_N/dF was calculated by

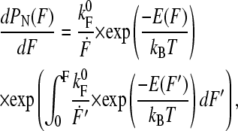(1)

where 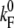denotes the folding rate at zero force, F′ the loading rate dF/dt, E(F) the additional barrier due to folding under force (for details, see Results), and k_BT the Boltzmann energy. The loading rate is calculated from a WLC model with fixed polypeptide contour lengths of L_C = 130 nm at a pulling velocity v_P = 5 nm/s. The scattering of the contour lengths within the data was <15 nm and therefore using a fixed contour length is justified.

Modeling of the lifetime distribution

To analyze the folding intermediate lifetime distribution, we performed Monte Carlo simulations of the experiment in Rief et al. (15). The effective folding rate k(F) was calculated following Eq. 3.

RESULTS

Lock-in force spectroscopy

Low frequency noise due to detector drift is the dominant factor limiting force resolution in force spectroscopy experiments. There are various experimental sources for this drift like thermal bending of the lever (16) or density fluctuations in the buffer affecting the optical path of the detection. Inspired by earlier AC-measurements that had been used to measure polymer elasticity (7–10), we devised a strategy using small amplitude oscillations to overcome the drift problem and increase force resolution. The basic idea is to oscillate the sample with a small amplitude (∼5 nm) at a low frequency of 20 Hz in addition to the slow distance ramp (v_P = 5 nm/s) applied in force-versus-distance curves. At such a low frequency, the internal dynamics of a polypeptide is fast (17) and the polypeptide response is entirely elastic. Lock-in detection then allows us to measure the elastic response and hence the polypeptide spring constant. An illustration of the experimental scheme can be found in Fig. 1 b. Both the oscillating reference signal from a frequency generator and the deflection signal were recorded simultaneously. In a post-experimental processing, the in-phase multiplication of the reference signal and the DC-offset deflection signal returned the relative amplitude transmission through the polypeptide to the cantilever and therefore gives information about the elasticity of the polypeptide between surface and cantilever. Integration of the in-phase multiplied signal resulted in a low-noise lock-in force versus distance trace. Force calibration of the integrated signal was achieved by multiplication with a scaling factor S = 2 × 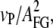where v_P is the actual pulling velocity and A_FG is the oscillation amplitude. Multiplication of the data with the reference signal shifted by 90° yields the viscous response of the system. We compared the viscous signal of the system with and without an attached molecule and could not detect any significant difference in the low force regime. This shows that in the low-force regime, elastic properties dominate the polypeptide behavior and viscous effects are negligibly small. Fig. 1 a shows the integrated elasticity curve of an unfolded polypeptide during a relaxation (dark blue line) and an extension (dark red line) trace. As a comparison, the conventional force curve at full bandwidth of f_S = 5 kHz (gray and dark gray) is shown. This curve is dominated by thermal noise with peak-to-peak amplitudes of ∼30 pN at a typical cantilever spring constant of k_C = 6 pN/nm. We also show the commonly used method of bandwidth reduction using a low-pass filter (25 Hz cutoff) (light blue line). The tremendous advantage of the AC lock-in technique for both drift correction and resolution becomes immediately obvious. The filtered conventional force curve certainly reduces peak-to-peak noise, but it still shows erratic excursions of the force signal due to drift (see also the inset in Fig. 1 a showing a zoom into the low force low extension regime). In contrast, the lock-in curves follow precisely a smooth curve. Fitting the lock-in curve to the WLC model of polypeptide elasticity (18), we find that a persistence length of 5 Å ± 0.2 Å fits the data best (green dashed line). From the deviations from the best WLC fit (Fig. 1 a, top) we estimate the force resolution of the lock-in technique to 400 fN, especially at low forces. Low-frequency lock-in detection therefore increases the force resolution of AFM force spectroscopy experiments by 1–2 orders of magnitude.

Refolding force distributions

We employed the lock-in technique to detect active refolding forces of the immunoglobulin (Ig) domain ddFLN4 from the rod of Dictyostelium discoideum filamin (ddFLN) (11,19). We used a polyprotein comprising five immunoglobulin domains from the ddFLN rod. Only domain 4 (ddFLN4) will fold fast (20) while, after a first unfolding cycle, the other domains in the chain remain permanently unfolded, thus serving as polypeptide spacers. In Fig. 1 c, such a mechanical folding and subsequent unfolding cycle of ddFLN4 at a pulling velocity of v_P = 5 nm/s is shown. Again, unfiltered data (gray), low-pass-filtered data (light blue and red), and lock-in data (dark blue and red) are shown. The blue traces show the relaxation during which ddFLN4 folds while the red traces correspond to the subsequent unfolding of ddFLN4 proving that ddFLN4 must have folded. The unfolding traces exhibit the characteristic three-state unfolding behavior of ddFLN4 due to a mechanical unfolding intermediate (11). It is important to note that the integrated lock-in data (dark traces) do not exhibit any discontinuous transitions since such signals will not lock to the 20-Hz driving frequency. However, the unfolding transitions are characterized by a sudden change in elasticity due to lengthening of the polypeptide upon unfolding, which leads to kinks in the integrated lock-in curves (red arrows). Similarly, refolding events should also manifest themselves in the lock-in data by a kink in the slope of the signal. Such a refolding event is clearly visible in the dark-blue curve at an extension of ∼38 nm, where the dark-blue curve joins the dark-red curve (blue arrow). The lock-in detection now enables us to unequivocally distinguish true refolding events from signal fluctuations caused by cantilever drift. This is essential since drift can easily exceed the refolding signals as can be seen from the low-pass filtered data trace of Fig. 1 c (light blue). For clarity, the sections of the lock-in curve between the folding/unfolding transitions can now be shifted such that the familiar appearance of a force-versus-distance curve is restored (for details, see Reconstruction of Lock-in Curves at Nonequilibrium Transitions). Such a restored curve is shown in Fig. 1 d. It is important to note that the restoring of curves is just a guidance to the eye but not a prerequisite for the analysis. Based on the postulated change in elasticity upon refolding, we then implemented an automated refolding detection algorithm to base our analysis on objective grounds. In brief, the algorithm exploits the fact that the second derivative of a signal with a discontinuity of the slope will exhibit a global minimum at the position of the kink (see bottom graphs in Fig. 2 a). We cross-checked the reliability of this algorithm by testing it against curves where refolding had not occurred, as shown in Fig. 2 b (see also Automatic Kink Detection). A selection of two more folding/unfolding cycles is shown in Fig. 2 a. The zoom insets of the two traces show both a clear refolding event in the direct force extension traces and the kink in the lock-in trace.

We now measured the distribution of refolding forces. To minimize force measurement errors we calculated refolding forces from the measured polypeptide extension at the kink in the lock-in trace (for details, see Materials and Methods). We find a narrow distribution of refolding forces centered at ∼4 pN (Fig. 3 a). Many models have been presented to describe unfolding force distributions of proteins (21–23). Generally, these models describe the unfolding kinetics under load using a load-independent transition state position and a zero-load unfolding rate. The assumption of a fixed, load-independent or only slightly dependent transition state position, however, does not hold in the case of a polypeptide contracting against an external load. This becomes obvious by plotting the energy landscape of a polypeptide held at constant load. Fig. 3 b shows such an energy landscape for a 19.5-nm-long polypeptide at loads of 4 pN and 8 pN, respectively (green and red trace on the left coordinate system). The shape of this energy landscape follows directly from the measured entropic elasticity at low loads as shown in Fig. 1 a leading to a parabolic shape to first-order. The applied load drastically shifts the energy minimum of the unstructured polypeptide to higher values because the polypeptide becomes more and more extended. In contrast, small forces of 4 and 8 pN leave the energy landscape of the structured polypeptide almost unaffected because the transition state lies very close to the folded state (blue lines on right coordinate system in Fig. 3 b) (23). As reaction coordinate in Fig. 3 b, we plot the end-to-end distance of the protein chain. It is important to note that the reaction coordinate for relaxing an unfolded polypeptide chain is nevertheless distinct from the reaction coordinate for pulling the folded structure. For relaxing the unfolded polypeptide, the reaction coordinate contains the additional boundary condition that all residues be unstructured. The reaction coordinate for pulling the folded structure is constrained to those subsets of protein conformations where all residues are structured and assume conformations close to the crystal structure.

To model the distribution of folding forces, we calculated at each possible initial folding force F_i all the additional energetic costs that load imposes on the folding protein as compared to folding in the absence of load. These contributions are the bending energy of the cantilever E_L(F_i), the stretching energy of the polypeptide spacer E_S(F_i), and the entropic elastic energy gain due to contraction of the folded domain E_domain(F_i). The energy needed to bend the cantilever is calculated by E_L(F_i) = 0.5 × (l_i(F_i) − l_f(F_f)) × (F_i + F_f), where l_i(F_i) denotes the extension on the initial WLC at the initial force F_i (at which refolding would happen) and l_f(F_f) is the extension at the final force F_f on the final WLC curve reached after folding. The energy needed to stretch the polypeptide spacer against its entropic elasticity is calculated by

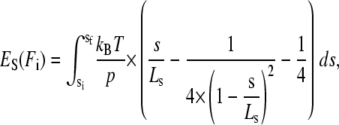where s_f = s_f(F_f) denotes the spacer's final extension on the polypeptide WLC curve, s_i = s_i(F_i) is the spacer's initial extension on its WLC curve, k_BT is the Boltzmann energy, p is the persistence length of the polypeptide spacer (in our case p = 0.5 nm), and L_S is the contour length of the polypeptide spacer. The energy gain E_domain(F_i) is calculated by

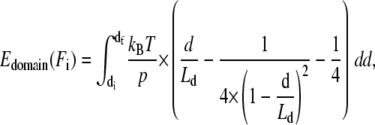where d_f ≠ d_f(F_f) denotes the domain's final extension on its WLC curve (which is independent of the final force F_f), and in our case zero extension, d_i = d_i(F_i) is the initial extension, and L_d is the contour length of the domain. The sum of all these energetic costs,

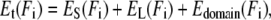(2)

then slows down the folding rate k_f as compared to the force-free folding rate k₀ according to

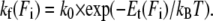(3)

In earlier work, we had determined the force-free folding pathway of ddFLN4. We could show that, in the absence of load, ddFLN4 folds via an obligatory intermediate state according to 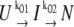with k₀₁ = 55 s⁻¹ and k₀₂ = 179 s⁻¹ (20). Our measured force-distribution can be fully reproduced using the values of the force free folding rate of 55 s⁻¹ and a polypeptide contour length decrease of ΔL_C = 19.5 nm for the amino acids contained in the folding intermediate (see black curve in Fig. 3 a). Also, for comparison, the distribution expected for a full contraction of all amino acids in the polypeptide chain with L_C = 36.5 nm is shown (green dashed line). This result also indicates that, under load, the folding pathway of ddFLN4 proceeds via a folding intermediate.

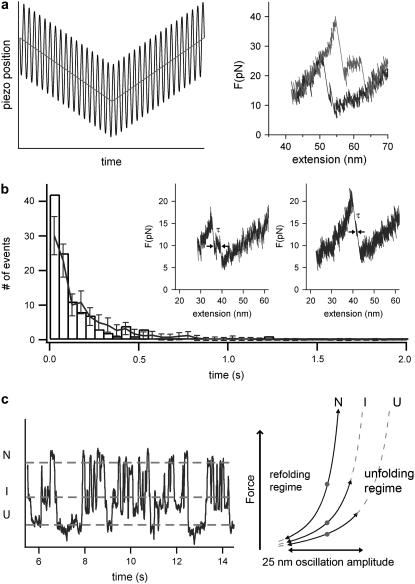
Large amplitude oscillations—apparent equilibrium

Due to limitations of the time resolution of the lock-in experiment the transiently populated intermediate cannot be seen directly in the refolding traces of Fig. 2 a. However, to show the population of the folding intermediate under load, we developed another experimental protocol distinct from lock-in detection that allows observation of the folding intermediate directly. To this end, we applied large amplitude oscillations of A = 20 nm at f_FG = 52 Hz to the sample piezo during a force curve. Due to the large oscillation amplitude, the protein experiences high and low forces in rapid succession at each point of the force curve (see Fig. 4 a, left). We now record the apparent force averaged over two oscillation periods as a function of the average extension. A refolding and subsequent unfolding cycle of ddFLN4 is shown in Fig. 4 a (right). The large oscillations reduce the observed apparent unfolding forces and, at the same time, increase the observed apparent refolding forces. This can be easily understood by considering that, at each point of the force curve, the polypeptide experiences a succession of much higher and much lower forces than the average force almost at the same time. In the refolding traces, the population of the refolding intermediate under load can now be clearly observed (Fig. 4 b, insets). The distribution of lifetimes τ of the intermediate is shown in Fig. 4 b and can be well fitted by a Monte Carlo simulation using a zero force folding rate of 200 s⁻¹ and a contour length of the folding portion of the protein of ΔL_C = 15 nm.

FIGURE 4.

The refolding pathway under force is not changed. (a) (Left) Schematic illustration of an experiment with large amplitudes. The protein is subject to an oscillation amplitude of 20 nm at 52 Hz during each relaxation and extension cycle. (Right) Typical folding/unfolding cycle at such high amplitudes (black and gray trace, respectively). Forces averaged over two oscillation periods are plotted versus average extension. (b) Distribution of lifetimes of the folding intermediate as observed in a 20-nm 52-Hz oscillation experiment. The lifetime τ was measured as illustrated in the two insets showing typical refolding traces at high amplitudes. The lifetime distribution can reproduced by a Monte Carlo simulation (line with error bars) using a contraction length of ΔL_C = 15 nm and at a zero-force folding rate of k₀₂ = 200 s⁻¹. (c) Time trace of ddFLN4 held at a fixed average extension with a large oscillation amplitude A = 25 nm. ddFLN4 populates all three different states (unfolded U, intermediate I, and native N), both during the folding and the unfolding pathway. On the right side we show a schematic illustration, where the average forces of each folding state are illustrated as gray dots.

Since the constantly changing forces reach from the folding regime to the unfolding regime within one period, hopping of the protein between the three states (folded N, intermediate I, and unfolded U) can be observed at a fixed average extension of the protein, leading to a state of apparent equilibrium (average apparent forces in the states N, I, and U are schematically shown as gray dots in Fig. 4 c, right). As an example for such a behavior, a trace is shown in Fig. 4 c, where all possible transitions under external load between the three mechanical stable states can be clearly observed.

DISCUSSION

A polypeptide behaves as an ideal entropic spring even at low forces

Many groups use entropic elasticity models like the wormlike chain (WLC) model of polymer elasticity to model the force-versus-extension relation of unfolded polypeptide chains (24). It is important to note that, due to the limited force resolution of AFM force spectroscopy, persistence lengths are generally inferred from fitting high force data (F > 30 pN). However, so far it is by no means evident that, in the low force regime, entropic elasticity is the sole determinant of polypeptide elasticity since chain collapse due to hydrophobic interactions or secondary structure formation may lead to deviations from ideal behavior. The relevant low force range (<10 pN) has not been experimentally accessible to AFM force spectroscopy experiments due to resolution limits imposed by drift. A first important achievement of our lock-in force spectroscopy is the possibility to look for deviations from ideal entropic elasticity in the low force regime of force-versus-distance curves. Fig. 1 a shows a relax-stretch cycle of the polypeptide chain formed by three unfolded immunoglobulin (Ig) domains. In this cycle, none of the three domains underwent a folding transition. Therefore, this curve can be used to study the elastic behavior of unfolded polypeptide in the low force regime. Surprisingly, the high resolution lock-in traces show no deviation from the predicted entropic elasticity within the resolution of 400 fN (see upper trace in Fig. 1 a). This observation holds down to at least a relative extension of the polypeptide of ∼0.2 (see inset in Fig. 1 a). Lower extensions are difficult to probe since unwanted tip-surface interactions may complicate the measurement. Our results indicate that the polypeptide elasticity is indeed dominated by entropic elasticity even down to low forces of ∼1.7 pN. We can now attempt to give an upper limit for the free energy contribution of intrachain interactions due to secondary structure formation and hydrophobic collapse of a polypeptide chain before folding. For three Ig domains, we observe no deviation from conformational entropy elasticity down to forces of 1.7 pN. Even if below this extension, the force would stay constant at 1.7 pN due to chain collapse, the maximum free energy of the collapse interactions can be, at most, 1.3 k_BT per domain. This is consistent with the idea that nonnative interaction energies in an unfolded protein are generally not stable compared to thermal energies (25). Consistent with our results, Hoffmann et al. (26) using single molecule fluorescence recently found that the conformation of unfolded CspTm can be described by Gaussian chain models. However, at our lowest extensions, the end-to-end distance is larger by a factor of 2.4 as compared to the folded state. Thus, our experiments complement those observations toward more highly stretched conformations.

One may argue that the linear Hookean elasticity we observe in the low force range could be a property not exclusive to entropic elasticity but that also hydrophobic interactions and secondary structure formation may lead to a force-extension curve similar to the one we observe. However, in single-stranded DNA, intrachain interactions have led to clear plateaulike deviations from entropic elasticity at <10 pN of force (27). Moreover, theoretical models of hydrophobic polymer collapse predict a force plateau rather than Hookean elasticity (28). We therefore consider the most likely interpretation of our results is that conformational entropy dominates polypeptide elasticity down to 1.7 pN. It is important to note that our observation is still consistent with the idea of considerable interresidue interaction or residue-solvent interactions (29) as long as those interactions only lead to apparently changing persistence length but still retain an overall Gaussian behavior of the chain. We cannot exclude that, below such extensions, a hydrophobic collapse of the chain deviating from Gaussian behavior still may occur. Hence, direct elasticity measurement of the low force regime of the polypeptide gives a first indication that the two discrete folding transitions we observe for ddFLN4 do not proceed from a thermodynamically distinct collapsed intermediate or molten globulelike state, like an unspecific collapse of the complete polypeptide chain. Instead, a relaxed polypeptide chain mechanically behaves like an ideal entropic spring down to forces of ∼1.7 pN.

Folding of ddFLN4 does not require a distinct collapsed state

The histogram of refolding forces shown in Fig. 3 a offers a possibility to test models for load-dependent refolding kinetics. In earlier work, Carrion-Vazquez et al. proposed a model for refolding of I27 from titin assuming that folding proceeds from a distinct thermodynamic state that they called condensed denatured (24). In those early measurements, refolding forces could not be detected directly. Instead, unfolded proteins were relaxed to a nonzero extension and successful folding events were detected in a subsequent unfolding cycle. Moreover, the sequential folding of many domains in polyproteins complicates the analysis since the applied force increases with every folding event if the protein ends are held at a constant distance. Lock-in force-spectroscopy allows measuring refolding force histograms for single domains directly. The energetic costs of folding against mechanical load are measurable quantities as detailed in Eqs. 2 and 3. Hence, the only remaining free parameter is the length contraction that the protein chain has to undergo to reach the folded state. We find that the measured force distribution is reproduced best using a contour length change of 19.5 nm. For comparison, the expected force distribution for a full contraction of the 36.5-nm-long polypeptide yields much lower forces than the measured ones (see green dashed curve in Fig. 3 a). This result is a strong indication that the folding pathway under load also proceeds via the same intermediate we reported in our earlier study for force-free folding (20).

Our results exclude a scenario where the complete polypeptide chain collapses into a distinct condensed conformation before final folding occurs. For such a scenario, we would expect a refolding force distribution at lower forces as given by the green dashed line in Fig. 3 a, which is not consistent with our data. Moreover, if such a completely collapsed state existed, the kinetics of all subsequent folding steps, first to the intermediate and then to the fully folded state, would be force-independent, since no additional contraction of the polypeptide chain would be necessary. In contrast, we found a clear force-dependence for the lifetime τ of the intermediate. Folding from the intermediate to the native state under load is slowed by a factor of ∼20 (10 s⁻¹, histogram in Fig. 4 b) as compared to the force-free case (200 s⁻¹) (20). Our data would only be consistent with a scenario of two sequential collapses: a first collapse comprising those amino acids that form the intermediate and a second collapse of the remaining amino acids that occurs only after complete folding of the intermediate. However, such collapses could no longer be called nonspecific, since the collapsed states would already bear precise knowledge about the primary structure of both the intermediate state and the final folded state.

There are certainly examples in the literature where molten globulelike or hydrophobically collapsed states have been reported (30–33). Specifically for RNase H, Cecconi et al. reported such a state in mechanical folding traces (6). For RNase H, however, this state had been described in bulk folding studies. Recently, Fernandez et al. (2) and Bullard et al. (34) have used a constant force assay to measure folding forces of ubiquitin and Ig domains of projectin. In contrast to the discrete folding behavior observed in our study as well as by Cecconi et al. (6), those authors report a slow nonspecific collapse of the complete multidomain chain followed by the refolding of several domains at once. However, the interpretation of constant force refolding data is somewhat controversial (35).

LIMITS FOR PROTEIN REFOLDING FORCES

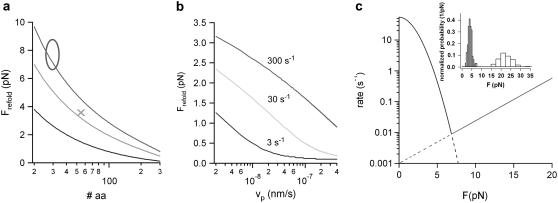
The model we have developed in this article for folding under load makes predictions about the range of forces at which two-state refolding of proteins can be expected. In Fig. 5, a and b, calculated average folding forces for proteins with three different zero-force folding rates are shown. Fig. 5 a shows the dependence of average refolding forces as a function of the length of the folding polypeptide chain. In Fig. 5 b, the average refolding forces of a 100-amino-acids protein is calculated as a function of pulling velocity. It becomes clear that refolding forces, even at an extreme choice of folding parameters, will hardly exceed 8–10 pN. Quantitative measurements of refolding forces are rare. Recent results for the fast folding 33-residues-long protein ankyrin agree well with our calculations (see open circle in Fig. 5 a) (4). The predictions of Fig. 5, a and b, can serve as a guideline for the forces that can be expected in future mechanical refolding experiments. In addition, it is important to note that for most proteins, refolding under load will occur far from equilibrium as is also assumed in our model.

FIGURE 5.

A minimal model prediction for protein folding forces. (a) Average calculated refolding forces as a function of the number of folding amino acids. The average folding force was calculated at three different zero-force refolding rates of 3 s⁻¹ (black), 30 s⁻¹ (light gray), and 300 s⁻¹ (gray) using a pulling velocity of v_P = 5 nm/s and a spacer of the length L₀ = 150 nm. (x) Average refolding force of ddFLN4 from the unfolded to the intermediate state. (o) The range of refolding forces observed for ankyrin taken from Lee et al. (4). (b) Average refolding force of a 100-amino-acids protein calculated for three different zero-force folding rates (color code as in panel a) as a function of the pulling velocity with a polypeptide spacer of L₀ = 150 nm. (c) Calculated folding and unfolding rate (black and gray line, respectively) for the transitions between the unfolded and the intermediate state of ddFLN4 as a function of the external force. The folding rate was calculated following Eq. 3. The unfolding rate parameters were extracted from a Bell equation fit to the unfolding force distribution (gray bars) shown in the inset. The intersection of both functions reveals an equilibrium force of ∼7 pN.

Recent experiments with RNA and DNA demonstrated the richness of information that can be obtained when observing a folding biomolecular system close to equilibrium (36,37). Are similar equilibrium conditions also achievable for proteins? Even at a low pulling velocity of 5 nm/s the folding/unfolding transition of the intermediate of ddFLN4 is still far from equilibrium, as can be seen from the comparison of unfolding and refolding force histogram shown in the inset of Fig. 5 c: The two distributions show no overlap. The equilibrium force at which unfolding rates equal refolding rates can be estimated to 7 pN. For this purpose, we calculated a force chevron plot (Fig. 5 c). The folding branch (black line) was calculated following Eq. 3, while the unfolding branch was calculated according to Bell's equation k_u(F) = k_u0 × exp(F × Δx/k_BT) (38). The unfolding transition state distance Δx = 13 Å and the unloaded unfolding rate k_u0 = 0.001 s⁻¹ was obtained by fitting the unfolding force distribution shown in the inset of Fig. 5 c. At this equilibrium force of F_eq ∼ 7 pN, folding and unfolding transitions will occur approximately once every 120 s. Current limitations in drift stability make experiments with such timescales almost impossible, especially if several transitions are to be observed. Given the associated experimental difficulties, the large amplitude oscillation experiments shown in Fig. 3 c offer an attractive possibility to study the system in an equilibriumlike situation where rapid transitions between the possible states can be observed.

Population of the refolding intermediate allows high refolding forces

From a mechanical point of view, what is a potential advantage for an immunoglobulin domain of an actin crosslinking protein to fold via a stable intermediate state? Certainly, one immediately obvious advantage is that average refolding forces of the domain can be twice as high if the domain refolds via an intermediate as compared to a two-state folding process, because the refolding distance to the transition state is shorter since less polypeptide spacer is contracting (see Fig. 2 b, black versus green distributions). This can already be seen by a simple calculation of folding lifetimes. One can assume that, in a very simplified picture, an external force F increases the folding lifetimes by a factor exp(F × x/k_BT), where x is a length of the contracting polypeptide strand, which is proportional to the number of amino acids in the strand. A full one-step contraction of all amino acids will then be slowed down by the factor A = exp(F × l_all/k_BT), while, at the same force, two consecutive partial contractions of 50% of the total amino acids will each be slowed by B = exp(F × 0.5 × l/k_BT). For the one-step folding scenario, the total folding time under force τ_total(F) for a full contraction scenario will be slowed by τ_total (F) = A × τ_total(0). Instead, for the partial folding scenario each step is slowed down by B resulting in τ_total (F) = B × τ₁(0) + B × τ₂(0) = B × (τ₁(0) + τ₂(0)) = B × τ_total(0). Considering that A = B² and that A and B are both numbers >1, the full contraction step will always be at least slowed down by the square of the partial steps, even if the folding time in the absence of force are identical for the two scenarios. This simple consideration explains why an intermediate state can increase the speed of folding under load.

The high refolding forces fit ideally to the suggested role of ddFLN4 as an extensible element in a cross-linked actin network. Unfolding of ddFLN4 occurs at significantly lower forces than unfolding of all other two-state Ig domains in ddFLN (11). The significantly increased refolding forces can now make sure that even in the presence of mechanical tension, filamin can contract to its native structure. If ddFLN4 were to generate an average force of 4 pN by folding in a two-state fashion, it would have to fold at a rate on the order of 3000–4000 s⁻¹ (theoretical distribution is shown as black dotted line in Fig. 2 b). Such a high refolding rate is orders of magnitudes above the fastest folding rates ever observed for an Ig-fold (39).

CONCLUSION

In this study, we introduced low frequency lock-in detection that increases the force resolution of conventional AFM force spectroscopy by 1–2 orders of magnitude, allowing us to measure protein refolding forces directly. We could demonstrate that mechanical control of protein refolding offers new possibilities to study pathways of protein folding. We anticipate that similar studies will help unravel the folding dynamics and pathways of many complex proteins in the future.