Abstract
We have employed the recently described crystallohydrodynamic approach to compare the time-averaged domain orientation of human chimeric IgG3wt (wild-type) and IgG4wt as well as two hinge mutants of IgG3 and an IgG4S331P (mutation from serine to proline at position 331, EU numbering) mutant of IgG4. The approach involves combination of the known shape of the Fab and Fc regions from crystallography with hydrodynamic data for the Fab and Fc fragments and hydrodynamic and small angle x-ray scattering data for the intact IgG structures. In this way, ad hoc assumptions over hydration can be avoided and model degeneracy (uniqueness problems) can be minimized. The best fit model for the solution structure of IgG3wt demonstrated that the Fab regions are directed away from the plane of the Fc region and with a long extended hinge region in between. The best fit model of the IgG3m15 mutant with a short hinge (and enhanced complement activation activity) showed a more open, but asymmetric structure. The IgG3HM5 mutant devoid of a hinge region (and also devoid of complement-activation activity) could not be distinguished at the low-resolution level from the structure of the enhanced complement-activating mutant IgG3m15. The lack of inter-heavy-chain disulphide bond rather than a significantly different domain orientation may be the reason for the lack of complement-activating activity of the IgG3HM5 mutant. With IgG4, there are significant and interesting conformational differences between the wild-type IgG4, which shows a symmetric structure, and the IgG4S331P mutant, which shows a highly asymmetric structure. This structural difference may explain the ability of the IgG4S331P mutant to activate complement in stark contrast to the wild-type IgG4 molecule which is devoid of this activity.
INTRODUCTION
One of the most important functions of IgG is to react with the complement system initiated by the binding of two or more IgGs to the surface of pathogens followed by an interaction with C1q (1) leading to complement activation and subsequent elimination of pathogenic agents. An important factor initiating this activation process is the spatial orientation of the domains of the IgG molecule. This may be a time-averaged orientation because of potential flexibility in the hinge region, the extent of this flexibility depending on the IgG subclass. Despite the high degree of amino-acid sequence homology, the four human IgG subclasses differ markedly in their ability to activate the classic complement pathway. IgG1 and IgG3 can active-complement effectively, IgG2 only activates complement when the target antigens are in high concentration (1,2), and IgG4 is inactive (3,4). Sequence homology analysis has shown the greatest difference among the human IgG subclasses resides in the hinge region (5).
In general, the hinge element can be divided into three structurally discrete regions: the upper, middle, and lower hinges (6). The upper hinge (UH) was defined by Beale and Feinstein (7) and depicted by Burton (8) as the number of amino acids between the end of the first heavy-chain constant region domain (CH1) and the first cysteine forming an inter-heavy-chain disulphide bridge. The middle hinge (MH) stretching from the first to the last inter-heavy-chain cysteine is believed to be rigid due to the inter-heavy-chain disulphide bridging and the formation of polyproline helices (9,10). The lower hinge (LH) begins at the last hinge disulphide and connects to the amino terminus of the CH2 domain. The LH is postulated to be flexible and have an extended conformation independence on the presence of the Fab arms but be critically modulated by the MH (6).
It has long been considered that the hinge region serves as a spacer and mediates the segmental flexibility allowing the two Fab arms to assume a variety of orientations in space relative to the Fc (11–14). Using nanosecond fluorescence depolarization technique, Dangl and co-workers (12) have observed correlations between segmental flexibility and complement fixation activity with the relative length of the upper hinge (UH) region. However, we have found that segmental flexibility and spacer properties of the genetic hinge were of little importance to complement activation (15,16). In a more recent study (17), the authors have systematically generated 26 hinge variants by site-directed mutagenesis to investigate the relationship between the hinge characteristics and the human IgG1 effector functions. The hinge length or amino-acid sequence, and thereby presumably the flexibility (or rigidity) of the UH or middle hinge (MH), resulted in changes in effector functions.
These mutation studies have provided evidence that the hinge may module complement activation in an indirect mode by influencing the conformation of the binding sites in the molecule or possibly altering the overall conformation of the antibody molecule in solution (17–19). Structural analysis of antibodies will therefore facilitate the design of novel antibodies that possess optimal combinations of effector functions and hence allow for more specific and defined manipulation of the protective activities of IgG molecules.
Unfortunately, the application of high-resolution structural techniques like x-ray crystallography to immunoglobulins have proved difficult, due to the inherent flexibility of an intact antibody rendering crystallization or interpretation of electron density maps problematic (10,20). Crystal structures of the intact antibody molecules are currently only confined to the hingeless mutants Dob (21), Mcg (22), and Kol (23), and the wild-type intact IgGs Mab231 (24,25), Mab61.1.3 (26), and human IgG1 b12 molecule (27). Comparisons of the crystal structures of these intact antibodies have indicated that the differences in the orientation of the two Fab regions relative to the Fc region influence the effector function (20,28). This structure-function correlation has also been reported in immune complex formation studies using electron microscopy—studies indicating that the two Fab arms can adjust their orientations to accommodate the particular orientation of any cognate epitope array (29–32).
To gain an insight into the structure-function relationship of antibodies in solution, we have previously proposed the crystallohydrodynamics approach for describing the time-averaged domain orientation of antibodies in solution. The approach is to combine x-ray crystallography of the IgG Fab and Fc fragments with data from the measured hydrodynamic properties of the fragments and the intact IgG molecule (33,34) to specify possible low-resolution domain orientations without the ad hoc assumptions concerning time-averaged hydration used by other approaches (35–38). The methodology has been further refined by combining sedimentation, small angle x-ray scattering, and viscometry techniques to reduce the degeneracy or model uniqueness problem (39). The domains are represented as low-resolution bead-shell ellipsoids linked together by a hinge region. A range of 100+ possible domain orientations are generated by the model-producing algorithm MONTESUB (40) and the best model or models are selected on the basis of agreement of modeled hydrodynamic parameters with experimental hydrodynamic parameters. In this way, the low-resolution domain orientation of human IgG3 has been described (39).
The structural approximations for individual Fab and Fc regions as simple ellipsoids allow us to concentrate on the spatial arrangements within the antibody molecule that may modulate its effector function (33,34,39,41). The Fab regions can be approximated as prolate ellipsoid shapes (with two equal minor axes, of semi-axial length b, and one longer major axis, of semi-axial length a, and shape defined by the axial ratio a/b). The Fc domain is approximated by an oblate ellipsoid shape (with two equal major axes, of semi-axial length a, and one shorter minor axis, of semi-axial length b, and shape also defined by the axial ratio a/b). To facilitate calculation of the hydrodynamic properties of the intact antibody molecule, the surface of each ellipsoidal region is then represented by an array of beads. The hinge region joining the Fab and Fc regions is represented by linear arrays of frictionless beads.
We now use this procedure to study the time-averaged Fab-Fc orientation of a chimeric IgG3 and two of its hinge mutants, one with 15 amino-acid hinge IgG3m15 (IgG3 normally has 62 amino acids in the hinge) and one altogether without hinge, IgG3HM5. Changes in orientations caused by the mutations may correlate with the different abilities of these antibodies to activate the complement cascade. IgG3m15 has a greater complement activation ability than wild-type IgG3 (15,16,42), while IgG3HM5 is completely devoid of complement activation activity (16). We also adopt a similar approach to investigate how a single amino-acid substitution from Ser to Pro at position 331 in human IgG4 alters the overall conformation of the molecule—a change known to confer a dramatic improvement of complement-activation activity (19,43). Solution conformations of these IgG3 and IgG4 wild-type and mutant molecules are sought and an attempt made to relate the best-fit models with complement activation. In doing so, we were not able to follow the complete crystallohydrodynamics approach as there was insufficient material to obtain reliable viscosity data for the range of proteins analyzed. However, the measurement of sedimentation coefficient, radius of gyration, and maximum particle dimension, together with the known structure of the antibody regions, provided sufficient information to tackle the model degeneracy problem.
MATERIALS AND METHODS
Antibodies
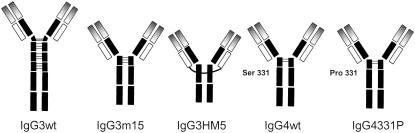
All the antibodies used in our study (Fig. 1) are chimeric (mouse/human) molecules that share specificity for the hapten 5-iodo-4-hydroxy-3-nitrophenacetyl. The production and purification of the IgG3 wild-type antibody and two hinge mutants (IgG3m15 with 15 amino acids in the hinge and IgG3HM5 without the genetic hinge) are as reported previously (15,16,42). Production of the chimeric IgG4 antibody and the mutant IgG4S331P with serine at position 331 (EU numbering) replaced by proline have been described in Brekke et al. (43). A comparison of the amino-acid sequences in the hinge region is given in Table 1.
FIGURE 1.
Schematic drawings of the five different chimeric IgG molecules analyzed in this study. The IgG3HM5 molecule has one S-S bridge between the two light chains. For the variants of IgG3 and IgG4, common gray shades represent common sequences.
TABLE 1.
Hinge-region amino acids
| IgG type | UH | MH | LH |
|---|---|---|---|
| IgG3 | ELKTPLGDTTHT | CPRCP(EPKSCDTPPPCPRCP)3 | APELLGGP |
| IgG3m15 | EPKS | CDTPPPCPRCP | APELLGGP |
| IgG3HM5 | — | — | APELLGGP |
| IgG4 | ESKYGPP | CPSCP | APELLGGP |
| IgG4S331P | ESKYGPP | CPSCP | APELLGGP |
Sedimentation velocity
Sedimentation velocity experiments were performed using a Beckman Optima XLA analytical ultracentrifuge (Palo Alto, CA) running at 40,000 rpm at 20°C. The solute concentrations were recorded as ultraviolet absorbance at 280 nm. Sedimentation profiles were analyzed by the least-squares g*(s) method as implemented in SEDFIT (44) and sedimentation coefficients were corrected to standard conditions (density and viscosity of water at 20°C) to give 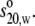
Small angle x-ray scattering (SAXS)
SAXS was performed in Station 2.1 at the Synchrotron Radiation Source (SRS, Daresbury, UK), employing camera lengths of 1.0 m (to cover a Q-range of 0.038 < Q < 0.32 Å−1) and 4.3 m (for 0.008 < Q < 0.18 Å−1). The detector was calibrated with wet rat tail collagen and silver behenate. Data were collected at different antibody concentrations (ranging from 0.4 mg/mL to 11.4 mg/mL). Using the standard Daresbury software package XOTOKO (45), data were then normalized to the intensity of the incident beam, radially averaged, and corrected for the detector response. The total scattering intensity from each of the time frames was determined to check for beam-induced aggregation in the sample. Those frames showing increasing counts were excluded from further analysis as the increase was considered to be due to radiation-induced aggregation.
After subtracting the buffer contribution, to correct for the interparticle interaction effects in the low-angle region of the high concentration measurement, the low-angle regions of the low concentration data were scaled to merge with the high-angle regions of the high concentration data using SigmaPlot (Systat Software, San Jose, CA). The distance distribution function p(r) and the maximum dimension (Dmax) were obtained by using GNOM (46). The radii of gyration (Rg) were determined by using both the Guinier approximation (47) and GNOM.
Hydrodynamic bead modeling
As described previously (39), the solution properties (including sedimentation coefficient, 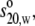 and the radius of gyration Rg) of an antibody molecule were determined experimentally. Their corresponding universal shape functions (Perrin P, and Mittelbach G functions) were then derived from the experimentally determined quantities (Table 2).
and the radius of gyration Rg) of an antibody molecule were determined experimentally. Their corresponding universal shape functions (Perrin P, and Mittelbach G functions) were then derived from the experimentally determined quantities (Table 2).
TABLE 2.
Experimental hydrodynamic data for the IgG3 and its hinge mutants (IgG3m15 and IgG3HM5), IgG4 and IgG4S331P
| Mw (Da) |
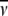 (mL/g) (mL/g) |
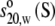 |
P | Rg (Å) | G | Dmax (Å) | |
|---|---|---|---|---|---|---|---|
| IgG3wt | 156943 | 0.725 | 6.11 ± 0.02 | 1.44 ± 0.04 | 71.6 ± 2.0 | 2.72 ± 0.08 | 195 ± 10 |
| IgG3m15 | 146771 | 0.726 | 6.77 ± 0.04 | 1.24 ± 0.04 | 54.2 ± 2.0 | 1.63 ± 0.05 | 165 ± 8 |
| IgG3HM5 | 143529 | 0.727 | 6.68 ± 0.03 | 1.23 ± 0.04 | 54.8 ± 2.0 | 1.65 ± 0.05 | 163 ± 8 |
| IgG4wt | 146076 | 0.725 | 6.66 ± 0.08 | 1.26 ± 0.04 | 54.0 ± 2.0 | 1.62 ± 0.05 | 161 ± 8 |
| IgG4S331P | 146096 | 0.726 | 6.46 ± 0.12 | 1.30 ± 0.04 | 55.4 ± 2.0 | 1.71 ± 0.05 | 163 ± 8 |
The partial specific volume (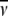 ) and molecular weight (Mw) of each antibody molecule in Table 2 are calculated using the SEDNTERP algorithm (52) from the amino-acid sequence and carbohydrate content. Errors associated with each measurement are shown in italics. Table headings:
) and molecular weight (Mw) of each antibody molecule in Table 2 are calculated using the SEDNTERP algorithm (52) from the amino-acid sequence and carbohydrate content. Errors associated with each measurement are shown in italics. Table headings: 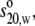 sedimentation coefficient; P, Perrin function; Rg, radius of gyration; G, reduced radius of gyration function; and Dmax, maximum dimension of the scattering particle.
sedimentation coefficient; P, Perrin function; Rg, radius of gyration; G, reduced radius of gyration function; and Dmax, maximum dimension of the scattering particle.
Bead-shell modeling (i.e., the surface of the particle is represented by a shell-like assemblage of many identical minibeads) was chosen as our modeling strategy based on the recognition that shell models are hydrodynamically more appropriate as hydrodynamic resistance mainly takes place on the surface of the particle (48). However, it is worth reiterating that the filling bead procedure (i.e., the particle is filled with scattering elements), as opposed to the shell bead procedure for the calculation of hydrodynamic properties, was included in the calculation of the radius of gyration and other scattering related properties that are specifically dependent on the particle volume.
Candidate bead-shell models (>100) of differing domain orientations were constructed for each hinge arrangement using MONTESUB (40), and chosen to cover a representative range of possible orientations. The hydrodynamic properties of the candidate models were then calculated using HYDROSUB (49) and SOLPRO (50,51). Matches were then sought between the set of calculated shape functions (Table 2) for the models with the experimental set. The maximum distance parameter Dmax from x-ray scattering data was used as an additional filter in the selection of the appropriate model(s).
RESULTS
Hydrodynamic characterization of the IgGs
Experimental values for the sedimentation coefficient, 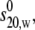 radius of gyration Rg, and maximum particle dimension Dmax for each antibody are given in Table 2. The corresponding universal shape functions are then calculated using Eqs. 1–4 as described in Lu et al. (39), taking into account the effects of the apparent hydration: a value of (0.59 ± 0.07)g/g for the latter is used, based on the crystal structure and hydrodynamic data for the antibody domains (33). The experimental errors associated with each measurement have been considered and evaluated as described in Lu et al. (39).
radius of gyration Rg, and maximum particle dimension Dmax for each antibody are given in Table 2. The corresponding universal shape functions are then calculated using Eqs. 1–4 as described in Lu et al. (39), taking into account the effects of the apparent hydration: a value of (0.59 ± 0.07)g/g for the latter is used, based on the crystal structure and hydrodynamic data for the antibody domains (33). The experimental errors associated with each measurement have been considered and evaluated as described in Lu et al. (39).
Under the same experimental conditions (namely rotor speed, buffer, and temperature), the wild-type IgG3 sediments were slowest (6.11 ± 0.02 S) among all the intact antibodies investigated, consistent with previous findings (33,53–55) that the extended hinge in IgG3 exerts an increased translational friction for the sedimentation of the molecule. The truncations of the hinge region in IgG3m15 and IgG3HM5 result in a more compact solution structures of these molecules as demonstrated by the increase in sedimentation coefficients, despite the lower molecular weight. By contrast, sedimentation velocity experiments demonstrate that the single amino-acid substitution, from Ser to Pro at position 331 in IgG4S331P, decreases the sedimentation coefficient—indicative of a change to a less compact solution structure.
These qualitative findings appear to be reinforced by the data from SAXS (Table 2). The radius of gyration Rg is a measure of the size and elongation of the scattering particle (56–58) and G is the corresponding size-independent universal parameter (39). Dmax, which can be obtained by transformation of the scattering profile into the distance distribution function p(r) of scattering vectors (59), represents the maximum dimension of the scattering particle.
Interestingly, both the ultracentrifuge and scattering data show that the hingeless mutant IgG3HM5 behaves more like an IgG4 molecule in solution (see Table 2). In comparison with the two hingeless mutants Dob and Mcg, IgG3HM5 has a sedimentation coefficient more akin to Mcg (6.79 ± 0.10 S) than Dob (6.30 ± 0.05 S) (33,54).
To get a more quantitative picture in terms of the time-averaged domain orientations, we have employed hydrodynamic bead modeling.
Hydrodynamic bead modeling strategy for the IgGs
As described earlier (33,34,39,60), the two Fabs in an antibody molecule can be approximated to prolate ellipsoids and the Fc as an oblate ellipsoid. The dimensions of the hydrated ellipsoids used for representing the Fab and Fc domains are shown in Table 3.
TABLE 3.
Dimensions of the ellipsoids for representing the Fab and Fc domains
| Longest semiaxis (Å) | Shortest semiaxis (Å) | |
|---|---|---|
| Fab | 39.30 | 24.35 |
| Fc | 36.60 | 21.63 |
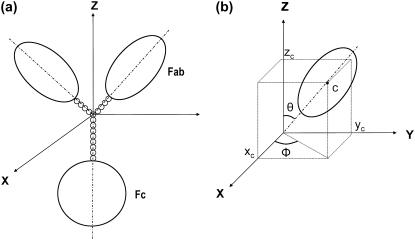
The hinge region (when significant) in an antibody model is represented as a Y-shape with each arm of the Y connected to the Fab and the body of the Y linked to the Fc (Fig. 2). The upper part (i.e., the arm) of the Y-shape represents the flexible upper hinge (UH) and the body part the Y-shape represents the rigid middle hinge (MH). Therefore, we can incorporate the known hinge sequence information in constructing the hinge region for a certain antibody molecule. For instance, the body of the Y-hinge in IgG3 was constructed four times longer than the arm of the Y, based on the sequence information that the MH in IgG3 is four times longer than the UH (see Table 1). Using a defined U-U-M index for the beads arrangement in the hinge, in which U is the number of beads in each branch of the upper hinge and M is the number of beads in the middle hinge (39), the generic hinge of IgG3 can be typically assigned as 2-2-8, 3-3-12, 4-4-16, etc., providing that a uniform bead size (radius of 1.8 Å in our study) is used.
FIGURE 2.
Scheme for the construction of an intact antibody model. (a) A model with a 4-4-8 hinge arrangement. (b) The position of the center of the symmetrical axis of the ellipsoid is represented as the Cartesian coordinates (xc,yc,zc) and two spherical-polar angles (θ and ϕ). The value θ is the angle subtended by the main particle axis and the Z axis, and ϕ is the angle subtended by the projection of the main particle axis on the (X,Y) plane and the X axis. Figure adapted from Lu et al. (39).
In our modeling strategy (39), hinge flexibility was modulated by altering the length and orientation of the arm and body in the hinge using the Monte Carlo procedure as implemented in MONTESUB (40). The advantage of using the Monte Carlo procedure lies in that it generates a representative set of conformations covering all the possible spatial arrangements allowed for the two Fab ellipsoids relative to the Fc. The routine HYDROSUB calculates the values for the set of universal shape functions (P, G, and ν) for each conformation—matches are then sought for the values of P, G, and ν calculated from experimental data, namely 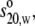 Rg, and ν, respectively, together with the time-averaged hydration value of (0.59 ± 0.07)g/g obtained by comparing crystal structure with hydrodynamic data for the domains. Allowance is made for experimental errors (see Table 2) in selecting candidate models. The number of possible models is further reduced by the employment of the Dmax parameter from the scattering data.
Rg, and ν, respectively, together with the time-averaged hydration value of (0.59 ± 0.07)g/g obtained by comparing crystal structure with hydrodynamic data for the domains. Allowance is made for experimental errors (see Table 2) in selecting candidate models. The number of possible models is further reduced by the employment of the Dmax parameter from the scattering data.
We have already described the solution conformation of the wild-type IgG3 antibody when we described the extended crystallohydrodynamic approach (39). Following a similar procedure, candidate models for the other four antibodies (IgG3m15, IgG3HM5, IgG4, and IgG4S331P) have now been found.
Bead modeling of the wild-type IgG3 (39)
A model (with U-U-M index of 6-6-24) that best reproduces the shape functions (P and G) and the Dmax parameter was found for the wild-type IgG3 antibody (39). Details of this model are given in Table 4 and Table 5(a), in which θ and ϕ are the spherical-polar angles referring to the orientation of the main axis of each ellipsoid. The projection on the Z axis for each Fab is the projection of the arm in the Y-shape hinge (i.e., UH) on the Z axis, while for Fc is the projection of the body in the Y-shape hinge (i.e., MH). Hinge distance between Fab and Fc can be referred to as the sum of the UH and MH lengths on the Z axis. A negative value for the projection on the Z axis indicates that the Fab arm is bent toward the Fc, which could be also demonstrated by an obtuse value for θ (i.e., θ > 90°) of the main axis of the Fab.
TABLE 4.
Shape functions from the best-fit models for the IgG3 and its hinge mutants (IgG3m15 and IgG3HM5) IgG4 and IgG4S331P
| Best-fit model (s) | P | G | Dmax (Å) | |
|---|---|---|---|---|
| IgG3wt | 1.40 | 2.70 | 196 | |
| IgG3m15 | 1.28 | 1.68 | 163 | |
| IgG3HM5 | 1.27 | 1.60 | 164 | |
| IgG4wt | A | 1.27 | 1.58 | 162 |
| B | 1.28 | 1.65 | 162 | |
| IgG4S331P | A | 1.28 | 1.66 | 160 |
| B | 1.29 | 1.66 | 160 |
Note: Only one best-fit model was found for IgG3wt, IgG3m15, and IgG3HM5, two equivalent models (models A and B, see descriptions below) were found for IgG4wt and IgG4S331P.
TABLE 5.
Parameters of the best-fit models for wild-type and mutant human IgG3s and IgG4s (39)
| Model | θ (degree) | ϕ (degree) | Projection on Z axis (Å) | Hinge distance between Fab and Fc (Å) | Angle between Fabs | Dmax (Å) |
|---|---|---|---|---|---|---|
| (a) Wild-type IgG3 | ||||||
| Fc arm | 90.0 | 0 | −88.2 | — | 80.2 | 196 |
| Fab1 arm | 111.9 | 243.6 | −8.7 | 79.5 | ||
| Fab2 arm | 99.4 | 326.8 | −3.8 | 84.4 | ||
| (b) IgG3m15 | ||||||
| Fc arm | 90.0 | 0 | −19.8 | — | 108.0 | 163 |
| Fab1 arm | 64.0 | 17.9 | 3.9 | 23.7 | ||
| Fab2 arm | 69.0 | 254.2 | 3.2 | 23.0 | ||
| (c) IgG3HM5 | ||||||
| Fc arm | 90.0 | 0 | −1.8 | — | 108.0 | 164 |
| Fab1 arm | 64.0 | 17.9 | 7.1 | 8.9 | ||
| Fab2 arm | 69.0 | 254.2 | 5.8 | 7.6 | ||
| (d) Wild-type IgG4 model A with 2-2-2 hinge | ||||||
| Fc arm | 90.0 | 0 | −9.0 | — | 122.4 | 162 |
| Fab1 arm | 65.6 | 176.3 | 3.72 | 12.72 | ||
| Fab2 arm | 57.4 | 4.6 | 4.85 | 13.85 | ||
| (e) Wild-type IgG4 model B with 2-2-3 hinge | ||||||
| Fc arm | 90.0 | 0 | −12.6 | — | 122.4 | 162 |
| Fab1 arm | 65.6 | 176.3 | 3.72 | 16.32 | ||
| Fab2 arm | 57.4 | 4.6 | 4.85 | 17.45 | ||
| (f) IgG4S331P mutant model A | ||||||
| Fc arm | 90.0 | 0 | −12.6 | — | 108.0 | 160 |
| Fab1 arm | 64.0 | 17.9 | 5.52 | 18.12 | ||
| Fab2 arm | 69.0 | 254.2 | 4.52 | 17.12 | ||
| (g) IgG4S331P mutant model B | ||||||
| Fc arm | 90.0 | 0 | −12.5 | — | 108.0 | 160 |
| Fab1 arm | 64.0 | 17.9 | 5.17 | 17.67 | ||
| Fab2 arm | 69.0 | 254.2 | 4.23 | 16.73 | ||
As shown in Tables 4 and 5(a) and Fig. 3 a, it appears that the two Fabs adopt difference orientations relative to the Fc, which results in a slightly asymmetrical structure along the long axis of Fc. The hinge length (sum of UH and MH length) is ∼80 Å. This is in agreement with results from immunoelectron microscopy studies by our collaborators (31) that the mean hinge distance is 80 ± 23 Å and consistent with the earlier estimates of 90∼100 Å of Pumphrey (14), Gregory et al. (54), and Philips et al. (55).
FIGURE 3.
Best fit models for wild-type and mutant human IgG3s and IgG4s. In each case, the Fc domain (oblate ellipsoid) is displayed at the bottom linked by a bent hinge to the two Fab domains (prolate ellipsoids). The possible regions of the C1q-binding motif in the CH2 region of Fc are highlighted in white. (a) Model with a 6-6-24 hinge for wild-type IgG3. (b) Model with a 2-2-5 hinge index for IgG3m15, which has only 15 amino acids in the hinge region. (c) Model for the hingeless mutant IgG3 HM5 with a 4-4-0 hinge. (d) Model with a 2-2-2 hinge index for wild-type IgG4. (e) Model with a 3-3-3 hinge for the IgG4S331P mutant.
Bead modeling of IgG3m15
The IgG3m15 mutant possesses only 15 amino acids in the hinge. Bead models were constructed to try to reproduce the experimental parameters as described for the wild-type IgG3. Of the 1200 candidate models explored, one unique model was found (with U-U-M index of 2-2-5), which was consistent with the experimental P, G, and Dmax (Tables 4 and 5(b)).
Fig. 3 b shows the best-fit model. It appears that in this conformation the UH is not bent toward the Fc (suggested by the acute θ and positive values of projection on the Z axis in Table 5(b)). Despite a truncated hinge, the two Fab arms of the IgG3m15 seem to open up the molecule as demonstrated by the unbent hinge and a wide Fab-Fab angle. Judging by the projection on the Z axis, the hinge distances between the two Fab domains relative to the Fc are similar (∼23 Å). However, the two Fabs appear to distribute asymmetrically along the long axis of the Fc (i.e., the Z axis), exposing one side of the Fc ellipsoid proximal to the lower hinge region.
Bead modeling of IgG3HM5
The IgG3HM5 antibody is a hingeless antibody molecule. Therefore, we first tried to generate models without hinge space. However, models without hinge beads construction were unable to reproduce any of the experimental date (details not shown). This is consistent with our findings that the solution characteristics (see Table 2) of IgG3HM5 appear to resemble IgG4 rather than the compact hingeless antibody Dob (11,21,54).
Bead modeling was then performed by constructing models with a small but finite hinge or spacer-length between the domains by altering the number of beads in each side chain (39). Three models (with 2-2-3, 3-3-3, and 4-4-0 hinge indices, respectively) were found that successfully reproduced the experimental P- and G-values. Interestingly, the model with a 4-4-0 hinge has a Dmax value that best represents the experimental Dmax. The significance of 4-4-0 is that, instead of a conventional Y-shape hinge region, this model possesses a V-shape that modulates the orientations of the two Fabs. Since IgG3HM5 is genetically constructed in a way that no UH and MH are present, only the LH is retained (see Table 1) (16,42); it is unlikely that there will be UH and MH present in IgG3HM5, although they are present in IgG4. We could postulate that the V-shape hinge region found in the IgG3HM5 model is a feature of the LH in the molecule as the LH is also believed to be flexible (6). Another explanation here is the V-shape hinge does not represent the actual LH or the shape of the LH; instead, it is only an indicator of the spatial separations between the three ellipsoids. Nevertheless, the V-shape hinge does appear to confer considerable degree of flexibility within the IgG3HM5 molecule, which could be an explanation for the high level of ring dimers found in electron microscopy studies (32).
Details of this model are shown in Tables 4 and 5(c) and Fig. 3 c: the two Fabs of IgG3HM5 have the same domain orientations (thereby same Fab-Fab angle) as in IgG3m15. However, IgG3HM5 has, as expected, a much limited hinge length—only ∼8 Å compared to ∼24 Å for IgG3m15.
Bead modeling of wild-type IgG4
Of the 1600 candidate models, only two reproduced, within experimental error, the experimental data in Table 2 for P, G, and Dmax, which are described in Tables 4, 5(d), and 5(e): these models are very similar to each other. The Fab arms in one model (with a 2-2-2 hinge index, Fig. 3 d) and the other model (with a 2-2-3 hinge index) adopts the same orientation relative to the Fc. The difference in hinge length suggests that when the domain dispositions are fixed, the hinge length could vary from ∼13 Å to ∼17 Å, maintaining Dmax the same. Thus, both models could be valid, and the degeneracy in this case is simply an indication of some hinge flexibility in the wild-type IgG4.
Bead modeling of IgG4S331P
As with the case for wild-type IgG4, we found two equivalent and very similar models (i.e., same domain dispositions) for the IgG4S331P mutant (with hinge length varying from 17 Å to 18 Å). Tables 4, 5(f), and 5(g) give the parameters and Fig. 3 e shows the model with a 3-3-3 hinge for IgG4 S331P.
It is apparent that due to the single amino-acid substitution, there is a significant conformational change in IgG4S331P (Fig. 3 e) compared with the wild-type IgG4 (see Fig. 3 d). For both the mutant IgG4S331P and the wild-type IgG4, the Fab arms stretch out and away from the Fc. However, it is clear that one Fab arm in IgG4S331P rotates away from the Fc and leads to an extreme asymmetrical conformation in contrast to the conformation of IgG4, which shows itself as highly symmetrical. The bead modeling also suggests that the UH length and genetic hinge length of IgG4S331P is slightly longer than the wild-type IgG4. The correlation between the conformational changes with complement activation will be considered below.
Further validity check on the x-ray scattering data: superimpositions of the distance distribution function p(r)
The distance distribution function p(r) of a scattering particle is directly related to the angular dependence of scattered intensity that reflects the shape and mass distribution of the molecule (57,59) and is used to calculate Dmax as considered above. In the refined crystallohydrodynamic approach (39), we also proposed the inclusion of an ancillary procedure that compares the full features of the experimental p(r) from SAXS, with calculated p(r) from bead modeling using SOLPRO (50,51,61). The experimental distance distribution function from x-ray scattering can be normalized to unity to superimpose with the distance distribution function from modeling. Fig. 4 shows the superimposition of the experimental p(r) with the modeled p(r) for each antibody using SOLPRO.
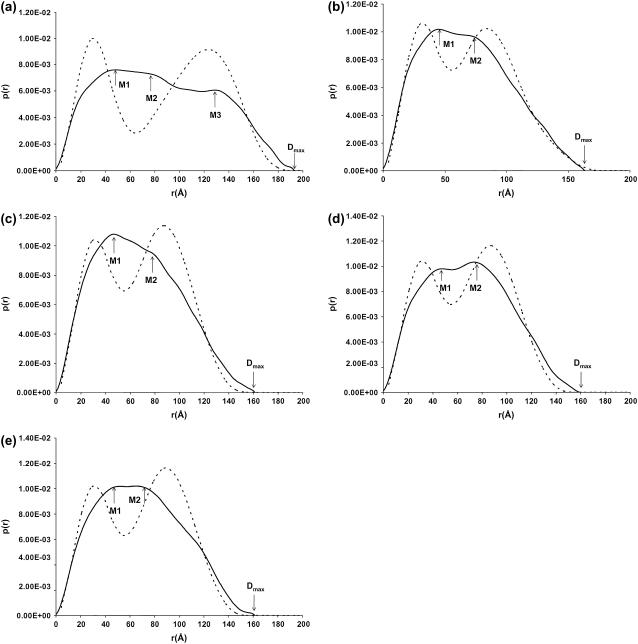
FIGURE 4.
Superimposition of the experimental (—) with the calculated p(r) plots (- - -) from bead modeling. (a) Wild-type IgG3; (b) IgG3m15; (c) IgG3HM5; (d) wild-type IgG4; and (e) IgG4S331P. In panel a, SAXS peaks M1, M2, and M3 occur at ∼46 Å, 83 Å, and 129 Å, respectively. The experimental maximum dimension of ∼195 Å is denoted as Dmax. In panels b–e, M1 occurs at ∼46 Å and M2 at 76–80 Å, respectively. For Dmax values, see Table 2.
The distance distribution function obtained from scattering represents a conformational average for a molecule with some degree of flexibility. By contrast, the SOLPRO calculation of p(r) is based on a static (filled) shell-bead model and this simplified structure may explain why the computed features in the p(r) distributions are blurred in the experimental data, as demonstrated by Diaz and co-workers (61). Polydispersity effects may also cause differences between the experimental and calculated p(r) as well as the simplifications we have made in representing the domains as (bead-shell) ellipsoids. Agreement, however, between the experimental and calculated values for the radius of gyration Rg and the maximum dimension Dmax indicate that the filled shell-bead models have captured the distribution of mass within the antibody molecule correctly. There are some exaggerated features (such as the bimodal peaks) in the computed p(r) plots but this is simply due to the use of well-defined shapes (ellipsoids) for the individual domains in the geometrical model (48).
The distance distribution function is a linear combination of all the intraparticle scattering vectors in SAXS experiments. The maxima M in a p(r) curve correspond to the most frequently occurring interatomic distances within the structure (37). In all five antibodies investigated, the first maximum M1 at 46–47 Å can be assigned to the most commonly occurring distance in a single Fab or Fc fragment, which is consistent with the average cross section (∼45 Å) found by x-ray crystallography for the Fab and Fc (10). Peak M2, between ∼76 and 83 Å, describes the most common distance within the whole antibody molecule. For the wild-type IgG3, M1 is the distance in a Fab or Fc, M2 is assigned to the distance between the two Fabs, and the third maximum M3 at (129 ± 1) Å is assigned to the greatest distance between the Fab and Fc fragments that are held apart due to the existence of the long hinge. This third maximum is not apparent in either the IgG3 hinge mutants or the two IgG4 antibodies, which indicates no distinguishable difference between the Fab-Fab distance and the Fab-Fc distance—an observation consistent with only a small (or no) hinge region within the molecule.
DISCUSSION
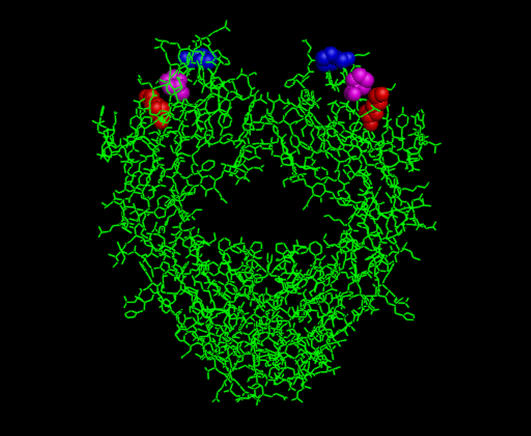
Activation of complement through the classical pathway is initiated by the interaction of the complement subcomponent C1q and IgG molecules complexed to a membrane target antigen. The C1q binding motif of mouse IgG2b seems to involve Glu318, Lys320, and Lys322 in the CH2 region (62), while human IgG1 and IgG3 appears to involve only Lys322, in addition to Asp270, Pro329, and Pro331 (63–65) (see Fig. 5). Here a rationalization for the topography of this complement-binding site on the Fc region is made and has been highlighted in the models (see Fig. 3, a–e).
FIGURE 5.
Crystal structure of a human Fc fragment taken from the Brookhaven Protein Data Bank (accession code No. 1Fc1). Residues considered most significant for C1q binding are Lys322 (red), Pro329 (blue), and Pro331 (magenta).
Wild-type IgG3 and its hinge mutants
For wild-type IgG3, the two Fabs are seen to bend toward the Fc; however, they are positioned far away from the Fc domain due to the existence of the long hinge (see Fig. 3 a). Therefore, the complement-binding motif located in the Fc region proximal to the lower hinge region is easy for C1q to access and therefore it is not surprising that IgG3 is efficient in complement activation. The hinge region of IgG3wt has also been visualized by electron microscopy as having a long extension of 100–110 Å between the Fab and Fc regions (31), slightly greater than 80–84 Å observed (under different conditions) in this report. The mean Fab angle estimated by EM was 136°, while our best-fit model is more consistent with a mean angle of 80°, but again under different conditions. Our present model of IgG3wt structure deviates considerably from our first crystallohydrodynamic approach (33) and reflects the refinement and the use of multiparameters in our new strategy, resulting in a more accurate and higher resolution of the IgG3wt model.
When focusing on the hinge mutants of IgG3, the enhanced complement-activation activity of IgG3m15 argue against the view that the upper hinge length influences the complement-activation activity (67). In fact, IgG3m15 forms fewer ring dimers with an anti-idiotypic antibody than IgG3wt, which indicates that IgG3m15 is less flexible than IgG3wt (32). Thus, enhanced complement activation of IgG3m15, compared to IgG3wt, has previously been interpreted to be due to C1q binding to the more rigid molecule. IgG3m15 may be more energetically favorable than binding to the flexible IgG3 molecule, as the loss of entropy on complex formation is greater for a flexible than for a rigid molecule (15). This is consistent with our modeling of the domain geometry, even at low resolution, that the solution conformations of IgG3 wild-type and IgG3m15 are both favorable for C1q binding, since IgG3m15 seems to expose the C1q binding site (see Fig. 3 b) and have a sufficient hinge space of 23 Å to allow C1q binding. It is also slightly asymmetric along the Fc axis, similar to the IgG3wt. Extensive studies of mutant chimeric human IgG3 have established that the efficiency of C1 activation is not directly determined by the length of the hinge region, but that at least one inter-heavy-chain disulphide bridge is required (15,16,42,66).
Bead modeling of IgG3HM5 appears to establish that there is no inter-heavy-chain disulphide bridge between the two heavy chains, as shown by a V-shape hinge area in Fig. 3 c. The lack of an S-S link between the heavy chains of IgG3HM5 (Fig. 1) is a structural consequence of hinge deletion and has been confirmed by SDS/PAGE analysis (16). Since the spatial orientations for each domain in the complement-inactive IgG3HM5 are the same as in the very complement-active IgG3m15 (see Fig. 3 b), this suggests that, if our hydrodynamic models are correct, the time-averaged orientation of the Fab and Fc domains—although of importance—is not the only controlling element in complement activation. Differences in the localization and positioning of the heavy-chain CH2 regions of IgG3HM5 compared to IgG3m15 might be unfavorable for C1q binding, differences our low-resolution methodology cannot pick up. However, our modeling shows a small hinge space of 8 Å, which might be too small to facilitate C1q binding (Fig. 6) .
FIGURE 6.
Best-fit models of IgG3m15 (dark shading) and IgG3HM5 (light shading) superimposed for comparison.
Wild-type IgG4 and IgG4 S331P mutant
Using point mutants of chimeric antibodies, residue 331 has been identified as a critical amino acid for determining the isotypic differences in complement activation for human IgG4 (18,19,43,67). It is here of interest to point out that IgG4S331P mutant only activates complement at high antigen concentration. Residue 331 is located in a peptide loop between the last two β-strands of CH2 and is in close proximity to the C1q-binding motif (19). Greenwood and colleagues (18) have postulated that the replacement of Pro (which exists in IgG1 and IgG3) at position 331 with Ser) may have a significant effect on the tertiary structure of the loop, such that elements of the IgG4 structure actively prevent binding to an otherwise suitable site.
In this study, bead modeling has shown that the replacement of Ser to Pro at position 331 has dramatically altered the domain orientations within the IgG4 molecule. As shown in Fig. 3 e, the two Fabs in IgG4S331P adopt a much more asymmetrical conformation when compared to the symmetrical wild-type IgG4 (see Fig. 3 d). This represents a significant refinement of our previously published attempt on human IgG4 (33) where, on the basis of sedimentation coefficient alone and its corresponding P-value (1.23 ± 0.02), we could only conclude on an open conformation (as opposed to compact with the Fab arms folded down toward the Fc). Most importantly, as with IgG3m15, one Fab arm in IgG4S331P stretches away from the Fc, thereby leaving the C1q binding site accessible. In the wild-type IgG4 molecule, however, docking of complement C1q is obstructed by the two Fab arms, which distribute symmetrically along the long axis of the Fc ellipsoid.
It is our view that domain orientation (or dispositions) seems to modulate the complement-activation ability for a given antibody molecule. Antibodies that adopt conformations allowing docking of complement C1q are favorable for complement activation, as demonstrated by IgG3m15 and IgG4S331P. However, the inability of IgG3HM5 to induce complement activation suggests that maintenance of at least one inter-H-chain disulphide bond linking heavy chains at the N-terminus of the lower hinge is a prior requirement for complement activation. This may throw some light on the role of the hinge region in controlling unrestricted flexibility, which would compromise the expression of biological effector function (15). Finally, our models all appear asymmetrical, with the exception of the wild-type IgG4. The limited amount of crystal structures available for the intact antibodies (24–27) are also asymmetrical. It would appear our low-resolution solution models are at least consistent with this theme. It is here relevant to mention that human IgG seems to expose only one C1q binding site, perhaps as a consequence of asymmetry (68).
Acknowledgments
We thank the United Kingdom Engineering and Physical Science Research Council for supporting this work, and the Council for the Central Laboratory of the Research Councils for access to the Synchrotron Radiation Source, Daresbury, UK.
Work at the University of Murcia and a predoctoral fellowship to A.O. were supported by grant No. CTQ2006-06381.
Editor: Jill Trewhella.
References
- 1.Lucisano Valim, Y. M., and P. J. Lachmann. 1991. The effect of antibody isotype and antigenic epitope density on the complement-fixing activity of immune complexes: a systematic study using chimeric anti-NIP antibodies with human Fc regions. Clin. Exp. Immunol. 84:1–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Michaelsen, T. E., P. Garred, and A. Aase. 1991. Human IgG subclass pattern of inducing complement-mediated cytolysis depends on antigen concentration and to a lesser extent on epitope patchiness, antibody affinity and complement concentration. Eur. J. Immunol. 21:11–16. [DOI] [PubMed] [Google Scholar]
- 3.Feinstein, A., N. Richardson, and M. J. Taussig. 1986. Immunoglobulin flexibility in complement activation. Immunol. Today. 7:169–174. [DOI] [PubMed] [Google Scholar]
- 4.Brüggemann, M., G. T. Williams, C. I. Bindon, M. R. Clark, M. R. Walker, R. Jefferis, H. Waldmann, and M. S. Neuberger. 1987. Comparison of the effector functions of human immunoglobulins using a matched set of chimeric antibodies. J. Exp. Med. 166:1351–1361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Kabat, E. A., T. T. Wu, H. M. Perry, K. S. Gottesman, and C. Foeller. 1991. Sequence of Proteins of Immunological Interest. National Institutes of Health, Bethesda, MD.
- 6.Burton, D. R. 1990. The conformation of antibodies. In Fc Receptors and the Action of Antibodies. H. Metzger, editor. American Society of Microbiology, Washington DC.
- 7.Beale, D., and A. Feinstein. 1976. Structure and function of the constant region of immunoglobins. Q. Rev. Biophys. 9:135–180. [DOI] [PubMed] [Google Scholar]
- 8.Burton, D. R. 1985. Immunoglobulin G: functional sites. Mol. Immunol. 22:161–202. [DOI] [PubMed] [Google Scholar]
- 9.Kim, H., C. Matsunaga, K. Yoshino, K. Kato, and Y. Arata. 1994. Dynamical structure of the hinge region of immunoglobulin G as studied by 13C nuclear magnetic resonance spectroscopy. J. Mol. Biol. 236:300. [DOI] [PubMed] [Google Scholar]
- 10.Padlan, E. A. 1996. X-ray crystallography of antibodies. Adv. Protein Chem. 49:57–133. [DOI] [PubMed] [Google Scholar]
- 11.Klein, M., N. Haeffner-Cavaillon, D. E. Isenman, C. Rivat, M. A. Navia, D. R. Davies, and K. J. Dorrington. 1981. Expression of biological effector functions by immunoglobulin G molecules lacking the hinge regions. Proc. Natl. Acad. Sci. USA. 78:524–528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Dangl, J. L., T. G. Wensel, S. L. Morrison, L. Stryer, L. A. Herzenberg, and V. T. Oi. 1988. Segmental flexibility and complement fixation of genetically engineered chimeric human, rabbit and mouse antibodies. EMBO J. 7:1989–1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Oi, V. T., T. M. Vuong, R. Hardy, J. Reidler, J. L. Dangl, L. A. Herzenberg, and L. Stryer. 1984. Correlation between segmental flexibility and effector function of antibodies. Nature. 307:136–139. [DOI] [PubMed] [Google Scholar]
- 14.Pumphrey, R. 1986. Computer models of the human immunoglobulins: shape and segmental flexibility. Immunol. Today. 7:174–178. [DOI] [PubMed] [Google Scholar]
- 15.Brekke, O. H., T. E. Michaelsen, R. Sandin, and I. Sandlie. 1993. Activation of complement by an IgG molecule without a genetic hinge. Nature. 363:628–630. [DOI] [PubMed] [Google Scholar]
- 16.Michaelsen, T. E., O. H. Brekke, A. Aase, R. H. Sandin, B. Bremnes, and I. Sandlie. 1994. One disulfide bond in front of the second heavy chain constant region is necessary and sufficient for effector function of human IgG3 without a genetic hinge. Proc. Natl. Acad. Sci. USA. 91:9243–9247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Dell'Acqua, W. F., K. E. Cook, M. M. Damschroder, R. M. Woods, and H. Wu. 2006. Modulation of the effector functions of a human IgG1 through engineering of its hinge region. J. Immunol. 177:1129–1138. [DOI] [PubMed] [Google Scholar]
- 18.Greenwood, J., M. R. Clark, and H. Waldmann. 1993. Structural motifs involves in human IgG antibody effector functions. Eur. J. Immunol. 23:1098–1104. [DOI] [PubMed] [Google Scholar]
- 19.Tao, M., R. I. F. Smith, and S. L. Morrison. 1993. Structural features of human immunoglobulin G that determine isotype-specific difference in complement activation. J. Exp. Med. 178:661–667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Harris, L. J., S. B. Larson, and A. McPherson. 1999. Comparison of intact antibody structures and the implications for effector function. Adv. Immunol. 72:191–209. [DOI] [PubMed] [Google Scholar]
- 21.Terry, W. D., B. W. Matthews, and D. R. Davies. 1968. Crystallographic studies of a human immunoglobulin. Nature. 220:239–241. [DOI] [PubMed] [Google Scholar]
- 22.Edmundson, A. B., M. Wood, M. Schiffer, K. D. Hardman, C. F. Ainsworth, K. Ely, and H. F. Deutsch. 1970. A crystallographic investigation of a human IgG immunoglobulin. J. Biol. Chem. 245:2763–2764. [PubMed] [Google Scholar]
- 23.Huber, R., J. Deisenhofer, P. M. Coleman, M. Matsushiman, and W. Palm. 1976. Crystallographic structure studies of an IgG molecule and an Fc fragment. Nature. 264:415–420. [DOI] [PubMed] [Google Scholar]
- 24.Larson, S. B., J. Day, A. Greenwood, E. Skaletsky, and A. McPherson. 1991. Characterization of crystals of an intact monoclonal antibody for canine lymphoma. J. Mol. Biol. 222:17–19. [DOI] [PubMed] [Google Scholar]
- 25.Harris, L. J., S. B. Larson, K. W. Hasel, J. Day, A. Greenwood, and A. McPherson. 1992. The three-dimensional structure of an intact monoclonal antibody for canine lymphoma. Nature. 360:369–372. [DOI] [PubMed] [Google Scholar]
- 26.Harris, L. J., E. Skaletsky, and A. McPherson. 1998. Crystallographic structure of an intact IgG1 monoclonal antibody. J. Mol. Biol. 275:861–872. [DOI] [PubMed] [Google Scholar]
- 27.Saphire, E. O., P. W. H. I. Parren, C. F. Barbas, D. R. Burton, and I. A. Wilson. 2001. Crystallization and preliminary structure determination of an intact human immunoglobulin b12: an antibody that broadly neutralizes primary isolates of HIV-1. Acta Crystallogr. D. 57:168. [DOI] [PubMed] [Google Scholar]
- 28.Saphire, E. O., R. L. Stanfield, M. D. Max, P. W. H. I. Crispin, R. P. M. Parren, R. A. Dwek, D. R. Burton, and I. A. Wilson. 2002. Contrasting IgG structures reveal extreme asymmetry and flexibility. J. Mol. Biol. 319:9–18. [DOI] [PubMed] [Google Scholar]
- 29.Roux, K. H. 1989. Immunoelectron microscopy of idiotype-anti-idiotype complexes. Methods Enzymol. 178:130–144. [DOI] [PubMed] [Google Scholar]
- 30.Phillips, M. L., V. T. Oi, and V. N. Schumaker. 1990. Electron microscopic study of ring-shaped, bivalent hapten, bivalent antidansyl monoclonal antibody complexes with identical variable domains but IgG1, IgG2a and IgG2b constant domains. Mol. Immunol. 27:181–190. [DOI] [PubMed] [Google Scholar]
- 31.Roux, K. H., L. Strelets, and T. E. Michaelsen. 1997. Flexibility of human IgG subclasses. J. Immunol. 159:3372–3382. [PubMed] [Google Scholar]
- 32.Roux, K. H., L. Strelets, O. H. Brekke, I. Sandlie, and T. E. Michaelsen. 1998. Comparisons of the ability of human IgG3 hinge mutants, IgM, IgE, and IgA2, to form small immune complexes: a role for flexibility and geometry. J. Immunol. 161:4083–4090. [PubMed] [Google Scholar]
- 33.Carrasco, B., J. Garcia de la Torre, K. G. Davis, S. Jones, D. Athwal, C. Walters, D. R. Burton, and S. E. Harding. 2001. Crystallohydrodynamics for solving the hydration problem for multi-domain proteins: open physiological conformations for human IgG. Biophys. Chem. 93:181–196. [DOI] [PubMed] [Google Scholar]
- 34.Longman, E., K. Kreusel, S. B. Tendler, I. Fiebrig, K. King, J. Adair, P. O'Shea, A. Ortega, J. Garcia de la Torre, and S. E. Harding. 2003. Estimating domain orientation of two human antibody IgG4 chimeras by crystallohydrodynamics. Eur. Biophys. J. 32:503–510. [DOI] [PubMed] [Google Scholar]
- 35.Boehm, M. K., J. M. Woof, M. A. Kerr, and S. J. Perkins. 1999. The Fab and Fc fragments of IgA1 exhibit a different arrangement from that in IgG: a study by x-ray and neutron solution scattering and homology modeling. J. Mol. Biol. 286:1421–1447. [DOI] [PubMed] [Google Scholar]
- 36.Aslam, M., J. M. Guthridge, B. K. Hack, R. J. Quigg, V. M. Holers, and S. J. Perkins. 2003. The extended multidomain solution structures of the complement protein Crry and its chimeric conjugate Crry-Ig by scattering, analytical ultracentrifugation and constrained modeling: implications for function and therapy. J. Mol. Biol. 329:525–550. [DOI] [PubMed] [Google Scholar]
- 37.Furtado, P. B., P. W. Whitty, A. Robertson, J. T. Eaton, A. Almogren, M. A. Kerr, J. M. Woof, and S. J. Perkins. 2004. Solution structure determination of monomeric human IgA2 by x-ray and neutron scattering, analytical ultracentrifugation and constrained modeling: a comparison with monomeric human IgA1. J. Mol. Biol. 338:921–941. [DOI] [PubMed] [Google Scholar]
- 38.Sun, Z., A. Almogren, P. B. Furtado, B. Chowdhury, M. A. Kerr, and S. J. Perkins. 2005. Semi-extended solution structure of human Myeloma Immunoglobulin D determined by constrained x-ray scattering. J. Mol. Biol. 353:155–173. [DOI] [PubMed] [Google Scholar]
- 39.Lu, Y., E. Longman, K. G. Davis, A. Ortega, J. G. Grossmann, T. E. Michaelsen, J. Garcia de la Torre, and S. E. Harding. 2006. Crystallohydrodynamics of protein assemblies: combining sedimentation, viscometry and x-ray scattering. Biophys. J. 91:1688–1697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Garcia de la Torre, J., H. E. Perez Sanchez, A. Ortega, J. G. Hernandez, M. X. Fernandes, F. G. Diaz, and M. C. Lopez Martinez. 2003. Calculation of the solution properties of flexible macromolecules: methods and applications. Eur. Biophys. J. 32:477–486. [DOI] [PubMed] [Google Scholar]
- 41.Harding, S. E., E. Longman, B. Carrasco, A. Ortega, and J. Garcia de la Torre. 2004. Studying antibody conformations by ultracentrifugation and hydrodynamic modeling. In Antibody Engineering: Methods and Protocols. B. K. C. Lo, editor. Humana Press, Totowa, NJ. [DOI] [PubMed]
- 42.Michaelsen, T. E., A. Aase, C. Westbye, and I. Sandlie. 1990. Enhancement of complement activation and cytolysis of human IgG3 by deletion of hinge exons. Scand. J. Immunol. 32:517–528. [DOI] [PubMed] [Google Scholar]
- 43.Brekke, O. H., T. E. Michaelsen, A. Aase, R. H. Sandin, and I. Sandlie. 1994. Human IgG isotype-specific amino acid residues affecting complement-mediated cell lysis and phagocytosis. Eur. J. Immunol. 24:2542–2547. [DOI] [PubMed] [Google Scholar]
- 44.Schuck, P. 2000. Size distribution analysis of macromolecules by sedimentation velocity ultracentrifugation and Lamm equation modeling. Biophys. J. 78:1606–1619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Boulin, C. J., R. Kempf, A. Gabriel, and M. H. J. Koch. 1988. Data acquisition systems for linear and area x-ray detectors using delay-line readout. Nucl. Instr. Methodol. Phys. Res. 269:312–320. [Google Scholar]
- 46.Semenyuk, A. V., and D. I. Svergun. 1991. GNOM-a program package for small-angle scattering data processing. J. Appl. Crystallogr. 24:537–540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Guinier, A., and G. Fournet. 1995. Small Angle Scattering of X-Rays. Wiley, New York.
- 48.Carrasco, B., and J. Garcia de la Torre. 1999. Hydrodynamic properties of rigid particles: comparison of different modeling and computational procedures. Biophys. J. 75:3044–3057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Garcia de la Torre, J., and B. Carrasco. 2002. Hydrodynamic properties of rigid macromolecules composed of ellipsoidal and cylindrical subunits. Biopolymers. 63:163–167. [DOI] [PubMed] [Google Scholar]
- 50.Garcia de la Torre, J., B. Carrasco, and S. E. Harding. 1997. SOLPRO: theory and computer program for the prediction of SOLution PROperties of rigid macromolecules and bioparticles. Eur. Biophys. J. 25:361–372. [DOI] [PubMed] [Google Scholar]
- 51.Garcia de la Torre, J., S. E. Harding, and B. Carrasco. 1999. Calculation of NMR relaxation, covolume and scattering of properties of bead models using the SOLPRO computer program. Eur. Biophys. J. 28:119–132. [DOI] [PubMed] [Google Scholar]
- 52.Laue, T. M., B. D. Shah, T. M. Ridgeway, and S. L. Pelletier. 1992. Computer-aided interpretation of analytical sedimentation data for proteins. In Analytical Ultracentrifugation in Biochemistry and Polymer Science. S. E. Harding, A. J. Rowe, and J. C. Horton, editors. Royal Society of Chemistry, Cambridge, UK.
- 53.Kilar, F., I. Simon, S. Lakatos, F. Vonderviszt, G. A. Medgyesi, and P. Zavodszky. 1985. Conformation of human IgG subclasses in solution. Small angle x-ray scattering and hydrodynamic studies. Eur. J. Biochem. 147:17–25. [DOI] [PubMed] [Google Scholar]
- 54.Gregory, L., K. G. Davis, B. Sheth, J. Boyd, R. Jefferis, C. Nave, and D. R. Burton. 1987. The solution conformations of the subclasses of human IgG deduced from sedimentation and small angle x-ray scattering studies. Mol. Immunol. 24:821–829. [DOI] [PubMed] [Google Scholar]
- 55.Philips, M. L., M. H. Tao, S. L. Morrison, and V. N. Schumaker. 1994. Human/mouse chimeric monoclonal antibodies with human IgG1, IgG2, IgG3 and IgG4 constant domains: electron microscopic and hydrodynamic characterization. Mol. Immunol. 31:1201–1210. [DOI] [PubMed] [Google Scholar]
- 56.Tanford, C. 1961. Physical Chemistry of Macromolecules. Wiley, New York.
- 57.Glatter, O., and O. Kratky. 1982. Small Angle X-Ray Scattering. Academic Press, London.
- 58.Perkins, S. J. 2001. High-flux x-ray and neutron solution scattering. In Protein-Ligand Iterations: Hydrodynamics and Calorimetry. S. E. Harding and B. Z. Chowdhry, editors. Oxford University Press, Oxford, UK.
- 59.Svergun, D. I. 1992. Determination of the regularization parameter in indirect transform using perceptual criteria. J. Appl. Crystallogr. 25:495–503. [Google Scholar]
- 60.Carrasco, B., J. Garcia de la Torre, O. Byron, D. King, C. Walters, S. Jones, and S. E. Harding. 1999. Novel size-independent modeling of the dilute solution conformation of the immunoglobulin IgG Fab′ domain using SOLPRO and ELLIPS. Biophys. J. 77:2902–2910. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Diaz, F. G., J. J. Lopez Cascales, and J. Garcia de la Torre. 1993. Bead-model calculation of scattering diagrams: Brownian dynamics study of flexibility in immunoglobulin IgG1. J. Biochem. Biophys. Methods. 26:261–271. [DOI] [PubMed] [Google Scholar]
- 62.Duncan, A. R., and G. Winter. 1988. The binding site for C1q on IgG. Nature. 332:738–740. [DOI] [PubMed] [Google Scholar]
- 63.Morgan, A., N. D. Jones, A. M. Nesbitt, L. Chaplin, M. W. Bodmer, and J. S. Emtage. 1995. The N-terminal end of the CH2 domain of chimeric human IgG1 anti-HLA-DR is necessary for C1q, FcγRI and FcγRIII binding. Immunology. 86:319–324. [PMC free article] [PubMed] [Google Scholar]
- 64.Thommesen, J. E., T. E. Michaelsen, G. A. Loset, I. Sandlie, and O. H. Brekke. 2000. Lysine 322 in the human IgG3 CH2 domain is crucial for antibody dependent complement activation. Mol. Immunol. 37:995–1004. [DOI] [PubMed] [Google Scholar]
- 65.Idusogie, E. E., L. G. Presta, H. Gazzano-Santoro, K. Totpal, P. Y. Wong, M. Ultsch, Y. G. Meng, and M. G. Mulkerrin. 2000. Mapping of the C1q binding site on rituxan, a chimeric antibody with a human IgG1 Fc. J. Immunol. 164:4178–4184. [DOI] [PubMed] [Google Scholar]
- 66.Coloma, M. J., K. R. Trinh, L. A. Wims, and S. L. Morrison. 1997. The hinge as a spacer contributes to covalent assembly and is required for function of IgG. J. Immunol. 158:733–740. [PubMed] [Google Scholar]
- 67.Tao, M., S. M. Canfield, and S. L. Morrison. 1991. The differential ability of human IgG1 and IgG4 to activate complement is determined by the COOH-terminal sequence of the CH2 domain. J. Exp. Med. 173:1025–1028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Michaelsen, T. E., J. E. Thommesen, O. Ihle, T. F. Gregers, R. H. Sandin, O. H. Brekke, and I. Sandlie. 2006. A mutant human IgG molecule with only one C1q binding site can activate complement and induce lysis of target cells. Eur. J. Immunol. 36:129–138. [DOI] [PubMed] [Google Scholar]