Abstract
Many enzymes mold their structures to enclose substrates in their active sites such that conformational remodeling may be required during each catalytic cycle. In adenylate kinase (AK), this involves a large-amplitude rearrangement of the enzyme's lid domain. Using our method of high-resolution single-molecule FRET, we directly followed AK's domain movements on its catalytic time scale. To quantitatively measure the enzyme's entire conformational distribution, we have applied maximum entropy-based methods to remove photon-counting noise from single-molecule data. This analysis shows unambiguously that AK is capable of dynamically sampling two distinct states, which correlate well with those observed by x-ray crystallography. Unexpectedly, the equilibrium favors the closed, active-site-forming configurations even in the absence of substrates. Our experiments further showed that interaction with substrates, rather than locking the enzyme into a compact state, restricts the spatial extent of conformational fluctuations and shifts the enzyme's conformational equilibrium toward the closed form by increasing the closing rate of the lid. Integrating these microscopic dynamics into macroscopic kinetics allows us to model lid opening-coupled product release as the enzyme's rate-limiting step.
Keywords: conformational equilibrium, rate-limiting step, single-molecule FRET, adenylate kinase
Proteins such as enzymes are flexible with a range of motions spanning from picoseconds for localized vibrations to seconds for concerted global conformational rearrangements (1). Despite their randomly fluctuating environment, in which stochastic collisions with solvent molecules drive changes in tertiary structure, enzymes have evolved to catalyze reactions efficiently and specifically. Indeed, conformational transitions have been postulated to play a central role in enzyme functions in a wide variety of ways, including direct contribution to catalysis (2), allosteric regulation (3), and large-scale conformational changes in response to ligand binding (4). Most of our current understanding of structural motions in solution comes from NMR experiments (5) as well as from molecular dynamics simulations (6), approaches that are best suited to study dynamics in the pico- to millisecond time scales. Because catalysis in enzymes frequently occurs in the submillisecond to minute time regime, our current understanding of the relationship between enzyme function and conformational dynamics comes from NMR experiments involving relatively localized motions of active site forming loops on the submillisecond time scale (7–10). However, many enzymes contain active sites located in between domains in which large-amplitude, low-frequency domain motions are required to complete their Michaelis–Menten enzyme–substrate complexes. Even simple questions regarding these transitions remain generally unanswered: What is the number and range of conformational states accessible to enzymes during their catalytic cycle? How does the enzyme's conformation respond to interaction with substrates? At which stage along an enzymatic cycle do these changes occur? These questions, although essential to the fundamental understanding of the structure–function relationship, are difficult to address because proteins do not move synchronously on this time scale, resulting in averaging away conformational dynamics in bulk experiments. We use adenylate kinase (AK) from Escherichia coli as a model to examine the aforementioned issues by monitoring the time-dependent FRET in dye-labeled AKs at the single-molecule level.
AK was chosen for this study because many aspects of this enzyme have been studied both experimentally (11–19) and theoretically (20–24). It is an ubiquitous enzyme that helps maintain the energy balance in cells by catalyzing the reversible reaction, Mg2+·ATP + AMP ⇌ Mg2+·ADP + ADP. This reaction has been regarded as exhibiting a random bi–bi mechanism in which the two unique ATP- and AMP-binding sites are independently and randomly occupied with substrate (11). It also is a classic example of an enzyme with a large conformational change critical to its function (18) and provides a very rich platform through which many basic ideas about the interplay between structure, function, and dynamics can be examined in detail. A comparison of >20 available crystal structures of AK in various ligand-bound states reveals that, upon binding substrates, the enzyme changes from an open (ligand-free) to a closed conformation to form the catalytically competent active site (Fig. 1), the basic structural motif of which is shared by many other kinases and ATPases. These hinge motions involve the ATP lid domain and the nucleoside monophosphate binding domain (the NMPbind domain) closing over their respective substrates to exclude water from the enzyme's active site during the phosphoryl transfer reaction (14, 25). The closed lid occludes AK's substrate binding site (Fig. 1b) such that the lid may need to be open in order for substrates to bind or for products to be released from the enzyme. The high catalytic efficiency of AK [kcat/KM,Mg·ATP = 4.3 × 106 M−1·s−1 (12), where KM,Mg·ATP is the Michaelis–Menten constant for Mg-ATP] suggests that if the lid is involved in the enzyme's mechanism, it has been optimized to help the enzyme achieve its high efficiency. A recent NMR study (19) performed on AK at equilibrium with nucleotides (ATP, ADP, and AMP; so that both forward and backward reactions are occurring) and a nucleotide analog (AMP-PNP and AMP; no turnover) has provided experimental evidence correlating the time scale of lid opening dynamics with the catalytic turnover rate for the forward, ADP-forming reaction. Despite these advances, the functional roles of conformational dynamics remain elusive. For example, because the forward and reverse reactions of this enzyme have distinct rates [kcat(forward) ≈ 3 × kcat(reverse) (12)], it is unclear how lid dynamics are involved in the overall reaction mechanism based on bulk results alone (19). Furthermore, these bulk experiments assume that AK only exists in its open form and that a two-state model is applicable when it interacts with substrates, assumptions that remain to be validated. Here, we demonstrate that data-driven, single-molecule experiments can resolve these issues and provide quantitative information about the functional roles of conformational dynamics in enzymes such as AK.
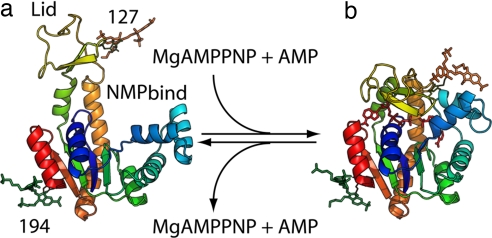
Fig. 1.
Modeling of AK with FRET dyes attached. Open (a) and closed (b) form E. coli AK illustrating the lid, NMPbind, and core domains, as well as the labeling positions used in single-molecule experiments (A127C and A194C). The closed form shows substrates modeled into the binding site. The distances between the center of mass of the two dyes are ≈44 Å (high-FRET state) and ≈53 Å (low-FRET state), respectively. Details of the modeling and computer simulation are included in SI Materials and Methods.
Results and Discussion
Conformational Distribution and Flexibility of AK.
A mutant protein was constructed to allow measurement of distance changes between AK's core and lid domains using single-molecule FRET (see Fig. 1). To characterize AK's innate flexibility, we performed experiments on the substrate-free enzyme. A sample emission intensity vs. time trace for a single substrate-free AK molecule, averaged every 10 ms, is displayed in Fig. 2a. This figure shows anticorrelated donor and acceptor emission that is indicative of conformational changes. Although fluorescence single-molecule methods have unveiled many dynamical aspects in nucleic acid interactions by following the on–off-like switching behavior in the signal (26–28), there are no apparent discrete transitions in AK's trajectories, underscoring the difficulties in analyzing protein single-molecule experiments. We attribute the lack of discrete states to the complexity of the energy landscape governing conformational motions in AK, a property that appears to be common in proteins (29). It is challenging to quantify rapid motions along a fluorescence single-molecule time trace (for a recent review, see ref. 30) because it generally requires 20–25 photons to make a statistically meaningful FRET measurement. To overcome experimental limitations, we have developed advanced statistical methods using ideas from information theory (31) that quantitatively resolve conformational dynamics, photon by photon, from counting-noise-limited, single-molecule data without any presumed kinetic model [see supporting information (SI) Materials and Methods for details]. When applied to the substrate-free AK intensity–time trace in Fig. 2a, this unbiased analysis yields the dye separation vs. time trajectory in Fig. 2b (x ≡ R/R0 is the normalized distance, where R is the dye separation), showing fast transitions in the enzyme's conformation as defined by the lid–core distance. Our direct single-molecule observation clearly shows that AK is capable of stochastically sampling a wide range of conformations on the millisecond time scale, even without its substrate.
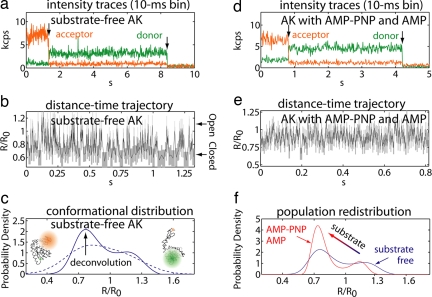
Fig. 2.
Raw single-molecule data and subsequent analysis. (a) Single-molecule FRET emission intensities for substrate-free AK (kcps, 1,000 counts per second) as a function of time averaged every 10 ms. Both acceptor (orange) and donor (green) dyes eventually photobleach (indicated by arrows in the trajectory), after which the background counts detected in each channel are displayed. (b) Donor–acceptor distance–time trajectory for substrate-free AK intensity trajectory in a, analyzed by using the kinetic-model-free maximum-likelihood method (31). The vertical and horizontal widths of each box (gray) represent the uncertainties in the distance and time resolution of the analysis. Larger distances come from more open enzyme conformations, and shorter distances come from closed conformations. R/R0 is the normalized distance, where R is the distance and R0 is the Förster radius characteristic of the dye pair that was used (R0 = 51 Å). (c) Probability distribution for substrate-free AK constructed using the Gaussian kernel density estimator (dashed line) and after entropy-regularized deconvolution (32) to remove broadening due to photon-counting noise (solid line) analyzed at a 2-ms time resolution. (d and e) Single-molecule intensity trajectory (d) and subsequent distance–time trajectory (e) for AK in the presence of 0.5 mM AMP-PNP and 0.5 mM AMP. (f) Comparison of deconvolved probability distributions at an ≈2-ms time resolution for substrate-free AK (blue line) and ligand-bound enzyme with 0.5 mM AMP-PNP (nonhydrolysable ATP analog) and 0.5 mM AMP (red), showing how the population of conformational states is shifted upon ligand binding.
To gain insight about the distribution of the conformational states available to the enzyme (another piece of information that is not available from bulk studies), we constructed a time-weighted probability density of the lid–core distance using a Gaussian kernel density estimator (Fig. 2c, dashed line). At this time resolution (≈2 ms), the distribution is significantly broadened by photon-counting noise; it appears nearly featureless except for a small shoulder toward more open conformations. This distribution could be equally well fit to a number of different models if one assumes the number of states present (e.g., one, two, or three) and their shapes (e.g., Gaussian or log-normal). To avoid subjective bias in interpreting the distribution, we applied our deconvolution technique to remove the broadening due to photon-counting noise (32). Based on the maximum entropy method, this procedure recovers the entire distribution of conformational states without a preassumed model regarding the number of states or the shape of the distribution. Applied to >400 trajectories, our analysis clearly reveals two distinct conformational modes in the lid–core coordinate of AK in the absence of substrates (Fig. 2c, solid line). The average distance in each deconvolved conformational mode, x ≈ 1.2 and 0.8, corresponds well to those predicted by crystal structures in the open and the closed conformations. Therefore, we were able to assign the modes observed in the probability distribution to an open and closed conformation of AK's lid. This, together with Fig. 2b, demonstrates that the lid domain of AK is in dynamical equilibrium between the open and closed conformational modes with each mode containing an ensemble of substates. Our results are in sharp contrast to the common view that AK's lid should remain open in the absence of substrates (13, 15–17), whereas binding would cause a global conformational change resulting in lid closure. That the substrate-free enzyme should remain in the open form has also been assumed (a reasonable supposition given the existing ensemble-averaged results) in the analysis of NMR relaxation-dispersion experiments performed on AK (19). Highlighting the information made available by single-molecule approaches, the direct observation of a conformational equilibrium between the open and closed modes in the substrate-free enzyme is evidence that large-scale conformational dynamics are an intrinsic feature of AK; substrate is not required to trigger the formation of the active-site cavity. Perhaps even more surprising with respect to the conventional view of AK's lid is the observation that the equilibrium favors the closed conformation in the absence of substrates. Intrinsic flexibility and a preference for the closed conformation of the lid are expected to contribute to minimizing the energy required to form the active configuration of this enzyme and help AK achieve it's high catalytic rate.
Effects of Ligand Binding on the Conformation Distribution.
Having revealed that large-amplitude conformational transitions exist in AK in the absence of ligands, we next evaluate how ligand binding may affect AK's conformation. Single-molecule experiments were performed as described above with both AMP-PNP (adenosine 5′-[β,γ-imido]triphosphate, a nonhydrolysable ATP analog) and AMP, each at 0.5 mM. This condition, rather than AK undergoing reaction, was chosen to probe the product release step of AK's reverse reaction. Similar to what was observed in the substrate-free case, the distance–time trajectory for AK in the presence of ligands shows a wide range of lid–core motions on the millisecond time scale (Fig. 2 d and e). A probability distribution constructed from >340 individual molecules is presented in Fig. 2f (red line) and compared with the distribution measured in the substrate-free enzyme (blue line). In the presence of ligands, the probability distribution measured along AK's lid–core coordinate also displays two conformational modes. It is clear that, instead of locking AK into a closed conformation, interaction with ligands results in a shift in AK's relative lid–core distribution while the enzyme continues to fluctuate dynamically between open and closed conformations. Fig. 2f also shows that ligands cause AK's conformational distribution to become more compact when compared with that observed in the substrate-free case, results made possible using our methodology (32). This narrowing of the distribution can be understood in terms of AK's interaction with ligands, which restricts the range of motion that AK can otherwise experience. These observations characterize the manner with which ligand-binding changes the equilibrium properties of AK's conformation. Previous ensemble-averaged FRET studies have reported shortening in AK's mean lid–core distance upon interaction with substrates (refs. 16 and 17 also reproduced in this study) (see SI Materials and Methods and SI Table 1), which has been used as evidence for substrate-induced lid closure. Our single-molecule data show that this bulk observation can now be understood as a reweighting in the relative lid–core distribution between the open and closed states while AK continues to fluctuate dynamically between conformations regardless of the presence or absence of the substrates. These features are masked in bulk experiments because they can measure only the mean distance of the entire ensemble of molecules.
Kinetics of Lid Movements.
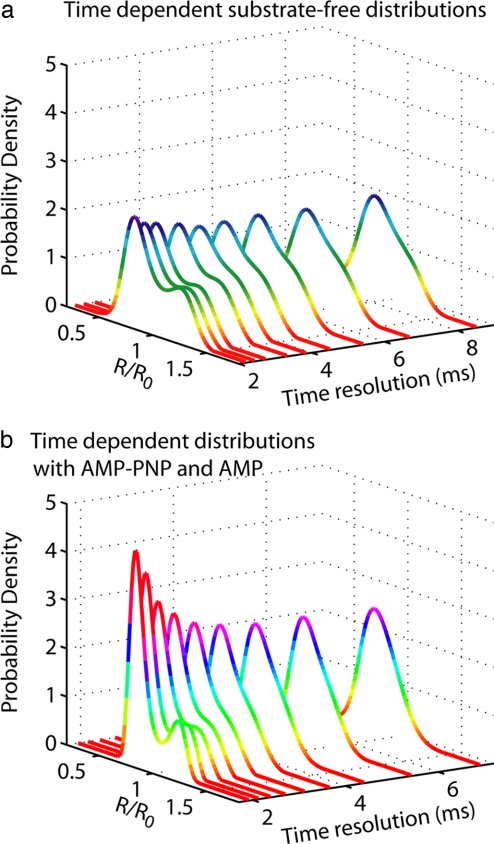
To link the stochastic microscopic dynamics of lid motions to macroscopic kinetic parameters, we need to determine the interconversion rates between the two conformational modes observed in the single-molecule probability distribution measured on AK. These rates will allow us to quantify how ligand-binding affects conformational motions and to place conformational dynamics in the overall kinetic scheme of this enzyme. The commonly used correlation method to extract kinetic rates from time series data are not practical because single-molecule traces are too short to allow adequate sampling of transitions; therefore, another strategy is needed. To this end, we further exploit our capability of quantitatively measuring single-molecule conformational distributions. We start by systematically changing the time resolution at which the deconvolution analysis was performed on a single data set. Fig. 3 shows that the two conformational modes gradually become unresolved as the data analysis time resolution was lowered from ≈2 ms to ≈8 ms. This is a clear indication that there are irresolvable motions that are beyond the time scale of our analyses; when the time resolution is insufficient to follow the dynamical switching between the two conformations, only a single mode, which is the time average of the two, is observed. These are in fact the basic ideas underlying the Kubo–Anderson motional narrowing model in spectroscopy (33, 34). We therefore used a simple two-state motional narrowing model to extract kinetic rates from finite-length FRET trajectories (35–37). The switching rate as well as the simplified equilibrium distribution of the two modes can be obtained by globally fitting the data sets in Fig. 3 to the solution of a two-state motional narrowing model. A fit of our data to this model yielded the following for substrate-free AK: kopen = 120 ± 40 s−1, kclose = 220 ± 70 s−1, xopen = 1.20 ± 0.03, and xclose = 0.76 ± 0.01 (see SI Fig. 5 and SI Table 2 for complete results). By fitting the experiments with AMP-PNP and AMP to the same model, we obtained kopen = 160 ± 40 s−1, kclose = 440 ± 110 s−1, xopen = 1.15 ± 0.03, and xclose = 0.73 ± 0.02 (see SI Fig. 6 and SI Table 2 for complete results). Our analysis shows that substrate binding does not substantially change the mean positions of AK's open and closed states, indicated by the normalized distance x. Rather, interaction with substrates changes the enzyme's conformational dynamics, doubling the lid closing rate upon ligand binding. The increase in the closing rate is likely driven by electrostatic interaction between positively charged residues in AK's binding pocket and the negatively charged phosphate groups on the ligand (13). Perhaps more interestingly, the opening rates of AK's lid domain are comparable within experimental errors. This experiment provides a direct observation that the rate of lid opening is an intrinsic feature of the enzyme itself, consistent with the recent domain-swapping experiments on AK (38), and that this opening is unaffected by ligand binding. That the lid opening rate appears to be commensurate with the kcat for the reverse reaction (12) leaves open the possibility that lid dynamics play a crucial mechanistic role in the function of this enzyme, the rate-limiting step. Indeed, previous NMR experiments have provided evidence correlating the time scales of the relatively small-amplitude intrinsic loop dynamics with the turnover rates in enzymes, including triosephosphate isomerase (7, 39), RNase A (9), dihydrofolate (8), and human cyclophilin A (10), hinting that structural dynamics are capable of playing a rate-limiting role in catalysis. However, it is not clear whether an analogous picture can be extended to such large-amplitude conformational fluctuations as are observed in AK.
Fig. 3.
Time-resolution-dependent motional narrowing of probability distributions. Deconvolved distributions from >300 AK single-molecule experiments at mean analysis time resolutions from ≈2 to ≈8 ms showing motional narrowing in both the free enzyme (a) and ligand-bound enzyme (b).
A Mechanistic Model for Lid Dynamics.
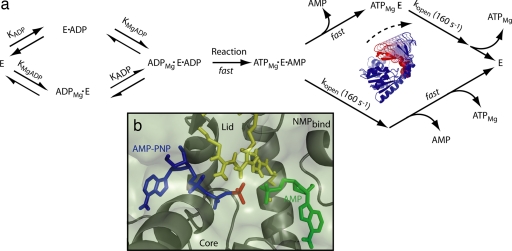
To understand the role of lid dynamics in the context of the enzymatic mechanism of AK, a thorough kinetic analysis of the reverse reaction of AK was undertaken. Bulk kinetic data in AK's reverse direction was collected on the mutant protein used in single-molecule experiments and found to be consistent (χ̃2 = 0.73) with the random bi–bi mechanism commonly assumed for AK (11). Parameters determined for kcat and disassociation constants for nucleotides are similar to those determined for the untagged WT protein (SI Fig. 7 and SI Table 3), indicating that mutations used in single-molecule experiments have not significantly perturbed the enzyme's reaction mechanism. The hypothesis that the rate-limiting step in the ATP-producing reaction is actually lid-opening-coupled product release and not catalysis itself was tested for consistency with the same bulk kinetic data. We fit the data to a kinetic model in which only the closed, tertiary enzyme–substrate complex can undergo catalysis (Fig. 4a). Although AK's reaction is reversible, the fast loss of product following catalysis renders it irreversible under our experimental conditions. Accordingly, our model predicts that the rate-limiting step in AK's reverse reaction will be lid-opening preceding the release of ATP. A fit of this model to the kinetic data measured in AK's reverse direction is presented in SI Fig. 8 and SI Table 4, demonstrating that this model describes the measured turnover for this enzyme very well (χ̃2 = 0.80). Therefore, that lid opening forms the rate-limiting step in AK's reverse reaction is consistent with the overall enzymatic reaction kinetics. Upon combining our single-molecule measurements with bulk kinetics and information from crystallography, a picture emerges (Fig. 4a) detailing how AK has optimized its structure to use large-amplitude conformational dynamics to achieve fast catalytic turnover. By following the fluctuations of individual enzyme molecules in real time, we show that AK stochastically samples a wide range of conformations on its catalytic time scale, even in the absence of ligands. Single-molecule experiments uniquely demonstrate that the extent of these fluctuations includes open and closed states of the enzyme, manifested as two distinct modes in the conformational distributions. This dynamic equilibrium is important because it allows the formation of the active site without significant energy cost, contributing to the efficiency of this enzyme. When ligands are interacting with the enzyme, the distribution of states underlying AK's conformational landscape is reconfigured, shifting the enzyme's conformational equilibrium to further favor the closed state. Substrate binding also restricts the range of motions available to the enzyme, likely to promote formation of the activated enzyme–substrate complex poising the system for catalysis. Once AK has formed its closed, tertiary complex, the β-phosphate of ADP is rapidly shuffled between the two nucleotides bound to the enzyme until the products are able to diffuse away, with the rate of ATP disassociation and the overall rate of the reaction controlled by lid opening. A closer look at AK's active site by crystallography (Fig. 4b) reveals that most of AK's interactions with the β-phosphate of AMP-PNP are through hydrogen bonds to three highly conserved arginine residues (R123, R156, and R167) in the lid (40, 41). In addition to direct contribution to catalysis (42), contact with these residues is likely to prevent ATP from diffusing out of AK's active site when the lid is partially open; only when the lid is fully open can ATP be released from the active site. This model provides a mechanism for product release in AK's reverse reaction that is gated by lid-opening, the rate of which is an inherent feature of AK's structure and is independent of ligand.
Fig. 4.
Kinetic modeling for AK with lid-opening coupled product release as the rate-limiting step. (a) Schematic representation of model used to fit bulk kinetic data for AK's reverse reaction (SI Fig. 8). The rate-limiting step for this model is lid-opening before release of MgATP. Opening of the lid domain is not coupled to release of AMP, illustrated by two alternative substrate release pathways. Substrate binding steps before lid opening are treated as if they were at equilibrium, whereas the phosphate transfer reaction and product release are modeled as fast, kinetically irresolvable steps [morph-generated with the Yale Morph Server, http://molmovdb.org (48)]. (b) Detail of AK's active site (Protein Data Bank ID code 1ANK) with AMP-PNP bound (blue) showing the specific contacts between the β-phosphate (red) of the nucleotide poised for transfer to AMP (green), as well as three arginine residues in the closed state of the lid (yellow) whose contacts with ATP are abolished upon lid opening (15).
Summary and Conclusion
Individual fluorescent molecules can now be detected routinely (43); yet, to realize the full potential of single-molecule spectroscopy and imaging, it is important to go beyond simple visualization when analyzing and interpreting data from these experiments (44). This report represents the application of several recent developments in fluorescence single-molecule techniques based on information theory that use the information carried by each detected photon in an unbiased way (31, 32, 45). Our data-driven approach allows us to quantitatively account for photon-detection statistics, follow the time-dependent FRET distance changes photon-by-photon with the best possible time and distance resolution, and to unambiguously recover the entire FRET distance distribution. The results are unprejudiced because these statistical procedures do not require any presumed models of kinetic schemes or number of states. We have been able to uncover many statistically significant features of enzyme structure–function dynamics that are not readily detectable either by ensemble-averaged techniques or simply visualizing single-molecule data.
By following the domain motions of a single AK from E. coli in real time, we have shown that substrates are not required for inducing large-amplitude domain reconfiguration, allowing this enzyme to sample its closed, active-site-forming conformation. We have been able to quantitatively recover the entire distribution of conformations available to AK, showing that the dynamic equilibrium favors the closed state of AK's lid domain, an unanticipated result. Furthermore, our experiments have demonstrated that the role of substrate binding is to dynamically reshape the entire distribution of an ensemble of conformational substates, illustrating that ligands restrict the range of conformational fluctuations and shift the dynamic equilibrium by increasing the closing rate. The unequivocal presence of two modes in our noise-free distributions suggests a two-state model for recovering kinetic parameters from short, stochastic single-molecule trajectories, which in turn allows us to combine single-molecule dynamics and bulk kinetic analysis, leading to the model that the rate-limiting step in the enzyme's reverse reaction involves the large-scale conformational change of the lid from a closed to fully open state before product release. The nature of these dynamic conformational transitions, although driven by random interactions with solvent molecules, is likely guided by the 3D structure of the enzyme and represents a delicate balance between configuration of the active site for catalysis, substrate recruitment, and product release. Using quantitative, unbiased single-molecule measurements and other powerful ensemble-averaged methods, we have begun to develop a predictive understanding of the functional role of structural dynamics in enzymes.
Materials and Methods
Single-Molecule Data Analysis.
To minimize error and bias in calculating time-dependent donor–acceptor distances from single-molecule trajectories (see SI Materials and Methods), a change-point analysis (45) was applied to the data to determine the precise moment at which the dyes bleach. Distance vs. time data were extracted from trajectories using the maximum-likelihood analysis method (31). Data were then combined to form a probability distribution function using the Gaussian kernel method. Photon-counting noise was removed with entropy-regularized deconvolution (32).
Two-State Motional Narrowing Model.
That the conformational distribution coalesces at lowered time resolutions is isomorphic to the spectral narrowing problem that has been solved by Anderson (33) and Kubo (34). The closed-form solutions (35–37) were used to model the observations under the simple kinetic scheme presented in equation (see SI Materials and Methods for details).
 |
By systematically changing the fixed relative uncertainty, α  (δx/x), used during data analysis (31, 32), the average time resolution in the calculations can be varied and effects on the distribution of the lid–core distances can be investigated. It is recognized that proteins are likely to exhibit motions on time scales that range several orders of magnitude (29). Thus, the approximately millisecond time experimental resolution averages over the dynamics as they are projected onto the one-dimensional FRET donor–acceptor coordinate and is likely to introduce additional time-resolution-dependent widths in the distribution. Dynamics of this origin, although extremely interesting, do not contribute significantly to kinetically resolvable conformations in single-molecule experiments. For simplicity, their contributions and contributions for the calibration errors (see SI Materials and Methods) are modeled as a Gaussian of width σα at a given time resolution (indicated by the analysis uncertainty, α) that are incorporated in the fitting via convolution, according to the treatment of Gopich and Szabo (37). The parameters that are to be optimized in the global fitting are kopen, kclose, a, b, and σα, where α = 0.07–0.15 with an increment of 0.1, b is the x position of the closed conformation, and (a + b) is the x position of the open conformation.
(δx/x), used during data analysis (31, 32), the average time resolution in the calculations can be varied and effects on the distribution of the lid–core distances can be investigated. It is recognized that proteins are likely to exhibit motions on time scales that range several orders of magnitude (29). Thus, the approximately millisecond time experimental resolution averages over the dynamics as they are projected onto the one-dimensional FRET donor–acceptor coordinate and is likely to introduce additional time-resolution-dependent widths in the distribution. Dynamics of this origin, although extremely interesting, do not contribute significantly to kinetically resolvable conformations in single-molecule experiments. For simplicity, their contributions and contributions for the calibration errors (see SI Materials and Methods) are modeled as a Gaussian of width σα at a given time resolution (indicated by the analysis uncertainty, α) that are incorporated in the fitting via convolution, according to the treatment of Gopich and Szabo (37). The parameters that are to be optimized in the global fitting are kopen, kclose, a, b, and σα, where α = 0.07–0.15 with an increment of 0.1, b is the x position of the closed conformation, and (a + b) is the x position of the open conformation.
Bulk Kinetic Model with Conformational Change.
AK activity was measured according to the protocol of Huss et al. (46) using the reverse reaction, Mg2+·ADP + ADP → Mg2+·ATP + AMP (46). A simple kinetic scheme for AK incorporating the LID conformational dynamics was used to model the bulk kinetic data (Fig. 4a). This model assumes that the rate-limiting step in AK's reaction is the lid-opening step that occurs after catalysis and before product release and that the catalytic step and disassociation of products are fast. The model was fit with the combined steady-state/rapid equilibrium approximation, for which ligand binding was considered to be at rapid equilibrium whereas the lid-opening coupled product release was assumed to be at steady state (47). Accordingly, Eq. 1 was used to model the initial-velocity data.
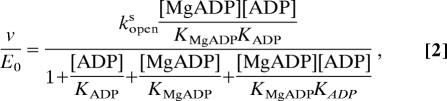 |
where KMgADP and KADP are the disassociation constants for Mg2+·ADP and ADP, respectively. Although we recognize that the subtle differences between AMP-PNP and ATP cannot be completely ignored, here we use the lid opening rate determined from single-molecule experiments in the presence of substrate and analog (AMP-PNP/Mg2+ and AMP), kopens, to approximate the lid opening rate in an actual reaction involving ATP. The assumption that product release is fast compared with the rate-limiting, lid opening step is reasonable if the association rate for products is diffusion-limited (kon ∼ 107–109 M−1·s−1). Given the literature values for product disassociation constants (KD = 85 μM for ATP), one would expect the off rate for ATP to be koff ∼ 9 × 102 to 9 × 104 s−1.
Supplementary Material
Acknowledgments
We thank Y.-W. Tan for critical reading of the manuscript; M. Glaser (University of Illinois at Urbana–Champaign, Urbana, IL) for the WT AK gene and protocols; S. Marqusee (University of California, Berkeley) for the use of a CD spectrometer; and J. M. Berger and R. Brem (University of California, Berkeley) for the use of plate readers. This work was supported by a National Science Foundation CAREER Award, U.S. Department of Energy Contract DE-AC03-76SF00098, and National Institutes of Health Contract R01 GM069937-01A3 (to the University of California, Berkeley). J.-W.C. was supported by the University of California, Berkeley. K.D. was supported by National Institutes of Health Molecular Biophysics Training Grant T32 GM008295 (to the University of California, Berkeley).
Abbreviations
- AK
adenylate kinase
- AMP-PNP
adenosine 5′-[β,γ-imido]triphosphate.
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/cgi/content/full/0708600104/DC1.
References
- 1.Frauenfelder H, Sligar SG, Wolynes PG. Science. 1991;254:1598–1603. doi: 10.1126/science.1749933. [DOI] [PubMed] [Google Scholar]
- 2.Hammes-Schiffer S, Benkovic SJ. Annu Rev Biochem. 2006;75:519–541. doi: 10.1146/annurev.biochem.75.103004.142800. [DOI] [PubMed] [Google Scholar]
- 3.Gunasekaran K, Ma BY, Nussinov R. Proteins. 2004;57:433–443. doi: 10.1002/prot.20232. [DOI] [PubMed] [Google Scholar]
- 4.Erzberger JP, Berger JM. Annu Rev Biophys Biomol Struct. 2006;35:93–114. doi: 10.1146/annurev.biophys.35.040405.101933. [DOI] [PubMed] [Google Scholar]
- 5.Boehr DD, Dyson HJ, Wright PE. Chem Rev. 2006;106:3055–3079. doi: 10.1021/cr050312q. [DOI] [PubMed] [Google Scholar]
- 6.Karplus M, McCammon JA. Nat Struct Biol. 2002;9:646–652. doi: 10.1038/nsb0902-646. [DOI] [PubMed] [Google Scholar]
- 7.Rozovsky S, McDermott AE. J Mol Biol. 2001;310:259–270. doi: 10.1006/jmbi.2001.4672. [DOI] [PubMed] [Google Scholar]
- 8.McElheny D, Schnell JR, Lansing JC, Dyson HJ, Wright PE. Proc Natl Acad Sci USA. 2005;102:5032–5037. doi: 10.1073/pnas.0500699102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Beach H, Cole R, Gill ML, Loria JP. J Am Chem Soc. 2005;127:9167–9176. doi: 10.1021/ja0514949. [DOI] [PubMed] [Google Scholar]
- 10.Eisenmesser EZ, Millet O, Labeikovsky W, Korzhnev DM, Wolf-Watz M, Bosco DA, Skalicky JJ, Kay LE, Kern D. Nature. 2005;438:117–121. doi: 10.1038/nature04105. [DOI] [PubMed] [Google Scholar]
- 11.Rhoads DG, Lowenstein JM. J Biol Chem. 1968;243:3963–3972. [PubMed] [Google Scholar]
- 12.Reinstein J, Vetter IR, Schlichting I, Rosch P, Wittinghofer A, Goody RS. Biochemistry. 1990;29:7440–7450. doi: 10.1021/bi00484a013. [DOI] [PubMed] [Google Scholar]
- 13.Berry MB, Meador B, Bilderback T, Liang P, Glaser M, Phillips GN. Proteins. 1994;19:183–198. doi: 10.1002/prot.340190304. [DOI] [PubMed] [Google Scholar]
- 14.Vonrhein C, Schlauderer GJ, Schulz GE. Structure (London) 1995;3:483–490. doi: 10.1016/s0969-2126(01)00181-2. [DOI] [PubMed] [Google Scholar]
- 15.Muller CW, Schlauderer GJ, Reinstein J, Schulz GE. Structure (London) 1996;4:147–156. doi: 10.1016/s0969-2126(96)00018-4. [DOI] [PubMed] [Google Scholar]
- 16.Bilderback T, Fulmer T, Mantulin WW, Glaser M. Biochemistry. 1996;35:6100–6106. doi: 10.1021/bi951833i. [DOI] [PubMed] [Google Scholar]
- 17.Sinev MA, Sineva EV, Ittah V, Haas E. Biochemistry. 1996;35:6425–6437. doi: 10.1021/bi952687j. [DOI] [PubMed] [Google Scholar]
- 18.Yan HG, Tsai MD. Adv Enzymol Relat Areas Mol Biol. 1999;73:103–134. doi: 10.1002/9780470123195.ch4. [DOI] [PubMed] [Google Scholar]
- 19.Wolf-Watz M, Thai V, Henzler-Wildman K, Hadjipavlou G, Eisenmesser EZ, Kern D. Nat Struct Biol. 2004;11:945–949. doi: 10.1038/nsmb821. [DOI] [PubMed] [Google Scholar]
- 20.Elamrani S, Berry MB, Phillips GN, McCammon JA. Proteins. 1996;25:79–88. doi: 10.1002/(SICI)1097-0134(199605)25:1<79::AID-PROT6>3.0.CO;2-F. [DOI] [PubMed] [Google Scholar]
- 21.Miyashita O, Onuchic JN, Wolynes PG. Proc Natl Acad Sci USA. 2003;100:12570–12575. doi: 10.1073/pnas.2135471100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Temiz NA, Meirovitch E, Bahar I. Proteins. 2004;57:468–480. doi: 10.1002/prot.20226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Maragakis P, Karplus M. J Mol Biol. 2005;352:807–822. doi: 10.1016/j.jmb.2005.07.031. [DOI] [PubMed] [Google Scholar]
- 24.Lou HF, Cukier RI. J Phys Chem B. 2006;110:24121–24137. doi: 10.1021/jp064303c. [DOI] [PubMed] [Google Scholar]
- 25.Jencks WP. Adv Enzymol Relat Areas Mol Biol. 1975;43:219–410. doi: 10.1002/9780470122884.ch4. [DOI] [PubMed] [Google Scholar]
- 26.Zhuang XW, Bartley LE, Babcock HP, Russell R, Ha TJ, Herschlag D, Chu S. Science. 2000;288:2048–2051. doi: 10.1126/science.288.5473.2048. [DOI] [PubMed] [Google Scholar]
- 27.Tan E, Wilson TJ, Nahas MK, Clegg RM, Lilley DMJ, Ha T. Proc Natl Acad Sci USA. 2003;100:9308–9313. doi: 10.1073/pnas.1233536100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.McKinney SA, Declais AC, Lilley DMJ, Ha T. Nat Struct Biol. 2003;10:93–97. doi: 10.1038/nsb883. [DOI] [PubMed] [Google Scholar]
- 29.Yang H, Luo GB, Karnchanaphanurach P, Louie TM, Rech I, Cova S, Xun LY, Xie XS. Science. 2003;302:262–266. doi: 10.1126/science.1086911. [DOI] [PubMed] [Google Scholar]
- 30.Michalet X, Weiss S, Jager M. Chem Rev. 2006;106:1785–1813. doi: 10.1021/cr0404343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Watkins LP, Yang H. Biophys J. 2004;86:4015–4029. doi: 10.1529/biophysj.103.037739. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Watkins LP, Chang H, Yang H. J Phys Chem A. 2006;110:5191–5203. doi: 10.1021/jp055886d. [DOI] [PubMed] [Google Scholar]
- 33.Anderson PW. J Phys Soc Jpn. 1954;9:316–339. [Google Scholar]
- 34.Kubo R. J Phys Soc Jpn. 1954;9:935–944. [Google Scholar]
- 35.Geva E, Skinner JL. Chem Phys Lett. 1998;288:225–229. [Google Scholar]
- 36.Brezhkovskii AM, Szabo A, Weiss GH. J Chem Phys. 1999;110:9145–9150. [Google Scholar]
- 37.Gopich IV, Szabo A. J Phys Chem B. 2003;107:5058–5063. [Google Scholar]
- 38.Bae EY, Phillips GN. Proc Natl Acad Sci USA. 2006;103:2132–2137. doi: 10.1073/pnas.0507527103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Williams JC, Mcdermott AE. Biochemistry. 1995;34:8309–8319. doi: 10.1021/bi00026a012. [DOI] [PubMed] [Google Scholar]
- 40.Berry MB, Bae EY, Bilderback TR, Glaser M, Phillips GN. Proteins. 2006;62:555–556. doi: 10.1002/prot.20699. [DOI] [PubMed] [Google Scholar]
- 41.Fukami-Kobayashi K, Nosaka M, Nakazawa A, Go M. FEBS Lett. 1996;385:214–220. doi: 10.1016/0014-5793(96)00367-5. [DOI] [PubMed] [Google Scholar]
- 42.Tsai MD, Yan HG. Biochemistry. 1991;30:6806–6818. doi: 10.1021/bi00242a002. [DOI] [PubMed] [Google Scholar]
- 43.Moerner WE, Fromm DP. Rev Sci Inst. 2003;74:3597–3619. [Google Scholar]
- 44.Lippitz M, Kulzer F, Orrit M. ChemPhysChem. 2005;6:770–789. doi: 10.1002/cphc.200400560. [DOI] [PubMed] [Google Scholar]
- 45.Watkins LP, Yang H. J Phys Chem B. 2005;109:617–628. doi: 10.1021/jp0467548. [DOI] [PubMed] [Google Scholar]
- 46.Huss RJ, Glaser M. J Biol Chem. 1983;258:13370–13376. [PubMed] [Google Scholar]
- 47.Huang CY. Methods Enzymol. 1979;63:54–84. doi: 10.1016/0076-6879(79)63006-9. [DOI] [PubMed] [Google Scholar]
- 48.Flores S, Echols N, Milburn D, Hespenheide B, Keating K, Lu J, Wells S, Yu EZ, Thorpe M, Gerstein M. Nucleic Acids Res. 2006;34:D296–D301. doi: 10.1093/nar/gkj046. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.