STOCHASTIC MODEL FOR ANALYSIS OF LONGITUDINAL DATA ON AGING AND MORTALITY

Abstract

Aging-related changes in a human organism follow dynamic regularities, which contribute to the observed age patterns of incidence and mortality curves. An organism’s “optimal” (normal) physiological state changes with age, affecting the values of risks of disease and death. The resistance to stresses, as well as adaptive capacity, declines with age. An exposure to improper environment results in persisting deviation of individuals’ physiological (and biological) indices from their normal state (due to allostatic adaptation), which, in turn, increases chances of disease and death. Despite numerous studies investigating these effects, there is no conceptual framework, which would allow for putting all these findings together, and analyze longitudinal data taking all these dynamic connections into account. In this paper we suggest such a framework, using a new version of stochastic process model of aging and mortality. Using this model, we elaborated a statistical method for analyses of longitudinal data on aging, health and longevity and tested it using different simulated data sets. The results show that the model may characterize complicated interplay among different components of aging-related changes in humans and that the model parameters are identifiable from the data.

1. Introduction

Current studies of mortality rates deal not only with analyses of available life span data. A substantial part of this research is going on within an analytical framework aiming to derive observed features of mortality curves using respective theoretical concepts. These studies include evolutionary biology theory of senescence [1], mutation-selection balance [2], reliability theory [3,4], and economic theory [5], among others. Such abstract analyses became possible because of remarkable regularities revealed in the shape of the mortality curve: the decline in the childhood, the exponential increase in the adult ages and the tendency to deceleration and leveling off at the oldest old ages. The studies intend to explain these regularities as natural phenomena resulting from the postulates of the respective theories.

Researchers studying aging/health/longevity still argue about regularities of aging-related deterioration in health and well-being status in humans. The lack of consensus in this area delays development of comprehensive models and theory. The revealed findings and regularities of the aging process remain largely disconnected and the high potential of data collected in many longitudinal studies remains underused. The typical situation is that only portions of available data are currently used and most of them are analyzed separately using formal statistical methods.

Such methods, however, largely ignore current knowledge and theory about aging in the process of data analyses. Meanwhile, it is clear that the progress in developing such modeling concepts would make combining distinct subsets of large-scale longitudinal data possible. The joint analysis of such data would allow for systemic addressing the issues on comprehensive interplay between different aging-related changes in a human organism. Ultimately this approach would help making a complete picture out of available mosaic details, findings, and regularities of aging-related changes in humans.

Overcoming these methodological problems is the matter of time. Development of several interesting concepts capable of capturing fundamental features of aging-related changes is now underway. They are related to the notion of allostatic load [6], the decline in adaptive capacity (homeostenosis) [7,8], the decline in resistance to stresses [9], the aging-related physiological norms, and heterogeneity in longitudinal data.

The formal approaches to the joint analysis of longitudinal and time-to-event data have been also developed during the last decades (see recent reviews in [10–12]). Joint longitudinal-survival models are the models that describe the joint behavior of the process generating the observed measurements and the survival (generally, time-to-event) process. The first, “longitudinal,” process is observed at respective times of measurement and the second, “survival,” process generates (possibly censored) event times that depend on the observations of the longitudinal process. The frequently used approach for a univariate case assumes that the longitudinal data follow a linear mixed-effects model [13] and that the hazard depends both on the random effects and other time-independent covariates through a Cox proportional hazard relationship [14–16]. Xu and Zeger [17] extended the model using the generalized linear model for the longitudinal process to allow for continuous or discrete covariates. Wang and Taylor [18] included a stochastic (an integrated Ornstein-Uhlenbeck) process into the model of longitudinal data to allow for random fluctuations of individual measurements around the population average. In Henderson et al. [19], a latent bivariate Gaussian process is introduced as a time-dependent variable in a proportional hazard model. Multivariate generalizations of such methods and the estimation procedures have been suggested recently [20–25].

The models mentioned so far use the Cox proportional hazards to characterize the relationship between the longitudinal and survival data. There are, however, many cases where the proportionality assumption fails. For such situations other models need to be used. Tseng et al. [26] used an accelerated failure time survival model as an alternative to the Cox model with longitudinal covariates following a linear mixed-effects model with measurement errors. Song and Huang [27] used a joint longitudinal-survival model with an additive hazard, where time-dependent covariates measured with errors are added to the baseline hazard.

An important class of models for analyses of longitudinal data is based on a biologically-motivated assumption of a quadratic hazard which is justified by J- or U-shapes of hazards considered as functions of risk factors observed in epidemiological studies [28]. These models were developed and intensively used in the studies of longitudinal data [29–33]. The advantageous feature of this approach is that it allows for incorporation of the new insights and ideas appearing in the course of research on aging.

In this paper we propose a new model of health, mortality, and aging, which will further develop this biologically-motivated approach by including all four major concepts of aging known to date, i.e., the notions of the age-dependent physiological norms, allostatic load, adaptive capacity and resistance to stress, and investigate the potential for the model application to the analysis of longitudinal data.

The reminder of the paper is organized as follows. Section 2 presents the model and outlines the estimation procedure. Section 3 describes the results of a simulation study checking the estimation procedure and the model performance. The last section summarizes the results and discusses perspectives of further research in this area.

2. Model

2.1. General description

The arguments discussed above allow us to formulate requirements for the model capable of connecting different aspects of aging and explore respective links in the analyses of longitudinal data. It is clear that it should be a dynamic model capable of describing random differences between individual trajectories of physiological or other indices. The values of such indices have to affect health or mortality risks. The model should be capable of describing the J-, or U-shape of the risk considered as a function of risk factors. The age trajectory in physiological space, for which the minimum value of the risk function is reached, will characterize the age-dependent physiological norm. Persistent deviations from the norm will characterize effects of allostatic adaptation and the magnitudes of such deviations for each physiological index will be associated with components of allostatic load. The narrowing of the U-shape of the risk function with age will characterize the decline in stress resistance. The dynamic model must include a feedback mechanism with coefficients of homeostatic regulation. The age-related changes in these coefficients will characterize the decline in adaptive capacity. To meet these requirements, we suggest the stochastic process model for continuously changing risk factors in the form of stochastic differential equation:

$$d{Y}_t=a(t)(Y_t-f_1(t))dt+b(t)d{W}_t,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{Y}_0.$$ (1)

Here Y_t (t is age) is a k-dimensional stochastic process describing continuously changing vector of risk factors (e.g., physiological characteristics), which approximates a human organisms’ functional state, W_t is a vector Wiener process with independent components, which describes exogenous challenges affecting these covariates. The process W_t is independent of the initial vector Y₀ with normally distributed components. Note that such a model preserves the Gaussian property: in the case of initial Gaussian distribution for Y₀, the distribution of Y_t among survivors is also Gaussian ([30,31,34]). Thus, our assumption on a Gaussian initial distribution defines the structure of the entire process Y_t. The strength of disturbances of W_t is characterized by a matrix of diffusion coefficients b(t).

The vector-function f₁(t) (having the same dimension as a vector Y_t) describes a functional state that organisms subject to allostasis [35] are forced to follow by the process of adaptive regulation at age t. This trajectory reflects aging-related changes in the organism’s functioning due to the average effect of a complicated interplay among the ontogenetic program, senescence, and environmental stresses exceeding limits of the homeostatic regulation in human organisms.

The matrix a(t) characterizes the rate of adaptive regulation. Specifically, the elements of matrix a(t) regulate age trajectories of the components of the physiological state approximated by the vector Y_t, i.e., the elements of matrix a(t) characterize the rate of the adaptive response for any deviation of a physiological index from the state f₁(t) which an organism tends to follow. The important feature of aging – the decline in adaptive capacity – has never been measured directly in longitudinal studies of aging, health and longevity. The use of matrix a(t) in our model allows for evaluating this effect. For example, in a simplified one-dimensional case, in the absence of random disturbances in equation (1) (b(t) = 0, for all t), and constant negative a(t) = a for all t, the parameter a is the coefficient of negative feedback in the equation for Y_t, which keeps the trajectory of Y_t close to f₁(t). When f₁(t) = f₁ is constant for all t, the value of Y_t asymptotically approaches f₁. The higher is the absolute value of a, the closer is Y_t to f₁, and the faster Y_t tends to f₁ in case of disturbances. That is why the value a(t) characterizes adaptive capacity. When the absolute value of coefficient a(t) declines with age, more time is needed for the trajectory of Y_t to approach f₁(t) at old ages compared to younger ages.

The process Y_t can be stopped randomly at time T. The conditional distribution of T given trajectories of Y_u, 0 ≤u≤t is completely characterized by the conditional hazard μ(t, Y_t), which is assumed to be:

$$\mu (t,Y_t)={\mu }_0(t)+{(Y_t-f(t))}^{\ast }Q(t)(Y_t-f(t)).$$ (2)

Here μ₀(t) is the background hazard characterizing the mortality rate which would remain if a vector of covariates Y_t follows the optimal trajectory coinciding with f(t). An asterisk in (2) and in formulas below denotes the transposition of respective vectors or matrices. Matrix Q(t) is a non-negative-definite symmetric matrix of respective dimension (k × k). Note that we assume column vectors throughout the text, thus the transposition of vectors in (2) is needed to produce the respective scalar quadratic term in the hazard rate. The one-dimensional version of (2) is

$$\mu (t,Y_t)={\mu }_0(t)+{\mu }_1(t){(Y_t-f(t))}^2,$$ (3)

where μ₁(t) is some non-negative function of age t.

The vector-function f(t) in (2) (or, correspondingly, the scalar function f(t) in (3)) is introduced to explicitly characterize age-related changes in the “optimal” physiological state corresponding to the minimum of hazard at a given age. It has a meaning of the age-dependent norm for a given functional state. It may differ from f₁(t) since the process of allostatic adaptation does not necessarily results in the optimal physiological state. Thus, the difference between f₁(t) and f(t) provides the measure of the allostatic load.

2.2. Estimation procedure

The model can be estimated using the maximum likelihood method. The survival function associated with the life span distribution is $P(T>t)=exp\left(-{\int }_0^t\overline{\mu }(u)du\right)$, where the marginal (unconditional) hazard $\overline{\mu }(u)$ has the form (see [32,36,37]):

$$\overline{\mu }(u)={\mu }_0(u)+{(m(u)-f(u))}^{\ast }Q(u)(m(u)-f(u))+Tr(Q(u)\gamma (u)).$$ (4)

Here Tr denotes the trace of a matrix and m(u) and γ(u) satisfy the following system of ordinary nonlinear differential equations:

$$\begin{array}{l}dm(t)/dt=a(t)(m(t)-f_1(t))-2\gamma (t)Q(t)(m(t)-f(t)),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}m(0),\\ d\gamma (t)/dt=a(t)\gamma (t)+\gamma (t)a{(t)}^{\ast }+b(t)b{(t)}^{\ast }-2\gamma (t)Q(t)\gamma (t),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\gamma (0).\end{array}$$ (5)

Here m(0) and γ(0) are the mean and the variance/covariance matrix of the normal distribution of initial vector Y₀. Note that in such a model the distribution of Y_t among survivors is also Gaussian at any age t ([30,31,34]). The mean and the variance/covariance matrix of this distribution at age t are given by m(t) and γ(t), respectively.

Let the sequence $y_{t_0^i}^i,y_{t_1^i}^i,\mathrm{...},y_{t_{n_i}^i}^i,{\tau }_i$ represent the results of measurements of the process Y_t and the life span (which may be censored) related to the i^th individual. The likelihood function for N individuals is (see [32,36,37]):

$$\begin{array}{l}{\prod }_{i=1}^N{\prod }_{j=0}^{n_i({\tau }_i)}{(2\pi )}^{-{}^k/_2}\parallel {\gamma }^i(t_j^i-){\parallel }^{-{}^1/_2}exp\left\{-\frac{1}{2}{\left(y_{t_j^i}^i-m^i(t_j^i-)\right)}^{\ast }{\gamma }^i{(t_j^i-)}^{-1}\left(y_{t_j^i}^i-m^i(t_j^i-)\right)\right\}\times \\ {\overline{\mu }}^i{({\tau }_i)}^{{\delta }_i}exp\left\{-{\int }_0^{{\tau }_i}{\overline{\mu }}^i(u)du\right\}.\end{array}$$ (6)

Here δ_i is a censoring indicator, mⁱ (t) and γⁱ (t) satisfy equations (5) at the intervals $\left[t_0^i,t_1^i\right);\left[t_1^i,t_2^i\right);\mathrm{...};\left[t_{n_i-1}^i,t_{n_i}^i\right);\left[t_{n_i}^i,{\tau }_i\right)$ with the initial conditions $y_{t_0^i}^i,y_{t_1^i}^i,\mathrm{...},y_{t_{n_i}^i}^i$, respectively. Here $m^i(t_j^i-)=\underset{t\uparrow t_j^i}{lim}{m}^i(t)$, and ${\gamma }^i(t_j^i-)=\underset{t\uparrow t_j^i}{lim}{\gamma }^i(t)$, and $t_{n_i}^i$ is the age of the latest measurement of a functional state before death/censoring at τ_i. Maximization of this likelihood function generates parameter estimates that characterize the dynamics of stochastic process Y_t describing trajectories of physiological aging. Note that the observed values $y_{t_0^i}^i,y_{t_1^i}^i,\mathrm{...},y_{t_{n_i}^i}^i$ are used as initial conditions for differential equations (5) at the beginning of subsequent intervals between the observation times. Therefore, the individual trajectories of mⁱ (t) and γⁱ (t) differ for different individuals. Consequently, the estimates of the chances of death for individuals having different observed values of the respective covariates also differ.

Note that, as mentioned above, the conditional distribution of Y_t among survivors is Gaussian, whereas most of physiological indices that can be represented by Y_t are positive. Thus, appropriate restrictions on parameters of respective functions defining the dynamics of Y_t are necessary in the estimation procedure. In addition to this, restrictions are necessary for functions in the mortality risk (2). These restrictions should reasonably impose constraints on parameters of: a) an initial distribution Y₀ (to ensure a negligible probability of negative values); b) functions f₁(t) and f(t) (to ensure non-negative values for each age); c) matrix a(t) (to ensure that the feedback coefficient in (1) does not become too small and the trajectories of Y_t tend to f₁(t)); d) the background hazard μ₀(t) (to ensure non-negative values for each age and a non-decreasing age pattern); and e) matrix Q(t) (to ensure that the matrix is non-negative definite for each age).

3. Simulation study

We performed a simulation study to check performance of the model in one-dimensional case. In computer simulations, we used a discrete-time version of the model (1), (3). We assumed that the background mortality in (3) is the Gompertz hazard, ${\mu }_0(t)=a_{{\mu }_0}{e}^{b_{{\mu }_0}(t-t_{min})}$, where t_min = 30. The trajectories f₁(t) and f(t) are approximated by linear functions, f₁(t) = a_f1 + b_f1 (t−t_min), f(t) = a_f + b_f (t−t_min). The functions a(t) and b(t) are assumed constant, a (t) = a_y, b (t) = σ₁. The initial distribution of Y_t0 is normal with the mean f₁ (t₀) and the variance ${\sigma }_0^2$. We considered the case of non-symmetric dependency of mortality on deviations of values of the process Y_t from the trajectory f(t), assuming that ${\mu }_1(t)=\{\begin{array}{c}{\mu }_{11}(t),\hspace{0.17em}\text{if\hspace{0.17em}}{Y}_t\le f(t)\\ {\mu }_{12}(t),\hspace{0.17em}\text{if\hspace{0.17em}}{Y}_t>f(t)\end{array}$, where μ_1j (t) = a_μ1j + b_μ1j (t−t_min) j = 1, 2. Parameters to be estimated in this model are: a_μ0, b_μ0, a_μ11, b_μ11, a_μ12, b_μ12, a_Y, σ₀, σ_1, a_f1, b_f1, a_f, and b_f. The age at entry into the study was simulated as a discrete random variable uniformly distributed over the interval from 30 to 60 years. The interval between observations of Y_t equals 2 years. The number of observations (surveys) is 25. This structure resembles the Framingham Heart Study (FHS) data [38]. The simulated values of parameters were taken similar to those obtained in our preliminary analyses of data on diastolic blood pressure for females in the FHS. We simulated 100 data sets with 2500 individuals in each data set (which is approximately equal to the number of females in the FHS data) and estimated the discrete model for different data sets using the MATLAB’s optimization toolbox [39,40]. Mean values, standard deviations and 95% ranges of the estimated parameters are presented in Table 1.

Table 1.

Means, standard deviations (st. dev.) and 95% lower (LCL) and upper (UCL) limits of parameter estimates in 100 simulated data sets

	aμ0 · 104	bμ0	aμ11· 104	bμ11 · 104	aμ12 · 104	bμ12 · 104	aY	σ0	σ1	af1	bf1	af	bf
Mean	1.052	0.109	0.968	0.012	0.495	0.0012	−0.140	12.980	6.005	85.014	−0.200	77.125	−0.065
St. dev.	0.224	0.004	0.307	0.010	0.094	0.0034	0.002	0.173	0.020	0.246	0.008	1.302	0.044
LCL	0.678	0.103	0.379	−0.006	0.325	−0.0054	−0.143	12.604	5.958	84.577	−0.219	74.603	−0.157
UCL	1.501	0.117	1.569	0.031	0.669	0.0066	−0.136	13.281	6.043	85.558	−0.186	79.489	0.008
True values	1	0.11	1	0.01	0.5	0.001	−0.14	13	6	85	−0.2	77	−0.06

The estimated age trajectories of ln μ₀(t), μ₁₁(t), μ₁₂(t), f₁(t), f(t) and the initial distribution of Y_t0 (p(Y_t0)) for 100 simulated data sets are shown in Fig. 1.

Fig. 1.

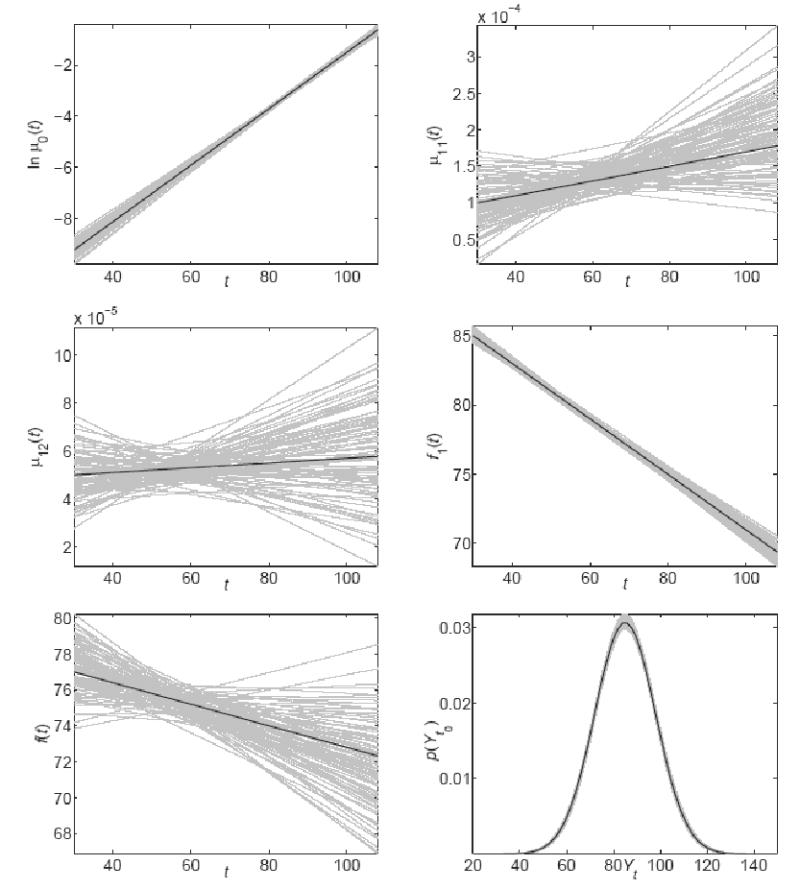
Estimated trajectories (grey lines) of lnμ₀(t) (left top panel), μ₁₁(t) (right top panel), μ₁₂(t) (left middle panel), f₁(t) (right middle panel), f (t) (left bottom panel) and p (Y_t0) (right bottom panel) for 100 simulated data sets. True trajectories are shown as black lines.

The table and the figure show that the parameters related to the dynamics of Y_t(a_Y, σ₀, σ₁, a_f1, b_f1) and the background mortality (aμ₀, bμ₀) are estimated better than those related to the optimal trajectory f(t) (a_f ,b_f). For example, the standard deviations of a_f and b_f are about five times larger than those of a_f1 and b_f1. As the result, the trajectory of f1(t) is estimated better than that of f(t). Nevertheless, the means of all parameters are close to the true values. Fig. 2 illustrates the estimated (mean for 100 data sets) and true mortality (μ(t, Y_t)) and relative risk (RR(t, Y_t)) over age (t) and values of Y_t.

Fig. 2.

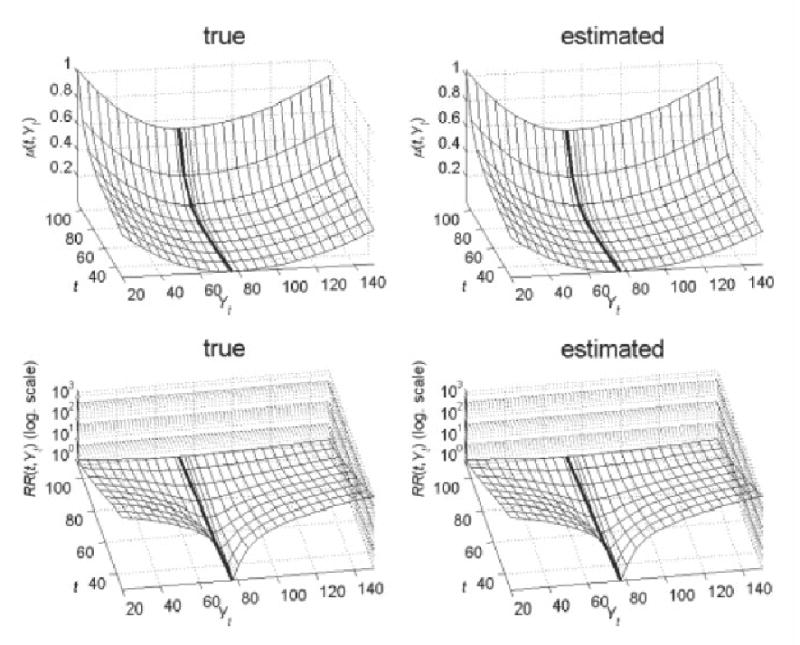
Estimated (mean for 100 data sets) and true mortality (μ(t, Y_t)) and relative risk (RR(t, Y_t)). Thick lines denote the “optimal” age trajectory of a physiological index (f(t)).

The figure shows that both estimated and true parameters specify two key features of dependence of mortality and relative risk on age and values of Y_t: the narrowing of U-shape of mortality and the decrease in the relative risk with age.

4. Discussion

Many researchers involved in population studies of aging and longevity continue considering mortality curves, as an important source of information about the rate of individual aging. In particular, the slope of the logarithm of the mortality curve is often associated with the aging rate at the adult and old ages. Such interpretations may be misleading: the changes in the slope and in many other features of mortality curve may occur because of many other reasons, which have nothing to do with the aging process [41]. Data on many such factors dynamically affecting chances of survival are collected in longitudinal data. Moreover, these data contain information about various aspects of senescence process and can be used for evaluating respective effects. That is why in situations characterized by the wide spectrum of longitudinal data and findings on aging, making speculations about the meaning of different properties of the mortality curve and ignoring the presence of other relevant information about aging-related changes affecting survival chances would be methodologically incorrect.

The urgent need for modifying a traditional experimental paradigm that associates the features of individual aging with properties of the age pattern of the mortality curve without developing an appropriate biological background has been also emphasized by Manton and Yashin [33]. The urgency stems from the lack of balance between data and theory currently existing in the area of research on aging: the abundance of the data and findings about aging and the development of aging-related disorders in humans and laboratory animals on the one hand and the weakness of methodological and theoretical concepts guiding the collection and analysis of data on the other hand. It became clear that working with data collected in human longitudinal studies of aging and longevity requires new models capable of not only describing mortality linked with longitudinally measured physiological or health indices. These models must have the ability to describe connections and evaluate joint effects of senescence, ontogenetic program, and environmental stresses in aging-related changes in health/well-being/survival characteristics measured in longitudinal studies.

An important attempt to connect the Gompertz model of mortality rate with the model describing longitudinal data has been performed using the quadratic hazard model of human mortality and aging (see [33] and references therein). The conditional mortality rate in this model is represented in the form

$$\mu (t,Y_t)={\stackrel{\sim }{Y}}_t^{\ast }\stackrel{\sim }{Q}{\stackrel{\sim }{Y}}_t{e}^{\theta t},$$ (7)

where ${\stackrel{\sim }{Y}}_t^{\ast }=(1,Y_t^{\ast })$ is an extended vector of covariates Y_t, t is age, $\stackrel{\sim }{Q}$ is an extended (constant) matrix, and θ is the Gompertz’s parameter [33].

In applications of this model to longitudinal data, the estimated value of the parameter θ has always been smaller than the respective parameter in the Gompertz’s model describing the total mortality rate evaluated for the same data. The reduction of the Gompertz’s growth parameter estimated in the presence of observed covariates has been interpreted as an effect of measurements: the new (reduced) value of parameter θ characterized the component of aging-related increase in the mortality rate remaining unexplained in this scheme of observations (i.e., which occurred due to unobserved processes). The difference between the old and the new estimates of θ characterized explanatory power of the observed covariates. To make this point clearer, we provide an equivalent formulation of the original one-dimensional quadratic hazard model:

$$\mu (t,Y_t)=({\mu }_0+{\mu }_1{(Y_t-c)}^2)e^{\theta t}={\mu }_0{e}^{\theta t}+{\mu }_1{e}^{\theta t}{(Y_t-c)}^2,$$ (8)

where μ₀, μ₁, and c are constants. The first term has been interpreted as a part of the Gompertz’s mortality remained after effects of observed covariates have been taken into account (the second term). Equation (8) clearly shows implicit assumptions used in the formulation of the original quadratic hazard model – a competing risks model of the hazard rate with two mortality components. Specifically, the first component is an exponentially increasing function of age. The second risk is a product of an exponentially increasing function of age and a quadratic function of observed covariates. The important limitation of this model is that the exponential multipliers in both components of risk function are the same. The second limitation is that the minimum of the second (quadratic hazard) term is reached at the constant level of observed covariates.

The model proposed in this paper is free of these two basic limitations. This can be seen in its one-dimensional formulation where the quadratic hazard is given by (3). First, our model assumes that the minimum value of the risk function can change over age. This is a realistic assumption since in epidemiologic and medical practice specialists often operate with the notion of age-dependent “norm”, i.e., values of the physiological indices that are “optimal” for a given age. The “optimal” age trajectory of physiological (or, more broadly, functional) state, f(t) (i.e., the trajectory for which the risk of death takes its minimum value), is explicitly included in the model description (compare equations (3) and (8)). Importance of this extension is that it allows one to statistically test hypotheses on an optimal physiological trajectory and, thus, rigorously justify respective age-dependent physiological “norms” of physiological state corresponding to the minimum of the hazard. The model also allows for evaluating the “price” for deviations from this norm in terms of mortality increase at different ages.

Second, our model distinguishes between the contribution of an additive term μ₀ (t) and the multiplier of the quadratic hazard μ₁ (t). Assuming differences between these functions allows for a completely new interpretation of these coefficients, which clarify the contribution of measured indices to mortality and evaluate the effects of senescence on behavior of risk functions. The function μ₀(t) can be considered as a component of competing risks associated with death from factors other than those involved in the quadratic term (i.e., unmeasured factors). The risk μ₀(t) is supposed to be smaller than the total mortality calculated when observed covariates are ignored. Therefore, μ₀(t) characterizes mortality remaining after all observed covariates follow the “optimal” trajectory and its interpretation remains similar to that used in the original model. Thus, this model allows us to evaluate a potential decline in the mortality rate (or an increase in the life expectancy) which would happen when the risk associated with all observed covariates is eradicated.

The term μ₁(t) captures changes in the mortality risk associated with deviations of the observed index Y_t from its normal age trajectory. It shows how the shape of the risk function changes with age. Since the quadratic hazard captures the U- (or J-) shape of the mortality risk considered as a function of risk factors, the increasing pattern of μ₁(t) indicates how the branches of respective U-shaped risk function are getting steeper with age. This means that the range of tolerant deviations of the resultant risk factor from its “optimal” value is getting narrower with age, which, in turn, is an indicator of decline in stress resistance with age.

Evaluating such behavior of risk functions in human data is extremely important to capture the connections between senescence, longevity, and stress-resistance. Although many aspects of such connections have been investigated in experimental animal studies [9], they were not adequately addressed for humans. Thus, the rate of increase in μ₁(t) (not the slope of the logarithm of the mortality curve) may characterize the rate of senescence. Thus, the important methodological finding is that the model is transformed to the form where effects of senescence on survival, longevity and disease development may be evaluated from longitudinal data.

The modified model includes the earlier version (8) as a particular case. The similarity between μ₀(t) and μ₁(t) can be easily tested using the likelihood ratio test. Changes in μ₁(t) with age indicate age-related narrowing of the U-shape of mortality risks (considered as function of Y_t), which is interpreted as a decline in stress resistance with age. One should expect that a similar decline in resistance to stresses represented by deviations of other (unobserved) risk factors from their norms also takes place, and contributes to an increase in the baseline hazard μ₀(t) Thus, both functions μ₁(t) and μ₀(t) reflect effects of senescence process but capture its different aspects.

Incorporating functions f₁(t), f(t) and matrix a(t) into the extended model allows one to test various hypotheses about dynamics of aging-related changes in a human organism. For example, one can test whether the age trajectory of physiological state, which an organism is forced to follow by the process of allostasis, f₁(t), coincides with the “optimal” trajectory corresponding to the minimal mortality at respective ages, f(t). The rejection of respective null-hypothesis would indicate that the processes of compensatory adaptation and remodeling do not tend to minimize the mortality risk. A testable hypothesis is also the one that the observed mean age-trajectories of the covariates in a population coincide with the age-dependent norm f(t). Estimating the model with fixed and non-fixed a(t), one can test the hypothesis about aging-related changes in the “adaptive capacity” of a human organism, i.e., how the rate of the adaptive response for any deviation of physiological indices from the “prescribed” state f₁(t) changes with age. Specifications of different forms of the matrix Q(t) allow for an analysis of relationships between covariates and evaluation of their joint effects on the mortality risk.

Contrary to the traditional association of the aging rate with the slope of the logarithm of the mortality curve, it seems more appropriate to relate the rate of decline in stress resistance (associated with the function μ₁(t) with this process. This function, however, characterizes the aspects of senescence associated with a selected risk factor. More generally, the increasing role of senescence in the mortality risk could be captured by the widening pattern of the U-shape of the relative risk, which would indicate a faster increase in μ₀(t) compared to μ₁(t). Our analysis shows that both characteristics can be evaluated from the longitudinal data. The performed analysis shows that the proposed model can be effectively used for evaluating features of the aging-related changes from data collected in longitudinal studies.

It is important to note that functions f(t) and f₁(t) introduced in the model are rough approximations of the reality. The physiological “norm” f(t), or the “optimal” age trajectory of physiological indices corresponds to the minimal value of the mortality risk at respective ages. The model assumes that all individuals have the same “optimal” age trajectory of physiological indices that depend solely on age. In some situations, this assumption looks oversimplified. For example, it is quite likely that the notion of “norm” may differ for individuals carrying different alleles or genotypes, or having different histories of life events (e.g., diseases, environmental exposures), etc. The lack of appropriate individual data is the only reason for considering f(t) as a “common” function for all individuals.

Similar considerations also take place for the function f₁(t) defined as the age trajectory of physiological state which an organism is forced to follow by the process of allostasis. This function is also likely to be more personalized and depend on various genetic and non-genetic factors. However, empirical evaluation of such trajectories is limited by the absence of respective data.

These observations indicate the need for developing a more general methodology, which could incorporate individualized notions of “norms” and the adaptive response. For example, the trajectories of f(t) and f₁(t) can be modeled as stochastic processes. Elaboration of respective models, specification of required data, and development of appropriate estimation procedures are beyond the scope of this paper.

The properties of the process Y_t depend on the assumption about the initial value Y₀. The model preserves the Gaussian property: in the case of initial Gaussian distribution for Y₀, the distribution of Y_t among survivors is also Gaussian. Note that such a distribution allows for negative values of respective variables with a positive probability, which is not appropriate for most physiological indices. In modeling practice, however, this property of Gaussian models does not limit the analyses. One can always consider a Gaussian approximation as a first description of the observed dynamic phenomenon. The advantage of such a model, however, is that it describes the probability distribution in terms of the first two moments, and, in this sense, it may serve as a two-moment approximation for many other distributions resulted from a non-Gaussian initial value or nonlinear effects in the physiological response.