Resource competition as a mechanism for B cell homeostasis

Abstract

Cellular competition for survival signals offers a cogent and appealing mechanism for the maintenance of cellular homeostasis [Raff, M. C. (1992) Nature (London) 356, 397–400]. We present a theoretical and experimental investigation of the role of competition for resources in the regulation of peripheral B cell numbers. We use formal ecological competition theory, mathematical models of interspecific competition, and competitive repopulation experiments to show that B cells must compete to persist in the periphery and that antigen forms a part of the resources over which B cells compete.

“The most basic qualities of a natural community are the kinds and numbers of species living in them.” This quotation from a classic ecological monograph (1) could equally well apply to immunology, where the communities in question are populations of lymphocytes present within individual organisms. Motivated by this similarity in basic questions we have used ecological competition theory in studies of B cell homeostasis and diversity. A combination of laboratory and mathematical models lead us to propose that the size of the peripheral B lymphocyte pool results from a process of immigration from the bone marrow, competition for resources in the periphery (2), and rapid death of cells that fail to secure resources. Our models allow us to quantify the contribution of each of these three processes to the final size of the peripheral B cell pool.

Immunologists often use the word competition and most would probably agree that they define competition as “an interaction between two populations, in which, for each, the birth rates are depressed or the death rates increased by the presence of the other population” (3). However, this type of interaction can arise through a number of different processes. In resource competition (1) the negative effects come about because the two populations both have a need for the same substrate that is in limited supply. In apparent competition (4) the two populations affect each others’ growth via a shared predator rather than a shared resource. Other schemes have been proposed where populations affect each other directly or indirectly via populations on the same trophic level (5). It is useful to be precise about which type of process is envisaged when competition is invoked. Because such a formalism already exists in the ecological literature, it makes sense to adapt it to the special situation of cells competing within an organism. To go further and ask “does the formalism fit the data?” it becomes necessary to express the formal model in mathematical equations and see if those equations behave like the populations that we observe. This is the strategy we have adopted in the work presented here. We have developed formal schemes for competition among B lymphocytes that give rise to two models; one of competition in its broadest sense and one that is specifically a model of resource competition. We show detailed comparisons of our first model with our data on B lymphocyte population dynamics. Our second model is a useful guide to the things we wished we knew about resources for B cells. The first model is summarized in Fig. 1 and its assumptions and equations are detailed below.

Figure 1.

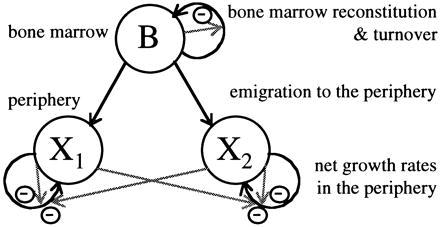
Mathematical model of competition among peripheral lymphocytes. The model includes the processes of bone marrow regrowth and turnover, emigration from the bone marrow to the periphery, and cell division and death in the periphery. Growth rates of bone marrow precursors decrease as a function of their number. Peripheral net growth rates (i.e. the difference between division and death rates) for each population X₁ and X₂ are down-regulated by the presence of their own numbers and the number of cells in the competing population. The model is, in fact, the Lotka–Volterra competition model with the addition of immigration.

There are established criteria accepted as evidence that resource competition shapes a community (6). The presence of competitors should alter the equilibrium size of a population and also the dynamics of the approach to that equilibrium. One would expect changes in morphology in response to the presence of competitors, allowing exploitation of a different niche, a process known as character displacement (7, 8). Finally the ability to shape the composition of populations by manipulating resources is an important test that the populations are engaged in competition to exploit shared resources.

METHODS

Competitive Repopulation.

Lethally irradiated (850–900 rads) host mice (8 week, female, C57BL/6, Iffa Credo, France) received i.v. a total of 4 × 10⁶ bone marrow cells from donor mice mixed at different ratios. The donor mice for the precursor populations in the graft were as follows: diverse 1, normal C57BL/6 IgH^b; diverse 2, the IgH congenic B6.IgH^a/BC-8; transgenic 1, the C57BL/6 transgenic line B6-SP6 carrying a transgene coding both μ^a heavy and light chains of a complete BALB/c antibody to 2,4,6-trinitrophenyl (TNP) (9); transgenic 2, the C57BL/6 line MD4 expressing a transgene coding for the μ^a+δ^a heavy and light chains of an antibody to hen eggwhite lysozyme (HEL) (10). All lines of transgenic mice were kept at the specific pathogen free barrier facilities of the Centre de Developpement des Techniques Avancées, Centre National de la Recherche Scientifique, Orleans, France. In all experiments mice were matched for age and sex. At different times postreconstitution (8 weeks for equilibrium) mice were sacrificed, spleens recovered, total nucleated cells counted, and their composition analyzed by flow cytometry (11).

Affinity Chromatography.

A column of CNBr-activated Sepharose (Pharmacia) to which was coupled an excess of RS3.1 anti-μ^a was equilibrated in a buffer (0.1 M Tris/0.5 M NaCl, pH 7.2). One hundred microliters of serum was mixed with 3 ml of Sepharose in 2 ml of the buffer turned end over end for 3 hr at 4°C in a 15-ml Corning Falcon tube, and then eluted in 45 ml of buffer. The eluate was concentrated and then tested for the presence of μ^a and μ^b by ELISA. After two passes through the column all samples were μ^a free.

Resource Manipulation.

Host mice were sublethally irradiated (750 rads) and then received 5 × 10⁶ splenocytes. The injected splenocytes were a mixture of freshly harvested cells from transgenic donors of the SP6 or MD4 line in the ratio 50:50 or 10:90. The mice received antigen from an Alzet osmotic pump (model 1007D, Alza) implanted in the dorso that delivered 42 μg of antigen (TNP-Ficoll) continuously over 7 days. On day 7 mice were sacrificed and spleens analyzed using flow cytometry to assess the proportion of cells of donor origin (μ^a allotype) derived from the SP6 donor cells (20.5 idiotype).

Experiments Establishing Competition Between B Lymphocytes

To explore B cell homeostasis we performed a series of experiments in which traceable populations of B lymphocyte precursors were introduced into mice whose own immune cells had been destroyed by irradiation. We had at our disposal two different populations with normal antibody diversity and two populations with reduced antibody diversity (from transgenic mice). When put into a mouse on their own each of these populations of B lymphocytes expands to form a population of comparable size. We created chimeric mice by injecting with seeding populations of bone marrow cells that were always of the same size (4 × 10⁶ bone marrow cells), but of differing composition (11).

Competition Affects Equilibrium Population Size.

Two months after the bone marrow transplant we counted cells in the spleen to assess the equilibrium size of the two different populations. In broad summary (Fig. 2) we found that a diverse population would outcompete a transgenic population, although not to exclusion (Fig. 2 A and B). Furthermore when comparable populations were pitched against each other (i.e. diverse vs. diverse or transgenic vs. transgenic) the resulting equilibrium population composition reflected the composition of the seeding cells (Fig. 2 C and D). Thus we showed that the equilibrium size of a population of B lymphocytes depended on the number and diversity of other B lymphocytes present. We compared these experimental results with the behavior of the model described in Fig. 1. For the equilibrium situation we were able to estimate independently all but one of this model’s parameters (Table 1). Thus in Fig. 2 A and B only one parameter is estimated from the data shown. In Fig. 2 C and D no parameters were estimated from the data shown. Without having to adjust more than one parameter the model fits well with the observed data. The model and its parameter values are discussed below.

Figure 2.

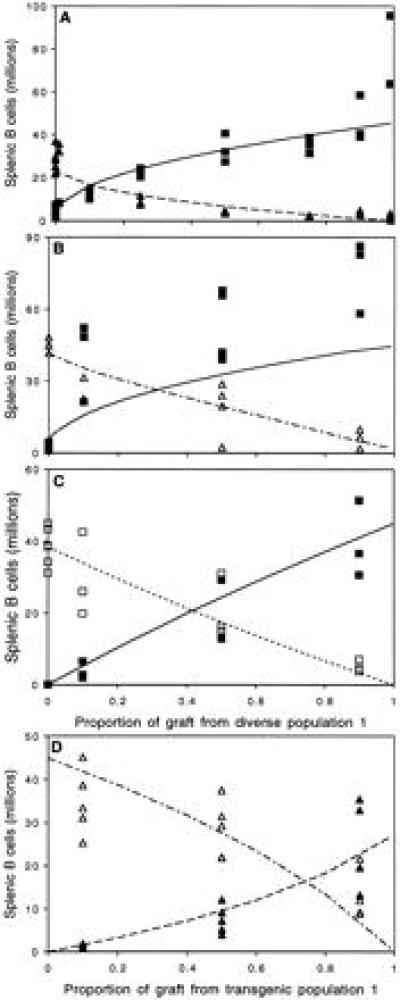
Equilibrium population sizes in mice with chimeric bone marrow. Graphs compare observed (symbols) and predicted (lines) population sizes at equilibrium for four pairs of populations matched against each other. (A) Diverse 1 (▪) versus transgenic 1 (▴). (B) Diverse 1 (▪) versus transgenic 2 (▵). (C) Diverse 1 (▪) versus diverse 2 (□). (D) Transgenic 1 (▴) versus transgenic 2 (▵). Predictions were made using the model in Fig. 1 (Eqs. 1–3). Parameters used in the predictions are listed in Table 1, parameter a₂₁ was estimated using a least-squares minimalization.

Table 1.

Parameters, data sources, and numerical values for the Lotka–Volterra competition equations with immigration

Parameter	Data source	Value
n	Known from the proportion of cells of type 1 in inoculum	0–1
a12, a21 like with like	Assumption	1
a12 transgenic on diverse	Data B6:μKO bone marrow chimeras (F.A. and A.A.F., unpublished data)	0
K	From data on mice without immigration from the bone marrow with a periphery reconstituted with normal peripheral cells (F.A. and A.A.F., unpublished data)	5 × 106 cells
ri for B6a	45.6 × 106 B cells in the spleen of a B6 mouse	0.028 cell−1·d−1
ri for B6b	38.5 × 106 B cells in the spleen of a B6b mouse	0.04 cell−1·d−1
ri for SP6	27.3 × 106 B cells in the spleen of an SP6 mouse	0.085 cell−1·d−1
ri for MD4	44.9 × 106 B cells in the spleen of an MD4 mouse	0.029 cell−1·d−1
a21 diverse on transgenic	Estimated from Fig. 2A and B	1
rB	Fig. 3A	0.8 cell-1·d−1
KB	Fig. 3A	2.6 × 106 cells
f	Estimated from Fig. 3	4

The parameters are arranged in the order in which we estimated their numerical values. Those whose values we could estimate from data sources external to the data presented here come first (rows 1 to 8). Thus the fit of the model to the data in Fig. 2 was achieved estimating only one additional parameter (a₂₁). Likewise, fitting the model to Fig. 3 B and C required the estimation of only one additional parameter (f). 

Competition Affects the Dynamics of Reconstitution.

We went on to study the dynamics of the approach to this equilibrium. Kinetic experiments showed that all populations had similar initial growth rates (Fig. 3 B and C), but as population sizes reached saturation levels, the growth rate of a transgenic B lymphocyte population depended on whether it was pitched against another transgenic population or a diverse population (compare solid triangles in Fig. 3B with those in Fig. 3C). A test of homogeneity of slopes comparing logged data from day 14 and after shows a significant difference (P < 0.001) in the growth rate of SP6 cells when competing against MD4 or B6 cells. Thus we established that the dynamics of the approach to equilibrium are affected by the presence and diversity of other lymphocyte populations. We once more compared our mathematical model’s predicted behavior with our data. Again only one additional parameter value was estimated, that which determines the rate at which cells migrate to the spleen from the bone marrow (f). Fig. 3C also shows prediction of a modified model, the better fit was achieved by estimating a further two parameter values. The dynamic version of the model is in good agreement with the data; details are discussed below.

Figure 3.

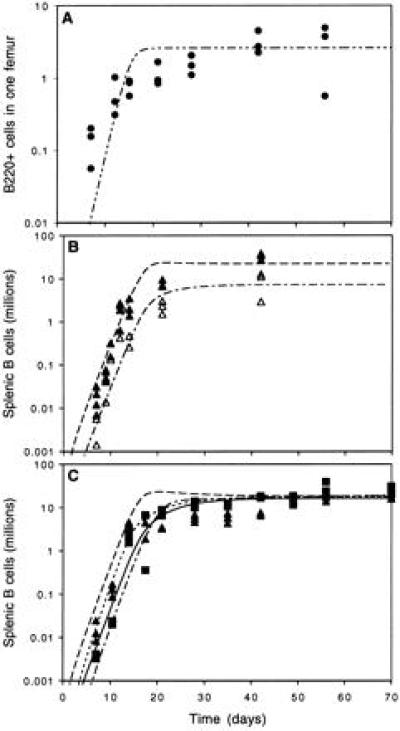
Observed and predicted dynamics of the repopulation of bone marrow B220+ and splenic B lymphocytes. (A) B220+ B cells (•) in the bone marrow modeled with a logistic growth function. (B) Peripheral competition between two transgenic populations, the influx from the bone marrow is 90% SP6 (▴) and 10% MD4 (▵) cells. (C) Peripheral competition between a transgenic population and a normal population, the influx from the bone marrow is 90% SP6 (▴) and 10% normal (▪). Predictions from the simple model of Fig. 1 using the parameter values of Table 1 are also shown (dashed lines predicted SP6, dash-dot line MD4, solid line normal). All parameter values are as in Table 1. A second model was investigated to see if an improved fit could be achieved in C. This model gives identical predictions for A and B. Two modifications were made to the model in Fig. 1. Instead of both populations sharing a single peripheral carrying capacity K each was allowed its own and the peripheral growth rate r was modified so that r_i′ = max{r_max (1 − (X_i + a_ijX_j)/K, r_i (1 − (X_i + a_ijX_j)/K)}, relaxing the strong assumption that the peripheral growth rate is a linear function of population size and allowing a better fit of the model to the transgenic data. In C the dashed line is the prediction for SP6 cells and the dash-dot line is the prediction for normal cells, these were drawn with f = 0.5, K₁ = 5, K₂ = 15, r₁ = 0.011, r₂ = 0.014, and r_max = 0.6.

Character Displacement.

Using a method for the quantitative analysis of Western blots (12) we studied changes in the binding patterns of a diverse population of B lymphocytes in the presence or absence of a transgenic population. The sites that we use to distinguish between normal and transgenic lymphocytes are also present on the immunoglobulin molecules that they shed into the circulation. We therefore were able to separate plasma IgM into that derived from normal B6 cells (bearing the μ^b allotype) or that derived from cells of transgenic origin (bearing the μ^a allotype). We exploited this ability to trace the provenance of secreted IgM in an experiment designed to test the prediction that competition should lead to character displacement. As shown in Fig. 4 we observed a shift in the binding reactivities of immunoglobulins shed by B cells that were in a competitive environment.

Figure 4.

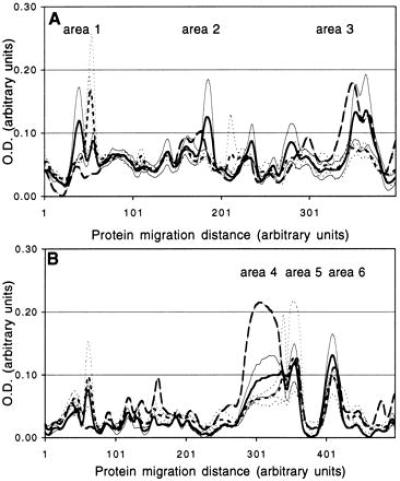
Character displacement in immunoglobulin reactivities. We used binding patterns in a quantitative Western blot (11) as a representative character for the populations of B lymphocytes we studied. We used affinity chromatography to purify immunoglobulins secreted by normal cells that had been in competition with transgenic cells for 2 months (dotted lines, average in bold). As a control, serum from normal B6 mice was subjected to the same procedures (solid lines average in bold). Purified supernatant from an SP6 hybridoma was used to reveal the proteins that SP6 cells bind well leading to intense competition (dashed line). Serum reactivities to two tissues were obtained; murine muscle (A) and murine liver (B). A threshold to define a peak was set at O.D. = 0.1. Theory predicts that solid lines and dotted lines will coexist in areas where no dashed peak is present (as in area 1) but will not if a dashed peak is present (as in areas 2, 3, 4, and 6 but not area 5). (P = 0.11).

Population Manipulation by Resource Manipulation.

Although the observations made above confirm that B lymphocytes compete to persist in the periphery they tell us nothing about what type of competition is involved. Thus, although the competitive superiority of the population with the more diverse antibody repertoire is indicative of a competition for antigen, we cannot (from the above data) rule out the possibility that all of the patterns that we observe are the result of regulation by other, unidentified cell populations (apparent competition). To test whether there is any element of resource competition in the competition we observe among peripheral B cells it is necessary to show that population composition can be manipulated by manipulating resource levels. The B lymphocytes from these transgenic mice are specific for known antigens. Cells from SP6 donors bind TNP and can respond to TNP-Ficoll in a manner that is independent of help from T cells (9, 13). We created MD4-SP6 splenocyte chimeras in which antigen levels were manipulated by continuous infusion of TNP-Ficoll from osmotic pumps. We found (Table 2) that splenocytes from SP6 donors were present in greater numbers when the host animal had received TNP-Ficoll, the specific antigen that these cells recognize, thus showing that population composition can be manipulated by manipulating resources (14).

Table 2.

Population composition can be shaped by manipulating resources

Ratio of splenocytes in the inoculum, SP6:MD4	Fraction of retrieved μa-ve cells of SP6 origin
	Without TNP-Ficoll	With TNP-Ficoll
50:50	0.3	0.5
	0.2	0.5
	0.3	0.6
10:90	0.05	0.1
	0.01	0.1
	0.02	0.4

As predicted, in the presence of their specific antigen the SP6-derived cells constituted a larger proportion of the cells of donor origin. 

Models of Resource Competition with Immigration

Need for New Theoretical Models.

There is an extensive body of theoretical work on competition between species (1–6, 15). However existing models assume that competition takes place in closed arenas, without any immigration of competitors. [Models of island biogeography (16) explicitly account for the immigration of new species, but then count the number of new species present, as opposed to the number of individuals of each species. Metapopulation models (17) allow migration between patches, but all recruitment is internal.] This is not an appropriate assumption for our experimental systems because there is a continuous flux of new B cells entering the competitive arena of the periphery. We modified existing ecological competition models to reflect this influx.

Lotka–Volterra Competition Equations with Immigration.

In our simplest model we simply added an immigration term to the Lotka Volterra competition equation (3). For modeling kinetic data we had to account for the dynamics of bone marrow repopulations. We therefore made a model for bone marrow B cell precursors and peripheral B cells.

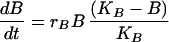1

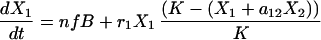2

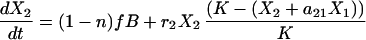3

The first equation describes the growth of B cell precursors in the bone marrow with a logistic equation. We model all bone marrow precursor cells as one group, reflecting our assumption that with respect to the export of cells to the periphery all four cell types have the same reconstitution kinetics. The second and third equations model the two peripheral B cell populations. The first term describes immigration of newly formed B cells from the bone marrow into the periphery. n is the proportion of bone marrow donor cells coming from a type 1 donor. As in Eq. 1 B is the number of bone marrow B cell precursors and f is just a constant fraction representing the relationship between the number of precursors in the bone marrow and the number of new cells arriving in the spleen. Thus immigration into the spleen is constrained by the number of B cells being produced in the bone marrow, a number that is very low during the first few weeks of reconstitution. The second terms of these equations are then simply the Lotka–Volterra competition equations. The terms r₁ and r₂ represent the peripheral net growth characteristics of each population (i.e. division rate—death rate), characteristics that always will be present even when no competing populations are present. The terms a₁₂ and a₂₁ are the Lotka–Volterra competition coefficients. They represent the per-cell competitive impact of each cell type on the other (3).

Parameter Estimation and Lotka–Volterra Competition Coefficients.

Table 1 gives estimates for numerical values used in Figs. 2 and 3. Four points are of particular interest. First is the Lotka–Volterra competition coefficient describing the effect of normal cells upon the growth of transgenic cells. According to the estimated value of this coefficient a normal cell has the same impact as a transgenic cells upon the peripheral growth rate of transgenic cells. This is despite the fact that the population of transgenic cells is several orders of magnitude less diverse than the population of normal cells. This estimate is robust, being sensitive only to the equilibrium numbers of normal and transgenic B cells in the spleens of intact mice, and to the peripheral carrying capacity K. Estimates for the maximum growth rate for each population imply that transgenic populations will expand more rapidly in the periphery than normal populations. This prediction arises because of the very strong assumption that this model inherits from the logistic growth model: that the peripheral growth rate r_i is a linear function of population size. We estimate rs from data on equilibrium population sizes, i.e. when the peripheral net growth rate is at its minimum and is negative. Because K is fixed for all populations, the population with the smallest equilibrium size (and hence the largest population clearance rate at equilibrium) will have the largest maximal growth rate. In Fig. 3C these two assumptions (r linear in population size and K equal for all population sizes) are dropped, achieving a much better fit between model and data. This better fit can be translated into two easily tested predictions: in the absence of influx from the bone marrow peripheral transgenic and normal cell populations will have the same initial growth rates, but they will stabilize at different population sizes. The small size of the peripheral carrying capacity K is somewhat surprising, but is in agreement with the well known finding that B cells cannot form a large self-renewing population. Taken together these parameter estimates imply that out of a steady-state population of around 50 million splenic B cells, 5 million (K) are in a resource-supported pool whereas the other 45 million cells are part of an immigration-death process in which competition modulates death rates.

Tilman Models for Resource Competition with Immigration.

The Lotka–Volterra equations are completely general in terms of the kind of competition they represent, simply describing a pair of populations that have a negative effect on each other’s growth rates. We developed a model that explicitly reflects the process of competition as being one in which cell populations must compete for resources. This model includes peripheral resources (R), produced at rate aS and decaying at rate a, their impact upon the growth of peripheral cell populations (r_iR/(R + k_i)) and their consumption by peripheral B cells (g).

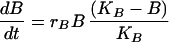4

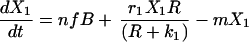5

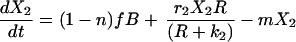6

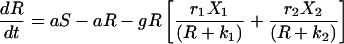7

This model is Tilman’s model for resource competition (1) with an additional term representing immigration of competitors into the periphery. As before, the population can be divided into that generated by the immigration death process and that supported by peripheral resources. Numerical solution of the model with reasonable parameter values generates curves consistent with the data (Fig. 5). However the main interest in this model lies in what it suggests we might wish we knew about resources for peripheral B cells.

Figure 5.

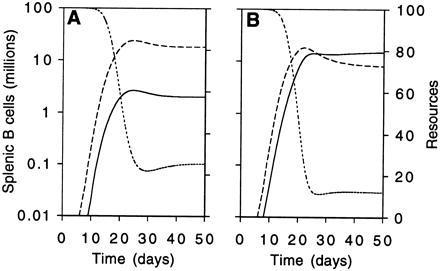
Modeling resources explicitly. The adapted Tilman model also can show behavior akin to that observed. (A) Two weak competitors pitted against each other, as in Fig. 3B. (B) A weak competitor pitted against a strong competitor with the weaker population making up 90% of immigrants. As we observed (Fig. 3C), the weaker competitor initially predominates, but as resources become in short supply, the superior competitive ability of the population making up 10% of immigrants is manifested in its predominance. The model is the second set of equations in the text, X₁ represented by the solid line X₂ by the dashed line and resources, R, by the dotted and dashed line. Parameter values are: r_B = 0.8, K_B = 2.6, f = 0.5, n = 0.1, r₁ = r₂ = 0.85, k₂ = 90, m = 0.25, a = 0.1, S = 100, g = 2; in A k₁ = 90 and in B k₁ = 30.

Of course, we would like a list enumerating the limiting substrates that allow B cells to mature and persist in the periphery. Furthermore, for each one we would want information on how different amounts affect population growth rates. In this version of the Tilman model populations grow in response to resources following a Monod (saturating) growth function that plateaus to a maximum for large amounts of resource. For antigen there is evidence to suggest that too much antigen is detrimental to the survival of peripheral B cells (18, 19) so that the curve describing the peripheral net growth rate in response to resources may fall off from its peak value as antigen concentrations exceed their optimum level. We also would like to know about the production and decay characteristics of each resource (a and S) and finally about the consumption of resources by B cells (g). A daunting list, it is nevertheless helpful in shaping strategic thinking toward a truly quantitative understanding of the role of resource competition in the generation of peripheral B cell pools (1).

DISCUSSION

We set out to examine whether competition for resources is a major force in determining the size and composition of the peripheral B cell pool. We did this with a series of four experiments that established that: the equilibrium size of peripheral populations is shaped by the number and nature of other populations present; the dynamics of the approaches to those equilibria are also dependent upon the other cell populations present; IgM secreted into the serum by normal cells exhibits different binding patterns according to the presence or absence of a population of transgenic cells; and, finally, we can change the composition of a peripheral B cell population by adding resources (in this case antigen), which boost the growth of only one of the two peripheral populations monitored. Furthermore we showed that the equilibrium sizes of two competing B cell populations are well described by a simple mathematical model of peripheral competition. We were able to independently estimate all but one of this model’s parameters and then show that the model’s predictions were in very close agreement with observations. To fit the dynamic data well we needed to invoke a nonlinear relationship between growth rate and population size at the periphery and also to allow a different peripheral-carrying capacity K for transgenic compared with normal cells: two easily testable predictions. It should be noted that the evolutionary forces that shape competition between cells within an individual host are quite different from those that lead to competition between different organisms.

Two important biological insights emerged from the exercise of fitting the model to the data. The first is that although transgenic cells represent a population with a vastly lower diversity than normal cells and are outcompeted in the periphery by normal cells, they put up a good fight. On average one normal cell down-modulates the growth of the transgenic population as much as one transgenic cells. The second important inference we make from these data is that the peripheral-carrying capacity for B cells (parameter K) is small, representing about 10% of cells in the spleen, the other 90% of cells being part of a simple process of immigration from the bone marrow followed by death or division and subsequent entry into the resource-supported pool.

How do these findings compare with previous work on competition among lymphocytes (20, 21)? Lymphocyte competition has been invoked as an explanation for thymic selection (22–24), graft tolerance (25, 26), and self–nonself discrimination (21, 27, 28). Our emphasis is different, we have chosen to concentrate upon the determinants of the number of cells found in the periphery; a better understanding of the processes underlying homeostasis should inform our understanding of its consequences for other immunological phenomena (20). Models of B cell population dynamics have mostly concentrated on individual clones (29) or sets of clones (30). Again a better understanding of the control of total cell numbers should inform our understanding of the determinants of clone size (31).

Finally, what of the division of the peripheral B cells into different life-history stages (20, 32, 33)? If one invokes competition as a major force in regulating cell numbers the division of the peripheral population into the immigration death pool and the resource-supported pool is very natural. But how does it fit with pre-existing dichotomies? The division of peripheral B cells into two pools, one rapidly renewed, the other more persistent is of very long standing (33–35), and the idea that those B cells that do divide in the periphery persist for longer is also well established (36). What is less clear is what correlations there are between membership of the resource-supported pool, activation, and differentiation into Ig-secreting cells. The resource-supported pool is by definition those cells that are present in the periphery in the absence of input from the bone marrow. The study of peripheral cells, transferred into mice incapable of exporting cells from the bone marrow, should therefore clarify this issue.

ABBREVIATION

TNP

2,4,6-trinitrophenyl