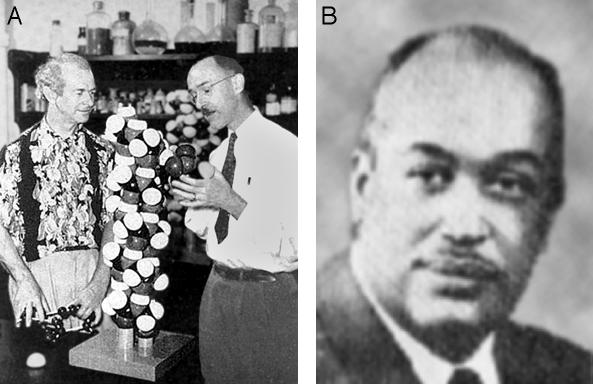The discovery of the α-helix and β-sheet, the principal structural features of proteins

Abstract

PNAS papers by Linus Pauling, Robert Corey, and Herman Branson in the spring of 1951 proposed the α-helix and the β-sheet, now known to form the backbones of tens of thousands of proteins. They deduced these fundamental building blocks from properties of small molecules, known both from crystal structures and from Pauling's resonance theory of chemical bonding that predicted planar peptide groups. Earlier attempts by others to build models for protein helices had failed both by including nonplanar peptides and by insisting on helices with an integral number of units per turn. In major respects, the Pauling–Corey–Branson models were astoundingly correct, including bond lengths that were not surpassed in accuracy for >40 years. However, they did not consider the hand of the helix or the possibility of bent sheets. They also proposed structures and functions that have not been found, including the γ-helix.

Adecade before the structures of entire proteins were first revealed by x-ray crystallography, Linus Pauling and Robert Corey of the California Institute of Technology (Fig. 1) deduced the two main structural features of proteins: the α-helix and β-sheet, now known to form the backbones of tens of thousands of proteins. Their deductions, triumphs in building models of large molecules based on features of smaller molecules, were published in a series of eight articles, communicated to PNAS in February and March 1951. Their work had a significance for proteins comparable to that 2 years later of the Watson–Crick paper for DNA, which adopted the Pauling–Corey model-building approach. Here I summarize the main points of these historic articles, and then mention some surprising omissions from them.

Fig. 1.

Linus Pauling and Robert Corey (A) and Herman Branson (B). Pauling's deep understanding of chemical structure and bonding, his retentive memory for details, and his creative flair were all factors in in the discovery of the α-helix. Robert Corey was a dignified and shy x-ray crystallographer with the know-how and patience to work out difficult structures, providing Pauling with the fundamental information he needed. Herman Branson was a physicist on leave at the California Institute of Technology, who was directed by Pauling to find all helices consistent with the rules of structural chemistry that he and Corey had determined. The wooden helix between Pauling and Corey has a scale of 1 inch per Å, an enlargement of 254,000,000 times. (A) Courtesy of the Archives, California Institute of Technology. (B) Courtesy of the Lincoln University of Pennsylvania Archives.

The most revolutionary of these articles is the first, submitted to PNAS on Pauling's 50th birthday, February 28th, 1951. It is The Structure of Proteins: Two Hydrogen-Bonded Helical Configurations of the Polypeptide Chain (1), in which Pauling and Corey are joined by a third coauthor, H. R. Branson, an African-American physicist, then on leave from his faculty position at Howard University (Fig. 1). In the opening paragraph, the authors state that “we have been attacking the problem of the structure of proteins in several ways. One of these ways is the complete and accurate determination of the crystal structure of amino acids, peptides, and other simple substances related to proteins, in order that information about interatomic distances, bond angles, and other configurational parameters might be obtained that would permit the reliable prediction of reasonable configurations of the polypeptide chain.” In other words, the structural chemist Pauling believed that with an accurate parts list for proteins in hand he would be able to infer major aspects of their overall architecture, and this proved to be so.

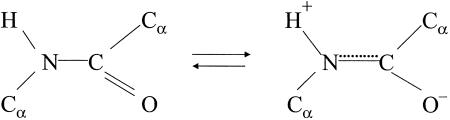
The next two paragraphs concisely set out the method: “The problem we have set ourselves is that of finding all hydrogen-bonded structures for a single polypeptide chain, in which the residues are equivalent (except for the differences in the side chain R).” That is, the authors sought all possible repeating structures (helices) in which the carbonyl CO group of each amino acid residue accepts an N—H hydrogen bond from another residue. Why did they believe that there would be only a small number of types of helices? This was because of the constraints on structure imposed by the precise bond lengths bond angles they had found from their past studies of crystal structures of amino acids and peptides, the components from which proteins are built up. These constraints are summarized in the third paragraph of their paper, which specifies to three significant figures the bond lengths and bond angles that they had found.† The most important constraint was that all six atoms of the amide (or peptide) group, which joins each amino acid residue to the next in the protein chain, lie in a single plane. Pauling had predicted planar peptide groups because of resonance of electrons between the double bond of the carbonyl group and the amide C—N bond of the peptide group (Scheme 1).

Scheme 1.

In fact, such planar peptide groups had been observed in the crystal structures of N-acetylglycine and β-glycylglycine. As the authors put it: “This structural feature has been verified for each of the amides that we have studied. Moreover, the resonance theory is now so well grounded and its experimental substantiation so extensive that there can be no doubt whatever about its application to the amide group.”

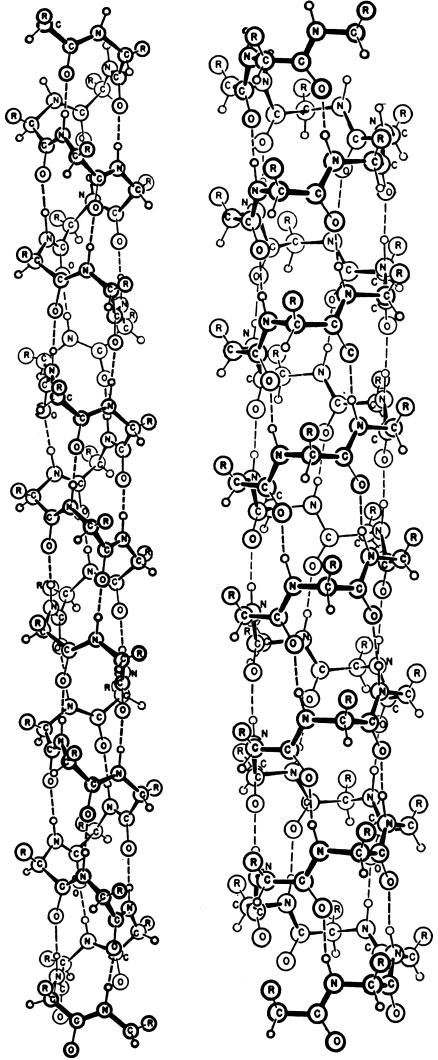
When Pauling, Corey, and Branson constructed helices with planar amide groups, with the precise bond dimensions they had observed in crystal structures, and with linear hydrogen bonds of length 2.72 Å, they found there were only two possibilities. These two they called the helix with 3.7 residues per turn and the helix with 5.1 residues per turn (Fig. 2), soon to be called the α-helix and the γ-helix.

Fig. 2.

The α-helix (Left) and the γ-helix (Right), as depicted in the 1951 paper by Pauling, Corey, and Branson (1). Biochemists will note that the CO groups of the α-helix point in the direction of its C terminus, whereas those of the γ-helix point toward its N terminus, and, further, that the α-helix shown is left-handed and made up of d-amino acids. (Reproduced with permission from Linda Pauling Kamb.)

Much of the rest of this short, brilliant paper is taken up with a comparison of these two helices with helices proposed earlier by others, most notably Bragg, Kendrew, and Perutz (2) in a paper the year before, that attempted to enumerate all possible protein helices, but missed these two. In their α-helix paper, Pauling et al. take a tone of triumph: “None of these authors propose either our 3.7-residue helix or our 5.1-residue helix. On the other hand, we would eliminate by our basic postulates all of the structures proposed by them. The reason for the difference in results obtained by other investigators and by us through essentially similar arguments is that both Bragg and his collaborators... discussed in detail only helical structures with an integral number of residues per turn, and moreover assume only a rough approximation to the requirements about interatomic distances bond angles, and planarity of the conjugated amide group, as given by our investigations of simpler substances. We contend that these stereochemical features must be very closely retained in stable configurations of polypeptide chains in proteins, and that there is no special stability associated with an integral number of residues per turn in the helical molecule.” In short, stereochemistry is important in determining which helices are possible, and integral symmetry has no role whatever.

Today, we accept without a second thought that helices do not need to have an integral number of monomer units per turn. But in 1950, the crystallo-graphic backgrounds of Bragg, Kendrew, and Perutz, three of the greatest structural scientists of the 20th century, saddled them with the notion of integral numbers of units per unit cell. They also missed the necessity of planar peptide groups. Working in the physics department at Cambridge University (Cambridge, U.K.), they were unaware of conjugation with nearby double bonds. The professor of organic chemistry at Cambridge at that time was Alexander Todd, who worked across the courtyard from Bragg and his team. Todd recalled (3) that “despite the proximity, Bragg never, to my knowledge, set foot in the chemical laboratory... until one day... he came to my room in a somewhat agitated state of mind, bearing a bunch of papers in his hand,” including the Pauling–Corey–Branson paper and his own on helices. Bragg asked Todd whether he preferred the α-helix over the helices that Bragg and his coworkers had invented. Todd responded, “I think that, given the evidence, any organic chemist would accept Pauling's view. Indeed, if at any time since I have been in Cambridge you had come over to the chemical laboratory, I... would have told you that.”

The idea of the nonintegral α-helix had come to Pauling 3 years before, when he was visiting professor at Oxford University. He caught cold in the damp weather and spent several days in bed. He recalled (4) that he was soon bored with detective novels and “I didn't have any molecular models with me in Oxford but I took a sheet of paper and sketched the atoms with the bonds between them and then folded the paper to bend one bond at the right angle, what I thought it should be relative to the other, and kept doing this, making a helix, until I could form hydrogen bonds between one turn of the helix and the next turn of the helix, and it only took a few hours of doing that to discover the α-helix.”

Why did Pauling delay 3 years in publishing this finding that came to him in only a few hours? He gave the answer in his banquet address at the third symposium of the Protein Society in Seattle in 1989. He was uneasy that the diffraction pattern of α-keratin shows as its principal meridional feature a strong reflection at 5.15-Å resolution, whereas the α-helix repeat calculated from his models with Corey was at 5.4 Å. As he says in his fourth paper of the PNAS series with Corey: “The 5.15-Å arc seems on first consideration to rule out the α-helix, for which the c-axis period must be a multiple of the axis distance per turn...” But then came the paper in 1950 by Bragg, Kendrew, and Perutz enumerating potential protein helices. Pauling told his audience in 1989: “I knew that if they could come up with all of the wrong helices, they would soon come up with the one right one, so I felt the need to publish it.”

The origin of the discrepancy between the repeat of the α-helix and the x-ray reflection of α-keratin was hit on a year later by Francis Crick (5), then a graduate student with Perutz, and also by Pauling. It is that keratin is a coiled-coil, with α-helices winding around each other. The wider excursion of the α-helix in the coiled-coil reduces its repeat distance to 5.1 Å. This knack of knowing which contradictory fact to ignore was one of Pauling's great abilities as a creative scientist.

The β-Sheets

The second paper of the series appeared as one of a group of seven in a single issue of PNAS. It was: The Pleated Sheet, A New Layer Configuration of Polypeptide Chains (6). In this article, Pauling and Corey report that they have discovered a hydrogen-bonded layer configuration of polypeptide chains, in which the planar peptide groups lie in the plane of the sheet, and successive protein chains can run in opposite directions, giving an antiparallel sheet, as well as a parallel sheet. In both, linear H-bonds are again formed, but between protein chains rather than within a single chain. This results in protein chains that are not fully extended: the rise per residue is 3.3 Å, a spacing seen in x-ray diffraction patterns of β-keratin, rather than 3.6 Å, expected for a fully extended protein chain.

Confirmation of the α-Helical and β-Sheet Models

Confirmation of the α-helix came from Max Perutz, one of the three authors of the 1950 article that had enumerated the wrong helices. One Saturday morning in spring 1951, he came across the PNAS paper (7). “I was thunderstruck by Pauling and Corey's paper. In contrast to Kendrew's and my helices, theirs was free of strain; all of the amide groups were planar and every carbonyl group formed a perfect hydrogen bond with an imino group four residues further along the chain. The structure looked dead right. How could I have missed it?... I cycled home to lunch and ate it oblivious of my children's chatter and unresponsive to my wife's inquiries as to what the matter was with me today.”

Suddenly Perutz had an idea: “Pauling and Corey's α-helix was like a spiral staircase in which the amino acid residues formed the steps and the height of each step was 1.5 Å. According to diffraction theory, this regular repeat should give rise to a strong x-ray reflection of 1.5 Å spacing from planes perpendicular to the fiber axis... In mad excitement, I cycled back to the lab and looked for a horse hair that I had kept tucked away in a drawer...” and put it in the x-ray beam at an angle of 31° to the beam to bring the 1.5-Å repeat into the reflecting position. “After a couple of hours, I developed the film, my heart in my mouth. As soon as I put the light on I found a strong reflection at 1.5-Å spacing, exactly as demanded by Pauling and Corey's α-helix.”

On Monday morning, Perutz showed his x-ray diffraction picture to Bragg. “When he asked me what made me think of this crucial experiment, I told him that the idea was sparked off by my fury over having missed building that beautiful structure myself. Bragg's prompt reply was, `I wish I had made you angry earlier!' because discovery of the 1.5-Å reflection would have led us straight to the α-helix.” Perutz also found the 1.5-Å reflection in diffraction from hemoglobin. He wrote to Pauling (8), “The fulfillment of this prediction and, finally, the discovery of this reflection in hemoglobin has been the most thrilling discovery of my life.” Perutz, along with his coworkers Dickerson, Kendrew, Strandberg, and Davies, was to make even more thrilling discoveries later, including seeing direct pictures of α-helices in myoglobin and hemoglobin.

β-Sheets and single-stranded β-ribbons were first seen in globular proteins as in the structure of egg white lysozyme in 1965 (9). An initial surprise was that both the strands and the sheets are twisted, unlike the straight strands and pleated sheets of Pauling and Corey. In 1989 Pauling recalled that as soon as he saw the structure of lysozyme with its twisted sheet he realized he should have incorporated the twist in the original model. More recently there have been thorough analyses of twist and shear in β-structures (10, 11).

Some Surprising Omissions from the 1951 Papers

Chemists who take a careful look at the α-helix of Fig. 2 will notice two surprising features: (i) It is a left-handed helix, unlike α-helices of biological proteins, which are now known to be right-handed. That is, if your left thumb points along the helix axis, the helix turns in the direction of the fingers of your left hand. (ii) The configuration of chemical groups around each α-carbon atom have the d-configuration, rather than the naturally occurring l-configuration of amino acid residues in proteins. That is, this model of Pauling et al. is the mirror image of an α-helix in a natural protein. In contrast, the γ-helix in Fig. 2 is a right-handed helix made up of d-amino acid residues. Why did the authors choose to draw the α-helix as left-handed, with d-amino acids?

The basis for this choice has recently been analyzed by Dunitz (12), who had been a postdoctoral fellow at the California Institute of Technology at the time of the Pauling–Corey research. In fact, it was Dunitz who persuaded Pauling to change his terminology from “spiral” to “helix” in describing the new protein structures. In his analysis, Dunitz notes that 1951, the year of the α-helix, was also the year in which J. M. Bijvoet established the absolute configuration of molecules by the anomalous scattering of x-rays. After recalling discussions of handedness at the California Institute of Technology in that year, Dunitz concludes: “Either Pauling was unaware of these developments when he wrote the α-helix paper, or he knew about them but was uninterested... I tend to believe that when they wrote the paper, or quite possibly even when they made the models, Pauling (or his colleague Robert B. Corey) simply picked one of the two amino acid configurations (as it happened, the wrong one) to illustrate the helical structures and did not give the problem of absolute configuration much thought... Problems of absolute configuration received little or no attention because there seemed to be no need for them then. Perhaps they were even regarded as a distraction from the task at hand. Sometimes one can focus more clearly by closing one eye.”

Also missing from the first paper is anything more than passing mention of the 3₁₀ helix, a component of globular proteins found rarely in short segments, but more common than the Pauling–Corey–Branson γ-helix, which is virtually never seen. The H-bonds of the 3₁₀ helix are somewhat too long and bent to have been acceptable by the stringent thresholds set by the authors. Their intuition about bent and long hydrogen bonds destabilizing structures was basically correct, but the thresholds they set are more stringent than those used today (13), now that we know nature accepts the 3₁₀ helix.

One other omission from the set of 1951 papers is the Ramachandran diagram. This is a 2D plot of the allowed values of rotation about the N—Cα and Cα—CO bonds in the protein backbone, introduced by Ramachandran and others in 1964 (14). This diagram shows that most values of rotation about these two bonds are forbidden by collisions of protein atoms. Only two major regions of the diagram are allowed: one corresponds to the α-helix, and one to the nearly extended chains of the β-sheets. Today the Ramachandran diagram is taught in all classes on protein structure and is featured in every textbook to give insight into the forces that determine the structures of proteins. But there is nothing in this diagram beyond what Pauling and Corey knew well: they built models of their proposed structures that embodied all features of the Ramachandran diagram. Apparently they understood the principles so well that they felt no need to explain them by a diagram of this sort. Another factor may have been that Pauling and Corey focused more on the stability provided by hydrogen bonds and less on the restrictions on possible structures dictated by collisions between nonbonded atoms.

The Other Six PNAS Articles by Pauling and Corey and the Wider Context

The remaining six articles in PNAS give the atomic coordinates of the models and interpret the diffraction patterns of fibrous proteins in terms of the models. There is much in these papers than has not been borne out, including a proposal that muscle contraction is a transition from extended β-strands to compact α-helices. Nevertheless, the breathtaking correctness of the α-helix and β-sheets and the bold approach of modeling biological structures from chemical principles overshadow the rest.

These papers are all the more remarkable when we consider the political context in which they were written. During this period, Pauling was also heavily involved in defending academics, including himself, against charges of disloyalty to the United States, brought about by the pressures of the Cold War and what became known as McCarthyism. He was subpoenaed to appear before various anticommunist investigating committees, he received hate mail for his work on liberal causes, and he faced cancellation of his major consulting contract and coolness from some California Institute of Technology colleagues. On the day after Pauling and Corey submitted their seven protein papers for publication, the House Un-American Activities Committee named Pauling one of the foremost Americans involved in a “Campaign to Disarm and Defeat the United States” (8). The press release read, “His whole record... indicates that Dr. Linus Pauling is primarily engrossed in placing his scientific attainments at the service of a host of organizations which have in common their complete subservience to the Communist Party of the USA, and the Soviet Union.” Somehow, even in the face of such false invective and multiple distractions, Pauling could maintain his focus as a top creative scientist.