Abstract
We construct a class of global exact solutions of the Einstein equations that extend the Oppeheimer–Snyder model to the case of nonzero pressure, inside the black hole, by incorporating a shock wave at the leading edge of the expansion of the galaxies, arbitrarily far beyond the Hubble length in the Friedmann–Robertson–Walker (FRW) spacetime. Here the expanding FRW universe emerges be-hind a subluminous blast wave that explodes outward from the FRW center at the instant of the big bang. The total mass behind the shock decreases as the shock wave expands, and the entropy condition implies that the shock wave must weaken to the point where it settles down to an Oppenheimer–Snyder interface, (bounding a finite total mass), that eventually emerges from the white hole event horizon of an ambient Schwarzschild spacetime. The entropy condition breaks the time symmetry of the Einstein equations, selecting the explosion over the implosion. These shock-wave solutions indicate a cosmological model in which the big bang arises from a localized explosion occurring inside the black hole of an asymptotically flat Schwarzschild spacetime.
We describe a cosmological model based on matching a critically expanding Friedmann–Robertson–Walker (FRW) metric to a metric that we call the Tolman–Oppenheimer–Volkoff (TOV) metric inside the black hole across a shock wave that lies beyond one Hubble length from the center of the FRW spacetime. This implies that the spacetime beyond the shock wave must lie inside a black hole, thus extending the shock matching limit of one Hubble length that we identified in ref. 1.
In the exact solutions constructed in this article, the expanding FRW universe emerges behind a subluminous blast wave that explodes outward from the origin r̄ = 0 at the instant of the big bang t = 0, at a distance beyond one Hubble length.¶ The shock wave then continues to weaken as it expands outward until the Hubble length eventually catches up to the shock, and this marks the event horizon of a black hole in the TOV metric beyond the shock. From this time onward, the shock wave is approximated by a zero pressure (k = 0) Oppenheimer–Snyder (OS) interface, and thus the OS solution gives the large time asymptotics of these solutions. Surprisingly, the equation of state p = ⅓ρ of early big bang physics is distinguished by the differential equations, and only for this equation of state does the shock wave emerge from the big bang at a finite nonzero speed, the speed of light. This is surprising because the equation of state p = ⅓ρ played no special role in shock matching outside the black hole (2). We find it interesting that such a shock wave emerging from the big bang beyond the Hubble length would account for the thermalization of radiation in a region well beyond the light cone of an observer positioned at the FRW center at present time, even though the FRW expansion is finite, and the model does not invoke inflation. Details will appear in our forthcoming article (3); here, we summarize this work and describe its physical interpretation.
1. Statement of the Problem
If there is a shock wave at the leading edge of the expansion of the galaxies, then we can ask what is the critical radius r̄crit at each fixed time t in a k = 0 FRW metric such that the total mass inside a shock wave positioned beyond that radius puts the universe inside a black hole? [There must be such a critical radius because the total mass M(r̄, t) inside radius r̄ in the FRW metric at fixed time t increases like r̄,¶ and so at each fixed time t we must have r̄ > 2M(r̄, t) for small enough r̄, while the reverse inequality holds for large r̄. We let r̄ = r̄crit denote the smallest radius at which r̄crit = 2M(r̄crit, t).] We show that when k = 0, r̄crit equals the Hubble length. Thus, we cannot match a critically expanding FRW metric to a classical TOV metric beyond one Hubble length without continuing the TOV solution into a black hole, and we showed in ref. 4 that the standard TOV metric cannot be continued into a black hole. Thus to do shock matching with a k = 0 FRW metric beyond one Hubble length, we introduce the TOV metric inside the black hole.
2. The TOV Metric Inside the Black Hole
When the metric anzatz is taken to be of the TOV form
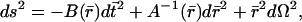 |
[2.1] |
and the stress tensor T is taken to be that of a perfect fluid comoving with the metric, the Einstein equations G = κT, inside the black hole, take the form
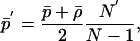 |
[2.2] |
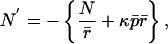 |
[2.3] |
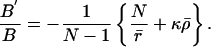 |
[2.4] |
We let 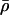 , p̄ denote the density and pressure, respectively, and r̄ is taken to be the timelike variable because we assume
, p̄ denote the density and pressure, respectively, and r̄ is taken to be the timelike variable because we assume
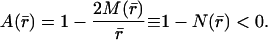 |
[2.5] |
Here, M(r̄) has the interpretation as the total mass inside the ball of radius r̄ when r̄ > 2M, but M does not have the same interpretation inside the black hole∥ because r̄ < 2M. The system 2.2–2.4 defines the simplest class of gravitational metrics that contain matter and evolve inside the black hole.
3. Shock Matching Inside the Black Hole
Matching a given k = 0 FRW metric to a TOV metric inside the black hole across a shock interface, leads to the system of ordinary differential equations
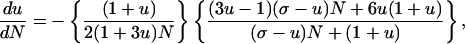 |
[3.1] |
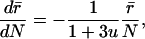 |
[3.2] |
with conservation constraint
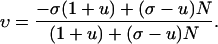 |
[3.3] |
Here
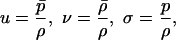 |
[3.4] |
ρ and p denote the (known) FRW density and pressure, σ = p/ρ, and all variables are evaluated at the shock. Solutions of 3.1–3.3 determine the (unknown) TOV metrics that match the given FRW metric Lipschitz continuously across a shock interface, such that conservation of energy and momemtum hold across the shock, and such that there are no delta function sources at the shock (4, 5).
For such solutions, the speed of the shock interface relative to the fluid comoving on the FRW side of the shock, is given by
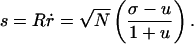 |
[3.5] |
Note that the dependence of 3.1–3.3 on the FRW metric is only through the variable σ. Since solutions of 3.1–3.3 are formally time-reversible but shock waves are not, system 3.1–3.3 must be augmented by an entropy condition for shocks that breaks the time symmetry. Since we are interested in solutions that model the “big bang” as a localized explosion with an outgoing blast wave emanating from r̄ = 0 at time t = 0, we impose the entropy conditions,
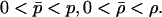 |
[3.6] |
Condition 3.6 for outgoing shock waves implies that the shock wave is compressive and is sufficient to rule out unstable rarefaction shocks in classical gas dynamics.
4. Exact Shock-Wave Solutions Inside the Black Hole
In the case when the FRW pressure is given by the equation of state
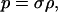 |
[4.1] |
σ assumed constant, 0 < σ < 1, the FRW equations have the exact solutions
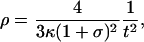 |
[4.2] |
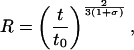 |
[4.3] |
which assumes an expanding universe, (Ṙ > 0), and initial conditions R = 0at t = 0, and R = 1, at t = t0. Since σ is constant, Eq. 3.1 uncouples from 3.2, and thus solutions of system 3.1–3.3 are determined by the scalar nonautonomous Eq. 3.1. Making the change of variable S = 1/N, which transforms the big bang N → ∞ over to rest point at S → 0, cf. ref. 1, we obtain,
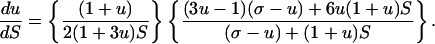 |
[4.4] |
We take as entropy condition 3.6, and in addition, we require that the TOV equation of state meet the physical bound
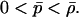 |
[4.5] |
The conditions N > 1 and 0 < p̄ < p restrict the domain of 4.4 to the region 0 < u < σ < 1, 0 < S < 1. Inequalities 3.6 and 4.5 are both implied by the single condition
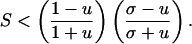 |
[4.6] |
We prove the following theorem:
Theorem 1. For every σ, 0 < σ < 1, there exists a unique solution uσ(S) of 4.4, such that 4.6 holds on the solution for all S, 0 < S < 1, and on this solution, 0 < uσ(S) < ū, limS→0 uσ(S) = ū, where ū = Min{1/3, σ}, and
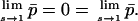 |
[4.7] |
Concerning the the shock speed, we have:
Theorem 2. Let 0 < σ < 1. Then the shock wave is everywhere subluminous, that is, the shock speed sσ(S) ≡ s(uσ(S)) < 1 for all 0 < S ≤ 1, if and only if σ ≤ 1/3.
By a careful analysis of the asymptotics of the solution near S = 0, we can prove
Theorem 3. The shock speed at the big bang S = 0 is given by:
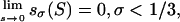 |
[4.8] |
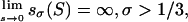 |
[4.9] |
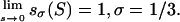 |
[4.10] |
5. Bounds on the Shock Position
Let r* be the FRW radial position of the shock wave at the instant of the big bang [the arclength distance r̄* = r*R(0) = 0 when R(0) = 0]. The analysis implies that the shock wave will first become visible at the FRW center r̄ = 0 at the moment t = t0 [R(t0) = 1], when the Hubble length 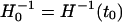 satisfies
satisfies
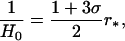 |
[5.1] |
where r* is the FRW position of the shock at the instant of the big bang. At this time, we prove that the number of Hubble lengths 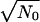 from the FRW center to the shock wave at time t = t0 can be estimated by
from the FRW center to the shock wave at time t = t0 can be estimated by
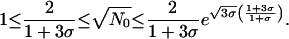 |
Thus, in particular, the shock wave will still lie beyond the Hubble length 1/H0 at the FRW time t0 when it first becomes visible. Furthermore, we prove that the time tcrit > t0 at which the shock wave will emerge from the white hole given that t0 is the first instant at which the shock becomes visible at the FRW center, can be estimated by
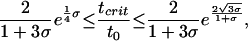 |
[5.2] |
for 0 < σ ≤ 1/3, and by the better estimate
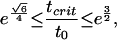 |
[5.3] |
in the case σ = 1/3. For example, 5.2 and 5.3 imply that at the OS limit σ = 0,
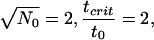 |
and in the limit σ = 1/3,
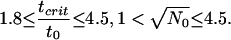 |
We conclude in these shock-wave cosmological models that the moment t0 when the shock wave first becomes visible at the FRW center it must lie within 4.5 Hubble lengths of the center. Throughout the expansion up until this time, the expanding universe must lie entirely within a black hole; the universe will eventually emerge from this black hole, but not until some later time tcrit, where tcrit does not exceed 4.5 t0.
6. Concluding Remarks
We have constructed global exact solutions of the Einstein equations in which the expanding FRW universe extends out to a shock wave that lies arbitrarily far beyond the Hubble length. The distance to the shock wave at any given value of the Hubble constant is determined by one free parameter that can be taken to be the FRW position of the shock wave at the instant of the big bang.
The critical OS solution inside the black hole is obtained in the limit of zero pressure and provides the large time asymptotics, but the shock-wave solutions differ qualitatively from the OS solution. For example, the shock wave models contain matter, and thus do not rely on any portion of the empty space Schwarzschild metric inside the black hole for their construction. In both models, the interface propagates outward from the FRW center r̄ = 0 at the instant of the big bang, but in the shock-wave model the mass function M(r̄, t) is infinite at the instant of the big bang and immediately becomes a finite decreasing function of FRW time, for all future times t > 0. And although the OS solution is time reversible, the directional orientation of the shock interface relative to the various observers is determined by an entropy condition (6–8). The entropy condition selects the explosion over the implosion, and the condition that the entropy condition be satisfied globally, determines a unique solution. Since the TOV radial coordinate r̄ is timelike inside the black hole, we can also say that the density 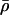 (r̄) and mass M(r̄) are both constant at each fixed time in the TOV spacetime beyond the shock wave.
(r̄) and mass M(r̄) are both constant at each fixed time in the TOV spacetime beyond the shock wave.
The shock interface that marks the boundary of the FRW expansion continues out through the white hole event horizon of an ambient Schwarzschild metric at the instant when the wave is exactly one Hubble length from the FRW center r̄ = 0, and then continues on out to infinity along a geodesic of the Schwarzschild metric outside the black hole. These solutions thus indicate a scenario for the big bang in which the expanding universe emerges from an explosion emanating from a white hole singularity inside the event horizon of an asymptotically flat Schwarzschild spacetime of finite mass. The model does not require the physically implausible assumption that the uniformly expanding portion of the universe is of infinite mass and extent at every fixed time, and it has the nice feature that it embeds the big bang singularity of cosmology within the event horizon of a larger spacetime, the Schwarzschild spacetime. Moreover, the model also allows for the uniform expansion of arbitrarily large densities within an arbitrarily large mass extended over an arbitrary number of Hubble lengths early on in the big bang, a prerequisite for the standard physics of the big bang at early times.
We conclude that these shock-wave solutions give the global dynamics of strong gravitational fields in an exact solution, the dynamics is qualitatively different from the dynamics of solutions when the pressure p ≡ 0, the solution suggests a big bang cosmological model in which the expanding universe is bounded throughout its expansion, and the equation of state most relevant at the big bang, p = 13 ρ, is distinguished by the differential equations. But these solutions are only rough qualitative models because the equation of state on the TOV side is determined by the equations and therefore cannot be imposed. That is, the TOV density 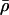 and pressure p̄ only satisfy the entropy conditions (3.6), together with the loose physical bounds (4.5); and on the FRW side, the equation of state is taken to be p = σρ, σ ≡ constant, 0 < σ < 1. Nevertheless, these bounds imply that the equations of state are qualitatively reasonable, and we expect that these solutions will capture the gross dynamics of solutions when more general equations of state are imposed. For more general equations of state, other waves, (e.g. rarefaction waves), would need to be present to meet the conservation constraint and thereby mediate the transition across the shock wave. Such transitional waves would be pretty much impossible to model in an exact solution, but the fact that we can find global solutions that meet our physical bounds, and that are qualitatively the same, for all values of σ ∈ (0, 1), and all initial shock positions, leads us to expect that such a shock wave would be the dominant wave in a large class of problems.
and pressure p̄ only satisfy the entropy conditions (3.6), together with the loose physical bounds (4.5); and on the FRW side, the equation of state is taken to be p = σρ, σ ≡ constant, 0 < σ < 1. Nevertheless, these bounds imply that the equations of state are qualitatively reasonable, and we expect that these solutions will capture the gross dynamics of solutions when more general equations of state are imposed. For more general equations of state, other waves, (e.g. rarefaction waves), would need to be present to meet the conservation constraint and thereby mediate the transition across the shock wave. Such transitional waves would be pretty much impossible to model in an exact solution, but the fact that we can find global solutions that meet our physical bounds, and that are qualitatively the same, for all values of σ ∈ (0, 1), and all initial shock positions, leads us to expect that such a shock wave would be the dominant wave in a large class of problems.
As a final remark, we note that because Einstein's theory by itself does not choose an orientation for time, it follows that if we believe that a black hole can exist in the forward time collapse of a mass through an event horizon as t → ∞, (the time t as observed in the far field), then we must also allow for the possibility of the time reversal of this process, a white hole explosion of matter out through an event horizon coming from t → –∞. That is, if we are willing to accept black holes in the forward time dynamics of astrophysical objects whose collapse appears so great as to form an event horizon in the future, then by symmetry, we may well also be forced to accept white holes in the backward time dynamics of astrophysical objects, which, like the expanding universe, appear to have expansions so great as to have emerged from an event horizon in the past. Given this, it is natural to wonder if there is a connection between the mass that disappears into black hole singularities and the mass that emerges from white hole singularities.
Acknowledgments
This work was supported in part by National Science Foundation Applied Mathematics Grants DMS-010-3998 (to J.S.) and DMS-010-2493 (to B.T.).
Abbreviations: FRW, Friedmann–Robertson–Walker; TOV, Tolman–Oppenheimer–Volkoff; OS, Oppenheimer–Snyder.
Footnotes
We let (t, r) denote standard FRW coordinates, so that r̄ = rR(t) measures arclength distance at each fixed value of the FRW time t, where R denotes the cosmological scale factor. Barred coordinates also refer to TOV standard coordinates, in which case r̄ = rR(t) also holds as a consequence of shock matching.
System 2.2–2.4 for A < 0 differs substantially from the TOV equations for A > 0 because, for example, the energy density T00 is equated with the timelike component Grr when A < 0, but with Gtt when A > 0. In particular, this implies that 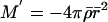 when A < 0, versus
when A < 0, versus 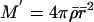 when A > 0, the latter being the equation that gives the mass function its physical interpretation outside the black hole.
when A > 0, the latter being the equation that gives the mass function its physical interpretation outside the black hole.
References
- 1.Smoller, J. & Temple, B. (2000) Commun. Math. Phys. 210, 275–308. [Google Scholar]
- 2.Smoller, J. & Temple, B. (1995) Phys. Rev. D 51, 2733–2743. [DOI] [PubMed] [Google Scholar]
- 3.Smoller, J. & Temple, B. (2003) Cosmology, Black Holes, and Shock Waves Beyond the Hubble Length, preprint.
- 4.Smoller, J. & Temple, B. (1997) Arch. Ration. Mech. Anal. 138, 239–277. [Google Scholar]
- 5.Israel, W. (1966) Nuovo Cimento Soc. Ital. Fis. B XLIV, 1–14. [Google Scholar]
- 6.Lax, P. D. (1957) Commun. Pure Appl. Math. 10, 537–566. [Google Scholar]
- 7.Smoller, J. (1983) Shock Waves and Reaction-Diffusion Equations (Springer, Berlin).
- 8.Glimm, J. (1965) Commun. Pure Appl. Math. 18, 697–715. [Google Scholar]


