Abstract
Under conditions where macromolecules are aligned very weakly with respect to an external magnetic field, Brownian diffusion no longer averages internuclear dipole–dipole interactions to zero. The resulting residual dipolar coupling, although typically 3 orders of magnitude weaker than in a fully aligned sample, can readily be measured by solution NMR methods. To date, application of this idea has focused primarily on pairs of nuclei separated by one or two covalent bonds, where the internuclear separation is known and the measured dipolar coupling provides direct information on the orientation of the internuclear vector. A method is described that allows observation of dipolar interactions over much larger distances. By decoupling nearest-neighbor interactions, it is readily possible to observe direct dipolar interactions between protons separated by up to 12 Å. The approach is demonstrated for the DNA dodecamer d(CGCGAATTCGCG)2, where direct interactions are observed between protons up to three base pairs apart.
In general, molecules diffusing in an environment with asymmetric boundary conditions sample orientational space in a nonuniform manner. When placed in a magnetic field, magnetic dipole–dipole interactions in such molecules no longer average to zero. As a result, NMR spectra of small organic solute molecules diffusing in a magnetically oriented liquid crystalline medium contain a wealth of such coupling information, which can reveal very precise information on the average geometry of the solute (1–3). The high degree of order of the solute molecule in such systems results in very large dipole–dipole couplings for proximate pairs of protons, up to 50% of what would be observed for a perfectly oriented molecule, and numerous smaller couplings to more remote protons. The resulting spectral complexity is such that complete analysis is not feasible for systems containing more than about a dozen magnetically active nuclei.
The spectral complexity resulting from the multitude of couplings that are larger than the resonance width will be reduced when the degree of alignment is scaled down. Very weak alignment (Aa), on the order of Aa = 10–4, can result from a molecule's intrinsic magnetic susceptibility anisotropy when placed in a sufficiently strong magnetic field. Use of this method of alignment frequently exploits the presence of a paramagnetic ion, either endogenous (4–6) or tagged to the protein by a synthetic chelating group (7, 8). Despite the weakness of such alignment, and the proportionately small-scale factor for the dipolar interaction, the effects of the largest dipolar interactions remain detectable. This was first demonstrated for the one-bond backbone 15N–1H interactions in paramagnetic myoglobin (4), where dipolar couplings with magnitudes up to several hertz were observed, smaller than the natural resonance width but nevertheless easily detectable from a change in the one-bond 1JNH splitting.
Measurement of these couplings, also in diamagnetic systems, became much easier when it was shown to be feasible to induce a tunable, weak degree of macromolecular alignment by using very dilute, aqueous, lyotropic liquid crystalline solutions (9). The first such medium used for this purpose contained so-called bicelles (10), which (over a limited temperature and concentration range) are self-assembling, highly porous α-lamellar bilayers (11, 12) consisting of dimyristoyl phosphatidyl choline and detergent. When placed in a magnetic field, the bilayers of this liquid crystalline medium align with their bilayer normal orthogonal to the field. Originally, this medium was developed to study, mainly by solid-state NMR technology, the structure and membrane binding properties of small lipophilic molecules, anchored to the highly ordered bilayers (13, 14). The application of the bicelle medium to water-soluble proteins is rather different and takes advantage of the very small deviation from a purely random distribution of orientations that is sterically imposed on asymmetrically shaped proteins when immersed in such an ordered environment. A host of other liquid crystalline systems, including nematic suspensions of filamentous bacteriophages (15, 16) or crystalline cellulose fibers (17), and polyethylene glycol (18) or cetylpyridinium-based lamellar phases (19), are available to induce the required weak degree of macromolecular alignment. More recently, the use of anisotropically compressed aqueous acrylamide gels has been added to this arsenal (20, 21). Such media make it easily possible to increase the degree of ordering to Aa ≈ 10–3, where spectral complexity has not yet increased much compared with the regular solution NMR spectrum, but smaller interactions such as the one-bond 13C–13C and 13C–15N, and two-bond 13C–1H and 15N–1H also become accessible in proteins (9, 22) and nucleic acids (23, 24).
So far, most measurements of residual dipolar couplings have focused on heteronuclear one-bond or two-bond interactions, where the internuclear distance is known accurately from covalent geometry. The size of the observed coupling then depends uniquely on the orientation of the internuclear vector with respect to the molecule's alignment frame. For structure calculation purposes, however, such simplicity offers little advantage, and homonuclear dipolar coupling between protons far apart in the covalent network can readily be measured (9) and incorporated in the structure calculation protocol (25). We recently demonstrated the measurement of nearly 200 1H-1H dipolar couplings for the DNA dodecamer d(CGCGAATTCGCG)2 (26), a palyndromic oligomer that has been studied extensively by x-ray crystallography (27–29), NMR (30–32), and computational methods (33, 34). The structure of the center six base pairs of the oligomer in the crystal structure agrees remarkably well with the solution NMR structure (26), whereas the conformation of the flanking base pairs is affected by crystal packing and Mg2+ coordination, absent in solution. NMR structures calculated from 1H–1H dipolar couplings agreed well with those derived from 1H–13C dipolar couplings, but no interactions between protons separated by >4 Å were observable (34).
The problem with observing 1H–1H dipolar couplings for the longest distances is not so much that the absolute value of the coupling becomes too small, but primarily that there are too many much larger 1H–1H interactions, which obscure the small magnetic dephasing effects from the more remote interactions. In proteins, we have demonstrated that perdeuteration can overcome this problem, essentially chemically removing the majority of 1H–1H interactions and permitting the study of the remaining amide protons, for distances of up to 7 Å (35). We now demonstrate that interactions between remote protons, separated by distances of up to 12 Å, become accessible in fully protonated biomolecules by appropriate manipulation of the nuclear spin Hamiltonian, which allows for effective decoupling of all protons outside a spectral region of interest.
Experimental Section
All NMR experiments were carried out at 35°C on a Bruker DRX spectrometer, operating at 600 MHz 1H frequency equipped with a triple resonance, three-axes pulsed-field gradient probe head, optimized for 1H detection. Samples contained 3 mM of unlabeled DNA duplex d(CGCGAATTCGCG)2, 50 mM KCl, 1 mM EDTA, and 10 mM potassium phosphate buffer (pH 7.0) in 99.9% D2O, in a 300-μl Shigemi microcell. For the aligned sample 324 μg of cetyltrimethylammonium bromide and 360 μl of a 10% (wt/vol) nonhydrolyzable ether bicelle stock solution (composed of 1,2-O-ditetradecyl-sn-glycero-3-phosphocholine and 1,2-O-dihexyl-sn-glycero-3-phosphocholine in a molar ratio 3:1) were mixed with 300 μl of the DNA solution. The sample was then lyophilized and redissolved in 300 μl of D2O. The final solution of DNA, containing 12% (wt/vol) bicelles, was characterized by a deuterium quadrupole splitting of 35.7 Hz. All data sets were processed and analyzed with the nmrpipe software system (36). The pulse sequence to detect long-range 1H–1H dipolar couplings, and the nmrpipe macro used to process the data are available on our laboratory web site: http://spin.niddk.nih.gov/bax.
Results
Band-Selective Removal of Coupling Interactions. In a weakly aligned molecule, the truncated spin Hamiltonian in the absence of external radiofrequency fields is given by
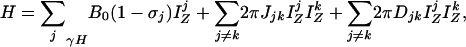 |
[1a] |
where the first and second term are the Zeeman (HZ) and the scalar coupling part (HJ) of the Hamiltonian, and the last one is the residual dipolar coupling term (HDD). The residual dipolar coupling between a pair of protons, j and k, is given by
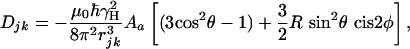 |
[1b] |
where θ and φ describe the orientation of the j-k vector relative to the molecular alignment tensor, rjk is the interproton distance, Aa is the magnitude of the alignment, and R is its rhombicity (9).
In the absence of alignment, HDD = 0, and spectral dispersion in the 1H NMR spectrum is dominated by differences in chemical shift, σ, of the individual protons, with a multiplet structure superimposed on each resonance, caused by HJ, the through-bond coupling to the magnetically active nuclei three or fewer bonds removed from it. In the absence of isotopic enrichment, only interactions to geminal and vicinal hydrogens need to be considered, and multiplet structures are simple. For example, the anomeric H1′ proton in a deoxyribose ring appears as a doublet of doublets, resulting from its interaction with the H2′ and H2″ protons. Frequently this interaction is comparable to the natural line width of the proton resonance, resulting in unresolved splittings and an apparent broadening of the resonance (Fig. 1B). In the presence of weak alignment, a multitude of 1H–1H dipolar interactions are also present, typically in the range from 0 to ±30 Hz. Because of the large number of such interactions and the spread in their magnitudes, these couplings usually do not result in resolved multiplets and manifest themselves as severe apparent broadening of the 1H resonance, and a concomitant loss in resolution (Fig. 1 A).
Fig. 1.
Comparison of the H1′/H5 region of 1D spectra of d(CGCGAATTCGCG)2, recorded without (A and B) or with (C) homonuclear decoupling. Spectrum A corresponds to the partially aligned state [12% (wt/vol) ether bicelle], and spectra B and C have been recorded on the corresponding isotropic sample of DNA. The duration of the sampled free induction decay equals 307 ms for spectra A and B. Apodization using a cosine-squared function, followed by zero-filling, was used before Fourier transformation. Spectrum C has been acquired and processed as described in the legend to Fig. 3. In C,H1′ and H5 protons are labeled by their nucleotide numbers, including * for H5 resonances.
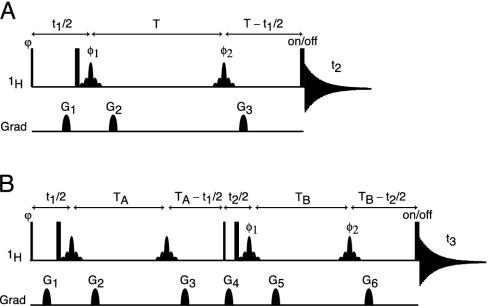
In principle, the loss in resolution caused by the homonuclear scalar and dipolar 1H–1H interactions can be eliminated by using the original homonuclear J spectroscopy experiment (37). In practice, however, the difficulty in obtaining absorption mode spectra limits the use of this approach. Instead, we describe a simple alternative method that removes the couplings between protons resonating in a selected band of the spectrum to all protons outside of this band. The pulse scheme is sketched in Fig. 2A. During a so-called constant-time evolution period (38) of duration 2 T, only the transverse magnetization of a narrow band of protons is selected by the application of appropriate gradients and a so-called REBURP 180° pulse (39), applied at time T + t1/2 after initial excitation. This pulse eliminates evolution of homonuclear coupling between protons inside and outside the selected band from the last 2 T – t1 fraction of the constant-time evolution period. Homonuclear coupling is eliminated from the remaining, first t1 fraction of this period by a nonselective 180°, band-selective 180° pulse pair, applied at time t1/2 after initial excitation. Temporarily ignoring couplings between protons within the selected band of resonances, chemical shift evolution during the constant-time evolution period has transformed an initial transverse spin operator, Iy, into Iycos(2πδit1) – Ix sin(2πδit1), where δi denotes the chemical shift of spin i. Signal detected during the subsequent detection period, t2, is described by
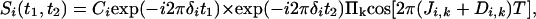 |
[2] |
where Ci is an experimental constant, depending on sample concentration and instrumental factors, and the product extends over all spins k, coupled to i and resonating within the selected band. A second experiment, which inserts a 180° pulse between the end of the evolution period and the start of the detection changes the exp(–i2πδit1) term to exp(i2πδit1), and the paired data sets can be used to generate purely absorptive 2D NMR spectra in the standard manner (40, 41).
Fig. 2.
Pulse schemes for homonuclear decoupled spectroscopy. (A) Basic pulse element for band-selective 1H homonuclear decoupling. (B) Selective constant-time COSY pulse scheme, in which band-selective decoupling is implemented to specifically detect internucleotide residual dipolar coupling. Narrow and wide pulses correspond to flip angles of 90° and 180°, respectively. Unless specified, pulses are applied along the x axis. Shaped 1H pulses are of the 180° REBURP type (39) (8-ms duration at 600 MHz, for a 500-Hz inversion bandwidth, centered at 5.8 ppm). Phase cycling: ϕ = x,–x; φ1 = 2(x),2(–x); φ2 = 4(x),4(–x); and receiver = y,–y,–y,y,–y,y,y,–y. (A) Quadrature detection in the indirect 1H dimension is achieved by applying an extra 1H 180° pulse just before the acquisition for half of the scans, storing signals separately, and using the usual “echo-antiecho” Fourier transform processing method (40, 41). All gradients are sine bell-shaped, with durations of 200 μs each, and (x,y,z) peak amplitudes in G/cm of (15,–33,20) for G1, (9,9,12) for G2, and (24,–24,32) for G3.(B) Quadrature detection in F1 is achieved by incrementing ϕ in the usual States-TPPI manner, and in F2 by insertion on alternate scans of the extra 1H 180° pulse just before acquisition (as in A). All gradients are sine bell-shaped, with durations of 200 μs, and (x,y,z) peak amplitudes in G/cm of (7,7,24) for G1, (5,5,–7) for G2, (12,12,17) for G3, (15,–33,20) for G4, (9,9,12) for G5, and (24,–24,32) for G6.
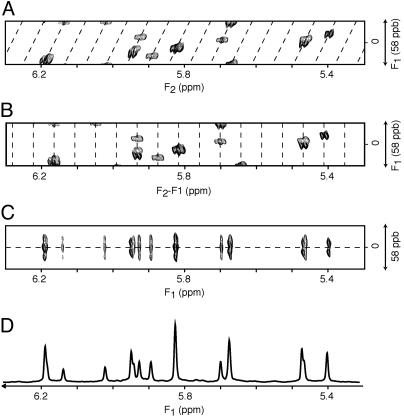
In the final spectrum, the F1 dimension yields the homonuclear decoupled resonances at frequencies δi, whereas in the F2 dimension the regular multiplet, centered around δi, is present (Fig. 3A). As demonstrated in Fig. 3A, extensive folding can be used in the F1 dimension without introducing resonance overlap. The constant-time evolution mode in the t1 dimension allows the use of mirror-image linear prediction (42) for further enhancement of the spectral resolution. A shearing transformation of the data matrix coordinates according to (F1′, F2′) = (F1, F2 –F1) yields a spectrum where the F1′ coordinate remains δi, but the F2′ dimension now represents the multiplet shape (Fig. 3B). Rearrangement of this data matrix (Fig. 3C) allows one to “unfold” such a spectrum, and a projection on its F1′ axis yields homonuclear decoupled spectra (Figs. 1C and 3D), which exhibit much improved spectral resolution.
Fig. 3.
Processing scheme for diagonal unfolding. (A) The original spectrum, processed in the standard manner, in which the diagonal signal (dashed line) is repeatedly folded in the F1 dimension. Spectra have been recorded with the pulse scheme of Fig. 2 A. The data matrix consists of 6*(t1) × 1,024*(t2) data points, with acquisition times of 144 ms (t1) and 307 ms (t2) (2T = 164 ms). Linear prediction was used to double the number of time-domain points in the F1 dimension, and both dimensions were apodized by cosine-squared functions and zero-filled by a factor of two before Fourier transformation. (B)An F1-dependent frequency shift is applied to the F2 dimension, such that the diagonal signals are now positioned vertically. (C) Vertical bands from the shifted spectrum are transposed and reassembled horizontally to construct an unfolded spectrum in the F1 dimension. (D) A 20-Hz band, corresponding to the center of the F2 dimension in C, is extracted, apodized by a sine-bell function, and then projected onto the F1 dimension, to yield a homonuclear decoupled 1D spectrum. The spectral widths for the horizontal and vertical dimensions are, respectively, 600 and 34.9 Hz. For display purposes, the vertical axis is expanded 2-fold relative to the horizontal axis.
Detection of Remote Dipolar Interactions. The above described homonuclear decoupling procedure only removes the couplings between protons resonating inside the spectral region selected by the band-selective pulse and those outside. When selecting, for example, the H1′ region in a DNA spectrum, which also contains the cytidine H5 resonances, dephasing resulting from couplings between different H1′ protons, or between H1′ and H5 protons remains active during the t1 evolution period. Considering that the distance between such pairs of protons almost always exceeds 4 Å, the corresponding dipolar couplings are very small. However, with all other large intranucleotide couplings effectively removed, these small couplings can readily be detected.
The pulse scheme used for this purpose (Fig. 2B) essentially duplicates the evolution period of Fig. 2 A and separates the first and second evolution period by a 90° mixing pulse, which serves the same function as the 90° mixing pulse in the classic COSY experiment (43). During the t1 and t2 evolution periods, and focusing on the spectral region encompassing the H1′ and H5 protons, HJ = 0, but Hz and HDD terms for H1′/H1′ and H1′/H5 interactions remain intact. As a result, at the end of the second constant time evolution period, of duration 2 TB, the signal originating on proton i and remaining on proton i is described by
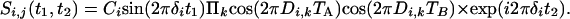 |
[3a] |
Magnetization transferred from i to in-phase magnetization of spin j is described by
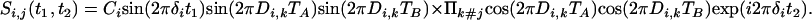 |
[3b] |
2D Fourier transformation with respect to t1 and t2 then yields a doubly constant-time, in-phase COSY spectrum, with an Fi,j(δi, δj) to Fi,i(δi, δi) intensity ratio given by tan(2πDi,j TA)tan(2πDi,j TB), neglecting the difference in relaxation of protons i and j. Similar j → i terms are obtained by interchanging the indices i and j. In practice, the experiment is recorded in a 3D mode, but as very extensive folding can be used (Fig. 3) relatively few complex points are required for the F2 dimension.
For each duration of t1, the (t2, t3) plane is processed as described above for generating the 1D homonuclear decoupled spectrum, resulting in a S(t1, F2) spectrum, which is then Fourier-transformed with respect to t1, yielding the final 2D spectrum. For extracting the homonuclear dipolar coupling directly from this projected 2D spectrum, an additional scale factor applies that depends on the mode of projection (skyline or integration) and apodization used in the projection process of each (t2,t3) plane. Its effect can be eliminated by calculating Di,j from:
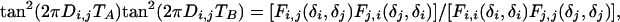 |
[4] |
where Fi,j(δi, δj) represents the cross peak intensity between protons i (F1 dimension) and j (F2 dimension).
Application to a B-Form DNA Oligomer. The experiments described above are demonstrated for a double-stranded B-form DNA oligomer: d(CGCGAATTCGCG)2. In the absence of 13C enrichment, transverse relaxation times of the H1′ resonances are quite favorable and are ∼150 ms. This allows the use of reasonably long durations of the constant time evolution periods. For example, for generating the spectrum of Fig. 1C, a t1 acquisition time of 144 ms was used, resulting in excellent resolution. For the constant-time COSY experiment of Fig. 2B, two such evolution periods are present, and for sensitivity considerations shorter transfer delays of 2 T = 81 ms are used for the constant-time evolution periods. The alignment of the dodecamer in the ether-bicelle medium (44) is described by a nearly axially symmetric alignment tensor (rhombicity, R = 0.25) of magnitude 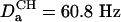 (Aa = 2.77 × 10–3). For a pair of protons, separated by 7 Å on a vector parallel to the unique axis of the tensor, this corresponds to a DHH dipolar coupling of 1.83 Hz, or a cross peak to diagonal peak ratio of 0.25. The smallest ratios observed in the spectrum are on the order of 0.006, corresponding to an internuclear separation of 12.7 Å if the vector were parallel to the unique axis of the alignment tensor.
(Aa = 2.77 × 10–3). For a pair of protons, separated by 7 Å on a vector parallel to the unique axis of the tensor, this corresponds to a DHH dipolar coupling of 1.83 Hz, or a cross peak to diagonal peak ratio of 0.25. The smallest ratios observed in the spectrum are on the order of 0.006, corresponding to an internuclear separation of 12.7 Å if the vector were parallel to the unique axis of the alignment tensor.
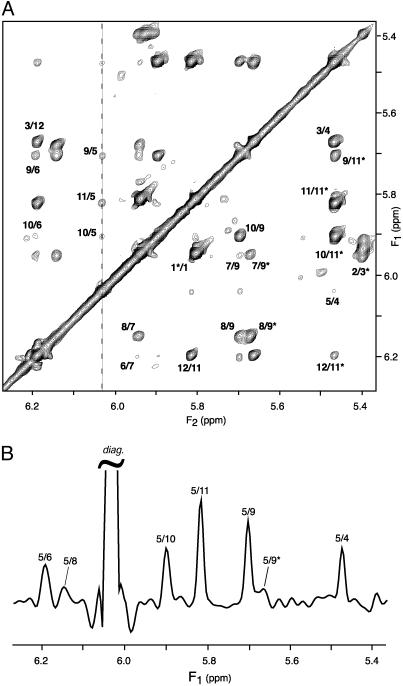
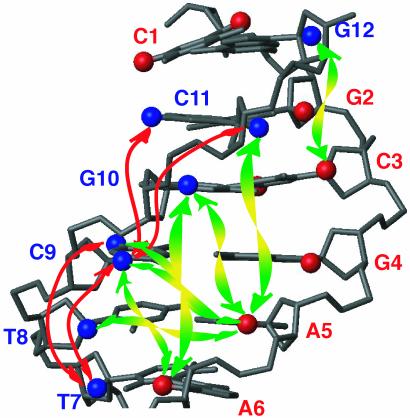
A cross section through the spectrum of Fig. 4, taken at the diagonal resonance of A5-H1′ reveals several of the weaker dipolar interactions, annotated with the corresponding pairs of protons involved in the structure. At 10.4 Å, the longest distance observed is that between A5-H1′ and C9-H5 on the opposing strand (Fig. 5), giving rise to a 0.3-Hz coupling. The orientation of this vector is nearly orthogonal to the helix axis (θ ≈ π/2 in Eq. 1b), and therefore corresponds to this relatively small coupling. The A5-H1′ to C11-H1′ vector is nearly parallel to the helix axis and at a comparable internuclear separation of 9.7 Å yields a >2-fold larger coupling and a correspondingly more intense cross peak (Fig. 4B).
Fig. 4.
1H-1H dipolar correlation spectra of d(CGCGAATTCGCG)2, homonuclear band-selectively decoupled, recorded at 600 MHz in 12% ether bicelle medium. (A) Projection of the 3D spectrum along the F3 axis onto the 2D (F1,F2) plane, displaying the dipolar connectivities between H1′ and H5 protons. (B)F1 cross section, taken at the frequency of A5-H1′ (6.03 ppm, marked by a dashed line in A). Spectra have been recorded with the pulse scheme of Fig. 2B. Total measurement time is 36 h, with the data matrix consisting of 40*(t1) × 20*(t2) × 256*(t3) data points, with acquisition times of 62.4 ms (t1), 60.8 ms (t2) and 51 ms (t3)(2 TA = 2 TB = 81 ms). Linear prediction was used to double the number of time-domain points in both the t1 and t2 dimensions, and all three dimensions were apodized by cosine-squared functions and zero-filled before Fourier transformation. Each (F2,F3) plane has been reduced to its homonuclear decoupled 1D equivalent, using the protocol of Fig. 3 (using a 60-Hz width for the projected central band). Intrastrand connectivities (intranucleotide, sequential, and long range) are labeled by their corresponding residue numbers on the lower right half of the spectrum, whereas the interstrand cross peaks are labeled in the upper left half of the spectrum. Only positive contour levels are displayed.
Fig. 5.
Long-range 1H-1H connectivities observed for the d(CGCGAATTCGCG)2 dodecamer, with only half of the palyndromic oligomer shown. H1′ and H5 are displayed as spheres. Nucleotides are labeled by their nucleotide numbers, with red and blue marking the opposing strands. Intrastrand and interstrand long-range connectivities are indicated by red and green arrows, respectively.
Discussion
Weak alignment offers numerous new opportunities in structural studies of macromolecules. They not only improve local structural characteristics, such as the Ramachandran map distribution when applied to proteins (45), but also can define global features at high accuracy, including DNA bending (32, 46, 47) and relative orientations of proteins in complexes (48). In addition, they potentially can reveal details about internal dynamics, including their amplitude and directions, provided the motional amplitudes are sufficiently large (49).
De novo structure determination on the basis of dipolar couplings has also been demonstrated, but remains challenging if only one-bond heteronuclear dipolar couplings are available (50–52). In this case, the lack of distance restraints makes it difficult to correctly translate elements of well-defined local structure relative to one another. 1H–1H dipolar couplings may prove to be a useful complement in this respect. Their measurement is not afflicted by spin diffusion effects and therefore can provide more accurate distance information, albeit with increased error bounds when the dipolar interactions are very weak. Our results demonstrate that 1H–1H dipolar interactions are detectable up to distances of at least 12 Å, well beyond the reach of direct nuclear Overhauser effect interactions (≤6 Å). These remote 1H–1H dipolar couplings may prove particularly useful in the assembly of parts of well-defined local structure, such as helical regions in complex nucleic acid structures, or elements of secondary structure in proteins.
The concept of band-selective homonuclear 1H decoupling is likely to be beneficial to a wide range of experiments, both in proteins and nucleic acids, and is not restricted to the measurement of dipolar couplings. Particularly in experiments that use direct observation of the 13C spectrum, where homonuclear couplings severely affect attainable resolution, significant gains may be achievable.
Although we demonstrated the application of homonuclear decoupling and remote dipolar coupling measurement for an unlabeled nucleic acid, where 1H transverse relaxation properties are favorable, comparably favorable relaxation characteristics are encountered when considering 1H–15N or aliphatic 1H–13C two-spin coherence terms. Therefore, extension of this approach to isotopically enriched proteins and nucleic acids also appears feasible.
Acknowledgments
We thank Dennis Torchia for useful suggestions. This work was supported by a fellowship from the Human Frontier Science Program (to J.B.).
This contribution is part of the special series of Inaugural Articles by members of the National Academy of Sciences elected on April 30, 2002.
References
- 1.Saupe, A. & Englert, G. (1963) Phys. Rev. Lett. 11, 462–464. [Google Scholar]
- 2.Emsley, J. W. (1996) in Encyclopedia of Nuclear Magnetic Resonance, eds. Grant, D. M. & Harris, R. K. (Wiley, Chichester, U.K.), Vol. 4, pp. 2788–2799. [Google Scholar]
- 3.Burnell, E. E. & DeLange, C. A. (2003) NMR or Ordered Liquids (Kluwer, Boston).
- 4.Tolman, J. R., Flanagan, J. M., Kennedy, M. A. & Prestegard, J. H. (1995) Proc. Natl. Acad. Sci. USA 92, 9279–9283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Banci, L., Bertini, I., Huber, J. G., Luchinat, C. & Rosato, A. (1998) J. Am. Chem. Soc. 120, 12903–12909. [Google Scholar]
- 6.Demene, H., Tsan, P., Gans, P. & Marion, D. (2000) J. Phys. Chem. B 104, 2559–2569. [Google Scholar]
- 7.Ma, C. & Opella, S. J. (2000) J. Magn. Reson. 146, 381–384. [DOI] [PubMed] [Google Scholar]
- 8.Gaponenko, V., Dvoretsky, A., Walsby, C., Hoffman, B. M. & Rosevear, P. R. (2000) Biochemistry 39, 15217–15224. [DOI] [PubMed] [Google Scholar]
- 9.Tjandra, N. & Bax, A. (1997) Science 278, 1111–1114. [DOI] [PubMed] [Google Scholar]
- 10.Bax, A. & Tjandra, N. (1997) J. Biomol. NMR 10, 289–292. [DOI] [PubMed] [Google Scholar]
- 11.Gaemers, S. & Bax, A. (2001) J. Am. Chem. Soc. 123, 12343–12352. [DOI] [PubMed] [Google Scholar]
- 12.Nieh, M. P., Glinka, C. J., Krueger, S., Prosser, R. S. & Katsaras, J. (2001) Langmuir 17, 2629–2638. [Google Scholar]
- 13.Sanders, C. R. & Schwonek, J. P. (1992) Biochemistry 31, 8898–8905. [DOI] [PubMed] [Google Scholar]
- 14.Sanders, C. R., Hare, B. J., Howard, K. P. & Prestegard, J. H. (1994) Prog. Nucl. Magn. Reson. Spectrosc. 26, 421–444. [Google Scholar]
- 15.Clore, G. M., Starich, M. R. & Gronenborn, A. M. (1998) J. Am. Chem. Soc. 120, 10571–10572. [Google Scholar]
- 16.Hansen, M. R., Mueller, L. & Pardi, A. (1998) Nat. Struct. Biol. 5, 1065–1074. [DOI] [PubMed] [Google Scholar]
- 17.Fleming, K., Gray, D., Prasannan, S. & Matthews, S. (2000) J. Am. Chem. Soc. 122, 5224–5225. [Google Scholar]
- 18.Ruckert, M. & Otting, G. (2000) J. Am. Chem. Soc. 122, 7793–7797. [Google Scholar]
- 19.Prosser, R. S., Losonczi, J. A. & Shiyanovskaya, I. V. (1998) J. Am. Chem. Soc. 120, 11010–11011. [Google Scholar]
- 20.Tycko, R., Blanco, F. J. & Ishii, Y. (2000) J. Am. Chem. Soc. 122, 9340–9341. [Google Scholar]
- 21.Sass, H. J., Musco, G., Stahl, S. J., Wingfield, P. T. & Grzesiek, S. (2000) J. Biomol. NMR 18, 303–309. [DOI] [PubMed] [Google Scholar]
- 22.Yang, D. W., Venters, R. A., Mueller, G. A., Choy, W. Y. & Kay, L. E. (1999) J. Biomol. NMR 14, 333–343. [Google Scholar]
- 23.Zidek, L., Wu, H. H., Feigon, J. & Sklenar, V. (2001) J. Biomol. NMR 21, 153–160. [DOI] [PubMed] [Google Scholar]
- 24.Yan, J. L., Corpora, T., Pradhan, P. & Bushweller, J. H. (2002) J. Biomol. NMR 22, 9–20. [DOI] [PubMed] [Google Scholar]
- 25.Tjandra, N., Marquardt, J. & Clore, G. M. (2000) J. Magn. Reson. 142, 393–396. [DOI] [PubMed] [Google Scholar]
- 26.Wu, Z., Delaglio, F., Tjandra, N., Zhurkin, V. B. & Bax, A. (2003) J. Biomol. NMR 26, 297–315. [DOI] [PubMed] [Google Scholar]
- 27.Wing, R., Drew, H., Takano, T., Broka, C., Tanaka, S., Itakura, K. & Dickerson, R. E. (1980) Nature 287, 755–758. [DOI] [PubMed] [Google Scholar]
- 28.Tereshko, V., Minasov, G. & Egli, M. (1999) J. Am. Chem. Soc. 121, 470–471. [Google Scholar]
- 29.Shui, X. Q., McFail-Isom, L., Hu, G. G. & Williams, L. D. (1998) Biochemistry 37, 8341–8355. [DOI] [PubMed] [Google Scholar]
- 30.Nerdal, W., Hare, D. R. & Reid, B. R. (1989) Biochemistry 28, 10008–10021. [DOI] [PubMed] [Google Scholar]
- 31.Denisov, A. Y., Zamaratski, E. V., Maltseva, T. V., Sandstrom, A., Bekiroglu, S., Altmann, K. H., Egli, M. & Chattopadhyaya, J. (1998) J. Biomol. Struct. Dyn. 16, 547–568. [DOI] [PubMed] [Google Scholar]
- 32.Tjandra, N., Tate, S., Ono, A., Kainosho, M. & Bax, A. (2000) J. Am. Chem. Soc. 122, 6190–6200. [Google Scholar]
- 33.Young, M. A., Ravishanker, G. & Beveridge, D. L. (1997) Biophys. J. 73, 2313–2336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.McConnell, K. J. & Beveridge, D. L. (2000) J. Mol. Biol. 304, 803–820. [DOI] [PubMed] [Google Scholar]
- 35.Wu, Z. R. & Bax, A. (2002) J. Am. Chem. Soc. 124, 9672–9673. [DOI] [PubMed] [Google Scholar]
- 36.Delaglio, F., Grzesiek, S., Vuister, G. W., Zhu, G., Pfeifer, J. & Bax, A. (1995) J. Biomol. NMR 6, 277–293. [DOI] [PubMed] [Google Scholar]
- 37.Aue, W. P., Karhan, J. & Ernst, R. R. (1976) J. Chem. Phys. 64, 4226–4227. [Google Scholar]
- 38.Bax, A., Mehlkopf, A. F. & Smidt, J. (1979) J. Magn. Reson. 35, 167–169. [Google Scholar]
- 39.Geen, H. & Freeman, R. (1991) J. Magn. Reson. 93, 93–141. [Google Scholar]
- 40.Bachmann, P., Aue, W. P., Müller, L. & Ernst, R. R. (1977) J. Magn. Reson. 28, 29–39. [Google Scholar]
- 41.Palmer, A. G., Cavanagh, J., Wright, P. E. & Rance, M. (1991) J. Magn. Reson. 93, 151–170. [Google Scholar]
- 42.Zhu, G. & Bax, A. (1990) J. Magn. Reson. 90, 405–410. [Google Scholar]
- 43.Aue, W. P., Bartholdi, E. & Ernst, R. R. (1976) J. Chem. Phys. 64, 2229–2246. [Google Scholar]
- 44.Ottiger, M. & Bax, A. (1999) J. Biomol. NMR 13, 187–191. [DOI] [PubMed] [Google Scholar]
- 45.Tjandra, N., Omichinski, J. G., Gronenborn, A. M., Clore, G. M. & Bax, A. (1997) Nat. Struct. Biol. 4, 732–738. [DOI] [PubMed] [Google Scholar]
- 46.Vermeulen, A., Zhou, H. J. & Pardi, A. (2000) J. Am. Chem. Soc. 122, 9638–9647. [Google Scholar]
- 47.Barbic, A., Zimmer, D. P. & Crothers, D. M. (2003) Proc. Natl. Acad. Sci. USA 100, 2369–2373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Clore, G. M. (2000) Proc. Natl. Acad. Sci. USA 97, 9021–9025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Meiler, J., Prompers, J. J., Peti, W., Griesinger, C. & Bruschweiler, R. (2001) J. Am. Chem. Soc. 123, 6098–6107. [DOI] [PubMed] [Google Scholar]
- 50.Delaglio, F., Kontaxis, G. & Bax, A. (2000) J. Am. Chem. Soc. 122, 2142–2143. [Google Scholar]
- 51.Hus, J. C., Marion, D. & Blackledge, M. (2001) J. Am. Chem. Soc. 123, 1541–1542. [DOI] [PubMed] [Google Scholar]
- 52.Rohl, C. A. & Baker, D. (2002) J. Am. Chem. Soc. 124, 2723–2729. [DOI] [PubMed] [Google Scholar]