Abstract
Although the binding change mechanism of rotary catalysis by which F1-ATPase hydrolyzes ATP has been supported by equilibrium, kinetic, and structural observations, many questions concerning the function remain unanswered. Because of the importance of this enzyme, the search for a full understanding of its mechanism is a key problem in structural biology. Making use of the results of free energy simulations and experimental binding constant measurements, a model is developed for the free energy change during the hydrolysis cycle. This model makes possible the development of a kinetic scheme for ATP hydrolysis by F1-ATPase, in which the rate constants are associated with specific configurations of the β subunits. An essential new element is that the strong binding site for ADP,Pi is shown to be the βDP site, in contrast to the strong binding site for ATP, which is βTP. This result provides a rationale for the rotation of the γ subunit, which induces the cooperativity required for a tri-site binding change mechanism. The model explains a series of experimental data, including the ATP concentration dependence of the rate of hydrolysis and catalytic site occupation for both the Escherichia coli F1-ATPase (EcF1) and Thermophilic Bacillus PS3 F1-ATPase (TF1), which have different behavior.
The F1Fo-ATP synthase is a widely distributed enzyme that couples the translocation of protons through biological membranes to ATP synthesis or hydrolysis (1–3). The Fo portion forms a transmembrane proton conduction path, but its atomic resolution structure has not been determined. The nonmembrane-bound F1 complex hydrolyzes ATP and is, therefore, called F1-ATPase. The structure of F1-ATPase from bovine heart mitochondria (MF1) with the stoichiometry of α3β3δγε, has been determined with a variety of ligands (1, 2, 4, 5). The three α and three β subunits are arranged in alternation around a central α-helical coiled-coil that is part of the γ subunit. Each of the β subunits has a catalytic nucleotide-binding site, whereas the α subunits have noncatalytic nucleotide-binding sites (3–5). In the x-ray structures of the bovine mitochondrial F1-ATPase (1), the three catalytic sites have different conformations due primarily to their different interactions with the γ subunit. In ATP hydrolysis or synthesis by F1Fo-ATP synthase, the γ subunit, together with the Fo complex, undergoes rotation with respect to the α and β subunits (1, 2, 4–7). The γ subunit is asymmetric, and it has been suggested that its rotation modulates the structure, and by extension, the nucleotide-binding affinities of the catalytic sites (8, 9), in accord with single molecule experiments (10, 11) and macroscopic measurements (12–14). The relation between the rotation of the γ subunit and the conformational changes in the β subunits has been investigated by use of a structural interpolation scheme (15), and more recently by molecular dynamics simulations (16, 17), which also provide information concerning the forces involved.
F1-ATPase hydrolyzes ATP to ADP plus Pi (Pi corresponds to 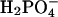 ) under optimum conditions with a kcat of 40 and 600 s–1, depending on the organism and mutant type that was studied (4, 5). This rate corresponds to an acceleration by a factor of 5 × 108 to 8 × 109, relative to the rate constant for hydrolysis in solution (8 × 10–8 s–1) (18). Unisite measurements for the Escherichia coli F1-ATPase (EcF1) have shown an acceleration of the hydrolysis reaction, per se, to 0.12 s–1, but the overall unisite rate is only 1.2 × 10–3 s–1 (8) because product release is rate limiting. The rotation of a noncatalytic subunit (the γ subunit), as embodied in the binding change mechanism proposed by Boyer (9), leads to an increase in the observed hydrolysis rate by a factor of up to 5 × 105. This enhancement arises from two complementary contributions. The first is the separation of the chemical step from the product release step with a speed-up of the latter by multisite catalysis; i.e., catalysis takes place in one conformation of the β subunit and product release in another. In addition, the chemical step is accelerated by a factor of 300 or more, relative to its rate in unisite catalysis, to achieve the overall observed rate of 40 to 600 s–1; the exact value is not known because only overall rates have been measured. (We note that, for ATP synthesis, the separation of the chemical step, synthesis of ATP, and the physical step, binding of ADP and Pi and not of ATP, is also an essential part of the mechanism.) Rotary catalysis accelerates a nonchemical step (i.e., product release) and in addition accelerates the chemical step so that it keeps up with the accelerated product release step.
) under optimum conditions with a kcat of 40 and 600 s–1, depending on the organism and mutant type that was studied (4, 5). This rate corresponds to an acceleration by a factor of 5 × 108 to 8 × 109, relative to the rate constant for hydrolysis in solution (8 × 10–8 s–1) (18). Unisite measurements for the Escherichia coli F1-ATPase (EcF1) have shown an acceleration of the hydrolysis reaction, per se, to 0.12 s–1, but the overall unisite rate is only 1.2 × 10–3 s–1 (8) because product release is rate limiting. The rotation of a noncatalytic subunit (the γ subunit), as embodied in the binding change mechanism proposed by Boyer (9), leads to an increase in the observed hydrolysis rate by a factor of up to 5 × 105. This enhancement arises from two complementary contributions. The first is the separation of the chemical step from the product release step with a speed-up of the latter by multisite catalysis; i.e., catalysis takes place in one conformation of the β subunit and product release in another. In addition, the chemical step is accelerated by a factor of 300 or more, relative to its rate in unisite catalysis, to achieve the overall observed rate of 40 to 600 s–1; the exact value is not known because only overall rates have been measured. (We note that, for ATP synthesis, the separation of the chemical step, synthesis of ATP, and the physical step, binding of ADP and Pi and not of ATP, is also an essential part of the mechanism.) Rotary catalysis accelerates a nonchemical step (i.e., product release) and in addition accelerates the chemical step so that it keeps up with the accelerated product release step.
For a detailed understanding of the binding change mechanism, it is necessary to relate (19) the macroscopic thermodynamic and kinetic measurements to the four different conformations of the catalytic β subunits (βTP, βDP, βE, βHC) observed in the x-ray structures (1, 2). There are three measured binding constants, referred to as “tight,” “loose,” and “open” (1–3) or H, M, and L, respectively (5). Although the identification of the open (L) site with βE is generally accepted, it has not been possible experimentally to determine which of the βTP and βDP sites are the tight and loose binding sites, respectively, (see, e.g., refs. 1, 2, and 20). It was demonstrated recently by use of a combination of simulation and experimental data (19) that the βTP is the tight site for ATP binding. Also, the agreement between the calculated free energies of the reaction and the experimental data (see Table 1) provides support for the conclusion that the crystal structures represent the structures of the sites in solution. Given this result, it is now possible to begin to develop a mechanism for F1-ATPase that couples the structural information with the experimental thermodynamic and kinetic data.
Table 1. Binding constants KD, binding affinities (kcal/mol), and standard free energy differences between ATP and ADP+Pi (kcal/mol) at various binding sites.
| βTP | βDP | βE | βHC | |
|---|---|---|---|---|
| KD for ATP | 0.2 nM* (-13.24) | 2 μM† (-7.78) | 25 μM* (-6.28) | 5 mM‡ (-3.14) |
| KD for ADP | 29 μM* (-6.19) | 0.05 μM* (-9.96) | 29 μM* (-6.19) | 25 μM‡ (-6.27) |
| KD for Pi | 0.5 M§ (-0.37) | 0.5 M§ (-0.37) | 0.5 M§ (-0.37) | 1 mM‡ (-4.09) |
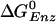 (est.)¶ (est.)¶
|
-0.63 | -9.8 | -7.8 | -14.3 |
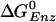 (cal.)∥ (cal.)∥
|
1.4 | -9.2 | — | -12.7 |
From ref. 5.
From ref. 24 and see text.
From ref. 25.
Estimated for the βTP site as in the text. In the absence of data, it was assumed to be the same for all three sites involved in ATP hydrolysis. Senior (29) obtained a lower limit for all sites under the hydrolysis condition of >10 mM.
Estimated numbers from the present work for EcF1. The one for βTP is taken from ref. 8.
From ref. 19 for MF1.
A number of insightful pictorial models for the function of F1-ATPase has been proposed (2, 4, 5, 14, 21), but none of them have been used to give a quantitative description of the thermodynamics and kinetics of the enzyme. In addition, Wang and Oster (15) proposed a detailed model of the enzyme based on fitting some experimental results. Their chemomechanical model (15) uses the unisite catalysis measurements with certain assumptions and the introduction of several empirical factors to obtain the high rate constants observed in multisite catalysis. The present approach is very different from that of Wang and Oster. We introduce a chemical kinetic model for ATP hydrolysis by F1-ATPase based on experimental and simulation results. The model takes into account explicitly the negative cooperativity of ATP and ADP,Pi binding and its role in the positive cooperativity of the kinetics. The different properties of the βTP, βDP, and βE catalytic sites, which are identified by the free energy simulations, play an essential role in associating the structural results with the kinetic data.
A free energy profile for the β subunit catalytic sites during the hydrolysis cycle is constructed. It is based on the binding free energies of ATP and ADP,Pi in the βTP, βDP, and βE sites. The profile is significantly different from that obtained from unisite measurements for the tight binding site (5, 15). Using the free energy profile, we identify the measured rate constants with specific sites and propose a kinetic mechanism that explains a large body of the available experimental data, including the ATP concentration dependence of the hydrolysis rate and the occupation of the catalytic sites. The dynamics of the coupling between the β and γ subunits are not considered explicitly; i.e., we formally treat the process as “adiabatic” in that the binding of the reactant and products of the hydrolysis reaction to the β subunits leads to certain conformational changes that induce the rotation of the γ subunit.
Thermodynamic Aspects of F1-ATPase
Free Energy Analysis. An essential quantity involved in the binding change mechanism of Boyer (3, 4) is the free energy difference, 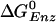 , between ATP(+H2O) and ADP+Pi, at each catalytic site of the β subunits, Pi corresponding to
, between ATP(+H2O) and ADP+Pi, at each catalytic site of the β subunits, Pi corresponding to 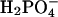 . Given the identification of the βTP and βDP sites as the tight and loose site for ATP from the free energy simulations of MF1 (19), we use experimental measurements for EcF1 of the binding constants for ATP and ADP,Pi to obtain quantitative values of
. Given the identification of the βTP and βDP sites as the tight and loose site for ATP from the free energy simulations of MF1 (19), we use experimental measurements for EcF1 of the binding constants for ATP and ADP,Pi to obtain quantitative values of 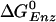 for each of the sites in the latter enzyme (see Table 1 and see section A of Supporting Text, which is published as supporting information on the PNAS web site, www.pnas.org). These values can be obtained by employing the thermodynamic cycle shown in Scheme 1 where
for each of the sites in the latter enzyme (see Table 1 and see section A of Supporting Text, which is published as supporting information on the PNAS web site, www.pnas.org). These values can be obtained by employing the thermodynamic cycle shown in Scheme 1 where 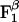 refers to each of the catalytic subunits βTP, βDP, βE, or βHC identified in the crystal structures. The quantity
refers to each of the catalytic subunits βTP, βDP, βE, or βHC identified in the crystal structures. The quantity 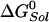 is the standard hydrolysis free energy of ATP in solution in the presence of physiological concentrations of Mg2+ [
is the standard hydrolysis free energy of ATP in solution in the presence of physiological concentrations of Mg2+ [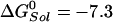 kcal/mol for Mg2+ equal to 3 mM (22)]. The quantities,
kcal/mol for Mg2+ equal to 3 mM (22)]. The quantities, 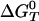 and
and 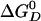 are the standard binding free energies of ATP and ADP+Pi at the
are the standard binding free energies of ATP and ADP+Pi at the 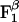 site under consideration. Thus,
site under consideration. Thus,
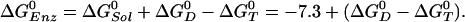 |
[1] |
Scheme 1.
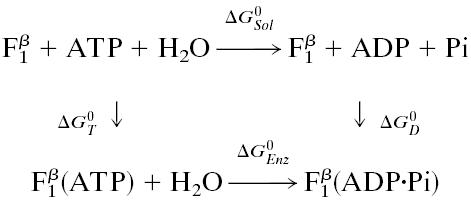
Based on the nucleotide concentration dependence of the number of occupied sites, Senior and coworkers (13) obtained three ATP binding constants for EcF1; they are <0.1 μM, ≈0.5 μM and ≈25 μM. Using the same technique, the binding constants for ADP, in the presence of 5 mM Pi, were determined to be 0.05 μM, 29 μM, and 29 μM (23). Grüber and Capaldi (24) studied ATP binding to EcF1 with the β and γ subunits crosslinked so that no multisite hydrolysis could occur; they obtained the values of <0.1 μM, 2 μM, and 30 μM, respectively. Also, the binding constant of ATP at the tight binding site in EcF1 has been determined directly to be ≈0.2 nM by using radioactive ATP (5, 8). All these experimental values were obtained at 2.5 mM Mg2+, the physiological concentration. For the dissociation constant of Pi from a β site, a lower limit of 10 mM for all three sites was estimated for EcF1 by Senior and coworkers (5).
To determine the tight site for ADP,Pi, we use experimental data and simulation results (19). The measured ATP binding affinity is 5.5 kcal/mol greater in the tight site [KD = 0.2 nM (5)] than in the loose site [KD = 2 μM (24)]). Combining this value with the fact that the calculated 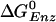 decreases by 10.6 kcal/mol in going from the tight to the loose ATP site (i.e., the calculated values are 1.4 and –9.2 kcal/mol, respectively; see Table 1), we find that the binding affinity for ADP+Pi is ≈5.1 kcal/mol greater in the βDP site than in the βTP site (see Supporting Text, section A). The measured
decreases by 10.6 kcal/mol in going from the tight to the loose ATP site (i.e., the calculated values are 1.4 and –9.2 kcal/mol, respectively; see Table 1), we find that the binding affinity for ADP+Pi is ≈5.1 kcal/mol greater in the βDP site than in the βTP site (see Supporting Text, section A). The measured 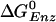 [–0.63 kcal/mol (8)] for the tight site then yields a value of 0.5 M for the KD of Pi, consistent with the experimental limits (5). Moreover, with this value (KD = 0.5 M) for Pi, and the measured values 2 μM and 0.05 μM for the KD of ATP and ADP binding, respectively, in the loose site for ATP, we obtain
[–0.63 kcal/mol (8)] for the tight site then yields a value of 0.5 M for the KD of Pi, consistent with the experimental limits (5). Moreover, with this value (KD = 0.5 M) for Pi, and the measured values 2 μM and 0.05 μM for the KD of ATP and ADP binding, respectively, in the loose site for ATP, we obtain 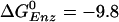 kcal/mol, again consistent with the simulation result [–9.2 kcal/mol (19)]. Thus, we conclude that the tight site for ATP binding is the loose site for ADP binding and the tight site for ADP is the loose site for ATP. This result plays an essential role in the proposed mechanism for F1-ATPase hydrolysis, as described below.
kcal/mol, again consistent with the simulation result [–9.2 kcal/mol (19)]. Thus, we conclude that the tight site for ATP binding is the loose site for ADP binding and the tight site for ADP is the loose site for ATP. This result plays an essential role in the proposed mechanism for F1-ATPase hydrolysis, as described below.
The 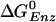 value of the βE and βHC sites can be estimated in a similar way. If the KD for Pi (0.5 M) is assumed to hold for the βE site, by using the measured KD of ATP [25 μM (5)] and ADP [29 μM; (5)], the
value of the βE and βHC sites can be estimated in a similar way. If the KD for Pi (0.5 M) is assumed to hold for the βE site, by using the measured KD of ATP [25 μM (5)] and ADP [29 μM; (5)], the 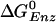 for the βE site is ≈–7.8 kcal/mol; no simulation was made for this site because of the uncertainty of placing the ligands in an empty site. For the βHC site, we assume that the binding parameters correspond to those observed under synthesis conditions (i.e., in the presence of a proton motive force) in accord with the analysis of Menz et al. (2), which indicates that the Pi site in βHC is accessible; it is occupied by sulfate. The measured KD values in the presence of a proton motive force are 5 mM for ATP and 1 mM for Pi (25). For ADP, it has been shown that the binding is not significantly altered in the presence of a proton motive force (25), so we use the highest value of 29 μM, measured in the absence of a proton motive force (5, 25). With these values, the
for the βE site is ≈–7.8 kcal/mol; no simulation was made for this site because of the uncertainty of placing the ligands in an empty site. For the βHC site, we assume that the binding parameters correspond to those observed under synthesis conditions (i.e., in the presence of a proton motive force) in accord with the analysis of Menz et al. (2), which indicates that the Pi site in βHC is accessible; it is occupied by sulfate. The measured KD values in the presence of a proton motive force are 5 mM for ATP and 1 mM for Pi (25). For ADP, it has been shown that the binding is not significantly altered in the presence of a proton motive force (25), so we use the highest value of 29 μM, measured in the absence of a proton motive force (5, 25). With these values, the 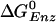 for βHC is estimated to be –14.3 kcal/mol, in satisfactory agreement with the simulation result of –12.7 kcal/mol (19). The free energy results are summarized in Table 1.
for βHC is estimated to be –14.3 kcal/mol, in satisfactory agreement with the simulation result of –12.7 kcal/mol (19). The free energy results are summarized in Table 1.
Free Energy Profile for the Hydrolysis Reaction. The results in Table 1 provide the information necessary for the construction of a free energy diagram that describes the change in the binding free energies and occupations of the three sites (βE, βTP, and βDP) during a 120° rotation of the γ subunit, the elementary cycle of the F1-ATPase hydrolysis mechanism. With the measured rotation direction of the γ subunit during ATP hydrolysis [counter-clockwise as viewed from the membrane (10)], each catalytic β subunit changes its conformation in the sequence: βE → βTP → βDP → (βHC →)βE as the γ subunit rotates by 360°.
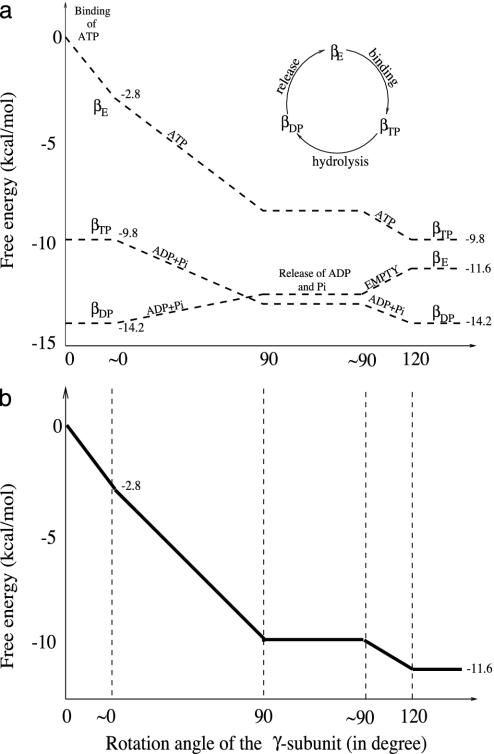
The free energy profiles of each of the three sites and that of the whole system are shown in Fig. 1 a and b for the 120° rotation cycle, respectively. The dominant species bound in each site is indicated. In constructing the diagram, we have made use of the results of Yasuda et al. (11), which show that the 120° rotation cycle consists of two parts: a 90° rotation followed by a 30° rotation with a time delay of 2 ms between the two; the measured rotation rate of the 90° and 0° steps is in the submillisecond range. In accord with one of their suggestions, we assume that the delay at 90° involves release of the hydrolysis products ADP and Pi. The delay at 30° occurs at low concentrations of ATP and is assumed to be due to the waiting time for ATP binding to the βE site.
Fig. 1.
Free energy (kcal/mol) profile for ATP hydrolysis in the trisite mechanism. (a) The individual free energy changes as a function of the conformational transitions βE → βTP, βTP → βDP, and βDP → βE are depicted for a 120° rotation of the γ subunit. The symbols (e.g., ATP) on each of the lines for the individual subunit represent the principal occupation of that site. (b) The change of the total free energy, which is the sum of the free energy changes of the three sites. It begins at 0 with βE empty and decreases by the amount corresponding to ATP hydrolysis at the end of hydrolysis cycle: i.e., ΔGT is ≈–11.6 kcal/mol with cellular concentrations corresponding to [ATP] ≈ 3 mM, [ADP] ≈ 0.4 mM, and [Pi] ≈ 6 mM (26). The free energy curves between “≈0°” and “120°” are independent of the ATP concentration. In both a and b, we connected the various crystallographic states by straight lines, as a function of the γ rotation, in accord with the analysis of Panke et al. (6) of ATP hydrolysis by the E. coli F1Fo-ATP synthase. The detailed behavior is not known, but activation barriers are expected for both the ligand-binding and release processes, as well as the chemical reactions. We show ranges for each of the important angles (0°, 90°, and 120°) to have room to indicate the molecules occupying the site and the processes that take place (i.e., ATP binding and hydrolysis and ADP,Pi release without rotation). The specific values of the angles used in the figure correspond to those in the crystal structures and the single molecule experiments and are not meant to imply that the angles are fixed in solution; i.e., fluctuations about the equilibrium positions are expected to occur.
As can be seen from Fig. 1a, an ATP binds to the empty (βE) site with a free energy change of –2.8 kcal/mol, as determined from KD = 25 μM and the cellular concentration of ATP, which is equal to 3 mM (26). The conformation of the βE site then changes to that of the βTP site due to the free energy stabilization of ≈–7.0 kcal/mol (corresponding to the decrease of KD from 25 μM to 0.2 nM, as given in Table 1). The inward movement of the β subunit involved in this conformational change drives the γ subunit rotation, as suggested by simulations (16, 17); i.e., it is the first source of energy coupling that is an essential part of the rotary binding change mechanism. The free energy difference between ATP and ADP+Pi is nearly zero at the βTP site, so that ATP hydrolysis could begin once the βTP site is formed; however, a conformational change toward that of βDP is likely to be involved because the hydrolysis rate is faster than in unisite catalysis. With the γ subunit rotation, which is induced by the change of βE to βTP, the former βTP site is transformed to a βDP site. During this process, the ATP hydrolysis reaction is expected to be essentially complete because 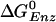 in the βDP site is –9.8 kcal/mol. Because the βDP site has a higher binding affinity for ADP+Pi than βTP, the transformation of βTP to βDP provides a second driving force for γ subunit rotation; the free energy stabilization is ≈–4.4 kcal/mol, corresponding to the free energy difference of –0.63 kcal/mol between ATP and ADP+Pi at the βTP site plus the KD changes for ADP from 29 to 0.05 μM, with KD for Pi unchanged. The rotation of the γ subunit results in the opening of the βDP site and the release of ADP, Pi. This process requires ≈2.6 kcal/mol, which is the binding free energy of ADP,Pi at the βDP site.
in the βDP site is –9.8 kcal/mol. Because the βDP site has a higher binding affinity for ADP+Pi than βTP, the transformation of βTP to βDP provides a second driving force for γ subunit rotation; the free energy stabilization is ≈–4.4 kcal/mol, corresponding to the free energy difference of –0.63 kcal/mol between ATP and ADP+Pi at the βTP site plus the KD changes for ADP from 29 to 0.05 μM, with KD for Pi unchanged. The rotation of the γ subunit results in the opening of the βDP site and the release of ADP, Pi. This process requires ≈2.6 kcal/mol, which is the binding free energy of ADP,Pi at the βDP site.
The overall free energy change in the 120° rotation cycle (Fig. 1b) is obtained by summing the contributions of the individual sites. It is equal to –11.6 kcal/mol, the hydrolysis free energy of 1 mole of ATP, given the solution concentration (see Fig. 1b legend). The present analysis shows that the release of ADP and Pi is induced by the opening of the βDP subunit (βDP → βE) and requires energy. This feature is an essential aspect of the cooperativity involved in the binding change mechanism of F1-ATPase.
We note that the free energy diagram in Fig. 1 differs from a proposal by Wang and Oster (15) in their analysis of the hydrolysis cycle of F1-ATPase. As they point out (15), their proposal is essentially a transcription of the unisite catalysis measurements (8). In the present model, the different properties of the other sites (βDP and βE) play an important role in explaining the entire hydrolysis cycle of F1-ATPase (see also Supporting Text, section C).
Kinetic Mechanism for Hydrolysis by F1-ATPase
The thermodynamics of the binding change mechanism in Fig. 1 serves as a basis for a detailed chemical kinetic model, which provides an interpretation of the macroscopic kinetic measurements in terms of the structural features of F1-ATPase. We use experimental data, where available, for the required rate constants; the rate constant kr (see Fig. 2 legend), which has not been measured for either enzyme, is the single fitted parameter of the model. A full kinetic scheme with all possible occupations of the three β subunits would require 53 = 125 states (each of the three types of sites can either be empty or be occupied by ATP, ADP,Pi, or ADP+Pi) and is beyond the scope of this article. However, it is possible to develop a “minimal” model with 6 states that correctly describes multisite ATP hydrolysis and explains how F1-ATPase functions in the absence of significant solution concentrations of ADP and Pi. The experiments (5, 11) we consider were performed under conditions such that the tight ATP site (βTP) is always occupied by ATP; i.e., the ATP concentrations are always higher than the dissociation constant at the βTP site [KD is 0.2 nM for EcF1 and 1 pM for TF1 (5)].
Fig. 2.
(a) Kinetic scheme for multisite hydrolysis of ATP by F1-ATPase. S represents an ATPase with the βTP site occupied, because it is always occupied by ATP under the condition considered (see text). S(βE,T) has βTP and βE both occupied by ATP; S(βDP,T) has βTP and βDP both occupied by ATP, whereas S(βDP,D) has βTP and βDP occupied by ATP and ADP, respectively. All three catalytic sites of S(βE,T;βDP,T) and S(βE,T;βDP,D) are occupied. The symbol T represents an ATP and the D stands for an ADP+Pi. The ki values are rate constants (see text and legend of Fig. 3). (b) Schematic diagram for the ATP hydrolysis reaction, where only the species important for ATP hydrolysis (see text) are shown.
Given the solution conditions (see also Supporting Text, section D), the kinetic scheme that describes the hydrolysis reaction to a reasonable accuracy is shown in Fig. 2. The kinetic equations are given in Fig. 2a, with the states of the F1-ATPase species illustrated in Fig. 2b (see the Fig. 2 legend for the notation). The figure starts with an initiation step S → S(βE,T) → S(βDP,D). With increased nucleotide binding, the system proceeds to the trisite mechanism S(βDP,D) → S(βE,T;βDP,D) → S(βDP,D), corresponding to the fully active F1-ATPase. In initiation, an F1-ATPase with the βTP site occupied by an ATP (species S) can bind a second ATP to either the βE or βDP subunits, forming S(βE,T) or S(βDP,T). A third ATP can then be bound to the remaining subunit, yielding the species S(βE,T;βDP,T) with all three sites occupied by ATP; the latter does not contribute significantly to the reaction (see below), but does play a role in the measured occupation of the β sites.
The binding of an ATP to the βE site to yield S(βE,T) is associated with a stabilization energy of ≈2.8 kcal/mol at cellular conditions, but this step generates no free energy gradient for rotation, because there is already an ATP in the βTP site. The next step in the reaction is the transformation of S(βE,T) into S(βDP,D) with a rate constant kr. This reaction involves both the hydrolysis of ATP to ADP,Pi and the rotation of the γ subunit by 120°. (Although we do not consider the details here, the latter is likely to involve Brownian motion biased by the free energy gradient arising from the different stabilities of the two species.) The overall standard free energy change of this process (with an ATP always bound to the βTP site) is equal to the free energy difference between an ATP bound to the βE site and an ADP,Pi bound to the βDP site; the change is 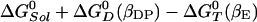 , which is ≈–11.4 kcal/mol (see Table 1). The hydrolysis of ATP to ADP,Pi provides a free energy gradient that contributes to the transformation of βTP site to a βDP site because the latter subunit binds ADP+Pi more strongly that the former subunit (the βTP to βDP line in Fig. 1). In unisite catalysis, this gradient is by itself not sufficient to induce the rotation on the time scale of the reaction. However, in the presence of higher concentrations of ATP, this rotational free energy contribution is strengthened by the fact that the βE site, containing an ATP, is simultaneously transformed to βTP (the βE to βTP line in Fig. 1). Once S(βDP,D) is formed, an ATP binds to the βE site and the trisite ATP hydrolysis mechanism becomes operational. The overall ATP hydrolysis rate under trisite conditions is denoted in Fig. 2 by kt. It corresponds to the ATP hydrolysis rate [i.e., S(βE,T;βDP,D) → S(βDP,D)] at saturating concentrations of ATP. The standard free energy change in the full 120° rotation is
, which is ≈–11.4 kcal/mol (see Table 1). The hydrolysis of ATP to ADP,Pi provides a free energy gradient that contributes to the transformation of βTP site to a βDP site because the latter subunit binds ADP+Pi more strongly that the former subunit (the βTP to βDP line in Fig. 1). In unisite catalysis, this gradient is by itself not sufficient to induce the rotation on the time scale of the reaction. However, in the presence of higher concentrations of ATP, this rotational free energy contribution is strengthened by the fact that the βE site, containing an ATP, is simultaneously transformed to βTP (the βE to βTP line in Fig. 1). Once S(βDP,D) is formed, an ATP binds to the βE site and the trisite ATP hydrolysis mechanism becomes operational. The overall ATP hydrolysis rate under trisite conditions is denoted in Fig. 2 by kt. It corresponds to the ATP hydrolysis rate [i.e., S(βE,T;βDP,D) → S(βDP,D)] at saturating concentrations of ATP. The standard free energy change in the full 120° rotation is 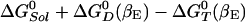 , which is ≈–7.5 kcal/mol. We note that binding of an ATP to the βDP site of a βTP-occupied F1-ATPase to form S(βDP,T) (see Fig. 2) is a side reaction because it does not change the β subunit conformations, since there is no driving force for the rotation of the γ subunit.
, which is ≈–7.5 kcal/mol. We note that binding of an ATP to the βDP site of a βTP-occupied F1-ATPase to form S(βDP,T) (see Fig. 2) is a side reaction because it does not change the β subunit conformations, since there is no driving force for the rotation of the γ subunit.
Analysis of Experiments
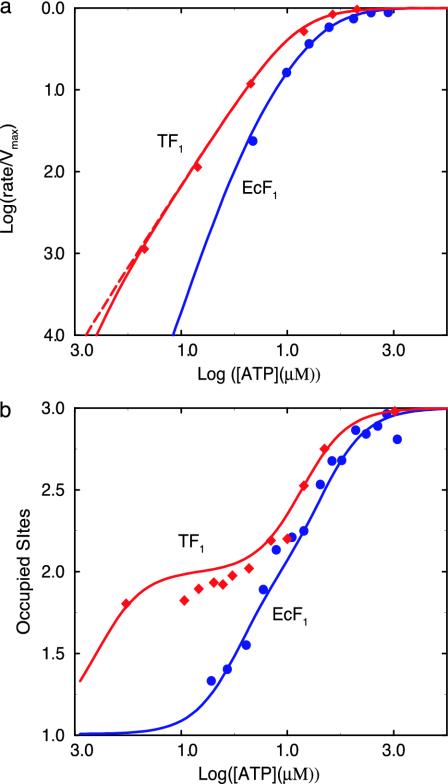
Rate of ATP Hydrolysis. We now use the reaction scheme in Fig. 2 to analyze experimental results for EcF1, and TF1; the first was studied in solution by the Senior group (5) and the second by the group of Yoshida by using single molecule techniques (11). To obtain the rate of ATP hydrolysis, kt[S(βE,T;βDP,D)], the steady-state approximation is used for the concentrations of all six species (see Supporting Text, section F). The calculated ATP hydrolysis rate as a function of the ATP concentration is given in Fig. 3a (see legend for details) and is in good agreement with experimental results for both TF1 and EcF1 over the entire concentration range.
Fig. 3.
(a) A log-log plot of the ATP hydrolysis rate, normalized to the maximum hydrolysis rate, as a function of the ATP concentration in the medium. Diamonds are experimental results for TF1 (11), circles are experimental results for EcF1 (5), and solid lines are the calculated results. The rate constants used for TF1 to obtain the calculated values are kt = 401 s–1 (11), k1 = 3 × 107 M–1 s–1 (11), k–1/k1 = 2 μM. [Because KM of the observed simple Michaelis–Menten kinetics was found to be ≈15 μM and KM = (k–1 + kt)/k1, k–1/k1 is ≈2 μM.] The actual values of k–1 and k1 have very little influence on the calculated results as long as KM is 15 μM. k–2 = 0.0016 s–1 (8), where k–2 is the experimentally measured ADP dissociation rate constant from its tight (βDP) site and kr is fitted (see text). To obtain good agreement with the experimental results, one needs kr ≥ 0.01 kt; the value used in the present calculations is 0.01 kt for the solid line and 0.1 kt for the dashed line. The values of k3 and k–3 have essentially no influence on the calculated results when k–3/k3 is in the nM to mM range; a value of 2 μM was used in the calculations. The rate constants used for EcF1 are as follows: kt = 40 s–1 (5), k1 = k3 = 2 × 106 M–1 s–1 (5), k–1/k1 = 25 μM, k–3/k3 = 2 μM (24), k–2 = 0.0016 s–1 (8), and the fitted kr is 0.001 kt.(b) The occupation of catalytic sites is a function of the ATP concentration for EcF1 and TF1. The experimental results are from refs. 5 and 27. The rate constants used to obtain this figure are those used in obtaining a.
Weber and Senior (5) measured the ATP hydrolysis rate for EcF1, and they observed a non-Michaelis–Menten dependence of the ATP hydrolysis rate for ATP submicromolar to millimolar concentrations of ATP (13). This behavior is reproduced in Fig. 3a; i.e., the rate becomes nonlinear in the μM range. As we describe below, the result is consistent with the catalytic site occupation measurements. Surprisingly, by using single molecule spectroscopic techniques, Yasuda et al. (11) showed that the rotation rate of the γ subunit in TF1 follows simple Michaelis–Menten kinetics over an ATP concentrations range extending from 20 nM to 3 mM. This result, which is different from the behavior of EcF1, was confirmed by ensemble hydrolysis rate measurements (11). By using the binding constants of the β sites (see Table 1), on average only one site would be occupied by an ATP at concentrations as low as 20 nM, whereas at concentrations >100 μM, all three sites would be highly occupied (see Figs. 4 and 5, which are published as supporting information on the PNAS web site). If the number of ATP bound to the β subunits determined the hydrolysis mechanism, one would expect that F1-ATPase would function by different mechanisms (bi- and trisite mechanisms, respectively) at low (lower than the two larger ATP dissociation constants but higher than the smallest one) and high ATP concentrations. This result would mean that, in the 20-nM and 3-mM ATP concentration range, at least two apparent Michaelis–Menten constants would be observed, in disagreement with experiment.
However, as described above (see Fig. 2b), during steady-state ATP hydrolysis, the ADP,Pi bound to the βDP site comes from the hydrolysis of ATP in the βTP site. As long as the βTP site is occupied by an ATP and at the same time the βDP site is occupied by ADP,Pi, binding of ATP to the βE site leads to the trisite mechanism. The βTP site is always occupied under the conditions considered here, and the βDP site is occupied as long as the release of ADP,Pi from the βDP site of S(βDP,D) with a rate constant k–2 [which is ≈2 × 10–3 s–1 (8)] is slow compared with the rate of the reaction S(βE,T) → S(βDP,D), as determined by kr (the fitted parameter, see Fig. 2). Thus, although there is no ADP,Pi in the solution, the βDP site is expected to be occupied by ADP,Pi during steady state ATP hydrolysis even when the ATP concentration is lower than the ATP dissociation constant of the βDP site, and F1-ATPase functions by the trisite mechanism. The main difference between TF1 and EcF1 is that both k1 (measured) and kr (fitted) are larger for the former, which together lead to a faster rate of S(βDP,D) formation and thus a higher steady-state concentration of S(βDP,D) at low concentrations of ATP for TF1 than that for EcF1. As a result, the linear (Michaelis–Menten) dependence of ATP hydrolysis on the ATP concentration continues to the concentration of 20 nM (or lower) for TF1, as seen in Fig. 3a.
Occupation of the β Sites. A quantity of interest for understanding the hydrolysis mechanism and for comparison with experiments is the average total occupancy by nucleotides (both ATP and ADP) of catalytic sites, N, as a function of ATP concentration (see also Supporting Text, section F). The results calculated for EcF1 and TF1 are shown in Fig. 3b and compared with the experimental values measured by Senior and coworkers (28) and by Allison and coworkers (27); the latter results are very recent and were found by us only after the present work was completed.
In steady state hydrolysis at high concentrations of ATP (e.g., 1 mM), all three catalytic sites are calculated to be occupied by nucleotides, in agreement with the three binding constants obtained for mutant F1-ATPase (13, 24). It has been shown (11) that the rate-limiting step for ATP hydrolysis at cellular conditions is the release of ADP,Pi. This release of ADP,Pi is expected to involve a conformation near βE, with the βDP site also occupied by ADP,Pi and the βTP site occupied by ATP (see Figs. 1a and 2). Consequently, during ATP hydrolysis at high concentrations of ATP, two ADP and one ATP are expected to be bound on average [the species S(βE,D;βDP,D) in Fig. 2b], in agreement with experiment (28) (see also Fig. 4). As seen in Fig. 3b, the main difference between TF1 and EcF1 is that there exists a large plateau with an occupation of two nucleotides in the TF1 curve, reflecting the higher concentration of S(βDP,D) at these ATP concentrations. In fact, S(βDP,D) is the dominant species for TF1 as long as the ATP concentration is higher than nM (see Fig. 5), so that the trisite mechanism is operational and simple Michaelis–Menten kinetics is a good approximation (Fig. 3a), as indicated above.
Other results of the present model, such as the dependence of the speed of the rotation on the concentrations of ADP, Pi, and ATP (30), and occupations of the catalytic sites are described in Supporting Text, sections F and H.
Concluding Discussion
A model is proposed for the hydrolysis of ATP by the F1-ATPase. It serves to connect the structure, thermodynamics, and kinetics of this enzyme. The model is based on the binding change mechanism (3), and leads to trisite kinetics (5). By combining experimental measurements of binding affinities with molecule free energy simulations, we have identified the two closed sites (βTP and βDP sites, respectively) of the observed x-ray structures with the tight binding sites for the reactant and products of the hydrolysis reaction (ATP and ADP,Pi), respectively. Given this result and the binding data of Senior et al. (5, 24), we have constructed a diagram of the free energy change of the three catalytic β sites as a function of the rotation angle of the γ subunit. This result makes possible the construction of a consistent kinetic model for the binding change mechanism proposed by Boyer (3, 9, 12).
Under conditions where an ATP is always bound to the βTP site, the free energy gradient that biases the motion of the γ subunit to produce the observed cooperative rotation arises from two sources: namely, the free energy gained in binding ATP to the βTP site vs. the βE site and that gained by binding the hydrolysis product ADP,Pi to the βDP site vs. the βTP site. The only process that requires energy is the transformation of the βDP site to the βE site for release of products. Thus, under physiological conditions, the three catalytic sites function in a cooperative manner, with the binding to two sites providing the driving force required to open the third one and release the products. The enzyme shows negative cooperativity in ATP binding and positive cooperativity in ATP hydrolysis. The negative cooperativity of ATP and ADP,Pi binding is responsible for the sources of free energy for the conformational change. ATP hydrolysis with only the high affinity site occupied is slow (unisite hydrolysis), which is important for avoiding ATP hydrolysis uncoupled from the mechanical steps (e.g., proton pumping induced by the γ subunit rotation). The coupling of the negatively cooperative ATP (ADP,Pi) binding with the γ subunit rotation leads to the positive cooperativity in catalysis so that trisite hydrolysis is substantially faster than the unisite reaction. The cooperative interactions also play an important role in the synthesis of ATP by the F1Fo-ATP synthase.
The thermodynamics results were used to develop a minimal kinetic model that describes the hydrolysis reaction of F1-ATPase over a wide range of ATP concentrations. By calculating the occupancy of the β sites during the steady-state ATP hydrolysis, it was shown that the maximum hydrolysis rate is obtained during a trisite cycle. Moreover, the kinetic scheme also describes the initiation of the trisite mechanism from a nucleotide-depleted enzyme and shows how TF1, unlike EcF1, is able to function by using the trisite mechanism even at very low ATP concentrations. As a result, TF1 shows Michaelis–Menten behavior (a single KM value) down to an ATP solution concentration in the nanomolar range (30), whereas EcF1 does not.
Finally, we describe briefly the implications of the present analysis for ATP synthesis. This aspect is of particular interest because it is known that ATP hydrolysis by F1-ATPase and ATP synthesis by FoF1-ATPase in the presence of a proton motive force can occur at the same (physiological) concentrations of the substrates: i.e., with [ATP] ≈ 3 mM, [ADP] ≈ 0.4 mM, and [Pi] ≈ 6 mM (26). This behavior requires that the initial step of the reaction (i.e., binding of ATP in hydrolysis and binding of ADP+Pi in synthesis) must involve β subunits with different binding affinities and, therefore, with different structures. One possibility is that the βE site is the “open” (reactant, ATP-binding) site for hydrolysis and that the βHC site plays the corresponding role (reactants, ADP,Pi-binding) in synthesis. If the βE site serves as the “open” site for ATP hydrolysis, it should bind ATP but not ADP+Pi (25). Given the binding constants for the βE site (see Table 1) and the solution concentrations of ATP, ADP, and Pi, we find that the ratio of ATP to ADP+Pi bound in the βE site is ≈725. (When the lower limit of 10 mM is used for the Pi dissociation constant, a lower limit of 14 is obtained for this value.) Moreover, the KD for Pi is too high to bind Pi at normal concentrations to any β site under hydrolysis condition. For synthesis, one would expect the opposite: i.e., that at the beginning of the synthesis cycle, the “open” subunit binds ADP+Pi and not ATP. The βHC site satisfies this condition because it binds ADP+Pi much more strongly than ATP under synthesis conditions; the ratio of ADP+Pi bound to ATP bound is ≈145. Given the above, it seems that the ATP synthesis is not a direct inverse of ATP hydrolysis.
In this article, we have proposed a model connecting the thermodynamic and kinetic data for F1-ATPase with its structural elements. The model is similar in spirit to the one developed for connecting the structural and thermodynamic data in the cooperative ligand binding by hemoglobin (31). As shown by the single molecule experiments (10, 11), the rate-limiting step in ATP hydrolysis under the conditions described in the text is the binding of the reactant at low concentrations of ATP and the release of product(s) at high concentrations of ATP. Because the rotation time of the γ subunit is always faster, the ATP hydrolysis by F1-ATPase can be treated as a chemical process. The specifics of the chemomechanical coupling, including the diffusive aspect of the rotation of the γ subunit, will have to be considered explicitly in describing the function of F1-ATPase in the presence of an external load. Additional atomic level simulations and experiments are needed for the elaboration and validation of the present model of this “splendid molecular machine” (4, 9).
Supplementary Material
Acknowledgments
We thank Aaron Dinner and George Oster for helpful comments on the manuscript. This work was supported in part by a grant from the National Institutes of Health (to M.K.) and grants from the National Science Foundation and the Office of Naval Research (to R.A.M.).
References
- 1.Abrahams, J. P., Lesile, A. G. W., Lutter, R. & Walker, J. E. (1994) Nature 370, 621–628. [DOI] [PubMed] [Google Scholar]
- 2.Menz, R. I., Walker, J. E. & Leslie, A. G. W. (2001) Cell 106, 331–341. [DOI] [PubMed] [Google Scholar]
- 3.Boyer, P. D. (1993) Biochim. Biophys. Acta 1140, 215–250. [DOI] [PubMed] [Google Scholar]
- 4.Boyer, P. D. (1997) Annu. Rev. Biochem. 66, 717–749. [DOI] [PubMed] [Google Scholar]
- 5.Weber J. & Senior, A. E. (1997) Biochim. Biophys. Acta 1319, 19–58. [DOI] [PubMed] [Google Scholar]
- 6.Panke, O., Cherepanov, D. A., Gumbiowski, K., Engelbrecht, S. & Junge, W. (2001), Biophys. J. 81, 1220–1233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Junge, W., Panke, O., Cherepanov, D. A., Gumbiowski, K., Muller, M. & Engelbrecht, S. (2001) FEBS Lett. 504, 152–160. [DOI] [PubMed] [Google Scholar]
- 8.Senior, A. E. (1992) J. Bioenerg. Biomembr. 24, 479–484. [DOI] [PubMed] [Google Scholar]
- 9.Boyer, P. D. (1979) in Membrane Bioenergetics, ed. Lee, C. P., Schatz, C. & Ernster, L. (Addison–Wesley, Reading, MA), pp. 461–477.
- 10.Noji, H., Yasuda, R., Yoshida, M. & Kinosita, K. (1997) Nature 386, 299–302. [DOI] [PubMed] [Google Scholar]
- 11.Yasuda, R., Noji, H., Yoshida, M., Kinosita, K. & Itoh, H. (2001) Nature 410, 898–904. [DOI] [PubMed] [Google Scholar]
- 12.Boyer, P. D. (2000) Biochim. Biophys. Acta 1458, 252–262. [DOI] [PubMed] [Google Scholar]
- 13.Weber, J., Wilke-Mounts, S., Lee, R. S. F., Grell, E. & Senior, A. E. (1993) J. Biol. Chem. 268, 20126–20133. [PubMed] [Google Scholar]
- 14.Allison, W. S. (1998) Acc. Chem. Res. 31, 819–826. [Google Scholar]
- 15.Wang, H. & Oster, G. (1998) Nature 396, 279–282. [DOI] [PubMed] [Google Scholar]
- 16.Ma, J., Flynn, T. C., Cui, Q., Leslie, A., Walker, J. E. & Karplus, M. (2002) Structure 10, 921–931. [DOI] [PubMed] [Google Scholar]
- 17.Böckmann, R. A. & Grubmüller H. (2002) Nat. Struct. Biol. 9, 198–202. [DOI] [PubMed] [Google Scholar]
- 18.Khan, M. M. T. & Mohan, M. S. (1973) J. Inorg. Nucl. Chem. 35, 1749–1755. [Google Scholar]
- 19.Yang, W., Gao, Y. Q., Cui, Q., Ma, J. & Karplus, M. (2003) Proc. Natl. Acad. Sci. USA 100, 874–879. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Nakamoto, R. K., Ketchum, C. J. & Al-Shawi, M. K. (1999) Annu. Rev. Biophys. Biomol. Struct. 28, 205–234. [DOI] [PubMed] [Google Scholar]
- 21.Milgrom, Y. M., Murataliev, M. B. & Boyer, P. D. (1998) Biochem. J. 330, 1037–1043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Stryer, L. (1995) Biochemistry (Freeman, New York), p. 446.
- 23.Weber, J., Wilke-Mounts, S., Grell E. & Senior, A. E. (1994) J. Biol. Chem. 269, 11261–11268. [PubMed] [Google Scholar]
- 24.Grüber G. & Capaldi, R. A. (1996) Biochemistry 35, 3875–3879. [DOI] [PubMed] [Google Scholar]
- 25.Nakamoto, R. K., Ketchum, C. J., Kuo, P. H., Peskova, Y. B. & Al-Shawi, M. K. (2000) Biochim. Biophys. Acta 1458, 289–299. [DOI] [PubMed] [Google Scholar]
- 26.Kashket, E. R. (1982) Biochemistry 21, 5534–5538. [DOI] [PubMed] [Google Scholar]
- 27.Bandyopadhyay, S., Valder, C. R., Huynh, H. G., Ren, H. & Allison W. S. (2002) Biochemistry 41, 14421–14429. [DOI] [PubMed] [Google Scholar]
- 28.Weber, J., Bowman, C. & Senior, A. E. (1996) J. Biol. Chem. 271, 18711–18718. [DOI] [PubMed] [Google Scholar]
- 29.Weber, J. & Senior, A. E. (1998) Biochemistry 37, 10846–10853. [DOI] [PubMed] [Google Scholar]
- 30.Yasuda, R., Noji, H., Kinosita, K. & Yoshida, M. (1998) Cell 93, 1117–1124. [DOI] [PubMed] [Google Scholar]
- 31.Szabo, A. & Karplus, K. (1972) J. Mol. Biol. 72, 163–197. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.