Genetically engineered mice with an additional class of cone photoreceptors: Implications for the evolution of color vision

Abstract

Among eutherian mammals, only primates possess trichromatic color vision. In Old World primates, trichromacy was made possible by a visual pigment gene duplication. In most New World primates, trichromacy is based on polymorphic variation in a single X-linked gene that produces, by random X inactivation, a patchy mosaic of spectrally distinct cone photoreceptors in heterozygous females. In the present work, we have modeled the latter strategy in a nonprimate by replacing the X-linked mouse green pigment gene with one encoding the human red pigment. In the mouse retina, the human red pigment seems to function normally, and heterozygous female mice express the human red and mouse green pigments at levels that vary between animals. Multielectrode array recordings from heterozygous female retinas reveal significant variation in the chromatic sensitivities of retinal ganglion cells. The data are consistent with a model in which these retinal ganglion cells draw their inputs indiscriminately from a coarse-grained mosaic of red and green cones. These observations support the ideas that (i) chromatic signals could arise from stochastic variation in inputs drawn nonselectively from red and green cones and (ii) tissue mosaicism due to X chromosome inactivation could be one mechanism for driving the evolution of CNS diversity.

In vertebrates, color vision is subserved by a family of homologous visual pigments, each of which resides within a dedicated class of cone photoreceptors. Among different vertebrate species, the number and absorption maxima of the cone pigments vary, leading to diverse color vision systems. For example, most nonprimate mammals have only two cone pigments, whereas many birds and fish have four. Humans and other Old World primates have three cone pigments, which subserve a system of trichromatic color vision.

The evolution of trichromatic color vision in Old World primates appears to have occurred in two stages (1–3). Comparison of visual pigment gene sequences shows that an ancient color vision system, comprising one longer wavelength-sensitive pigment (absorption maximum >500 nm) and one shorter wavelength-sensitive pigment (absorption maximum <500 nm), predated the vertebrate radiation. This ancestral arrangement has been retained in essentially its original form in nonprimate mammals, but in Old World primates the gene encoding the longer wavelength pigment has duplicated, giving rise to two adjacent and highly homologous genes arranged in a head-to-tail configuration on the X chromosome. These two genes code for the green pigment (also called the middle wavelength or M pigment) and the red pigment (also called the long wavelength or L pigment).

A second pathway to trichromacy has evolved in most New World monkeys (2). In these species, sequence polymorphisms within the single X chromosome-linked visual pigment gene have created three alleles, with each allele encoding a pigment with a distinct spectral sensitivity. Males and homozygous females invariably exhibit dichromatic color vision, whereas heterozygous females possess trichromatic color vision. In these heterozygous females, random X inactivation early in embryogenesis produces a retinal mosaic of two spectrally distinct cone types that leads to chromatically diverse retinal ganglion cell responses as determined from the response properties of neurons in the lateral geniculate nucleus (4, 5).

In studying the evolution of vertebrate color vision, it would be highly desirable to work with an experimental animal amenable to genetic manipulation. As a first step along these lines, we report here the use of genetically engineered mice to model the evolution of New World primate red–green color vision.

Materials and Methods

Construction of the Human Red Pigment Knock-In Mouse. The knock-in construct contains at its 5′ end an 11.7-kb mouse genomic DNA segment, which extends upstream from a BbsI site in exon 2 of the green pigment gene (within the amino acid sequence VVVASVFTNG). By site-directed mutagenesis, the single BbsI site in the human red cDNA clone hs7 (in exon 4; ref. 6) was eliminated by the introduction of silent nucleotide substitutions, and a BbsIsite was created within exon 2 at the location corresponding to the BbsI site in exon 2 of the mouse green pigment gene. The 11.7-kb mouse 5′ region and the human red pigment cDNA segment, modified as described above and containing the 3′ untranslated region including a consensus poly(A) addition site, were joined at their BbsI sites. The 3′ end of the knock-in construct contains a 2.8-kb EcoRI–BamHI mouse genomic segment from intron 5 of the mouse green pigment gene. The EcoRI site at the 5′ edge of this fragment was destroyed to permit Southern blot screening of EcoRI-digested genomic DNA with a 3′ flanking probe. For positive selection in G418, a loxP-phosphoglycerate kinase promoter–neomycin resistance gene-loxP cassette was inserted immediately distal to the human red pigment cDNA segment. For negative selection with gancyclovir, a thymidine kinase gene was inserted distal to the 3′ homology region. The loxP-flanked neo marker was subsequently excised by crossing to mice expressing cre in the germ line (7).

Immunostaining of Mouse Retinae. Ten-micrometer cryostat sections of paraformaldehyde-fixed mouse eyecups were processed for immunocytochemistry with anti-cone pigment antibodies (8) as described (9).

5-Bromo-4-chloro-3-indolyl β-d-galactoside (X-Gal) Staining and Analysis of Retinal Flatmounts. Retinas from four adult female mice heterozygous for an X-linked hydroxymethylglutaryl-CoA reductase promoter-lacZ reporter transgene were prepared as whole mounts, processed for X-gal histochemistry, dehydrated and embedded flat in glycol methacrylate, sectioned at 5 μm in the plane of the retina, and counterstained with neutral red (10).

Cone Electroretinogram (ERG) Measurements. The equipment and general procedures have been described (11, 12). Recording was performed in a room illuminated to provide 100 lux at the position of the test eye. Stimuli were derived from a three-beam optical system with the outputs imaged in register on the retina in Max-wellian view (59° circular spot). Three types of measurements were made. (i) Spectral sensitivity functions were obtained with an ERG flicker photometric technique. In these experiments, light pulses (12.5 Hz) that originated from a test light (monochromatic; 15-nm half-bandwidth) and a reference light (achromatic; 3,700 trolands) were temporally interleaved. ERGs obtained from averaging over 4 s (50 responses to the test and reference lights) were compared. For each animal, flicker photometric equations were obtained for test lights varying in steps of 10 nm. Two complete spectral scans were made, and the resulting values were averaged. (ii) A test for spectral response univariance was performed using the flicker photometric paradigm. ERG flicker photometric equations were made between a 500-nm test light and a 600-nm reference light (pulse rate 12.5 Hz; 15-nm half-bandwidth) in the alternate presence of steady adapting lights having wavelengths of either 500 or 600 nm. The two adaptation lights were first equated in intensity so that each elevated the threshold for a flickering 530-nm test light by 0.5 log units. (iii) Cone response amplitude vs. intensity (V-log I) functions were obtained. Amplitudes of the fundamental component of the ERG signal, reflecting the cone response, were recorded to 12.5-Hz flickering lights. A 455-nm long-pass filter was inserted into the test beam to minimize contributions from the mouse UV photopigment. Responses were collected for a series of intensities starting at the response threshold and increasing, in 0.2 or 0.3 log unit steps, until the response saturated. For this experiment, the intensity of the test light was scaled according to each animal's spectral sensitivity function, such that the intensities used in the test had the same effectiveness irrespective of the pigments present in the animal's retina. At each intensity, five separate response amplitudes were measured; each averaged over 50 presentations (4 s) of test light stimulation. The intensity/response functions were best fitted using the Michaelis–Menten equation, V/V_max = Iⁿ/(Iⁿ + kⁿ), where V is the amplitude measured for intensity I, and the parameters are the saturation voltage (V_max), the intensity required for half-maximal response (k), and the slope of the function at the half-saturation amplitude (n). This function has been used to describe intensity/response relationships for a wide variety of cone-based measurements (13).

Recording of Ganglion Cell Action Potentials. Spike trains were recorded extracellularly from the ganglion cell layer of mouse retinas with a multielectrode array as described (14, 15). The animals were dark-adapted for at least 1 h before enucleation. The retina was isolated into oxygenated Ringer's solution (110 mM NaCl/2.5 mM KCl/1 mM CaCl₂/1.6 mM MgCl₂/10 mM d-glucose buffered with 22 mM NaHCO₃/5% CO₂/95% O₂, pH 7.4) under infrared illumination. A piece of retina 2–3 mm on a side was cut from the superior part of the retina and placed ganglion cell side down on an array of 61 electrodes spaced 70 μm apart. The isolated retina was continuously superfused with oxygenated Ringer's solution (1 ml/min) and maintained at 36°C.

Visual Stimulation for Array Recordings. The combination of an LCD panel (Sharp QA-1750) and an overhead projector (Eiki OHP-4100) was used to deliver visual stimuli that were projected through an objective lens onto the retina, generating a 3.25-mm diameter image on the photoreceptor layer. The average light intensity, calculated in terms of the time-average rate of photoisomerizations in a rod, was 10⁵ R* per rod per s, enough to saturate the rod pathway (9). For the random-flicker stimuli used for spectral sensitivity measurements, the field was divided into a checkerboard of 105- or 50-μm² size. In each square, each of the three color channels of the LCD panel (red, green, and blue) was turned on or off by an independent random choice. These assignments were randomized every 30 ms, yielding a checkerboard that flickered rapidly with eight different colors (14).

Spectral Sensitivity Measurements for Retinal Ganglion Cells. The spatio-temporal receptive fields of all ganglion cells were measured by reverse correlation to the flickering-checkerboard stimulus (14). The receptive field was approximated as the product of a spatial profile and a temporal filter (16). The receptive field center was estimated as the region where the spatial profile was larger than one-third of its maximum value. The ganglion cell's spectral sensitivity was estimated from the relative sensitivity to the red, green, and blue lights of the stimulator. Sensitivity was measured as the rms amplitude of the reverse correlation function in the region of the receptive field center. The spectrum of each of the LCD panel's color channels was measured using a spectrophotometer (PR-650 SpectraScan Colorimeter, Photo Research, Chatsworth, CA).

The absorption spectra of the human red pigment and the native mouse green and UV pigments were approximated by using the nomogram of Baylor et al. (17) at 556, 512, and 359 nm, respectively. The measured spectral sensitivity of a ganglion cell was expressed as a linear combination of the spectral sensitivities of these three pigments. The relative weightings in this mixture were taken to represent the relative contribution from the three cone types to the ganglion cell's response. Strictly speaking, this rests on the assumption that the ganglion cell sums the various cone inputs linearly. The average contribution of the UV cones to a ganglion cell's spectral sensitivity was 2.5 ± 0.73% (mean ± SEM, n = 86), consistent with the small number of UV cones and small content of UV pigment in the superior retina (18, 19). Therefore, we have presented only the relative weightings of the red and green cones.

To estimate the variance of the distribution of cone weightings in a population of ganglion cells, the variance due to measurement error was subtracted from the total variance. For a given cell, the measurement error was estimated by computing the spectral sensitivity from two independent stretches of data (even and odd minutes in the experiment). For Figs. 4A and 6, the measurement error was averaged over all cells in the population.

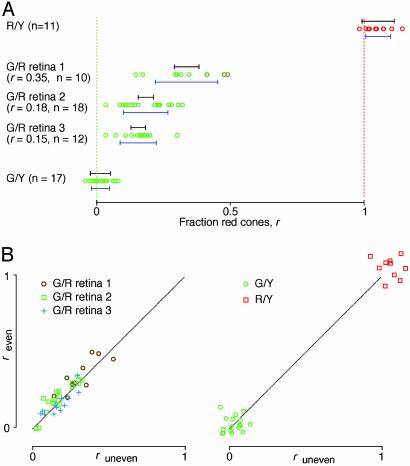
Fig. 4.

Relative weightings of red and green cone inputs in the ganglion cell population. Results shown are from five different animals. Each data point represents the fraction of red cone input, r, for an individual ganglion cell. (A) Results from an R/Y hemizygote, three G/R heterozygotes, and a G/Y hemizygote. Blue error bars below the data points represent the spread of the data points (mean ± SD). Black error bars above the data points denote the experimental uncertainty (2 × SD of the noise) in each measurement, averaged over all cells in the experiment. n, number of ganglion cells. The skew of the R/Y data points from the expected value of 1.0 likely reflects a combination of uncertainties in the red pigment spectral sensitivity curve and the spectral output of the LCD panel. (B) Scatter plots of two independent measurements of r; “even” and “uneven” refer, respectively, to data obtained during the interleaved even and odd minutes of the recording session (see Materials and Methods). Each data point represents one cell. (Left) Three G/R retinas. (Right) G/Y and R/Y retinas. The dotted line represents identical values. In G/R retinas, the cell-to-cell variation in r exceeds the variation from measurement error.

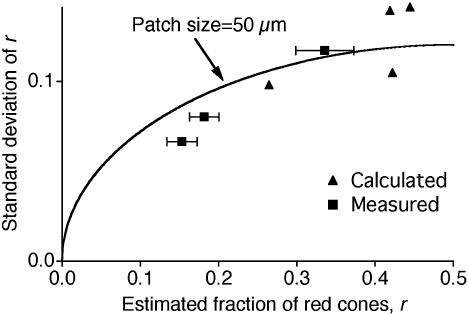
Fig. 6.

The measured spectral variation among retinal ganglion cells can be explained by the spatial heterogeneity of X inactivation. The SD of the red cone fraction, r, within a ganglion cell population is plotted against the average fraction. Squares, measured values (mean ± SEM) for ganglion cells in three G/R retinas (Fig. 4). Triangles, calculated values from the four patchy cone mosaics in Fig. 5, assuming that each ganglion cell pools input from the overlying cones with a Gaussian weighting function (SD 65 μm). The curve, the expected dependence if the cone mosaic consists of 50-μm² tiles, was assigned randomly to red and green cones with probability r and 1 – r, respectively.

Simulation of Spectral Weighting of Retinal Ganglion Cells by Using X-Gal-Stained Retinal Flatmounts. Color images of the X-gal-stained retinal flatmounts (Fig. 5) were converted to binary images by thresholding the red color channel; the threshold value was chosen to maximize the correlation with the original image. The resulting binary map reflects X-inactivation patches with cones in a given region (white or black) expressing either the red or the green opsin. To estimate the distribution of red/green weightings in a ganglion cell population nonselectively connected to such a cone mosaic, the binary images were filtered with a two-dimensional Gaussian representing the average ganglion cell-receptive field profile. Each point in the filtered image thus represented a possible spectral mix for a ganglion cell that is sampling the cone mosaic. The average size of a ganglion cell's receptive field was determined by fitting a two-dimensional Gaussian to the cell's spatial receptive field profile. The mean width (2 × SD) of the Gaussian fit was 130 μm (range 70–250 μm).

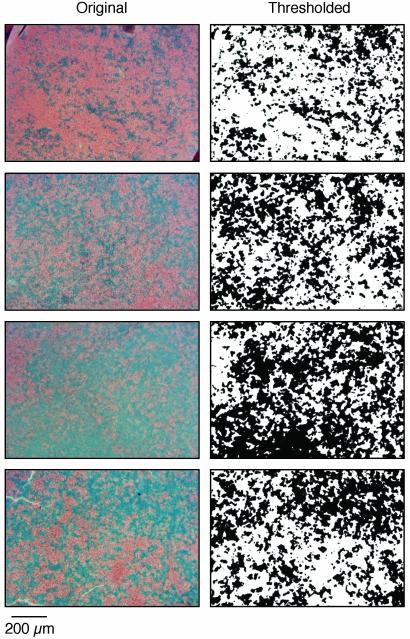
Fig. 5.

X-inactivation mosaicism in four β-galactosidase transgenic retinas. Retinas were obtained from adult female mice heterozygous for the hydroxymethylglutaryl CoA (HMGcoA) reductase promoter-lacZ transgene as described in ref. 10. (Left) Original images of X-gal-stained retinal flatmounts sectioned in the plane of the retina at the level of the outer nuclear layer. Blue, X-gal; red, neutral red staining of nuclei. (Right) The same images processed with an intensity threshold to obtain binary maps of the X-gal-stained regions.

Results

Design of the Red Knock-In Allele. In all mammals examined to date, the gene(s) coding for the longer wavelength cone pigment(s) reside on the X chromosome. Therefore, engineering a new cone pigment gene in place of the endogenous mouse gene on the X chromosome should create a mosaic of spectrally distinct cones in the retinas of heterozygous females, recapitulating the arrangement seen in New World primates. For these experiments, the X-linked mouse pigment [absorption maximum ≈511 nm (20, 21); referred to hereafter as the mouse green pigment] was replaced by a derivative of the human red cone pigment [with a polymorphic alanine at position 180; absorption maximum ≈556 nm (22–25)], thereby providing heterozygous females with a pair of cone pigments with a ≈45-nm spectral separation.

In the knock-in construct, both the first exon and the first intron of the mouse green pigment gene were left intact, and a hybrid coding region was constructed in which the amino-terminal 92 amino acids are coded by exon 1 and the 5′ half of exon 2 of the mouse green pigment gene, and the carboxyl-terminal 266 amino acids are coded by a human red pigment cDNA (hs7, ref. 6; amino acids 98–364 in the human numbering system; Fig. 1). In this hybrid pigment, nearly the entire chromophore binding pocket is derived from the human red pigment, as determined by comparison with the three-dimensional structure of bovine rhodopsin (26). Moreover, the two amino acid differences previously shown to account for the different absorbance spectra of the mouse green and human red pigments (Fig. 1C; positions 197 and 308 in the human red pigment; ref. 21) fall within the region derived from the human red pigment. Based on these considerations, the absorbance spectrum of the hybrid pigment would be predicted to closely resemble that of the human red pigment, a prediction subsequently borne out by ERG measurements (see below). Therefore, we will refer to this hybrid pigment as the human red or R pigment and the cones that contain it as red or R cones. Similarly, we will refer to hemizygous malemiceasR/YorG/Y if their X chromosome carries the human red or mouse green pigments, respectively, and homozygous and heterozygous female mice as G/G, R/R, or G/R.

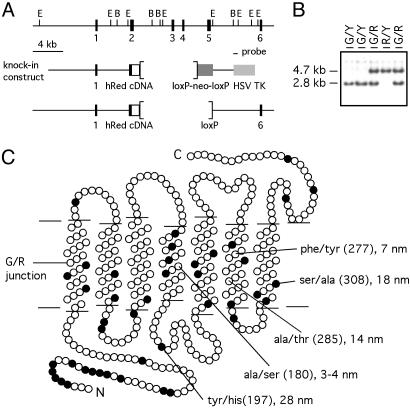
Fig. 1.

Generation of the human red knock-in allele. (A) Restriction map of the mouse green pigment gene showing exons 1–6 (black bars) and the 0.7-kb EcoRI–BamHI probe used for embryonic stem cell screening and mouse genotyping (Top). The human red pigment knock-in construct in which the 5′ half of mouse exon 2 is joined in-frame to the corresponding region of human red pigment cDNA hs7 (Middle; ref. 6), and the final floxed human red knock-in allele from which the phosphoglycerate kinase-neo selection cassette has been removed (Bottom). Brackets indicate the region deleted. (B) Southern blot genotyping of mouse tail DNA using the 0.7-kb probe. Samples are from male mice hemizygous for the mouse green pigment gene (G/Y) or the human red pigment knock-in allele (R/Y), and heterozygous female mice (G/R). Y, Y chromosome. (C) Schematic of the transmembrane disposition of the human red pigment showing the junction used to create the mouse green/human red hybrid pigment in the center of transmembrane helix 1 (horizontal line). Amino acids that differ between the mouse green and human red pigments are shown as filled circles. The five amino acid dimorphisms that determine the different wavelengths of maximal absorption among members of the long wavelength visual pigment subfamily are labeled. Positions 197 and 308 account for the different absorption maxima of the mouse green and human red pigments (21).

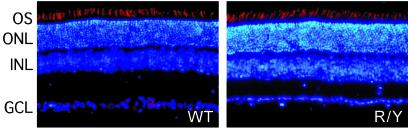
Red Cone Function in the Knock-In Mouse. As a first test of the functionality of the human red knock-in allele, we analyzed retinas from adult G/Y and R/Y males by immunostaining with an antiserum that binds both the mouse green and human red pigments (Fig. 2). This comparison revealed indistinguishable patterns of immunostained cone outer segments and no evidence for cell loss or retinal disorganization. These data suggest that the red pigment is expressed at roughly normal levels within cone photoreceptors and is efficiently transported to the outer segment.

Fig. 2.

Normal numbers of longer wavelength cones in the R/Y retina. Tenmicrometer sections of dorsal retina were immunostained with anti-human red/green carboxyl-terminal antibodies and Texas red secondary antibody (red). Nuclei are counterstained with 4′,6-diamidino-2-phenylindole (blue). The number and lamination of nuclei and the density of immunoreactive cone outer segments are indistinguishable between WT and R/Y retinas.

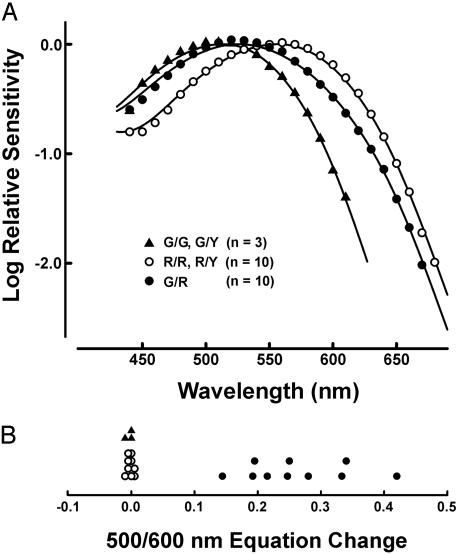
Fig. 3A shows the averaged spectral sensitivity functions for three classes of mice (G/YorG/G, G/R, and R/YorR/R) determined by ERG flicker photometry. As the spectral sensitivity of hemizygous males seemed indistinguishable from that of the corresponding homozygous females (i.e., G/Y males and G/G females, and R/Y males and R/R females), data from each of these subgroups were pooled. To obtain peak spectral sensitivities, optimal fits for these two groups were made to the photopigment templates of Govardovskii et al. (27). The spectral sensitivity of the green cones in G/Y and G/G mice peaked at 512.6 ± 0.5 nm, in good agreement with previous ERG measurements (20). The spectral sensitivity of the red cones in R/Y and R/R mice peaked at 556.5 ± 1.0 nm, in good agreement with previous analyses of the recombinant red pigment in vitro (22, 23) and of red cones in the living human eye (24, 25).

Fig. 3.

ERG spectral sensitivity functions from red cone knock-in mice. (A) The data points are mean values for 3 G/G and G/Y mice, 10 R/Y and R/R mice, and 10 G/R mice. The data from mice expressing only a single longer wave pigment are fit to the photopigment templates of Govardovskii et al. (27). The best curve fit to the data from the G/R mice is a linear summation of the green (57%) and red (43%) curves. For the R/Y and R/R group and the G/R group, in which 10 mice each were analyzed over the same 25 wavelengths, the average SDs were 0.054 log units (R/Y and R/R) and 0.089 log units (G/R). The larger SD in the G/R group presumably derives from interanimal variability in the ratio of red:green cones. (B) Results from an ERG test for spectral response univariance. Plotted are the differences (in log units) for the 500- and 600-nm photometric equations obtained in the alternate presence of 500- and 600-nm adapting lights. Values near zero indicate spectral univariance; positive values imply the presence of two independently adaptable spectral mechanisms.

The peaks of the spectral sensitivity functions for ten G/R heterozygotes were between those of the other two groups (Fig. 3A), reflecting contributions from both green and red cones. That conclusion is further supported by results from a test for response univariance in which we measured the relative sensitivity of the retina to 500- and 600-nm test lights after exposing the eye to adapting lights of either 500 or 600 nm (Fig. 3B). If a single cone type is at work, this sensitivity ratio should be unaffected by adaptation. As expected, equations obtained from hemizygous males and homozygous females remained invariant irrespective of whether the eye was adapted to lights of either 500 or 600 nm. By contrast, each of the G/R mice showed clear shifts in their equation values. This failure of response univariance means that the heterozygous mice have two functional cone types in this spectral region, and, accordingly, the mean spectral sensitivity for this group was fit to a linear combination of green and red cone spectra.

On average, signals from green and red cones provided contributions of 57% and 43%, respectively, to the spectral sensitivity of the heterozygous retinas. Interestingly, there were significant individual deviations from this average value, with red cone contributions varying from 17% to 78% across the 10 animals. Repeat testing indicated that these individual variations are reliable; for example, red cone contributions of 36% and 42% were obtained from one animal when spectra were recorded with a 14-day interval between the two tests. Most likely, these individual differences arise from stochastic variation in X chromosome inactivation and embryonic cell migration and proliferation (28) with consequent fluctuations in the ratio of red:green cones.

We also compared intensity/response functions obtained by ERGs from G/G and R/R mice. The three parameters of the fits (V_max, n, and k; see Materials and Methods) made to the averaged functions were not statistically different for the two groups of animals. This result suggests that the human red pigment is linked to the ERG signal with an efficiency similar to that of the native green pigment. Finally, separate ERG measurements demonstrated the presence and normal functioning of the UV cones in R/Y, R/R, and G/R mice.

Retinal Ganglion Cell Responses in Red Knock-In Retinas. Using a multielectrode array, we recorded spike trains from ganglion cells in the superior retinas of G/Y, R/Y, and G/R mice. The stimulus was a checkerboard in which each field flickered randomly with eight possible colors. By correlating the spike trains with the stimulus, we determined each cell's spatial receptive field, temporal response function, and spectral sensitivity. Ganglion cells in G/Y, R/Y, and G/R retinas showed similar distributions of receptive field sizes and temporal responses, suggesting that much of retinal processing is unaffected by the knock-in modification.

From the measurement of spectral sensitivity, we computed the relative contribution that the different cone pigments made to the ganglion cell's response. As expected, ganglion cells in the G/Y retina had a spectral sensitivity matching that of the native mouse green pigment, and ganglion cells in the R/Y retina showed a spectral sensitivity matching that of the human red pigment (Fig. 4A). Ganglion cells in G/R retinas received a mixture of input from the red and the green pigments (Fig. 4A), with no evidence for center-surround chromatic antagonism. Interestingly, the relative fraction of red cone input, which we will call r, varied considerably within the ganglion cell population. The difference in the average value of r (0.23) obtained by multielectrode array recording relative to that observed in the ERG experiments (0.43) is not significant given the large spread of red cone contribution across animals and the small number of heterozygous retinas examined. In the G/Y and R/Y retinas, the range of r was considerably smaller. This residual variation in hemizygous retinas reflects the experimental uncertainty in measuring r, and any variation among G/R ganglion cells in excess of this value can be assigned to true variation in the relative red and green cone inputs. We obtained a direct estimate of experimental uncertainty in r by measuring it twice for each ganglion cell. In G/R retinas, the values for different ganglion cells scattered much more than the replicate measurements for the same ganglion cell (Fig. 4B). Overall, the observed variation in red cone input among G/R ganglion cells was 2- to 3-fold greater than the experimental uncertainty (Fig. 4A), indicating that most of the variation is due to genuine differences in cone inputs. Finally, we note that in comparing different G/R retinas, r showed greater variability the closer its mean approached 0.5. As discussed below, this trend is predicted if each ganglion cell samples randomly from a mixed population of red and green cones.

Modeling Retinal Ganglion Cell Responses in the G/R Retina. The spectral properties of retinal ganglion cells can provide some insight into the routing of cone signals within the retina. Consider two extreme wiring schemes. In one case, individual ganglion cells get excitatory input from a single cone type, as seen in the blue–yellow system in the primate retina (29, 30). In this case, color information is carried by cells with stereotyped response properties. In the G/R retina, a system of this type would lead to just two discrete spectral types of ganglion cells, with the spectral sensitivities of the red and green pigments. In the second case, each ganglion cell draws its excitatory input nonselectively from the overlying mosaic of red and green cones, as has been proposed for the red–green system in the peripheral primate retina (30). Such indiscriminate wiring would result in a continuous distribution of spectral sensitivities among ganglion cells, the shape of which depends on the irregularities of the cone mosaic. The retina's capacity for relaying color information would then depend on the range of spectral sensitivities across the ganglion cell population.

Our finding of a continuous and unimodal distribution of spectral sensitivities in G/R mice (Fig. 4A) strongly speaks for the random sampling hypothesis. To determine more quantitatively whether the observed spread in ganglion cell spectral sensitivities can be explained by nonselective wiring, we computed the distribution that would be expected given the observed spatial layout of X-inactivation patches within the mouse retina. For this purpose, we used transgenic mice that carry a ubiquitously expressed β-galactosidase transgene on the X chromosome to reveal the patterns of X inactivation in heterozygous female retinas (10). These mice exhibit prominent, radially distributed clusters of X-gal-stained cells, with tangential dispersion of certain neurons, including cones. However, cone dispersion is a relatively short-distance phenomenon (≈15 μm; ref. 28) compared with the average diameter of ganglion cell-receptive fields measured here (≈130 μm). For the present purpose, we assumed that the X-gal staining pattern in the photoreceptor layer of β-galactosidase transgenic mice provides a reasonable estimate of the patchiness of red and green cones in G/R retinas.

Four transgenic retinas that are representative of the observed variation in X inactivation patchiness were flatmounted, X-gal stained, and sectioned (Fig. 5 Left). The images were then thresholded, resulting in binary images of the pattern of X inactivation (Fig. 5 Right). In each image, we assigned the more abundant territory to the X chromosome carrying the mouse green pigment gene to match the excess green cone weighting observed among the experimental G/R retinas (Fig. 4A). Assuming that each ganglion cell collects inputs nonselectively from this cone mosaic, we calculated the probability distribution of r, the relative fraction of red cones contributing to the ganglion cell response.

Fig. 6 shows the SD of r in a ganglion cell population plotted as a function of the average value of r for each of the four X-gal-stained retinas. The SDs obtained from the calculation are a good match to the SDs measured physiologically in G/R retinas (Fig. 4). This indicates that nonselective wiring to a patchy mosaic of red and green cones can indeed account for the observed spread in the ganglion cell spectral sensitivities. It is also consistent with the working assumption that the red and green pigments are each expressed in dedicated cone types and that these red and green cones are arranged with a patchiness that approximates the radial territories set up by X inactivation.

The variability seen in both the measured and the calculated spectral sensitivities increased as the average red cone fraction approached 0.5. This is the expected outcome if the average cone weighting in a given retina simply reflects the fraction of retinal surface area populated by the different cone types. If we assume that the retina is composed of equally sized single-pigment patches, of which a fraction r is red, then the cone input ratio of a ganglion cell sampling some random set of these patches would follow the binomial distribution. The SD of this distribution depends on the patch size, the receptive field size of the ganglion cell, and the fraction of red patches (r) and will vary proportionally with 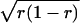. By fitting this relationship to the data in Fig. 6 and assuming a Gaussian ganglion cell receptive field (SD 65 μm), we estimated an effective patch size of 50 μm.

Discussion

In the experiments reported here, we have used genetically engineered mice in an attempt to recapitulate one step in the evolution of New World primate trichromacy. By replacing the single murine X chromosomal cone pigment gene with one that encodes a human red pigment, we have generated hemizygous male and homozygous female mice with a ≈45-nm red shift in retinal sensitivity. Given the close correlation between retinal sensitivity and behavioral sensitivity previously reported for WT mice (20), we presume the red knock-in mice are endowed with enhanced sensitivity to long-wavelength lights, although this remains to be demonstrated. More significantly, we observe a newly acquired chromatic diversity among retinal ganglion cells in G/R females. If chromatic diversity persists at higher CNS levels, it may be possible to train G/R mice to perform chromatic discrimination tasks that G/G and R/Rmice cannot perform.

The present work complements and extends that of Shaaban et al. (31) and Jacobs et al. (12) who generated and studied mice in which the human red cone pigment was expressed as a transgene. In those experiments, the human red pigment transgene was shown to confer increased sensitivity to long wavelength light as determined both by ERG and behavioral testing, but no evidence could be found for enhanced chromatic discrimination. The latter observation would be expected if, as was likely, the transgenic human red pigment and each of the endogenous mouse pigments were expressed together at fixed ratios in cone photoreceptors. Such pigment mixtures would generate an extended envelope of spectral sensitivity but would not lead to increased chromatic diversity among retinal ganglion cells.

It is interesting that even with relatively large receptive fields, ganglion cells in the mouse can be engineered to exhibit significant chromatic diversity simply by providing them with an overlying cone mosaic that is sufficiently coarse-grained. In the mosaic retinas of heterozygous New World primates, the small receptive fields of the midget ganglion cells permit a finer sampling of the patchy cone mosaic, which presumably accounts for the greater chromatic diversity of New World primate ganglion cells relative to those in the G/R mouse, despite the smaller spectral separation among the primate polymorphic cone pigments. If, as some authors have suggested, midget ganglion cells in Old World primates draw inputs nonselectively from longer wavelength cones (32–34), then small receptive fields might be essential for generating chromatic diversity from the fine-grained mosaic of red and green cones characteristic of these species (35, 36).

Could mosaicism based on X inactivation be of selective value in the generation of cellular diversity in other contexts? In the nervous system, cellular diversity is advantageous as a general strategy for enhancing the efficiency of signal processing and transmission. For example, an ensemble of neurons with different excitabilities would have a larger dynamic range than would a comparable ensemble with identical excitabilities. X chromosome inactivation represents a particular form of transcriptional regulation that has the potential to create cellular diversity on an extremely rapid evolutionary time scale. This is possible because functional mosaicism depends only on the presence of random X chromosome sequence polymorphisms and does not require the evolution of novel or altered gene regulatory circuits. Moreover, the small size of X-inactivation patches within the mammalian CNS (37) ensures that virtually any structure of appreciable size within the brain of a heterozygous female will be mosaic. Finally, we note that stochastic variation in X inactivation-based mosaicism could generate physiologic diversity among heterozygous females that might be advantageous at the level of group selection. These considerations suggest that it would be of general interest to search for polymorphisms in mammalian X-linked genes that might contribute to other types of neuronal diversity in heterozygous females.