Reaching the global minimum in docking simulations: A Monte Carlo energy minimization approach using Bezier splines

Abstract

The docking problem faces two major challenges: the global optimization of a multivariable function, such as the energy, and the ability to discriminate between true and false positive results, i.e., native from nonnative structures based on the input energy function. Among all energy evaluation tools, only a local energy-minimization method using an accurate enough potential function is able to discriminate between native and nonnative structures. To meet these requirements, a Monte Carlo with energy-minimization method has been incorporated into a new ECEPP/3 docking program. The efficiency of the simulation results from the use of an energy-grid technique based on Bezier splines and from a simplification of the receptor by switching on the energy of only important residues of the active site. Simulations of a thrombin-inhibitor complex show that the global minimum of the energy function was reached in every independent run within less than 3 min of time on an IBM RX 6000 computer. For comparison, 10 standard independent Monte Carlo simulations with 10⁶ steps in each were carried out. Only three of them led to a conformation close to the x-ray structure. The latter simulations required an average of 24 min and about 10 hr with and without the grid, respectively. Another important result is that the Bezier spline technique not only speeds up the calculation by reducing the number of operations during the energy evaluation but also helps in reaching the global minimum by smoothing out the potential energy surface.

Determination of the structure of a receptor-ligand complex is a prerequisite for estimating the binding affinity or binding free energy between the two molecules. In a typical drug design project, this energy estimation should be accomplished for a large number of candidate molecules. The problem thus amounts to determining the structure of the bound ligand accurately, for the binding free energy calculation to be correct, and fast enough for screening a large molecular database in a reasonable amount of time. Much effort has been devoted to developing efficient automatic procedures to calculate the structures of ligands bound to their receptors.

This task faces two major challenges. The first one is to find the global minimum (GM) of a multivariable scoring or energy function that measures the fit between the ligand and the receptor. This is the multiple-minima problem that depends strongly on the size of the system. However, for docking simulations, the problem can be simplified by assuming the structure of the receptor and/or the ligand to be fixed or partially flexible. The second challenge is to find an energy function or an energy-evaluation tool that is able to discriminate between native and nonnative structures. Because the “energy” of the scoring function is the only criterion available for selecting the correct bound structure, it should have the property that its GM value corresponds to the native conformation of the complex.

Many approaches have been proposed for docking a ligand onto its receptor. They are based mostly on geometric or energetic criteria or on a combination of the two. Geometric criteria use the idea of shape complementarity between the ligand and the receptor (1–22). This can be implemented in different ways, by least-squares fitting the positive and negative images of the ligand and the receptor, respectively (4, 7, 8), by using three-dimensional (3D) correlation techniques (6, 13, 17, 21, 22), or by using computer vision-based methods (10, 11). These methods have proven to be efficient for selecting a reasonable number of candidates for the bound structure of the ligand. These candidates then are re-evaluated according to some energetic criteria. This consists of calculating the energy of the bound ligand complex with an heuristic potential function or with a standard mechanical force field. The second approach makes use only of the energetic criteria without geometrical evaluation of the shape complementarity between the two molecules. The energy function involved refers to the standard types of molecular interactions such as hydrogen bond, electrostatic interaction, van der Waals contact, hydrophobic forces, solvation energy, etc. Currently, the methods used for sampling the conformational space are based on combinatorial or random search using a graph-theoretical approach (8, 9, 15, 20), genetic algorithms (23–27), Monte Carlo (MC) (28–39), or molecular dynamics (40–43).

All of the methods and approaches mentioned above face the same problem: the existence of what might be called “false-positive” results among the set of solutions, i.e., native-like structures with higher energy than some nonnative structures. Shoichet and Kuntz (3) have tested the reliability for differentiating the native conformation from nonnative ones with different energy evaluation methods such as buried surface area, free energy of solvation, mechanical constraints, packing, electrostatic complementarity, and energy minimization using standard mechanical force fields. They found that only the energy-minimization technique was able to discriminate, in most cases, the native from nonnative conformations. Electrostatic complementarity using a delphi type of calculation showed significant improvement (3). Guida et al. (30) used the energy-minimization technique coupled with a MC method to calculate the bound structure of four inhibitors of thermolysin. They found that, in each case, the crystallographically observed conformations were among the low-energy conformers discovered, with three of them having the lowest energy. Caflisch et al. (31) also applied the local energy-minimization technique, but within a different scheme, to the HIV type 1 aspartic acid proteinase complex. Their results also did not lead to any false-positive results; their lowest-energy conformation was the closest to the x-ray structure.

It is necessary to use a local energy-minimization technique to discriminate between a native and a nonnative structure because a structure close to the GM but with some atomic clashes will have a high energy value, higher than some unrelated nonnative structure. In that case, the native-like structure will be ranked very high unless this structure is refined by energy minimization, in which case the GM is obtained. The reason the energy-minimization method is not used extensively for screening potential candidates is its computational cost. The computational time varies, of course, with the system, but for a typical complex with a small rigid ligand and a rigid receptor and with a distance cutoff of 8–10 Å, one energy minimization might take several minutes of computer time on a current workstation. Screening many candidates or implementing the minimization technique into a MC scheme would take hours of calculations. This frustrates the accepted goal of obtaining the docked structure in less than an hour or if possible within a few minutes of simulation per ligand molecule.

In this paper, we present two techniques that make the MC energy minimization (MCM) method competitive, especially for docking simulations. The first one is an approximation of the molecular system and turns out to be well adapted for the rigid docking problem. It consists of docking the ligand onto a small part of the active site: only certain residues of the active site of the receptor are considered during the simulation. The rest of the atoms, including those blocking accessibility to the active site, are not taken into account. For example, instead of considering all of the active site residues, only those lying at the “bottom” are seen by the ligand. When an approximate bound structure of the ligand is obtained, additional residues of the active site then are added to the system. This approach has the advantage of lowering the number of interactions and also finding the bound structure of the ligand by starting from the open form of the receptor when the closed form is not available.

The second improvement is the incorporation of a grid-based energy evaluation technique using a Bezier splines interpolation scheme developed recently in our laboratory (44). This technique enables one to evaluate, on a 3D grid, not only the energy but its gradient as well. Full advantage of the grid now can be applied to an energy-minimization procedure. The speed-up increases with the size of the rigid part of the system that is incorporated into the grid. This technique, together with the simplification of the receptor, lowers the time of one energy minimization to less than 1 s for a rigid ligand and a rigid receptor, compared with several minutes when the grid is absent and the whole rigid receptor is taken into account in the energy calculation, i.e., without a cutoff distance.

This paper presents an adaptation of the MCM method (45, 46) for the docking simulation. Calculations were carried out for the noncovalent binary complex of human α-thrombin with the tripeptide NH₂-d-Phe-Pro-Arg-COOH (FPR). This substrate is analogous to PPACK (d-Phe-Pro-Arg-chloromethylketone), which is an inhibitor of the fibrinogen interaction site of thrombin. The structure of the covalent complex, thrombin-PPACK, has been determined by x-ray crystallography at 2.3 Å resolution (47, 48). Besides its biological relevance, thrombin presents interesting structural characteristics for the active site: this is a serine protease that cleaves the Arg-16–Gly-17 peptide bond of the Aα-chain of human fibrinogen. The arginine side chain of the ligand is inserted into a deep narrow pocket of the enzyme making the docking difficult by a pure MC technique (see Results). Two insertion loops flank each side of the thrombin pocket. They play the role of a lid that opens and closes during the binding of fibrinogen to thrombin (47, 48).

Both molecules were considered as rigid in this study. To test the ease or difficulty of the docking of FPR onto thrombin, we carried out comparative calculations using the standard Metropolis MC without energy minimization but using our grid-based technique. This approach is similar to the approach used by many authors (12, 28, 29, 32, 38). The efficiency of the grid technique has been measured by the savings in computational time and also in the number of MC steps necessary to reach the GM. The results show that the Bezier spline not only decreases the simulation time by lowering the number of operations per energy evaluation but also has the nice property of smoothing out the potential energy surface, which is particularly helpful in searching for the GM (49). This program is part of a new modeling ECEPP/3 package developed recently in our laboratory.

METHODS

Regularization.

The coordinates of human α-thrombin were taken from the file 1ppb in the Protein Databank (50). The reference structure of the complex that will be used for comparison with the calculated structure was prepared as follows: the x-ray structures of the ligand and the A and B chains of human α-thrombin were regularized independently, using the protocol that will be described elsewhere; i.e., the structures were forced to have the standard bond lengths and bond angles of ECEPP/3. After regularization, the structure of the whole complex (internal degrees of freedom) was energy-minimized in several stages by using harmonic distance constraints with decreasing weights. At each stage, 2,000 minimization iterations were carried out except for the last stage in which minimization was carried out until convergence (rms-gradient = 10⁻⁴ kcal/mol.rad). The values of the weight, associated with each minimization stage were: 100.0, 10.0, 1.0, 0.1, and 0.0. The purpose of the constraint energy was to prevent the complex from departing significantly from its crystal structure during the early stages of minimization. The last energy minimization was carried out without x-ray constraints. No cutoff distance was used, which is an important point. If a cut-off distance is introduced during minimization, the final structure after complete minimization will not be at the energy minimum when a new list of nonbonded interactions is recalculated from the final structure. Because of this, convergence cannot be attained with a cutoff distance, no matter how many successive energy minimizations are carried out. At the end of the complete minimization, the rms deviation (rmsd) between the regularized structure and the x-ray structure was 1.9 Å for thrombin and 1.0 Å for the FPR portion of PPACK.

Docking.

At the beginning of the simulation, the orientation and the position of the ligand were generated randomly in such a way that the Pro2-C^α atom of FPR was located uniformly inside a sphere of 3 Å or 15 Å radius (computational experiments I and II, respectively) centered at point P (6.2, 9.5, 13.5 Å) near the catalytic residue Ser-195 (with respect to the coordinate system of the Protein Databank structure). A harmonic distance constraint was applied when the ligand atom Pro2-C^α moved outside of the sphere. The docking thus consists of tumbling the ligand inside the active site region. Only seven degrees of freedom were considered, three for translation and four quaternions for rotation. The constraint concerning the norm of the quaternion was incorporated in the energy function (unpublished work). The step sizes for the quaternions were large enough for two successive rotations to be uncorrelated. The step size for the translation move was chosen in such a way that the displacement of the center of mass of the ligand was about 0.1–0.3 Å per MC move.

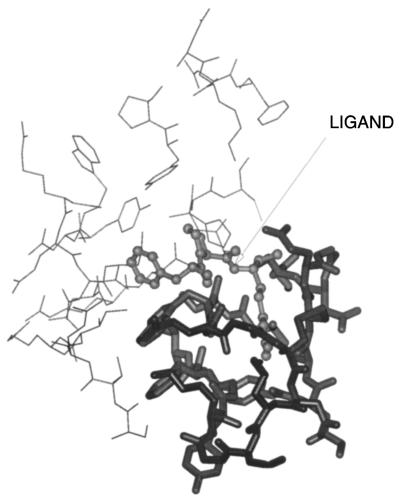
To facilitate the docking, a large part of the receptor was disregarded in the computation. For experiment I, the only residues taken into account were the residues of the binding pocket of thrombin (Fig. 1). They correspond to segment nos. 14 and 16 of the B chain of thrombin (Table 1). All of the other segments of thrombin were turned off in the energy calculation, in particular, the surrounding loops “Trp-148” and “Trp-60D” that are located at the entrance of the active site (47, 48). For experiment II, all of the active site segments were turned on during the simulation (see Table 1). In our simulation, all residues were considered in their neutral charge state in order not to bias the simulations, because Arg-3 of FPR can make an electrostatic bridge with Asp-109 of thrombin, which is located at the bottom of the active site at about 2.5 Å from the guanidinium group of Arg-3. The calculations were carried out on a single node of the IBM-SP2 RX 6000 Super-Computer at the Cornell Theory Center.

Figure 1.

Active site residues of human α-thrombin that were considered during the simulation. Thick line: residues taken into account in experiment I. Thin line: additional residues added for experiment II. The ligand FPR is indicated by an arrow.

Table 1.

List of segments for which the energy has been switched on or switched off during the rigid docking of FPR onto human α-thrombin

Segment number	Residue number in the sequence	Chymotrypsin numbering	Energy turned off or turned on for experiment I	Energy turned off or turned on for experiment II
FRP
1.	1-3	1-3	ON	ON
Thrombin A chain
1.	1-36	1-15	OFF	OFF
Thromin B chain
1.	1-40	16-54	OFF	OFF
2.	41-44	55-58	OFF	ON
3.	45-46	59-60	OFF	OFF
4.	47-48	60A-60B	OFF	ON
5.	49-51	60C-60D	OFF	OFF
6.	52-54	60E-60H	OFF	ON
7.	55-89	60I-93	OFF	OFF
8.	90-99	94-102	OFF	ON
9.	100-140	103-140	OFF	OFF
10.	141-156	141-151	OFF	OFF
11.	157-175	152-170	OFF	OFF
12.	176-180	171-175	OFF	ON
13.	181-197	176-187	OFF	OFF
14.	198-206	188-196	ON	ON
15.	207-224	197-212	OFF	OFF
16.	225-241	213-229	ON	ON
17.	242-259	230-247	OFF	OFF

The residues of the active site of thrombin are listed in bold type, even though the energies of all of them were not turned on. 

Grid Calculation.

In this study, the contribution of the nonbonded and electrostatic field of all of the atoms of the rigid segments of the receptor that were considered during the simulation (switched on) was incorporated into a 3D grid. The principle and the manner in which the grid is calculated have been presented elsewhere (44). The grid was defined as a cube of 56 ų volume with a constant spacing of 0.666 Å, whose center is located at point P1 = (6, 20, 13 Å) somewhere inside the active site. The 3D grid was actually split up into 15 different grids: one for the electrostatic field and 14 for the nonbonded energy associated with each of 14 atom types. The value of the field at a given point of the active site was estimated by using two layers of neighbors, i.e., the 64 nearest points of the grid. The interpolation of the value of the field at the position of any atom of the ligand, from these 64 grid points, was carried out with Bezier splines. The major advantage of this interpolation scheme is that the splines are smooth, i.e., continuous and differentiable everywhere on the grid. The energy as well as the gradient could be estimated from the grid points, making the energy minimization very efficient. The calculation of the grid was carried out only twice, once for each experiment (I and II).

RESULTS AND DISCUSSION

The first series of experiments consisted of docking the FPR ligand onto a small part of the active site consisting of two segments, nos. 14 and 16. The ligand was generated inside a sphere of radius 3 Å. Twenty independent rigid-docking simulations using the MCM method and the 3D grid energy evaluation were carried out. The simulation stopped when the GM was reached, i.e., when the energy was less than 0.4 kcal/mol above the GM (−40.7 kcal/mol); this corresponds to a rmsd from the reference structure of the ligand of less than 0.1 Å. Our results showed that all 20 simulations reached the GM. On average, 49 ± 34 MC steps were required to reach the GM corresponding to an average simulation time of 35 s with a SD of 20 s.

The same types of simulations also were carried out without the grid. The grid calculation was replaced by the calculation of all of the atomic interactions between the ligand and the two segments. The GM was reached again in all 20 simulations. The average number of MC steps to reach the GM was 126 ± 108 with a time of 411 ± 347 s, where the error corresponds to one SD. The computational time is thus about 12 times longer than simulations with the grid. This factor depends, of course, on the size of the system. The result is that an average of 2–3 times more MC steps are required to reach the GM when the simulations are carried out without the grid. This suggests that it is easier to locate the GM when the original function is replaced by Bezier splines. This is because of the smoothing property of the Bezier splines. By smoothing out the potential energy surface, it is easier to overcome the energy barriers and reach the GM.

To assess the complexity imposed by the narrowed active site of thrombin, we compared our MCM procedure with a current MC procedure used for docking (12, 28, 29, 32, 38). Simulations were carried out using the same procedure as previously, i.e., with the ligand initially placed randomly in a sphere of 3 Å radius around the active site, and the grid-based energy calculation but with standard MC without minimization. Ten independent standard MC simulations of 10⁶ steps were carried out. The results showed that none of them reached the GM (Table 2). However, the lowest energy value, which is about 3 kcal/mol above that of the GM corresponds to a structure close to the native (rmsd = 0.4 Å). The average time per simulation was about 24 min. The chance of reaching the GM thus can be estimated at 10% (1/10) for the standard MC procedure. The MCM protocol is about 40 times faster with a chance of success of 100% for this system. This series of standard MC simulations also showed false-positive results (Table 2). Structures with low energy values have comparatively high rmsd values and, conversely, high-energy structures have low rmsd values. This shows the importance of reaching the GM in a docking simulation, because, after a certain threshold above the GM, the energy and the rmsd value are no longer correlated, i.e., it is no longer possible to predict the native conformation from the energy value.

Table 2.

Results of the 10 independent MC simulations (without energy minimization) of experiment I

Energy*	rmsd†, Å
−37.7	0.4
−29.8	0.6
−22.6	7.6
−22.3	1.2
−22.2	0.8
−21.7	5.9
−21.5	6.8
−21.3	7.8
−21.3	6.8
−21.2	7.4

^*The GM is defined to be the set of energies for which the rmsd is less than 0.1 Å, i.e. E is in the range [−40.7; −40.3] kcal/mol. 

^†The rmsd is calculated between the lowest-energy structure of the ligand FPR and its reference structure, which is the structure obtained after energy-minimizing the x-ray structure of the complex, human α-thrombin-FPR. 

To test the robustness of the method, a second series of computer experiments was carried out. This time, almost all of the residues of the active site were taken into account, and the ligand was generated randomly inside a sphere of 15 Å centered in the middle of the active site. As before, 20 independent MCM simulations, using the grid, were carried out. We again obtained 100% success in reaching the GM. The average number of steps was 208 ± 202, corresponding to an average time of 140 ± 128 s. Without the grid, 19 of 20 simulations led to the GM within an average time of 2,284 s. The computer time savings with the grid in this case was about 16-fold. For comparison, 10 independent MC simulation of 10⁶ steps, without energy minimization and without the grid, were carried out. Each simulation took about 10 hr of computer time. None of them led to the GM. All of the lowest energy conformations of the complex were 10–20 kcal/mol higher in energy than that of the GM with rmsd values ranging from 6 to 8 Å.

CONCLUDING REMARKS

The MCM method using Bezier splines for the grid interpolation scheme meets the two major requirements for docking ligands onto proteins: robustness and accuracy. Robust enough to reach the GM with great reproducibility (in our case, 100%) and accurate because no false-positive results were obtained. The lowest energy value corresponds to the native structure. The reasons for the absence of false-positive results are, first, the use of local energy minimization after each MC step. Therefore, only energy-refined structures without atomic clashes are considered. Second, the ECEPP/3 force field with an all atom model is sufficiently accurate to describe the x-ray structure of the complex as the GM. In this study, the energy-minimized complex was the reference system. If the reference structure were not energy-minimized, then conformations with lower energy could be obtained by MCM simulation.

The results show that it is sufficient to consider only a small part of the active site to determine the bound conformation of the ligand. When the ligand is rigid, the GM of the reduced molecular system turns out to correspond to the native bound structure. This means that the orientation and location of the ligand are determined entirely by a few particular active site residues, such as those of the active site pocket. The other residues do not influence the orientation and position of the ligand. In flexible docking, this might not be true. Even if some part of the ligand is correctly localized in the active site, a portion of the ligand might change its internal conformation to adapt to the perturbation of the active site. This is demonstrated in a study with a flexible ligand and/or a flexible receptor (M. C. Maurer, J.-Y.T., C. C. Lester, E. E. DiBella, and H.A.S., unpublished results).

ABBREVIATIONS

MC

Monte Carlo

MCM

MC energy minimization

FPR

NH₂-d-Phe-Pro-Arg-COOH

rmsd

rms deviation

GM

global minimum

3D

three-dimensional