Characterizing semilocal motions in proteins by NMR relaxation studies

Abstract

The understanding of protein function is incomplete without the study of protein dynamics. NMR spectroscopy is valuable for probing nanosecond and picosecond dynamics via relaxation studies. The use of ¹⁵N relaxation to study backbone dynamics has become virtually standard. Here, we propose to measure the relaxation of additional nuclei on each peptide plane allowing for the observation of anisotropic local motions. This allows the nature of local motions to be characterized in proteins. As an example, semilocal rotational motion was detected for part of a helix of the protein Escherichia coli flavodoxin.

The functions of proteins are dictated by their three-dimensional structures as well as by their dynamic behavior. In many cases, dynamics such as flap and domain movements as well as overall conformational changes are essential for the full and correct function of proteins (1–4).

One way to measure the dynamic behavior of proteins on the nanosecond and picosecond time scale is via NMR relaxation (5–7). Relaxation is caused by fluctuations of interaction energies, e.g., dipole-dipole energies, as the internuclear interaction vectors are reoriented by thermal motion. For example, the time constant for longitudinal dipolar relaxation of spin I by spin S, T₁, is given by

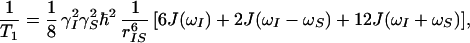1

where γ_I and γ_S are the gyromagnetic ratios of I and S, r_IS is the internuclear distance between I and S, and ℏ = Planck’s constant/2π. The spectral density functions, J(ω), which represent the intensity of the internuclear vector motion at the NMR frequencies ω (typically 10⁹ rad/s), are the actual reporters of the reorientational dynamics of the internuclear interaction vectors (8, 9).

Relaxation measurements are typically carried out with ¹⁵N-labeled proteins (10–11). By using two- or three-dimensional NMR techniques, the values for the J(ω) can be obtained for virtually all N-NH vectors in the molecule. Using the model-free approach (12, 13), one obtains from J(ω) the overall tumbling with characteristic correlation time τ_c and the local mobility characterized by the correlation time τ_e, on a residue specific basis, according to

2

The order parameter, S², describes the amount of local mobility, with S² = 1 for no local motion and S² = 0 for completely unrestricted local motion of the NH vectors. For a typical relaxation study, S², τ_c, and τ_e are reported for the different NH sites. This is a powerful method that has allowed the detection of extensive local dynamics, especially of loops and termini, in many proteins. A general shortcoming, however, is that these existing methods cannot identify what the local motions are. This seriously hampers our understanding of the biological significance of the local motions.

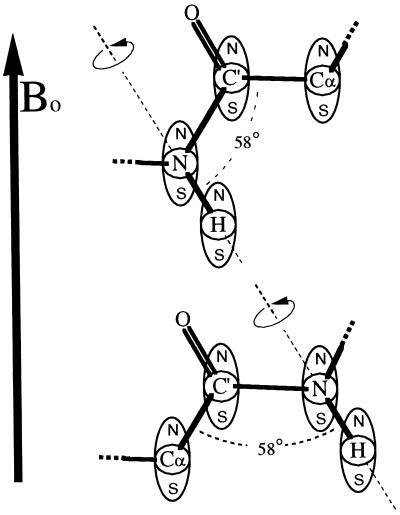
We propose here that to better obtain insight into the nature of the local motion, one must measure, at any given location, the relaxation of two or more interactions corresponding to internuclear vectors that lie at some fixed angle to each other. Thus, the reorientation of each of these vectors is characterized by an order parameter, S², which reports on the same motion. The combined values put restraints on the possible local motions. For the protein backbone, this can be accomplished by measuring the relaxation of amide ¹⁵N by the ¹⁵N-¹H dipolar interaction and the relaxation of carbonyl ¹³C′ by the ¹³C′-¹³Cα dipolar interaction, because it is known that each peptide plane unit moves essentially as a rigid entity (14). These two vectors (N-NH, C′-Cα) make a fixed angle of 58°. As an example, consider Fig. 1 where a peptide plane in an external magnetic field, B_o, is shown rotating about the N-NH bond axis. The N-NH dipolar and the C′-Cα dipolar interactions are represented schematically by magnetic dipoles centered on the N, H, C′, and Cα nuclei. As the peptide plane rotates about the N-NH bond, the N-NH dipolar interaction is not affected: this motion does not cause additional ¹⁵N dipolar relaxation and will not affect the order parameter S²_N-NH. In contrast, the C′-Cα dipolar interaction changes considerably (the interaction actually changes sign for the motion drawn): this motion may be detected in ¹³C′ dipolar relaxation, and it strongly affects S²_C′-Cα. Note that this particular local motion, because of its anisotropic nature, would go undetected if only the ¹⁵N relaxation were measured.

Figure 1.

A peptide plane in an external magnetic field, B_o, showing the anisotropic effect of an 180° rotation about the N-NH bond axis upon the N-NH and C′-Cα dipolar interactions. The N-NH and C′-Cα dipolar interactions are represented schematically by magnetic dipoles centered on N, H, C′, and Cα. The N-H dipolar interactions are seen to be invariant on this rotation, whereas the C′-Cα dipolar interactions vary significantly, even changing sign. The figure illustrates a fast local motion superimposed on a slower overall isotropic motion.

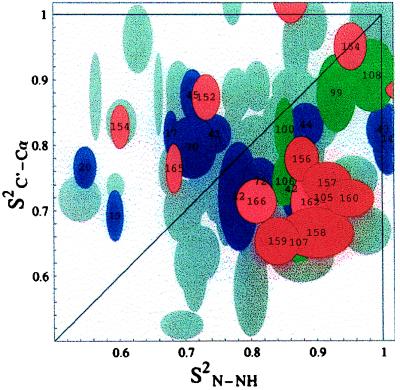
In this study of Escherichia coli flavodoxin (175 residues, τ_c ≈ 14 nsec, assignments taken from ref. 15), the order parameter S²_N-NH was measured in a conventional way from ¹⁵N T₁, T₂, T_1ρ, and nuclear Overhauser effect (NOE) experiments, whereas the S²_C′-Cα order parameters were measured from carbonyl relaxation data (16–20). We used experiments developed in our group (16) that exclusively determine the contribution of the Cα-C′ dipole-dipole interaction to the C′ relaxation by measuring homonuclear Cα → C′ NOE and C′ T₁ relaxation. By selecting for the Cα-C′ dipole-dipole interaction, we can interpret the C′ relaxation data in terms of an exclusive order parameter for the Cα-C′ internuclear vector. The results of these measurements are shown in Fig. 2, where each point corresponds to one peptide plane. Typical error ranges (± one SD) were obtained by computing the order parameters for a range of synthetic input data with distributions corresponding to the primary uncertainties of the experimental input data as estimated from signal-to-noise ratios.

Figure 2.

The order parameters S²_C′-Cα versus S²_N-NH for E. coli flavodoxin. Data for most peptide planes are shown as overlapping gray ellipsoids representing the experimental uncertainties. The error ranges (± one SD) were obtained by computing the order parameters for a range of synthetic input data with distributions corresponding to the primary uncertainties of the raw input relaxation data as estimated from spectral signal-to-noise ratios. Red and pink ellipsoids correspond to the peptide planes of helix 5 as indicated by the residue numbers. Residues 163 and 153 are on the top and right-hand side of the figure, respectively. The green ellipsoids show helix 4, and the purple ellipsoids show all other helical residues for which data was obtained. Note: The coordinates of data point i correspond to the order parameters of the vectors C′(i)-Cα(i) and N(i + 1)-NH(i + 1). The order parameters S²_N-NH were measured from ¹⁵N T₁, T_1ρ, and nuclear Overhauser effect data. The T_1ρ data for these residues were found to be independent of spin locking rf power. Hence, we conclude that the order parameters for these residues have no exchange component, and therefore, that the anisotropic motions are confined to the nanosecond to picosecond time domain. The order parameters S²_C′-Cα were measured from Cα-C′ nuclear Overhauser effect experiments combined with ¹³C′ T₁ relaxation as described in ref. 16. Because T_1ρ and T₂ were not used, the C′ order parameters also have no exchange component. Experimental details are given in ref. 29.

If all the motions of the peptide planes were isotropic, the order parameters S²_N-NH and S²_C′-Cα would be identical at each site, and all of the points would fall along the diagonal within the given error margins. Thus, the presence of off-diagonal points corresponding to peptide planes with very different reorientational dynamics for N-NH and C′-Cα suggests an abundance of anisotropic local motions in this protein. The anisotropic motion of the peptide planes could be global, semilocal, or purely local. The anisotropy of the global tumbling is a function of the shape of the protein and, for nearly spherical molecules such as flavodoxin (calculated principal diffusion tensor components relate as 1.0:1.17:1.45 excluding the last 10 highly unstructured residues) (21), may be neglected (see below). Purely local motion occurs when each peptide plane moves independently, whereas semilocal motion is characterized by regions of the protein undergoing more or less concerted motions. A concerted motion might occur when a loop or flap of the protein moves as a rigid unit like a door swinging on its hinges or when a helix moves as an entity (1–3, 22).

Further inspection of the data in Fig. 2 reveals the existence of five consecutive residues (156–160) that have very similar order parameters. These residues, indicated in red, are characterized by values for S²_N-NH that are significantly larger than those for S²_C′-Cα. The probability that the clustering of these five residues in the area defined by S²_N-NH 0.8–1.0 and S²_C′-Cα 0.62–0.82 is caused by pure chance is 0.12% using a standard Z-score test in both dimensions. We conclude from these small probabilities that the observed clustering is statistically significant and merits further investigation.

Residues 156–160 form part of a regular alpha helix (helix 5, residues 152–165) in the crystal structure and NMR secondary structure of E. coli flavodoxin (15, 21). We suggest here that part of helix 5 is subject to semilocal motions that affect the C′-Cα vectors more strongly than the N-NH vectors. A simple model for this motion is limited rotational diffusion of the helix about its axis, which reorients the N-NH vectors of that helix much less than the C′-Cα vectors. Specifically, all N-NH vectors are roughly aligned with the helical axis, within 15° for an ideal helix whereas the C′-Cα vectors are oriented more perpendicular to that axis, ≈46° for an ideal helix.

For a specific local motion, we can rigorously calculate the order parameter for an internuclear vector. The model and magnitude of a local motion can be expressed as the probability P_a(θ_a, φ_a) of finding internuclear vector a at the angles (θ_a, φ_a) relative to the molecular frame. The auto correlation order parameter, S_a², then can be expressed as (12, 23, 24)

3

where the averages of the spherical harmonics, Y_2m, are probability weighted as follows

4

The order parameter for a different internuclear vector b at the same site, S_b², may be calculated in a similar manner but in most cases will differ because the probability P_b(θ_b,φ_b) will differ from P_a(θ_a,φ_a) depending on the specific local motion chosen. Using these expressions we calculate that a helix rotation of ±30° about the helix axis would explain the typical observed values S²_N-NH = 0.88 and S²_C′-Cα = 0.72.

Our data cannot distinguish between a concerted, in-phase rotational motion for this helical fragment or more disjointed twisting motions for the individual residues in this fragment. However, we prefer to think of the motion as a more concerted one, as that more easily would explain the similarity of the order parameters. A lower limit for the time scale of the motion is set at the overall rotational correlation time of the protein, which is 14 ns. We have not been able to obtain reliable numbers for the local correlation time, τ_e, associated with the nitrogen relaxation because of limited sensitivity of the relaxation data. Note, however, that S²_N-NH and S²_C′-Cα values are much less sensitive to the raw relaxation data sensitivity (25), allowing us to derive the order parameters shown. Other workers typically observe local correlation times of 100 ps or shorter for local NH vector dynamics (10, 11), using the model-free formalism. We have no indication that the time scale of the semilocal dynamics would be different for this case. The question arises whether the peptide planes of all alpha-helical residues in flavodoxin are characterized by a larger S²_N-NH than S²_C′-Cα. This is generally not the case, because the order parameters of the other helical residues in flavodoxin span the entire distribution, as is indicated by green and purple symbols in Fig. 2. An exception is helix 4 (residues 98–108) for which a similar indication of anisotropic motion exists. However, the number of data points and their clustering is too small for this helix to make statistically sound identifications.

An alternate explanation for the relatively large S²_N-NH values observed for the residues of helix 5 (and 4) that does not require the introduction of anisotropic local motions must be considered. Because helices 4 and 5 are nearly parallel (within 12°) it is possible that they, and therefore the N-NH vectors they contain, are aligned (on average) with a preferred global rotational axis of the molecule. That is, if the molecule were nonspherical and its long axis were aligned with helices 4 and 5, then the larger-than-average values observed for S²_N-NH might be caused by global anisotropic tumbling and not the presence of a concerted helical motion. Alternatively, the anisotropy of the susceptibility of the flavin cofactor might cause the protein to be partially aligned in the external magnetic field (26, 27). If such a putative alignment axis were to lie parallel to helices 4 and 5, similar global rotational anisotropy would be observed. To explore these possibilities, the measured order parameters for those N-NH internuclear vectors that are aligned with helix 5 were examined. The results are summarized in Table 1. The order parameters for helix 5 alone (column 2) are clearly above the global mean (column 1). Using the Kolmorogov-Smirnov statistical test (28), we calculate that the large difference between these two averages is significant to an 80% confidence level. In contrast, the average for those N-NH vectors that are aligned with those in helix 5 but are not in helix 4 or 5 (column 3) is very near the mean S²_N-NH for the entire protein. The very small difference between these numbers is negligible to a 80% confidence level. The residues of both helices 4 and 5 were removed from the average in column 3 because there are some indications that helix 4 is undergoing an anisotropic motion similar to that of helix 5 (see the green ellipsoids in Fig. 2). Therefore, the N-NH order parameters for helix 4 also may be higher than the global average because of motion rather than alignment. The statistical results do indicate that to a high confidence level that the order parameters observed are larger than the global mean not because of their alignment with respect to the molecular frame, but because of some other characteristic of helix 5. We conclude, therefore, that there is not a preferred global rotational axis parallel to helix 5 and that the observed order parameters are, in fact, indicating the presence of an anisotropic semilocal rotational axis.

Table 1.

Dependence of N-NH order parameters on orientation relative to the molecular frame

Average S2 N-NH
All residues	Helix 5 alone	N-NH vectors aligned with those in helix 5 except for those helices 4 and 5
0.773  ± 0.014 (108)	0.854  ± 0.038 (13)	0.764  ± 0.033 (14)

The average order parameters (S²N-NH) were calculated for all internuclear N-NH vectors and for those internuclear vectors aligned (or anti-aligned) within 35° of the helix 5 axis. The number of residues used in each average is given in parentheses. Separate averages are calculated for those aligned N-NH vectors that are contained in helix 5 and those that are not. See text for details. 

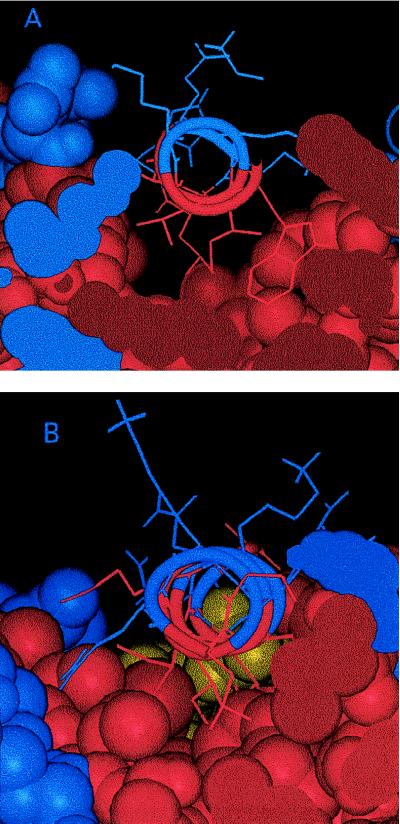
The known x-ray crystallographic structure of flavodoxin (21) was examined to evaluate the plausibility of the proposed limited helical rotation. One observes that the hydrophobic side of the amphipathic helix 5 binds to the core of the protein in a large, shallow, fairly smooth hydrophobic trough (Fig. 3A). The binding may be quite loose because this helix is near the C terminus (residue 175) and the patch against which it binds is saddle-shaped with no clear pockets or holes tightly binding specific side chains. The only “specific” binding is the burial of the polar end of the Arg-155 side chain. The long nonpolar hydrocarbon chain of this side chain, however, still would afford the helix considerable mobility. In addition, helix 5 could rotate on its axis without bringing any large hydrophilic side chains into contact with the hydrophobic surface of the trough. In contrast, another helix in flavodoxin, helix 1 (residues 12–25), appears to bind much more snugly in a hydrophobic trough like a wedge in a V-shaped slot (Fig. 3B). The binding surface is a much sharper valley than that for helix 5, which would inhibit rotational motion for helix 1. It thus appears that a plausible structural explanation in terms of loose packing exists for the observed semilocal anisotropic dynamics of helix 5.

Figure 3.

Views parallel to the helical axis of (A) helix 5 and (B) helix 1. Hydrophobic (apolar) residues and hydrophilic (polar) residues are rendered in red and blue, respectively. The yellow atoms in B belong to the flavin cofactor.

In conclusion, the measurement of the relaxation behavior and picosecond dynamics of two internuclear vectors on each peptide plane allows one to more accurately determine the mobile regions of proteins. This is demonstrated by the examination of helix 5 of flavodoxin. By the standard studies of ¹⁵N relaxation alone, helix 5 appears rather immobile relative to the rest of the protein. The additional measurement of ¹³C′ relaxation, however, reveals the presence of local motions experienced by the C′–Cα internuclear vectors. Moreover, these methods may be used to determine the nature or character of the local motion by deriving likely motional models that are consistent with the observed anisotropic relaxation behavior. The characterization becomes better when the reorientational dynamics of more internuclear vectors and the cross-correlations between relaxation pathways (29) are measured. Recently, order parameters have been correlated with entropy (30, 31). It is evident that the entropic contribution to protein stability from this particular helix motion would go undetected in measurements of N-NH dynamics alone. Similarly, a change in entropy on a binding event or conformational change also would go undetected if insufficient relaxation parameters were studied.