Nature of PEVK-titin elasticity in skeletal muscle

Abstract

A unique sequence within the giant titin molecule, the PEVK domain, has been suggested to greatly contribute to passive force development of relaxed skeletal muscle during stretch. To explore the nature of PEVK elasticity, we used titin-specific antibodies to stain both ends of the PEVK region in rat psoas myofibrils and determined the region’s force-extension relation by combining immunofluorescence and immunoelectron microscopy with isolated myofibril mechanics. We then tried to fit the results with recent models of polymer elasticity. The PEVK segment elongated substantially at sarcomere lengths above 2.4 μm and reached its estimated contour length at ≈3.5 μm. In immunofluorescently labeled sarcomeres stretched and released repeatedly above 3 μm, reversible PEVK lengthening could be readily visualized. At extensions near the contour length, the average force per titin molecule was calculated to be ≈45 pN. Attempts to fit the force-extension curve of the PEVK segment with a standard wormlike chain model of entropic elasticity were successful only for low to moderate extensions. In contrast, the experimental data also could be correctly fitted at high extensions with a modified wormlike chain model that incorporates enthalpic elasticity. Enthalpic contributions are likely to arise from electrostatic stiffening, as evidenced by the ionic-strength dependency of titin-based myofibril stiffness; at high stretch, hydrophobic effects also might become relevant. Thus, at physiological muscle lengths, the PEVK region does not function as a pure entropic spring. Rather, PEVK elasticity may have both entropic and enthalpic origins characterizable by a polymer persistence length and a stretch modulus.

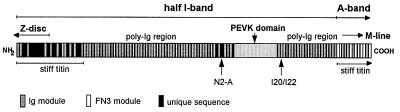
The molecular basis of muscle elasticity has become a subject of growing interest, thanks in particular to recent insights into the primary structure of the protein mainly responsible for passive force development in relaxed myofibrils (1). This protein, the giant polypeptide titin (or connectin; refs. 2 and 3), assumes unique functions in the sarcomeres, the unitary structures of a muscle fiber (for reviews, cf. refs. 4–6). Most importantly, the filamentous titin molecules provide an elastic link between the sarcomere’s Z-disc and A-band. Although a titin filament is >1 μm long, only a fraction of the molecule from the I-band region is functionally extensible (7–9) and involved in passive tension generation (10–12). However, the elastic I-band titin represents no uniform molecular spring, but consists of structurally distinct segments (Fig. 1), poly-Ig domain chains and a unique sequence, the PEVK region (1). Previously we showed that these two structural motif types contribute differently to I-band titin elasticity (13): the poly-Ig chains lengthen mainly within a low sarcomere length (SL) range where passive force is very small, whereas the PEVK domain elongates at moderate to long SLs where passive force increases more steeply. After the discovery of this two-stage extension mechanism (also see refs. 14 and 15), an important aim of current research on titin is to uncover the nature of elasticity of both I-band titin motif types.

Figure 1.

I-band titin domain architecture showing the splice variant likely to be found in psoas muscle (1, 13). The epitope positions of the two antibody types used in this study, N2-A and I20/I22, are indicated. Note that not the entire I-band titin is elastic; a 100 nm-long segment at the Z-disc end is functionally stiff. Ig, Ig-like; FN3, fibronectin type-3-like.

Micromechanical studies on isolated single titin molecules recently have demonstrated that the Ig domains can unfold at high external forces and thereby contribute to the extensibility of the sarcomere (16–18). However, at lower forces—those likely to be relevant during normal muscle function—it was suggested that an “entropic spring” mechanism may account for the elasticity of titin (summarized in ref. 19). According to this concept, the Ig domain segments and the PEVK domain may be in a partially collapsed state at the short SLs. Then, to extend these regions by an external force, it would be necessary to counteract the forces brought about by exposure of the molecular segments to thermal fluctuations. Whereas the entropic-spring concept appears to be valid for the poly-Ig chains of psoas muscle titin (20), this study was initiated to test whether it also can explain the elastic properties of the PEVK domain. We find that entropic theory alone cannot describe the region’s spring-like properties. Rather, PEVK stiffness also may be based on enthalpic contributions to elasticity, such as electrostatic and hydrophobic interactions. Our results point to a dual role of the PEVK region in acting as a compliant entropic spring at low stretch and a stiffer enthalpic spring at higher extensions.

METHODS

Myofibril Mechanics.

Myofibrils were isolated from freshly excised male Wistar rat psoas muscle as described (21). Under a Zeiss Axiovert 135 microscope, the ends of a myofibril were picked up with two glass microneedles, one connected to a micromotor, the other to a home-built force transducer (sensitivity, ≈5 nN). Force data collection and motor control were done with a 586 PC, data acquisition (DAQ) board (PCI-MIO-16-E1, National Instruments, Austin, TX) and custom-written labview software (21). SL was measured either with a sensitive charge-coupled device camera (Völker, Maintal, Germany) and frame grabber board including image processing software (Data Translation, Marlboro, MA) or by digitizing and analyzing the myofibril image, using a 512-element linear photodiode array (Reticon, Munich), the PC, DAQ board, and labview programs.

To record passive force, relaxed single myofibrils or preparations containing up to five myofibrils (to improve signal-to-noise ratio particularly at the short SLs) were stretched in stages from slack length to a series of desired SLs. Stretch duration was ≈10 s; the hold period (to wait for stress relaxation at constant length) was 1–2 min. After stretch to a maximum SL, the specimen was released in stages to slack length. Force data were recorded every 4 ms, stored in binary format, and median-filtered by applying labview algorithms. To obtain passive tension, the cross-sectional area of a preparation was inferred from the diameter of the specimens as described (20, 21). Finally, to also record titin-based stiffness in some experiments, we imposed small-amplitude, 20-Hz sinusoidal oscillations onto stretched myofibrils exposed to a Ca²⁺-independent gelsolin fragment (TL-40) for at least 20 min and measured the magnitude of force oscillations as reported (21).

Solutions contained enough protease inhibitor, particularly leupeptin (21), to largely prevent titin degradation (20). Experiments normally were performed at room temperature, pH 7.1, and ionic strength (IS) of 200 mM. In the stiffness experiments, actin-extracted myofibrils were exposed to relaxing buffers of different pH (5.9, 6.6, 7.0, 7.4, and 8.0, adjusted with KOH) and IS (170, 50, and 20 mM, adjusted with KCl; cf. ref. 22).

Antibodies.

Two affinity-purified polyclonal antibodies were used to label the PEVK region of titin at its N terminus and C terminus, respectively (Fig. 1). The first antibody, N2-A, has been described previously (13). The second, referred to as I20/I22, was raised to the nucleotide positions 13978–14826 of the human cardiac titin data library entry (GenBank accession no. X90568). Sequences were isolated by PCR, subcloned into His-tagged pET vectors, expressed in Escherichia coli, and purified according to standard protocols. Purity was confirmed by SDS/PAGE. Antisera against both N2-A and I20/I22 protein were generated in rabbits by Eurogentec (Brussels). Affinity purification of the antibodies was achieved by passing the sera over Sepharose columns charged with covalently bound antigen.

Immunofluorescence and Immunoelectron Microscopy.

Immunofluorescence studies were performed under the inverted microscope (epifluorescence mode; 100×, 1.4NA objective) on single myofibrils (13, 21). Typically, a specimen was stretched in relaxing buffer to a desired SL and was labeled with primary antibody and Cy3-conjugated anti-rabbit IgG (Rockland, Gilbertsville, PA, no. 3838). Sometimes, we first fixed a stretched myofibril in 4% formaldehyde solution for 20 min before carrying out the staining procedure. With both approaches, results were virtually identical; only data obtained from unfixed myofibrils are shown in this study. In some cases, myofibrils also were stained with the two primary antibody types together. Three images usually were recorded at a given SL and automatically superimposed by using a feature of the software. For measurements at another SL, a new preparation was used. The antibody epitope spacing across the Z-disc was measured with image analysis software (21) and divided by two to obtain the Z-disc-epitope distance in a half-sarcomere.

Immunoelectron microscopy was essentially carried out as follows: Rat psoas muscle was stretched to different degrees in situ, and fiber bundles were excised from freshly killed animals perfused previously with a solution containing 4% paraformaldehyde. Sometimes, we quickly excised muscle tissue without perfusing the animal and stretched the fibers in relaxing buffer before adding the fixative. Specimens then were processed for cryosectioning and immunolabeling with the titin antibodies and 10-nm gold particles as described (23, 24). Micrographs were taken with a Philips EM 301 at 80 kV. The center of the nanogold particles was used to measure the distance of a given antibody epitope from the center of the Z-disc.

Calculations.

We considered the PEVK region to behave as a polymer and tried to describe its mechanical properties with recent elasticity models. In a first model applied—a standard wormlike chain (WLC) model (25, 26)—the external force (f) is related to the fractional extension (z/L) of the chain by

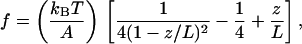1

where A is the persistence length, k_B is the Boltzmann constant, T is absolute temperature (300 K in our experiments), z is the end-to-end length, and L is the chain’s contour length. Eq. 1 is a good approximation to describe entropic elasticity of many biopolymers (26).

Two other models applied by us are a freely jointed chain model (27) and a WLC model developed by Odijk (28), both of which are based on entropic and enthalpic theory. The models use similar parameters as the standard WLC model to describe entropic elasticity, but also define an elastic modulus to incorporate enthalpic stretching.

A fourth model used by us is an extension of Eq. 1 with the addition of a stretch modulus, K_o, to describe enthalpic contributions to elasticity (29). According to this modified WLC model, the force is related to the fractional extension through

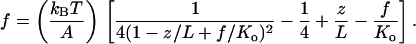2

The force necessary to extend the PEVK segment of one titin strand was deduced from the myofibrillar passive tension-SL curve by using a value of 1.2 ∗ 10⁹ titins per mm² cross-sectional area (30), which is comparable to assuming 3 titins per half thick filament (31). This ratio was considered more likely than a 6:1 ratio (12, 32), based on the results of a recent study, in which we modeled titin’s poly-Ig chains as entropic springs (20). To obtain z, we determined the difference between the N2-A and I20/I22 extension curves and subtracted a constant of 20 nm, to account for the length of some non-PEVK titin near the antibody binding sites (cf., Fig. 1). For L, we assumed a value of 476 nm, as estimated from the number of 1,400 residues per psoas PEVK segment (1, 13), multiplied by 0.34 nm for the maximal residue spacing. Calculation of A and K_o and curve fitting were done with a nonlinear least-squares method (Levenberg-Marquardt algorithm; Origin 5.0 software by Microcal, Amherst, MA).

RESULTS

PEVK Extension.

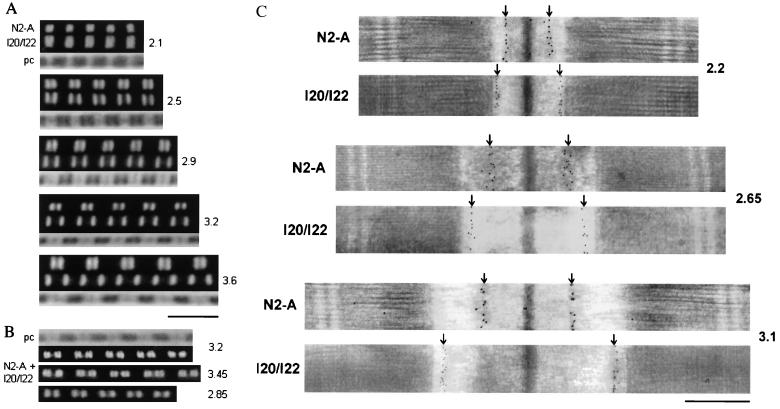
Extensibility of the PEVK region of psoas muscle titin was investigated by immunofluorescence microscopy on sarcomeres of single myofibrils stretched to varying degrees. Typical images of myofibrils extended to five different SLs and stained with antibodies specific to N2-A or I20/I22 are shown in Fig. 2A. When myofibrils were exposed to both antibody types together and repeatedly stretched and released at SLs above 3 μm, we could readily observe reversible extension of the PEVK region (Fig. 2B).

Figure 2.

Examples of immunostainings with titin antibodies flanking the PEVK region. (A and B) Immunofluorescence images of single psoas myofibrils stretched to different SLs (indicated on the right) and labeled with either the N2-A or the I20/I22 titin antibody (A) or both antibody types together (B). As secondary antibody, Cy-3-conjugated IgG was used. In B, the lower two images show the same myofibril both at high and moderate stretch; the spacing between two close fluorescent stripes indicates the length of the PEVK region. pc, phase-contrast images. (Scale bar, 5 μm.) (C) Immunoelectron micrographs of stretched psoas muscle sarcomeres stained with N2-A or I20/I22. The nanogold particles indicate the respective epitope positions (arrows). (Scale bar, 0.5 μm.)

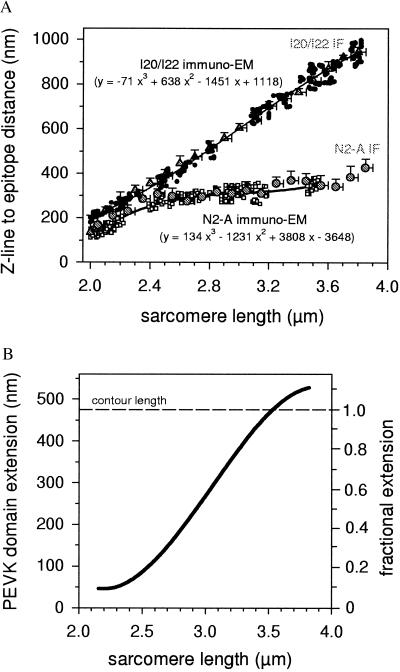
Because the immunofluorescence method did not provide enough resolution to measure the precise length between the N2-A and I20/I22 epitopes, we determined this parameter by using an immunoelectron microscopical technique (Fig. 2C). The N2-A epitope distance from the Z-disc center increased greatly on stretch from 2.0 to ≈2.6 μm SL, but little with further extension to ≈3.5 μm. On the other hand, the Z-disc–I20/I22 spacing increased almost linearly with SL. Small deviations occurred at the shorter lengths, at which the distance of the I20/I22 epitope from the A-band edge became longer on stretch, until a quasi-plateau value was reached between 2.6 and 2.8 μm SL. The results of the immunolabeling experiments (with electron microscopy data sets for each antibody type fitted by third-order regressions) are summarized in Fig. 3A.

Figure 3.

Extension behavior of the PEVK segment. (A) Summary of results of immunolabeling experiments. Immunoelectron microscopy data points for the Z-line center to epitope spacing are shown for both N2-A (□) and I20/I22 (•). The larger shaded circles (and triangles) and error bars indicate the mean distances from the Z-disc center and SD for N2-A (and I20/I22, respectively), measured by immunofluorescence microscopy (IF). Curve fitting parameters (electron microscopy data only) also are shown. (B) Extension of the PEVK region vs. SL. The left axis indicates the region’s end-to-end length, the right axis fractional extension (relative to the segment’s assumed contour length of 476 nm).

The N2-A fit curve and a constant of 20 nm (for rationale, cf. Methods) then were subtracted from the I20/I22 curve to obtain PEVK extension vs. SL (Fig. 3B). Substantial PEVK elongation began at ≈2.4 μm SL and then continued over the entire length of range investigated. At the average slack SL of ≈2.1 μm, the region’s end-to-end length was 46 nm, or, ≈10% of the estimated contour length (476 nm). One-hundred percent extension was reached at 3.5 μm SL.

Force-Extension Relation of the PEVK Region.

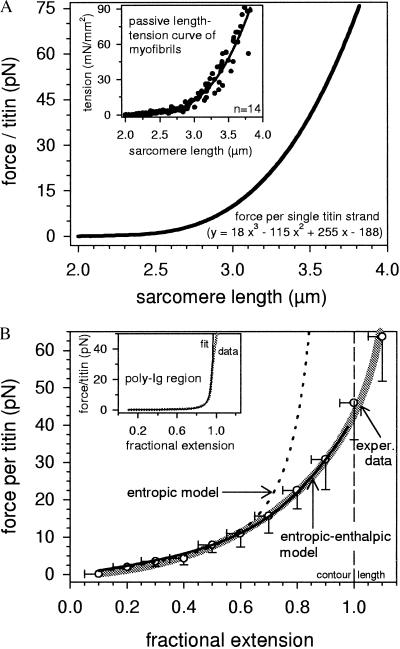
To determine this relation, it was necessary to know the force per titin strand. This parameter was deduced as described in Methods from the quasi steady-state, passive length-tension curve of rat psoas myofibrils (Fig. 4A, Inset), by assuming that (i) all titin molecules (≈1,000 parallel filaments per myofibril) behave independently of one another and have comparable elastic properties; and (ii) all parallel titin strands bear the same force at a given extension; the sum of these parallel forces is the force measured at the ends of the myofibril. With these assumptions, force per titin was calculated as shown in Fig. 4A.

Figure 4.

Force-length relations of titin. (A) Force per single titin molecule at different SLs, extrapolated from the steady-state passive tension vs. SL curve of isolated rat psoas myofibrils, shown in the Inset. The curve parameters also are indicated. (B) Force per titin vs. fractional extension of the PEVK region. Open circles and error bars indicate the mean force and SD of incrementally summarized data points and the thick shaded line the calculated fit to the experimental data, both deduced from A and Fig. 3B. The dotted black line represents the WLC model fit according to Eq. 1 (entropic elasticity), the continuous black line the modified WLC fit according to Eq. 2 (entropic-enthalpic elasticity). (Inset) For comparison, force vs. fractional extension (thicker shaded line) and fit according to the standard WLC model with A = 21 nm (thinner black line), calculated for the N-terminal poly-Ig segment of rat psoas titin (20).

To define the elastic properties of the PEVK segment, we plotted force per titin vs. fractional extension (Fig. 4B, thick shaded curve). Force increased from ≈1.5 pN at 20% relative extension (≈2.6 μm SL) to 8 pN at 50% extension (≈2.9 μm SL) and reached almost 45 pN at 100% fractional extension (3.5 μm SL).

Fits to Theory.

We tried to fit the experimental data with a number of recent elasticity models applicable to polymer chains. A standard WLC model of entropic elasticity (Eq. 1) has been used to simulate the elastic properties of whole titin filaments in vitro at low to moderate extensions (16, 18). However, we find that this model describes the PEVK force-extension curve sufficiently well only for forces below ≈12 pN (Fig. 4B, dotted line); a best fit returned a persistence length of ≈0.65 nm. At higher forces, there were large systematic deviations from the experimental data. Much better results for the moderate and high force regimes were obtained with the three entropic-enthalpic models, a freely jointed chain (27), Odijk (28), and modified WLC (29) models. Of these, the latter revealed by far the best fits. With this model (Eq. 2), the fit at lower forces was comparable to that obtained with Eq. 1, but the data curve was particularly well reproducible for forces >12 pN (Fig. 4B, continuous black line). For the best fit, the persistence length was 0.55 nm and the stretch modulus 185 pN. Because such calculations are valid only for a contour length assumed to be 476 nm, we performed the analysis also with different L-values ranging from 450 to 500 nm. These variations affected the stretch modulus, but had little impact on the persistence length. For example, with L = 450 nm, best fits were obtained for A = 0.60 nm and K_o = 150 pN; the respective values for L = 500 nm were 0.53 nm and 250 pN. The quality of the fits was similar to that shown in Fig. 4B. Importantly, in no case was it possible to describe the high-extension data with the purely entropic model. Thus, even in light of an unknown contour length, the above analysis is qualitatively valid. Further, when we used the different L-values also in the freely jointed chain and Odijk models, the fit results were generally better than those obtained with the standard WLC model, confirming the need to consider enthalpic factors. Still, the fit quality was never as good as with Eq. 2. Hence, the experimental findings apparently were described best by the modified WLC model.

For comparison, the inset in Fig. 4B shows results of related work on the elastic properties of the other extensible I-band titin regions, the Ig domain chains (20). In that study, the experimentally determined force-extension curve of the N-terminal poly-Ig segment of rat psoas titin could be correctly fitted up to forces of ≈35 pN with the purely entropic WLC model (A = 21 nm). Using this fit result and the values, A = 0.55 nm and K_o = 185 pN, respectively, from the entropic-enthalpic PEVK fit, we were able to correctly reproduce the measured passive length-tension curve of rat psoas myofibrils over the whole range of physiological SLs (data not shown).

Effect of pH and Ionic Strength on PEVK Stiffness.

In search of a possible origin of enthalpic PEVK elasticity, we took into account that the PEVK region is highly charged (15) and attempted to investigate whether pH changes and/or variable electrostatic screening of charges might affect the region’s stiffness. Therefore, we determined titin-based stiffness of psoas myofibrils from the force response to 20-Hz sinusoidal oscillations (21) under a variety of pH and IS conditions. These measurements were performed at 2.9–3.0 μm SL, at which force per titin is near 10 pN and PEVK extension is ≈50%. To exclude a possible contribution of actin-myosin interactions to stiffness, all preparations were exposed to a calcium-independent gelsolin fragment (TL-40, ≈0.2 mg/ml) to depolymerize the actin filaments (21). After 20–30 min of exposure to gelsolin fragment, myofibrils failed to respond to activation in pCa 5.0 solution with a measurable active tension or stiffness increase, as desired.

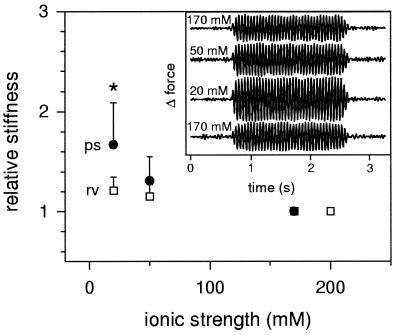
Varying pH of the relaxing solution between 5.9 and 8.0 did not result in noticeable stiffness changes of actin-extracted myofibrils (data not shown). However, on replacing normal-IS (200 or 170 mM) with mid-IS (50 mM) or low-IS (20 mM) relaxing buffer at pH 7.1, myofibrils became significantly stiffer (Fig. 5, Inset). On average, stiffness increased by ≈30% at mid IS and ≈70% at low IS (Fig. 5). This effect was unlikely to be caused by a contractile response (cf. ref. 22), because in control measurements, myofibrillar slack SL generally remained unchanged. On the other hand, when similar experiments were performed on actin-depleted myofibrils from rat right ventricle (at 2.3–2.4 μm SL), which express only a very short PEVK segment (1), a much smaller IS-dependent stiffening effect was observable (Fig. 5). At 20 mM IS, the difference in relative stiffness change between muscle types was statistically significant (P < 0.005, unpaired Student’s t test). We thus reasoned that the stiffening of rat psoas myofibrils in mid- to low-IS relaxing buffer might reflect changes in the elasticity of titin—probably the PEVK segment—brought about by electrostatic screening of charges.

Figure 5.

Titin-based stiffness of actin-extracted rat myofibrils at different ionic strengths. (Inset) Representative force oscillations of psoas myofibrils (raw data filtered with Butterworth bandpass filter) in response to 20-Hz oscillatory motor movement. The magnitude of force oscillation—a measure of myofibril stiffness—increases progressively as IS is lowered from 170 to 50 and 20 mM. The effect was reversible on returning to 170 mM. The main figure shows the average IS-dependent stiffness change (relative to the stiffness at normal IS) of actin-extracted psoas (ps; n = 6) and right ventricular (rv; n = 9) myofibrils.

DISCUSSION

Current understanding of the nature of titin elasticity has derived in part from recent mechanical experiments with single molecules (16, 18) or recombinant fragments (17), which have demonstrated that titin’s Ig domains can unfold at extreme stretch. These studies also confirmed previous findings in intact sarcomeres suggesting that Ig domain unfolding is unlikely to account for titin elongation at lower extension (13, 14). At low stretch forces, the titin molecule was proposed to act as an “entropic spring” showing WLC behavior. Taken simply, the stiffness of a WLC may be parameterized by its contour length, L, and a persistence length, A, which is a measure of the chain’s bending rigidity. Entropic compliance results when L ≫ A, because of the numerous configurations the polymer may adopt. As for the in vitro studies on titin, it must be reminded, however, that conclusions drawn from the results of mechanical analysis of isolated molecules are not unambiguous, because in vivo, titin filaments are functionally elastic only along part of their I-band portion. This portion has a heterogeneous structure (Fig. 1) and primarily is made up of poly-Ig regions and the PEVK domain (1). Therefore, to test whether the entropic spring concept is applicable to the physiologically extensible titin segments, it was desirable to “dissect” I-band titin into the structurally distinct regions and measure the elastic properties of each segment.

Whereas it has been shown elsewhere that entropic theory can indeed correctly describe the elastic properties of the N-terminal poly-Ig region of psoas muscle titin (20), this study focused on titin’s PEVK domain. By using immunofluorescence/immunoelectron microscopy and isolated myofibril mechanics, we determined the force-extension curve of the PEVK segment in situ. The relatively small dimensions of the myofibril preparation were advantageous in that they allowed extrapolation of the results down to the single molecule level and simulation of the experimental data by models of polymer elasticity. On the other hand, for valid application of WLC theory, we must assume independent mechanical behavior of individual titin strands—a situation not obvious in the sarcomere, which contains many parallel filaments. The possibility that weak interactions between filaments, for example, titin and actin, might affect passive force transiently (33), plays no role in our analysis, because we used only the force values after stress relaxation for the calculations. Whether filament-packing constraints in the I-band could hinder the random motion of titin molecules, thereby modifying entropic force, currently is unknown. However, some indication for such constraints not being a factor comes from the observation that selective removal of actin filaments from psoas muscle sarcomeres has no effect on passive force up to SLs far beyond 3 μm (33), at which we find enthalpic PEVK elasticity to dominate. Considering steric hindrance to be unimportant, we propose that the PEVK region behaves as a pure entropic spring only at forces (per titin) below ≈12 pN, or, relative extensions <60%. Up to such extensions, the titin region can be characterized as a WLC with A = 0.65 nm, a value at the low end of the persistence-length range of 0.6–220 nm known for amino acid homopolymers (34).

A few literature reports are available that have addressed the issue of PEVK elasticity in a similar context: in attempts to determine the persistence length of the PEVK region, the force-extension relation of whole titin filaments has been fitted with the WLC model (Eq. 1), by assuming either a single extensible component (16) or two such components connected in series (18). In the former approach, A was 2 nm, whereas in the latter, the persistence length of the component considered to be the PEVK region was ≈0.2 nm. The value found in the present study lies in between those numbers and would indicate that stretches of approximately two residues take on orientations that are correlated—a situation more likely than one in which the unitary length of the WLC is smaller than the average residue spacing. As for the value of 2 nm, it also was calculated for whole titin filaments and may not represent the true persistence length of the PEVK region. In this study, at least, it was impossible to obtain a reasonable fit of the experimental data by assuming A = 2 nm. In any case, it appears that the PEVK region of psoas titin acts as a pure entropic spring at extensions corresponding to small to moderate physiological SLs. Because of its relatively low bending rigidity, the PEVK domain extends at much higher forces than the poly-Ig regions of titin, which have an ≈35-fold greater persistence length (21 nm; ref. 20).

Toward the high end of the physiological SL range (2.2–3.2 μm for psoas muscle in situ; refs. 20 and 35), PEVK elasticity appears to become increasingly determined by enthalpic contributions. Such additional compliance at high forces can be characterized by including a stretch modulus, K_o, in the standard WLC equation, as suggested in a study on the elastic properties of single DNA molecules (29). The stretch modulus, which measures a polymer’s intrinsic resistance to longitudinal strain, was 185 pN in this study. Application of the entropic-enthalpic model (Eq. 2) permitted a satisfactory comparison of fit theory with experimental data over the full range of PEVK extension (Fig. 4B). It can be envisioned that enthalpic elasticity at high sarcomere stretch may be important in that it provides an additional extensible “buffer” element that is recruited before the onset of potentially more destructive events, such as Ig domain unfolding.

To explain enthalpic contributions to elasticity, we first argue that, if the polymer were an ideal WLC with uniform, isotropic elastic properties, A and K_o should be closely coupled and determined solely by geometry and the Young’s modulus (29). In the simplest possible case, A and K_o are linearly related through

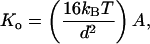3

where d is the diameter of a solid rod with circular cross section. Modeling the PEVK region as such a rod with the reasonable values of d = 0.34 nm and A = 0.60 nm would predict a stretch modulus of 345 pN, much higher than the value calculated with Eq. 2. Clearly, this simple scenario does not appear to be valid. Rather, we suggest that elastic anisotropy, electrostatic, and/or hydrophobic interactions are likely to contribute to PEVK elasticity.

Evidence for electrostatic stiffening of the charged PEVK region now is provided in this study. Reductions in electrostatic screening of charges, achieved by lowering IS, resulted in a significant increase in titin-based myofibril stiffness (Fig. 5). Interestingly, an increase in passive stiffness and tension of actin-extracted rabbit psoas fibers at 60 mM IS also had been reported previously (36), but the authors did not comment on this. In the present study, an important finding is that the stiffness increase was much more pronounced in skeletal myofibrils than in cardiac specimens. Considering the short PEVK length in cardiac muscle (1) and the fact that there are relatively few exposed charges along the poly-Ig regions of titin, we reason that the intrinsic properties of the PEVK segment may be responsible for the muscle type-dependent differences in stiffness change on lowering IS. Although in the sarcomere, PEVK stiffening may arise in part from increased electrostatic attraction between parallel segments, decreasing IS also should lead to a greater propensity for interactions between charged residues within the PEVK domain. The latter type of interactions may be much reduced in the fully extended PEVK region and, indeed, no IS-dependent stiffness changes have been observed in rabbit psoas sarcomeres stretched to 3.8–4.0 μm (22). This result also implies—because at high stretch, deviations of the experimental data curve from the purely entropic model are most dominant (Fig. 4B)—that electrostatic effects might not be the only cause of enthalpic elasticity. For example, enthalpic stiffening could result from exposure of hydrophobic residues (e.g., valine) to water, once the PEVK segment unravels greatly. Along this line of reasoning, both hydrophobic interactions and electrostatic bonds may define enthalpic contributions to PEVK elasticity. How electrostatic screening of charges might affect the persistence length and/or the stretch modulus, and whether the enthalpic stiffness also has other sources, remains to be established.

In summary, this study provides important insights into the nature of PEVK-titin elasticity. First, by using immunoelectron microscopy and isolated myofibril mechanics, we could determine the elastic properties of the rat psoas PEVK segment. Second, PEVK elasticity appears to have both entropic and enthalpic origins; whereas entropic elasticity is most relevant at low to moderate sarcomere stretch, enthalpic elasticity may be the dominant factor at large physiological extensions. And third, at least part of the enthalpic elasticity may originate in electrostatic interactions within the PEVK region.

Note Added in Proof

A related study by Trombitas et al. (37) appeared while this paper was under review. A comparative discussion of both studies’ results will be provided elsewhere.