Genetic evidence for a Paleolithic human population expansion in Africa

Abstract

Human populations have undergone dramatic expansions in size, but other than the growth associated with agriculture, the dates and magnitudes of those expansions have never been resolved. Here, we introduce two new statistical tests for population expansion, which use variation at a number of unlinked genetic markers to study the demographic histories of natural populations. By analyzing genetic variation in various aboriginal populations from throughout the world, we show highly significant evidence for a major human population expansion in Africa, but no evidence of expansion outside of Africa. The inferred African expansion is estimated to have occurred between 49,000 and 640,000 years ago, certainly before the Neolithic expansions, and probably before the splitting of African and non-African populations. In showing a significant difference between African and non-African populations, our analysis supports the unique role of Africa in human evolutionary history, as has been suggested by most other genetic work. In addition, the missing signal in non-African populations may be the result of a population bottleneck associated with the emergence of these populations from Africa, as postulated in the “Out of Africa” model of modern human origins.

Genetic approaches to the study of human population expansions previously have focused on variation at a single genetic locus, the “control region” of mtDNA (1). However, in the study of demographic history, single-locus studies suffer from pronounced statistical and biological limitations. The statistical problem is that the conclusions rely on only one particular realization of a gene genealogy, the “tree” determining the ancestral relationships among a set of alleles. The biological problem is that there are a large number of functional genes in the mitochondrion (2), and because there is complete linkage, a selective sweep for any one of the genes may lead to a spurious signal of expansion. Genome-wide data sets provide a promising alternative, overcoming most of the statistical and biological limitations inherent in single-locus studies. If genome-wide data sets are used, population expansions will be distinguishable from natural selection because expansions affect all loci, whereas selection only affects loci tightly linked to the selected locus.

DATA AND ANALYSIS

The markers we use in our tests are “microsatellites,” which first were identified in large-scale gene mapping projects but are increasingly used for inferring population parameters (3). Microsatellites, which exhibit extensive “length” variations, are widely distributed throughout the genome, seem to be selectively neutral, and appear to conform reasonably well to a simple mutation process (stepwise mutation model), whereby mutations change the length by one or occasionally two units (3). On the basis of this mutation model, we have developed two statistical tests to discern whether populations have been constant or growing in size.

Within-Locus k-Test for Population Expansion.

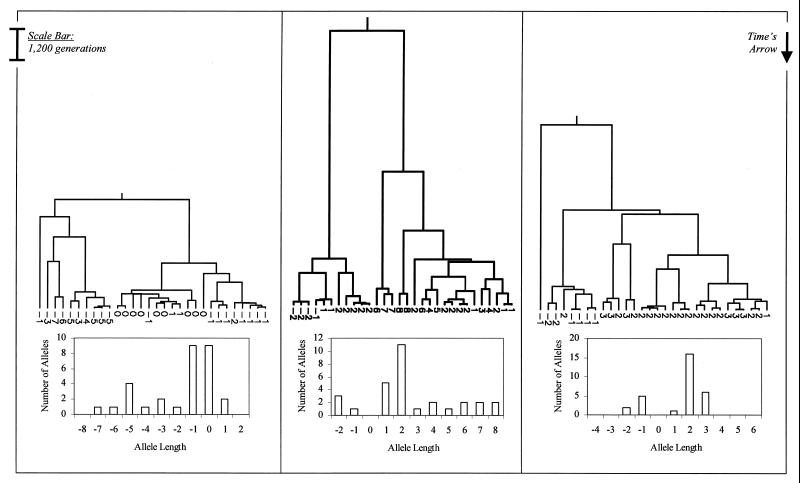
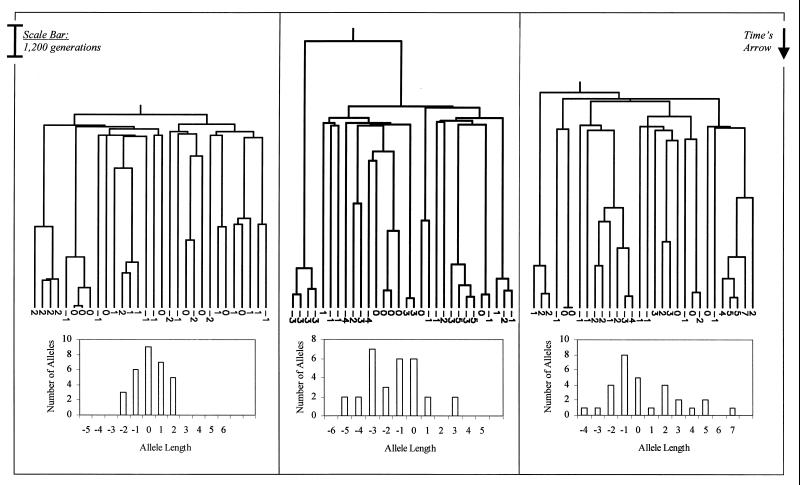
For a population of constant size, gene genealogies tend to have a single ancient bifurcation, implying that most pairs of alleles are either closely or distantly related, with few in between (4). The distribution of allele lengths, therefore, has discrete peaks that correlate with the descendants of each side of the ancient bifurcation (Fig. 1). For a growing population, in contrast, most of the bifurcations tend to date back to the time of expansion—the genealogical tree is “comblike,” and the resultant allele length distribution is more smoothly peaked (Fig. 2).

Figure 1.

Three examples of gene genealogies for constant-sized populations of 5,000 chromosomes from which 30 chromosomes are sampled randomly. Associated allele length distributions are shown below for each example and are obtained by distributing stepwise mutations along the genealogy with an average frequency of 0.00056 per generation. The numbers at the bottom of each genealogy show the change in allele length from the ancestral chromosome to each of the sampled chromosomes.

Figure 2.

Three examples of gene genealogies for 30 chromosomes sampled randomly from a population that currently includes 50,000. All three genealogies correspond to constant-sized populations that underwent sudden, 100-fold expansions 7,000 generations in the past. Associated allele length distributions are shown below for each figure and are obtained by distributing stepwise mutations along the genealogy with an average frequency of 0.00056 per generation. The numbers at the bottom of each genealogy show the change in allele length from the ancestral chromosome to each of the sampled chromosomes.

To differentiate between the ragged, multipeaked distribution expected for a constant population size, and the smooth, single-peaked distribution expected for an expansion, we construct a statistic, denoted k, which is a decreasing function of the fourth central moment of the sample, 1/n Σ_i=1ⁿ(X_i − 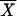)⁴, where n is the number of chromosomes, 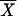is the average allele length, and the X_i values are the individual allele lengths. Because the fourth central moment is related to the kurtosis, which increases with peakedness, the statistic k tends to decrease systematically with the degree of peakedness caused by expansion (D.E.R., M. W. Feldman, and D.B.G., unpublished data) (note that the kurtosis is equal to the normalized fourth central moment plus an overall constant).

To set the parameters of the k statistic empirically, we use computer simulations based on the coalescent algorithm of R. Hudson (5). Genealogies are traced backward in time from the sampled individuals to their most recent common ancestors, and stepwise mutations are distributed along the genealogies according to a random Poisson process. We use the results of the simulations to set the parameters of the k statistic so that the probability of a locus being positive when the population is constant in size is constrained to a narrow range (between 0.515 and 0.55) for sample sizes greater than 10 and for a wide variety of population sizes and mutation rates. In this way, we derive the statistic k = 2.5*Sig⁴ + 0.28*S² − 0.95/n − Gam₄, where S² is the sample variance and Sig⁴ and Gam₄ are unbiased estimators for the variance squared and fourth central moment, respectively. Note that Sig⁴ and Gam₄ were derived specifically for this analysis (D.E.R. et al., unpublished data), and their validity was checked by computer simulation.

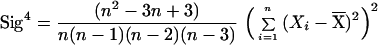1

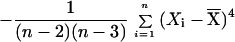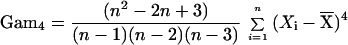2

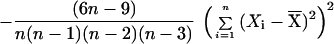To implement the approach, we set the probability of a positive k conservatively at 0.515, and use a simple one-tailed binomial test to determine whether fewer loci were associated with a positive k than would be expected for a constant-sized population. Because the expectation of k decreases with increasing kurtosis, such a reduction in the number of positive k values can be interpreted as a sign of population expansion.

Interlocus g Test for Population Expansion.

The second technique for detecting an expansion focuses on a feature of multilocus data sets that has no analog in studies of a single gene. When populations are of constant size, the dates of the most ancient bifurcations are subject to considerable variation from locus to locus (Fig. 1). Under conditions of growth, the most ancient bifurcations tend to have similar dates at all loci (Fig. 2). To distinguish between the demographic scenarios, we note that the characteristic differences associated with demography—so evident in a comparison of gene genealogies in Figs. 1 and 2—also will be reflected in the variance of the variance of the allele length distributions. Specifically, because the variance of an allele length distribution depends mainly on the ages of the few most ancient bifurcations (7), the variance of the variance is expected to be larger for constant-sized populations than for growing ones.

To test for this effect statistically, we take advantage of the fact that there is an analytical expectation for the variance of the variance in a constant-sized population, 4/3(E[V_j])² + 1/6E[V_j] (6, 8). To estimate this quantity, we substitute 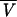, the average variance across loci, for E[V_j]. To formulate the test explicitly, we consider the ratio, g, of the observed value to the expected value.

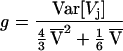3

A sufficiently low value of g is taken as a sign of expansion. A useful and interesting feature of this ratio is that, as shown by the computer simulations used to calculate P values, its expectation and confidence intervals are essentially independent of Nμ (mutation rate times population size) and nearly independent of sample size (D.E.R. et al., unpublished data). For sample size greater than 25, and 30 loci, a g ratio less than 0.35 is sufficient to reject the null hypothesis. A full look-up table of significant cutoffs is presented elsewhere (D.E.R. et al., unpublished data).

Paleolithic Human Population Expansion in Africa.

One tetranucleotide and one dinucleotide microsatellite data set, each of 30 unlinked loci, recently have become available, providing information about genetic diversity represented in hundreds of individuals and several populations around the world (9, 10).† In the tetranucleotide data, the “within locus” k test shows that only two populations give a significant signal of expansion, and they are both in Africa (San and Sotho-Tswana, both with P values of <0.01) (Table 1). The interlocus g test applied to these data also suggests a difference between African and non-African populations: the four lowest g values are in Africa and clearly lower than those found elsewhere in the world.

Table 1.

Analysis of human microsatellite diversity data using 30 tetranucleotide repeat microsatellites

Population	Average variance	No. of chromosomes	Within-locus (k) test		Interlocus (g) test
			Positive/total	P value	g ratio	P value*
San	5.0	20–30	8/30	P < 0.005	1.07	P < 0.49
Sotho-Tswana	5.2	28–38	9/30	P < 0.014	1.00	P < 0.50
Tsonga	5.4	24–28	13/30	P < 0.24	0.87	P < 0.32
Biaka Pygmy	6.3	10	16/28	P < 0.78	1.11	P < 0.47
Nguni	5.9	26–28	13/30	P < 0.24	1.81	P < 0.84
Mbuti Pygmy	4.6	10	15/26	P < 0.80	1.89	P < 0.80
Malay	3.4	10–12	15/23	P < 0.94	1.29	P < 0.64
Japanese	4.1	30–38	13/30	P < 0.24	1.32	P < 0.68
Chinese	4.5	30–34	11/30	P < 0.07	1.67	P < 0.82
Cambodian	5.4	20–24	17/30	P < 0.77	2.17	P < 0.88
Vietnamese	5.0	12–18	12/30	P < 0.14	2.47	P < 0.89
North European	5.4	130–140	12/30	P < 0.14	1.82	P < 0.84
French	5.5	36–40	14/30	P < 0.36	1.93	P < 0.84

P values for the within-locus test are calculated from a binomial distribution, with probability of a positive k taken conservatively at 0.515. P values for the interlocus g test are calculated from a distribution that is empirically generated using 1,000 computer simulations. For the inputs to the coalescent simulations, we use the actual number of loci and samples in our data and estimate Nμ (the mutation rate times population size) as half the variance. Note that inaccuracy in this estimate of Nμ is not a problem for the interlocus test because g has the useful property of being independent of Nμ (D.E.R. et al., unpublished data). 

^*The g values are biased high because of variation in the mutation rate. This also causes the P values to be biased high, and hence we only list adjusted P values that are obtained after correcting for variation in the mutation rate. 

In the dinucleotide data, the within-locus k test produces no significant P values, possibly because, as demonstrated by computer simulations, the test loses power for higher values of the mutation rate (D.E.R. et al., unpublished data) (Table 2). With the interlocus g test, however, the North-Central African population shows a significant sign of expansion (P < 0.037). The significance of the detected expansion increases even further, to P < 0.006, when we drop an exceptionally variable locus (D13S122), which has a variance in the worldwide sample of 89.2 compared with a range of 1.0 to 17.2 for the other 29 loci (11). In contrast, non-African populations fail to show signs of expansion when the high-variance locus (D13S122) is dropped, although g values for these populations are all below 1, suggestive of expansions.

Table 2.

Analysis of human diversity data from 30 dinucleotide repeat microsatellites

Population	Average variance	No. of chromosomes	Within-locus (k) test		Interlocus (g) test*		Adjusted P value
			Positive/total	P value	g ratio	P value
N. Central African	7.7	32–38	15/30	P < 0.51	0.32	P < 0.037	P < 0.0007
Zairian	9.1	16–20	15/30	P < 0.51	1.80	—	P < 0.23
European	9.0	34–58	17/30	P < 0.77	3.88	—	P < 0.11
Amerind	8.1	36–60	13/28	P < 0.24	3.08	—	P < 0.40
East Asian	10.0	32–60	18/30	P < 0.87	2.92	—	P < 0.20
Sahulland	9.0	22–40	19/26	P < 0.93	3.33	—	P < 0.10
Melanesian	8.7	14–20	16/23	P < 0.72	2.53	—	P < 0.43

The populations are clustered according to the convention established in earlier literature: “North-Central African” includes Lisongo and Central African Republic Pygmies; “European” includes North Europeans and Italians; “Amerind” includes Karitania, Surui, and Mayan; “East Asian” includes Cambodian, Chinese, and Japanese; and “Sahulland” includes Australian and New Guinean (11). 

^*The g values for the interlocus test are biased high because of variation in the mutation rate. This in turn causes the P values to be biased high, so we only list P values that are significant despite the bias. We also provide a list of adjusted P values that emerge when we drop the exceptionally variable locus D13S122 and correct for variation in the mutation rate. 

Correction for Variation in the Mutation Rate.

We can improve the power of the interlocus g test by taking into account variation in the mutation rate across loci, denoted σ_μ², which is certainly substantial for microsatellite loci, and which weakens the interlocus test by increasing the g ratio. We obtain an estimate of the variation in the mutation rate by considering the statistic Var[(δμ)²]/((δμ)²)², where (δμ)² is a genetic distance introduced by Goldstein et al. (11), and is defined as the square of the difference between the mean allele lengths at a locus in two populations. We then use computer simulations to show that the expected value of this ratio approaches 2(1+σ_μ²/μ²) as (δμ)² becomes large, as might be expected from theoretical calculations (D.E.R. et al., unpublished data; ref. 6). We are now able to use the equation Var[(δμ)²]/((δμ)²)² = 2(1+σ_μ²/μ²) to estimate σ_μ². Note that error in this estimate could arise because our calculations are based on analytical expectations for (δμ)² and Var[(δμ)²], which both derive from an assumption that populations are in mutation-drift equilibrium. However, such inaccuracies in our estimate of σ_μ² are likely to be only moderate, because demography has only a small effect on expectations for the (δμ)² genetic distance (12).

To extract σ_μ² from the data, we average Var[(δμ)²] and (δμ)² over all pairwise comparisons of African and non-African populations, and then use the ratio of averages to calculate σ_μ². To obtain a confidence interval on the resulting estimate, it is necessary to know the effective number of independent observations of the (δμ)² distance between African and non-African populations. The number of calculations of (δμ)² that were actually made is likely to be considerably larger than the effective number because of correlation resulting from shared genealogical history among the populations in our data set. By assessing the shape of the genealogical tree relating the populations, and specifically noting that the total branch length of the tree is likely to be more than twice the branch length of any single Africa/non-Africa comparison, we conclude that we have made at least two independent calculations of (δμ)² in both data sets (D.E.R. et al., unpublished data). The confidence intervals on the estimate can then be calculated empirically by using computer simulations.

From this procedure, we obtain a variance of the mutation rate of σ_μ² = 0.97 μ² for the tetranucleotides (90% CI: 0.20 μ² − 3.10 μ²), and σ_μ² = 1.30 μ² for the dinucleotides (90% CI: 0.14 μ² − 3.13 μ²). Incorporating these estimates into our analysis, and assuming that the mutation rate varies according to a truncated Gaussian distribution, the signal of expansion for the North-Central African population (dinucleotide data set) becomes highly significant at P < 0.0016, whereas g ratios for the non-African populations in both data sets come closer to the expectation for a constant population size. We can also combine the two approaches for correcting the interlocus g test—dropping the high-variance locus (D13S122) and adjusting for variance in the mutation rate among the remaining 29 loci (σ_μ² = 0.28 μ²)—to obtain a P value of <0.0007 in the North-Central African population. Table 2 shows other P values that result from this combined approach.

Effects of Inaccuracies in the Stepwise Mutation Model and the Demographic Model.

A known inadequacy of the stepwise mutation model is that occasional mutations occur that change allele lengths by more than a single repeat unit. For the within locus test, such multistep mutations have a conservative effect (D.E.R. et al., unpublished data). For the interlocus g test, multistep mutations can be accounted for explicitly by use of an analytical prediction (6), which shows that for reasonable frequencies of these mutations, any effect on g will be too slight to affect our primary conclusion that there is a clear difference in the signal of expansion between African and non-African populations (D.E.R. et al., unpublished data).

An additional problem with the stepwise mutation model is that it assumes an infinite range of allowable allele sizes, whereas in reality the range is known to be constrained (3). The effect of range constraints is potentially nonconservative, but if this were a cause for bias, genetic distances between the various humans populations, calculated by using the assumptions of the model, would be systematically inconsistent with inferences from other sources. Goldstein et al. showed, however, that for the dinucleotide data, inferences about the date of splitting of African and non-African populations are consistent with other estimates (11), indicating that range constraints do not substantially retard genetic differentiation among human populations. For the tetranucleotide data, on the other hand, range constraints may have an influence on human population differentiation. This conjecture is supported by the lower measure of genetic population differentiation (F_ST value) observed in tetranucleotide relative to dinucleotide microsatellite data sets (9, 10).

Real human populations are not perfectly isolated from one another and are internally structured. This could produce a deceptive signal of expansion if appropriate populations are not selected for testing. Indeed, structuring appears to be a serious problem for the within-locus test; the signal of expansion is consistently stronger in populations clumped into continental and whole-world samples than in populations that are considered separately. The interlocus g test, in contrast, seems relatively insensitive to clumping schemes, indicating that slight deviations from the correct demographic model are unlikely to produce a false-positive signal of expansion (D.E.R. et al., unpublished data).

Estimating a Date for the Expansion.

The observed values of g and the average variance across loci put constraints on the possible dates of the detected expansion. In estimating the date, we define an expansion time, as well as its associated preexpansion population size and factor of expansion, to be “allowable” if computer simulations using these three parameters generate 90% confidence intervals that include the observed values of g and the average variance across loci. With N as the preexpansion population size, we consider 60 values of Nμ between 0.05 and 25, 50 values of the expansion time from 0 to 10N generations in the past, and factors of sudden expansion ranging from 3 to 100. Applying this procedure to the data, we calculate allowed dates using 29 of the dinucleotide loci typed in the North-Central African population, neglecting the anomalously high-variance locus as before, and incorporating the estimated variation in the mutation rate, which in this case is 0.28 μ². With an average dinucleotide mutation rate that has been estimated at 5.3 × 10⁻⁴ per generation (13), and a generation time of 25 years, we are able to make the following inferences.

The maximum preexpansion population size for the North-Central African population is 6,600, the lower bound for the postexpansion population size is 8,400, and the allowed dates are between 49,000 and 640,000 years ago—certainly predating the advent of agriculture (14). Crude estimates of the maximum likelihood surface for the date, based on computer simulations, indicate that the distribution is bimodal, and thus that a point estimate may not be very informative (D.E.R. et al., unpublished data). The positions of the peaks for the various factors of expansion, however, constrain the maximum likelihood estimate to between 148,000 and 364,000 years, consistent with the expansion having occurred around or before the split of modern human populations in Africa [estimated to have occurred 75,000–287,000 years ago using the dinucleotide data, and dated to similar times using other data (11, 15)]. Note that the method of allowed dates seems to be robust in the sense that it produces similar ranges of dates for widely varying expansion factors; however, it must be remembered that the real pattern of growth is likely to have been considerably more complicated, involving repeated periods of expansion and possibly even contractions, and it is not clear how these complications would affect our inferences.

DISCUSSION

We have shown that a signal of population expansion in the Paleolithic appears in Africa but not elsewhere in the world. We observe the signal in two different data sets and in two separate statistical tests. Our strongest piece of evidence, a significant signal of expansion in the North-Central African population using the interlocus g test, appears to be conservative to most deviations from the biological and demographic assumptions.

In light of the robustness of the detected signal, it may seem surprising that the within- and between-locus tests do not always agree on a significant result in the same population. For example, the signals of expansion in the North-Central African population, San, and Sotho-Tswana populations, are not replicated in both tests. This is not unexpected, however, and indeed is related to one of the strengths of the tests. Because the tests are based on different principles, they are differently sensitive to deviations from the biological and demographic models that could mask the signal of expansion. In addition, as we discovered by using a variety of parameter combinations in our computer simulations, the time of maximum sensitivity of the within-locus test is about three times as recent as that of the interlocus test (D.E.R. et al., unpublished data). Thus, by combining the two approaches, we can obtain more statistical resolution, for a broader range of demographic and historical parameters, than by using either test alone. By comparing the results of the tests, we may even obtain new information about population history that could not be derived without such a comparison, a unique strength of combining the two approaches.

Whatever the reason for the lack of a signal of expansion outside Africa, our analysis, like many other genetic analyses, assigns a unique role to Africa in human evolution. If, as seems likely, the expansion we have detected in Africa predates the split of modern groups, it follows that non-Africans must have once carried the signal of expansion—a surprising fact because this signal of expansion is not now observed among these groups. Given the properties of the g statistic, however, a simple way to erase the signal of growth would be a population bottleneck that could have occurred in the history of non-African populations. In a bottleneck that is sufficiently severe and long-term, genetic drift causes the variances at individual loci to wander, raising the variance of the variance across loci and obscuring the signal of expansion (D.E.R. et al., unpublished data). The hypothesis of a bottleneck also is appealing because it explains why no new signals of expansion developed among non-African populations—for example, in the Americas, where colonization must have been associated with population growth. Assuming that the ancient bottleneck did not reduce the variances at all loci to zero, any new signals of expansion that could have arisen might have been obscured by residual variance of the variance, in order words, by elevated values of g inherited from before the time of the bottleneck.

If a bottleneck is indeed responsible for the high value of g outside of Africa, a compelling possibility is that it occurred during the emergence of the first anatomically modern human groups from that continent. Our analysis not only adds further support to the “Out of Africa” theory (16) but indicates an approach for characterizing the demographic nature of the emergence itself, putting constraints on the time frame and severity of the associated bottleneck (see Appendix). With only 30 loci, for example, we can conclude that the effective population size must at some point have dropped below 6,900; we may expect that analysis of larger data sets will reveal new details concerning this critical period of human history.

Appendix

Locus variances and genetic diversity tend to be significantly higher in Africa than elsewhere (14). By explaining this as the effects of variation lost during a severe bottleneck, the same bottleneck that we suggest has erased the signal of expansion outside of Africa, we can put a maximum on the effective population size during the bottleneck’s narrowest point. The dynamic for the change in variance from generation to generation is ΔV = [(2N-1)μ-V₀]/2N, where V₀ is the current population variance (17). The requirement for variance to decrease is that ΔV should be negative, and thus that N < V₀/μ + ½. Assuming that the prebottleneck variance is less than the current North-Central African variance, a reasonable assumption because the variance of the North-Central African loci should have been growing since the expansion, the effective population size during the bottleneck’s narrowest point is constrained to less than 6,900.