Skip to main content
NCBI home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2007 Nov 26.
Published in final edited form as: J Biomech. 2007 Jan 2;40(10):2199–2206. doi: 10.1016/j.jbiomech.2006.10.040

Tissue strain amplification at the osteocyte lacuna: A microstructural finite element analysis

Amber Rath Bonivtch a, Lynda F Bonewald b, Daniel P Nicolella a,*
PMCID: PMC2094105  NIHMSID: NIHMS16595  PMID: 17196968

Abstract

A parametric finite element model of an osteocyte lacuna was developed to predict the microstructural response of the lacuna to imposed macroscopic strains. The model is composed of an osteocyte lacuna, a region of perilacunar tissue, canaliculi, and the surrounding bone tissue. A total of 45 different simulations were modeled with varying canalicular diameters, perilacunar tissue material moduli, and perilacunar tissue thicknesses. Maximum strain increased with a decrease in perilacunar tissue modulus and decreased with an increase in perilacunar tissue modulus, regardless of the thickness of the perilacunar region. An increase in the predicted maximum strain was observed with an increase in canalicular diameter from 0.362 to 0.421 μm. In response to the macroscopic application of strain, canalicular diameters increased 0.8% to over 1.0% depending on the perilacunar tissue modulus. Strain magnification factors of over 3 were predicted. However, varying the size of the perilacunar tissue region had no effect on the predicted perilacunar tissue strain. These results indicate that the application of average macroscopic strains similar to strain levels measured in vivo can result in significantly greater perilacunar tissue strains and canaliculi deformations. A decrease in the perilacunar tissue modulus amplifies the perilacunar tissue strain and canaliculi deformation while an increase in the local perilacunar tissue modulus attenuates this effect.

Keywords: Bone, Osteocyte, Lacuna, Tissue strain, Finite element model

1. Introduction

It is well known that bone adapts to changes in its mechanical environment and that this adaptation is controlled at the cellular level through the coordinated actions of osteoblasts, osteocytes, and osteoclasts. Osteocytes make up over 90% of all bone cells (Marotti et al., 1995), and are hypothesized to be the mechanosensors in bone (Aarden et al., 1996; Burger et al., 1995; Burger and Klein-Nulend, 1999) that mediate the effects of bone loading through their extensive communication network. The application of force to the skeletal system produces several potential stimuli for osteocyte function including hydrostatic pressure, fluid flow-induced shear stress, and bone tissue strain. Theories based on fluid flow-derived shear stress stimulation of osteocyte cell processes within canaliculi have gained the most prominence (Weinbaum et al., 1994, 2003; You et al., 2001; Han et al., 2004) since it has been shown that direct mechanical strain applied to cells at levels measured to occur in humans in vivo do not stimulate bone cells in vitro (Owan et al., 1997; Smalt et al., 1997). In further comparisons of fluid flow stimulation to substrate stretching experiments on osteoblastic cells (You et al., 2000), it was found that substrate strain levels in the range of strains measured in vivo using a strain gages did not induce an increase in intercellular calcium and osteopontin mRNA, but higher strain levels did produce a calcium response in a significant number of cells. Furthermore, oscillatory fluid flow stimulation at 20 dy/cm2 produced both increased intercellular calcium as well as an upregulation of osteopontin mRNA. However, fluid flow and direct mechanical stimulation have been shown to have different effects on bone cells. Substrate stretching results in an increase of collagen or bone matrix production (Walker et al., 2000; Mullender et al., 2004) responses associated with the osteoblastic phenotype while fluid flow-induced shear stress stimulation results in increases in signals thought to be involved in osteocyte control of bone remodeling, including nitric oxide and prostaglandin E2 (PGE2, an osteogenic messenger) (Owan et al., 1997; You et al., 2000; Bacabac et al., 2004; Mullender et al., 2004).

The application of mechanical forces to whole bone does cause fluid to flow in vivo through the lacunar–canalicular system (Knothe Tate et al., 2000; Ciani et al., 2005). It is theorized that the fluid flow induced drag on the osteocyte and its processes results in the deformation of the cell membrane thus triggering a biological response (Han et al., 2004). Osteocytes have been shown to be more sensitive than osteoblasts by responding with a sustained release of PGE2 following both hydrostatic compression and fluid flow treatment. Moreover, dynamic fluid flow produces the more effective response (Klein-Nulend et al., 1995).

However, the basis used for studying the stimulatory effects of mechanical strain on bone cell biological responses in vitro has been the direct measurement of bone strain in humans during various physical activities (Burr et al., 1996; Milgrom et al., 1996; Hoshaw et al., 1997; Milgrom et al., 2004). The limitation of applying this strain magnitude data to cells in vitro, however, is that the in vivo strain gage measurements represent continuum measures of bone deformation. Clearly, at the spatial level of bone cells, cortical bone is not a continuum and microstructural inhomogeneities will result in inhomogeneous microstructural strain fields; local tissue strains will be magnified in association with microstructural features (Nicolella et al., 2001, 2006). A major source of the inhomogeneity in bone are osteocyte lacunae and canaliculi. Thus, it is important to quantify the local bone tissue deformation state surrounding the osteocyte since it is this deformation that is most likely acting on the osteocyte located within its lacuna and canaliculi.

Recently, new evidence has been reported (Tazawa et al., 2004) in the long standing debate that osteocytes can alter their lacuna tissue (Parfitt, 1977). In this study, it was shown that in rats treated continuously with human parathyroid hormone (PTH) for 4 weeks exhibited a significant increase in osteocyte lacunar size due to tissue resorption by the osteocyte. Furthermore, the authors provide evidence that suggests regeneration of the resorbed perilacunar tissue, indicating the potential for osteocytes to alter their tissue microenvironment. It has also been shown that the administration of glucocorticoids in a rat model results in an increase in lacunar size and hypomineralization of the mineralized matrix surrounding the osteocyte (Lane et al., 2006). Additionally, it has been shown that the perilacunar tissue has different material and mechanical properties compared to tissue not associated with an osteocyte although specific pharmacological treatments or age effects were not investigated (Ling et al., 2005). Moreover, using this data in a preliminary numerical analysis, it was shown that changes in the mechanical properties of the osteocyte perilacunar tissue can significantly alter the perilacunar tissue deformation, thus theoretically altering the mechanical signal sensed by osteocytes (Ling et al., 2005).

The objective of this study was to perform a more detailed investigation into the effect of changes to the perilacunar bone tissue structure and properties on microstructural bone tissue strains potentially transmitted to an embedded osteocyte.

2. Materials and Methods

A parametric finite element model of an osteocyte lacuna was developed to predict the microstructural tissue strains associated with lacunae in response to imposed macroscopic deformations. The model is composed of an osteocyte lacuna, its perilacunar tissue, canaliculi, and the surrounding bone tissue. The osteocyte lacuna was modeled as a revolved ellipsoid with minor and major axes equal to 3.9 and 8.9 μm, respectively (McCreadie et al., 2004). Similar representations of the lacuna have been used previously (McCreadie and Hollister, 1997; McCreadie, 2000). The size of the lacuna was kept constant for all simulations. Ten canaliculi were modeled using diameters of 0.362 and 0.421 μm and lengths of 15 μm (Beno et al., in press; You et al., 2004). A simulation was also run where the canaliculi were not included in the model. The perilacunar tissue thickness was varied between 3 and 10 μm to determine whether the parameter has an effect on the maximum predicted strain.

The parametric finite element model was developed using TrueGrid (XYZ Scientific Applications, Inc., Livermore, CA). The geometry of the lacuna, perilacunar tissue, and canaliculi were described as above within TrueGrid and a hexahedral finite element mesh was mapped to the geometry. By changing the parameters describing the geometry (i.e. canaliculi diameter, thickness of the perilacunar tissue), updated meshes were automatically created. The parametric variables in this model include the size of the lacuna, the perilacunar thickness, the diameter and length of the canaliculi, and the material properties of the perilacunar and surrounding tissues (Fig. 1).

Fig. 1.

Fig. 1

Open in a new tab

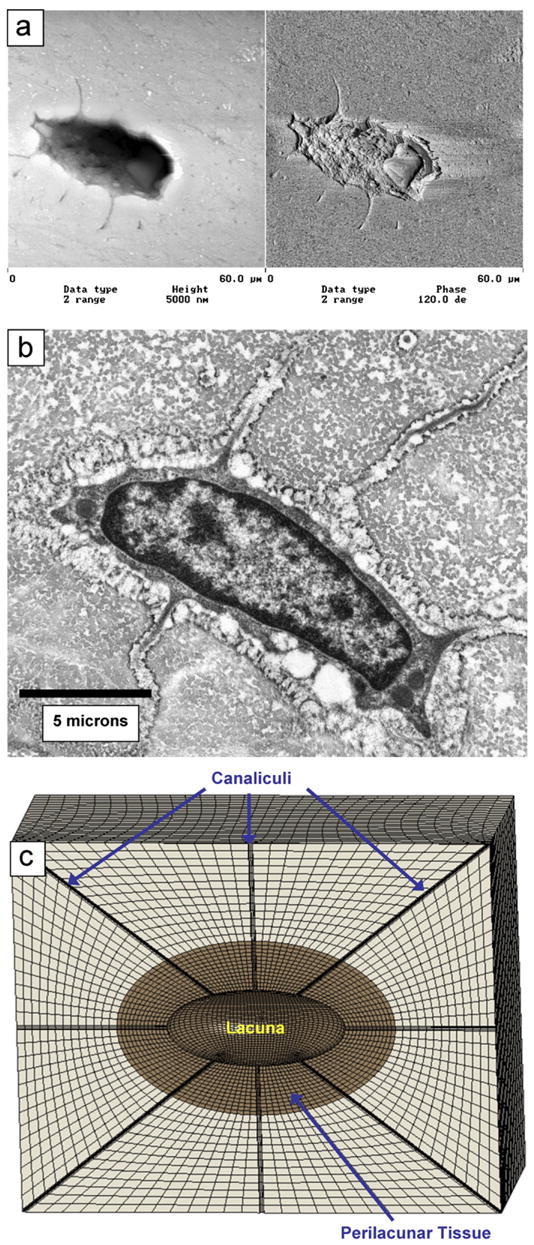
(a) Atomic force microscopy image of an osteocyte lacunae on a polished section of cortical bone. (b) Transmission electron image of an osteocyte and its lacunae (courtesy of Jian Feng, University of Missouri at Kansas City, Department of Oral Biology). (c) Finite element mesh shown for a perilacunar thickness of 5 μm and canaliculi diameter of 0.425 μm. The canaliculi, lacuna, and perilacunar tissue are labeled.

The bone tissue was modeled as linearly elastic with two separate material regions. A material modulus of 25 GPa was used for the bone tissue surrounding the perilacunar tissue (Rho et al., 1999). A range of 15 to 35 GPa was considered for the material modulus of the perilacunar tissue, to determine the effects of changing this value on the maximum strain predicted. A Poisson’s ratio of 0.3 was used for all of the material models.

A prescribed axial displacement was applied to the model face perpendicular to its long axis (horizontal direction in Fig. 1) resulting in an overall model structural strain of 2000 microstrain. This strain was chosen since it is the range of maximum physiological strain experienced by bone under active conditions in the human body (Burr et al., 1996). The nodes on the model face opposing the applied displacement were constrained. Symmetry boundary conditions were applied to the nodes on the remaining model faces, which had the resultant effect of mirroring the model across each plane.

A mesh convergence study was conducted to determine the mesh density used in this analysis. The finite element mesh was increased in 10 steps from 15,480 nodes to 605,400 nodes. Mesh convergence was determined by comparing the predicted maximum principal strain from successively finer meshes until the difference was less than 2%. The maximum lacunar strain converged to less than a 2% difference from 508,176 nodes to 605,400 nodes (Fig. 2).

Fig. 2.

Fig. 2

Open in a new tab

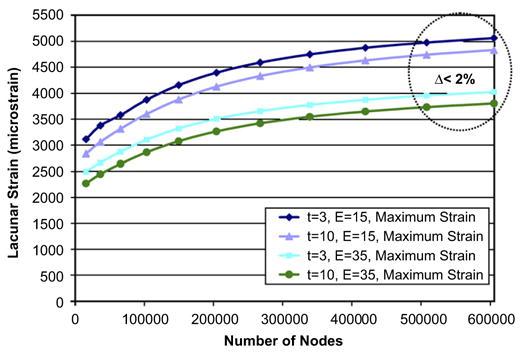
Mesh convergence results for maximum lacunar effective strain. Differences in model predicted strains converged to less than 2% at a mesh density of 605,400 nodes for both thicknesses (3 and 10 μm) and moduli (15 and 35 GPa) considered.

A total of 45 simulations were performed with varying canaliculi diameters, perilacunar material moduli, and perilacunar thicknesses (Table 1). Following the model simulation, the maximum first principle strain was recorded. The quasi-static simulations were run using LS-DYNA Version 970 (Livermore Software Technology Corporation, Livermore, CA) on a dual processor AMD Athlon 1.4 GHz Linux system with 4 GB of memory. The simulations took approximately 30 min each to run. The results were post-processed using LS-PrePost Version 2.1 (Livermore Software Technology Corporation, Livermore, CA).

Table 1.

Simulation parameter matrix of values used, resulting in 45 different models

Parameter Value
Canaliculi diameter (μm) No canaliculi 0.362 0.421
Perilacunar material modulus (GPa) 15 20 25 30 35
Perilacunar thickness (μm) 3 5 10
Open in a new tab

The maximum strain (first principle strain) in the perilacunar region was recorded and the strain amplification factor was computed as the maximum perilacunar tissue strain divided by the applied macroscopic strain.

3. Results

The maximum perilacunar tissue strain predicted using the model without any canaliculi present was 2957.3 microstrain, resulting in a strain amplification factor of 1.52 (Fig. 3). Inclusion of the canaliculi of 0.362 diameter resulted in a 97% increase in maximum perilacunar tissue strain to 6036.6 microstrain and an increase in the strain magnification factor to 3.12. Increasing the canaliculi diameter to 0.421 increased the maximum predicted perilacunar strain 2.31% to 6092.9 microstrain and resulted in a strain magnification factor of 3.14.

Fig. 3.

Fig. 3

Open in a new tab

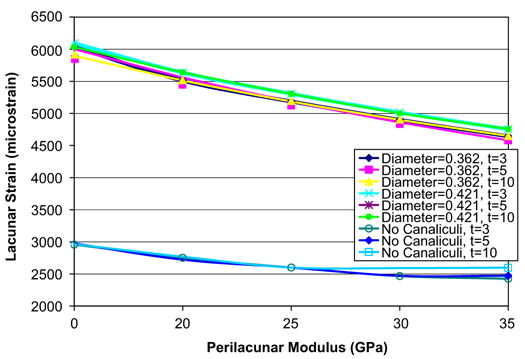
Perilacuna strain increased 97% when the canaliculi (of either diameter) were included in the model. An increase in the diameter of the canaliculi from 0.362 to 0.421 μm resulted in an increase of 2.31% in the measured maximum perilacunar.

The predicted maximum perilacunar strain increased with a decrease in perilacunar tissue modulus and decreased with an increase in perilacunar tissue modulus, regardless of the thickness of the perilacunar region (Fig. 4). An approximate 15% increase in maximum strain was predicted for a 40% decrease in the modulus of the perilacunar tissue for both canaliculi diameters, while a 40% increase in the perilacunar tissue modulus resulted in an approximate 10% decrease in maximum strain. There were no differences in the maximum predicted strain for varying perilacunar thicknesses.

Fig. 4.

Fig. 4

Open in a new tab

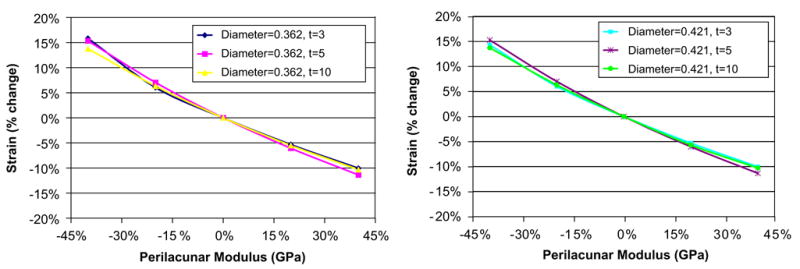
Both the measured maximum strain increased with a decrease in perilacunar modulus and decreased with an increase in perilacunar modulus, regardless of the thickness of the perilacunar region.

The maximum perilacunar strain occurs where the canaliculi enter the lacuna (Fig. 5). The contour plots also indicate the differences in the distribution of perilacunar tissue strain resulting from differences in perilacunar tissue modulus. Higher maximum perilacunar tissue strain values are predicted in the perilacunar region with a lower tissue modulus.

Fig. 5.

Fig. 5

Open in a new tab

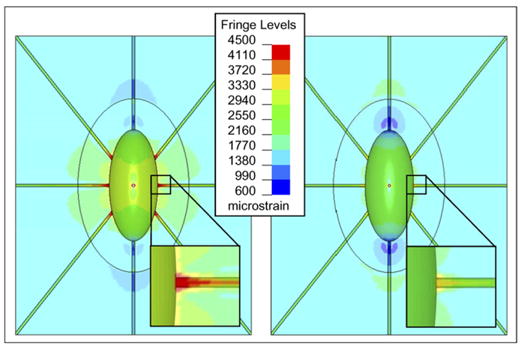
Fringe plots of the strain experienced by the perilacunar region and its surrounding material showing that a low perilacunar modulus led to higher strains than a high modulus: (left) a perilacunar region with a material modulus of 15 GPa (right) a perilacunar region with a material modulus of 35 GPa.

Strain magnification factors of 1.26 to 1.52 were predicted using the model without the canaliculi and magnification factors of over 3 were predicted for both canaliculi diameters considered (Fig. 6). For all of the perilacunar tissue property combinations considered that included canaliculi, the lowest magnification factor was 2.32. The average strain magnification factors were 2.68 and 2.73 for the model with canaliculi diameters of 0.362 and 0.425 μm, respectively.

Fig. 6.

Fig. 6

Open in a new tab

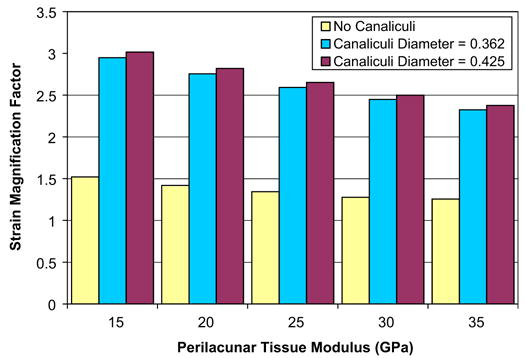
Strain magnification factor. There is an average strain magnification factor of 1.36, 2.68, and 2.73 for the model with no canaliculi, a canaliculi diameter of 0.362 μm, and a canaliculi diameter of 0.425 μm, respectively.

The applied global model deformation of 2000 microstrain (0.2%) results in increases in the diameter of the canaliculi from 0.795% to 1.017% across the perilacunar tissue properties (Fig. 7). A decrease in perilacunar tissue modulus results in an increase in canaliculi deformation while an increase in perilacunar tissue modulus results in a decrease in canaliculi deformation. In all cases, canaliculi deformation reaches its maximum at the intersection of the canaliculi and lacuna wall.

Fig. 7.

Fig. 7

Open in a new tab

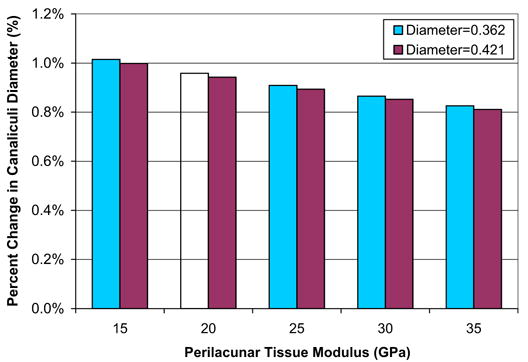
The measured percent change in canaliculi diameter ranges from 0.811% to 1.015% across the perilacunar tissue properties.

4. Discussion

In this analysis, a parametric microstructural bone tissue model was constructed to investigate the effect of perilacunar tissue properties and canaliculi geometry on computed perilacunar tissue strain and canaliculi deformation resulting from a globally applied deformation of 2000 microstrain. The results of this analysis indicate that a globally applied tissue strain of 2000 microstrain (0.2%) result in a perilacunar strain magnification of 1.52 without the inclusion of canaliculi to 3.14 when the canaliculi are included. This level of applied macroscopic strain also results in an increase in canaliculi diameter of approximately 1.0%. Local differences in perilacunar tissue modulus result in significant changes in predicted perilacunar strain.

Prior to discussing the implications of these results, the limitations of this analysis necessitate discussion. Idealized representations of the lacunae and canaliculi geometry were used. In reality, lacunae are not perfect ellipsoids nor are the canaliculi perfectly cylindrical (McCreadie et al., 2004). The size and shape of the lacuna can vary and the walls of the lacuna and canaliculi are not smooth but are irregular. Species-related and bone histology-related variations in lacuno-canalicular geometries that have been described previously could also correlate with non-uniform strain distributions that may not be demonstrated using the selected parameters in the present study (Marotti, 1980; Cane et al., 1982; Marotti et al., 1990; Metz et al., 2003). Variations in size and shape of the lacuna will lead to nonuniform strain distributions and depending on the orientation and geometry of the lacuna will further increase the maximum strain values sensed by the osteocyte. Non-smooth lacuna and canaliculi walls will also increase the maximum strain values. Imperfections and small indentations at the lacuna–canaliculi interface will lead to strain concentrations at that location.

A linear elastic material model was used to represent the deformational behavior of the bone tissue. The strains predicted are on the order of yield strain measured in cortical bone (Cowin, 1989) and may result in damage to the bone tissue (Fondrk et al., 1988). Furthermore, isotropic material was assumed. At this level, there may be material properties that exhibit a directionality resulting from the underlying organization of the collagen fibril (Giraud-Guille, 1988; Hofmann et al., 2005; Weiner and Traub, 1986). These limitations are the focus of ongoing investigations.

This finite element model also included a limited number of canaliculi. The estimated number of canaliculi per lacuna in human long bone is 41 (Beno et al., in press). One of the purposes of this model was to determine if the presence and size of the canaliculi influenced the strain at the osteocyte lacuna. Since it has been determined that by simply including the canaliculi in the model the measured maximum strain is doubled, the next step will be to create a model with the anatomically correct number of canaliculi, to investigate the effect on the strain at the osteocyte.

The perilacunar bone tissue strain magnitudes predicted in this study are consistent with tissue strain values measured in our previous work (Nicolella et al., 2001, 2005, 2006; Nicolella and Lankford, 2002). In these studies, microstructural osteocyte bone tissue strains were measured to be significantly larger than macroscopic applied strains resulting in strain magnifications factors of 1.1–3.8. However, detailed measurements of the strains and deformations of the canaliculi were not included due to limitations in the optical resolution of our microscope systems.

The tissue bone strains predicted in this analysis are consistent with applied substrate strain levels required to elicit a biological response from bone cells in culture. Biological responses, such as NO release and PGE2 release, have been reported to occur at strains ranging from 3400 microstrain to 5500 microstrain (Pitsillides et al., 1995; Owan et al., 1997, Fermor et al., 1998; Zaman et al., 1999; Kunnel et al., 2002). These strain levels were originally thought to be too high to be experienced in vivo in human bone since the maximum physiological strain experienced by bone under active conditions in the human body is approximately 2000 microstrain (Burr et al., 1996). However, it has been shown in this study, that an applied 2000 microstrain globally can result in maximum strain concentrations of 4000–6000 microstrain, consistent with in vitro substrate stretch levels sufficient to elucidate a biological response.

Similar to McCreadie and Hollister (1997), this study found that there is strain magnification at the osteocyte lacuna. McCreadie and Hollister (1997) did not include in the canaliculi and the lacuna in the same finite element model. The strain values presented in the current study taken into account the interface of the lacuna and canaliculi, which is the site of the maximum measured strain. Contrary to the results of McCreadie and Hollister (1997) the measured maximum strains were found to vary with changes in the tissue modulus.

The globally applied strain resulted in an increase in canaliculi diameters of 0.8% to over 1.0%. This change in diameter will result in direct application of deformation to the enclosed cell process via transverse tethering elements that connect the cell process to the canalicular wall (You et al., 2004). It is interesting to note that if there is no attenuation of the canaliculi deformation by the tethering element, the change in diameter of the canaliculi predicted using this model will result in a radial strain within the cell process of 10,000 microstrain. This cell process strain is in the range of applied substrate strain required to produce a cellular response in bone cells cultured in vitro. In addition, dimensional changes to the canaliculi will result in changes to the fluid flow, and therefore to the shear stresses, experienced within the canaliculi and lacunae.

There is increasing evidence that the osteocyte can affect changes to its local environment (Baylink and Wergedal, 1971; Rubin et al., 2002; Tazawa et al., 2004; Lane et al., 2006). Additional studies have shown similar results with chondrocytes in cartilage (Guilak et al., 1999, 2006; Alexopolous et al., 2005). Although osteocyte alteration of the perilacunar tissue is not well understood, the results from the present investigation indicate that alterations to the perilacunar tissue may act to control the strain signal sensed by the embedded osteocyte. The material around the osteocyte may be remodeled due to changes in overall bone loads or changes in systemic biochemical equilibrium. The results of the present investigation demonstrate that for a given macroscopic strain level, a change in perilacunar tissue modulus will result in a modification of the perilacunar bone tissue strain. This may provide a mechanism whereby the osteocyte can fine tune the local bone tissue strain signal to remain within an optimal range. For example, local increases in perilacunar tissue stiffness will result in a decrease in perilacunar tissue strain. Local microstructural changes such as these may be implicated in the reduced ability of the aging skeleton to respond to mechanical loading (Rubin et al., 1992; Turner et al., 1995). As the skeleton ages, there is an overall increase in bone tissue mineralization (Currey et al., 1996) which will increase the bone tissue modulus. Therefore, if this increase in overall mineralized tissue extends to perilacunar bone tissue, the local perilacunar bone tissue modulus increases as a function of age, the aged skeleton may be less able to sense and transduce normal skeletal loading. In other words, even if the global strain signal remains relatively constant, the transmission of this global strain to the embedded osteocytes in an older skeleton may be significantly reduced.

In summary, a parametric finite element model of an osteocyte lacuna was developed to predict the microstructural response of the lacuna to imposed macroscopic strains. An increase in the predicted maximum strain was observed for an increase in canalicular diameter. The measured maximum strain increased with a decrease in perilacunar tissue modulus and decreased with an increase in perilacunar tissue modulus, regardless of the thickness of the perilacunar region. Canaliculi diameters increased from 0.8% to over 1.0% depending on the perilacunar tissue modulus. Strain magnification factors of over 3 were predicted. These results indicate that the application of average macroscopic strains similar to strain levels measured in vivo can result in significantly greater perilacunar tissue strains and canaliculi deformations.

5. Uncited references

Cowin (2002), Stains and Civitelli (2005).

Acknowledgments

This research was funded by NIH/NIAMS P01 AR046798.

References

  1. Aarden EM, Nijweide PJ, van der Plas A, Alblas MJ, Mackie EJ, Horton MA, Helfrich MH. Adhesive properties of isolated chick osteocytes in vitro. Bone. 1996;18:305–313. doi: 10.1016/8756-3282(96)00010-5. [DOI] [PubMed] [Google Scholar]
  2. Alexopolous LG, Setton LA, Guilak F. The biomechanical role of the chondrocyte pericellular matrix in articular cartilage. Acta Biomaterialia. 2005;1:317–325. doi: 10.1016/j.actbio.2005.02.001. [DOI] [PubMed] [Google Scholar]
  3. Bacabac RG, Smit TH, Mullender MG, Dijcks SJ, Van Loon JJ, Klein-Nulend J. Nitric oxide production by bone cells is fluid shear stress rate dependent. Biochemical and Biophysical Research Communications. 2004;315:823–829. doi: 10.1016/j.bbrc.2004.01.138. [DOI] [PubMed] [Google Scholar]
  4. Baylink DJ, Wergedal JE. Bone formation by osteocytes. American Journal of Physiology. 1971;221:669–678. doi: 10.1152/ajplegacy.1971.221.3.669. [DOI] [PubMed] [Google Scholar]
  5. Beno T, Yoon YJ, Cowin SC, Fritton SP. Estimation of bone permeability using accurate microstructural measurements. Journal of Biomechanics. 2006 doi: 10.1016/j.jbiomech.2005.08.005. in press. [DOI] [PubMed] [Google Scholar]
  6. Burger EH, Klein-Nulend J. Mechanotransduction in bone—role of the lacuno-canalicular network. FASEB Journal. 1999;13(Suppl):S101–S112. [PubMed] [Google Scholar]
  7. Burger EH, Klein-Nulend J, van der PA, Nijweide PJ. Function of osteocytes in bone—their role in mechanotransduction. Journal of Nutrition. 1995;125:2020S–2023S. doi: 10.1093/jn/125.suppl_7.2020S. [DOI] [PubMed] [Google Scholar]
  8. Burr DB, Milgrom C, Fyhrie D, Forwood M, Nyska M, Finestone A, Hoshaw S, Saiag E, Simkin A. In vivo measurement of human tibial strains during vigorous activity. Bone. 1996;18:405–410. doi: 10.1016/8756-3282(96)00028-2. [DOI] [PubMed] [Google Scholar]
  9. Cane V, Marotti G, Volpi G, Zaffe D, Palazzini S, Remaggi F, Muglia MA. Size and density of osteocyte lacunae in different regions of long bones. Calcified Tissue International. 1982;34:558–563. doi: 10.1007/BF02411304. [DOI] [PubMed] [Google Scholar]
  10. Ciani C, Doty SB, Fritton SP. Mapping bone interstitial fluid movement: displacement of ferritin tracer during histological processing. Bone. 2005;37:379–387. doi: 10.1016/j.bone.2005.04.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Cowin SC. Bone Mechanics. CRC Press; Boca Raton, FL: 1989. [Google Scholar]
  12. Cowin SC. Mechanosensation and fluid transport in living bone. Journal of Musculoskeletal and Neuronal Interactions. 2002;2:256–260. [PubMed] [Google Scholar]
  13. Currey JD, Brear K, Zioupos P. The effects of ageing and changes in mineral content in degrading the toughness of human femora (published erratum appears in Journal of Biomechanics 1997; 30 (9), 1001) Journal of Biomechanics. 1996;29:257–260. doi: 10.1016/0021-9290(95)00048-8. [DOI] [PubMed] [Google Scholar]
  14. Fondrk M, Bahniuk E, Davy DT, Michaels C. Some viscoplastic characteristics of bovine and human cortical bone. Journal of Biomechanics. 1988;21:623–630. doi: 10.1016/0021-9290(88)90200-x. [DOI] [PubMed] [Google Scholar]
  15. Giraud-Guille MM. Twisted plywood architecture of collagen fibrils in human compact bone osteons. Calcified Tissue International. 1988;42:167–180. doi: 10.1007/BF02556330. [DOI] [PubMed] [Google Scholar]
  16. Guilak F, Jones WR, Ting-Beall HP, Lee GM. The deformation behavior and mechanical properties of chondrocytes in articular cartilage. Osteoarthritis Cartilage. 1999;7(1):59–70. doi: 10.1053/joca.1998.0162. [DOI] [PubMed] [Google Scholar]
  17. Guilak F, Alexopoulos LG, Upton ML, Youn I, Choi JB, Cao L, Setton LA, Haider MA. The pericellular matrix as a transducer of biomechanical and biochemical signals in articular cartilage. Annals of the New York Academy of Sciences. 2006;1068:498–512. doi: 10.1196/annals.1346.011. [DOI] [PubMed] [Google Scholar]
  18. Han Y, Cowin SC, Schaffler MB, Weinbaum S. Mechanotransduction and strain amplification in osteocyte cell processes. Proceedings of the National Academy of Science USA. 2004;101:16689–16694. doi: 10.1073/pnas.0407429101. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Hofmann T, Heyroth F, Meinhard H, Franzel W, Raum K. Assessment of composition and anisotropic elastic properties of secondary osteon lamellae. Journal of Biomechanics. 2005 doi: 10.1016/j.jbiomech.2005.07.009. [DOI] [PubMed] [Google Scholar]
  20. Hoshaw SJ, Fyhrie DP, Takano Y, Burr DB, Milgrom C. A method suitable for in vivo measurement of bone strain in humans. Journal of Biomechanics. 1997;30:521–524. doi: 10.1016/s0021-9290(96)00176-5. [DOI] [PubMed] [Google Scholar]
  21. Klein-Nulend J, van der PA, Semeins CM, Ajubi NE, Frangos JA, Nijweide PJ, Burger EH. Sensitivity of osteocytes to biomechanical stress in vitro. FASEB Journal. 1995;9:441–445. doi: 10.1096/fasebj.9.5.7896017. [DOI] [PubMed] [Google Scholar]
  22. Knothe Tate ML, Steck R, Forwood MR, Niederer P. In vivo demonstration of load-induced fluid flow in the rat tibia and its potential implications for processes associated with functional adaptation. Journal of Experimental Biology. 2000;203(Pt 18):2737–2745. doi: 10.1242/jeb.203.18.2737. [DOI] [PubMed] [Google Scholar]
  23. Kunnel JG, Gilbert JL, Stern PH. In vitro mechanical and cellular responses of neonatal mouse bones to loading using a novel micromechanical-testing device. Calcified Tissue International. 2002;71:499–507. doi: 10.1007/s00223-001-1073-3. [DOI] [PubMed] [Google Scholar]
  24. Lane NE, Yao W, Balooch M, Krumme A, Habelitz S, Kinney JH, Bonewald LF. A proposed mechanism for increased bone fragility in patients treated with glucocorticoids: enlargement and hypomineralization of bone matrix surrounding osteocyte lacunae. Journal of Bone and Mineral Research. 2006 in press. [Google Scholar]
  25. Ling J, Miller M, Moravits D, Lankford J, Bonewald L, Nicolella D. Microstructural compositional changes associated with osteocyte lacunae detected using Raman imaging. Journal of Bone and Mineral Research. 2005;20:S149–S150. [Google Scholar]
  26. Marotti G. Three dimensional study of osteocyte lacunae. Metabolic Bone Disorder and Related Research. 1980;2:S223–S229. [Google Scholar]
  27. Marotti G, Cane V, Palazzini S, Palumbo C. Structure–function relationships in the osteocyte. Italian Journal of Mineral & Electrolyte Metabolism. 1990;4:93–106. [Google Scholar]
  28. Marotti G, Ferretti M, Remaggi F, Palumbo C. Quantitative evaluation on osteocyte canalicular density in human secondary osteons. Bone. 1995;16:125–128. doi: 10.1016/s8756-3282(94)00019-0. [DOI] [PubMed] [Google Scholar]
  29. McCreadie BR. Structural and material changes in osteoporosis: their impact on the mechanical environment of the osteocyte. Ph.D. University of Michigan.; 2000. [Google Scholar]
  30. McCreadie BR, Hollister SJ. Strain concentrations surrounding an Ellipsoid model of lacunae and osteocytes. Computational Methods in Biomechanical Biomedical Engineering. 1997;1:61–68. doi: 10.1080/01495739708936695. [DOI] [PubMed] [Google Scholar]
  31. McCreadie BR, Hollister SJ, Schaffler MB, Goldstein SA. Osteocyte lacuna size and shape in women with and without osteoporotic fracture. Journal of Biomechanics. 2004;37:563–572. doi: 10.1016/S0021-9290(03)00287-2. [DOI] [PubMed] [Google Scholar]
  32. Metz LN, Martin RB, Turner AS. Histomorphometric analysis of the effects of osteocyte density on osteonal morphology and remodeling. Bone. 2003;33(5):753–759. doi: 10.1016/s8756-3282(03)00245-x. [DOI] [PubMed] [Google Scholar]
  33. Milgrom C, Burr D, Fyhrie D, Forwood M, Finestone A, Nyska M, Giladi M, Liebergall M, Simkin A. The effect of shoe gear on human tibial strains recorded during dynamic loading: a pilot study. Foot & Ankle International. 1996;17:667–671. doi: 10.1177/107110079601701104. [DOI] [PubMed] [Google Scholar]
  34. Milgrom C, Finestone A, Hamel A, Mandes V, Burr D, Sharkey N. A comparison of bone strain measurements at anatomically relevant sites using surface gauges versus strain gauged bone staples. Journal of Biomechanics. 2004;37:947–952. doi: 10.1016/j.jbiomech.2003.10.008. [DOI] [PubMed] [Google Scholar]
  35. Mullender M, el Haj AJ, Yang Y, van Duin MA, Burger EH, Klein-Nulend J. Mechanotransduction of bone cells in vitro: mechanobiology of bone tissue. Medical and Biological Engineering and Computing. 2004;42:14–21. doi: 10.1007/BF02351006. [DOI] [PubMed] [Google Scholar]
  36. Nicolella DP, Lankford J. Microstructural strain near osteocyte lacuna in cortical bone in vitro. Journal of Musculoskeletal and Neuronal Interactions. 2002;2:261–263. [PubMed] [Google Scholar]
  37. Nicolella DP, Nicholls AE, Lankford J, Davy DT. Machine Vision Photogrammetry: a technique for measurement of microstructural strain in cortical bone. Journal of Biomechanics. 2001;34:135–139. doi: 10.1016/s0021-9290(00)00163-9. [DOI] [PubMed] [Google Scholar]
  38. Nicolella DP, Bonewald LF, Moravits DE, Lankford J. Measurement of microstructural strain in cortical bone. European Journal of Morphology. 2005;42:23–29. doi: 10.1080/09243860500095364. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Nicolella DP, Moravits DE, Gale AM, Bonewald LF, Lankford J. Osteocyte lacunae tissue strain in cortical bone. Journal of Biomechanics. 2006;39:1735–1743. doi: 10.1016/j.jbiomech.2005.04.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Owan I, Burr DB, Turner CH, Qiu J, Tu Y, Onyia JE, Duncan RL. Mechanotransduction in bone: osteoblasts are more responsive to fluid forces than mechanical strain. American Journal of Physiology. 1997;273:C810–C815. doi: 10.1152/ajpcell.1997.273.3.C810. [DOI] [PubMed] [Google Scholar]
  41. Parfitt AM. The cellular basis of bone turnover and bone loss: a rebuttal of the osteocytic resorption—bone flow theory. Clinical Orthopaedics and Related Research. 1977:236–247. [PubMed] [Google Scholar]
  42. Pitsillides AA, Rawlinson SC, Suswillo RF, Bourrin S, Zaman G, Lanyon LE. Mechanical strain-induced NO production by bone cells: a possible role in adaptive bone (re)modeling? FASEB Journal. 1995;9:1614–1622. doi: 10.1096/fasebj.9.15.8529841. [DOI] [PubMed] [Google Scholar]
  43. Rho JY, Roy ME, Tsui TY, Pharr GM. Elastic properties of microstructural components of human bone tissue as measured by nanoindentation. Journal of Biomedical Materials Research. 1999;45:48–54. doi: 10.1002/(sici)1097-4636(199904)45:1<48::aid-jbm7>3.0.co;2-5. [DOI] [PubMed] [Google Scholar]
  44. Rubin CT, Bain SD, McLeod KJ. Suppression of the osteogenic response in the aging skeleton. Calcified Tissue International. 1992;50:306–313. doi: 10.1007/BF00301627. [DOI] [PubMed] [Google Scholar]
  45. Rubin C, Judex S, Hadjiargrou M. Skeletal adaptation to mechanical stimuli in the absence of formation or resorption of bone. Journal of Musculoskeletal and Neuronal Interactions. 2002;2:264–267. [PubMed] [Google Scholar]
  46. Smalt R, Mitchell FT, Howard RL, Chambers TJ. Induction of NO and prostaglandin E2 in osteoblasts by wall-shear stress but not mechanical strain. American Journal of Physiology. 1997;273:E751–E758. doi: 10.1152/ajpendo.1997.273.4.E751. [DOI] [PubMed] [Google Scholar]
  47. Stains JP, Civitelli R. Cell–cell interactions in regulating osteogenesis and osteoblast function. Birth Defects Research C. Embryo Today. 2005;75:72–80. doi: 10.1002/bdrc.20034. [DOI] [PubMed] [Google Scholar]
  48. Tazawa K, Hoshi K, Kawamoto S, Tanaka M, Ejiri S, Ozawa H. Osteocytic osteolysis observed in rats to which parathyroid hormone was continuously administered. Journal of Bone and Mineral Metabolism. 2004;22:524–529. doi: 10.1007/s00774-004-0519-x. [DOI] [PubMed] [Google Scholar]
  49. Turner CH, Takano Y, Owan I. Aging changes mechanical loading thresholds for bone formation in rats. Journal of Bone and Mineral Research. 1995;10:1544–1549. doi: 10.1002/jbmr.5650101016. [DOI] [PubMed] [Google Scholar]
  50. Walker LM, Publicover SJ, Preston MR, Said Ahmed MA, el Haj AJ. Calcium-channel activation and matrix protein upregulation in bone cells in response to mechanical strain. Journal of Cellular Biochemistry. 2000;79:648–661. doi: 10.1002/1097-4644(20001215)79:4<648::aid-jcb130>3.0.co;2-q. [DOI] [PubMed] [Google Scholar]
  51. Weinbaum S, Cowin SC, Zeng Y. A model for the excitation of osteocytes by mechanical loading-induced bone fluid shear stresses. Journal of Biomechanics. 1994;27:339–360. doi: 10.1016/0021-9290(94)90010-8. [DOI] [PubMed] [Google Scholar]
  52. Weinbaum S, Zhang X, Han Y, Vink H, Cowin SC. Mechanotransduction and flow across the endothelial glycocalyx. Proceedings of the National Academy of Sciences. 2003;100:7988–7995. doi: 10.1073/pnas.1332808100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Weiner S, Traub W. Organization of hydroxyapatite crystals within collagen fibrils. FEBS Letters. 1986;206:262–266. doi: 10.1016/0014-5793(86)80993-0. [DOI] [PubMed] [Google Scholar]
  54. You J, Yellowley CE, Donahue HJ, Zhang Y, Chen Q, Jacobs CR. Substrate deformation levels associated with routine physical activity are less stimulatory to bone cells relative to loading-induced oscillatory fluid flow. Journal of Biomechanical Engineering. 2000;122:387–393. doi: 10.1115/1.1287161. [DOI] [PubMed] [Google Scholar]
  55. You LD, Cowin SC, Schaffler MB, Weinbaum S. A model for strain amplification in the actin cytoskeleton of osteocytes due to fluid drag on pericellular matrix. Journal of Biomechanics. 2001;34:1375–1386. doi: 10.1016/s0021-9290(01)00107-5. [DOI] [PubMed] [Google Scholar]
  56. You LD, Weinbaum S, Cowin SC, Schaffler MB. Ultra-structure of the osteocyte process and its pericellular matrix. Anatomical Record Part A: Discoveries in Molecular, Cellular, and Evolutionary Biology. 2004;278:505–513. doi: 10.1002/ar.a.20050. [DOI] [PubMed] [Google Scholar]
  57. Zaman G, Pitsillides AA, Rawlinson SC, Suswillo RF, Mosley JR, Cheng MZ, Platts LA, Hukkanen M, Polak JM, Lanyon LE. Mechanical strain stimulates nitric oxide production by rapid activation of endothelial nitric oxide synthase in osteocytes. Journal of Bone and Mineral Research. 1999;14:1123–1131. doi: 10.1359/jbmr.1999.14.7.1123. [DOI] [PubMed] [Google Scholar]

RESOURCES