Effects of Economic Shocks on Children’s Employment and Schooling in Brazil

Abstract

This paper uses longitudinal employment survey data to analyze the impact of household economic shocks on the schooling and employment transitions of young people in metropolitan Brazil. The paper uses data on over 100,000 children ages 10–16 from Brazil’s Monthly Employment Survey (PME) from 1982 to 1999. Taking advantage of the rotating panels in the PME, we compare households in which the male household head becomes unemployed during a four-month period with households in which the head is continuously employed. Probit regressions indicate that an unemployment shock significantly increases the probability that a child enters the labor force, drops out of school, and fails to advance in school. The effects can be large, implying increases of as much as 50% in the probability of entering employment for 16-year-old girls. In contrast, shocks occurring after the school year do not have significant effects, suggesting that these results are not due to unobserved characteristics of households that experience unemployment shocks. The results suggest that some households are not able to absorb short-run economic shocks, with negative consequences for children.

1. Introduction

Does economic volatility have negative long-term consequences for children in developing countries? It is often argued that households feeling the pinch of financial crises or structural adjustment programs will reallocate their resources to best weather the negative economic shock. In the case of poor urban households, the time allocation of family members may be one of the major resources available for adjustment. This paper focuses on the question of whether households reallocate the time of children in ways that have important consequences for children’s current and future welfare. In particular, do households under economic stress transfer children’s time out of school and studying and into labor force work? If households are not able to buffer short-term economic downturns then children who were previously not employed may be sent to work, potentially causing interruptions to their education or reduced progress in school. In addition to direct policy concern about the effects of economic shocks on children, researchers are interested in whether such effects exist because of what they reveal about households’ ability to smooth transitory economic shocks. If an adult becoming unemployed leads to increased work activity of children, this suggests that households are not able to fully insure against short-term income volatility. The extent to which households can buffer short-run shocks is an important issue in thinking about the policy implications of economic crises such as those experienced in Latin America during the 1980s or in East Asia in the late 1990s.

In this paper we analyze the relationship between household economic shocks and child employment in Brazil’s six largest cities. Brazil has had relatively high levels of child employment, especially considering the country’s relatively high per capita income. As we will see below, employment rates for 14-year-old boys were around 20% in the 1980s. Concern that high rates of youth employment may be competing with schooling are reinforced by Brazil’s poor schooling performance in recent decades (Birdsall and Sabot 1996). Brazil’s case is also interesting because of the economic volatility experienced during the 1980s and 1990s. After two decades of rapid economic growth in the 1960s and 1970s, the country experienced an economic crisis in the early 1980s, followed by large fluctuations that left per capita income in 1990 at roughly the 1980 level. Brazil’s economic performance was better in the 1990s, although it continued to be characterized by considerable volatility. Our analysis uses Brazil’s Monthly Employment Survey (PME), a survey with a longitudinal design that allows us to observe month-to-month transitions in and out of employment by all household members ages ten and over. We take advantage of this component to investigate our question of primary interest: do negative economic shocks at the household level cause children to move into employment or impede their educational attainment?

We begin with a review of related literature analyzing the impact of income volatility on children’s work and schooling in developing countries. We follow this with a discussion of the PME data, including consideration of attrition bias. In order to place our results in the context of changing patterns of children’s work in Brazil, we use the PME to document large declines in child labor from 1982 to 1999. Using the panel data to estimate transitions in and out of work, we show that the probability of a non-working child entering employment falls over time, and the probability of a working child leaving employment rises over time, with both factors helping explain the decline in youth employment. We then present our probit regression results, which indicate that unemployment shocks have a significant impact on the probability that children enter employment, drop out of school, and fail to advance in school. As a key robustness check, we show that shocks occurring after the end of the school year do not affect outcomes during the school year, suggesting that we are not simply picking up unobserved heterogeneity across households. The magnitude of our estimated effects is quite large. Unemployment shocks to the male household head increase the probability that children enter the labor force by 30–50%, and increase the probability of failing to advance in school by 14–34% in our examples. We conclude the paper with a discussion of how these short-run effects may cumulate to substantial disadvantages over a child’s school-age years.

2. Related literature on household shocks

Asia, Latin America, and Africa have all gone through periods of substantial economic volatility in recent decades. Policy makers and international agencies have focused attention on how households are affected by and respond to the economic shocks associated with this volatility, including fluctuations in prices, wages, unemployment, and exchange rates. Researchers have studied the impact of these shocks on a wide variety of outcomes at the household level, including poverty, employment, health, fertility, and schooling (e.g., Fallon and Lucas (2002), Frankenberg et al. (2003) and Tapinos et al. (1997). Concern about the impact of economic shocks on children has been an important focus in this literature, stimulated in part by the concerns voiced by organizations such as UNICEF about the impact of structural adjustment programs on children (Jolly, 1991). Fallon and Lucas (2002) summarize the evidence of the impact of economic crises on households, with particular attention to the 1990s financial crises in southeast Asia and Mexico. They find evidence of declines in school enrollment, especially among poor children, during periods of economic crisis. Funkhouser (1999) finds that school attendance declined in Costa Rica during a recessionary period in the early 1980s. Thomas et al. (2004), using panel data from the Indonesia Family Life Survey, find that the Indonesian financial crisis of 1998 caused a decline in schooling expenditures, with the largest declines among households that were poorest in 1997. Enrollment also declined, especially for younger children. They interpret this as evidence that families focused on keeping older children in school, at the expense of the schooling of younger children.

This research has built on the broader literature on the extent to which short-run income variability affects child labor and schooling in developing countries. Jacoby and Skoufias (1997) show that child labor and school attendance adjust in response to seasonal income fluctuations in rural India, adjustments which they interpret as evidence of incomplete financial markets. Using exchange rate fluctuations as an instrument for household income, Rucci (2004) finds effects of the Argentine crisis of 1998–2002 on school attendance and labor supply for 14–17-year-olds. Beegle et al. (2005), using panel data from Tanzania, find that accidental crop loss leads to increased child labor. Like Jacoby and Skoufias and Rucci, they interpret this as evidence of credit constraints, and find that the effect is mitigated when households have collateralizable assets. Edmonds (2005), taking advantage of the sharp discontinuity in age eligibility for South Africa’s old age pension, concludes that pension income, which should be entirely anticipated, significantly decreases child labor and increases school attendance of 10–17-year-olds. Looking at a very different level of data, Dehejia and Gatti (2005) interpret aggregate cross-national data as supporting a link between credit constraints and child labor, finding a negative relationship between the extent of financial development in a country and the employment level of children.

In this paper we look at the impact of short-run economic shocks to households in large metropolitan areas. The shock we focus on is job loss by the household head during a four-month period. Since there are few longitudinal data sets from developing countries with data on short-term work and school transitions, previous research in this area is limited. Brazil and Mexico have what may be the most interesting data for these purposes. Skoufias and Parker (2006) and Cunningham and Maloney (2000) use the Mexico National Urban Employment Survey (ENEU), which follows households over five consecutive quarters, to analyze issues related to those we consider here. Looking at youth aged 12–17 in the ENEU from 1987–1997, Cunningham and Maloney find weak evidence that parental job loss causes children to leave school and enter employment, with some evidence that girls are more affected than boys. Skoufias and Parker use the ENEU panels during the economic crisis period 1995–97 to look at the effects of adult job loss on the time allocation of both adults and children. They find some evidence that job loss by the head leads to increased work activity for girls, though there is no effect on time allocated to school. They find no significant effects of job loss on the time allocation of boys, and conclude that children appear to be largely unaffected by household economic shocks. In research using Brazil’s PME, Duryea (1997) finds that children are less likely to advance to the next grade if their father becomes unemployed during the school year. This study expands on that research, looking at the impact of unemployment shocks on both schooling and employment outcomes.

This paper expands our understanding of the impact of short-run economic shocks in several ways. The unusual Brazilian panel data allow us to look at the impact of shocks over almost two decades, a much longer period than covered in most previous research. Large sample sizes allow us to measure the impact of shocks that occur to a small fraction of households in any given period, permitting us to see effects that would be statistically insignificant in smaller samples. We are able to study household responses to idiosyncratic shocks in the very short run, an important indicator of a household’s ability to do intertemporal smoothing. The responses we consider take place during a four-month period, a short-run response that would be impossible to observe in panel surveys with one or more years between waves. The data also permit us to test for the contaminating influence of unobserved household heterogeneity in a way that has not been possible in most previous research. By showing that ex post shocks do not affect the probability that children enter the labor force, we provide some of the strongest evidence to date that job loss by fathers has an unexpected component that causes large and immediate negative effects on children.

3. Overview of data and trends

3.1 Brazil’s Monthly Employment Survey

Our empirical analysis uses Brazil’s Monthly Employment Survey, the Pesquisa Mensal de Emprego (PME). The PME is organized with a panel structure similar to the United States Current Population Survey (CPS). Respondent households are surveyed once per month for four consecutive months, rotate out of the sample for eight months, and then rotate back in for four final months. The appendix provides a detailed discussion of the data, including an analysis of sample attrition. As discussed in the appendix, it is possible to match individuals across waves in the PME, even though the survey is not designed primarily for the purpose of longitudinal analysis. During the period we analyze, the PME covered Brazil’s six largest metropolitan areas – São Paulo, Rio de Janeiro, Belo Horizonte, Porto Alegre, Recife, and Salvador – surveying 4,500 to 7,500 households in each metropolitan region per month. Our analysis is based on PME surveys in the period bracketed by February 1982 and August 1999.

Our sample includes 10–16-year-olds and male heads of their households. Because the PME is based on dwellings rather than households, and because it is not designed explicitly for longitudinal analysis, attrition across waves is relatively high. As shown in Table A.1 in the appendix, we lose about 30% of our sample of 10–16-year-olds between their first month in the survey and their fifth interview one year later. Table A.1 also shows, however, that there is very little systematic relationship between attrition and month 1 variables such as the schooling and employment of the child or head. Given the scarcity of longitudinal data for developing countries, and given the large sample size, time span, and methodological consistency of the PME data, we conclude from our analysis of sample attrition that the data are well worth using to analyze short-run adjustments to economic shocks. While potential selection biases in the data must be kept in mind, we believe the data provide valuable evidence that would otherwise never be available about short-run household dynamics during the highly volatile 1980s and 1990s.

Table A1.

Measures of sample attrition and selection bias, children aged 10–16 in metropolitan Brazil, PME 1982–99

Sample	Number of observations	Percent of Sample A	Mean child schooling month 1	Percent children working month 1	Mean father’s schooling month 1	Percent fathers working month 1
A. Child present in month 1	277,021	100%	4.36	11.0%	-	-
B. Child and father present in month 1	227,139	82%	4.41	10.4%	5.48	87.5%
C. Child in sample in months 1–13	162,142	59%	4.51	9.9%	-	-
D. Child and father in sample in months 1–13	156,733	57%	4.52	9.8%	5.52	87.8%
Sample conditional on month 1 activity
E. Child in school, child not working, head working in	165,572	60%	4.43	0%	6.03	100%
F. Same as E plus all sample restrictions for regression in	99,184	36%	4.53	0%	6.12	100%

3.2 Trends in youth employment in Brazil

The PME data provide a detailed picture of trends in youth employment over the 1980s and 1990s. Figure 1 shows employment rates for 14-year-old and 16-year-old males and females for the population-weighted average of the six Brazilian cities in the PME from 1982 to 1999.¹ The 14-year-olds are especially interesting since they are the oldest age group still considered to be children under most international definitions. Figure 1 shows that employment rates of 14-year-olds in Brazil have been relatively high, with over 20% of boys and over 10% of girls working in the early 1980s. Employment rates for 16-year-olds reach levels as high as 50% for boys and 30% for girls in the 1980s. During the 1980s there is relatively little decline in youth employment rates, and even evidence of rising employment rates in the mid-1980s. There are, however, substantial declines in employment rates for males and females in both age groups from the early 1980s to the late 1990s. In most cases employment rates in 1998 are about half what they were in 1982.

Figure 1.

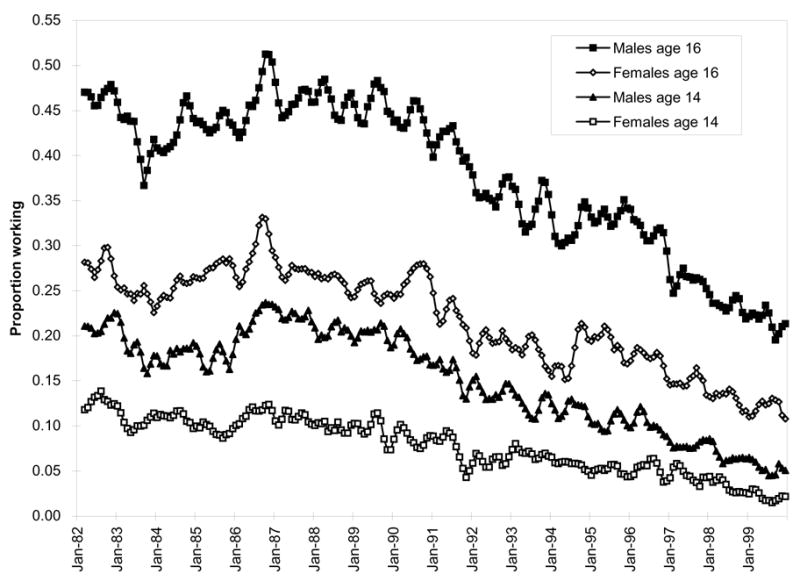
Proportion of 14-year-old and 16-year-old males and females working, 6 metropolitan areas, 1982–1999, Brazil, 3-month moving averages

The longitudinal dimension of the PME makes it possible to estimate month-to-month labor force transitions. Figure 2 shows monthly employment transitions for 14-year-old males and females in the combined six PME cities. The exit rate for month t is the number of children who move from the category “working in month t” to “not working in month t+1” divided by the number who were working in month t. The entry rate is defined analogously using the number who move from “not working in month t” to “working in month t+1.” In the early 1980s the probability that a 14-year-old boy who is not working in a given month is observed working in the next month is about 10%, while the entry rate for girls is about 5%. The probability that a working boy leaves employment by the next month is around 25%, with similar estimates for girls.² The transition rates in Figure 2 suggest that the lower employment rates for girls in Figure 1 are explained almost entirely by the fact that girls have lower entry rates than boys. Exit rates for boys and girls are fairly similar, suggesting that girls who do enter employment have similar job attachment as boys.

Figure 2.

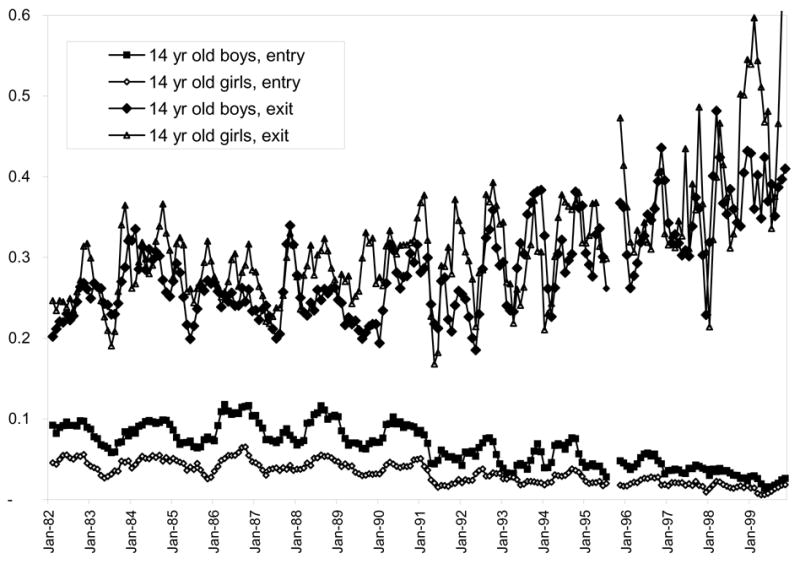
Rates of entry into and exit from employment, 14-year-old boys and girls, 6 metropolitan areas, 1982–99, 3-month moving averages, Brazil PME

The large declines in employment rates over time, shown in Figure 1, appear to result from both decreasing entry rates and increasing exit rates. Exit rates rise to levels around 30% by the end of the 1990s for both males and females. In other words, about one-third of the children who are working in a given month are not working in the following month, a high degree of labor force mobility.³ While all of these estimates may be subject to measurement error, it seems unlikely that measurement error can explain either the large increases in exit rates over time or the differences in entry rates by gender and socioeconomic status. Duryea et al. (2003) provide additional detail on these transition rates, including breakdowns by mother’s education. These breakdowns indicate that the fact that boys with less educated mothers have roughly twice the employment rates of those with more educated mothers is almost entirely due to the fact that the disadvantaged boys are twice as likely to enter employment each month. Once they take a job, the estimates suggest that boys in the two groups are about equally likely to stay employed.⁴

The high degree of mobility in and out of employment suggests that the percentage of children who work at some point during the year may be much higher than the rates estimated for any particular month. The PME data allow us to confirm this empirically. Levison et al. (2006) use the PME panels to construct a measure of whether a child works at any point during a consecutive four-month period. These results indicate that the proportion of 14-year-old girls who work at least once in a four-month period is roughly twice as high as the one-month employment rates shown in Figure 1. For 14-year-old boys, calculating employment on this four-month basis raises the employment rate about 15 percentage points in the 1980s, and about 10 percentage points in the 1990s, bringing the employment rate in 1998 to around 20%.

3.3 Trends in schooling and other variables

Table 1 shows means of child schooling and other outcomes by year from 1982 to 1998.⁵ The table focuses on 14-year-olds in order to provide a clearer picture of trends over time for a single age group. Table 1 shows large improvements in schooling in Brazil between 1982 and 1998. Mean completed years of schooling of 14-year-olds rises from 4.7 to 5.7 years, and enrollment rates rise from 85% to 94%. These improvements in schooling are consistent with the decline in youth employment shown in Figure 1. As shown in Table 1, the proportion of 14-year-olds working in the labor force falls from 17% to 5.5% over this period. Columns 4 and 5 of Table 1 show the percentage working and mean schooling of male household heads. The percentage of male heads working averages 87% for the entire period, with annual volatility of 3 to 4 percentage points in both decades. The 13% of male heads who were not working in Table 1 are made up of 2.6% unemployed (searching for work), 8.5% retired, and 2% in other categories. Mean schooling of male heads rose by over two years, from 4.5 to 6.7. As shown by Levison (1991), Barros and Lam (1996), and Lam and Duryea (1999), there is a strong relationship between parental schooling and children’s schooling and work in Brazil, so these improvements in adult schooling may have had an important direct role in explaining the rising schooling and falling rates of youth employment.

Table 1.

Sample means for selected variables by year for children age 14, Brazil PME 1982–98

Year	Values for child and head in Month 1					Outcomes conditional on state in Month 1
	Child in school	Child’s years of schooling	Child working	Male head working	Male head’s schooling	Child starts working by month 4	Child leaves school by month 4	Child fails to advance in school	Head loses job by month 4
	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)
1982	0.847	4.72	0.170	0.875	4.47	0.130	0.030	0.370	0.038
1984	0.842	4.71	0.148	0.841	4.36	0.121	0.024	0.350	0.062
1986	0.868	4.81	0.166	0.873	4.73	0.129	0.026	0.368	0.025
1988	0.851	4.79	0.163	0.878	5.11	0.101	0.020	0.345	0.036
1990	0.866	4.97	0.150	0.890	5.46	0.111	0.015	0.396	0.037
1992	0.890	5.11	0.109	0.867	5.77	0.076	0.014	0.344	0.048
1994	0.917	5.28	0.096	0.869	5.93	0.065	0.009	0.314	0.042
1996	0.938	5.55	0.090	0.866	6.48	0.061	0.008	0.279	0.039
1998	0.942	5.74	0.055	0.833	6.70	0.053	0.009	0.242	0.066
Total	0.884	5.06	0.129	0.866	5.40	0.094	0.017	0.334	0.043
N	39,393	39,385	39,393	31,930	31,919	34,283	29,383	26,366	17,571

Note: Means are estimated for largest possible sample for each outcome in each year. Column 6 is conditional on not working in month 1. Columns 7 and 8 are conditional on school enrollment in month 1. Column 9 is conditional on head employed in month 1

The last four columns of Table 1 show means for the key transitions that are the focus of our analysis. Column 6 shows the probability that a child who is not working in month 1 begins working by month 4. This probability is 13% for 14-year-olds in 1982, changes relatively little in the 1980s, then falls to around 5% by 1998. Column 7 shows dropout rates between month 1 and month 4. Only 3% of 14-year-olds enrolled in school in month 1 were out of school in month 4 in the early 1980s, a rate that fell to less than 1% in the late 1990s. While few children are reported as dropping out of school during a school year, a much higher percentage fail to advance to the next grade. Column 8 shows the proportion who fail to advance a grade between the first month of observation and one year later, conditional on enrollment in month 1. Among 14-year-olds in school in 1982, 37% did not advance to the next grade. This rate stayed between 34% and 40% until 1992, then fell to 24% in 1998. The failure to advance grades is primarily a reflection of grade repetition rather than dropping out. Taking all 14-year-olds ever enrolled in school in month 1 over the 1982–1999 period, 33% failed to advance a grade from month 1 to month 13. Of this 33% who failed to advance, 88% were enrolled in school in month 13.

3.4. Unemployment shocks to male household heads

Column 9 of Table 1 shows the prevalence of the economic shock variable that will be the focus of our analysis – the transition from employed to unemployed by the male household head between month 1 and month 4. As the table shows, 3.8% of male heads lost their job between month 1 and month 4 in 1982. This rate stays around 3% to 5% in most years, rising to almost 7% in 1998. The shock we will be focusing on can thus be seen to be a relatively unusual event for households. Nonetheless, given our very large sample sizes, a substantial number of heads are observed to lose their jobs during the period of our study. Unemployment shocks are more common among heads with less human capital. For men with less than one year of schooling (13% of male heads), the probability of an unemployment shock is 6.7% over the entire period, compared to 2.2% for men with 11 or more years of schooling (not shown).

Table 2 provides additional detail about these unemployment shocks, and helps illustrate the logic of our econometric analysis. We define male household heads as experiencing an unemployment shock if they move from employed to unemployed (searching for work) between month 1 and month 4.⁶ The first seven rows of Table 2 show all combinations of employment sequences that generate this shock, using the sample of male heads in households with 10–16-year-olds that will be used in our regression in Table 4 below. The first line shows that we observe 282 cases in which the male head is employed in month 1 but is unemployed in months 2, 3, and 4, 0.3% of the 106,648 cases. Summing up all sequences that include at least one month of unemployment in months 2, 3, or 4, we see that 3.16% of heads experienced an unemployment shock between month 1 and month 4. In just under half these cases, the head is employed again in month 4. The rows at the bottom of the table show that 90% of the heads were employed in months 1–4 and month 13, 2% were employed in all of the first four months but were unemployed in month 13, and 4.7% left the labor force between month 1 and month 13.

Table 2.

Summary of monthly employment sequences for male household heads employed in month 1, Brazil PME 1982–99

Sequence of employment and unemployment for male head employed in month 1	Age 10–16		Age 15–16	Percentage of 15–16 year-olds who:
	Frequency	Weighted percent	Weighted percent	Start working by month 4	Leave school by month 4	Fail to advance to next grade
Lost job month 2, 3, or 4:
Sequence 1000	282	0.27	0.29	17.8	9.3	33.7
Sequence 1001	276	0.23	0.17	17.9	8.3	42.1
Sequence 1010	129	0.11	0.08	13.3	0.0	49.0
Sequence 1011	728	0.66	0.51	18.0	4.2	38.0
Sequence 1100	418	0.39	0.36	18.2	0.8	36.0
Sequence 1101	723	0.60	0.48	23.7	1.6	37.6
Sequence 1110	963	0.90	0.77	16.8	2.8	36.3
Sum of rows above	3,519	3.16	2.67	18.5	3.5	37.3
Employed all months 1–4
Employed month 13	95,660	90.20	89.85	11.7	1.3	30.5
Unemployed month 13	2,049	1.96	1.81	13.7	1.6	35.0
Left labor force by month 13	5,420	4.68	5.67	12.8	1.4	33.7
Total	106,648	100	100	12.0	1.4	30.9

Note: Sample is restricted to children of a male head who are in school and not working in month 1, with head working in month 1. In job sequence, 1 indicates employed, 0 indicates unemployed; for example, job sequence 1000 means head was employed month 1, unemployed months 2, 3, 4.

Table 4.

Probit regressions: Impact of unemployment shock on work and school transitions, age 10–16, Brazil PME 1982–1999

Variable	Enter labor force by month 4	Leave school by month 4	Fail to advance to next grade in school
Head’s transitions (continuously employed omitted)
Unemployment shock in month 2–4	0.091 (0.050)**	0.179 (0.075)**	0.086 (0.033)***
Unemployment shock in month 5–13	0.016 (0.064)	0.074 (0.108)	0.017 (0.039)
Left labor force	0.016 (0.040)	−0.103 (0.066)	0.047 (0.026)*
Child’s age (age 16 omitted)
Child age 10	−1.294 (0.041)***	−0.438 (0.066)***	−0.165 (0.022)***
Child age 11	−1.169 (0.037)***	−0.434 (0.066)***	−0.115 (0.022)***
Child age 12	−0.938 (0.034)***	−0.296 (0.061)***	−0.075 (0.021)***
Child age 13	−0.739 (0.033)***	−0.296 (0.062)***	−0.023 (0.021)
Child age 14	−0.447 (0.030)***	−0.165 (0.058)***	−0.003 (0.022)
Child age 15	−0.210 (0.030)***	−0.124 (0.057)**	0.014 (0.023)
Male child	0.395 (0.019)***	−0.019 (0.034)	0.167 (0.010)***
Child 2+ years behind in school	0.100 (0.021)***	0.520 (0.040)***	0.194 (0.014)***
Father’s age	−0.010 (0.010)	−0.046 (0.018)***	−0.014 (0.007)**
Mother’s age	0.029 (0.012)**	0.017 (0.022)	−0.017 (0.007)**
Father’s age squared/100	0.011 (0.011)	0.050 (0.018)***	0.015 (0.007)**
Mother’s age squared/100	−0.042 (0.014)***	−0.027 (0.026)	0.017 (0.009)**
Father’s schooling	−0.027 (0.008)***	−0.022 (0.015)	−0.015 (0.005)***
Mother’s schooling	−0.036 (0.008)***	−0.036 (0.017)**	−0.029 (0.005)***
Father’s schooling squared/100	−0.064 (0.054)	−0.002 (0.112)	−0.026 (0.032)
Mother’s schooling squared/100	0.002 (0.063)	0.142 (0.133)	0.096 (0.035)***
Metro Area (São Paulo omitted)
Salvador	−0.037 (0.029)	−0.120 (0.057)**	0.426 (0.017)***
Belo Horizonte	0.082 (0.024)***	0.161 (0.048)***	0.148 (0.015)***
Recife	−0.030 (0.028)	0.007 (0.052)	0.299 (0.017)***
Rio de Janeiro	−0.338 (0.028)***	−0.023 (0.053)	0.276 (0.016)***
Porto Alegre	−0.150 (0.027)***	0.154 (0.051)***	0.277 (0.017)***
Year (1982 omitted)
Year 1984	−0.058 (0.034)*	−0.055 (0.061)	−0.124 (0.023)***
Year 1986	0.044 (0.034)	−0.028 (0.061)	−0.005 (0.022)
Year 1988	−0.086 (0.039)**	−0.028 (0.068)	−0.062 (0.025)**
Year 1990	−0.062 (0.037)*	−0.086 (0.065)	0.039 (0.023)*
Year 1992	−0.274 (0.040)***	−0.055 (0.071)	−0.068 (0.024)***
Year 1994	−0.251 (0.038)***	−0.290 (0.070)***	−0.117 (0.024)***
Year 1996	−0.230 (0.038)***	−0.379 (0.076)***	−0.235 (0.024)***
Year 1998	−0.304 (0.041)***	−0.187 (0.076)**	−0.268 (0.026)***
Month of first observation (February omitted)
March	−0.055 (0.036)	0.011 (0.067)	0.008 (0.022)
April	−0.060 (0.036)*	−0.122 (0.070)*	0.013 (0.022)
May	−0.024 (0.035)	−0.127 (0.069)*	−0.052 (0.022)**
June	−0.005 (0.035)	−0.073 (0.067)	−0.048 (0.022)**
July	0.005 (0.034)	−0.011 (0.065)	−0.057 (0.022)***
August	0.011 (0.035)	−0.035 (0.065)	−0.05 (0.021)**
Constant	−0.967 (0.266)***	−1.203 (0.506)**	0.255 (0.164)
Number of Observations	106,648	106,648	106,648

Note: Robust standard errors in parentheses; Significance levels:

^*=.10,

^**=.05,

^***=.01 Sample is conditional on child in school and not working in month 1 and male head working in month 1.

While many of the shocks documented in the first seven rows of Table 2 are of short duration, the last three columns show evidence that they nonetheless have significant negative effects on child outcomes. This example is limited to the age 15–16 group in order to keep the analysis focused on a narrow age range. Among 15–16-year-olds whose male head experiences an unemployment shock, 18.5% start working between months 1 and 4. This compares to 11.7% when the head is employed from month 1 to month 13. Looking at heads who experience a shock after month 4 (employed months 1–4 but unemployed month 13), 13.7% of 15–16-year-olds start working between months 1 and 4. Heads who experience a shock after month 4 will be used as an important control group in our regressions in Table 4, since they help us rule out the possibility that it is simply unobserved heterogeneity that explains the relationship between unemployment shocks and child outcomes. The last two columns show that unemployment shocks are also associated with higher dropout rates and higher failure rates in school. These relationships will be more convincingly analyzed in our regressions below, where we control for a large number of individual and household variables.

Tables 1 and 2 suggest that there was a high degree of flexibility in the Brazilian labor market during the 1980s and 1990s. Unemployment for prime-aged males was relatively low, and many unemployment spells were short. Although the unemployment spells in Table 2 are often short, they have a large impact on household income. In the sample used in the regressions below, male household income is on average 86% of joint husband-wife income, with 65% of wives having zero income.⁷ Joint husband-wife income fell an average of 69% between months 1 and 4 for those who experienced an unemployment shock, compared to the average income change for all couples, controlling for variables such as month 1 income, age, schooling, city, and month/year. Among men who experienced an unemployment shock but returned to work by month 4, earnings fell by 27% compared to the average change between months 1 and 4 for all workers, controlling for month 1 earnings, age, schooling, city, and month/year.

4. The impact of unemployment shocks on work and school transitions

4.1 Consumption smoothing and children’s time allocation

The above results demonstrate that youth employment is not a rare event in Brazil’s cities, and that this employment is characterized by a high degree of volatility. We have also seen that significant fractions of children fail to advance in school, and that unemployment shocks to male household heads, while relatively rare, appear to be associated with increased labor force entry and poorer school outcomes for youth. The possibility that even very short unemployment spells could affect children’s work and schooling has important implications for human capital accumulation and may indicate that some households are unable to smooth consumption.

As shown by Jacoby and Skoufias (1997), if households have access to perfect capital markets we would not expect transitory income fluctuations to affect the time children allocate to work or school. Investments in children’s human capital should be based on long-run optimization, with borrowing or insurance used to smooth consumption in response to negative income shocks. If a household is credit constrained, however, short-run income shocks may force adjustments in the labor supply of other household members, including children. If children are pushed into employment as a result of the shock, it may come at the expense of time spent attending school or doing homework. This may affect their probability of grade advancement, even if they do not drop out of school, by affecting the likelihood of passing end-of-year exams. School effort may be disrupted even if there is not an increase in employment. Children may be pulled out of school, even temporarily, because of problems paying school fees or transport costs. Some children, especially girls, may be pulled into increased domestic duties if the mother increases employment in response to the father’s job loss. ⁸ Increased stress in the household may disrupt the child’s school performance even in the absence of direct effects on enrollment. Although we cannot isolate all of the mechanisms through which job loss affects work and school transitions, we will be able to look directly at whether the child starts working, drops out of school, or fails to advance to the next grade in school in response to the male head becoming unemployed.

4.2 Estimation strategy

Taking advantage of the PME’s panel structure, we follow male household heads and the children living with them over the first four months in which they are interviewed in the PME. The sample used for the regressions consists of children aged 10–16 who are enrolled in school and not working at the time of the first interview. The sample is restricted to children who live in households with a male head present (we sometimes refer to this male head as the “father,” although he may have some other relationship to the child). We restrict the analysis to children who are a son, daughter or other relative of the household head.⁹ We drop all children for whom the first four PME interview months include the long summer break between the end of a school year and the beginning of the next school year. This means that the unemployment shocks and children’s entry into work all occur during a school year. A major focus of our analysis is on the timing of shocks and responses. As in Duryea (1997), an important issue in looking at the effects of household economic shocks is that the observation of a shock such as unemployment may simply be a proxy for household characteristics that are correlated with outcomes such as grade repetition or child employment. In other words, the observed child outcome may not be causally linked to the shock itself, but will be correlated with the shock in the data. Our panel data make it possible to separate the effect of shocks that occur during the school year from shocks that occur after the school year, allowing us to control, at least to some extent, for household heterogeneity that may cause spurious correlations between shocks and negative child outcomes.

The dependent variable capturing entry into labor force employment, L, is equal to 1 if a child who was not employed in month 1 is employed in month 2, 3, or 4. If the child is not employed in all four months then L=0. Children’s optimal work hours are based on the difference between the market wage and the reservation wage. Formally, the reservation wage is

$$w_{i,t}^r=f(Y_{i,t}^T,Y_i^P,X_i,m_t,a_t),$$ (1)

where X_i is a vector of demographic characteristics for the household and the child, $Y_i^p$ is a vector of permanent income variables for the family, and the vector $Y_i^t$ is an indicator of transitory shocks to household income. Month dummies m_t are included to control for seasonal variation in the reservation wage. To control for intertemporal changes we include period-specific constant terms a_t representing the different year-to-year panels from 1982–83 to 1998–99. The market wage includes productivity-related components of X such as the child’s age and progress through school, as well as seasonal and annual components. The child’s optimal hours L* are a function of the difference between the market wage and the reservation wage,

$$L_{it}^{\ast }=X_i^{\prime }\theta +Y_i^{\prime p}\sigma +T_{it}^{\prime }\delta +m_t+a_t+v_{it},$$ (2)

where the coefficients pick up effects from both the reservation wage and the market wage, and where v_it is a zero-mean normally distributed stochastic term that combines stochastic components in both the reservation wage and market wage. The child is observed working if $L_{it}^{\ast }>0$,

$$L_{it}=1\hspace{0.17em}\text{if\hspace{0.17em}}{v}_{it}\ge -X_i^{\prime }\theta -Y_i^{\prime p}\sigma -T_{it}^{\prime }\delta -m_t-a_t$$ (3)

We will estimate a probit version of Equation (3), where the transitory shock is indicated by the husband moving from unemployment into unemployment. If households could perfectly smooth consumption, we would not expect them to use child labor as a buffer against volatility, and would therefore expect θ in Equation (3) to be zero.

If the child starts working in response to a shock (and perhaps even if the child does not) the child may withdraw from school. We estimate a probit identical to Equation (3) in which the dependent variable is dropping out of school rather than entering work. Since dropping out may be directly related to the work decision, we use the same set of regressors. As shown above, dropping out during the school year is rare for the age group we are studying, but failing to advance a grade in school is much more common. We therefore consider the possibility that adjustments in the child’s time allocation in response to the shock may have a negative effect on school progress. This could be because of a shift into child labor, but could also occur even if the child does not start working. We define a variable indicating advancement in school, S, where S = 1 if the child passed the grade he or she was attending in month 1 and advanced to the next grade as of the month 13 interview, one year later. If the child does not advance to the next grade then S = 0. This could occur either because the child drops out of school or because the child repeats the grade, a relatively common outcome in Brazilian schools. Note that while the four months we observe occur in one year, evidence of the successful completion of the grade is not observed until the next year, given the eight-month gap between the fourth and fifth interviews. If the child is attending grade 5 in March through June 1994, evidence that the child passed grade 5 is not observed until the child is re-interviewed in March 1995 (in the household’s fifth interview).

More formally, achievement in school is assumed to be a function of the child’s effort spent on schoolwork with a stochastic component:

$$S_{it}^{\ast }=X_i^{\prime }\theta +Y_i^{\prime p}\sigma +T_{it}^{\prime }\delta +m_t+a_t+{\mu }_{it},$$ (4)

where we include the same variables defined for Equation (1), with the stochastic component μ_it reflecting the fact that parents and children cannot perfectly predict the amount of effort necessary to pass a grade. We will normalize such that the child advances in school if S_it >0,

$$S_{it}=1\hspace{0.17em}\text{if\hspace{0.17em}}{u}_{it}\ge -X_i^{\prime }\theta -Y_i^{\prime p}\sigma -T_{it}^{\prime }\delta -m_t-a_t$$ (5)

Since our other outcome measures are the “bad” outcomes of entry into employment and dropping out of school, for ease of interpretation we will use the failure to advance in school, F=1−S, as our dependent variable for the probit corresponding to Equation (5).

We use job loss by the male household head to indicate a negative transitory household income shock. We focus on male heads because they tend to be primary income earners with high labor force attachment. Ideally we would want to measure deviations from the head’s lifetime earnings profile to capture the existence and magnitude of transitory income shocks. Since the PME is a short panel of 8 interviews over a 16-month period, however, it is impossible to know whether a drop in earnings signals a return to the head’s long-run income path or a short-run deviation from that path. We also prefer to use transitions into unemployment rather than earnings changes because of several complications with the PME earnings variable. In addition to dealing with missing values, measuring changes in monthly earnings is complicated by periods of hyperinflation that reached over 50% per month in the 1980s. A further complication is that earnings are reported as zero if the job held at the time of the interview is different that the job held during the previous month (the reference period for earnings). This mismatch of earnings and jobs happens when the respondent changes jobs between monthly interviews, a relatively common occurrence given Brazil’s large informal labor sector.¹⁰

Given the problems with using changes in earnings, we use transitions to unemployment as the indicator of a negative income shock. Capturing the transitory nature of the shock is only a sufficient step in our estimation strategy. If we find that the father’s move into unemployment affects a child’s entry into the labor force or advancement in school, there are at least two possible explanations for the result. The first is that the income shock is unanticipated and affects children’s work and schooling. The second is that there is some permanent characteristic of the family related to the unemployment that affects work and school transitions. In other words, it is possible that unemployment is negatively associated with children’s work and school outcomes because of some persistent unobserved heterogeneity that drives all of the outcomes. For example, fathers with low ability and many labor force changes may have children with unsteady performance in school and frequent employment transitions, even if there is not a direct causal relationship between one particular shock and the child’s work and school transitions.

We leave it as an empirical question whether unemployment shocks are anticipated. If they are anticipated, then shocks occurring after the school year could affect outcomes during the school year. Since we observe shocks both during and after the school year, we can test directly whether shocks are anticipated. While we will see that shocks appear to be unanticipated, we do allow some flexibility in the sequence of shocks and outcomes. Since we do not expect job loss to be entirely without warning in the very short run (at least one or two weeks), and since the precise timing of transitions may not show up perfectly in our data, we do not require strictly that the head becomes unemployed before the child begins work. If the head becomes unemployed any time in month 2, 3, or 4, and the child enters employment in month 2, 3, or 4, we interpret the head’s employment as causing the child’s transition. On the other hand, we let the data tell us whether unemployment that occurs during the gap between months 5 and 13 has an impact on child transitions in months 2–4.

In our first set of regressions the unemployment variables are constructed with the aim of comparing the impact of an unemployment shock occurring during a given school year with the impact of a shock occurring after the end of the school year. This provides evidence about whether children’s work and school transitions are a response to a transitory, unanticipated shock rather than the result of persistent unobserved heterogeneity. Our control group is male heads who are employed in months 1, 2, 3, 4 and 13 (we sometimes refer to this as “continuously employed in months 1–13,” but it should be kept in mind that we have no data on employment in months 5–12). Our treatment group is male heads who are employed in month 1 but are unemployed at least once in months 2, 3, or 4. If the child was in grade 5 in March 1994 and the father became unemployed in April through June 1994, we examine whether the child started work or left school in April, May, or June, and whether the child was in grade 6 in March 1995. As a robustness test we also consider the case of an ex-post unemployment shock occurring after the school year. Since the shock occurs after month 4, it should have no impact on whether the child became employed between months 1 and 4 as long as the shock was unanticipated and unrelated to persistent heterogeneity with respect to characteristics that drive child employment and schooling. Heads that leave the labor force after month 1 are treated as a separate category since they may not represent the same kind of negative shock as unemployment. Leaving the labor force may be associated with advantageous changes, such as pension eligibility, or with negative changes such as disability. These transitions are dummied out to keep the main contrasts regarding unemployment shocks clean. If unemployment precedes leaving the labor force, the head is categorized as unemployed.

After analyzing the issue of ex-ante versus ex-post shocks in Regression 1, in Regression 2 we use a simpler shock measure that allows us to include interactions with a number of other variables. In these regressions the control group continues to be heads who are employed in every month of observation from month 1 through month 13. The “shock” variable will be defined equal to 1 for all heads who become unemployed between month 1 and month 4, independent of what happens after month 4. The case of ex-post unemployment and leaving the labor force are dropped from the sample to simply the shock versus no-shock comparison.

In summary, the sample is restricted to 10–16-year-olds who are attending school but are not employed in the first interview. This is about 85% of all 10–16-year-olds who can be followed from month 1 to month 13. The male household head (who is either the father or a relative of the child) must be present in the household and must be employed in the first interview. All other children are excluded from the sample. We also control for the sex and age of the child and whether the child is more than two years behind schedule in school. To control for household’s permanent income we include quadratic functions of the age and schooling of the father and the mother. To control for local conditions, we include dummies for the metropolitan area, with São Paulo as the omitted area. We include dummies for month to control for seasonal patterns, and we include dummies for year pairs to capture time trends.¹¹ We omit all cases in which the first four months of interviews do not fall fully within a single school year. Households observed for the first time in September through January are thus excluded from the regressions.

Table 3 gives mean characteristics for the samples used in our regressions. Regression 1 will include the more detailed breakdown of employment transitions, allowing us to analyze whether ex-post unemployment affects child transitions between months 1 and 4. Regression 2 will use the simpler shock variable with interactions for decade, gender, age, and father’s schooling. The sample size for Regression 1 is 106,648 10–16-year-olds for whom the impact of shocks on school and work transitions can be studied over the 1982–99 period. The sample for Regression 2 is about 7,000 observations smaller, the result of dropping cases where shocks occur after the school year or heads leave the labor force. Looking at the means of our dependent variables, shown in the first three rows, about 5% enter employment by month 4, about 1% drop out of school by month 4, and about 29% fail to advance to the next grade in school by month 13. The next rows of Table 4 show that 90% of the male heads are employed in interview rounds 1 through 5 (month 2, 3, 4, and 13), 3.2% become unemployed in month 2, 3, or 4, 2.1% become unemployed after month 4, and 4.7% leave the labor force after month 1.

Table 3.

Sample means for samples used in probit regressions in Tables 4 and 5, children age 10–16 in metropolitan Brazil, 1982–99

	Sample for Regression 1 (N=106,648)		Sample for Regression 2 (N=99,184)
Variable	Mean	Std. Dev.	Mean	Std. Dev.
Dependent variables
Child enters employment by month 4	0.052	0.221	0.051	0.220
Child drops out of school by month 4	0.008	0.089	0.008	0.089
Child fails to advance in school	0.287	0.452	0.285	0.452
Male head’s unemployment transitions, Regression 1
Continuously employed months 1–4 and 13	0.902	0.297
Loses job by month 4	0.032	0.175
Employed months 1–4, unemployed month 13	0.021	0.144
Leaves labor force after month 1	0.047	0.211
Male head’s unemployment transitions, Regression 2
Unemployment shock: Head loses job by month 4			0.034	0.181
Shock * 1990s			0.020	0.142
Shock * (Age 10–14)			0.028	0.165
Shock * Father’s education			0.160	1.076
Shock * Male child			0.017	0.130
Male child	0.495	0.500	0.495	0.500
Child more than 2 years behind in school	0.184	0.388	0.181	0.385
Age of child	12.60	1.91	12.59	1.91
Age of father	42.83	7.23	42.63	7.06
Age of mother	39.14	6.54	39.00	6.43
Years of schooling of child	4.52	2.15	4.53	2.15
Years of schooling of father	6.04	4.45	6.12	4.48
Years of schooling of mother	5.47	4.05	5.53	4.06
Metropolitan area
Salvador	0.072	0.258	0.070	0.256
Belo Horizonte	0.097	0.296	0.095	0.293
Recife	0.070	0.255	0.069	0.253
Rio de Janeiro	0.261	0.439	0.265	0.441
Porto Alegre	0.074	0.262	0.074	0.262
São Paulo	0.426	0.495	0.426	0.494

Note: Both samples are conditional on child enrolled in school and not working in month 1, male head working in month 1

4.3 Probit regression results

Table 4 presents our first set of regressions. Robust standard errors are estimated to correct for potentially correlated error terms across multiple children from a household. Looking at the coefficients on the main unemployment shock variable, we see that an unemployment shock to the male head during the three months after the first interview has a statistically significant positive effect on the probability of entering work by month 4, the probability of dropping out of school by month 4, and the probability of failing to advance to the next grade. The magnitude of these effects is relatively large, as will be discussed below. These are the effects we might predict if households are credit constrained and use children’s time allocation as a way to buffer a transitory income shock. The coefficient on the variable indicating an ex-post unemployment shock (that is, a shock after month 4) is not statistically significant for any of the three outcomes, with point estimates that are much smaller than the coefficients for the ex-ante shock. This is strong evidence that the apparent effect of an ex-ante unemployment shock is not simply due to a correlation between unemployment shocks and unmeasured household characteristics that cause both unemployment for the head and bad outcomes for the child. It also suggests that unemployment shocks occurring several months in the future are not fully anticipated. Looking at the impact of the permanent household characteristics included as regressors in Table 4, we find that males are considerably more likely to enter the labor force and fail to advance in school. We estimate large and statistically significant effects of mother’s and father’s education on all three outcomes. Significant differences across cities and across years are also observed for both sets of outcomes. These effects will be discussed in more detail below when we calculate predicted probabilities.

Table 5 presents a similar set of regressions using a simpler measure of the unemployment shock and including interactions of this shock with several key variables. The shock variable in Table 5 simply compares the control group of male heads who are continuously employed in months 1–4 and 13 with the group that becomes unemployed in months 2, 3, or 4 (whether or not they are employed in month 13). Cases in which heads become unemployed after month 4 and cases in which heads go from employed to out of the labor force are dropped from the regression. The unemployment shock variable is interacted with the male dummy, the 1990s decade dummy, a dummy indicating that the child is age 10–14, and father’s schooling. As in Table 4, we estimate statistically significant positive effects of the unemployment shock on the probability of labor force entry, the probability of leaving school, and the probability of failing to advance to the next grade in school. The interaction with the 1990s dummy is only significant in the dropout regression, where it indicates increased sensitivity of dropout to shocks in the 1990s. For the other two outcomes the point estimates of the interaction indicates less sensitivity to shocks in the 1990s. The interaction on the 10–14 dummy indicates a significantly smaller magnitude of the unemployment shock on the probability that younger children enter employment. The point estimates for the interactions with the male dummy suggest that boys are less affected by unemployment shocks on all three outcomes, although these coefficients are not statistically significant at the 10% level.

Table 5.

Probit regressions with interactions: Impact of unemployment shock on work and school transitions, age 10–16, Brazil PME 1982–1999

Variable	Enter labor force by month 4	Leave school by month 4	Fail to advance to next grade in school
Head’s transitions (continuously employed omitted)
Unemployment shock in month 2–4	0.354 (0.137)**	0.358 (0.179)**	0.225 (0.097)**
Unemployment shock * 1990s	−0.168 (0.105)	0.291 (0.151)*	−0.084 (0.067)
Unemployment shock * age 10–14	−0.203 (0.106)*	−0.230 (0.159)	−0.072 (0.081)
Unemployment shock * father’s schooling	−0.011 (0.017)	−0.051 (0.028)*	0.003 (0.010)
Unemployment shock * male child	−0.003 (0.098)	−0.014 (0.155)	−0.089 (0.055)
Child’s age (age 16 omitted)
Child age 10	−1.283 (0.042)***	−0.420 (0.067)***	−0.155 (0.023)***
Child age 11	−1.154 (0.039)***	−0.400 (0.068)***	−0.102 (0.023)***
Child age 12	−0.921 (0.036)***	−0.279 (0.064)***	−0.065 (0.022)***
Child age 13	−0.722 (0.034)***	−0.281 (0.065)***	−0.018 (0.022)
Child age 14	−0.436 (0.031)***	−0.149 (0.060)**	0.003 (0.023)
Child age 15	−0.201 (0.031)***	−0.115 (0.059)*	0.020 (0.023)
Male child	0.391 (0.020)***	−0.012 (0.036)	0.175 (0.011)***
Child 2+ years behind in school	0.107 (0.022)***	0.517 (0.041)***	0.194 (0.015)***
Father’s age	−0.018 (0.011)	−0.050 (0.019)***	−0.015 (0.007)**
Mother’s age	0.035 (0.013)***	0.034 (0.022)	−0.014 (0.007)*
Father’s age squared/100	0.022 (0.012)*	0.056 (0.020)***	0.016 (0.008)**
Mother’s age squared/100	−0.049 (0.016)***	−0.048 (0.027)*	0.014 (0.009)
Father’s schooling	−0.024 (0.008)***	−0.014 (0.016)	−0.015 (0.005)***
Mother’s schooling	−0.033 (0.009)***	−0.043 (0.017)**	−0.032 (0.005)***
Father’s schooling squared/100	−0.077 (0.057)	−0.048 (0.116)	−0.022 (0.033)
Mother’s schooling squared/100	−0.031 (0.066)	0.188 (0.135)	0.111 (0.036)***
Metro Area (São Paulo omitted)
Salvador	−0.016 (0.030)	−0.113 (0.059)*	0.424 (0.018)***
Belo Horizonte	0.090 (0.025)***	0.158 (0.051)***	0.153 (0.016)***
Recife	−0.018 (0.029)	−0.010 (0.055)	0.303 (0.018)***
Rio de Janeiro	−0.326 (0.029)***	−0.012 (0.054)	0.278 (0.016)***
Porto Alegre	−0.149 (0.029)***	0.141 (0.053)***	0.275 (0.017)***
Year (1982 omitted)
Year 1984	−0.081 (0.036)**	−0.070 (0.063)	−0.125 (0.023)***
Year 1986	0.015 (0.035)	−0.033 (0.063)	−0.003 (0.023)
Year 1988	−0.096 (0.040)**	−0.047 (0.071)	−0.063 (0.025)**
Year 1990	−0.078 (0.039)**	−0.134 (0.068)**	0.047 (0.024)*
Year 1992	−0.279 (0.042)***	−0.068 (0.073)	−0.063 (0.025)**
Year 1994	−0.266 (0.039)***	−0.311 (0.073)***	−0.115 (0.025)***
Year 1996	−0.231 (0.040)***	−0.401 (0.082)***	−0.228 (0.025)***
Year 1998	−0.307 (0.043)***	−0.234 (0.083)***	−0.263 (0.027)***
Month of first observation (February omitted)
March	−0.058 (0.038)	0.009 (0.070)	0.005 (0.023)
April	−0.066 (0.037)*	−0.11 (0.072)	0.007 (0.023)
May	−0.020 (0.037)	−0.133 (0.072)*	−0.055 (0.022)**
June	−0.013 (0.037)	−0.065 (0.070)	−0.052 (0.022)**
July	0.006 (0.036)	−0.024 (0.068)	−0.064 (0.023)***
August	0.018 (0.036)	−0.028 (0.067)	−0.058 (0.022)***
Constant	−0.911 (0.290)***	−1.482 (0.505)***	0.217 (0.176)
Number of Observations	99,184	99,184	99,184

Note: Robust standard errors in parentheses; Significance levels:

^*=.10,

^**=.05,

^***=.01 Sample is conditional on child in school and not working in month 1 and male head working in month 1.

The interactions with father’s education are included as a test of whether poor households are more affected by unemployment shocks, treating father’s education as an indicator of permanent income. If credit constraints play a role in causing a link between unemployment shocks and changes in children’s time allocation, then households with higher permanent income may be less affected by the shock. Although there is good reason to think that poor households would be less able to buffer a shock, these interaction terms are only statistically significant for the dropout regression. Although the negative point estimates in the other two regressions are in the expected direction, we cannot reject the hypothesis that there is no interaction between shocks and the schooling of the head. We have experimented with other measures of household socioeconomic status, including measures of month 1 income, and continue to find insignificant interactions with the shock variable in the regressions for entering work and failing to advance in school. It is possible that the low frequency of shocks makes it difficult to precisely identify this interaction effect. It is also possible that even these better off households are seriously affected by an unemployment shock, with young people becoming more likely to enter employment and with disruptions to school performance.

4.4 Robustness checks

Our results are robust to a variety of changes in specification. The results in Table 4 and 5 do not use the PME earnings measures because of our concern about missing values, measurement error related to hyperinflation, and the problem of incorrect earnings reports in the case of job changes. Using earnings does not significantly change the results, however. We have added the logarithm of the male head’s earnings in month 1 as an additional control in the regressions shown in Table 5. This lowers our sample size about 10% due to missing incomes, but has very little impact on the coefficients or standard errors on our shock variable in any of the three regressions. We have also created an alternative shock measure in which heads who experience a 50% decline in earnings between months 1 and 4 are also considered to have experienced a shock, increasing the percentage experiencing a shock from 4% to 7%. We estimate somewhat smaller, but still statistically significant, impacts of the shock on our three outcomes, suggesting that income changes alone are not as disruptive as job loss. Interacting this broader shock with month 1 income, we still find no evidence that shocks have smaller impacts in higher income households.

4.5 Predicted impact of shocks

Table 6 illustrates the magnitude of the effects of unemployment shocks implied by our regressions in Table 5. The baseline used for simulating the impact is a 16-year-old female in São Paulo in February 1982 who is not behind in school and whose parents have zero schooling. The first line shows that her predicted probability of entering work, conditional on being enrolled in school and not working in month 1, is 24.2% if the male head remains continuously employed. If the head loses his job in month 2, 3, or 4, the probability she enters employment rises to 36.5%, an increase of over 50%. Her probability of leaving school between months 1 and 4 more than doubles from 2.3% to 5% if the head becomes unemployed. The impact on school advancement is also substantial. In the absence of an unemployment shock she has a 31.1% chance of failing to advance to the next grade. This rises to 39.4% if he loses his job, an increase of 27%.

Table 6.

Impact of unemployment shock to male head on child’s work and school transitions

Case	Predicted probability with no employment shock			Predicted probability with employment shock			Percentage increase due to employment shock
	Enter labor force	Drop out of school	Fail to advance grade	Enter labor force	Drop out of school	Fail to advance grade	Enter labor force	Drop out of school	Fail to advance grade
	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)
Case 1: Baseline (see note for definition)	0.242	0.023	0.311	0.365	0.050	0.394	51%	121%	27%
Baseline, but with:
Case 2: Child male instead of female	0.379	0.022	0.375	0.517	0.047	0.427	37%	116%	14%
Case 3: Parental schooling 8 years instead of 0	0.110	0.009	0.208	0.192	0.022	0.278	74%	149%	34%
Case 4: Year 1998 instead of 1982	0.157	0.013	0.224	0.206	0.056	0.269	31%	344%	20%
Case 5: Child age 12 instead of 16	0.053	0.011	0.288	0.071	0.016	0.342	35%	39%	19%
Percentage difference from
Case 1:
Case 2: Child male instead of female	57%	−3%	21%	42%	−5%	8%	−28%	−5%	−48%
Case 3: Parental schooling 8 years instead of 0	−54%	−60%	−33%	−47%	−56%	−30%	46%	22%	26%
Case 4: Year 1998 instead of 1982	−35%	−44%	−28%	−44%	12%	−32%	−39%	184%	−26%
Case 5: Child age 12 instead of 16	−78%	−50%	−7%	−81%	−69%	−13%	−31%	−68%	−30%

Note: Baseline is 16 year-old female in São Paulo, father age 45, mother age 40, father and mother with zero schooling, father continuously employed between months 1–4 and 13. Based on probit regressions with interactions in Table 5.

The remaining rows of Table 6 consider other simulated examples to show how the impact of the shock varies with alternative baseline assumptions. Row 2 shows the case in which other baseline characteristics are kept the same but the child is male instead of female. Looking down column 1, boys are 57% more likely than girls to start working and 21% more likely to fail to advance in school in the absence of a shock. Looking across the row for Case 2, the predicted probability of a 16-year-old boy entering work is 38% if the head remains employed, rising to 52% if the head loses his job. The probability of dropping out rises from 2.2% to 4.7%, and the probability of failing to advance a grade rises from 38% to 43%. The percentage impact of the shock is slightly smaller for boys than girls based on the point estimates, although it should be recalled from Table 5 that the male interaction terms were not statistically significant.

Case 3 in Table 6 returns to the original baseline characteristics, but changes both parents’ schooling from 0 years to 8 years. Looking down column 1, the probability of labor force entry falls from 24% to 11% with this increase in parental schooling. Children with better educated parents are also much less likely to drop out of school and much more likely to advance a grade in school. Looking across the row for Case 3, an unemployment shock to the head increases the probability of entering work from 11% to 19% when both parents have 8 years of schooling. The probability of dropping out of school more than doubles and the probability of failing to advance in school increases 34% in response to an unemployment shock. So while children with better educated parents have significantly lower probabilities of bad outcomes, we find no evidence that these children are less affected by unemployment shocks. This is especially surprising given the fact that we are looking at short-term shocks that sometimes last only one or two months.

Case 4 in Table 6 changes the year used for predicted values from 1982 to 1998. This causes the predicted probabilities of entering employment, dropping out of school, and failing to advance in school to fall considerably. The large secular changes documented in Figure 1 and Table 1 continue to be evident after controlling for both permanent and transitory household variables. The impact of the unemployment shock on entering work and failing to advance in school is smaller in 1998 than in 1982, but is still quite high, with an unemployment shock to the head causing a 31% increase in the probability of a child entering work and a 25% increase in the probability that a child fails to advance in school, given the other baseline characteristics. The impact of the shock on dropping out of school is larger in 1998, although the levels are low. Only 1.3% of 16-year-old girls are predicted to drop out of school between month 1 and month 4 in 1998 if the head remains employed, rising to 5.6% if the head becomes unemployed.

Case 5 in Table 6 changes the age of the child from 16 to 12. Given other baseline characteristics, the predicted probability of a 12-year-old girl entering employment is only 5.3% if the head remains employed, rising to 7.1% if the head loses his job. This is an increase of 35% in the probability of entering employment, somewhat smaller than the effect for a 16-year-old. The impact of the shock on school advancement is also smaller for a 12-year-old than it is for a 16-year-old, consistent with the smaller effect on employment.

The overall picture from the predicted values shown in Table 6 is that an unemployment shock to the male head of household has substantial negative effects on children in Brazil. These shocks increase the probability that children enter the labor force, increase the probability that they leave school during the school year, and decrease the probability that they advance in school. It is interesting to compare the effect of a short-run shock with the effect of more permanent household characteristics. Put in this perspective, the effects of the shocks can be seen to be very large.

Taking the same baseline child used in Table 6, the 51% increase in the probability of entering employment that results from the head becoming unemployed is about the same as the effect of changing the head’s education from 8 years to 0 years. Interestingly, the 27% impact of the shock on the probability of failing to advance in school is also very similar to the effect of changing the head’s schooling from 8 years to 0 years.

4.6 Long-term impacts of shocks

The shocks we analyze are short-term shocks. The unemployment spell may last as little as one month, although some impact persists in the form of lower earnings. We have seen that these short-term shocks lead to substantial impacts on child work and schooling in the months immediately during and after the shock. An important policy question is whether these short-run adjustments in children’s time allocation have long term consequences. A key point in this regard is that failing to advance a grade in school, the most common negative outcome in our results, has long-term consequences almost by definition. Grade repetition is an important predictor of ultimate schooling attainment in Brazil. Students who drop an additional year behind in grade for age will face additional problems at older ages, as indicated by the negative impact of being behind in school in our regression results. It is interesting to contrast our results with those of Jacoby and Skoufias (1997). They find that unanticipated income shocks reduce school attendance immediately after the shock, but conclude that eliminating this effect would have only modest effects on children’s ultimate human capital attainment. We find, on the other hand, that very few children actually drop out of school during the school year in which the shock occurs, but significant percentages fail to advance to the next grade. This is partly a reflection of the historically high levels of grade repetition in the Brazilian school system, with a relatively modest adjustment in short-run time allocation potentially having a substantial impact on progress through school.

While we would like to get a better direct estimate of the longer-term impact of unemployment shocks, the combination of the short PME panels and the rarity of the unemployment shocks make it difficult to learn much in our data. The data do indicate that children who experienced a shock in months 1–4 are more likely to be working and less likely to be in school in month 13. In many cases these children still have an unemployed head, however, so it is difficult to distinguish the persistent effect of a shock in the prior year from the ongoing impact of the household’s poor economic condition. If we limit the analysis to cases in which the head is back at work in month 13, the effect of the shock is not statistically significant, but the small sample size makes this a weak test of the persistent impact of the shock.

While the estimated effects of unemployment shocks are quite large when compared to effects of large changes in permanent household characteristics, it is important to note that the effects of unemployment shocks per se appear to play a relatively small role in explaining the levels of work and school transitions and their changes over time. As shown in Table 1, about 4% of male heads experience an unemployment shock, rising to around 7% in 1998. Given the predicted values in Table 6, having 7% of heads becoming unemployed in a given 4-month period versus 0% of heads becoming unemployed implies a difference in the proportion of children who enter the labor force of 25.1% versus 24.2%. So while there is a large impact on children in households that experience these shocks, the low prevalence of the shocks means that their elimination in and of itself would have only a modest effect on overall child labor. On the other hand, it is important to recognize that the unemployment shock we are analyzing can be thought of as a proxy for more general negative income shocks. While it is relatively uncommon for male heads to become unemployed in a given four month period, large unexpected income shocks may occur for many other reasons. Our results suggest that these shocks could have significant impacts on child labor and schooling.

It is also worth noting that these probabilities can translate into much larger probabilities of shocks occurring over the full range of schooling years. For simplicity, suppose that the probability of the head becoming unemployed is independent across four-month periods and across years. If 95% of children experience no shock in one four-month school period, then about 90% experience no shock over two such periods, roughly representing one school year. Over ten years of schooling the probability of experiencing no shock would be 0.9¹⁰=0.35, implying that about 65% of children would experience a shock at some point in their schooling. Given the large impact of these shocks on the probability of entering work and falling behind in school, and given the potential for further long-term impact from falling behind in school, the effects we estimate imply substantial costs of short-term unemployment shocks on schooling attainment.

Finally, we note that child labor declined significantly in the 1990s, in spite of an increase in the prevalence of unemployment shocks. Based on Table 1, the mean probability of a male head becoming unemployed in a given four month period in the 1980s was 4%, with the probability increasing to 4.6% in the 1990s. While this increase in and of itself should have increased child labor and decreased progress in school, other factors clearly offset these effects and led to large declines in child labor and improvements in school outcomes. Factors working in this direction include increased parents’ education, reduced numbers of siblings, and reductions in the size of the school-age population beginning around 1990 (Lam and Marteleto, 2005). The 1990s also saw increased investments in education and the introduction of conditional grant programs such as Bolsa Escola and the Program to Eradicate Child Labor (PETI). Although there is evidence that these programs may have increased schooling and reduced child labor, they were introduced too late to explain the large improvements of the early 1990s (Cardoso and Souza, 2004).

5. Conclusion

The rotating panel structure of Brazil’s Monthly Employment Survey provides a unique opportunity to analyze the impact of economic shocks on children’s schooling and employment transitions over almost two decades. The PME data indicate relatively high levels of employment for 10–16-year-olds in the early 1980s in metropolitan Brazil, with considerable short-run volatility. About 20% of 14-year-old boys were working in a given month in 1982, with about 10% of non-working boys entering work each month and about 20% of working boys leaving work each month. Employment levels for 10–16-year-olds dropped substantially in the 1990s, driven both by decreasing probabilities of entering employment and increasing probabilities of leaving employment. Taking advantage of the PME’s longitudinal structure, we estimate significant impacts of household economic shocks on the probability that children enter employment, leave school, and fail to advance in school. The shock we analyze – the male household head becoming unemployed between months 1 and 4 of the survey – is a relatively rare event, occurring to about 4% of male heads in any given month. With our sample size of over 100,000 10–16-year-olds we are nonetheless able to estimate statistically significant impacts of the shocks. The magnitudes of the estimated effects are large. For a 16-year-old girl who was in school and not working in São Paulo in 1982, we estimate that the male head becoming unemployed increased her probability of entering the labor force in a 4-month period from 24% to 37%. Her probability of failing to advance a grade in school increased from 31% to 40%. Shocks occurring after the school year do not have significant effects on the outcomes observed during the school year, suggesting that these results are not being driven by unobservable characteristics of households that would have resulted in poorer child outcomes even in the absence of shocks.

Our results suggest that Brazilian youth adjust their school and labor force behavior in response to an unexpected, transitory economic shock to the household, with their increased labor force activity linked to a decline in school performance. This implies that programs that improve the ability of households to buffer short-run economic shocks may have beneficial impacts on investments in human capital. While the large impact of unemployment shocks on youth outcomes should be of concern to policy makers, it is also important to note that child and youth employment declined substantially in Brazil over the two decades analyzed in this paper. Most of these declines took place in the 1990s, a decade in which adult unemployment actually increased. Factors such as steady increases in parental schooling more than offset the effect of rising unemployment rates, suggesting that improvements in long-run economic conditions are also important in driving employment and schooling outcomes of young people.

Although the shock we study in this paper – the male head becoming unemployed in a given four-month period – occurs to a relatively small fraction of households, our shock measure can be thought of as a proxy for more general negative income shocks. Since unexpected income variation is not unusual in Brazil, our results suggest that short-run income volatility has substantial negative effects on young people. If households experience frequent short-run income fluctuations, the results can cumulate to have a large impact on schooling attainment.

Appendix

This appendix provides an overview of our data, including an analysis of sample attrition. The Pesquisa Mensal de Emprego (PME), collected by Brazil’s national statistical agency, the Instituto Brasileiro de Geografia e Estatística, is Brazil’s primary source of information on employment. It is organized with a panel structure similar to the United States Current Population Survey (CPS). Households are surveyed once per month for four consecutive months, rotate out of the sample for eight months, then rotate back in for four months. Unlike the CPS, the PME operates with two-year rotation windows in which most households enter the sample in even-numbered years, completing their second year in the survey in odd-numbered years. Beginning in February 1982 the PME includes questions on earnings, schooling, and employment for everyone in the household aged 10 and over. Our analysis is based on PME surveys in the period bracketed by February 1982 and August 1999. We only use households that first enter the sample between February and August in order to focus only on months during the regular school year (February – November). During the period we consider the PME covered Brazil’s six largest metropolitan areas – São Paulo, Rio de Janeiro, and Belo Horizonte in the Southeast; Porto Alegre in the South; and Recife and Salvador in the Northeast – surveying 4,500 to 7,500 households in each metropolitan region.

Like many national employment surveys with rotating panel designs, the PME’s panel structure is designed primarily to reduce volatility in estimates of month-to-month and year-to-year changes in unemployment. It is not designed explicitly for analyzing longitudinal transitions of individuals. Dwellings are the focus of the sample design. Households only remain in the sample if they continue to live in the sampled dwelling. Public release versions of the data are not designed for longitudinal analysis, although they do contain household identification numbers that make it possible to link households across months. Individuals in households must be linked using month and year of birth, a process that provides relatively straightforward matching for most individuals. We impose a set of filters on matches of individuals across months, using variables such as sex, month/year of birth, and schooling. As shown below, sample attrition is relatively high in the PME over the 16-month period that households theoretically are included in the sample. Since linking individuals across months is critical to our analysis, we analyze the magnitude and selectivity of sample attrition in Table A1.

Table A1 presents summary statistics for children aged 10–16 using alternative data restrictions. Sample A is the set of all 10–16-year-olds who are related to the household head who are ever observed in a month corresponding to the first month a household enters the PME sample. As shown in Table A1, we observe 280,535 such individuals between March 1982 and August 1999.¹² Sample B adds the restriction that the head of household in month 1 is male, a restriction required for our analysis of the impact of a male head becoming unemployed. As seen in Table A1, 82% of the children in Sample A resided with a male household head in month 1. Sample C adds the restriction that the child is observed in the sample for the first five rounds of the PME for their rotation group – months 1, 2, 3, 4, and 13. About 69% of children in Sample A meet this test. Sample D adds the restriction that both the child and the head are observed from month 1 through month 13, restrictions required for our analysis of children’s labor force entry and advancement in school. This is about 56% of the sample of all children in Sample A.

As shown in Table A1, over 30% of our initial sample of children disappears before the month 13 interview. This is similar to attrition rates estimated for the U.S. CPS by Peracchi and Welch (1995), who found that 35% of individuals could not be matched over the one year period 1990 to 1991. Given attrition of this magnitude, it is important to consider the extent to which the sample that remains is different than the sample of all children. Given the PME’s design, households are lost from the sample if they move residences, a potential source of selection bias that may be related to the outcomes we are studying. No information is provided on why households disappear from the sample. While overall attrition is high, it is less disturbing in a survey like the PME than it would be in a survey more explicitly designed to follow households longitudinally. This is because much of the attrition occurs for reasons unrelated to household characteristics. For example, we lose a large number of matches due to occasional changes in sample design, such as a 25% sample size reduction in 1986. Problems such as coding inconsistencies across years sometimes make it difficult to match households for reasons that have nothing to do with household characteristics.

While we can never know whether households that disappear from the sample were more likely to experience an unemployment shock, we can analyze attrition with respect to characteristics observed in month 1. Table A1 analyzes the extent to which sample attrition is non-random using three month 1 variables directly relevant to our analysis – child’s schooling, child’s employment, and male head’s employment. Table A1 shows that there are relatively small differences in means for these variables across the sub-samples. Children observed continuously from month 1 to month 13 (Sample C) have mean month 1 schooling of 4.51 years, compared to 4.36 years for the sample of all children observed in month 1. Restricting to the sample in which both the child and head are observed from month 1 to month 13 (Sample D), 9.8% of 10–16-year-olds were working in month 1, compared to 11% in the sample of all month 1 children. As expected, children who remain in the sample are less likely to have been working in month 1 and have higher schooling for both the child and the head. The differences between samples are quite small, however, suggesting that most of the attrition is not selective with respect to these characteristics. Comparing the father’s characteristics in Sample B and Sample D, mean schooling and the percent employed are very similar in the sample observed in all five months compared to the sample observed in month 1.

The last two rows of Table A1 provide additional evidence regarding sample attrition bias. Sample E imposes the restrictions on initial conditions we use for our regressions, requiring that children are enrolled in school and not working in month 1, and that the father is working in month 1. Sample E includes all such children observed in our data, a total of 165,572 children. Sample F includes only the children that satisfy the initial conditions, are observed over the entire period from month 1 to month 13, and have non-missing data for both the mother and the father, a total of 99,184 children. About 60% of the children who meet the first-period restrictions are also observed in month 13, allowing us to determine whether they have advanced to the next grade in school. Comparing sample means between Sample E and Sample F, we see once again that there is surprisingly little selectivity on two key observable characteristics – child’s schooling and head’s schooling. The sample observed over the full period from month 1 to month 13 has slightly higher mean schooling for both the child and the head. The differences are only around 2%, however, suggesting that the sample we use for our analysis looks quite similar to the full sample of children, at least in terms of variables we can observe.