Precisely Timed Spatiotemporal Patterns of Neural Activity in Dissociated Cortical Cultures

Abstract

Recurring patterns of neural activity, a potential substrate of both information transfer and transformation in cortical networks, have been observed in the intact brain and in brain slices. Do these patterns require the inherent cortical microcircuitry of such preparations or are they a general property of self-organizing neuronal networks? In networks of dissociated cortical neurons—which lack evidence of the intact brain’s intrinsic cortical architecture—we have observed a robust set of spontaneously repeating spatiotemporal patterns of neural activity, using a template-matching algorithm that has been successful both in vivo and in brain slices. The observed patterns in cultured monolayer networks are stable over minutes of extracellular recording, occur throughout the culture’s development, and are temporally precise within milliseconds. The identification of these patterns in dissociated cultures opens a powerful methodological avenue for the study of such patterns, and their persistence despite the topological and morphological rearrangements of cellular dissociation is further evidence that precisely timed patterns are a universal emergent feature of self-organizing neuronal networks.

The means by which information is reliably stored, propagated, and processed within biological neural networks is unknown, though several candidate mechanisms exist (Vogels et al., 2005). Of these theories, perhaps the most influential is that of Donald Hebb, who proposed information storage and processing via dynamically linked assemblies of cells, formed through simple activity-dependent learning rules (Hebb, 1949). Spontaneously recurring spatiotemporal patterns of neuronal action potentials, variously referred to as “motifs” (Ikegaya et al., 2004), “sequences” (Nadasdy et al., 1999), “synfire chains” (Abeles, 1991), and “information trains” (Frostig et al., 1984), might be an observable and quantifiable instantiation of Hebb’s proposed cell assemblies. Such precisely timed patterns of neuronal action potentials are well-documented in vivo in various cortical structures (Abeles et al., 1993, Nadasdy et al., 1999, Ikegaya et al., 2004, Luczak et al., 2006), and have also been shown in neocortical slices (Ikegaya et al., 2004). These preparations retain the brain’s inherent microcircuitry, comprised of a specific laminar and columnar architecture ostensibly critical for normal function (Mountcastle, 1998). But is such structure crucial for the brain’s elaboration of precisely timed activity patterns like those observed above?

Computational models of large-scale neuronal networks suggest that spontaneously recurring patterns of action potentials, termed “polychronous groups” by Izhikevich (2006), are an emergent property of loosely structured networks with realistic conduction delays governed by spike timing–dependent plasticity (STDP), and thus are not reliant on the brain’s intrinsic cortical circuitry (Izhikevich et al., 2004, Izhikevich, 2006). But to our knowledge, the modeling work’s conclusions have not been verified with unstructured networks in vitro. Is the Izhikevich model correct in implying that precisely timed spatiotemporal activity patterns are produced independently of the brain’s inherent cortical architecture?

To directly answer the above questions, we employed a well-established template-matching algorithm (Abeles and Gerstein, 1988) successfully utilized in two of the above-mentioned studies describing precisely timed activity patterns, one in vivo (Nadasdy et al., 1999) and one in vitro in brain slices (Ikegaya et al., 2004). This algorithm was applied to recordings of spontaneous action potentials from highly interconnected networks of dissociated cortical neurons, cultured on multielectrode arrays (Gross, 1979, Pine, 1980, Taketani and Baudry, 2006). Such neuronal networks are well studied and their constituent neurons physiologically normal, but there is no evidence that dissociated networks retain or reestablish the brain’s laminar and columnar microstructure (Dichter, 1978, Banker and Goslin, 1998). Moreover, the biological network’s size (~50,000 cells) and diameter (~5 mm) approximates that used in the modeling study (100,000 model cells and an 8 mm radius) (Izhikevich et al., 2004). Finding comparable patterns in large networks of cultured dissociated cortical neurons to those found in vivo and in slices will provide strong evidence that such patterns are a general property of self-organizing neural networks and not dependent on the brain’s intrinsic cortical microcircuitry, as it is constructed through the organism’s development and experience.

Experimental Procedures

Cell culture

The data analyzed in this paper derive from a subset of the recordings described in Wagenaar et al. (2006b), where full details of the cell culture and recording conditions may be found. Briefly, neocortex from embryonic (E18) Wistar rats, excluding the hippocampal anlage, was dissected according to NIH protocols, and dissociated in papain followed by trituration. Approximately 50,000 cells were plated in a 5 mm diameter droplet on top of a multielectrode array (MEA) containing 59 electrodes arranged in a rectangular grid with 200 μm spacing. Cultures were maintained at 35 °C, 9% O₂, and 5% CO₂ in a DMEM-based medium for up to two months, which was partially replaced periodically. To avert infection and maintain the culture’s osmolarity by preventing evaporation, the MEA dishes were covered with gas-permeable, water-impermeable Teflon membranes (Potter and DeMarse, 2001). Daily, 30 minutes of spiking activity was recorded using the MEA, inside the incubator where the cultures were maintained.

Extracellular recording

The MEA’s signals were amplified and sent to a data acquisition computer, using a MultiChannel Systems MEA60 preamplifier and MC_Card A/D board (MultiChannel Systems, Reutlingen, Germany), sampling at 25 kHz. Data acquisition and visualization was performed by our lab’s custom-written software package, MeaBench¹ (Wagenaar et al., 2005a). Extracellular recordings were obtained from 59 electrodes on each MEA and action potentials (i.e., spikes) were detected using a threshold-based detector as upward or downward excursions beyond 4.5× the estimated RMS noise (Wagenaar et al., 2005a). Spike waveforms were stored and used to remove duplicate detections of multiphasic spikes. A variety of spike waveform shapes was observed on many electrodes, but distinct clusters in waveform space, as determined using the wavelet-based method of Quiroga et al. (2004), were typically not seen, presumably because many cells contributed to the spike train at each electrode in these dense cultures, especially during bursts. Also during bursts, overlapping waveforms were a common occurrence, making spike sorting problematic. Thus, all results in this paper are based on unsorted multiunit data. Recordings were ultimately reduced to a series of ordered pairs, consisting of the precise time of each detected action potential’s peak and the electrode on which it occurred.

Template-matching algorithm

The template-matching algorithm used here is identical to that in Ikegaya et al. (2004) and Nadasdy et al. (1999) and based on that of Abeles and Gerstein (1988). Briefly, a 200 ms template is constructed for each detected action potential. For the dataset’s i^th spike occurring at time t_i on electrode e_i, a template temp_i is constructed as a vector containing the latencies and electrode numbers of all spikes occurring within 200 ms of t_i. That is, temp_i = <t_j − t_i, t_k − t_i, … ; e_j, e_k, … >, where t_j, t_k, … are less then t_i + 200 ms but greater than t_i. Each template from a spike detected on electrode e_i is then compared to all other templates from the same electrode. A match is declared when two latency/electrode pairs are identical within some specified precision (e.g., 1 ms), meaning that at least three matching spikes have recurred with a variation in firing times more tightly bound than the specified precision. These matches are later sorted into sequence families (see below). The matching process is repeated for all templates on all electrodes, resulting in the analysis of all the dataset’s spikes (>10,000/min of recording). It should be noted that templates with reference spikes occurring within the specified precision of a prior template’s reference spike (on the same electrode) are not included in the analysis, since this will result in many trivial matches.

The method, as described, would overestimate the number of sequences present in each dataset. As an example, say that a template consisting of spikes on electrodes 5, 10, 34, 7, and 8 recurs in a precise temporal order five times. The first run of the template-matching algorithm would find four matches (i.e., repetitions) of the pattern as it serially searched through the data. When the algorithm eventually repeats with the second instance of the pattern as its reference template, it will find an additional three matches, and so on. Moreover, the algorithm would experience the same problem as it searched through subsets of the pattern’s repetitions (e.g., {10, 34, 7, 8} and {34, 7, 8}). To alleviate this overcounting and to exactly replicate previous studies’ implementations of the template-matching algorithm, matched spikes are removed from the dataset during each iteration of the algorithm, while mismatched spikes are retained, as in Ikegaya et al. (2004). Overcounting is thus prevented, while every spike is still analyzed at least once. As an added benefit, such spike removal results in a significantly faster implementation by reducing the dataset during each cycle of the algorithm. It took roughly 30 minutes to analyze one minute of multielectrode data on a standard desktop computer with MATLAB 7.2 (MathWorks, Natick, MA).

When several sequences match a given reference template, it is unclear a priori whether identical or different subsets of the template’s spikes are matched. Due to this limitation of the algorithm, matches to one template form a collection of distinct subtypes or sequence families (e.g., one set of matches may be to spikes 2 5, while another may be to spikes 6 9, leaving only one spike, the trigger spike, in common between the two subtypes). Because we wish to identify repeating sequences of action potentials, and not repeating abstract templates, we conservatively collected instances of each sequence family separately by assigning a different sequence identification number to each family. Henceforth, sequence family will refer collectively to all instances of the same identified recurring spatiotemporal pattern of neural activity (i.e., all matches of a given subtype), and sequence repetition will refer to the individual occurrences of these families.

Shuffling

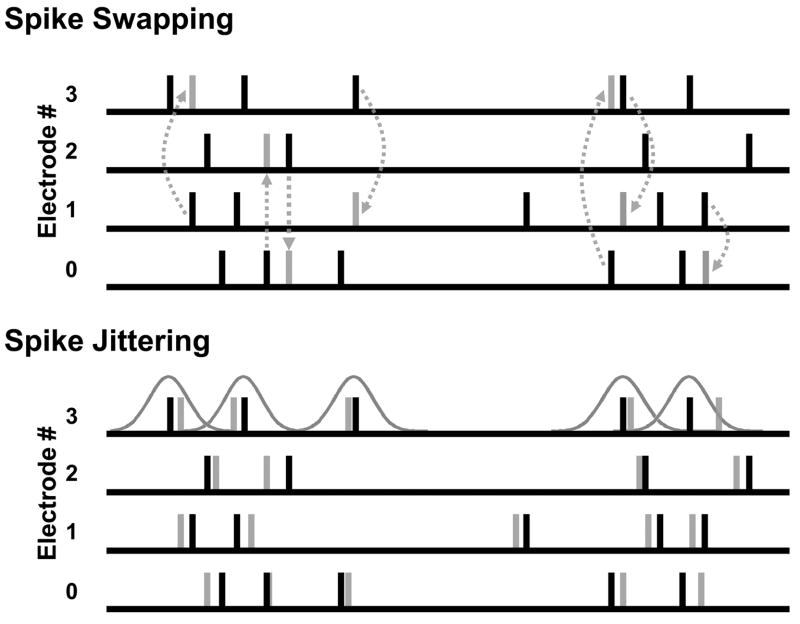
To evaluate the significance of our results, we ran the template-matching algorithm on shuffled versions of the same one-minute dataset and compared the number of identified sequences obtained from each. Two methods of shuffling were used, spike swapping and spike jittering (Fig. 1). Spike swapping can be thought of as exchanging the electrode numbers of two randomly selected spikes, and repeating this process throughout the entire dataset. Formally, spike swapping takes the length N vector of electrode numbers from the dataset, where N is the total number of spikes, and then assigns a new electrode number from this vector by sampling without replacement. Thus, the dataset retains identical spike times after shuffling and an identical distribution of spikes per electrode per recording, but presumably lacks any biologically-induced correlations between spike times.

Fig. 1.

Shuffling methods. (Top) Spike swapping preserves the dataset’s spike-timing distribution and electrode distribution. Note that swapping can be pair-wise (i.e., between two electrodes, as demonstrated with the two swaps to the left) or higher-order (as demonstrated with the three-wise swap to the right). (Bottom) Spike jittering preserves population modulations in firing rate and each electrode’s ISI distribution approximately, and the dataset’s electrode distribution exactly.

While spike swapping preserves the number of spikes per electrode and the overall timing of spikes, it fails to preserve each cell’s interspike interval (ISI) distribution, thereby distorting its firing rate. Shuffling methods that fail to respect local firing rate fluctuations may in some cases lead to an overestimation of the significance of observed patterns (Oram et al., 1999), so in addition to spike swapping, we employed spike jittering, wherein each spike’s time was perturbed by a random amount drawn from a Gaussian distribution with mean zero and a small standard deviation (this paper used 2 and 20 ms, depending on the experiment). Because the perturbing Gaussian distribution has a mean of zero, the ISI distribution for each cell remains closely preserved. Similarly, population modulations in firing rate are on average unchanged and the number of spikes per cell remains identical to the unshuffled data.

Pattern persistence

To determine the persistence of observed sequences, spike trains recorded in the ten minutes following the previously analyzed episodes were scanned exhaustively for a subset of the most frequently recurring patterns discovered in the original data. Unlike the template-matching algorithm above, this round of pattern finding did not discard matched spikes. The number of observed sequence repetitions in actual data at subsequent times was compared to the number of repetitions observed in shuffled versions of the same data. Twenty shuffles were used for each dataset: if the actual data contained more sequence repetitions than all 20 shuffled datasets, we concluded that these sequences occurred significantly more often than chance with P < 0.05.

Statistical Methods

The Wilcoxon signed-rank test was used to calculate significance by comparing the number of detected sequence families in each actual dataset to the number of detected sequence families in a single shuffled version of the same dataset. This captures the likelihood of all 10+ cultures having more sequence families than their shuffled counterparts, which is not expected by chance. Further, p-values were calculated directly for the three most frequently recurring sequence families in each culture by generating multiple shuffled datasets (see Pattern Persistence section above). When multiple comparisons were necessary, the Bonferroni adjustment, the most stringent correction for multiple comparisons (Bland and Altman, 1995), was used to protect against type I errors.

Results

Thirty minutes of spontaneous activity was recorded from each of 12 cultures, aged 21 DIV, derived from four separate platings (Wagenaar et al., 2006b). From these datasets, one minute (arbitrarily the 16^th minute of recording time) was examined with a template-matching algorithm (see Methods) to determine the number of repeating sequences. The algorithm used a precision of 1 ms and a window size T = 200 ms, following Nadasdy et al. (1999). On average, 2993 ± 1077 unique sequence families were found in each recording, repeating 2.01 ± 0.1 times/min (range 2–6), consisting of 4.3 ± 6.3 spikes (range 3–475) and spanning 125 ± 55 ms. Several example sequences are shown in Fig. 2.

Fig. 2.

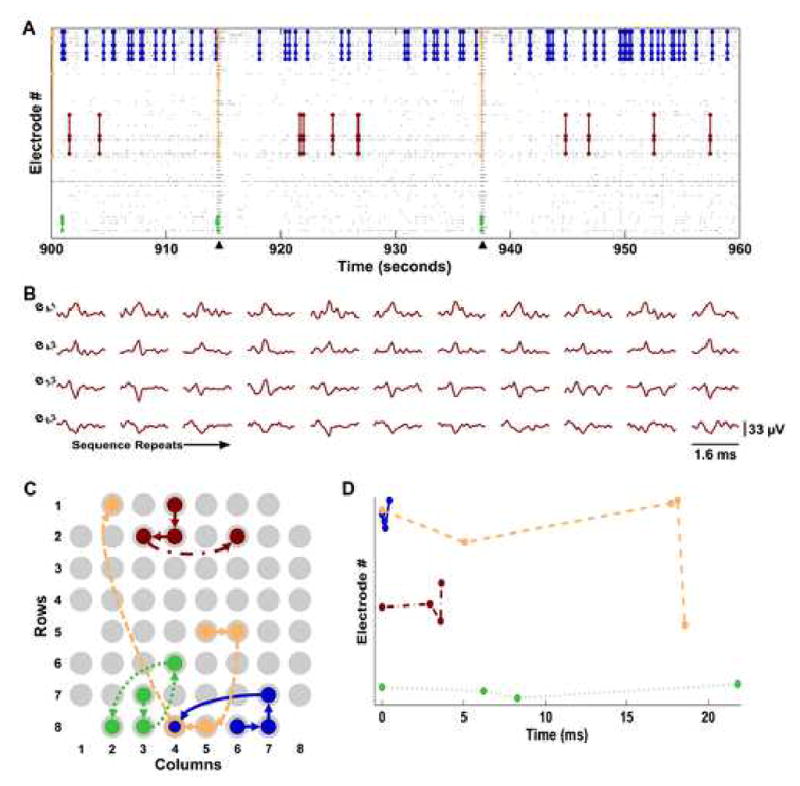
Precisely timed sequences of neural activity repeat spontaneously in networks of dissociated cortical neurons. (A) Raster plot showing sequence repetitions. Each gray dot represents an action potential detected on a specific electrode. Sixty-two instances of a repeating four-spike sequence are traced in dark blue lines, seven instances of a five-spike sequence in orange, four instances of a four-spike sequence in green, and eleven instances of a three-spike sequence in red (fewer instances may be visible due to overlap when displayed at this resolution). Arrowheads indicate population bursts. In this panel, the ordering of electrodes is not related to MEA geometry, but was chosen to avoid the overlapping of sequence traces. (B) Action potential waveforms for the eleven repetitions of the red sequence in A. Each row shows the waveforms recorded from one electrode and each column is one sequence repetition. Electrode labels indicate the column, row location of the electrode on the MEA (see panel C). (C) Spatial propagation of each sequence shown in A. Each electrode of the MEA is represented by a light gray circle. The dark blue solid arrows show the propagation of the dark blue sequence from A. The red dot-dashed arrows represent the red sequence depicted in panels A and B. The orange dashed arrows represent the orange sequence depicted in panel A and the green dotted arrows represent the green sequence. Arrows indicate the sequence’s origin and direction of propagation. The empty space at column 1, row 5 is the approximate location of the ground electrode. (D) The time course of the four sequence families, using the same color coding as panels A–C and the same line style as C. Electrode ordering as in panel A. These patterns were detected with a template-matching algorithm using a window size T = 200 ms and a precision of 1 ms (see Methods).

To demonstrate that the finding of precisely timed sequences was not limited to dissociated cultures at a particular developmental stage, we examined cultures aged 35 DIV as well. Using 11 cultures from three separate platings (8 from the previously analyzed 21 DIV cohort and three additional cultures), we found similar patterns to those observed at 21 DIV. In one minute of spontaneous activity, there were 1312 ± 341 unique sequence families per culture, repeating 2.1 ± 4 times (range 3–62), consisting of 8.0 ± 36.3 spikes (range 3–1408) and lasting 122 ± 61 ms.

Because of their precision and frequency of recurrence, it is appealing to interpret the observed precisely timed sequences as evidence of spatiotemporal attractors. Since sequences that recur frequently in our data are more likely to represent such attractors than those sequences that repeat only a few times, we can quantify this idea by tracking solely those sequences repeating three or more times, on the assumption that patterns recurring only twice are likely to be spurious. At 21 DIV, there were 26.3 ± 10.5 such frequently recurring sequence families per culture, repeating 3.1 ± 0.4 times/min, consisting of 3.1 ± 0.3 spikes (range 3–6) and spanning 105 ± 63 ms. At 35 DIV, there were 36.7 ± 14.1 sequence families per culture, repeating 3.8 ± 1.9 times, consisting of 3.1 ± 0.4 spikes (range 3–6) and lasting 99 ± 61 ms.

The average time between sequence repetitions was 13.7 ± 13.0 seconds and many of the repetitions appeared to recur in close succession (Fig. 3A, black bars). This tendency toward short inter-sequence intervals (the leftmost peak of Fig. 3A) can be explained by cultured cortical networks’ frequent display of brief, concerted increases in firing rate, known variously as “bursts,” “population bursts,” “barrages,” and “network spikes” (Droge et al., 1986, Eytan and Marom, 2006, Wagenaar et al., 2006b), which may be similar to the UP states observed in vivo and in slices (Robinson et al., 1993, Steriade et al., 1993, Steriade, 2001). More than half of all sequence spikes occur during bursts, so it is not surprising that the time between sequences reflects this short length of bursts typical in cultures at these ages (~200 ms; leftmost peak of Fig. 3A). Two additional peaks around 14 and 23 seconds reflect the burst pattern of the most active culture we examined (which accounted for, amongst all cultures, 21% of sequence families repeating three or more times). This particularly active culture had three bursts during the 16^th minute, with inter-burst intervals of 14.1 and 23 seconds. The histogram with this highly active culture removed is shown in gray in Figure 3A.

Fig. 3.

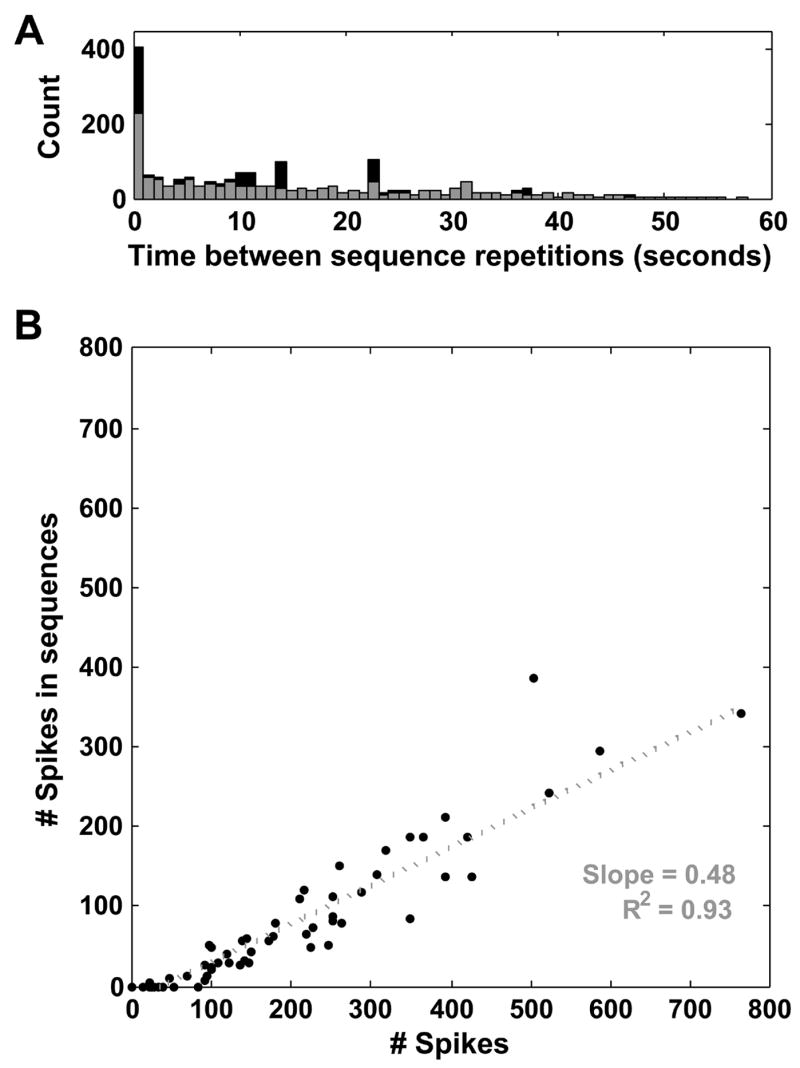
Properties of detected sequences. (A) Histogram of times between sequence repetitions from those sequences repeating three or more times (black bars). Sequences repeated with a mean interval of 13.7 ± 13.0 seconds, though many occur in close succession (left peak of histogram), due to the frequent occurrence of sequences in population bursts (see text). Additional peaks at 14 and 23 seconds are due to bursts in the most active culture studied, which contained three bursts with inter-burst intervals of 14.1 and 23 seconds. The histogram with this culture excluded is shown in gray. (B) Participation of each electrode in sequences, data from one representative culture. The total number of spikes detected on an electrode (x-axis) is plotted vs. the total number of spikes detected on the same electrode that take part in any sequence (y-axis). Each electrode is represented by one point. The slope of the best-fit line through these points can be used to estimate the percentage of spikes taking part in sequences on an electrode, 48% in this culture (R² = 0.93) (if every spike detected on an electrode participated in a sequence, the best-fit line would have a slope of one).

Interestingly, the likelihood of a spike being part of a sequence appears to be roughly the same—or even a bit lower—during bursts as outside of bursts, despite a burst’s greater concentration of spikes: Using the SIMMUX algorithm to detect population bursts (Wagenaar et al., 2005a), we determined that 52% of the spikes that were part of detected sequence repetitions occurred during bursts at 21 DIV, while of all spikes recorded at 21 DIV, 59% occurred in bursts. At 35 DIV, these numbers were 79% and 87%, respectively. These proportions—sequence spikes in bursts over all sequence spikes, and spikes in bursts over all spikes—are very nearly the same, though there are fewer sequence spikes in bursts at both developmental stages. This finding is even more striking if the analysis is limited to those sequence families repeating three or more times: at 21 DIV, 30% of sequence spikes occurred during bursts and, at 35 DIV, 48% occurred during bursts. To further restrict the possibility of a causative role for culture-wide bursting in the generation of sequences, we examined the relationship between each culture’s propensity for sequences (defined as the total number of sequence families detected in a culture, divided by the total number of spikes in the same recording) and the burstiness of each culture, quantified with the “burstiness index” of Wagenaar et al. (2005b). This analysis revealed no significant correlations between a culture’s burstiness and propensity for exhibiting precisely timed patterns (data not shown).

From looking at Figure 2, it is unclear whether some electrodes participate more frequently than others in the observed sequences. To investigate this in more detail, we made scatter plots, with the number of action potentials detected on each electrode as the abscissa and the number of action potentials taking part in sequence repetitions (from any sequence family repeating three or more times) as the ordinate, representing each electrode as a point (Fig. 3B). The slope of the best-fit line through these points provides an estimate of the percentage of each electrode’s spikes that participate in sequences. If every spike detected on each electrode took part in a sequence, these points should fall on a line with slope 1. In the data shown in Figure 3B (from one representative culture), this slope is 0.48 (R² = 0.93). No discernible patterns emerged from this analysis across cultures (the slope changes from culture to culture, but the best-fit curve is always linear), suggesting that electrodes participate roughly with a constant proportion of their firing rates.

To determine the significance of detected sequences, we compared the number of observed sequence families to the number of observed sequence families in shuffled versions of the same data. Two shuffling methods were used, spike swapping and spike jittering (see Methods; Fig. 1). Spike swapping is a balanced rearrangement of spikes over electrodes, leaving each electrode with precisely the same number of spikes, but occurring at different times. In essence, each spike’s electrode number is reassigned to that of another spike, though each spike can give its electrode number to only one other spike. This method preserves both temporal and spatial population modulations, but fails to preserve the ISI distribution of individual cells. Spike jittering randomly perturbs the timing of each spike by an amount drawn from a Gaussian distribution of mean zero and standard deviation 2 ms. Because the perturbation has zero mean, the ISI distribution of each electrode is closely preserved, along with modulations in population activity. Additionally, the number of spikes per electrode remains unchanged, making spike jittering the more stringent of the two shuffling methods. There were more observed sequence families (repeating 2 or more times) in the unshuffled data than in both spike-swapped and spike-jittered data (P < 0.05 and P < 0.01, respectively; Wilcoxon signed-rank test), indicating that the high number of observed sequences did not arise by chance.

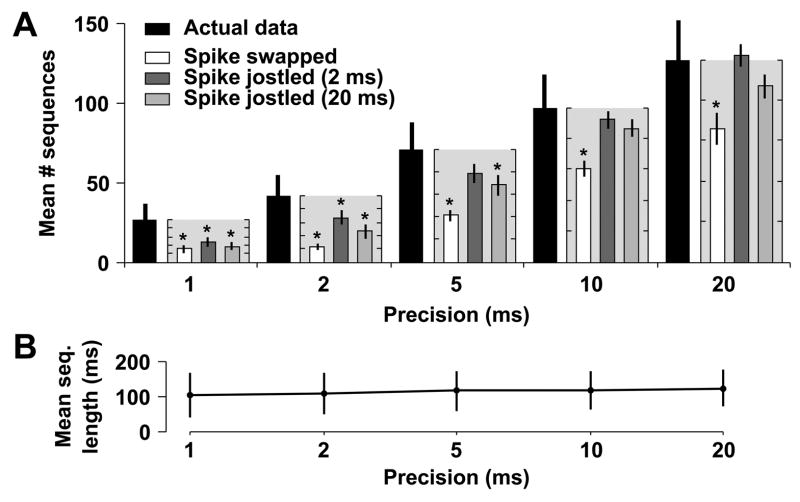
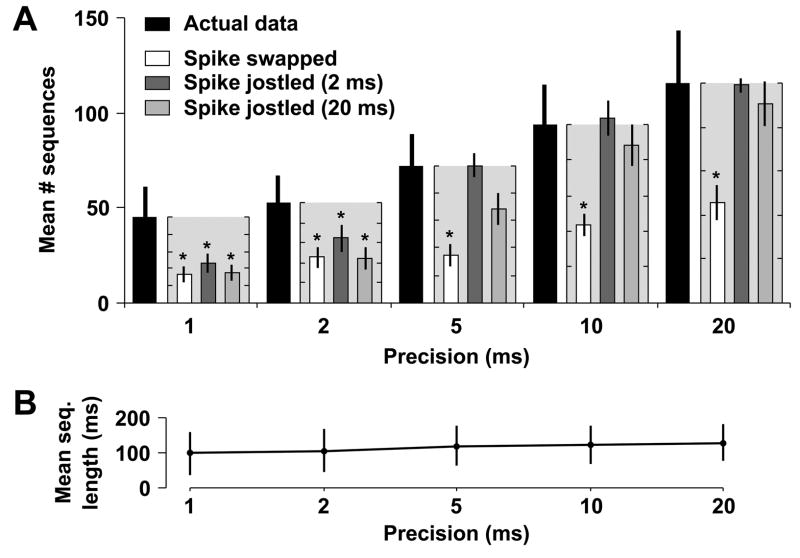
When our analysis is restricted to those sequences repeating three or more times (those sequence families most likely to represent neural attractors), we found that the number of such frequently repeating sequence families in the actual data was significantly higher than in spike swapped data (P < 0.001 at 21 DIV; P < 0.005 at 35 DIV). Furthermore, these positive results were not affected by the choice of precision, 1 ms, as was determined by examining the data at various other precisions, from 2 to 20 ms (Figs. 4A and 5A). Similarly, the number of detected sequence families was higher in actual data than in spike jittered data (P < 0.01 at 21 DIV; P < 0.005 at 35 DIV). However, unlike spike swapping, the results for spike jittering were affected by precision. Specifically, at a precision of 5 ms, the results became non-significant at 21 and 35 DIV (P > 0.05; Bonferroni-adjusted Wilcoxon signed-rank test). This is anticipated, however, because the Gaussian distribution used in spike jittering has a standard deviation of 2 ms, meaning that >95% of jittered spikes are within 4 ms (two standard deviations) of their original, unshuffled times. When using a precision ≥ 5 ms, this jittering should not be apparent. To account for this interplay between jittering and precision, we used an additional spike jittering kernel with a standard deviation of 20 ms. Surprisingly, a similar cutoff in precision was observed: at 21 DIV there were significantly more sequences in the actual data than jittered data at 1, 2, or 5 ms, but not 10 ≥ ms (Fig. 4A; P < 0.05 and P = 0.28, Bonferroni-adjusted Wilcoxon signed-rank test) and at 35 DIV there were significantly more sequences at 1 and 2 ms, but not 5 ≥ ms (Fig. 5A; P < 0.05 and P = 0.59, Bonferroni-adjusted Wilcoxon signed-rank test). This implies that frequently recurring sequence families in dissociated culture have an inherent precision of about or less than 5 ms, in agreement with the similar analysis of Beggs and Plenz on field potential patterns recorded in cultured slices (Beggs and Plenz, 2004).

Fig. 4.

Sequences repeat more frequently in actual data from cultures aged 21 DIV than in shuffled data. The template-matching algorithm was run at various precisions (1, 2, 5, 10, and 20 ms) and the number of detected sequences was compared to the number of sequences observed in shuffled versions of the same dataset. (A) The mean number of detected sequence families repeating 3 or more times in the actual data (solid black bars, ±SEM), along with the mean percentage of these sequences explained by shuffled data (spike-swapped white bars; jittered with 2 ms Gaussian kernel dark grey bars; jittered with 20 ms Gaussian kernel light grey bars). Percentages are calculated as the number of sequence families detected in shuffled data divided by the number detected in actual data, and the mean ±SEM of these ratios is plotted (light gray boxes next to black bars of unshuffled data) with the ordinate, ranging from 0–100%, scaled to the number of sequences detected in the actual data. Tick marks are at 20% intervals for these minor axes. Significant differences are indicated by asterisks. (B) Average length (±SD) of sequences repeating three or more times at each precision. The similarity between lengths indicates that our choice of precision does not affect the average length of detected sequences.

Fig. 5.

Sequences repeat more frequently in actual data than in shuffled data at 35 DIV. This figure mirrors Figure 4, but uses 11 cultures derived from 3 separate platings, aged 35 DIV, instead of 21 DIV. The observation of significant precisely timed sequences at both stages of development argues against any developmental transience of this phenomenon.

Since the template-matching algorithm allows multiple spikes from a single electrode to occur within the same template, it is possible that a single cell’s pattern of intrinsic bursting could comprise a repeating sequence. For example, if a cell on electrode 12 fires several three-spike bursts at 40 Hz, this three-spike burst would be detected as a unique sequence family. To confirm that the significance of our sequence counts cannot be ascribed to such single-electrode sequences, we reanalyzed our data using a modified version of our template-matching algorithm which declared two templates matched only if the matching spikes came from at least three separate electrodes. With this modification and a precision of 1 ms, there were still significantly more sequence families repeating three or more times at both 21 DIV and 35 DIV than in shuffled datasets: 21 ± 9 unique sequence families per culture at 21 DIV and 28 ± 14 at 35 DIV (P < 0.005 at 21 DIV and P < 0.05 at 35 DIV using spike jittering and the Wilcoxon signed-rank test).

Ideally, the choice of precision should only affect the number and not the character of detected sequences. We therefore verified that the choice of precision did not affect the average length of detected frequently recurring sequences (repeating three or more times) at either 21 or 35 DIV (Figs. 4B and 5B). Consequently, we feel confident that these sequences are not an artifact of particular precision choices, but instead may reflect the ongoing attractor-like dynamics of dissociated cortical networks.

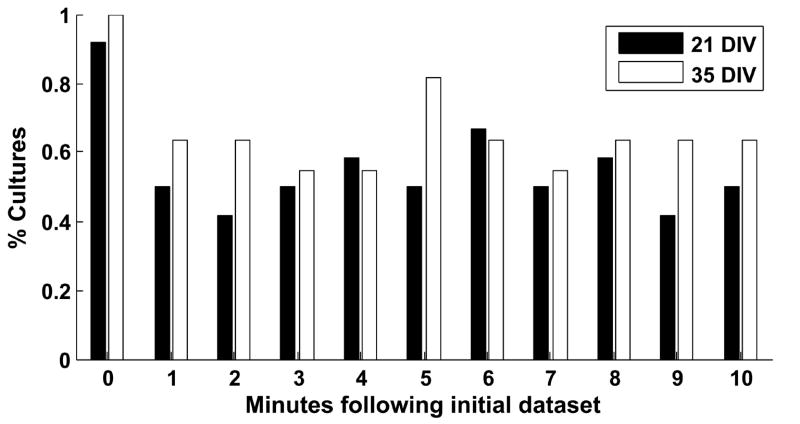
Since the above data were taken from short, one minute segments of larger recordings, we decided to track the detected patterns as they developed over longer times. To this end, we counted how often the three most frequently detected sequence families, from the original data, occurred in each of the ten one-minute data segments following the original data and, as a control, the original data itself. Because this method does not discard matched spikes (in contrast to the template-matching algorithm above), its use as a control helps verify that our discovered sequences truly occurred more frequently than they would by chance. With these data, we compared the number of times the three most frequently recurring patterns occurred in the actual data versus spike-jittered (2 ms Gaussian kernel) versions of the same datasets, shuffling each dataset 20 times. Those cultures for which the actual data contained more sequence repetitions than all 20 shuffled versions of the same data can be said to contain significantly more sequence repetitions with P < 0.05. The number of cultures satisfying this criterion was graphed as a function of time segment (Fig. 6), showing that, in more than half of the cultures, the three most frequently recurring sequences persist for at least ten minutes, and recur frequently during that time. Note that only one culture (at 21 DIV) failed the control validation.

Fig. 6.

Persistence of detected sequences. The three most frequently recurring sequences were sought in actual data during the ten minutes following the 16^th minute. The number of sequences observed in the actual data was compared to the number observed in 20 shuffled versions of the same data, using the most stringent shuffling method (i.e., spike jittering with a 2 ms Gaussian kernel). When searching the shuffled datasets, the three most frequently recurring sequences from the shuffled data were sought. If the actual data had more observed sequences than any of the 20 shuffles, it was considered to contain significantly more of the three most frequently occurring sequences than shuffled data (P < 0.05). The percentage of cultures passing this test is shown for both 21 DIV (black bars) and 35 DIV datasets (white bars) for each minute. Most or all of the cultures (11 of 12 at 21 DIV, 12 of 12 at 35 DIV) passed this test at minute zero, even though the method for tracking persistence does not discard matched spikes, thus providing a control for the template-matching algorithm. These results suggest that the most frequently recurring patterns are stable over several minutes following their initial observation.

Discussion

We have shown the presence of persistently recurring, precisely timed sequences of action potentials in dissociated networks of cortical neurons, using an algorithm with noted success both in vivo in the rat hippocampus (Nadasdy et al., 1999) and in vitro in neocortical slices (Ikegaya et al., 2004). Examination of the persistence of these patterns suggests that the most frequently recurring sequences are maintained for at least several minutes following their initial observation. The patterns were observed throughout multiple developmental stages and were found to occur both within and outside network bursts.

Precisely timed sequences have a rich history of inquiry (Abeles, 1991, Herrmann et al., 1995, Aertsen et al., 1996, Bienenstock, 1996) and have been shown to be useful as substrates for computational learning rules (Gutig and Sompolinsky, 2006), suggesting that such sequences may fulfill the idea of dynamically linked cell assemblies postulated by Hebb decades ago (Hebb, 1949). Recently, precisely timed sequences of bursts of action potentials were described and characterized in dissociated cortical cultures grown on MEAs (Wagenaar et al., 2006a), although these patterns were limited to a defined developmental period, typically the second week in vitro. Also, the sequence of neural activation during bursts has been shown to be non-random and repetitive (Segev et al., 2004, Eytan and Marom, 2006, Madhavan et al., submitted). The idea that such patterns are a general property of self-organizing networks, rather than being limited to developmentally and anatomically structured networks, is bolstered by computational studies of loosely-structured model neural networks of comparable size to our cultured neuronal networks (Izhikevich et al., 2004, Izhikevich, 2006). They found that recurring patterns of neural action potentials spontaneously developed in simulated networks as a result of the spike timing dependent plasticity (STDP) learning rule (Dan and Poo, 2006), despite a wide range of parameters and varying degrees of thalamic afferentation (Izhikevich, 2006).

While precisely timed sequences of action potentials have been observed repeatedly in vivo and in slices (Nadasdy et al., 1999, Ikegaya et al., 2004, Shmiel et al., 2005, Luczak et al., 2006, Shmiel et al., 2006), their existence remains controversial. In particular, the work of Oram et al. (1999), Baker and Lemon (2000), and Mokeichev et al. (2007) illustrates how more sophisticated methods of surrogate data generation can often account for a significant portion of detected precisely timed sequences. The specific methods of Oram et al. (1999) and Baker and Lemon (2000) are not applicable to our data because, with our stimulus-free, single trial data, we cannot construct accurate peristimulus time histograms, nor can each electrode’s ISI distribution be accurately modeled with a fixed order gamma process. We addressed the concerns raised by these studies by using spike jittering, wherein each cell’s firing rate modulation during the recording is preserved, along with population-wide modulations. Mokeichev et al. (2007) employed three advanced methods of surrogate data generation: time domain interval shuffling, phase randomization, and Poisson simulation. All three methods rely on continuous-time processes for their computations, rather than the point process data used in our analyses. The third, distinctly, uses a computational model of a single compartment neuron receiving Poisson inputs from three other neurons (two excitatory, one inhibitory), then uses the generated subthreshold activity as a surrogate. Interestingly, Poisson input to artificial neurons is the exact tactic utilized by Izhikevich et al. (2004) to generate a rich repertoire of precisely timed sequences in a large, loosely connected neural network, although the formation of these neuronal groups was only possible when the neurons interacted via STDP.

It has previously been suggested, by examining local field potentials (LFPs) with MEAs, that the neural networks of acute brain slices and organotypic cultures obey the principle of self-organized criticality (SOC) (Bak et al., 1987, Bak, 1996, Beggs and Plenz, 2003). Moreover, these precisely timed sequences of LFPs spontaneously recur, like the sequences we observed above (Beggs and Plenz, 2004). Might sequences of action potentials in dissociated cultures show similar behavior? One characteristic of critical processes is that their event sizes obey a power law probability distribution, P(n) ≈ n^−α, where n is the event size and P(n) is the probability of observing a size n event. Fitting a power law to our distribution of sequence sizes, in terms of number of electrodes taking part in a sequence, results in an exponent α = −3.1 ± 0.2 (±95% confidence interval (CI)) using linear regression in log-log space (R² = 0.97; Fig. 7A). However, when the same procedure is done on spike-swapped and spike-jittered data, similar fits are obtained (α = −3.2 ± 0.2, R² = 0.97 and α = −3.3 ± 0.2, R² = 0.97 for electrode-shuffled and spike-swapped data, respectively; Fig. 7B–C). This suggests that the observed scale invariance of sequence sizes—in these data—does not prove anything inherent to significant pattern generation (Reed and Hughes, 2002, Bedard et al., 2006).

Fig. 7.

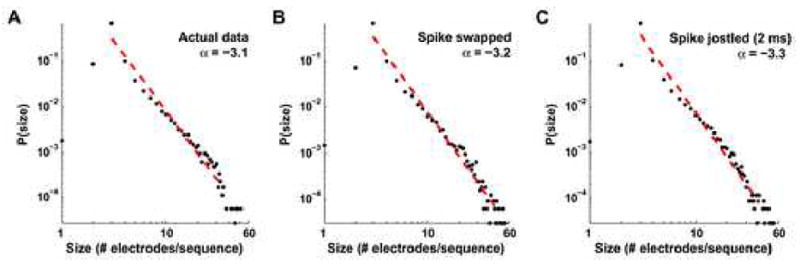
The distribution of sequence sizes obeys a power law probability distribution. When the number of electrodes taking part in each detected sequence is graphed against its probability of occurrence, the distribution can be fit by a power law (red dashed line), P(n) ~ n^{− α}, where n is the event size, P(n) is its normalized frequency of occurrence in our datasets, and α is the power law’s exponent. On log-log plots, such as these, graphed power laws appear linear, with slope α. For the observed sequences in the actual data α = −3.1 ± 0.2 (±95% CI, R² = 0.97; A). However, we find similar scale invariance in our spike-swapped (α = −3.2 ± 0.2, R² = 0.97; B) and spike-jittered data (α = −3.3 ± 0.2, R² = 0.97; C), minimizing the importance of scale invariance in explaining our significantly repeating patterns.

Finding precisely timed sequences in cultures presents three important advances for the study of neural information processing. First, the observation of such sequences in dissociated cultures, combined with their illustration in multiple in vivo preparations and in brain slices, argues for their robustness, as evidenced by their persistence in multiple species and across various degrees of deafferentation, from simple anesthesia to surgical excision. Second, the further study of such sequences can now be performed in dissociated cultures, a simple preparation allowing detailed control of the culture’s inputs and chemical environment, including relevant neuromodulators like dopamine (Lapish et al., 2007), as well as comprehensive long-term morphological imaging (Potter, 1996, Potter, 2005), potentially granting us a window into the morphological substrates underlying the formation of precisely timed sequences. Lastly, finding repeating sequences of neural action potentials in dissociated cultures argues against the necessity of innate cortical structure in their formation—not only are the sequences robust in the sense of not requiring afferent input, just as in slices (MacLean et al., 2005), but they are robust in the sense that the neural network spontaneously self-organizes in a way that generates them. While the brain’s intrinsic organization is likely to add new subtlety to these patterns, their existence appears to be a general feature of any self-organizing neuronal network. The reasons for such robustness are still unknown, but present an intriguing avenue for further research into repeating spatiotemporal patterns of neural activity.

Abbreviations

A/D

analog-to-digital

DIV

days in vitro

ISI

interspike interval

LFP

local field potential

MEA

multi-electrode array

RMS

root mean square

SBE

spontaneous bursting event

SEM

standard error of the mean

SD

standard deviation

STDP

spike timing–dependent plasticity