Sensitive Ultrasonic Detection of Dystrophic Skeletal Muscle in Patients with Duchenne's Muscular Dystrophy using an Entropy-Based Signal Receiver

Abstract

The dystrophinopathies comprise a group of X-linked genetic diseases that feature dystrophin deficiency. Duchenne and Becker muscular dystrophy are characterized by progressive weakness and wasting of skeletal, smooth, and/or cardiac muscle. Duchenne's Muscular Dystrophy (DMD) is the most severe dystrophinopathy, and with an incidence of 1:3500 male births. Despite understanding the structural and genetic basis for DMD, the pathogenesis and clinical basis for more severe involvement in specific skeletal muscle groups and the heart are poorly understood. Current techniques, such as strength testing, for monitoring progress of disease and therapy in DMD patients, are imprecise and physically demanding for test subjects. Ultrasound is well-suited to detect changes in structure and organization in muscle tissue in a manner that makes low demands on the patient. Therefore, we investigated the use of ultrasound to quantitatively phenotype the remodeling process in patients with DMD. Beam-formed RF data were acquired from the skeletal muscles of nine DMD and five normal subjects imaged with a clinical imaging system (HDI5000 w/7 MHz probe applied above left biceps muscle). From these data, images were reconstructed using B-mode (log of analytic signal magnitude) and information-theoretic receivers (H_f -receiver). H_f images obtained from dystrophic muscle contained extensive “mottled” regions (i.e. areas with heterogeneous image contrast) that were not readily apparent from the B-Mode images. The two dimensional autocorrelation of DMD H_f images have broader peaks than those of normal subjects, which is indicative of larger scatterer sizes, consistent with pathological changes of fibers, edema, and fatty infiltration. Comparison of the relative peak widths (Full width measured at 60% maximum) of the autocorrelation of the DMD and normal H_f images shows a quantitative difference between the two groups (p < 0.005, student two-tailed paired t-test). Consequently, these imaging techniques may prove useful for longitudinal monitoring of disease progression and therapy.

1. Introduction and Literature

The dystrophinopathies comprise a group of X-chromosome linked genetic diseases that include dystrophin deficiency Duchenne muscular dystrophy (DMD), Becker muscular dystrophy, and X-linked dilative cardiomyopathy. Duchenne and Becker muscular dystrophy are characterized by progressive weakness and wasting of skeletal, smooth, and cardiac muscle but without primary structural abnormalities in the lower motor neurons.(Emery, 2002; Finsterer and Stollberger, 2003; Ishikawa et al., 1999; Roland, 2000) DMD is the most severe dystrophinopathy, and with an incidence of 1 in 3500 male births, it accounts for over 80% of the dystrophinopathies.(Emery, 2002; Finsterer and Stollberger, 2003) Afflicted boys typically present with weakness by the age of 5 years and, if left untreated, are unable to walk without assistance by age 10 years. Despite understanding the structural and genetic basis for DMD, the pathogenesis and clinical basis for more severe involvement in specific skeletal muscle groups and the heart are poorly understood.

Dystrophin is a cell membrane-associated protein located within the sarcolemma of both cardiac and skeletal muscle cells. The protein serves multiple functions important to the maintenance of structural integrity and cardiac dynamic function.(Grady et al., 1997; Vatta et al., 2002) As a component of the dystrophin-glycoprotein complex within the sarcolemma, dystrophin also serves an important role in the transduction of physical forces in striated muscle.(Vatta et al., 2002) Dystrophin contributes to signaling within cardiac and skeletal muscle cells, as its presence within the dystrophin-glycoprotein complex enables molecules such as neuronal nitric oxide synthase and voltage gated sodium channels to attach onto this complex.(Ashford et al., 2005) Dystrophin interacts with calmodulin, a regulator of calcium dependent kinases and hence contractility.

Generally, the clinical appearance of skeletal muscle weakness associated with DMD triggers a diagnostic workup that includes phenotyping, genotyping and, if necessary, muscle biopsy. A variety of imaging modalities have been studied as a possible adjunct to physical examination or as a means for further exploring the pathophysiology of DMD. Both conventional and quantitative ultrasonography have revealed variations in muscle volume, echogenicity, and attenuation related to the degree of fatty infiltration in boys with DMD and other neuromuscular disorders.(Heckmatt et al., 1980a; Berger et al., 1987; Lamminen et al., 1988; Hete and Shung, 1995; Reimers et al., 1996)

Several techniques have been examined as a means to increase the contrast between pathological and surrounding normal tissue when imaged with ultrasound.(Heckmatt et al., 1980a; Berger et al., 1987; Lamminen et al., 1988; Hete and Shung, 1995; Reimers et al., 1996; Maurits et al., 2004, 2003; Heckmatt et al., 1980b, 1982; Heckmatt and Dubowitz, 1983; Heckmatt et al., 1988a,b, 1989; Manzur et al., 1992) To the best of our knowledge, all of these studies have been conducted ex-vivo or been based on digital analysis of B-mode images taken from video tape. A major distinction between previous studies and ours is the use of beam-formed radio frequency (RF) acquired with the same inter-subject power and gain settings. Moreover, use of the raw RF permits reconstruction of not only conventional B-mode grayscale images but also the investigation of other, perhaps, more sensitive signal processing techniques.

Pursuing this approach, we have applied information-theoretic detectors (ITD), proposed previously for materials characterization to find and size flaws not detectable by conventional methods.(Hughes, 1992a; Hughes et al., 2005c) These detectors frequently do not require setting time domain gates prior to signal analysis, which contrasts with more conventional ultrasonic analysis techniques that require prior information concerning the time of arrival of relevant information. ITD methods work by analyzing the statistical distribution of digitized voltage levels from an acoustic signal and are expected to be sensitive to diffuse, low amplitude features of the signal that are often obscured by noise or lost in large specular echoes which may preclude detection by a human observer. In this study we will focus on one of these detectors: H_f , an entropy-based receiver. Our goal is to determine whether or not it can be used to differentiate normal from dystrophic muscle. In order to provide a basis for comparison with earlier results we also examine sensitivity of the signal energy E_f , defined as the sum of the squares of the digitized waveform, for differentiation of normal from dystrophic muscle. E_f is essentially equivalent to the integrated backscatter metric utilized by Hete and Shung.(Hete and Shung, 1995)

1.1. Entropy Analysis: Theory

We begin with a backscattered radio frequency (RF) acoustic waveform, f(t), assumed to be defined on the interval [0, 1], and digitized into N_α discrete voltage levels on a discrete time lattice of N_σ points. The resulting data is an array of points which are integers falling in a range of values between 1 and N_α ; e.g. for an eight bit digitizer, N_α = 256. Subsequent to this digitization process, a histogram of the voltage levels of the digitized waveform is computed and normalized by the total number of data points N_σ to obtain a probability distribution p_i for the occurrence of the i^th symbol (where 1 ≤ i ≤ N_α ) in the digitized signal. Shannon entropy may then be computed via the standard formula(Cover and Thomas, 1991)

$$H_S=-\sum _{i=1}^{N_{\alpha }}{p}_i\log \left[p_i\right].$$ (1)

H_S depends critically on the characteristics of the digitizer: N_α and N_σ. In the limiting case of an ideal digitizer having infinite dynamic range and sampling rate, H_S → ∞ linearly with log[N_α ]. However, with use of a suitable mathematical limiting process we may extract a well-defined finite part from H_S and thus obtain an expression that is independent of digitizer characteristics.(Hughes, 1992a) This limiting form, denoted H_f , (where the subscript f indicates the relation to the sampled waveform) is also useful as a detector.(Hughes, 1992b,a, 1993a,b, 1994; Hughes et al., 2004, 2005c,b,a, 2006) In this ideal limit, the probabilities, p_i are replaced by the density function of the underlying continuous waveform, f(t). This function, which we denote by w_f (y), is a well-defined mathematical object possessed by every measurable function.(Wheeden and Zygmund, 1977) Measurable functions include all experimental waveforms as well as all random functions. With these substitutions, we obtain

$$H_f={\int }_{f_{min}}^{f_{max}}{w}_f\left(y\right)\log \left[w_f\left(y\right)\right]dy.$$ (2)

The density function, w_f (y), satisfies the fundamental relation

$${\int }_0^1\phi \left(f\left(t\right)\right)dt={\int }_{f_{min}}^{f_{max}}\phi \left(y\right)w_f\left(y\right)dy,$$ (3)

for any continuous function ℱ(y). Equation (3) is just the generalization of the usual rule for changing variables in an integral, which is usually stated in a form that holds only for a monotonic change of variable, to the case of a non-monotonic change variable: y = f(t). Equation (3) should also be compared with the expression for the expectation value of a function φ of a random variable X with density p_X(x), given by

$$\int \phi \left(x\right)p_X\left(x\right)dx,$$

which explains why w_f (y) is referred to as the density function for f(t).(Wheeden and Zygmund, 1977, see pages 68−69)

As the logarithm in Eq. (2) suggests, H_f “lives” in the “log-domain”. This can be shown mathematically using the scaling properties of w_f (y):

$$\mid \sigma \mid w_{\sigma f}\left(\sigma y\right)=w_f\left(y\right),$$ (4)

which may be obtained by inspection of Eq. (3). From this expression it can be shown that H_f obeys the scaling law:

$$\begin{array}{cc}\hfill H_f& ={\int }_{f_{min}}^{f_{max}}{w}_f\left(y\right)\log \left[w_f\left(y\right)\right]dy\hfill \\ \hfill & ={\int }_{f_{min}}^{f_{max}}\mid \sigma \mid w_{\sigma f}\left(\sigma y\right)\log \left[\mid \sigma \mid w_{\sigma f}\left(\sigma y\right)\right]dy\hfill \\ \hfill & ={\int }_{\sigma f_{min}}^{\sigma f_{max}}{w}_{\sigma f}\left(\xi \right)\log \left[\mid \sigma \mid w_{\sigma f}\left(\xi \right)\right]d\xi \hfill \\ \hfill & ={\int }_{\sigma f_{min}}^{\sigma f_{max}}{w}_{\sigma f}\left(\xi \right)\log \left[w_{\sigma f}\left(\xi \right)\right]d\xi +\log \left[\mid \sigma \mid \right]\hfill \\ \hfill & =H_{\sigma f}+\log \left[\mid \sigma \mid \right]\hfill \end{array}$$ (5)

In image quantitication applications we almost always utilize differences (or variations) in receiver output between different points within an image or between corresponding points within images of the same portion of the anatomy that are acquired serially. In general, gain settings may be adjusted between acquisitions at different time points. The “log”-like scaling of H_f shown in Eq. (5) makes such comparisons possible.

If we take φ(y) = δ(s − y) then Eq. (3) becomes

$$\begin{array}{cc}\hfill {\int }_0^1\delta (s-f\left(t\right))dt& ={\int }_{f_{min}}^{f_{max}}\delta (s-y)w_f\left(y\right)dy\hfill \\ \hfill & =w_f\left(s\right).\hfill \end{array}$$ (6)

Using the well-known representation for the Dirac δ-function

$$\delta (s-y)=\sum _{k=-\infty }^{\infty }{e}^{i\pi k(s-y)}$$ (7)

in Eq. (6), together with Eq. (3), we obtain

$$w_f\left(s\right)=\sum _{k=-\infty }^{\infty }{e}^{i\pi ks}{\int }_0^1{e}^{-i\pi kf\left(t\right)}dt.$$ (8)

This Fourier series expansion will be used to compute w_f (y) from the experimental waveform, i.e., the backscattered RF.

1.2. E_f and log[E_f] Analysis

By analogy with the expression for the kinetic energy for a spring, the signal energy of a waveform, f(t), is usually defined as

$$E_f={\int }_0^{1}f{\left(t\right)}^{2}dt.$$ (9)

Using Eq. (3), this may be rewritten using w_f (y) according to

$${\int }_{f_{min}}^{f_{max}}{y}^2{w}_f\left(y\right)dy,$$ (10)

which shows that the traditional signal energy analysis may be placed in the same mathematical framework that is used for entropy analysis.

As discussed above, image quantification applications frequently utilize differences (or variations) in receiver output. E_f suffers from the drawback that it is not invariant with respect to rescaling of f(t). This problem is solved by using log[E_f ] instead.

2. Materials and Methods

2.1. Patient Recruitment

Thirteen patients confirmed to have DMD by biopsy, elevated creatine kinase, or DNA analysis were recruited from the Neuromuscular Clinic at Washington University in St Louis, Mo, by one of the authors (A.M.C.). Nine age-matched healthy males were recruited independently by staff members of the Cardiovascular Magnetic Resonance Laboratory from a population of children who were relatives or friends of the authors. An attempt was made to recruit patients of approximately the same age as the DMD patients. These patients were enrolled in the study over a 20-month period. All subjects were under the age of 21 years. Written informed consent was obtained from each parent before the study, which was approved by the institutional review board of the Washington University Medical Center.

2.2. Statistical Analysis

All statistical analyses were performed with the use of the Open Source Gnumeric spreadsheet program. An unpaired Student two tailed t-test was used to assess differences in the means between groups where appropriate. Mean and standard deviation for the variables of interest were determined for both groups, and probability values 0.05 were considered significant.

3. Results

3.1. Physcial Characteristics of Patients

The physical attributes of our patient population are shown in Table 1, A summary of steroid treatment for each of the nine DMD subjects is shown in Table 2. P values comparing the mean values of age, weight, height, and body mass index, for control and DMD groups were computed. They show no statistically significant difference between the two groups.

Table 1.

Physical attributes of subjects used in this study

	DMD(n=9)	Control(n=5)	P
Age (y)	11.40 ± 1.84	7.40 ± 1.44	0.11
Weight (kg)	48.55 ± 8.53	28.27 ± 5.45	0.07
Height (cm)	139.20 ± 8.28	123.19 ± 6.77	0.16
Body Mass Index	23.57 ± 2.67	17.90 ± 1.65	0.10
Amublatory	5 of 9	All	—
Corticosteroid Use	All	None	—

Table 2.

Treatment history of DMD subjects appearing in this study The mean treatment time, as a percentage of age was 35±7%

Age(mo)	Therapy(mo)	%
108	44	41
180	75	42
180	120	67
60	20	33
192	41	21
264	25	9
60	3	5
96	65	68
108	36	33

3.2. Ultrasound tissue characterization of skeletal muscle

3.2.1. Data Acquisition

A modified commercial clinical imaging system (Philips HDI 5000, Philips Medical Systems) containing a radiofrequency capture board was used to collect individual beam-summed backscattered RF from the biceps of 10 DMD subjects, ranging in age from 5 to 22 years, and 5 normal subjects, ranging in age from 4 to 9 years. Imaging was accomplished using a linear array (CL7−15) with a nominal center frequency of 8 MHz (with bandwidth 3 dB down points at 5.7 and 10.2 MHz) placed on the left biceps so that the long axis of the array was parallel to the humerus bone. This permitted acquisition of beam-formed RF image data comprised of 256 917-point long A-lines. The sampling for each A-line was 24 MHz, thus, each panel represents a spatial region that is 2.94cm deep× 2.3mm wide. In addition, imager gain and power transmit levels were kept identical across all subjects by the use of stored “presets” in order to facilitate quantitative inter-subject comparisons.

Each of the RF lines in the beam-formed data was first up-sampled to 8192 points using a cubic spline fit to the original data set. This was done in order to numerically stabilize the thermodynamic receiver algorithms, as previous work has shown benefit from increased input waveform length.(Hughes, 1993a) Next, a moving window analysis was performed on the highly sampled data set with a 2.38 μs window (512 points) moved in 0.037 μs steps (8 points) to yield 961 window positions within the original data set. The values for the receivers (log signal energy, log[E_f ] and entropy H_f ) within the moving window are used to compute pixel values for the image reconstructed using each receiver type. For comparison, conventional gray-scale B-mode images were also produced.

Subsequently, all images were rescaled to a 256 × 256 pixel format to facilitate Fourier-based correlation analysis using the NIH ImageJ image processing program (http://rsb.info.nih.gov/ij/).

3.2.2. Image Analysis

A typical set of normal (left column) and DMD (right column) images are shown Figure (1). The DMD data are from the subject (nine years old) whose age most closely matches the group mean value. The top row are images of the logarithm of the analytic signal magnitude of the backscattered ultrasound, i.e., grayscale B-mode images. The images in the middle row are the logarithm signal energy, log[E_f ]. The bottom row was made using the same moving window parameters, but the data within each window were used to compute H_f . All images show a bright vertical region at the top, corresponding to the specular reflection from the transducer-skin interface. One goal of this study was to identify a method of analysis that did not require gating out this feature prior to analysis, thus eliminating a subjective and potentially difficult step from the analysis. Previous work has demonstrated that H_f can satisfy this requirement.(Hughes et al., 2005c)

Fig. 1.

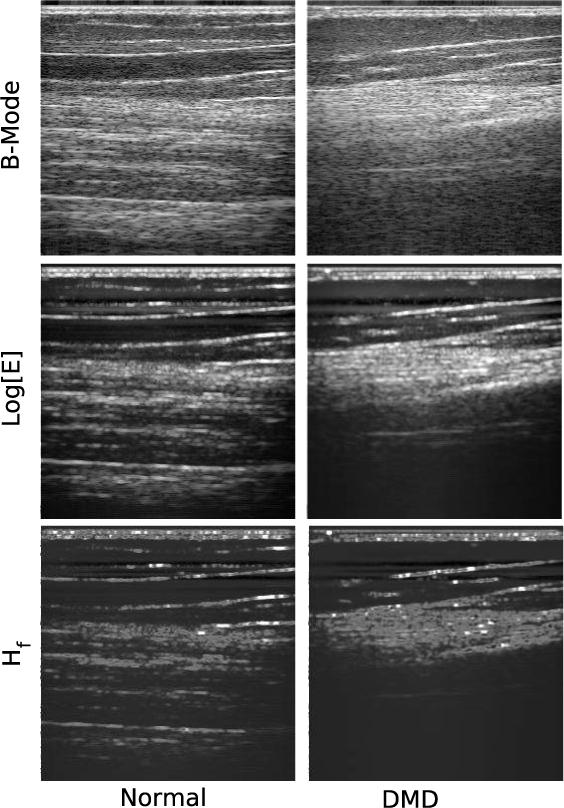
Images showing a comparison of backscattered ultrasound in normal (left column) vs. DMD (right column) muscle tissue. The top row are images of the logarithm of the analytic signal magnitude of the backscattered ultrasound, i.e., grayscale B-mode images. The direction of insonification is from top to bottom. The middle row was made by sliding a square window of 2.38μs over the backscattered RF lines in 0.037μs steps and computing the signal energy, E_f in each window (resulting in an image size of 961×256 pixels). Subsequently this image was rescaled to 256×256 pixels for presentation and processing purposes. The bottom row was made using the same window and subsequent rescaling, but the data within each window were used to compute H_f . Each panel represents a spatial region that is 2.94cm×2.3cm. The DMD date are from the subject (nine years old) whose age most closely matches the group mean value.

While there are some differences between the two columns, the images within each column all exhibit the same qualitative features, although they do so with obvious quantitative differences. The most notable is the presence of reflections from the muscle layers in the normal subject, which are absent in the DMD subject. Comparison of the normal vs. DMD sets of images reveals that the controls all possess numerous sharply defined features, while the DMD images contain rather diffuse features not quantitatively very different from the average image value. This suggests that an autocorrelation analysis might quantify the differences between backscatter from normal and dystophic muscle.

Specifically, for an image represented by a two variable function, g(x, y), the auto correlation is defined by

$$g\ast \ast g(x,y)={\int }_{\infty }^{-\infty }{\int }_{\infty }^{-\infty }g(x_1,y_1)g(x+x_1,y+y_1)d{x}_{1}d{y}_1.$$ (11)

For our analysis this integral was computed using the Fourier-based correlation function built into the NIH ImageJ image analysis program. This approach provides a basis for quantification of the differences, i.e. the relative magnitude between sharp features and average image background, observed in images made using the different signal processing schemes. Applying this autocorrelation analysis to the images of the panels in Figure (1) we obtain Figure (2). As expected the correlations of the normal images exhibit a bright central peak and numerous secondary peaks due to the multiple layer structure evident in the time-domain images. This differs noticably from the correlation images from the DMD group which have one central peak with one secondary peak on each side. Again this is to be expected from inspection of the time-domain images. These results are typical of the data acquired from both groups.

Fig. 2.

Correlation images of the panels shown in Figure (1). Each image shows a bright central region, as expected. The widths of these regions are significantly different when grouped according to whether they are from normal or dystrophic muscle. This suggests that the width might be used to differentiate the two groups. The dashed indicates the position of pixels in the normal and DMD H_f images used to plot the curves shown in Figure (3).

3.3. Ultrasonic Imaging

Figure (2) suggests that the next step in analysis should be quantification of the relative peak widths, for instance along a cross-sectional line drawn vertically across the images as shown in the normal H_f image. The exact position and orientation of this line does not effect the outcome of our analysis. It was chosen “by hand” to be near a vertical line in the center of the image since the goal of this study was to demonstrate the existance of an alogrithm capable of identifying dystrophic pathology that might be applied quickly and easily in a clinical setting. The plot of cross-sections thus obtained is shown in Figure (3). Both curves have been normalized to unity peak value to facilitate comparison. The plots show a broader central peak for DMD correlation cross-section, as expected. Also evident are the numerous secondary peaks in the cross-section from the normal subject. Arrows indicate the 60% height on both curves. We will subsequently discuss quantification of the correlation images using this width. During data analysis all widths from 5% to 95%, in 5% steps, were measured and a T-test performed to compare the normal (N = 5) and DMD (N = 9) peak widths. For the H_f images it was found that the 60% level shown in the figure produced peak widths with the lowest p-value. For log[E_f ] images the lowest p-value occured at the 70% level. For the B-mode images there were no cutoff levels that produced p-values indicating statistical significance.

Fig. 3.

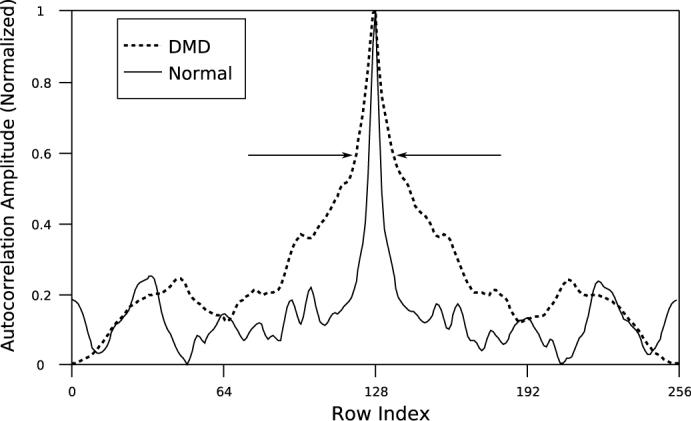
A cross-sectional slice through the mid-sections of the H_f images shown in Figure (2). The the 60% level is indicated. At this level the widths of the cross-sections are obviously different, reflecting differences in the H_f images shown in Figure (2).

The mean values of cross-sections of log[E_f ] images using the cutoff at 70% is shown in Figure (4). The two groups separate with a p-value that is less than 0.02 with the peak widths for the DMD group averaging nearly twice that for the normal group.

Fig. 4.

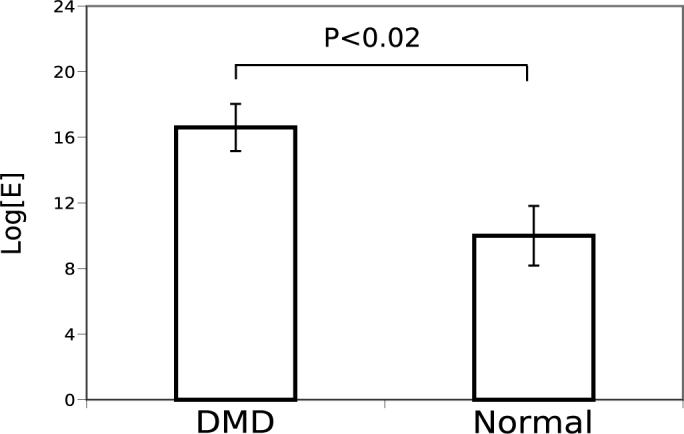
A comparison of mean width, at the 70% level of the central peaks of log[E] images of normal (N = 5) and dystrophic (N = 9) muscle. The two groups are significantly different (P < 0.02).

The corresponding results obtained using the H_f images is shown in Figure (5). In this case the correlation peak widths for the DMD group are consistently greater than the normal group with a greater statistical significance of p < 0.005.

Fig. 5.

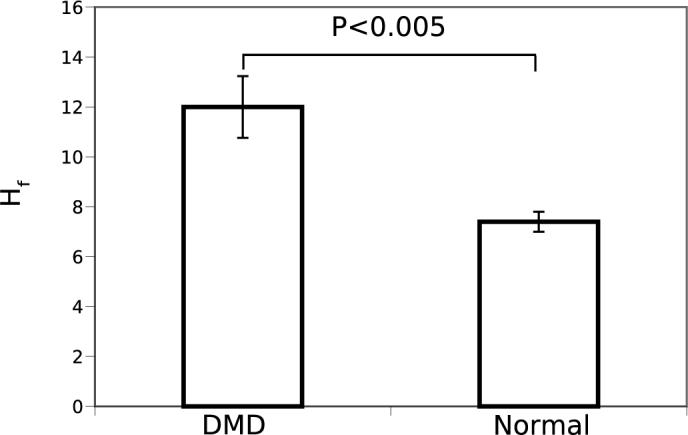
A comparison of mean width, at the 60% level of the central peaks of H_f images of normal (N = 5) and dystrophic (N = 9) muscle. The two groups are significantly different (P < 0.005).

4. Results and Discussion

4.1. Qualitative Comparison of B-Mode, Signal Energy, and Entropy Analyses

The gray-scale images used in medical ultrasound, B-mode, are displays of the logarithm of the envelope (i.e., analytic signal magnitude) of the backscattered signal, which is well-known to represent the energy contained in the waveform over the sampling interval.(Ziomek, 1995; Szabo, 2004) As discussed above, energy contained in longer intervals may be estimated using the sum of the squares of digitized values contained in a “moving window”. The physical motivation is based on analogy with the kinetic energy of a spring, which is proportional to amplitude of spring extension squared. Viewed this way, signal energy analysis of backscattered RF is a generalization of conventional B-mode imaging obtained by averaging energy over a longer time interval. Consequently, the usual benefits of signal averaging may be obtained by using log[E_f ] imaging, although at the cost of lower spatial resolution induced by the use of a moving window.

Previous investigations have shown that in some cases entropy-based imaging can offer further improvements in sensitivity.(Hughes, 1992b,a, 1993a,b, 1994; Hughes et al., 2005b, 2004, 2005c,a, 2006) The mechanism for the increased sensitivity of thermodynamic receivers relative to conventional receivers may be understood by appealing to the geometric picture of the signal space as an infinite dimensional vector space. Energy-based detection schemes, such as envelope detection or signal energy, separate vectors (digital waveforms) having different energy. Geometrically, this is equivalent to dividing the signal space into concentric spheres centered at the origin. If ultrasonic images are formed using signals that have propagated through media with similar average acoustic properties, differentiation of waveforms within the data set may be difficult, as all waveforms in the data set will lie on roughly the same sphere in the signal space. However, it is possible to divide the signal space into different shapes than spheres and some of these may provide much greater separation between vectors, such as those backscattered from contrast-labeled tissue in a tumor and those backscattered from normal tissue. This may be accomplished mathematically by performing the separation based on geometric characteristics other than vector length. Entropy is such a quantity. Qualitatively, it resembles a volume. Moreover, if we apply the constant energy constraint, it may be shown that(Kullback, 1997)

$$\infty >H_f\ge \log \left[1∕(E_f\sqrt{2\pi e}\right)].$$ (12)

This inequality suggests the potential utility for tissue characterization of the entropy receiver,H_f , since it takes on values covering an infinite range and has the potential to separate signals indistinguishable to the signal energy receiver.

Ultrasound has previously been employed for quantitative evaluation of muscle from DMD subjects.(Heckmatt et al., 1980a; Berger et al., 1987; Lamminen et al., 1988; Hete and Shung, 1995; Reimers et al., 1996; Heckmatt et al., 1989) To our knowledge, all of these studies have either been based on digital analysis of B-mode images taken from video tape or conducted ex-vivo. Most of these studies report that backscatter from DMD subjects is much more homogeneous with increased backscatter from all components of the muscle.(Heckmatt et al., 1989) A major distinction between previous studies and ours is the use of beam-formed RF acquired with the same inter-subject power and gain settings. Although our correlation analysis is based on the shapes of image features and may thus appear to be independent of these imager settings, it is important to remember that many imager controls have a nonlinear impact on not only the displayed image but also, through power-dependent propagation mechanisms in tissue, on the beam-formed RF. These are ruled out in our study.

Finally, several of the previous studies were based on the use of integrated backscatter. This quantity is very similar to log[E_f ], which we have included in our analysis in order to facilitate qualitative comparisons with the results of other researchers. Our study also employs entropy-based signal analysis, which we were motivated to use based our application of this technique for detection of molecularly targeted tissue.(Hughes et al., 2005b, 2004, 2005a, 2006) Its utility in this application is demonstrated by the greater significance it produces in distinguishing normal from dystrophic tissue.