Time-frequency characterization of interdependencies in nonstationary signals: application to epileptic EEG

Abstract

For the past decades, numerous works have been dedicated to the development of signal processing methods aimed at measuring the degree of association between EEG signals. This interdependency parameter, which may be defined in various ways, is often used to characterize a functional coupling between different brain structures or regions during either normal or pathological processes. In this paper we focus on the time-frequency characterization of the interdependency between signals. Particularly, we propose a novel estimator of the linear relationship between nonstationary signals based on the cross correlation of narrow band filtered signals. This estimator is compared to a more classical estimator based on the coherence function. In a simulation framework, results show that it may exhibit better statistical performances (bias and variance or mean square error) when a priori knowledge about time delay between signals is available. On real data (intracerebral EEG signals), results show that this estimator may also enhance the readability of the time-frequency representation of relationship and thus can improve the interpretation of nonstationary interdependencies in EEG signals. Finally, we illustrate the importance of characterizing the relationship in both time and frequency domains by comparing with frequency-independent methods (linear and nonlinear).

I. Introduction

Electroencephalographic (EEG) signals provide information about cerebral activity with an excellent time resolution (in the order of 1 ms). Quantitative analysis of EEG signals is generally performed using signal processing (SP) methods which may substantially complement the visual inspection of time series.

For the past decades, numerous works have been dedicated to the development of SP approaches aimed at evaluating the degree of association (in a general sense, i.e. interdependency). Indeed, the statistical relationship between signals acquired from different brain structures or regions may be used to characterize the functional coupling between recorded sites during normal (cognitive, for instance) or pathological (epileptic, for instance) processes.

These methods may be divided into two categories depending on whether or not the nonlinear nature of the relationship is taken into account.

Linear methods were developed first. Many estimators based on linear cross-correlation or coherence function were proposed and used to study functional couplings between brain regions during cognitive tasks (Chapman et al. [1]) or during epileptic processes like seizures. In this latter field, works based on the coherence function were initiated by Brazier [2] who studied the propagation of epileptic activities from intracerebral recordings. They were followed by Gotman [3] who studied interhemispheric relations in partial seizures and by Duckrow et al. [4] and Franaszczuk et al. [5, 6] who analyzed possible synchronization mechanisms occurring at the seizure onset.

The development of nonlinear methods is more recent (Pikovsky et al. [7]). A first family of methods based on mutual information (Mars et al. [8]) or on nonlinear regression (Pijn et al. [9], Wendling et al. [10]) was first introduced in the EEG field. A second family is currently developing, based on works related to the study of nonlinear dynamical systems and chaos (Iasemidis [11], Lehnertz [12]).

Recently, a comparative study of different synchronization measures in real EEG data was performed by Quian Quiroga et al. [13]. Authors first confirmed that linear methods (coherence and cross-correlation) as well as nonlinear methods (mutual information, phase synchrony) are useful in EEG analysis and provide information that is not accessible by the visual inspection. They also showed that all these measures (except entropy) may give similar results, qualitatively.

If nonlinear methods have the capability to account for the nonlinearity of relationship, they are generally independent from frequency, a key parameter in the EEG analysis that can be related to the oscillatory behavior of recorded neural populations. On the opposite, linear methods can not be used to analyze the nonlinear property of relationship but they can characterize its dependence on frequency. However, as underlined by Zaveri et al. [14] who give a review on the use of coherence in the EEG field, proposed estimators generally have strong bias and variance which make the interpretation of real data intricate. To alleviate these difficulties, frequency bands may be defined. For instance, classical delta, theta, alpha, beta and gamma EEG bands can be used to average the coherence function (Razoumnikova [15]) or to compute the cross-correlation of filtered signals (Nikolaev et al. [16], Wendling et al. [17]). Again, this is not entirely satisfactory since the choice of frequency bands becomes critical in this case (relevant phenomena may overlap two bands).

In this paper, we present a novel estimator for characterizing the evolution of linear relationship between signals both in the time and frequency domains. This estimator is based on the computation of the Pearson Product-Moment correlation between EEG signals filtered, in narrow and overlapping frequency bands, using a continuous filter bank. Asymptotically, it gives the same value as that obtained with the classical coherence estimator (squared modulus of coherence function, periodogram method). However, application to simulated nonstationary signals shows that its performances (in terms of bias and variance) can be better. In addition, contrary to aforementioned methods, no assumption on frequency bands is required. The method has also been applied to real EEG signal intracerebrally recorded in epileptic patients candidate to surgery (Stereoelectroencephalography, SEEG). Results show that the method is able to track the evolution of relationship between signals in the time-frequency plane with a good resolution. They also show that the method may help to better analyze paroxysmal phenomena that occur at the onset of epileptic seizures.

II. Problem Statement and Methods

We are interested in measuring the degree of statistical time-frequency relationship between real signals. Our reference method is the coherence function computed in a sliding window. We compare this method with the linear correlation coefficient computed between corresponding outputs of a narrow-band filter bank applied to the two signals of interest.

We show, in the case of stochastic wide sense stationary signals, that these two kinds of measure correspond asymptotically to the same theoretical quantity.

We compare then these two estimators (in term of bias and variance) in different simulated situations for which the target is either derived by mathematical calculation or estimated by Monte-Carlo simulation. To make the two estimators comparable, the lengths of observation window and the frequency resolution (the shape and length of weighting functions) have to be the same.

Two kinds of simulation models are chosen to encompass different physiological situations that may be encountered in real data. In the first simulation (model M1), shared information of two analyzed signals has stochastic nature; whilst in the second simulation (model M2), it has deterministic nature.

The delay parameter between channels (generally optimized in correlation method) can be imposed in the case of having a priori information about its value (possibly zero); we investigate here the effect of this information on the estimator performances.

Finally, the application of these measures to real signals recorded during an epileptic seizure with typical signatures are presented and commented.

Problem statement

We assume an observation vector X(t) = {x₁(t), …, x_M(t)}; t ∈ [0, T] where x_i(t) is the signal recorded from the ith sensor. The problem is to characterize the statistical relationship, both in the time and frequency domains, between nonstationary signals x_i(t) and x_j(t), t ∈ [0, T] for a given pair (i, j) ∈ {1 … M}²; i ≠ j. Indeed, this relationship may be interpreted as a functional coupling between two brain sites recorded by sensors i and j. The coupling evolution provides essential information about the organization of epileptic processes during seizures.

Numerous functionals Ψ(P_{t, δ}), where P_{t, δ} is the joint probability of (x_i, x_j) over an interval of [t−δ/2, t + δ/2[, can be introduced for characterizing the statistical relationship between x_i and x_j in the time-frequency plane. In this paper we focus on the comparison of two of them: i) the squared modulus of a local coherence function |ρ_ij(t, f)|² and ii) a local linear correlation coefficient $R_{ij}^2(t,f)$, computed at the outputs of narrow band-pass filter, as the function of frequency and time, which is maximized for time delay. To our knowledge, the application of this latter method in the EEG field has never been reported.

Coherence function and frequency-dependent correlation coefficient

The squared modulus of the local coherence function is defined as below (Haykin et al. [18]):

$${\mathrm{\Psi }}_{\rho }(P_{t,\delta })=\mid {\rho }_{ij}(t,f){\mid }^2=\frac{\mid {\gamma }_{x_i{x}_j}(t,f){\mid }^2}{{\gamma }_{x_i{x}_i}(t,f)\mathrm{\hspace{0.17em} }{\gamma }_{x_j{x}_j}(t,f)}$$ (1)

where f is the frequency, γ_xixj, γ_xixi, and γ_xjxj designate the local power cross-spectral density or power auto-spectral densities during an interval [t−δ/2, t + δ/2] defined as:

$${\gamma }_{x_i,x_j}(t,f)=E\left\{FT({\stackrel{\sim }{x}}_i)(t,f)F{T}^{\ast }({\stackrel{\sim }{x}}_j)(t,f)\right\}$$

where FT(x̃_i) is the Fourier transform computed with respect to θ of locally weighted signal x̃_i(θ, t) = x_i(θ)h₀(θ−t), θ ∈ ℝ with h₀(θ), θ ∈ [−δ/2, δ/2] a weighting function (hamming window for example), and * stands for complex conjugate.

The local linear correlation coefficient $R_{ij}^2(t,f)$ is defined as follows:

$${\mathrm{\Psi }}_r(P_{t,\delta })=R_{ij}^2(t,f)=\underset{{\tau }_{\text{m}}\le \tau \le {\tau }_M}{max}(r^2(x_{i,f}(t),x_{j,f}(t+\tau )))$$ (2)

where

$$r^2(x_{i,f}(t),x_{j,f}(t+\tau ))=\frac{{cov}^2[x_{i,f}(t),x_{j,f}(t+\tau )]}{var[x_{i,f}(t)]·var[x_{j,f}(t+\tau )]}$$ (3)

is the linear correlation coefficient between signals x_i,f and x_j,f outputs of a band-pass filter whose impulse response is h(t, f) = h₁(t)cos(2πft), t ∈ ℝ (characterized by a central frequency f). τ_m and τ_M are respectively minimum and maximum a priori bounds for the time delay between signals x_i,f and x_j,f. Since τ_m and τ_M are very small relatively to δ, we can neglect their effects and choose h₁ identical to h₀.

In theory, both quantities |ρ_ij(t, f)|² and $R_{ij}^2(t,f)$ are equal to 0 for x_i independent from x_j and increase, up to a maximum value of +1, for increasing linear dependence between x_i and x_j.

In the stationary case, and if δ → ∞ we have:

$$\mid {\rho }_{ij}(t,f){\mid }^2\to \mid {\rho }_{ij}(f){\mid }^2=\frac{\mid {\gamma }_{x_i{x}_j}(f){\mid }^2}{{\gamma }_{x_i{x}_i}(f)\mathrm{\hspace{0.17em} }{\gamma }_{x_j{x}_j}(f)}$$

where ρ_ij(f) is the classical coherence function associated to a pair of stationary random signals (Bendat and Piersol [19]). Furthermore, when relaxing the constraint τ_m≤τ≤τ_M to τ ∈ ℝ and for h₁(t)cos(2πft), t ∈ ℝ, being the impulse response of a very-narrow band filter, (1) and (2) become asymptotically equivalent as demonstrated in appendix A. So, in the following, |ρ_ij(t, f)|² will be taken as a reference and we introduce estimators for (1) and (2) to measure it.

In practice, to be computed on digital signals sampled at frequency Fs, an estimation Ψ̂_t,δ(x_i, x_j) of Ψ(P_t,δ) must be introduced in each case. For discrete time signals |ρ_ij(t, f)|² in (1) becomes |ρ_ij[t, f]|², t ∈ ℤ and |f|<F_S/2. Estimators use N₀ = [δF_S] (where [.] designates the integer part of its argument) samples of x_i[n] ≜ x_i(n/F_S), n/F_S ∈ [t−δ/2, t + δ/2] for i =1, 2, (N₀ is thus the length of a discrete sliding observation window)

Typically, the squared modulus of the local coherence function is estimated using the periodogram method over a sliding window (divided into Nb overlapped blocks) with the central point at time t:

$$\mid {\widehat{\rho }}_{ij}[t,f]{\mid }^2=\frac{{\mid \sum _{k=1}^{Nb}{X}_i^k[f]X_j^{k^{\ast }}[f]\mid }^2}{\sum _{k=1}^{Nb}\mid X_i^k[f]{\mid }^2\sum _{k=1}^{Nb}\mid X_j^k[f]{\mid }^2}$$ (4)

where $X_i^k[f]$ is the Discrete Fourier transform (DFT) of x_i[n] weighted by Hamming window, with length L, in kth block of the sliding observation window.

The estimation of the local linear correlation coefficient $R_{ij}^2(t,f)$ is:

$${\widehat{R}}_{ij}^2[t,f]=\underset{{\tau }_{\text{m}}<\tau <{\tau }_M}{\mathit{max}}\left(\frac{{\left(\sum _{k=-H/2}^{H/2}{y}_{i,f}[k]·y_{j,f}[k+\tau ]\right)}^2}{\sum _{k=-H/2}^{H/2}{y}_{i,f}^2[k]·\sum _{k=-H/2}^H{y}_{j,f}^2[k+\tau ]}\right)$$ (5)

where y_.,f[t] = x_.,f[t−k] − x̄_.,f and x̄_.,f is the mean of x_.,f over a sliding window of duration H. Here H = N₀ − L to ensure using the same information from observed signals (it is worth to mention that here also we have neglected the effects of τ_m and τ_M because they are very small compared to L).

For 0 < f < Fs/2, an appropriate filter bank can be derived using the Short-Time Fourier Transform (STFT), as described in appendix B. To ensure to have the same frequency resolution for two estimators, the discrete impulse response of the band-pass filter is set to h[n]cos(2πfn/F_S) where h is the Hamming window used in (4).

Comparison of the two estimators

First, we compare the performance of two estimators in terms of bias and MSE (mean square error) through simulations in which the linear relationship between simulated signals x_i and x_j may vary as a function of time. In each simulation, target values for |ρ[t, f]|² are derived mathematically or computed by Monte-Carlo simulation using a large number of realizations. Then, both estimators are evaluated on real SEEG signals recorded from internal brain structures during seizure in a case of temporal lobe epilepsy (TLE).

• 1) Simulated signals: Comparative analyses of the two estimators are based upon two simulation models M1 and M2. These models are simple but rely on some physiological considerations.

Let S_i and S_j be two sensors whose outputs are x_i[t] and x_j[t]. Furthermore, let P_i and P_j be two neural populations recorded respectively by sensor S_i and S_j (P_i and P_j belong to two distinct brain structures). Our physiological hypothesis is that we have two partitions P_i = P_i1 ∪ P_i2 and P_j = P_j1 ∪ P_j2 where the two subpopulations P_i1 and P_j1 are interconnected by long neuronal fibers (the axons of pyramidal cells, see Martin [20]) and may synchronize with each other during ictal activities probably with a short mean time delay τ between activities of P_i1 and P_j1 (Nunez and Cutillo [21]). P_i2 and P_j2 are the neuronal subpopulations corresponding to the background activity without statistical relation with activities of P_i1 and P_j1. In our simulations, and without loss of generality, we imposed τ_m = τ_M = 0. The ictal activity of P_i1 and P_j1 may have, in many instances, less complexity (as defined in nonlinear dynamic systems theory; see Kantz and Schreiber [22]) than the background activities of P_i2 and P_j2.

These facts motivated the choice of model M1 and M2. In model M1 activities of P_i1 and P_j1 are random (non-deterministic), while in model M2 they are quasi-deterministic and may frequently exhibit dynamics similar to nonlinear oscillator’s outputs.

Model M1 is described by the following equations:

$$\begin{array}{l}{x}_1[t]=(1-\alpha [t])B_1[t]+\alpha [t]B_3[t]\\ x_2[t]=(1-\alpha [t])B_2[t]+\alpha [t]B_3[t]\end{array}$$ (6)

where B₁, B₂ and B₃ are three independent wide sense stationary (IWSS) random signals having power spectral density (PSD) γ_i(f), i=1,2,3 and 0≤α[t]≤1 represents the time-varying degree of relationship between generated signals. B₃ is interpreted as the shared physiological activity whereas B₁ and B₂ represent independent background activities.

The second model M2 is proposed to encompass the case in which a deterministic signal influences both x₁ and x₂ signals. In M2, simulated signals x₁ and x₂ are given by:

$$x_1[t]=B_1[t]+\alpha [t]C[t]\mathrm{\hspace{0.17em} };\mathrm{\hspace{0.17em} }{x}_2[t]=B_2[t]+\alpha [t]C[t]$$ (7)

where B₁ and B₂ are as before two background activities; C[t] and α[t] are respectively the deterministic signal and the degree of relationship.

• 2) Estimation of the bias, variance and MSE: Theoretical values of |ρ[t, f]|² are mathematically derived when α[t] is a constant in the model M1. For the cases of non-constant α[t] in M1 or M2 model, |ρ[t, f]|² is computed by Monte-Carlo simulation. They are used as target to estimate the bias and mean square error (MSE) of both estimators on signals generated with model M1 and M2. Bias, variance and MSE are respectively defined by E(θ̂−θ), E{(θ̂−E(θ̂))²} and E{(θ̂−θ)²} where θ = |ρ[t, f]|²and θ̂ = |ρ̂[t, f]|²or θ̂ = R̂²[t, f]. These expectations are estimated over a sufficiently large number of realizations (also by Monte-Carlo simulation).

The effects of the various parameters used in the estimator |ρ̂_ij[t, f]|² and R̂_ij²[t, f] were studied: the width of the sliding window, number of blocks for calculation of DFT, percentage of overlapping, and the time resolution of the STFT. For comparison purpose, the width of the sliding windows as well as the length and shape of the weighting functions were chosen the same for the two estimators.

• 3) Real SEEG signals: An illustrative example of nonstationary real EEG signals was chosen for direct comparison of both methods on real data. In this example, signals are recorded from two internal limbic structures (anterior hippocampus and amygdala) in a patient suffering from mesial TLE during a seizure. These two structures are anatomically interconnected. Several studies already reported that they may play an active role in the triggering of seizures in the temporal lobe.

In the presented case, they were found to be involved at the onset of seizures and to give rise to a characteristic electrophysiological pattern (spiking background activity followed by a rapid tonic discharge that gradually slows down, see Maldonado et al. [23]). Recordings were performed using multiple lead electrodes (10 to 15 leads, length: 2 mm, diameter: 0.8 mm, 1.5 mm apart) placed intracranially according to Talairach’s stereotactic method [24]. The positioning of electrodes was determined from available non-invasive information and hypothesis about the localization of his epileptogenic zone (defined as the cerebral regions simultaneously discharging at seizure onset). Signals are sampled at 256 Hz, digitized with precision of 16 bits/sample and stored on hard disk for further processing.

III. Results

Model M1, stationary situation

In the case where α is not dependent on time, signals x₁ and x₂ are stationary and the theoretical value of |ρ[t, f]|² can be derived:

$$\mid \rho [t,f]{\mid }^2=\frac{{\alpha }^4{\stackrel{\sim }{\gamma }}_{B_3}^2(f)}{\left({(1-\alpha )}^2{\stackrel{\sim }{\gamma }}_{B_1}(f)+{\alpha }^2{\stackrel{\sim }{\gamma }}_{B_3}(f)\right)\left({(1-\alpha )}^2{\stackrel{\sim }{\gamma }}_{B_2}(f)+{\alpha }^2{\stackrel{\sim }{\gamma }}_{B_3}(f)\right)}$$

where γ̃_Bi(f) is the PSD of product of discrete time signal B_i and weighting window h₀ in section 2.2. Here, we choose γ_B1(f) = γ_B2(f) = γ_B3(f) and hence:

$$\mid \rho [t,f]{\mid }^2=R^2[t,f]=\frac{{\alpha }^4}{{\left({(1-\alpha )}^2+{\alpha }^2\right)}^2}$$

Bias and MSE values (variance is equal to MSE minus squared bias) were computed for different lengths of the sliding window duration N₀ and different coupling parameter α (N₀ = 256 × k₁, k₁= 2,…,5; α = 0.1 × k₂, k₂ = 0, …,10). The length L, of blocks used in (4), was set to 256 points. Consequently, the frequency resolution of both estimators |ρ̂[t, f]|² and R̂²[t, f] is the same.

The overlapping percentage of two successive blocks in the computation of |ρ̂[t, f]|² was chosen by minimizing the mean square error (MSE) between theoretical and estimated values. The optimal overlapping rate was found to be equal to 0.8 although the MSE does not decrease considerably for percentages beyond 50% (this result corroborates those published in Carter [25]).

Bias and MSE values were first computed by Monte-Carlo simulation over the time-frequency plane (1 frequency bin corresponds to 1 Hz) and were found to be approximately constant. This result shows that in this case both estimators are independent from frequency and time. Thus, bias and MSE values can be averaged over time-frequency. Fig. 1 represents the bias and the MSE of both methods for 4 different values of N₀ and 11 values of α uniformly distributed between 0 and 1.

Fig. 1.

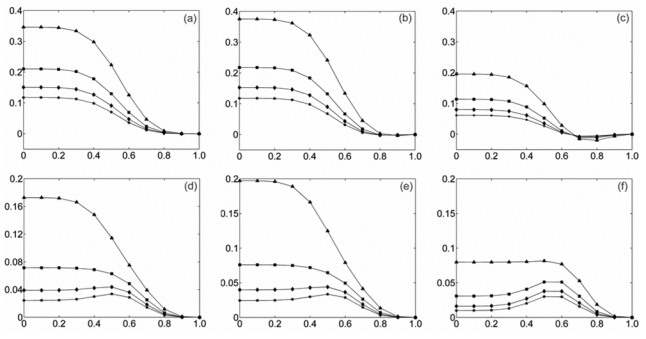
Bias and MSE of both estimators for model M1 (stationary situation, constant α[t]) for different duration N₀ of the sliding window a) Bias of |ρ̂[t, f]|². b) Bias of R̂²[t, f] with τ_M = −τ_m = 5. c) Bias of R̂²[t, f] with τ_m = τ_M = 0. d) MSE of |ρ̂[t, f]|². e) MSE of R̂²[t, f] with τ_M = −τ_m = 5. f) MSE of R̂²[t, f] with τ_m = τ_M = 0. These curves are obtained by Monte Carlo simulation for long duration signals and by averaging over time-frequency plane.

As depicted on this figure, bias and MSE are approximately equal when we use the constraint τ_M = −τ_m = 5 and for τ_m = τ_M =τ₀ (corresponding to the case where the time delay is known and equal to τ₀; here τ₀ = 0 = 0) the R̂²[t, f] has clearly smaller bias and MSE than |ρ̂[t, f]|².

This result was obtained for two different kinds of PSD: similar bias and MSE curves were obtained when B₁, B₂ and B₃ are white Gaussian noises or colored Gaussian noises with a 1/f power spectrum distribution similar to that of normal background EEG activity.

Model M1, nonstationary situation

Arbitrary profiles of evolutionary relationship were chosen for generating nonstationary signals x₁ and x₂. A scenario is provided in Fig. 2-a (dashed line) in which the evolution of α[t] was defined on four successive periods: linear increases from 0 to 1, constant period where α[t] = 1, constant period where α[t] = 0, linear decreases from 1 to 0. The target curve (Fig. 2-a, solid line) was computed from (Haykin et al. [18]):

Fig. 2.

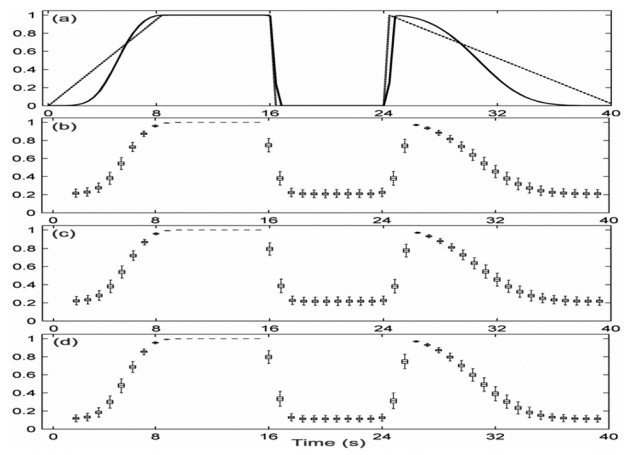
Performances of both estimators for model M1 (nonstationary situation, time-varying α[t] for N₀ =768. a) Time course of parameter α[t] (dashed line) and target relationship curve (solid line) averaged over frequency axis. Standard boxplots obtained by Monte-Carlo simulation for different estimators: b) |ρ̂[t, f]|², c) R̂²[t, f] with τ_M = −τ_m = 5, d) R̂²[t, f] with τ_m = τ_M = 0.

$$\mid \rho [t,f]{\mid }^2=\frac{{\mid \sum _{n=1}^N{X}_1^{(n)}[t,f]X_2^{\ast (n)}[t,f]\mid }^2}{\sum _{n=1}^N\mid X_1^{(n)}[t,f]{\mid }^2\sum _{n=1}^N\mid X_2^{(n)}[t,f]{\mid }^2}$$

where $X_i^{(n)}[t,f]$ denotes the STFT’s of the signal x_i, and the superscript (n) denotes the nth of N=10000 realizations of two signals. In the computation of STFT we have used Hamming temporal window of length of L=256 to ensure having the same frequency resolution for target and for both estimators.

As in the stationary case, both estimators were found to be frequency independent and thus estimated values of bias and variance were obtained by averaging along the frequency axis in order to facilitate their comparison to the target curve. Quantitative results displayed in Fig. 2, using boxplots, show that R̂²[t, f] has smaller bias and variance values compared to those of |ρ̂[t, f]|² when the time delay is known and equal to τ₀ (τ_m = τ_M = τ₀; here τ₀ = 0) and that the two estimators have similar performances, when the constraint τ_M = −τ_m = 5 is used, with however a better behavior of R̂²[t, f] around the rupture occurring at 16s and after the time instant 24 s.

Model M2, multi-component nonstationary situation

The common part C of x₁ and x₂ in (7) was extracted from a SEEG recording during an ictal period. It corresponds to a reproducible quasi-deterministic pattern observed during different ictal episodes of a patient.

The independent background activities B₁ and B₂of M2 where simulated by surrogating (randomization of phase in Fourier transform of same signal, see Schreiber and Schmitz [26]) a segment of real background SEEG of patient.

A large number of realizations (x₁[k], x₂[k]), 0≤k≤K, K/F_S = 40s,F_S =200Hz were simulated with $\overline{C^2}/{\sigma }_B^2=1.27$, where $\overline{C^2}$ denotes the temporal mean square value of C (estimated over its time support) and ${\sigma }_B^2={\sigma }_{B_1}^2={\sigma }_{B_2}^2$ is the variance of the surrogated data.

The target |ρ[t, f]|² was computed by Monte-Carlo procedure as in M1 for the case of time-varying α[t]. The visual inspection of the results, depicted on Fig. 3, reveals that the two estimators have similar behaviors (Fig. 3-b vs. 3-d) for τ_M = −τ_m= 5 and for known time delay τ_m = τ_M = τ₀ (here τ₀ = 0) the R̂²[t, f] seems to exhibit less bias than |ρ̂[t, f]|². In an attempt at quantifying the differences between the two estimators, mean of absolute values of bias, mean of variances and mean of MSE values over the time-frequency plane were calculated. The obtained values, reported in Table I, indicate that the R̂²[t, f] estimator has better performances than |ρ̂[t, f]|².

Fig. 3.

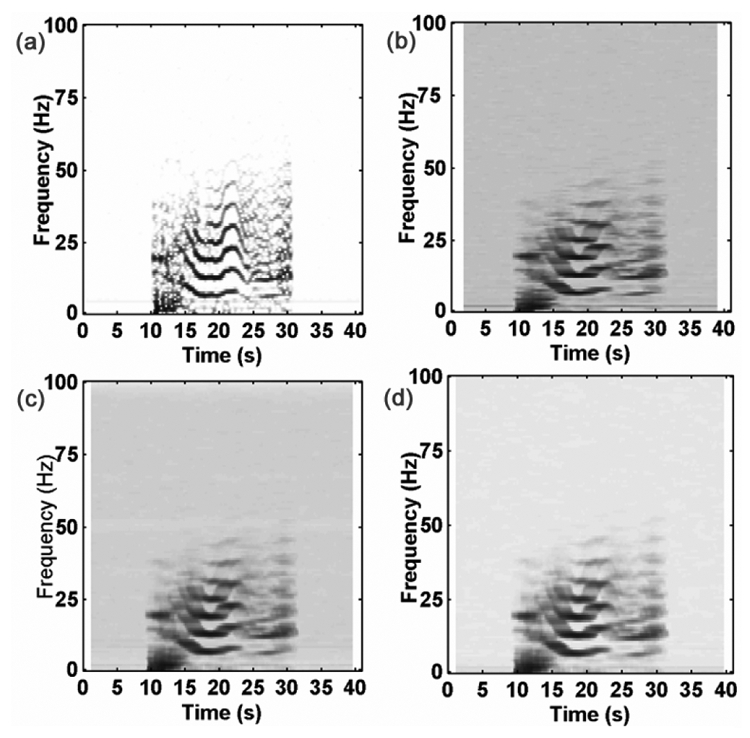
Model M2, nonstationary multi-component situation, a) Target time-frequency relationship obtained by Monte-Carlo simulation. Different estimations of target: b) |ρ̂[t, f]|², c) R̂²[t, f] with τ_m = τ_M = 0, d) R̂²[t, f] with τ_M = −τ_m = 5.

Real EEG signals

Results obtained on simulated signals using relatively short duration analysis windows show that statistical performances of R² estimator i) are equivalent to those of the coherence estimator when R² is maximized with respect to time delay τ and ii) are better (in terms of bias and mean square error) than those obtained with the coherence estimator when time delay τ is known.

This ability of both estimators to characterize a relationship between signals in the time-frequency plane is of great interest in the analysis of intracerebral SEEG signals recorded in epileptic patients candidate to surgery. Indeed, interdependencies between signals can be interpreted in terms of functional couplings between brain structures (possibly well localized in frequency) and thus provide essential information about the organization of the epileptogenic zone.

In order to verify if the results obtained on simulations also apply on real SEEG recordings, we chose an example of two SEEG signals recorded from temporal lobe brain structures (see section 2.3.3). These signals are representative of an observation that is often made at seizure onset. They are displayed in Fig. 4-a: after a period of background activity with sporadic spikes, a higher frequency activity (rapid discharge) is observed on both signals. The amplitude of this narrow band activity abruptly decreases and then gradually increases again while its frequency slows down. Both signals are nonstationary as depicted on Fig. 4-b that provides their respective spectrogram.

Fig. 4.

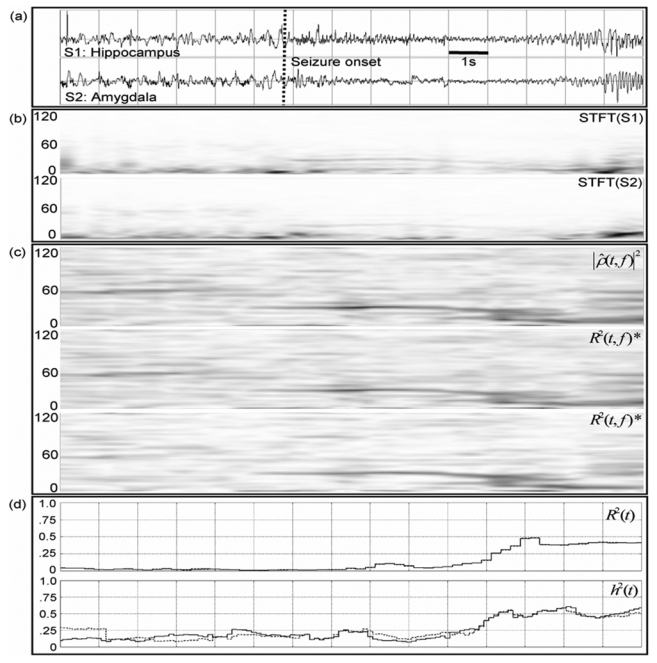
Results obtained on real data, a) Two SEEG signals recorded from hippocampus (top) and amygdala (bottom) in an epileptic patient (TLE) and b) corresponding spectrograms, c) Estimated relationship in the time-frequency plane for both methods. (*) Time-frequency representations of R̂²[t, f] maximized for time delay τ (middle, range −20 to 20 ms) and for fixed τ (bottom, τ_m = τ_M = 4 ms). d) Estimated relationship by two frequency-independent methods, one linear (r²[t], top) and the other nonlinear (h²[t], bottom).

The time-frequency characterization of the relationship between signals is illustrated in Fig. 4-c when performed with the estimator based on the coherence (first rectangle) and on the linear correlation coefficient maximized with respect to time delay τ (second rectangle, ranging from −20 ms to 20 ms).

As observed on simulated signals, both estimators lead to similar results: they reveal a similar signature characterized by a strong relationship that takes place over the narrow frequency band activity previously observed on spectrograms (around 30 Hz).

However, for fixed time delay τ (τ_m = τ_M =4ms), R̂²[t, f] provides a time-frequency representation of the relationship with enhanced readability when all the other parameters are set to provide identical time and frequency resolution in both methods. This result, displayed in Fig. 4-c (third rectangle), shows that the abrupt transition between SEEG dynamics (from background activity to rapid discharge) is also associated to an abrupt change of the frequency location of the linear relationship. As also noticed in simulations, the lower MSE of R̂²[t, f] with fixed τ leads to a time-frequency representation less noisy (in the sense of “easier to interpret”) than that obtained with the two previous estimators.

We also noticed that it is crucial to take frequency into account in some cases. Indeed, frequency-independent methods may not be able to reveal such a phenomenon of narrow band frequency hypersynchronization at seizure onset. We plotted the curves (Fig. 4-d) obtained with a linear estimator (linear correlation coefficient r²[t] maximized for the time delay, top) and with a nonlinear estimator (nonlinear correlation coefficient h²[t] maximized for the time delay, bottom) on the same analyzed signals. For detailed presentation regarding these two estimators, the reader may refer to Pijn [27]. One can notice that the two curves (Fig. 4-d) do not show significant changes during the transitions in EEG dynamics at seizure onset and are consequently unable to render some relevant information (i.e. the strong relationship between signals located on the narrow frequency band - about 30 Hz - and the abrupt jump of the relationship from the low to the higher frequency when background spiking activity changes into rapid discharge).

IV. Discussion and Conclusion

In the study of brain activity, the natural question about the functional coupling among cerebral structures or regions that generate EEG signals arises in numerous cases. It is addressed here through the characterization of linear interdependencies between SEEG signals in the context of epileptic processes. There are three main results in this study. First, characterizing the relationship in both time and frequency domains may be essential in some situations where this relationship is circumscribed within a particular region of the time-frequency plane (e.g. frequency-independent methods can be blind to relationships establishing on a narrow frequency band). Second, a novel estimator of the linear relationship as function of time and frequency which introduces a frequency dependent time delay has been proposed for nonstationary signals. On various simulations, this estimator has been shown to exhibit better statistical performances (bias and MSE) in comparison with a standard estimator based on the coherence function when a priori information is given about frequency dependent time delay value. Hence the user has the possibility to constrain coherence estimation using this information. Third, the proposed estimator has been used on real data and has also been found to enhance the readability of the time-frequency representation of the relationship for fixed time delay τ. Thus it can improve the interpretation of nonstationary interdependencies between SEEG signals. The choice of the relevant value of τ in a given time interval and in a given frequency band is actually under investigation. The key idea is to make use of a priori anatomical and physiological knowledge (neural pathways and their activations) and statistical results about propagation time delays in a data set built from a large number of patients: if generic reliable information about possible values of delays is available, this information can be used to improve performances of analysis methods of frequency dependent statistical relationship.

Table I.

Mean of the absolute values of bias, mean of the variances, and mean of MSE values computed over the time-frequency (TF) plane, for |ρ̂[t, f]|² and R̂²[t, f] (with τ_m = τ_M = 0; τ_M = −τ_m = 5).

Estimation	Mean of absolute value of bias over TF plane	Mean of variance over TF plane	Mean of MSE over TF plane
|ρ̂[t, f]|2	0.19014	0.0261	0.0702
R̂2[t, f], τm = τM = 0	0.09135	0.01278	0.02627
R̂2[t, f], τM = −τm = 5	0.1539	0.0178	0.04746

Appendix A

Let x₁ and x₂ be two real zero mean wide sense stationary stochastic process with covariance function: C_xi, _xj (τ) = E(x_i(t)x_j(t–τ)), τ∈ℝ; i,j ∈ {l,2} and corresponding power spectral density: γ_xi,_xj (f) = FT(C_xi,_xj)(f), f ∈ℝ where FT stands for the Fourier Transform.

The Coherence function between x₁ and x₂ is defined as:

$${\rho }_{x_1,x_2}(f)=\frac{{\gamma }_{x_1,x_2}(f)}{\sqrt{{\gamma }_{x_1,x_1}(f)·{\gamma }_{x_2,x_2}(f)}}$$

Property

Let us consider the real band-pass filter defined by:

$G\left(f\right)=\mathsf{1}(|f-f_0|<\mathrm{\Delta }f\mathit{\text{ OR }}|f+f_0|<\mathrm{\Delta }f)$, where $\mathsf{1}\left(A\right)=1$ if A is true and otherwise $\mathsf{1}\left(A\right)=0$, whose output is z₁ or z₂ when input is respectively x₁ or x₂ Let:

$$\mid r({\tau }^{\ast })\mid \simeq \underset{\tau }{max}\frac{\mid E(z_1(t)z_2(t-\tau ))\mid }{\sqrt{E({z_1}^2(t))E({z_2}^2(t-\tau ))}}$$

which is the absolute value of the correlation coefficient between the two zero mean real variables z₁ (t) and z₁,(t - τ), maximized relatively to the delay τ (the maximum is reached when τ = τ*). Then if Δf is small and γ_xixj is a continuous function at f = f₀ we have:

$$\mid r({\tau }^{\ast })\mid \simeq \mid {\rho }_{x_1,x_2}(f_0)\mid$$

Proof

$$\mid r({\tau }^{\ast })\mid =\underset{\tau }{max}\frac{C_{z_1,z_2}(\tau )}{\sqrt{C_{z_1,z_1}(0)C_{z_2,z_2}(0)}}=\underset{\tau }{max}\frac{\int {\gamma }_{z_1,z_2}(f)e^{i2\pi f\tau }df}{\sqrt{\int {\gamma }_{z_1,z_1}(f)df\int {\gamma }_{z_2,z_2}(f)df}}.$$

For small values of Δf:

$$\begin{array}{l}\mid r({\tau }^{\ast })\mid \simeq \underset{\tau }{max}\frac{({\gamma }_{x_1,x_2}(f_0)e^{i2\pi f_0\tau }+{\gamma }_{x_1,x_2}(-f_0)e^{-i2\pi f_0\tau })\mathrm{\Delta }f}{\sqrt{2{\gamma }_{x_1,x_1}(f_0)\mathrm{\Delta }f·2{\gamma }_{x_2,x_2}(f_0)\mathrm{\Delta }f}}\\ =\underset{\tau }{max}\frac{Re({\gamma }_{x_1,x_2}(f_0)e^{i2\pi f_0\tau })}{\sqrt{{\gamma }_{x_1,x_1}(f_0)·{\gamma }_{x_2,x_2}(f_0)}}\end{array}$$

since C_x1,_x2 (τ) ∈ℝ ⇒ {γ_x1,_x2 (f₀) = γ*_x1,_x2 (−f₀)} and since γ_xi,_xj is continuous at f = f₀.

For a complex number z and θ real $\underset{\theta }{max}Re(z{e}^{i\theta })=\mid z\mid$ (it is sufficient to equalize θ with −arg(z)) and hence:

$$\mid r({\tau }^{\ast })\mid \simeq \frac{\mid {\gamma }_{x_1,x_2}(f_0)\mid }{\sqrt{{\gamma }_{x_1,x_1}(f_0)·{\gamma }_{x_2,x_2}(f_0)}}=\mid {\rho }_{x_1,x_2}(f_0)\mid .$$

Appendix B

The continuous filter bank used is defined in the time domain as follows:

$$h_{v_0}(t)=h(t)·cos2\pi v_{0}t$$

where h(t) has the characteristics of a low-pass filter and is even, ν₀ an arbitrary frequency, and h_ν0(t) is the real part of h̃ν₀(t) = h(t).e^i2πν₀t. Thus for any real signal x(t), x*h_ν0 = Re(x*h̃_ν0); hence:

$$(x\ast {\stackrel{\sim }{h}}_{v_0})(t)=\left({\int }_{\Re }x(u)·h(t-u)·e^{-i2\pi v_{0}u}du\right)·e^{i2\pi v_{0}t}$$

As h is even:

$$(x\ast {\stackrel{\sim }{h}}_{v_0})(t)=\left({\int }_{\Re }x(u)·h(u-t)·e^{-i2\pi v_{0}u}du\right)·e^{i2\pi v_{0}t}$$

$$(x\ast {\stackrel{\sim }{h}}_{v_0})(t)=\mathit{STF}{T}_x(t,v_0)·e^{i2\pi v_{0}t}$$

where STFT_x is the short term Fourier transform of the x while using h for windowing.