Abstract
Degradable thiol-ene photopolymer networks were formed through radically mediated step growth reactions. Variations in the network structure were used to alter the initial and temporal moduli, mass loss profiles, and equilibrium swelling ratios. Mass loss rates varied with changes in the solvent concentration, monomer molecular weight, average monomer functionality, and concentration of degradable linkages. The time required for the networks to degrade completely ranged from 1.20 ± 0.01 to 24.5 ± 0.1 days, which corresponded to hydrolysis rates of 0.18 ± 0.01 and 0.021 ± 0.0003 days-1. Initial moduli also varied considerably as a function of network structure, ranging from 150 ± 35 to nearly 5000 ± 100 kPa, and initial equilibrium swelling ratios ranged from 2.5 ± 0.01 to 18.7 ± 2. Collectively, these results demonstrate how the material properties and the mass loss behavior of thiol-ene networks can be independently tuned for specific applications.
Keywords: degradable, thiol-ene, photopolymer
Introduction
As the fields of tissue engineering and sustained drug delivery have grown and expanded, so has the demand for improved biomaterials. In response to this demand, much research has focused on developing new biomaterials or improving existing systems.[1-12] While the design criteria driving this research cover as broad a range of material properties as diverse as the array of end-applications, they also share some common goals. Included among these goals is the desire to create biocompatible materials that have tunable material properties which allow optimal tissue regeneration and controllable drug delivery. Crosslinked, polymeric biomaterials are particularly attractive for these types of applications due to the wide range of material properties they are capable of achieving, their ability to degrade hydrolytically or enzymatically when properly designed, and their ability to imbibe large quantities of water while maintaining their mechanical integrity.
Crosslinked, degradable photopolymers are a set of polymeric biomaterials which are well suited for many tissue engineering and drug delivery applications. Previous research has demonstrated numerous advantages of using photopolymers for both bone and soft-tissue regeneration, as well as for the sustained delivery of growth factors, encapsulated proteins, and plasmid DNA.[3, 5, 13-24] One of the key advantages displayed by these photopolymeric materials is their ability to form highly crosslinked networks rapidly under physiological conditions while providing spatial and temporal reaction control. Additionally, many of the material properties and the degradation rate are strongly influenced by network structure. Network structure, in turn, is influenced by monomer chemistry and the polymerization conditions during network formation.
Previously, networks formed from the photoinitiated chain polymerization of multifunctional monomers have been studied and modeled, and the influence of a number of parameters, such as monomer molecular weight and solvent concentration present during polymerization, on network degradation was explored.[25, 26] Research involving hydrolytically degradable networks that were formed through Michael-type addition step growth reactions has qualitatively probed the impact of monomer molecular weight, monomer functionality, and the solvent concentration present during network formation on the swelling ratio, elastic modulus, and protein release rates.[27, 28] Additionally, the influence of monomer molecular weight on swelling ratios and cell invasion rates in enzymatically degradable Michael-type addition networks has also been documented.[29] Recent work by DeBose et al.[30] has focused more specifically on discovering how network structure in these Michael-type addition networks is controlled through variations in monomer functionality and solvent concentration. These researchers also quantified how variations in network structure impact the controlled release of molecules that were tethered to the network through a degradable linkage (i.e. a model protein: didansyl cysteine).
Here, the network structure of crosslinked thiol-ene photopolymers formed from PEG-based diallyl ethers and multifunctional thiol monomers was systematically varied through changes in solvent concentration, monomer molecular weight, monomer functionality, and the concentration of degradation sites (ester functionalities originating from the thiol monomers supply hydrolytically degradable sites throughout the network [31]). The impact of each of these parameters on the networks’ mass loss behavior, equilibrium swelling ratios, and compressive moduli were quantified initially and throughout network degradation. Additionally, mass loss and moduli profiles were predicted as functions of degradation time using a model developed for degradable step-growth networks.
Materials and Methods
Poly(ethylene glycol)-diallyl ether
Difunctional allyl ether monomers were synthesized from three different poly(ethylene glycol) (PEG) molecular weights using the following procedure. Tetrahydrofuran (THF) was dried overnight with sodium sulfate (both from Fisher Scientific), and 100 mL was added to every 10 g of each of the different PEGs (, 2000, or 4600 Da, Aldrich). This mixture was gently heated until the PEG dissolved and then cooled in an ice bath before sodium hydride (Aldrich) was slowly added in multiple portions (1.05 molar eq. NaH for the PEG R-OH groups). After the release of H2 gas ceased, the system was purged with argon and allyl bromide (1.1 molar eq. per PEG R-OH, diluted 1:10 in THF, Aldrich) was added dropwise using an addition funnel, after which the reaction mixture was transferred to an 85°C oil bath and refluxed overnight. Vacuum filtration was used to remove the sodium bromide side products and rotary evaporation was used to reduce the concentration of THF before the PEG-allyl ether products were precipitated from solution using iced diethyl ether (Fisher Scientific, 10:1 v:v diethyl ether:THF solution). The final product was analyzed by 1H NMR using a 500 mHz Inova by Varian and was shown to be at least 99% functionalized with allyl ether groups. The following data was obtained by the 1H NMR analysis: (CDCl3): 3.65 ppm (m, 91, 170, and 420 H for PEGs with of 1000, 2000, or 4600 Da, PEG-O-CH2-CH2-), 4.00 ppm (d, 3.96-4.06 H, PEG-O-CH2-CH=CH2), 5.17 ppm (d, 2.01 H, PEG-O-CH2-CH=CH2), 5.22 ppm (d, 2.00 H, PEG-O-CH2-CH=CH2), 5.88 ppm (q, 2.00 H, PEG-O-CH2-CH=CH2).
Monomer formulations
For all of the monomer formulations used in this study, equivalent moles of allyl ether and thiol functional groups were used, 0.1 wt% 1-[4-(2-Hydroxyethoxy)-phenyl]-2-hydroxy-2-methyl-1-propane-1-one (Irgacure 2959, I2959, Ciba) was added as a photoinitiator, and 50 wt% methylene chloride (Fisher Scientific) was used unless otherwise stated.
To ascertain how changing the solvent concentration present during photopolymerization impacts degradation behavior, monomer formulations containing 0, 30, and 50 wt% methylene chloride were prepared using PEG1000diallyl ether and pentaerythritol tetrakis(3-mercaptopropionate) (Figure 1, 1, Aldrich). The impact of monomer molecular weight on polymer degradation was probed using pentaerythritol tetrakis(3-mercaptopropionate) in combination with either the PEG1000diallyl ether, PEG2000diallyl ether, or PEG4600diallyl ether. The influence of average monomer functionality on network structure and degradation behavior was explored using mixtures prepared from PEG4600diallyl ether and varying ratios of pentaerythritol tetrakis(3-mercaptopropionate) and glycol dimercaptopropionate (Figure 1, 2, Evan’s Chemicals) such that the total mol% of the thiol groups coming from the tetrafunctional thiol monomer were 20, 50, and 80 mol%. Similarly, to study the impact of changes in the concentration of degradation sites within the network on degradation behavior, mixtures were prepared from 50 mol% PEG4600diallyl ether, 25 mol% pentaerythritol tetrakis(3-mercaptopropionate), and varying ratios of a degradable (glycol dimercaptopropionate) and non-degradable (2,2′-(Ethylenedioxy) diethanethiol, Figure 1, 3, Aldrich) difunctional thiol such that the fraction of functional groups coming from the nondegradable thiol monomer was ∼10, 15, or 20 mol%. The monomer formulations used for the various studies are summarized in Table 1.
Figure 1.
Thiol monomers used to make the thiol-allyl ether hydrogels: degradable tetrathiol: 1 pentaerythritol tetrakis(3-mercaptopropionate), degradable dithiol: 2 glycol dimercaptopropionate, non-degradable dithiol: 3 2,2′-(Ethylenedioxy) diethanethiol
Table 1.
Monomer formulations used to synthesize degradable thiol-ene photopolymer networks:
| mol% Functional Groups From: | ||||||
|---|---|---|---|---|---|---|
| Formulation | Solvent Concentration (wt%) | PEG Molecular Weight (Da) | Allyl Ether | Tetrathiol | Degradable Dithiol | Non-Degradable Dithiol |
| 1 | 0 | 1000 | 50 | 50 | ||
| 2 | 30 | 1000 | 50 | 50 | ||
| 3 | 50 | 1000 | 50 | 50 | ||
| 3 | 50 | 1000 | 50 | 50 | ||
| 4 | 50 | 2000 | 50 | 50 | ||
| 5 | 50 | 4600 | 50 | 50 | ||
| 6 | 50 | 4600 | 50 | 10 | 40 | |
| 7 | 50 | 4600 | 50 | 25 | 25 | |
| 8 | 50 | 4600 | 50 | 40 | 10 | |
| 9 | 50 | 4600 | 50 | 25 | 10 | 15 |
| 10 | 50 | 4600 | 50 | 25 | 15 | 10 |
| 11 | 50 | 4600 | 50 | 25 | 20 | 5 |
Formulations 1-3 vary the initial solvent concentration.
Formulations 3-5 vary the PEG molecular weight in the diallyl ether monomers.
Formulations 6-7 vary the average thiol monomer functionality by incorporating various ratios of a degradable dithiol.
Formulations 9-11 vary the concentration of degradable sites by replacing various amounts of the degradable dithiol with a nondegradable dithiol.
Polymer formation
The components of each monomer mixture were combined and stirred until completely mixed. The no solvent formulation (mixture 1, Table 1) was heated slightly before mixing to melt the PEG1000diallyl ether. Monomer formulations were injected into molds formed from two glass slides that were separated by a 0.9 mm thick layer of silicon rubber. Each of the monomer samples was exposed to 70 mW/cm2 of collimated UV light for 900 s before being removed from the molds, cut into smaller samples, dried under vacuum to remove the methylene chloride, and swollen in deionized water for a minimum of 18 hours. Evaporation of the methylene chloride polymerization was not observed during network formation using these conditions. Samples of each monomer formulation reached or exceeded 99% conversion of both the thiol and allyl ether functional groups using a technique that measures functional group concentration with real-time with mid IR (thiol conversion determined from the change in peak area at 2610-2490 cm-1, allyl ether conversion determined from change in peak area at 3110-3050 cm-1 [32, 33]).
Monitoring degradation behavior
Samples, swollen in water to equilibrium, were weighed wet, transferred to labeled tissue cassettes, placed in large jars of pH 8.0, 0.1 M phosphate buffer,[31] and placed in an incubated shaker (37°C, 100 rpm, MAXQ 4000, Barnstead/LabLine). Three samples of each polymer were not placed into the degradation buffer but were dried and reweighed to determine the average initial mass equilibrium swelling ratio (q) for the different polymer formulations. These initial q’s and the individual wet polymer weights were used to calculate the initial dry weight of each sample. At regular time intervals, samples were removed from the buffer, weighed wet, and transferred to deionized water to remove any buffer salts. A 5 mm disk was punched from each swollen sample and its modulus determined from the stress-strain curves generated when the disks were deformed at 0.1 mm/min in unconfined compression at room temperature (Synergie 100, MTS, cylindrical parallel plates, 1.9 cm in diameter). All samples were then frozen, lyophilized, and weighed dry, allowing their mass equilibrium swelling ratio and percent mass loss to be determined.[26, 32] The compressive moduli reported in this work were further normalized to account for variations in equilibrium swelling ratio as the networks degrade using eqn. 1 where Knorm is the normalized compressive modulus, K is the measured modulus, and q is the mass equilibrium swelling ratio.
| (1) |
Predicting mass and modulus changes as a function of degradation
A model was recently developed to describe changes in modulus and mass loss in degrading step-growth networks. The equations used to predict mass loss and modulus are described briefly in this publication, derivations of the equations are available in the appendix at the end of this work.
The effect of varying solvent concentration and monomer molecular weight on mass loss for thiol-ene networks synthesized from a tetrathiol and diene was predicted using eqn. 2. This equation accounts for the initial network composition, the extent of primary cycle formation, and the extent of degradation.
| (2) |
Here, WSH4 and WSH2 are the polymer weight fractions contributed by the degradable tetra and di functional thiol monomers; WSH2′ is the weight fraction contributed by the nondegradable dithiol monomer; Wene is the weight fraction contributed by the ene monomer; x and y are the probabilities that an ene or a thiol functional group, respectively, are part of a finite network and are not part of a cycle; fSH4,4, fSH4,2, and fSH4,0 are the fractions of degradable tetrathiol monomer that contain 0, 1, and 2 primary cycles, respectively; fSH2,0 and fSH2,2 are the fractions of degradable dithiol monomer molecules that are either part or not part of a primary cycle, respectively; fSH2′,0 and fSH2′,2 are the fractions of nondegradable dithiol monomers that are either part or not part of a primary cycle, respectively; fene2, is the fraction of ene monomers which are not part of a primary cycle; fene1, is the fraction of ene monomers which are part of a cycle on a thiol monomer that contains 1 cycle; fene0 is the fraction of ene monomers which are part of a cycle on a thiol monomer that contains 2 cycles; and P is the fraction of esters in the network that have degraded.
Equations 3-12 were used to describe how fSH4,4, fSH4,2, fSH4,0, fSH2,2, fSH2,0, fSH2′,2, fSH2′,0, fene2, fene1, and fene0 depend on the fraction of thiol monomers that are tetrafunctional (a4), the fraction of ene monomers that are part of a primary cycle (c), and the fraction of dithiol monomers that are degradable (A1). Equation 13 was used to determine P where khyd is the pseudo-first order rate constant for ester hydrolysis in these materials and t is the degradation time. Equations 14-15 were used to determine x and y. This model assumes 100% conversion during polymerization. Incomplete conversion would be accounted for through slight modifications to the expressions defining x and y.
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
Model predictions of the observed changes in compressive modulus as a function of the extent of degradation are correlated to changes in crosslinking density within these materials. For all of the thiol-ene networks investigated in this study, compressive moduli were predicted using eqn. 16 where K is the normalized compressive modulus at time t, and K0 is the normalized compressive modulus at time 0.
| (16) |
Calculating the extent of primary cyclization and predicting the initial modulus
In these swollen hydrogel materials, the crosslinking density and the compressive modulus are directly related,[26, 34, 35] and a decrease in compressive modulus corresponds to a decrease in crosslinking density. Changes in compressive modulus are expected when network structure is altered by changes in monomer molecular weight, monomer functionality, or the inclusion of network nonidealities such as primary cycles. This section describes how compressive modulus measurements were used to calculate c, the fraction of ene monomers that are part of a primary cycle.
Ideally, in the thiol-ene networks studied here, each tetrathiol monomer acts as a crosslink that connects two elastically active chains. When two thiol functional groups on the same monomer molecule react with two allyl ether groups on one PEG diallyl ether monomer, a primary cycle is formed. Every tetrathiol monomer that contains a primary cycle no longer acts as a crosslinking molecule. Instead, it behaves like a dithiol monomer, directly reducing the network’s crosslinking density. When a tetrathiol monomer contains two primary cycles, it is no longer connected to the network. Instead, these species are part of the soluble fraction that is extracted when the polymer networks are swollen in water prior to degradation. These three different tetrathiol reaction species are shown in Figure 2 where c‴ is the probability that a tetrathiol monomer contains one primary cycle, c″ is the probability that a tetrathiol monomer contains two primary cycles, and c‴ is the probability that a tetrathiol monomer contains no primary cycles.
Figure 2.

Schematic depicting tetrathiol monomers that contain one (c′), two (c″), or no c‴) primary cycles. Only c‴ contributes to the network’s crosslinking density, c′ acts as a linear chain extender but does not act to connect two elastically active chains, and c″ is part of the soluble fraction that is extracted from the network prior to degradation.
The relationships between the fraction of pairs of thiol functional groups that are part of primary cycles, c, and the fraction of thiol monomers that contain 0, 1, or 2 primary cycles are shown in eqns. 17-19. These equations are based on the probability of having thiol monomers that contain 0, 1, or 2 primary cycles at a given extent of primary cycle formation.
| (17) |
| (18) |
| (19) |
In an ideal network no primary cycles are formed and c′ = c″ = 0, while c‴ = 1. In these networks, the crosslinking density (ρx) is equivalent to twice the concentration of tetrathiol monomer (eqn. 20) because each arm of the thiol monomer is attached to half of an infinite chain. In reality, the formation of primary cycles decreases the network crosslinking density, and c‴ = 1 − c′ − c″. This decrease in crosslinking density decreases the experimentally measured compressive moduli from values that are predicted for networks where c‴ = 1. Since the theoretically predicted moduli (Ktheo) are based on a c‴ of 1 and the actual moduli are based on a c‴> = 1 − c′ − c″, the ratio of the measured and theoretical moduli is useful in determining the actual degree of cyclization (eqns. 21 and 22). In eqn. 21, K0 is the initial modulus that has been normalized to account for the initial swelling ratio (q0) and the swelling ratio during network formation (qNF). This adjustment is achieved using eqn. 22 where Kmeasured is the compressive modulus that was measured experimentally.
| (20) |
| (21) |
| (22) |
The theoretical compressive modulus, Ktheo, is easily calculated from eqns. 23 and 24 when the correct monomer molecular weights and densities are used to approximate the ideal crosslinking densities.[36, 37] In these equations, Etheo is the theoretical Young’s modulus; R is the gas constant; T is the temperature in Kelvin; and ρx is the ideal crosslinking density (assuming no cyclization). Equation 20 was used to calculate ρx where the moles of tetrathiol monomer directly equate to twice the moles of crosslinks, and the polymerization volume was calculated from the monomer molecular weight, monomer functionality, and monomer density (1.28 g/mL and 1.09 g/mL for the tetrathiol and PEG, respectively). Equation 24 was used to transform the theoretical Young’s moduli to theoretical compressive moduli, Ktheo.[38] A Poisson ratio (νp) of 0.42 was used for this correlation.[39, 40]
| (23) |
| (24) |
Results and Discussion
The aim of this research was to explore systematically how network structure at the molecular level impacts mass loss behavior and mechanical properties of degradable thiol-ene based photopolymer systems. To this end, four variables that impact network structure were selected and the mass loss behavior and mechanical properties of the thiol-allyl ether photopolymers that resulted were investigated. The parameters chosen for this study were the solvent concentration present during network formation, the monomer molecular weight, the monomer functionality, and the concentration of degradable groups in the crosslinked network. Each of these parameters alters network structure and should impact the measurable quantities of interest: mass loss, equilibrium swelling ratio, and compressive modulus.
Concentration of solvent present during network formation
The first parameter, solvent concentration, has the potential to impact the extent of primary cyclization during network formation (Figure 3). An increase in primary cyclization in networks formed through step growth reactions reduces the crosslink density, reducing the number of ester groups that must hydrolyze to release portions of the network that contain primary cycles.
Figure 3.
Schematic of how an increase in cyclization, which may occur when the solvent concentration present during network formation is increased, impacts network structure.
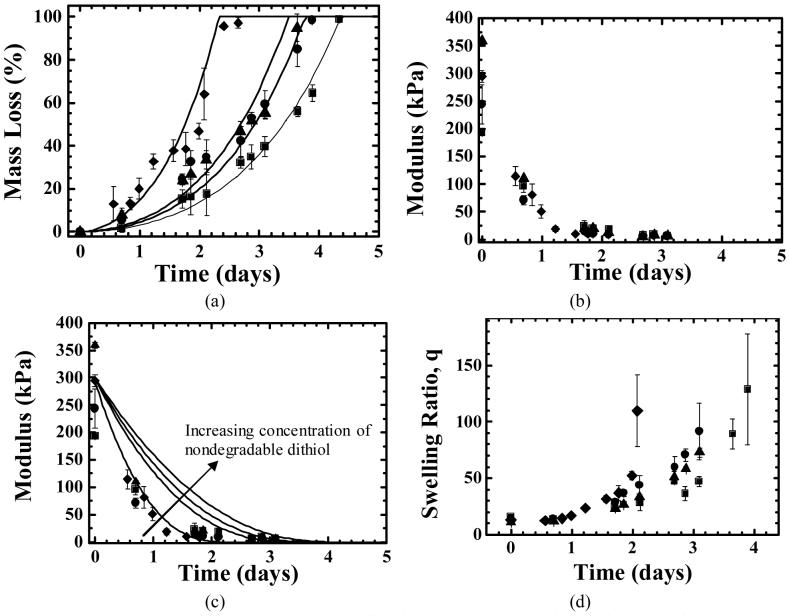
The data in Figure 4 shows how the mass loss profiles, compressive moduli, and equilibrium swelling ratios changed as a function of degradation time for thiol-allyl ether networks synthesized in the presence of 0, 30, and 50 wt% solvent. Examining the data in Figure 4a reveals that as the solvent concentration was increased, the degradation rate also increased, shifting the mass loss profiles to the left and reducing the time required for the networks to reach complete mass loss from 25.5 ± 0.1 to 14.8 ± 0.1 days. The data in Figure 4b confirm that as the initial solvent concentration was increased, the initial normalized compressive modulus (K0) decreased. Additionally, as these networks degraded, ester groups were being hydrolyzed, decreasing the crosslinking density. This change in network structure is reflected in the time-dependent changes in the normalized compressive modulus profiles, which revealed a nearly exponential decrease with increasing degradation time. In Figure 4c, the mass equilibrium swelling ratio (q) data reveal that as the solvent concentration was increased, the rate at which the equilibrium swelling ratio increased was accelerated. The initial swelling ratios also increased with increasing solvent concentration from 2.5 ± 0.005, to 2.9 ± 0.02, to 3.6 ± 0.2. These observations make sense since increasing the extent of ester hydrolysis and increasing the initial solvent concentration both decrease crosslinking density, which is inversely related to the equilibrium swelling ratio.
Figure 4.
a) Mass loss (%), b) normalized compressive modulus (kPa), and c) mass equilibrium swelling ratio as a function of time for thiol-allyl ether networks synthesized in the presence of 0 (▲), 30 (∎), and 50 (◆) wt% methylene chloride. Mass loss and compressive moduli predictions were made using the khyd and c values in Table 2. Model predictions of the mass loss and moduli curves are also included (solid lines). Note: the last point on the swelling ratio curve for the 50 (◆) wt% methylene chloride data is at 14.6 days and a q of 85 ± 38 but is not shown because it is off the y-axis’ scale.
The model predictions of the mass loss extent and compressive modulus as a function of degradation time are also shown in Figure 4. These curves were calculated using eqns. 2-16 and experimentally determined extents of primary cyclization and ester hydrolysis rate constants (c and khyd). The khyd and c values used to predict the moduli and mass loss profiles of these three networks are presented in Table 2. The c values in this table were calculated from deviations between the ideal, calculated initial compressive moduli and the experimentally observed values using eqn. 21, and khyd values were determined using regression analysis to minimize the error between compressive modulus measurements and predictions (which assume a pseudo first order degradation rate). Examining the khyd values reveals similar ester hydrolysis rate constants for the networks made with 30 and 50 wt% solvent. Interestingly, a significantly smaller khyd value was calculated for the networks made in the absence of solvent.
Table 2.
khyd, c, a4, and (1-a4)A1 values used to predict mass loss and changes in compressive moduli for the various thiol-allyl ether networks studied.
| Formulation | khyd (days-1)α | cβ | a4γ | (1-a4)A1γ |
|---|---|---|---|---|
| 1 | 0.021 ± 0.004 | 0.01 ± 0.00 | 1 | |
| 2 | 0.032 ± 0.002 | 0.06 ± 0.02 | 1 | |
| 3 | 0.034 ± 0.001 | 0.11 ± 0.03 | 1 | |
| 3 | 0.034 ± 0.001 | 0.11 ± 0.03 | 1 | |
| 4 | 0.063 ± 0.003 | 0.31 ± 0.05 | 1 | |
| 5 | 0.09 ± 0.010 | 0.18 ± 0.03 | 1 | |
| 6 | 0.18 ± 0.01 | 0.19 ± 0.09 | 0.2 | 0.8 |
| 7 | 0.14 ± 0.01 | 0.29 ± 0.01 | 0.5 | 0.5 |
| 8 | 0.10 ± 0.005 | 0.25 ± 0.01 | 0.8 | 0.2 |
| 9 | 0.08 ± 0.003 | 0.39 ± 0.00 | 0.5 | 0.1 |
| 10 | 0.10 ± 0.002 | 0.35 ± 0.05 | 0.5 | 0.2 |
| 11 | 0.11 ± 0.01 | 0.21 ± 0.01 | 0.5 | 0.3 |
The rates of ester hydrolysis (khyd) were determined from experimental fits of the modulus data for each monomer formulation.
The extents of cyclization (c) were determined from deviations between the measured and ideal initial moduli. Ideal initial moduli were based on the initial moduli of formulation 1 and account for variations in initial swelling ratio and the concentration of solvent present during network formation.
a4 and (1-a4)A1 values are the fraction of thiol functional groups coming from the degradable tetrathiol and dithiol monomers, respectively. These values are calculated from the monomer formulation data shown in Table 1.
One possible explanation for this observation is that, for networks where the initial swelling ratio is less than 10, differences in the initial water concentration cannot be neglected and have the potential to impact khyd. For example, the initial water content of the networks made with 0 and 50 wt% solvent are 60 and 73%, which corresponds to more than a 20% increase in water concentration. Furthermore, while this difference in initial water concentration may not entirely explain the increase in khyd that was observed when the solvent concentration was increased from 0 to 50 wt%, it may allude to differences in the availability of the ester groups for hydrolysis between these two networks, which could be responsible for the observed differences in khyd.
Further, all three networks exhibit low soluble fractions (less than 4 wt%, values listed in Table 3), and while the sol fraction did increase three-fold when the solvent concentration was increased from 0 to 50 wt%, the magnitudes of the measured sol fractions are too small to influence the khyd significantly. Finally, while the mechanism responsible for this deviation in khyd is not completely understood, similar behavior has been observed by others for degradable polymer networks formed from chain growth and step growth reaction mechanisms.[26, 30, 35]
Table 3.
Experimental and predicted sol fractions for the various polymer networks investigated in this study.
| sol faction (%) | ||
|---|---|---|
| Formulation | Experimental | predicted |
| 1 | 0.9 ± 0.4 | 0.01 |
| 2 | 3 ± 1 | 0.3 |
| 3 | 3 ± 1 | 1 |
| 3 | 3 ± 1 | 1 |
| 4 | 9 ± 1 | 10 |
| 5 | 5 ± 3 | 3 |
| 6 | 19 ± 2 | 17 |
| 7 | 11 ± 1 | 15 |
| 8 | 9 ± 2 | 8 |
| 9 | 16 ± 2 | 23 |
| 10 | 19 ± 5 | 19 |
| 11 | 11 ± 3 | 10 |
The increase in the number of primary cycles formed in networks synthesized from monomer solutions with increasing solvent concentration is most likely due to decreases in the bulk concentration of reactive functional groups. The formation of primary cycles depends heavily on the relative ratio of local and bulk reactive group concentrations.[36, 41] Increasing solvent concentration effectively decreases the bulk concentration of reactive groups without impacting the local concentration, creating an environment that favors intramolecular reactions. While this phenomena is well documented for polymerizations that occur by chain growth mechanisms,[41] much lower concentrations of primary cycles are expected to form in the thiol-ene polymers investigated in this study because the ratio of local and bulk reactive groups are substantially lower.[41] The c values that were calculated from the initial, experimentally determined moduli agree with experimentally determined[30, 42] and theoretically predicted[36] values reported in the literature.
Monomer molecular weight
As monomer molecular weight increases, so does the molecular weight between crosslinks, inversely affecting the crosslinking density. The data in Figure 5 show how mass loss profiles, compressive moduli, and equilibrium swelling change as a function of degradation time for polymer networks made from diallyl ether monomers with PEG1000, PEG2000, and PEG4600 cores. The mass loss profiles shown in Figure 5a for these networks display slow rates of mass loss at early stages of degradation. As the degradation time increases, however, the extent of mass loss steadily increases, displaying a nearly exponential increase in mass loss with increasing degradation time. The data in this figure also reveals an increase in the mass loss rate with increasing diallyl ether monomer molecular weight. The mass loss predictions from equations 2-15 and the c and khyd values listed in Table 2 fit the behavior exhibited by the networks made from the PEG1000 and PEG2000 dially ethers. Additionally, while the model does not capture the mass loss behavior exhibited by the PEG4600 networks, the model and the experimental data both exhibit the same trends in mass loss profiles with increasing monomer molecular weight: the PEG4600 allyl ether degraded the fastest, followed by the PEG2000 networks, and then the PEG1000 networks. The c and khyd values used to predict mass loss for these three networks were determined using the same procedures outlined for the networks made with varying solvent concentrations and are listed in Table 2.
Figure 5.
a) Mass loss (%), b) normalized compressive modulus (kPa), and c) mass equilibrium swelling ratio as a function of degradation time for thiol-allyl ether networks made from PEG-based diallyl ether monomers with of 4628 (◀), 2000 (●), and 1000 (◆) Da. Mass loss and compressive moduli predictions were made using the khyd and c values listed in Table 2. Model predictions of the mass loss and moduli curves are also included (solid lines).
The model predictions and experimentally determined modulus data in Figure 5b are in excellent agreement. This figure also confirms that increasing the PEG molecular weight in the diallyl ether monomers decreased the initial compressive modulus and increased khyd. Increasing PEG molecular weight also accelerated the rate at which the equilibrium swelling ratios increased (Figure 5c) and increased the initial equilibrium swelling ratios (3.6 ± 0.2, 7.4 ± 0.3, and 7.6 ± 0.1 for networks made from PEG1000, PEG2000 and PEG4600 diallyl ethers, respectively). This observed increase in equilibrium swelling behavior is expected since an increase in PEG molecular weight increases the network’s PEG weight fraction and decreases the crosslinking density.
Monomer functionality
In these step-growth networks, different ratios of dithiol and tetrathiol monomers were mixed with the PEG4600 diallyl ether to create monomer mixtures having systematically varying average monomer functionalities ranging from 2.4 to 3.6 thiol groups per monomer. The data in Figure 6 show how mass loss profiles, compressive moduli, and equilibrium swelling ratios change as a function of degradation time for networks containing various amounts of dithiol monomer. The results shown in Figure 6a indicate that an increase in the amount of dithiol in these networks increases the mass loss rate and decreases the time required to reach complete mass loss from 4.45 ± 0.05 to 1.20 ± 0.01 days. Model predictions that account for variations in crosslinking density and khyd capture the mass loss trends observed for the experimental data quite well.
Figure 6.
a) Mass loss (%), b) normalized compressive modulus (kPa), and c) mass equilibrium swelling ratio as a function of time for step-growth networks made from PEG4628 diallyl ether and varying ratios of tetrathiol and dithiol monomers where 80 (∎), 50 (◆), or 20 (▲) mol% of the thiol functional groups are contributed by the dithiol. Mass loss and compressive moduli predictions were made using the khyd and c values in Table 2, respectively. Model predictions of the mass loss and moduli curves are also included (solid lines).
The data shown in Figure 6b indicate that an increase in the amount of dithiol in these networks decreases the initial compressive modulus. Additionally, the model predictions for changes in compressive modulus capture the trends observed for all of these networks where the average thiol monomer functionality was varied, but they only accurately predict the changes in compressive moduli for the networks that had 50 and 80 % of their thiol functional groups originating from the dithiol monomer. The model fails to predict the observed changes in modulus for the networks made from 20 mol% dithiol
The equilibrium swelling data shown in Figure 6 display an acceleration in the rate that the swelling ratio increases when the concentration of dithiol was increased. The initial equilibrium swelling ratios increased from 9.1 ± 0.2 to 12.9 ± 0.01 to 18.7 ± 2.0 as the dithiol concentration was increased from 20 to 50 to 80 percent of the total thiol functional groups within the networks. Since an increase in the amount of dithiol in these systems corresponds to a decrease in crosslink density, increasing the amount of dithiol increases the amount of water the crosslinked networks imbibes at equilibrium.
The model parameters used to predict the mass loss profiles and changes in compressive moduli for these networks are found in Table 2. While changes to network structure through variations in initial solvent concentration and monomer molecular weight have corresponded to significant changes in the ester hydrolysis rate constant, increasing the concentration of dithiol from 20 to 50 mol% only slightly increases khyd, and a further increase to 80 mol% dithiol does not impact khyd at all. This result is not surprising considering the similarities in the tetrathiol and dithiol monomer chemistries and the Wene for the different networks, and is a significant outcome because it identifies a set of polymer networks where variations in network structure are primarily responsible for the observed variations in mass loss profiles.
Varying the concentration of degradation sites
Thiol-allyl ether networks were fabricated from diallyl ether, tetrathiol, and dithiol monomers with a portion of the original dithiol monomer replaced with a dithiol that did not contain any hydrolyzable ester groups (Figure 7). Prior to degradation, this change in monomer composition is not expected to impact the structure of the polymerized networks. However, once ester hydrolysis commences, the network compositions with a higher concentration of nondegradable thiol monomers will lose mass more slowly.
Figure 7.
Schematic of how decreasing the concentration of degradable groups through the incorporation of a nondegradable dithiol into the crosslinked network impacts network structure both initially (a) and part way through degradation (b).
Replacing degradable dithiol monomers with similar nondegradable dithiol monomers should decrease the observed mass loss rates. The data in Figure 8a confirm that this trend is observed when the amount of nondegradable dithiol monomer is decreased. The model’s mass loss predictions capture the trends observed in the experimental data. Additionally, for samples made with 20-80 % non degradable dithiol, the khyd values used to predict the mass loss behavior are identical. The observed variations in the predicted mass loss profiles are only due to differences in the network’s structures caused by different concentrations of degradable sites. The best agreement between the model predictions and the experimental data was observed for the networks made from monomer mixtures that had 10 and 50 % of their thiol functional groups contributed by the degradable dithiol.
Figure 8.
a) Mass loss (%), b) normalized compressive modulus (kPa), and c) mass equilibrium swelling for step-growth networks made from PEG4628 diallyl ether and varying ratios of degradable tetrathiol, degradable dithiol, and nondegradable dithiol monomers where 0 (◆), 10 (▲), 20 (●), or 30 (∎) mol% of the thiol functional groups are contributed by the nondegradable monomer. Mass loss and compressive moduli predictions were made using the khyd and c values in Table 2, respectively. Model predictions of the mass loss and moduli curves are also included (solid lines).
Figure 8b plots the normalized compressive modulus as a function of degradation time for these four networks. Interestingly, the initial compressive moduli are statistically different, and with the exception of the data set that contains no nondegradable dithiol, appear to increase as the concentration of nondegradable dithiol decreases. This result was unexpected since the changes in polymer composition between the various networks should not affect their initial crosslinking density, and are therefore not expected to alter the initial compressive modulus. Additionally, similar compressive moduli were observed for all of these samples once degradation commenced. This behavior is not captured by the model results shown in Figure 8c, which predict an increase in modulus with increasing concentration of nondegradable dithiol. While the factors responsible for this behavior are far from understood, these observations identify a set of materials that warrant further research due to their potential to afford control of the network’s mass loss behavior independently from the its compressive modulus.
A slight difference in the equilibrium swelling ratios is observed in Figure 8d as degradation time increased when the amount of non-degradable dithiol was increased. This subtle change is expected since the nondegradable dithiol monomers decrease the amount of ester hydrolysis that occurs throughout the network and allow the networks to maintain its structural integrity, as seen in Figure 7b. Increasing the nondegradable dithiol within the networks caused only small changes in the initial swelling ratio (12.9 ± 0.01, 16.0 ± 0.01, 14.1 ± 1.7, 11.3 ± 0.2 for 0, 10, 20, and 30 mol% of the entire thiol group population being contributed by the nondegradable thiol monomer).
Conclusions
Degradable thiol-ene photopolymers can be systematically synthesized to exhibit a wide range of degradation behavior and mechanical properties. The polymer network compositions studied here examined how four different parameters impact network structure for thiol-ene step growth materials. The parameters that were chosen were 1) the solvent concentration present during network formation, 2) the monomer molecular weight, 3) the average monomer functionality, and 4) the concentration of degradable groups within the network. The influence of each of these parameters was determined from three different types of measurements: mass loss, modulus, and equilibrium swelling ratio. Mass loss rates were observed to vary significantly with increasing solvent concentration, monomer molecular weight, and monomer functionality, with the fastest and slowest degrading samples reaching complete mass loss in 1.2 and 25 days, respectively. These observations correspond to hydrolysis rates of 0.15 and 0.021 days-1. Initial moduli also varied considerably in response to variations in network crosslinking density, ranging from 150 to nearly 5000 kPa, while initial equilibrium swelling ratios ranged from 2.5 to 18.7.
Further, a model was used to understand better changes in the mass loss and modulus profiles as functions of degradation time for the different networks investigated in this study. In general, the predicted curves capture the trends exhibited by the experimentally measured data, and the model equations used to calculate both the fractional decrease in crosslinking density and the fractions of the different network components that are released at a given extent of network degradation strongly depend on network structure. In summary, this work highlights how many of the material properties and mass loss behavior of thiol-ene photopolymers may be independently tuned for specific biomaterial applications.
Supplementary Material
Acknowledgments
The authors thank their funding sources for this work, a grant from the NIH (R01 DE12998), an NSF Industry/University Cooperative Research Center for Fundamentals and Applications of Photopolymerization, and a Department of Education GAANN fellowship and a University of Colorado Beverly Sears Graduate Student Grant to AER.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Anseth KS, Metters AT, Bryant SJ, Martens PJ, Elisseeff JH, Bowman CN. Journal of Controlled Release. 2002;78(13):199–209. doi: 10.1016/s0168-3659(01)00500-4. [DOI] [PubMed] [Google Scholar]
- 2.Anseth KS, Quick DJ. Macromolecular Rapid Communications. 2001;22(8):564–572. [Google Scholar]
- 3.Bryant SJ, Anseth KS. Biomaterials. 2001;22(6):619–626. doi: 10.1016/s0142-9612(00)00225-8. [DOI] [PubMed] [Google Scholar]
- 4.Bryant SJ, Bender RJ, Durand KL, Anseth KS. Biotechnology and Bioengineering. 2004;86(7):747–755. doi: 10.1002/bit.20160. [DOI] [PubMed] [Google Scholar]
- 5.Burdick JA, Anseth KS. Biomaterials. 2002;23(22):4315–4323. doi: 10.1016/s0142-9612(02)00176-x. [DOI] [PubMed] [Google Scholar]
- 6.Cellesi F, Tirelli N, Hubbell JA. Macromolecular Chemistry and Physics. 2002;203(1011):1466–1472. [Google Scholar]
- 7.Elbert DL, Hubbell JA. Biomacromolecules. 2001;2(2):430–441. doi: 10.1021/bm0056299. [DOI] [PubMed] [Google Scholar]
- 8.Lutolf MP, Raeber GP, Zisch AH, Tirelli N, Hubbell JA. Advanced Materials. 2003;15(11):888–892. [Google Scholar]
- 9.Sawhney AS, Pathak CP, Hubbell JA. Macromolecules. 1993;26(4):581–587. [Google Scholar]
- 10.West JL, Hubbell JA. Macromolecules. 1999;32(1):241–244. [Google Scholar]
- 11.Langer R, Peppas NA. Aiche Journal. 2003;49(12):2990–3006. [Google Scholar]
- 12.Wang Y, Ameer GA, Sheppard BJ, Langer R. Nature Biotechnology. 2002;20:602–606. doi: 10.1038/nbt0602-602. [DOI] [PubMed] [Google Scholar]
- 13.Nuttelman CR, Tripodi MC, Anseth KS. Matrix Biology. 2005;24(3):208–218. doi: 10.1016/j.matbio.2005.03.004. [DOI] [PubMed] [Google Scholar]
- 14.Quick DJ, Macdonald KK, Anseth KS. Journal of Controlled Release. 2004;97(2):333–343. doi: 10.1016/j.jconrel.2004.03.001. [DOI] [PubMed] [Google Scholar]
- 15.Masters KS, Shah DN, Walker G, Leinwand LA, Anseth KS. Journal of Biomedical Materials Research Part A. 2004;71A(1):172–180. doi: 10.1002/jbm.a.30149. [DOI] [PubMed] [Google Scholar]
- 16.Nuttelman CR, Tripodi MC, Anseth KS. Journal of Biomedical Materials Research Part A. 2004;68A(4):773–782. doi: 10.1002/jbm.a.20112. [DOI] [PubMed] [Google Scholar]
- 17.Rice MA, Martens P, Bryant SJ, Mahoney MJ, Bowman CN, Anseth KS. Abstracts of Papers of the American Chemical Society. 2004;228:U391–U391. [Google Scholar]
- 18.Quick DJ, Anseth KS. Pharmaceutical Research. 2003;20(11):1730–1737. doi: 10.1023/b:pham.0000003368.66471.6a. [DOI] [PubMed] [Google Scholar]
- 19.Bryant SJ, Anseth KS. Journal of Biomedical Materials Research Part A. 2003;64A(1):70–79. doi: 10.1002/jbm.a.10319. [DOI] [PubMed] [Google Scholar]
- 20.Poshusta AK, Burdick JA, Mortisen DJ, Padera RF, Ruehlman D, Yaszemski MJ, Anseth KS. Journal of Biomedical Materials Research Part A. 2003;64A(1):62–69. doi: 10.1002/jbm.a.10274. [DOI] [PubMed] [Google Scholar]
- 21.Bryant SJ, Anseth KS. Journal of Biomedical Materials Research. 2002;59(1):63–72. doi: 10.1002/jbm.1217. [DOI] [PubMed] [Google Scholar]
- 22.Burdick JA, Mason MN, Hinman AD, Thorne K, Anseth KS. Journal of Controlled Release. 2002;83(1):53–63. doi: 10.1016/s0168-3659(02)00181-5. [DOI] [PubMed] [Google Scholar]
- 23.Burdick JA, Padera RF, Huang JV, Anseth KS. Journal of Biomedical Materials Research. 2002;63(5):484–491. doi: 10.1002/jbm.10298. [DOI] [PubMed] [Google Scholar]
- 24.Burdick JA, Mason MN, Anseth KS. Journal of Biomaterials Science-Polymer Edition. 2001;12(11):1253–1265. doi: 10.1163/156856201753395789. [DOI] [PubMed] [Google Scholar]
- 25.Metters AT, Anseth KS, Bowman CN. Journal of Physical Chemistry B. 2001;105(34):8069–8076. [Google Scholar]
- 26.Metters AT, Anseth KS, Bowman CN. Journal of Physical Chemistry B. 2000;104(30):7043–7049. [Google Scholar]
- 27.Van de Wetering P, Metters AT, Schoenmakers RG, Hubbell JA. Journal of Controlled Release. 2005;102:619–627. doi: 10.1016/j.jconrel.2004.10.029. [DOI] [PubMed] [Google Scholar]
- 28.Lutolf MP, Hubbell JA. Biomacromolecules. 2003;4(3):713–722. doi: 10.1021/bm025744e. [DOI] [PubMed] [Google Scholar]
- 29.Lutolf MP, Lauer-Fields JL, Schmoekel HG, Metters AT, Weber FE, Fields GB, Hubbell JA. Proceedings of the National Academy of Sciences of the United States of America. 2003;100(9):5413–5418. doi: 10.1073/pnas.0737381100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.DuBose JW, Cutshall C, Metters AT. Journal of Biomedical Materials Research. 2005;74A:104–116. doi: 10.1002/jbm.a.30307. [DOI] [PubMed] [Google Scholar]
- 31.Rydholm AE, Bowman CN, Anseth KS.Acta Biomaterialia 2007. In Press [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Rydholm AE, Bowman CN, Anseth KS. Biomaterials. 2005;26(22):4495–4506. doi: 10.1016/j.biomaterials.2004.11.046. [DOI] [PubMed] [Google Scholar]
- 33.Rydholm AE, Reddy SK, Anseth KS, Bowman CN. Biomacromolecules. 2006;7(10):2827–2836. doi: 10.1021/bm0603793. [DOI] [PubMed] [Google Scholar]
- 34.Anseth KS, Bowman CN, Brannon-Peppas L , Biomaterials. 1996;17(17):1647–1657. doi: 10.1016/0142-9612(96)87644-7. [DOI] [PubMed] [Google Scholar]
- 35.Metters AT, Anseth KS, Bowman CN. Polymer. 2000;41(11):3993–4004. [Google Scholar]
- 36.Reddy SK. Chemical and Biological Engineering. University of Colorado; Boulder, CO: 2004. Mechanistic Modeling, Network Evolution, and Advanced Applications of Novel Thiol-Vinyl Systems. [Google Scholar]
- 37.Ilavsky M, Dusek K. Macromolecules. 1986;19:2139–2146. [Google Scholar]
- 38.Cowie JMG. Polymers: Chemistry and Physics of Modern Materials. 2nd ed. Nelson Thornes Ltd; Cheltenham, UK: 1991. [Google Scholar]
- 39.Johnson BD, Beebe DJ, Crone WC. Materials Science and Engineering. 2004;c 24:575–581. [Google Scholar]
- 40.Sudipto KD, Aluru NR, Johnson B, Crone WC, Beebe DJ, Moore J. Journal of Microelectromechanical Systems. 2002;11(5):544–555. [Google Scholar]
- 41.Elliott JE, Anseth KS, Bowman CN. Chemical Engineering Science. 2001;56(10):3173–3184. [Google Scholar]
- 42.Metters AT, Hubbell JA. Biomacromolecules. 2005;6:290–301. doi: 10.1021/bm049607o. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.