Spreading out of perturbations in reversible reaction networks

Abstract

Using an example of physical interactions between proteins, we study how a perturbation propagates in the equilibrium of a network of reversible reactions governed by the law of mass action. We introduce a matrix formalism to describe the linear response of all equilibrium concentrations to shifts in total abundances of individual reactants, and reveal its heuristic analogy to the flow of electric current in a network of resistors. Our main conclusion is that, on average, the induced changes in equilibrium concentrations decay exponentially as a function of network distance from the source of perturbation. We analyze how this decay is influenced by such factors as the topology of a network, binding strength, and correlations between concentrations of neighboring nodes. We find that the minimal branching of the network, small values of dissociation constants, and low equilibrium free (unbound) concentrations of reacting substances all decrease the decay constant and thus increase the range of propagation. Exact analytic expressions for the decay constant are obtained for the case of equally strong interactions and uniform as well as oscillating concentrations on the Bethe lattice. Our general findings are illustrated using a real network of protein–protein interactions in baker’s yeast with experimentally determined protein concentrations.

1. Introduction

Equilibria in a broad class of microscopically reversible processes where the direct and reverse reaction rates are proportional to the product of concentrations of reactants are described by the law of mass action (LMA). It has been rigorously proven that such processes have a unique equilibrium state which is completely defined by the set of initial concentrations and reaction constants [1]. Well-known examples include equilibria in chemically or physically reacting systems such as e.g. a pair of molecules reversibly binding each other. Large sets of interacting substances are often represented by networks, with nodes and links corresponding to reactants and their propensity for pairwise interactions correspondingly. One of the best-studied examples of such networks is that formed by all protein–protein physical interactions (pairwise bindings) in a given organism. In this case, the LMA determines the equilibrium free (unbound) concentrations of individual proteins as well as those of complexes formed by two or more proteins bound to each other given the set of dissociation constants of all pairwise protein–protein interactions and abundances (total concentrations) of all participating proteins. The protein abundances are subject to both stochastic fluctuations in the course of their production and degradation as well as to systematic changes in response to external and internal stimuli. This results in dynamical fluctuations in the LMA equilibrium state of the network.

A surprising feature observed in virtually all recent large-scale studies of these networks in a wide-ranging variety of biological organisms is their globally connected topology. Indeed, most pairs of protein nodes are linked to each other by relatively short chains of interactions. A change in the total abundance of a protein modifies free and bound concentrations of its immediate neighbors, which in their turn influence their neighbors, etc. Thus a fluctuation localized on just one reactant to some degree affects equilibrium concentrations of all nodes in the same weakly-connected topological component of the network. In biology such propagation of fluctuations far away from their source presents a great threat of undesirable cross-talk between different functional processes, simultaneously taking place in an organism. Thus it is important to understand whether and how this propagation gets attenuated and under what conditions it is minimized. On the other side, it has been shown that sometimes changes in equilibrium concentrations propagating beyond immediate neighbors of the perturbed protein are used for meaningful biological regulation or signaling. An example is a sensitive balance of interactions between sigma-factors, anti-sigma factors, and anti-anti-sigma-factors in bacteria [2]. In this case, a relevant question is under what conditions the propagation of the signal in a desirable direction is least attenuated while its indiscriminate spread is minimized.

In this work, we numerically and analytically study how localized perturbations such as changes of concentrations of individual reactants affect the binding equilibrium at all nodes of a reaction network. Our main conclusion is that under a broad range of conditions such perturbations exponentially decay with the network distance away from the perturbed node. Luckily, this makes protein binding networks poor conduits for indiscriminate propagation of fluctuations which would have led to a chaotic mutual influence between biologically distinct pathways. On the other hand, we also show that under carefully selected conditions, a perturbation can propagate relatively far with a minimal attenuation. We first develop a linear response theory and numerical methods for a general case of propagation of perturbations in a network of an arbitrary topology, concentrations and dissociation constants. A realistic protein binding network of baker’s yeast is used for illustration. Then several simpler analytically solvable case studies are shown to confirm the predictions of linear response theory and numerical results.

2. Methods and results

2.1. LMA equilibrium

In what follows we will use a simple case of our general formalism in which the reaction network is fully determined by a network of pairwise binding interactions between N distinct types of proteins (or any other molecules for that matter). The existence of a link between vertices i and j means that these proteins reversibly bind each other to form a two-protein complex (hetero- or homo-dimer) ij. Throughout this paper, we will consider only such dimers and ignore the existence of multi-protein complexes consisting of three or more proteins. However, our main results could be easily extended to an arbitrary composition of complexes or even to a more general situation of a set of substances that reversibly convert into each other and the equilibrium of every reaction is determined by the LMA (see appendix for this most general scenario).

The LMA states that free concentrations of proteins F_i and those of dimers D_ij obey

$$F_i{F}_j=k_{ij}{D}_{ij},$$ (1)

where K_ij is the corresponding dissociation constant. A dissociation constant has units of concentrations, the smaller is k_ij, the higher is the binding affinity of a pair i and j. Taking into account the conservation of mass of each substance i, one obtains the following system of equations that relates total concentrations C_i of proteins to their free concentrations F_i

$$C_i=F_i+{\displaystyle \sum _{j\leftrightarrow i}{D}_{ij}}=F_i+{\displaystyle \sum _{j\leftrightarrow i}\frac{F_i{F}_j}{k_{ij}}}.$$ (2)

Here and below the notation ∑_j↔i means a sum over all vertices j that are the network neighbors of the vertex i. In a general case of four or more interconnected interacting pairs this system of non-linear equations allows for only numerical solution. One particularly convenient computational method involves rewriting the equation (2) as

$$F_i=\frac{C_i}{1+{\displaystyle {\sum }_{j\leftrightarrow i}{F}_j/k_{ij}}},$$ (3)

and successively iterating it starting with F_i = C_i until the LMA is satisfied with a desired precision. The proof presented in [1] guarantees the uniqueness of the solution found this way.

2.2. Propagation of concentration perturbations in LMA equilibrium

As a concrete example, we consider the propagation of small concentration perturbations in the protein binding network of baker’s yeast, Saccharomyces cerevisiae. The set of protein–protein physical interactions (PPI) from the BIOGRID dataset [3] was automatically curated to include only interactions which were reported in at least two publications. Total concentrations of proteins for yeast grown in rich growth medium conditions were taken from a genome-wide experimental study in which Tandem-affinity precipitation (TAP) of individual proteins was followed by the Western blot analysis [4]. The resulting dataset consists of 4185 interactions among 1740 proteins with total concentrations ranging between 50 and 1 million molecules/cell with the median concentration of ~3000 molecules/cell. In the absence of genome-wide information regarding the value of dissociation constants in our simulations we assume them all to be the same k_ij = K_d. It turns out that apart from their overall strength the assignment and distribution of equilibrium concentrations to individual links in the network is relatively unimportant. In a follow up study we found [6] that Spearman and Pearson correlation coefficients between all equilibrium concentrations calculated using different assignments of dissociation constants of a given strength is usually as high as 0.8–0.95.

We observe that the magnitude of relative changes in free concentrations exhibits a universally exponential decay with the network distance from the source of perturbation (figure 1(A)). Approximately the same exponential damping was observed in response to a small 20% decrease of a protein abundance (which is roughly the range of intrinsic noise reported in [5]) as well as to a complete elimination of individual protein (which is experimentally realizable as a gene knock-out or inactivation). Stronger binding (smaller values of K_d) generally results in a longer range of propagation (slower decay) of perturbations.

Figure 1.

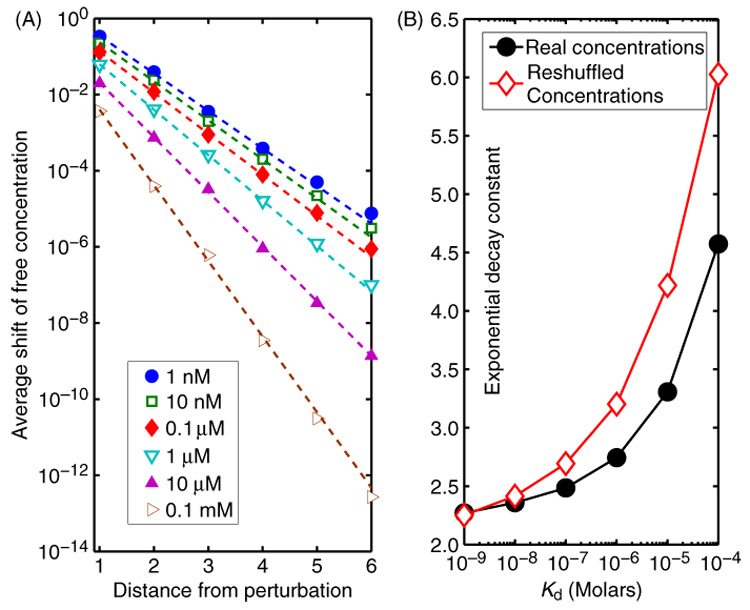
(A) The averaged over perturbation of all nodes magnitude of normalized changes in free concentrations |δF_i/F_i| per unit of δC₀/C₀ plotted as a function of the distance l_i0 from the perturbed node 0. The propagation of perturbations (equation (7)) was computed in a highly curated yeast PPI network [3] with real-life total concentrations of individual proteins [4]; the dissociation constant K_d was increased in 10-fold increments starting from 1 nM (or 34 molecules/cell) and up to 0.1 mM (the steepest decaying curve). (B) The exponential decay constant γ(K_d) obtained as the best fit of the form A exp[−γ(K_d)l_i0] to curves shown in the panel A with the real-life concentrations (filled circles), and for randomly reshuffled concentrations (open diamonds).

A much less computationally demanding (and, as shown below, quite heuristic) approach to find δF_j induced by a small perturbation of total concentrations δC_i is to invert the matrix Λ̂ obtained by linearizing equation (2) around the equilibrium point:

$$\frac{\delta C_i}{C_i}={\displaystyle \sum _j{\mathrm{\Lambda }}_{ij}\frac{\delta F_j}{F_j}},$$ (4)

with Λ̂ defined as

$${\mathrm{\Lambda }}_{ij}=A_{ij}\frac{F_i{F}_j/k_{ij}}{C_i}+{\delta }_{ij}\frac{(F_i+{\displaystyle {\sum }_{m\leftrightarrow i}{F}_i{F}_m/k_{im})}}{C_i}=A_{ij}\frac{D_{ij}}{C_i}+{\delta }_{ij}.$$ (5)

Here, A_ij is the adjacency matrix of the network. If complexes consisting of more than two proteins were included into consideration, D_ij would have been replaced by the total concentration of all complexes containing both i and j among their constituents⁵. It follows from equation (4) and equation (5) that when the change in total concentration is limited to just one node 0, the induced relative change of free concentration of any other node i ≠ 0 satisfies

$$\frac{\delta F_i}{F_i}=-{\displaystyle \sum _{j\leftrightarrow i}\frac{D_{ij}}{C_i}}\frac{\delta F_j}{F_j}.$$ (6)

This equation shows that changes in free concentrations on nearest neighbors tend to be of the opposite sign. Also, since ∑_j↔i D_ij/C_i = 1 − F_i/C_i < 1, the absolute magnitude of perturbation |δF_i/F_i| on any node away from the source is less than or equal to its maximal value among its neighbors: max_j↔i |δF_j/F_j|. Bonds with higher D_ij/C_i are better transmitters of perturbations from node j to node i. Note, that this quantity is non-symmetric: the transmission along any particular edge is directional with preferred direction pointing from the higher total concentration to lower one.

Inverting equation (4) one obtains the desired expression for the linear response of any free concentration to an arbitrary perturbation in total concentrations

$$\frac{\delta F_i}{F_i}={{\displaystyle \sum _j({\mathrm{\Lambda ̂}}^{-1})}}_{ij}\frac{\delta C_j}{C_j}.$$ (7)

The physical meaning of each column j of the inverse matrix Λ̂⁻¹ is that it determines relative changes in free concentrations of all proteins per relative change δC_j/C_j in the total concentration of the protein j.

While the linear response approximation (7) describes infinitesimally small perturbations, we observed that it approximates the response to a finite perturbation (even in the extreme case of a gene knock-out) rather well. The exponential decay of perturbation was found to be identical to that calculated using equation (3) and (with the exception of dimers containing the knocked-out protein) the overall magnitude of changes in free concentration is comparable to the full numerical solution.

2.3. Analogy with resistor network

To develop a better understanding of the developed matrix formalism, first consider the case when the underlying network is bipartite (but not necessarily acyclic). To take into account the natural sign-alternation of δF_i/F_i on immediate neighbors in the network (see equation (6)), we introduce new variables ϕ_i = (−1)^s_i δF_i/F_i where index s_i is 0 on one sublattice and 1 on the other. This allows us to rewrite the equation (4) and equation (5) as

$$\delta {\tilde{C}}_i={\displaystyle \sum _j{\sigma }_{ij}{\varphi }_j}.$$ (8)

Here δC̃_i = (−1)^s_i δC_i and σ̂ is given by

$${\sigma }_{ij}=-A_{ij}\frac{F_i{F}_j}{k_{ij}}+{\delta }_{ij} \left(F_i+{\displaystyle \sum _m{A}_{im}\frac{F_i{F}_m}{k_{im}}}\right)=-A_{ij}{D}_{ij}+{\delta }_{ij} \left({\displaystyle \sum _{k\leftrightarrow i}{D}_{ik}+F_i}\right).$$ (9)

In the situation when δC̃_i = δ_i0δC₀ (i.e. when the perturbation is limited to a single node 0), the equation (8) and equation (9) can be interpreted as describing ‘electric potentials’ ϕ_i in the network of resistors with resistances R_ij = 1/σ_ij = 1/D_ij subject to the injection of the current δC₀ at the node 0. Each node is also shunted to an auxiliary ‘ground node’ with potential ϕ_G = 0 by the resistance R_iG = 1/F_i. Potential gradients along edges ϕ_i − ϕ_j = (−1)^s_i δF_i/F_i −(−1)^s_j δF_j/F_j = (−1)^s_i δD_ij/D_ij determine relative (dimensionless) changes in concentrations of heterodimers, while currents I_ij= (ϕ_i − ϕ_j)/R_ij = (−1)^s_i δD_ij—the absolute (dimensional) changes. Similarly, currents to the ground I_iG = ϕ_i/R_iG = (−1)^s_i δF_i are equal to changes in free concentrations of proteins. As in resistor networks, the Kirchoff law here follows from the mass conservation which states that everywhere the total current flowing out of node i, I_iG + ∑_j↔i I_ij = (−1)^s_i (δF_i + ∑_i↔j δD_ij) = (−1)^s_i δC_i = δC̃_i is equal to the external current δC̃_i = δ_i0δC₀ of changes in total concentrations.

2.4. Effects of network topology and concentration assignment

The interpretation of the free concentrations F_i as ‘shunt conductivities’ leaking the ‘current’ to the ground means that the smaller they are, the weaker is the decay of both currents δD and δF with the distance. Since stronger binding generally decreases free concentrations of all proteins, it naturally reduces the rate of decay of perturbations (visible in figure 1(A)). However, the exponential decay constant γ(K_d) appears to saturate around 2.25 as K_d → 0 (figure 1(B)). This saturation is easy to understand. Indeed, consider the most ideal scenario in which all free concentrations F_i are very small and thus the ‘current’ δD is approximately conserved (loss to the ground is negligible). The exponential growth in the number of neighbors N_n(l) ~ (〈d(d − 1)〉/〈d〉)^l as a function of distance l from the perturbation source means that even in this ideal setup the average current at distance l would be proportional to 1/N_n(l) and thus exponentially small. The same rate of decay describes the ‘potentials’ δF_i/F_i as well.

However, it is important to emphasize that the ideal scenario outlined above almost never occurs with real-life concentrations. Indeed, the limit of infinitely strong binding k₁₂ → does not make all but only some of free concentrations F_i to go to zero. One can see it clearly already for two interacting proteins. When their concentrations C₁ and C₂ are not equal to each other, in the strong binding limit k₁₂ → 0 the free concentration of the more abundant protein (say 1) remains nonzero F₁ → C₁ − C₂, while the free concentration of its less abundant partner F₂ → 0. Consider another simple example of a chain of three proteins with initial concentrations C₁, C₂ and C₃ reacting to form dimers 1–2 and 2–3 with the same dissociation constant k. In this case one could still analytically calculate all free and bound concentrations,

$$\begin{array}{l}{D}_{12}=\frac{C_1}{2(C_1+C_3)}\left[C_1+C_2+C_3+k-\sqrt{{(C_1+C_2+C_3+k)}^2-4C_2(C_1+C_3)}\right],\\ D_{23}=\frac{D_{12}{C}_3}{C_1},\end{array}$$

and F₁ = C₁ − D₁₂, F₂ = C₂ − D₁₂ − D₂₃, F₃ = C₃ − D₂₃. The logarithmic derivative,

$${\mu }_{1\to 3}=\frac{\partial F_3}{\partial C_1}\frac{C_1}{F_3},$$

quantifies the propagation of perturbation of the node 1 through this three-node channel and in the strong binding limit has a maximum around C₂ = C₁ + C₃ (see figure 2). i.e. when all three substances are completely bound: {F₁, F₂, F₃} → 0. In a general case of a PPI network of arbitrary topology the only situation in which free concentrations of all proteins would approach zero as k_ij → 0 is when their total concentrations C_i are proportional to their degrees d_i. For a given topology of the network such concentration setup has the slowest decay of perturbations.

Figure 2.

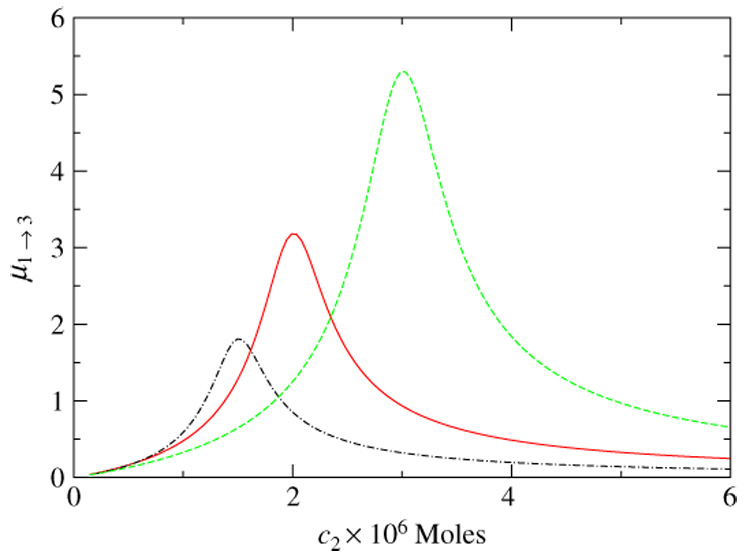
The propagation ratio µ_1→3 defined in the text in a linear chain C₁ → C₂ → C₃ with strong binding (k = 1 nM) as a function of concentration of the intermediate substance C₂. All curves have the same concentration of the target protein C₃ = 1 µM and different concentrations of the source of the signal C₁ = 2 µM (green dashed line), C₁ = 1 µM (red solid line), and C₁ = 0.5 µM (black dot-dashed line). In the strong binding limit the propagation ratio reaches its maximum when all three substances are completely bound, C₂ = C₁ + C₃. Note also that the peak propagation is higher in the direction opposite to the concentration gradient, i.e. when C₁ > C₃.

Most real-life PPI networks are characterized by a positive correlation between total concentrations of interacting proteins. In the yeast network used in this study we observed this effect to be present and highly statistically significant, (the Spearman rank correlation coefficient was 0.27 with a P-value of 10⁻⁵⁴). Such correlation improves the balance between total concentrations of interacting nodes and thus somewhat lowers the average free concentration of proteins compared to a case where this correlation is absent. Based on this we expect that real protein–protein networks would be more prone to propagating perturbations than their counterparts in which concentrations of proteins are randomly reshuffled and thus the correlation between concentrations of interacting nodes is destroyed. This theoretical expectation was indeed verified in figure 1(B) (compare filled circles and open diamonds for the network with real concentrations and the reshuffled ones).

Naturally occurring PPI networks are not bipartite. Fortunately, due to a relative sparsity of links the number of odd-length loops in them is small and our resistor network analogy provides a reasonable approximation. For any starting point of perturbation 0 the optimal way to define sign-alteration in variables ϕ_i = (−1) ^s_i δF_i/F_i is by using s_i = l_i0 (here l_i0 is the distance from the source of perturbation 0 to the node i). The majority of links would connect nodes with opposite ‘parities’, while the remaining non-bipartite links could be treated as a small but important correction to the ideal case. Like shunt conductivities to the ground, they contribute to the dissipation of the ‘current’. Indeed, if a link i ↔ j is of this anomalous kind, its contributions to the current leaving nodes i and j are equal to each other and given by D_ij(ϕ_i + ϕ_j). One example of such anomalous (non-bipartite) links is given by homodimers (see footnote 6). In general, these anomalous links lead to the loss of the total current from the system and thus tend to suppress the propagation of perturbations.

2.5. Analytical solution for Bethe lattice

To illustrate and rigorously validate conclusions of the previous section, we analytically investigate a simple example of a bipartite network, the Bethe lattice, where each vertex has the same number of interaction partners (degree) d_i = d. In addition, we assume that all dissociation constants are equal, k_ij = k. When total concentrations of all proteins are also identical C_i = C, the equilibrium concentrations of all monomers and heterodimers are given by

$$\begin{array}{ll}{F}_i=F=\frac{k}{2d}\left(\sqrt{1+\frac{4dC}{k}}-1\right),& D_{ij}=D=\frac{k}{2d}\left(\frac{2C}{k}+\frac{1}{d}-\frac{1}{d}\sqrt{1+\frac{4dC}{k}}\right).\end{array}$$ (10)

For arbitrary concentrations C_i, using the mass conservation and LMA, it is also simple to derive the following recurrent in the lattice index l relation for free concentrations

$$C_l-F_l=\frac{F_l}{k}[(d-1)F_{l+1}+F_{l-1}].$$ (11)

Assuming that the total concentration is perturbed from its universal for all network value C at node 0, and the deviation δF_l of free concentrations from their equilibrium value given by equation (10) are small, equation (11) yields

$$-\left(d+\frac{k}{F}\right) \delta F_l=(d-1)\delta F_{l+1}+\delta F_{l-1}.$$ (12)

It has an exponentially decaying solution δF_l = δF₀λ^l, where

$$\mathrm{\lambda }=-\frac{1}{d-1}\left[\frac{d+k/F}{2}-\sqrt{{\left(\frac{d+k/F}{2}\right)}^2-(d-1)}\right].$$ (13)

As expected, −1 < λ < 0 which means that perturbations sign alternate and exponentially decay as a function of l. In a strong binding limit the combination of equation (13) and equation (10) yields

$$\mathrm{\lambda }=-\frac{1}{d-1}\left(1-\frac{1}{d-2}\sqrt{\frac{dk}{C}}\right)+O \left(\frac{dk}{C}\right).$$ (14)

This confirms our qualitative prediction that in the ‘ideal’ scenario when no current is lost to the ground, the perturbation still decays exponentially due to branching of the current at each node. For a linear chain of proteins (d = 2), the complete solution in terms of C and k looks particularly elegant

$${\mathrm{\lambda }}_{d=2}=-\frac{{(1+8C/k)}^{1/4}-1}{{(1+8C/k)}^{1/4}+1}.$$ (15)

As one expects heuristically, in the limit of strong binding, a perturbation in a linear chain propagates indefinitely, |λ_d=2| → 1.

To explore the effect of non-ideal concentration setup on propagation of perturbation, we solve for the decay exponent in the linear chain (d = 2) with oscillating total concentrations,

$$C_i=C[1+{(-1)}^{i}a].$$ (16)

Response to perturbation of the even- and odd-numbered vertices has different amplitudes A_2i and A_2i+1 yet decays with the same exponential coefficient λ_1D±.

$$\begin{array}{ll}\delta F_{2i}=A_{2i}{\mathrm{\lambda }}^{2i},& \delta F_{2i+1}=A_{2i+1}{\mathrm{\lambda }}^{2i+1}.\end{array}$$ (17)

Substitution of (17) into linearized around the equilibrium concentration recursion relation (12) yields the system of two equations for the relative amplitude A_2i/A_2i+1 and λ with the solutions

$$\frac{A_{2i}}{A_{2i+1}}=\sqrt{\frac{F_{2i}(k+2F_{2i})}{F_{2i+1}(k+2F_{2i+1})},}$$ (18)

$${\mathrm{\lambda }}_{\pm }=-\frac{4\mathrm{\chi }\sqrt{1-a^2}-\sqrt{2f(1+4\mathrm{\chi })-2f^2}}{1+4\mathrm{\chi }-f},$$ (19)

where χ = C/k and $f=\sqrt{16a^2{\mathrm{\chi }}^2+8\mathrm{\chi }+1}$. Evidently, |λ_±(C/k, a)| ⩽ |λ_d=2(C/k)| with equality being achieved only for a = 0. For example, for k/C → 0 and a small

$${\mathrm{\lambda }}_{\pm }\to -(1-\sqrt{2a}).$$

Thus, as it was discussed above, any variation in C_i/d_i, which results in larger average unbound concentrations F_i, leads to a faster decay of perturbations.

3. Conclusions

We investigated the propagation of perturbations caused by change of concentrations of individual reactants in a reaction network whose equilibrium is governed by the LMA. We found that in general, such perturbations decay exponentially in the network distance from the perturbation source. It was also observed and explained that the concentration perturbations propagate with less attenuation along the links between highly sequestered (low free concentration) reacting substances. While the reaction network itself is non-directional, the concentration perturbation preferably propagates down the abundance gradient, i.e. from the substance with higher total concentration to that with the lower one. To illustrate the propagation of concentrational perturbations, we constructed an effective resistor network with edge and shunt resistivities inversely proportional to the dimer and free concentrations. Current flow in such a weighted network provides a good approximation to propagation of small concentrational perturbations. In the case of perfect sequestration, i.e. when neighboring concentrations are perfectly balanced and binding is strong, the perturbation is still attenuated by a factor $\frac{1}{d-1}$ at each node due to the branching of the ‘outgoing current’.

While only the case of pairwise interaction has been considered, our numeric and analytic approaches can be easily generalized to include the three- and higher-molecular complexes. We considered the protein binding network of baker’s yeast as the example, yet the methods developed here are very general and can be applied to any reaction network with the LMA equilibrium. A more detailed account of the biological implication of our analysis of perturbations of protein–protein binding equilibrium can be found in [6]. Future studies will include the temporal effects of the perturbation propagation, which could be reaction- or diffusion-limited; effects of correlated and uncorrelated multiple small abundance perturbations (noise, see [6] and references therein), fluctuations of free and bound concentrations around LMA equilibrium for fixed abundances, and non-LMA interactions such as catalytic reactions.

Appendix

The most general formalism suitable to any set of reversible reactions whose equilibrium is governed by the LMA is as follows:

Consider a network of R reactions labeled by Greek letters α = 1, …, R with equilibrium constants K_α and M substances labeled by Latin letters, i = 1, …, M. Each elementary act of reaction α produces n_iα molecules of substance i (negative numbers indicate that the substance is consumed). The M × R matrix n̂ = {n_iα} = is referred to as the stoichiometric matrix of the reaction network. The system is prepared in an initial state where each substance i has the concentration C_i. After the equilibrium is reached the concentrations become equal to F_i, defined by the LMA ${\displaystyle {\prod }_i{F}_i^{n_{i\alpha }}}=K_{\alpha }$. In our general case of both production and consumption of substances, F_i could be either larger or smaller than C_i. The approach to equilibrium in every reaction channel α is characterized by the reaction coordinate r_α, equal to the number of direct elementary reactions minus the number of reverse ones. The mass conservation dictates that

$$C_i=F_i+{\displaystyle \sum _{\alpha }{n}_{i\alpha }{r}_{\alpha }},$$ (A.1)

while the LMA can be written in the logarithmic form as

$${\mathrm{n̂}}^T\overrightarrow{\ln F}=\overrightarrow{\ln K}.$$ (A.2)

Evidently, the rank of stoichiometric matrix cannot be larger than M − 1 so that equation (A.2) has a continuous family of solutions for varying initial concentrations. A small perturbation C_i → C_i + δC_i leads to shifts in both equilibrium concentrations: F_i → F_i + δF_i and equilibrium reaction coordinates: r_α → r_α + δr_α. These R + M unknowns could be calculated from the linearized LMA equations ∑_i n_iα δF_i/F_i = 0 and conservation laws δC_i = δF_i + ∑_α n_iαr_α δr_α/r_α. In vector notation the solution of these two sets of equations is given by

$$\overrightarrow{\delta r}={Û}^{-1}{\mathrm{n̂}}^T\overrightarrow{\delta C/F},$$ (A.3)

and

$$\overrightarrow{\delta F}=\overrightarrow{\delta C}-\mathrm{n̂}\overrightarrow{\delta r},$$ (A.4)

where the R × R matrix Û is defined as U_αβ = ∑_i n_iαn_iβ/F_i. Here, we assumed that R < M so the condition rank (n̂) < M is satisfied and the inverse matrix Û⁻¹ is well defined.