Abstract
Thermally induced aggregates of α-chymotrypsinogen A and bovine granulocyte-colony stimulating factor in acidic solutions were characterized by a combination of static and dynamic light scattering, spectroscopy, transmission electron microscopy, and monomer loss kinetics. The resulting soluble, high-molecular weight aggregates (∼103–105 kDa) are linear, semiflexible polymer chains that do not appreciably associate with one another under the conditions at which they were formed, with classic power-law scaling of the radius of gyration and hydrodynamic radius with weight-average molecular weight (Mw). Aggregates in both systems are composed of nonnative monomers with elevated levels of β-sheet secondary structure, and bind thioflavine T. In general, the aggregate size distributions showed low polydispersity by light scattering. Together with the inverse scaling of Mw with protein concentration, the results clearly indicate that aggregation proceeds via nucleated (chain) polymerization. For α-chymotrypsinogen A, the scaling behavior is combined with the kinetics of aggregation to deduce separate values for the characteristic timescales for nucleation (τn) and growth (τg), as well as the stoichiometry of the nucleus (x). The analysis illustrates a general procedure to noninvasively and quantitatively determine τn, τg, and x for soluble (chain polymer) aggregates, as well as the relationship between τn/τg and aggregate Mw.
INTRODUCTION
Nonnative protein aggregation is a type of protein self-assembly in which the resulting soluble or insoluble aggregates are composed of monomers with secondary structures that are significantly altered from the native (monomer) state. Nonnative protein aggregation is a common problem in bioprocessing operations such as drying, reconstitution, and storage (1). The presence of soluble aggregates in a protein pharmaceutical may decrease its effectiveness or putatively elicit an adverse immune response (2). Nonnative protein aggregation has also been implicated in a variety of debilitating diseases such as Alzheimer's and Huntington's (3). Recent evidence suggests that soluble aggregate precursors rather than mature, insoluble fibrils are the primary cytotoxic species in a number of cases (4–6).
Common structural and morphological characteristics of fibril-forming systems are reasonably well established (7). However, similarly detailed characterization and categorization of afibrillar or “amorphous” soluble and insoluble aggregates are not typically reported (8,9). A small but growing body of literature indicates that a range of afibrillar aggregate morphologies are possible (10,11). Interestingly, unwanted aggregates in biotechnology applications are most often broadly classified as amorphous or afibrillar (1,12). A more complete understanding of the underlying mechanism and its relation to the resulting structure and morphology of nonnative aggregates may ultimately suggest more effective strategies for preventing or inhibiting their formation. From a more fundamental perspective, nonnative aggregates present an intriguing problem in understanding protein folding and assembly in that they offer a potentially lower free energy state than that of the folded monomer, provided that the total protein concentration exceeds the theoretical threshold value below which isolated monomers are thermodynamically stable (13). Their formation can involve a complex set of competing (mis)folding and assembly reactions that are difficult to resolve directly via experiment (12,14–20), or to access via molecular theory or simulation due to the long time- and length-scales involved (21). Together, these observations suggest that an improved understanding of the factors controlling the formation and properties of nonnative aggregates without higher-order, supramolecular assembly (e.g., before mature fiber assembly) would aid in both fundamental and applied research in this field.
At a qualitative level, the overall or observed rate of monomer loss or extent of conversion to aggregates can be broadly categorized by the location of the slow step(s) in the process. Unfolding-limited aggregation occurs when the timescale for monomer unfolding greatly exceeds that for all subsequent kinetic events, and is characterized by an observed rate coefficient that is independent of concentration and comparable to that for unfolding (22–26). In the alternative, aggregation-limited case, the rate-determining steps occur after the transition from folded to partially or completely unfolded monomer. Aggregation-limited cases can be further classified in terms of the growth mechanism of the aggregates (24,25). If the predominant growth route is aggregate-aggregate association, or condensation, this generally leads to relatively low number concentrations of each aggregate size and a wide distribution of sizes. If growth instead occurs primarily by (chain) polymerization, the aggregate size distribution is predicted to have lower polydispersity. The latter scenario is qualitatively implied in most models of nucleated growth or nucleated polymerization (27–30). Beyond these qualitative features, comparatively little has been shown experimentally regarding general relationships between kinetics and the morphology, structure, and size distribution of the resulting aggregates before appreciable condensation. For systems in which condensation steps are appreciable throughout the aggregation process, a small but increasing number of cases have been well described by approaches that either include a priori knowledge of the morphology of uncondensed and condensed aggregates (31–33), or require the aggregates to condense to form insoluble, macroscopic particles (34).
This report presents a detailed structural and morphological characterization of thermally induced, soluble nonnative aggregates of α-chymotrypsinogen A (aCgn) and bovine granulocyte-colony stimulating factor (bG-CSF). Here structure refers to the characteristic dimensions and conformational state of the monomers within the aggregate, whereas morphology refers to the spatial arrangement of these elements relative to each other in the aggregate as a whole. Aggregates composed of monomers of similar structure may, in principle, adopt dramatically different morphologies (e.g., linear chains, dendrimers, fibrils) (35). The proteins investigated are model systems for the study of nonnative aggregation relevant to biopharmaceutical stability (36–38), product formulation (36,37,39), and mechanistic interpretation of the underlying kinetics (24,40). The results reported here therefore offer an improved and more quantitative picture for the underlying morphology of soluble aggregates that potentially extends beyond aCgn and bG-CSF.
aCgn is a 25.7 kDa protein with pI = 9.2 and mixed α-helix/β-sheet secondary structure in its native and thermally unfolded states, while bG-CSF is ∼19 kDa with pI = 6.8 and essentially all α-helix in its native state. aCgn is the inactive, zymogen precursor to the digestive enzyme chymotrypsin (41). bG-CSF is the bovine homolog to the recombinant human G-CSF available as a commercial therapeutic agent to ameliorate white blood cell loss during chemotherapy (42). Both proteins are natively monomeric and able to form nonnative, relatively high molecular weight aggregates—i.e., the average number of monomers per aggregate, or degree of polymerization, is of order 10 or greater. Aggregation rates for both proteins are greatly accelerated at temperatures near and above their midpoint unfolding temperatures (36,38,40). Despite being structurally dissimilar monomers, the results here show that soluble aggregates of each protein share common characteristics in terms of morphology and structure that suggest similarities in the mechanisms by which they form.
The structure of the aggregates at a protein chain level is probed via circular dichroism (CD) spectroscopy and fluorescence upon thioflavine T (ThT) binding. These were selected because for both fibrillar and afibrillar systems, CD spectra of aggregates often display characteristic β-sheet signals (14,15), while ThT binding and fluorescence is often considered to be indicative of fibrillar, amyloid, and/or cross-β-sheet structures and morphologies (43,44). For systems that form fibrils (i.e., condensed filaments), nonnative aggregate structures are often high in β-sheet content, with long, rigid-rod morphologies (45,46). The opposite extreme is that of small, globular aggregates in which a reasonably conserved β-sheet structure is less established (14,47).
The data are further analyzed within the context of nucleated polymerization, utilizing a recently proposed mathematical model of nonnative aggregation kinetics (27). This allows development of quantitative relationships between the aggregate size and the number (x) of monomers in the nucleus, the number (δ) of monomers required to complete a kinetic step during growth, and the ratio of characteristic timescales for nucleation (τn) and growth (τg). Combining these results with measurements of the kinetics of aggregation provides self-consistent estimates of τn and τg that cannot otherwise be obtained without invasive approaches such as seeding or chemical labeling (48,49), or by incorporating a priori knowledge of the aggregate morphology (33).
MATERIALS AND METHODS
Solution preparation
aCgn (lyophilized powder, 6× crystallized, lot No. 105K7690) was purchased from Sigma-Aldrich (St. Louis, MO) and used without further purification. bG-CSF (lyophilized powder) was donated by Pfizer Global Research and Development (Bioprocess Research and Development, Groton, CT) and used without further purification (36–38). Stock solutions of 10 mM citrate buffer were prepared by dissolving citric acid monohydrate (Fisher Scientific, Pittsburgh, PA) in distilled, deionized water from a Millipore (Billerica, MA) Milli-Q filtration system with a Quantum EX ultrapure Organex cartridge, and titrating to the desired pH with 5 M sodium hydroxide solution (Fisher Scientific). aCgn samples at concentrations between 0.5 and 8 mg/mL were gravimetrically prepared by dissolving lyophilized powder in 10 mM citrate buffer (pH 3.5). bG-CSF samples at concentrations between 0.5 and 1 mg/mL were gravimetrically prepared by dissolving lyophilized powder in 10 mM citrate buffer (pH 3.0). The smaller concentration range for bG-CSF was necessary to ensure that the aggregation timescale remained within a reasonable range (∼1–100 min) for the purposes of this study. All concentrations were computed from purity specifications based on UV extinction coefficient measurements (36–38,40). Aggregation was accelerated by thermostatting samples at 65°C ± 0.2°C in a circulating water bath for a range of times (∼3–400 min) previously determined to yield a mass fraction of aggregates of 0.95 ± 0.02. Samples were quenched in an ice water bath immediately after each predetermined hold time and refrigerated (2–8°C) for a maximum of three days before use. Subsequent measurements to characterize aggregate structure, size, and morphology were performed at 20°C unless otherwise noted.
Static light scattering (SLS) and dynamic light scattering (DLS)
Light scattering ampules (1 mL) were purchased from Wheaton (Millsville, NJ), triple-rinsed with distilled and deionized water and dried. SLS and DLS data were acquired at 20°C ± 0.2°C using a Brookhaven (Holtsville, NY) BI9000AT correlator and a BI200SM goniometer, and a Lexel (Fremont, CA) model 95 argon ion laser operating at 488 nm. All light scattering measurements were performed at 20°C ± 0.2°C, with sample temperature controlled by an external circulating bath.
The scattered intensity of samples containing protein aggregates was recorded at 37 scattering angles between 30° and 120°. The (isotropic) scattered intensity of buffer solutions and a toluene reference were measured over five angles between 88° and 92° and subsequently averaged. For selected measurements, the average intensity measured over the entire angle range from 30° to 120° was confirmed to give identical values within instrument precision to that measured between 88° and 92°. The excess Rayleigh ratio was calculated as
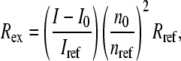 |
(1) |
where I is the scattered intensity of the sample, I0 is the averaged scattered intensity of the buffer, Iref is the averaged scattered intensity of a toluene standard, n0 is the refractive index of the buffer, nref is the refractive index of toluene, and Rref is the Rayleigh ratio of toluene (39.6 × 10−6 cm−1) (50). The standard Zimm expression (51),
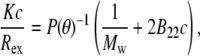 |
(2) |
relates the form factor, P(θ), to the optical constant, K, the mass concentration, c, the weight-average molecular weight, Mw, and the osmotic second virial coefficient, B22. The refractive index increment needed to calculate K was taken to be 0.19 cm3/g at 20°C, a value typical of small, globular proteins (52). P(θ) depends only on the geometry of the scattering object, and is usefully written in the Guinier approximation as 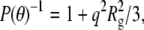 where Rg is the square-root of the z average of the square of the radius of gyration (
where Rg is the square-root of the z average of the square of the radius of gyration (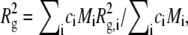 where
where 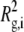 is the square of the radius of gyration of an aggregate of size i) and q is the magnitude of the scattering vector, q = 4πn0 sin (θ/2)/λ0, where n0 is the refractive index of the solvent, θ is the scattering angle, and λ0 is the wavelength of the light in vacuo. Equation 2 can then be written as
is the square of the radius of gyration of an aggregate of size i) and q is the magnitude of the scattering vector, q = 4πn0 sin (θ/2)/λ0, where n0 is the refractive index of the solvent, θ is the scattering angle, and λ0 is the wavelength of the light in vacuo. Equation 2 can then be written as
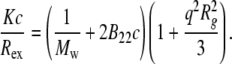 |
(3) |
For a given aggregated sample with initial protein concentration c0, different concentrations (c) were prepared gravimetrically by dilution with buffer. Previous work established that dilution does not change the size or structure of the protein aggregates, and was confirmed for all samples here by a lack of measurable change in aggregate size upon dilution (data not shown). SLS data across all concentrations and angles were globally regressed to Eq. 3 with a Levenberg-Marquardt nonlinear least-squares algorithm using the lsqcurvefit function in MATLAB (The MathWorks, Natick, MA) to obtain values and confidence intervals for each of the three fitted parameters: Mw, B22, and Rg. To assess the robustness of the regression, outliers were identified and excluded based on a two-tiered statistical test (53,54). For a given data set, points with residuals that fell outside of two standard deviations of the mean residual value from a fit including all data were identified as potential outliers. These points were excluded from a second regression, and then compared to their predicted values from that second regression. A potential outlier was subsequently rejected only if it fell outside the 90% confidence interval of the second regression. For all data reported, the average percentage of points rejected as outliers was 3%, and did not exceed 5% for any data set. Including or excluding outliers did not change the values of Mw and Rg within statistical uncertainty, suggesting the fitted values of these parameters from global regression against Eq. 3 are robust. Conversely, the large variability in fitted B22 values and the weak dependence of the scattered intensity on concentration precluded reliable determination of B22 values. Specifically, the 95% confidence intervals for the fitted B22 values were comparable to or larger than the magnitude of the values themselves. This was attributed in part to the fact that the fitted B22 values were invariably near zero (∼10−5–10−6 mol mL g−2).
For DLS measurements, all samples were diluted with buffer as needed to nominally 0.2 mg/mL protein. The intensity autocorrelation function of each sample was recorded at 20 angles between 25° and 120°. The measured intensity autocorrelation function was analyzed via an adaptation of the method of cumulants (55,56), by nonlinear regression of G(2)(τ) data as
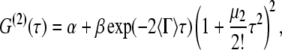 |
(4) |
where α is an average baseline intensity, β is an instrument constant, 〈Γ〉 is the average decay constant (or first cumulant), and μ2 is the second moment about the average decay constant. The reduced second moment, or polydispersity index, defined as
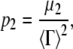 |
(5) |
is a dimensionless parameter that gives a direct measure of the width of the underlying distribution of particle sizes (55,57). 〈Γ〉 depends on q and can be written as
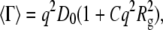 |
(6) |
where D0 is the z-average translational diffusion coefficient (D0 = 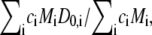 where D0,i is the translational diffusion coefficient of an aggregate of size i) and C is a numerical constant (58). D0 is related to the effective hard-sphere hydrodynamic radius (Rh) via the Stokes-Einstein equation (Rh = kBT/6πηD0, where kB is Boltzmann's constant, T is the thermodynamic temperature, and η is the viscosity of the solvent).
where D0,i is the translational diffusion coefficient of an aggregate of size i) and C is a numerical constant (58). D0 is related to the effective hard-sphere hydrodynamic radius (Rh) via the Stokes-Einstein equation (Rh = kBT/6πηD0, where kB is Boltzmann's constant, T is the thermodynamic temperature, and η is the viscosity of the solvent).
Size exclusion chromatography (SEC)
Monomer concentrations in protein samples were determined using either an Agilent Technologies (Santa Clara, CA) HP1050 with a G1306A photodiode array detector or a Waters (Milford, MA) Alliance 2695 separations module with a 2996 photodiode array detector. Each instrument was equipped with a Protein-Pak 7.8 × 300 mm size exclusion column maintained at room temperature during the measurements. Sample injections of 100 μL were eluted isocratically at 1 mL/min in a mobile phase composed of 0.5% (v/v) phosphoric acid (Fisher Scientific) and distilled and deionized water (pH adjusted to 2.5 with sodium hydroxide). Previous work established that this mobile phase composition and pH minimize interactions with the column and ensure consistent performance (36,40). All injected material was recovered (conserved total integrated peak area), and all detectable aggregates formed during incubation eluted in the void volume. For this column the practical molecular weight cutoff is estimated to be 80 kDa (manufacturer specification; J. Andrews, unpublished data). Peak areas recorded at an absorption wavelength of 280 nm were converted to concentration measurements by comparison with independently prepared calibration standards over the previously determined linear range of the assay (24,36).
Circular dichroism (CD)
Equilibrium, isothermal far-UV circular dichroism measurements were made using a Jasco (Easton, MD) J-810 spectropolarimeter and a Jasco PTC-424S Peltier temperature controller at 20°C ± 0.2°C. Spectra were recorded from 260 to 190 nm at a scanning rate of 20 nm/min in a 1 × 10 mm Hellma (Plainview, NY) cuvette. Samples contained either native or fully aggregated (mass fraction of aggregate = 0.95 ± 0.02) aCgn or bG-CSF at 0.2 mg/mL. Seven spectra were recorded and averaged. The mean residue ellipticity ([θ] deg cm2 dmol−1) was calculated as 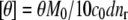 where θ is the average ellipticity in mdeg, M0 is the molecular weight of the protein monomer in g/mol, c0 is the mass concentration of the protein in mg/mL, d is the path length of the cuvette in cm, and nr is the number of amino-acid residues in the monomer.
where θ is the average ellipticity in mdeg, M0 is the molecular weight of the protein monomer in g/mol, c0 is the mass concentration of the protein in mg/mL, d is the path length of the cuvette in cm, and nr is the number of amino-acid residues in the monomer.
Fluorescence spectroscopy and thioflavine T (ThT) binding
A 7.78 mM stock solution was prepared by dissolving ThT (MP Biomedicals, Solon, OH) in distilled, deionized water. Samples were prepared for fluorescence measurements by diluting the ThT stock solution into aCgn and bG-CSF solutions to yield a 15× molar excess of the dye over the monomer. Equilibrium fluorescence measurements were made using a Jasco J-810 spectropolarimeter equipped with a FMO-427S fluorescence detector and a Jasco PTC-424S Peltier temperature controller at 20°C ± 0.2°C. Excitation and emission bandwidths were 10 nm. Emission spectra were recorded at 20°C in a 1 × 1 cm cuvette over a wavelength range of 460–600 nm (1 nm intervals) for an excitation wavelength of 450 nm. Seven spectra were recorded and averaged for each sample.
Cryogenic transmission electron microscopy (cryo-TEM)
Samples for cryo-TEM were examined using a Tecnai G2 12 TEM at an acceleration voltage of 120 keV. Specimens were prepared using a Vitrobot Mark II (FEI, Hillsboro, OR), a semiautomated preparation apparatus that allows for computer-controlled blotting of grids in a temperature- and humidity-controlled environment. Quantifoil grids (SPI Supplies, West Chester, PA) were submerged in a liquid sample, blotted once for 1 s to produce a thin liquid film, allowed to relax for 20 s to eliminate shear-induced artifacts, and then vitrified by rapid immersion into liquid ethane held at its freezing temperature. The temperature within the sample preparation chamber was maintained at 25 ± 0.5°C and at least 95% relative humidity. Vitrified grids were transferred to a Gatan (Pleasanton, CA) single tilt cryogenic holder cooled with liquid nitrogen. The temperature of the grids was maintained below −170°C during investigation in the TEM. Digital images were recorded using a Gatan multiscan charge-coupled device camera and processed with DigitalMicrograph software (Gatan).
RESULTS
Monomer loss kinetics
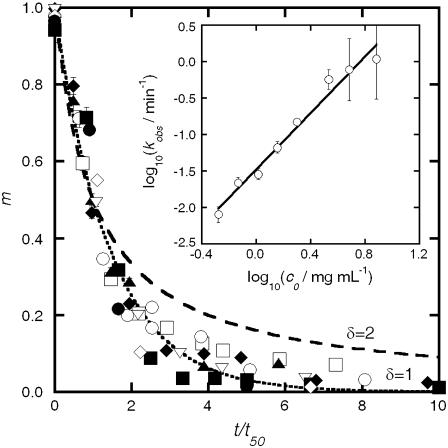
Monomer loss for a range of initial protein concentrations was measured via SEC as a function of incubation time at 65°C. The resulting kinetic profiles for aCgn were each fit using a nonlinear least-squares regression to the equation, 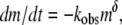 where m = c/c0, c is the monomer concentration, c0 is the initial monomer concentration, kobs is the observed rate coefficient ([=]1/time), t is the incubation time, and δ is expected to be an integer (22). The data over all c0 values are best fit with δ = 1, although profiles with δ-values as high as 2 were also reasonable approximations in some cases. The corresponding half-life value (t50), when m = 0.5, is
where m = c/c0, c is the monomer concentration, c0 is the initial monomer concentration, kobs is the observed rate coefficient ([=]1/time), t is the incubation time, and δ is expected to be an integer (22). The data over all c0 values are best fit with δ = 1, although profiles with δ-values as high as 2 were also reasonable approximations in some cases. The corresponding half-life value (t50), when m = 0.5, is 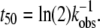 Equivalent values of t50 were also obtained from visual interpolation of m versus t. Fig. 1 (main panel) shows m versus t/t50 for aCgn with c0 ranging from 0.5 to 7.7 mg/mL. The values of log kobs versus log c0 are shown in the inset to Fig. 1. They follow the scaling relationship log kobs = log k0 + ξ log c0, with ξ = 1.9 ± 0.3 (95% confidence interval) from linear regression, and illustrate that kobs and t50 are strongly dependent on initial protein concentration. Plotting on a t/t50 scale allows data from a wide range of t50 values to be collapsed in a single panel, and also illustrates that the data are reasonably represented by a first-order decay (dotted line in Fig. 1). Monomer loss profiles for bG-CSF were qualitatively similar to those for aCgn, but with a different range of t50 values.
Equivalent values of t50 were also obtained from visual interpolation of m versus t. Fig. 1 (main panel) shows m versus t/t50 for aCgn with c0 ranging from 0.5 to 7.7 mg/mL. The values of log kobs versus log c0 are shown in the inset to Fig. 1. They follow the scaling relationship log kobs = log k0 + ξ log c0, with ξ = 1.9 ± 0.3 (95% confidence interval) from linear regression, and illustrate that kobs and t50 are strongly dependent on initial protein concentration. Plotting on a t/t50 scale allows data from a wide range of t50 values to be collapsed in a single panel, and also illustrates that the data are reasonably represented by a first-order decay (dotted line in Fig. 1). Monomer loss profiles for bG-CSF were qualitatively similar to those for aCgn, but with a different range of t50 values.
FIGURE 1.
(Main panel) Monomer fraction, (m), versus reduced time, (t/t50), for aCgn as a function of initial protein concentration. c0/mg mL−1 = 0.5 (open squares), 0.7 (solid triangles), 1.0 (open circles), 1.4 (solid diamonds), 2.0 (open triangles), 3.4 (solid squares), 4.8 (open diamonds), and 7.7 (solid circles). Dotted and dashed lines represent purely first order (δ = 1) and purely second order (δ = 2) decay, respectively. (Inset) Scaling of kobs with c0 for aCgn. Solid line is a linear fit to the data set on a log-log scale.
Static and dynamic light scattering
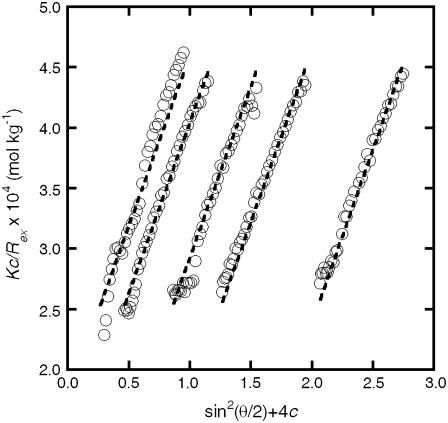
Static and dynamic light scattering were used to characterize each fully aggregated aCgn or bG-CSF sample. Samples were considered fully aggregated when m = 0.05 ± 0.02, as determined by SEC. Samples held at 65°C for incubation times that were a factor of two or greater than that needed to reach m = 0.05 were also tested and shown to give the same results within statistical uncertainty (not shown). All samples were optically transparent, without indications of precipitation or visual particulate formation, even after prolonged storage (>2 weeks) under refrigeration. Fig. 2 shows a representative Zimm plot generated from SLS measurements on a fully aggregated aCgn sample, c0 = 0.7 mg/mL, with dashed lines indicating the best fit to Eq. 3. Qualitatively similar results were observed for bG-CSF in all cases. Fitted values and 95% confidence intervals were obtained for Mw and Rg; these values are presented and discussed further below. As noted in Materials and Methods, the concentration dependence of the scattered intensity was typically insufficient to determine values of B22 that were statistically different from zero.
FIGURE 2.
Representative Zimm plot generated from static light scattering measurements of aCgn aggregates showing experimental data points (circles) and nonlinear least-squares fit to Eq. 3 (dashed lines). Data shown are for c0 = 0.7 mg/mL. Outliers (3% of the points) are not shown.
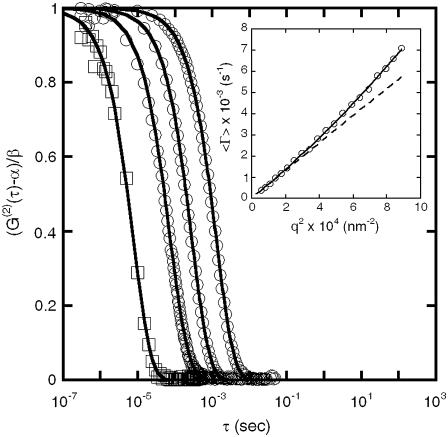
Fig. 3 shows representative examples of multi-angle DLS data for aCgn for a single value of c0, and for different scattering angles. The solid lines are best fits to Eq. 4, and the autocorrelation function for a native, monomeric sample (20°C, c0 = 5 mg/mL) is shown for reference. Qualitatively similar results were observed for bG-CSF in all cases. The inset to Fig. 3 shows the fitted values of 〈Γ〉 for the aggregate plotted as a function of q2. The solid line indicates a least-squares fit to Eq. 6 without assuming a zero y-intercept. The value of C was calculated from the fitted parameter  using the value of
using the value of  from the corresponding SLS data. Combining the fitted value of D0 with the Stokes-Einstein equation yielded Rh. The dashed line shows the limiting slope of the solid line as q2 approaches zero, emphasizing the deviation of 〈Γ〉 from linearity at high q2. This behavior is characteristic of a variety of molecular architectures, including semiflexible polymer chains, provided that the mobility of the internal domains is substantially different from that of the center of mass (35,58,59).
from the corresponding SLS data. Combining the fitted value of D0 with the Stokes-Einstein equation yielded Rh. The dashed line shows the limiting slope of the solid line as q2 approaches zero, emphasizing the deviation of 〈Γ〉 from linearity at high q2. This behavior is characteristic of a variety of molecular architectures, including semiflexible polymer chains, provided that the mobility of the internal domains is substantially different from that of the center of mass (35,58,59).
FIGURE 3.
(Main panel) Representative, normalized autocorrelation function as a function of delay time and scattering angle for aCgn monomer (90°, c = 5.0 mg/mL, squares) and aggregate (120°, 55°, 25°, c0 = 0.7 mg/mL, circles). For clarity, every other autocorrelation data point is omitted from each curve. All data are included in all analyses and fitting. (Inset) 〈Γ〉 versus q2 for the aggregate data represented in the main panel (circles). The solid line indicates a fit to Eq. 6. The dashed line shows the limiting slope as the scattering angle approaches zero.
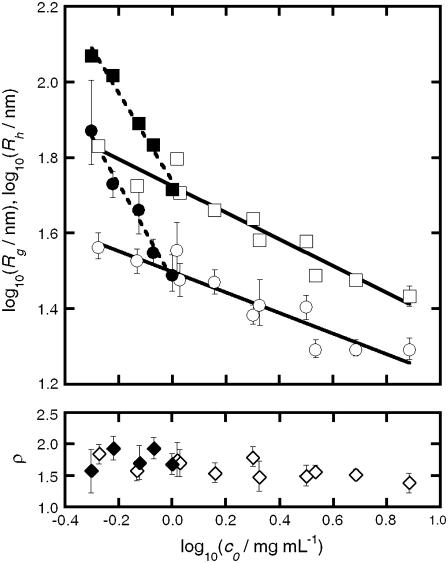
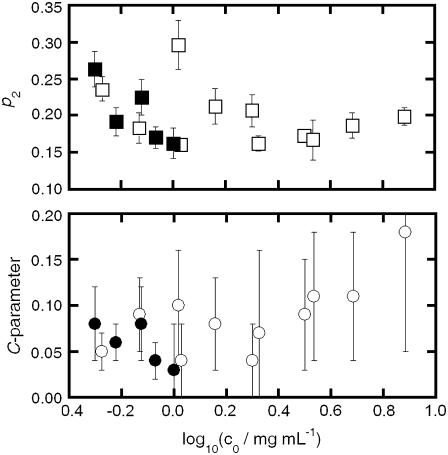
The upper panel of Fig. 4 shows the scaling behavior of Rg and Rh for both aCgn and bG-CSF aggregates as a function of the c0 value of the initial, unaggregated sample. The solid and dashed lines represent log-log fits to the data. The lower panel of Fig. 4 shows that values of the ratio ρ = Rg/Rh remain reasonably constant versus c0 for both aCgn and bG-CSF aggregates. The upper panel of Fig. 5 shows the values of the polydispersity index (p2, Eq. 5) as a function of c0, while the lower panel shows the corresponding C-parameter values (Eq. 6). The p2 values indicate that the distribution of aggregate sizes for both proteins is relatively narrow (57,60). The ρ-values together with values of the C-parameter are consistent with a semiflexible chain morphology (35,58,59,61).
FIGURE 4.
(Top panel) Scaling of Rg (squares) and Rh (circles) with c0 for aCgn aggregates (open symbols) and bG-CSF aggregates (solid symbols). The solid and dashed lines are linear fits to the data on a log-log scale for aggregates of aCgn and bG-CSF, respectively. (Bottom panel) ρ-ratio versus c0 for aCgn aggregates (open diamonds) and bG-CSF aggregates (solid diamonds).
FIGURE 5.
(Top panel) p2 versus c0 for aggregates of aCgn (open squares) and bG-CSF (solid squares) aggregates. (Bottom panel) C-parameter versus c0 for aggregates of aCgn (open circles) and bG-CSF (solid circles).
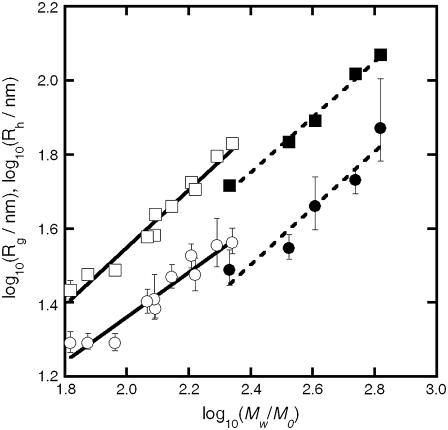
Fig. 6 shows the scaling behavior of Rg and Rh with respect to the reduced molecular weight (Mw/M0) of the aggregates, where M0 is the molecular weight of the monomer for aCgn (25.7 kDa) or bG-CSF (19 kDa). The solid and dashed lines again represent log-log fits. Fitted values of Mw for different c0 ranged from ∼1700–5600 kDa (∼70–220 M0) for aCgn aggregates, and ∼4200–13,000 kDa (∼220–680 M0) for bG-CSF aggregates. The scaling exponents (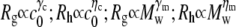 ) from the log-log fits in Figs. 4 and 6, average values of ρ from Fig. 4, and 95% confidence intervals for each are given in Table 1. Scaling exponents calculated from fits to a power law relationship without first converting to a log-log scale were the same as those reported in Table 1 within statistical uncertainty. Values of the scaling exponents γm and ηm are also consistent with a semiflexible, unbranched chain morphology (35,62,63).
) from the log-log fits in Figs. 4 and 6, average values of ρ from Fig. 4, and 95% confidence intervals for each are given in Table 1. Scaling exponents calculated from fits to a power law relationship without first converting to a log-log scale were the same as those reported in Table 1 within statistical uncertainty. Values of the scaling exponents γm and ηm are also consistent with a semiflexible, unbranched chain morphology (35,62,63).
FIGURE 6.
Scaling of Rg (squares) and Rh (circles) with reduced Mw for aggregates of aCgn (open symbols) and bG-CSF (solid symbols). The solid and dashed lines are linear fits on a log-log scale for the respective data sets.
TABLE 1.
Summary of scaling exponents and average ρ-ratio values
| γc | ηc | Avg ρ-ratio | γm | ηm | |
|---|---|---|---|---|---|
| aCgn | −0.3 ± 0.1 | −0.27 ± 0.07 | 1.65 ± 0.1 | 0.74 ± 0.16 | 0.64 ± 0.12 |
| bG-CSF | −1.13 ± 0.34 | −1.25 ± 0.34 | 1.76 ± 0.13 | 0.74 ± 0.15 | 0.8 ± 0.4 |
Definitions of the scaling exponents are provided in the text. The statistical uncertainties are 95% confidence intervals.
Cryo-TEM
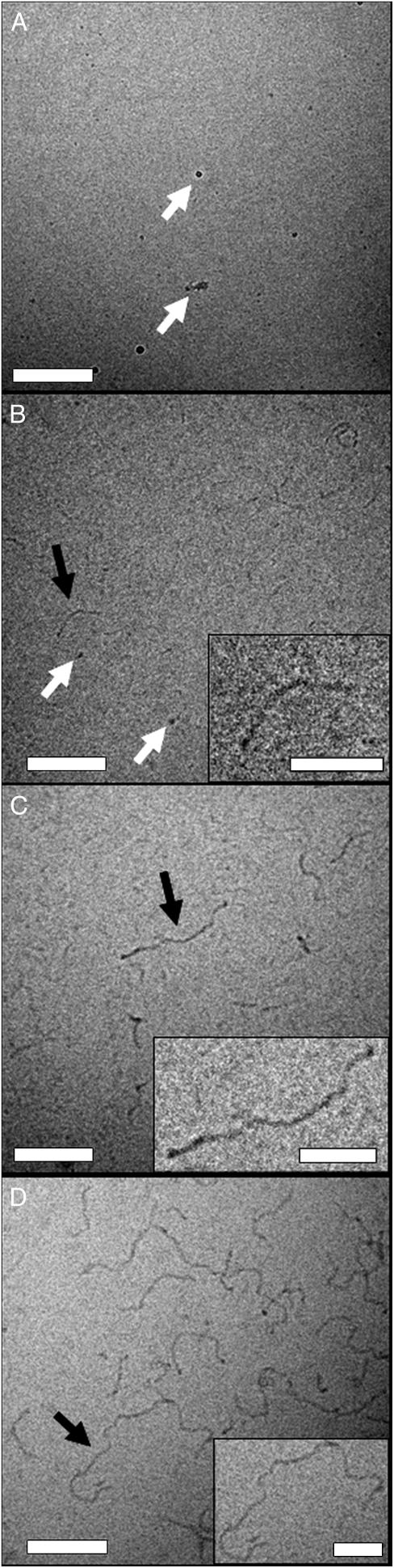
Cryo-TEM measurements were performed on a series of aCgn samples as a function of incubation time at 65°C for c0 = 1.0 mg/mL. Representative images for fully monomeric (m = 1), partially aggregated (m = 0.42 ± 0.06) and fully aggregated (m = 0.05 ± 0.02) samples are shown in Fig. 7, A–C. The protein monomers (native state crystallographic diameter ∼4 nm) (64) are too small to be quantified with this technique. The mature, linear aCgn aggregates have an apparent contour length of ∼150–250 nm and apparent width of ∼8–10 nm, without obvious branching. Aggregates from other intermediate time points shared the same width and qualitative shape as those in Fig. 7, B and C, consistent with growth by linear polymerization. A representative image from a similar measurement for a fully aggregated bG-CSF sample (c0 = 0.5 mg/mL) is shown in Fig. 7 D. Aggregates of bG-CSF appear to have the same qualitative morphology as those of aCgn, with a slightly greater width (∼10–13 nm) and much greater contour length (∼200–800 nm). Crystallographically, native bG-CSF is roughly cylindrical with dimensions of ∼ 2.5 × 4.5 nm (65). The lack of a rigid-rod morphology was apparent in all cryo-TEM images.
FIGURE 7.
Cryo-TEM micrographs of aCgn samples (c0 = 1 mg/mL) at m = 1 (A), m = 0.42 ± 0.06 (B), and m = 0.05 ± 0.02 (C) and a bG-CSF sample (c0 = 0.5 mg/mL) at m = 0.05 ± 0.02 (D). The white arrows in panels A and B indicate artifacts caused by crystallization of water vapor on the grid. The black arrows indicate sections of the main image that appear as insets for greater clarity. Main panel scale bar: 200 nm. (Inset scale bar) 50 nm.
Circular dichroism and ThT fluorescence
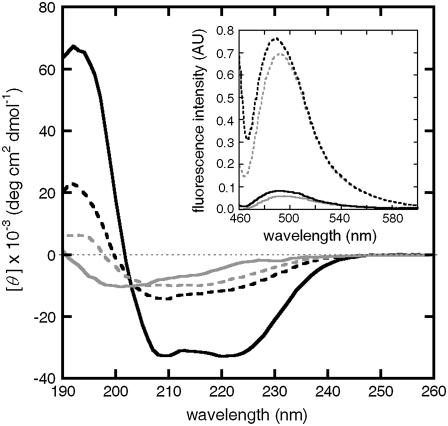
The main panel of Fig. 8 shows the mean residue ellipticity ([θ]) as a function of wavelength for both native and fully aggregated samples of aCgn (c0 = 1.0 mg/mL) and bG-CSF (c0 = 0.5 mg/mL). In both cases, the aggregate spectra are indicative of an increased β-sheet structure, and this is distinct from both the native and unfolded monomers (37,40). The inset of Fig. 8 shows the fluorescence enhancement of ThT in the presence of aCgn (c0 = 1.0 mg/mL) and bG-CSF (c0 = 0.5 mg/mL) aggregates compared to that in a corresponding solutions of only native monomers. Such increases are similar to those typically reported for a variety of systems that undergo nonnative aggregation (43,66).
FIGURE 8.
(Main panel) Far-UV CD spectra of aCgn monomer (solid gray line) and aggregate (dashed gray line), and bG-CSF monomer (solid black line) and aggregate (dashed black line) at 20°C ± 0.2°C. (Inset) Fluorescence emission spectra of ThT in the presence of aCgn monomer (solid gray line) and aggregate (dashed gray line), and bG-CSF monomer (solid black line) and aggregate (dashed black line) at 20°C ± 0.2°C.
DISCUSSION
Aggregate size, morphology, and polydispersity
It is important to establish whether appreciable aggregate condensation or coalescence occurs during aggregate growth. For aggregates that remain soluble throughout the course of assembly, all of the following experimental signatures are expected if appreciable coalescence occurs: Mw increases without a concomitant decrease in monomer concentration, e.g., at long times once monomer concentration does not change appreciably; high polydispersity values for the resulting aggregates (p2 values ≫ 0.3); and evidence of higher order structure in microscopy, e.g., crosslinking, bundling, or evidence that aggregates are composed of distinct subunits that are themselves discernable aggregates. Our light scattering and TEM data clearly show no evidence of any of these experimental signatures for aCgn and bG-CSF aggregates, and therefore indicate that the aggregates are uncondensed. Additional details regarding the morphology of the aggregates can be deduced from the analysis below.
Values of the ratio ρ = Rg/Rh correlate with the compactness of the underlying polymer architecture, increasing as the morphology becomes more open and extended and as the polydispersity increases (35). The bottom panel of Fig. 5 shows that the values of ρ are reasonably independent of c0 for aggregates of both aCgn and bG-CSF, while Fig. 6 shows the monotonic relationship for Rg(Mw) and Rh(Mw). Together, these results indicate that the underlying morphology is conserved across aggregates from these two proteins, even though the resulting sizes are significantly different. The average values for ρ given in Table 1 are intermediate between those for a theoretical Gaussian chain (ρ = 8/(3π1/2) ≈ 1.505) (58) and a rigid rod (ρ > 2) (35). The values for p2 shown in the top panel of Fig. 5 indicate that the polydispersity of the aggregated samples was relatively low (average p2 = 0.2). For comparison, a typical condensation polymerization (Mw/Mn ≈ 2) with chains of similar flexibility would yield p2 ≈ 0.3, while monodisperse chains (Mw/Mn = 1) would yield p2 = 0 (57,60).
The value of the C-parameter is determined by the longest internal mode of the polymer relative to its center of mass, and is a measure of the flexibility of the polymer molecular architecture (35,58,59,61). The calculated values for aggregates of aCgn and bG-CSF shown in the bottom panel of Fig. 5 lie between the values for a theoretical hard sphere (C = 0) (35) and a fully flexible chain (C ∼ 0.2) (59). Values of the scaling exponent γm for both aCgn aggregates and bG-CSF aggregates (Table 1) lie between those for a Gaussian chain (γm = 0.5) and a rigid rod (γm = 1) (35), and values of ηm also fall in the theoretical range for semiflexible chains (0.6 < ηm < 1) (62,63). Together the light scattering data show convincingly that soluble, nonnative aggregates of aCgn and bG-CSF are each well described as linear, semiflexible polymer chains with relatively low polydispersity.
The size and morphology of the aCgn and bG-CSF aggregates indicated by light scattering measurements are confirmed by the cryo-TEM micrographs shown in Fig. 7. The aggregates are linear chains without appreciable branching or evidence of aggregate-aggregate condensation. In keeping with this description, SLS measurements yield Rg values of 63 ± 2 nm and 117 ± 2 nm for the aggregates of aCgn and bG-CSF shown in panels C and D, respectively. Upper estimates of the corresponding end-to-end distances (Re) are ∼150 nm and ∼300 nm, respectively (based on the Gaussian limit, 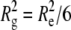 ) (67), which are also consistent with the micrographs. The corresponding rigid rod limits for the contour length (L) of aggregates with these Rg values are ∼220 nm and ∼400 nm for aCgn and bG-CSF, respectively (
) (67), which are also consistent with the micrographs. The corresponding rigid rod limits for the contour length (L) of aggregates with these Rg values are ∼220 nm and ∼400 nm for aCgn and bG-CSF, respectively (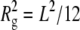 ) (67). Caution must be exercised in extracting length scales from cryo-TEM micrographs. As the images are two-dimensional projections of a three-dimensional sample, the degree to which aggregate chains protrude above and below the image plane is difficult to quantify.
) (67). Caution must be exercised in extracting length scales from cryo-TEM micrographs. As the images are two-dimensional projections of a three-dimensional sample, the degree to which aggregate chains protrude above and below the image plane is difficult to quantify.
Monomer structure in aggregates
The main panel of Fig. 8 indicates the secondary structure changes upon aggregation for aCgn and bG-CSF. While both proteins have appreciably different native secondary structure, their aggregate far-UV CD spectra are semiquantitatively similar. It is difficult to reliably quantify or distinguish different types of β-sheet structures using only far-UV CD. However, for aCgn, the red shift compared to the unfolded monomer spectra (40) along with the broad single minimum near 212 nm are taken here to indicate a small but discernible increase in β-sheet content. The data are insufficient to draw quantitative conclusions regarding the extent of β-sheet conversion, or to assess whether a cross-β-sheet structure is present. Doing so would presumably require techniques such as infrared spectroscopy and/or x-ray diffraction. It should be noted that structural analysis of model systems (68,69) indicates that only relatively short series of amino acids within a polypeptide chain are needed to stabilize nonnative polymerization. For bG-CSF, the aggregate is conclusively nonnative, but the CD spectrum is not sufficient to conclude that more than a small fraction of the residues in a given monomer have adopted a β-sheet structure. Based on all of the above considerations, a reasonable hypothesis is that the aggregates are composed of subunits in which only a fraction of the amino acids from each (nonnative monomer) protein chain have undergone large conformational rearrangements to form stabilizing interprotein contacts.
Thioflavine T (ThT) binds to various types of β-sheet architectures (44) and has been used as an indicator for the presence of amyloid fibrils (43). The approximately sevenfold increase in the fluorescence intensity maxima between native and aggregated samples at comparable mass concentration of protein (inset, Fig. 8) demonstrates specific binding to the aggregates for both proteins. This is despite the relatively small changes in CD spectra and the observation that the aggregates do not form (amyloid) fibrils or other higher-order structures resulting from aggregate-aggregate condensation under these conditions. This finding is consistent, however, with previous work demonstrating ThT binding to nonamyloid samples (44,70), and adds confirmatory evidence that ThT binding alone cannot be used to accurately infer specific aggregate morphologies or underlying monomer structure.
Scaling with c0 and relation to a nucleated-growth mechanism
The observed scaling behavior of Mw with c0, and thus Rg and Rh with c0, may at first appear counterintuitive. However, a recent model of nucleated polymerization (27) naturally produces such behavior as a result of the different dependencies of nucleation and growth rates on initial protein concentration, and provides quantitative relationships between this behavior and the relative stoichiometries of nucleation and growth. Increasing c0 decreases the characteristic timescales of both nucleation (τn) and growth (τg). However, τn scales as 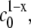 while τg scales as
while τg scales as 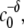 where x denotes the number of monomers in the nucleus and δ denotes the number of monomers needed to advance polymer growth by one kinetic step. When x > δ + 1, the limiting Mw of the aggregates is predicted to decrease with increasing c0 at fixed temperature, pressure, and solvent conditions (27). To the best of our knowledge, the results in Fig. 4 are the first experimental confirmation of this behavior, and are analyzed further below using the LENP model. The particular relationships of interest are (27)
where x denotes the number of monomers in the nucleus and δ denotes the number of monomers needed to advance polymer growth by one kinetic step. When x > δ + 1, the limiting Mw of the aggregates is predicted to decrease with increasing c0 at fixed temperature, pressure, and solvent conditions (27). To the best of our knowledge, the results in Fig. 4 are the first experimental confirmation of this behavior, and are analyzed further below using the LENP model. The particular relationships of interest are (27)
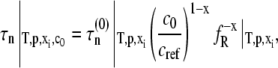 |
(7a) |
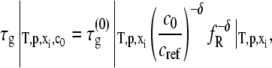 |
(7b) |
where 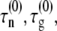 and fR are, respectively, the intrinsic nucleation timescale, intrinsic growth timescale, and fraction of monomeric protein that exists in the reactive (unfolded) conformational state. Each of these parameters is independent of c0, and constant for a given protein at fixed temperature, pressure, and solvent composition (T, p, and xi) (27), such as the conditions for all data reported here. cref is an arbitrary, fixed reference concentration that sets the values of
and fR are, respectively, the intrinsic nucleation timescale, intrinsic growth timescale, and fraction of monomeric protein that exists in the reactive (unfolded) conformational state. Each of these parameters is independent of c0, and constant for a given protein at fixed temperature, pressure, and solvent composition (T, p, and xi) (27), such as the conditions for all data reported here. cref is an arbitrary, fixed reference concentration that sets the values of 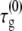 and
and 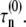 kobs from monomer loss kinetics or any extent-of-reaction based kinetics is given by (27)
kobs from monomer loss kinetics or any extent-of-reaction based kinetics is given by (27)
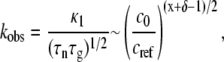 |
(8) |
where κ1 is a constant of order one that depends weakly on x and δ, and is otherwise independent of c0. In addition, the Mw of the soluble aggregates as m goes to zero is given by
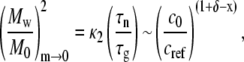 |
(9) |
where κ2 is again a constant of order one that depends weakly on x and δ, and is independent of c0. M0 is the molecular weight of the monomer, and the subscript m→0 indicates the quantity is evaluated as the mass fraction of remaining monomer approaches zero. Combining Eqs. 8 and 9 and neglecting the weak and c0-independent contributions of κ1 and κ2 gives
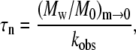 |
(10a) |
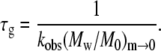 |
(10b) |
Equations 8–10 hold for conditions in which (Mw/M0)m→0 > ∼10 (27).
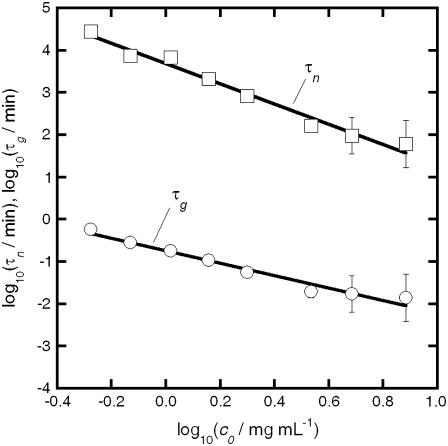
Fig. 9 shows τn and τg calculated from Eq. 10 and the experimental kobs and Mw data over a range of c0 for aCgn. If the nucleated polymerization model accurately represents the experimental data, τn and τg should scale with c0 according to Eq. 7, and the resulting x and δ values should be the same as those derived from the m(t/t50) profiles and the scaling of kobs with c0 (27,40). The slopes for τn and τg versus c0 in Fig. 9 are −2.4 ± 0.4 and −1.5 ± 0.3, respectively (95% confidence intervals). Using experimental values of kobs or t50 without assuming δ = 1 when fitting monomer loss data (e.g., using δ = 2) makes minor, c0-independent changes in the absolute values of τn and τg that are imperceptible on the log scale in Fig. 9. The slope of τn in Fig. 9 indicates a nucleus size (x) of 3–4 monomers, suggesting both trimers and tetramers act effectively as nuclei. This is consistent with a previous analysis based purely on the scaling behavior of kobs with c0, and the observation that at higher temperatures (75–80°C) a competition between two nucleus sizes is clearly evident (40). Unlike that previous analysis, the results for x and δ from the c0 scaling in Fig. 9 do not rely upon inferring a value of δ from m versus t. Furthermore, the analysis above provides separate values of τn and τg, while extent-of-reaction or monomer-loss data alone cannot provide more than the product of τn and τg (27,40). In addition, Eq. 9 provides a simple and useful relationship in that it shows the limiting value of Mw provides a quantitative estimate of the ratio of nucleation to growth timescales. For aCgn, the observed range of limiting Mw/M0 values (∼70–220) thus correspond to values of τn/τg ∼ 5 × 103 to 5 × 104, consistent with the vertical distance between the τn and τg curves in Fig. 9. A similar analysis to that above can be performed for bG-CSF, but is not included here. The much larger variability found for kobs values, and the much smaller c0 range over which they were measurable at 65°C presently preclude an accurate assessment of τn, τg, x, and δ. Equation 9 can still be applied, however, as it does not require accurate kobs values. Doing so yields τn/τg values of order 104–105, consistent with the larger aggregate sizes for bG-CSF compared to aCgn, as observed in Figs. 4, 6, and 7.
FIGURE 9.
Rate diagram for aCgn with nucleation (squares) and growth (circles) timescales as a function of c0. The solid lines are linear fits to the data on a log-log scale.
The results in Fig. 9 are particularly important in that they illustrate a general procedure for extracting distinct values of τn and τg for a given T, p, xi, c0, and protein of interest without the need for indirect experiments such as seeding and chemical labeling. Unlike previous approaches and models of nonnative aggregation in which nucleation and growth timescales were regressed from experimental kinetic and/or light scattering data (33,71,72), the above analysis is independent of the particular morphology of the aggregates, and it does not require one to impose a priori assumptions regarding τn/τg (73–75). That is, although the morphology and the relationship between Rg, Rh, and Mw have been determined in this report, this information is not needed to perform the timescale analysis described above, provided that the aggregates have not condensed appreciably before the monomer supply has been significantly depleted. If aggregate condensation is the predominant growth mechanism, then accurate information regarding morphology is required to employ light scattering to extract meaningful kinetic parameters (31,33,72). In either case, imposing assumptions regarding τn/τg will artificially constrain the predicted size distribution and the ability of the model to describe the light scattering data (27).
Eq. 7 shows that τn and τg are both functions of c0 and the free energy of unfolding of the monomer (via fR). These contributions can be factored out using experimental values for protein concentration and unfolding free energy (24,38,40). The resulting intrinsic timescales for nucleation and growth are then of further value in that they provide quantitative bounds on interpretations of the effects of protein sequence, charge, and sample conditions on factors such as prenuclei free energies and the rate-controlling step(s) for nucleation and growth (27,40).
In the simplest version of the nucleated growth model, x and δ are assumed to have integer values. The observation that intermediate values are obtained suggests that both nucleation and growth may more accurately be described as occurring via two competing species at this temperature, and solvent conditions, nucleation from both trimers and tetramers, and growth via addition of one to two monomers. The estimated width of the aggregates from cryo-TEM, ∼10 nm (approximately twice the diameter of the monomer), lends additional support to a qualitative mechanism in which each growth step during polymerization requires one or two monomers to progress to the next stable polymer length. In general, the value of δ is not necessarily the number of monomers in a cross-section of the aggregate chains. It is simply the number of monomers that must reversibly associate with a previously formed aggregate before the monomers forming the necessary stabilizing interprotein contacts to commit them (irreversibly) to that aggregate (27).
CONCLUSIONS
Thermally induced, nonnative aggregates of aCgn and bG-CSF were characterized using a combination of light scattering, spectroscopy, and microscopy. The combined results unambiguously indicate that the aggregates from both systems are linear, semiflexible polymer chains with relatively low polydispersity, and increased nonnative β-sheet secondary structure. The aggregates bind thioflavine T, without evidence for the formation of (amyloid) fibrils or higher-order structures resulting from association or condensation. Distinct values for the nucleation and growth timescales were calculated without the need for seeding or addition of chemical labels, or assumptions about the underlying structure and morphology of the aggregates. These timescales scale differently with initial protein concentration and provide a self-consistent explanation for the experimental observation that relatively few, large aggregates are formed at low c0, and a greater number of smaller aggregates are formed at high c0. Although suggested by recent theoretical work (27), to the best of our knowledge this is the first time such qualitative and quantitative scaling behavior and timescale analysis has been shown experimentally for aggregated proteins. In total, the t50-Mw method presented here produces scaling behavior and fitted stoichiometries for nucleation and growth that agree well with those of an alternative approach based exclusively on monomer loss kinetics (40), and has the added benefit of being able to separate the nucleation and growth timescales when aggregate condensation is not appreciable. This, and its more general form in which aggregate Mw and monomer loss are coupled as a function of time (27), offer a potentially powerful and widely applicable approach for determining key mechanistic parameters of protein nucleation and growth before subsequent condensation.
Acknowledgments
The authors gratefully acknowledge partial funding from the COBRE program of the National Center for Research Resources of the National Institutes of Health (grant No. P20 RR015588), Merck and Co., and the generous donation of bG-CSF by Pfizer Global R&D (Groton, CT).
Editor: Kathleen B. Hall.
References
- 1.Wang, W. 2005. Protein aggregation and its inhibition in biopharmaceutics. Int. J. Pharma. 289:1–30. [DOI] [PubMed] [Google Scholar]
- 2.Rosenberg, A. S. 2006. Effects of protein aggregates: an immunologic perspective. AAPS J. 8:E501–E507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Dobson, C. M. 2006. Protein aggregation and its consequences for human disease. Protein Pept. Lett. 13:219–227. [DOI] [PubMed] [Google Scholar]
- 4.Slow, E. J., R. K. Graham, and M. R. Hayden. 2006. To be or not to be toxic: aggregations in Huntington and Alzheimer disease. Trends Genet. 22:408–411. [DOI] [PubMed] [Google Scholar]
- 5.Bucciantini, M., G. Calloni, F. Chiti, L. Formigli, D. Nosi, C. M. Dobson, and M. Stefani. 2004. Prefibrillar amyloid protein aggregates share common features of cytotoxicity. J. Biol. Chem. 279:31374–31382. [DOI] [PubMed] [Google Scholar]
- 6.Bucciantini, M., E. Giannoni, F. Chiti, F. Baroni, L. Formigli, J. S. Zurdo, N. Taddei, G. Ramponi, C. M. Dobson, and M. Stefani. 2002. Inherent toxicity of aggregates implies a common mechanism for protein misfolding diseases. Nature. 416:507–511. [DOI] [PubMed] [Google Scholar]
- 7.Tycko, R. 2006. Molecular structure of amyloid fibrils: insights from solid-state NMR. Q. Rev. Biophys. 39:1–55. [DOI] [PubMed] [Google Scholar]
- 8.Relini, A., R. Rolandi, M. Bolognesi, M. Aboudan, G. Merlini, V. Bellotti, and A. Gliozzi. 2004. Ultrastructural organization of ex vivo amyloid fibrils formed by the apolipoprotein A-I Leu174Ser variant: an atomic force microscopy study. Biochim. Biophys. Acta. 1690:33–41. [DOI] [PubMed] [Google Scholar]
- 9.Schuler, B., R. Rachel, and R. Seckler. 1999. Formation of fibrous aggregates from a non-native intermediate: the isolated P22 tailspike beta-helix domain. J. Biol. Chem. 274:18589–18596. [DOI] [PubMed] [Google Scholar]
- 10.Shahi, P., R. Sharma, S. Sanger, I. Kumar, and R. Jolly. 2007. Formation of amyloid fibrils via longitudinal growth of oligomers. Biochemistry. 46:7365–7373. [DOI] [PubMed] [Google Scholar]
- 11.Moore, R., S. Hayes, R. Fischer, and S. Priola. 2007. Amyloid formation via supramolecular peptide assembly. Biochemistry. 46:7079–7087. [DOI] [PubMed] [Google Scholar]
- 12.Chi, E. Y., S. Krishnan, T. W. Randolph, and J. F. Carpenter. 2003. Physical stability of proteins in aqueous solution: mechanism and driving forces in nonnative protein aggregation. Pharma. Res. 20:1325–1336. [DOI] [PubMed] [Google Scholar]
- 13.Oliveberg, M., and P. G. Wolynes. 2005. The experimental survey of protein-folding energy landscapes. Q. Rev. Biophys. 38:245–288. [DOI] [PubMed] [Google Scholar]
- 14.Dobson, C. M. 2004. Principles of protein folding, misfolding and aggregation. Sem. Cell Dev. Biol. 15:3–16. [DOI] [PubMed] [Google Scholar]
- 15.Fink, A. L. 1998. Protein aggregation: folding aggregates, inclusion bodies and amyloid. Fold. Des. 3:R9–R23. [DOI] [PubMed] [Google Scholar]
- 16.Goers, J., S. E. Permyakov, E. A. Permyakov, V. N. Uversky, and A. L. Fink. 2002. Conformational prerequisites for alpha-lactalbumin fibrillation. Biochemistry. 41:12546–12551. [DOI] [PubMed] [Google Scholar]
- 17.Grillo, A. O., K. L. T. Edwards, R. S. Kashi, K. M. Shipley, L. Hu, M. J. Besman, and C. R. Middaugh. 2001. Conformational origin of the aggregation of recombinant human factor VIII. Biochemistry. 40:586–595. [DOI] [PubMed] [Google Scholar]
- 18.Khurana, R., J. R. Gillespie, A. Talapatra, L. J. Minert, C. Ionescu-Zanetti, I. Millett, and A. L. Fink. 2001. Partially folded intermediates as critical precursors of light chain amyloid fibrils and amorphous aggregates. Biochemistry. 40:3525–3535. [DOI] [PubMed] [Google Scholar]
- 19.Linding, R., J. Schymkowitz, F. Rousseau, F. Diella, and L. Serrano. 2004. A comparative study of the relationship between protein structure and beta-aggregation in globular and intrinsically disordered proteins. J. Mol. Biol. 342:345–353. [DOI] [PubMed] [Google Scholar]
- 20.Uversky, V. N., and A. L. Fink. 2004. Conformational constraints for amyloid fibrillation: the importance of being unfolded. Biochim. Biophys. Acta Proteins Proteomics. 1698:131–153. [DOI] [PubMed] [Google Scholar]
- 21.Bratko, D., T. Cellmer, J. M. Prausnitz, and H. W. Blanch. 2007. Molecular simulation of protein aggregation. Biotechnol. Bioeng. 96:1–8. [DOI] [PubMed] [Google Scholar]
- 22.Lumry, R., and H. Eyring. 1954. Conformation changes of proteins. J. Phys. Chem. 58:110–120. [Google Scholar]
- 23.Sanchez-Ruiz, J. M. 1992. Theoretical analysis of Lumry-Eyring models in differential scanning calorimetry. Biophys. J. 61:921–935. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Roberts, C. J. 2003. Kinetics of irreversible protein aggregation: analysis of extended Lumry-Eyring models and implications for predicting protein shelf life. J. Phys. Chem. B. 107:1194–1207. [Google Scholar]
- 25.Roberts, C. J. 2006. Non-native protein aggregation: pathways, kinetics, and shelf-life prediction. In Misbehaving Proteins: Protein Misfolding, Aggregation, and Stability. R. M. Murphy and A. M. Tsai, editors. Springer, New York.
- 26.Kurganov, B. I., E. R. Rafikova, and E. N. Dobrov. 2002. Kinetics of thermal aggregation of tobacco mosaic virus coat protein. Biochemistry (Mosc.). 67:525–533. [DOI] [PubMed] [Google Scholar]
- 27.Andrews, J. M., and C. J. Roberts. 2007. A Lumry-Eyring nucleated-polymerization model of protein aggregation kinetics I. Aggregation with pre-equilibrated unfolding. J. Phys. Chem. B. 111:7897–7913. [DOI] [PubMed] [Google Scholar]
- 28.Goldstein, R. F., and L. Stryer. 1986. Cooperative polymerization reactions. Analytical approximations, numerical examples, and experimental strategy. Biophys. J. 50:583–599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Oosawa, F., and S. Asakura. 1975. Thermodynamics of the Polymerization of Proteins. B. Horecker, N. O. Kaplan, J. Marmur, and H. Sheraga, editors. Academic Press, London.
- 30.Ferrone, F. 1999. Analysis of protein aggregation kinetics. Methods Enzymol. 309:256–274. [DOI] [PubMed] [Google Scholar]
- 31.Gibson, T. J., and R. M. Murphy. 2006. Inhibition of insulin fibrillogenesis with targeted peptides. Protein Sci. 15:1133–1141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Liu, L., and R. M. Murphy. 2006. Kinetics of inhibition of beta-amyloid aggregation by transthyretin. Biochemistry. 45:15702–15709. [DOI] [PubMed] [Google Scholar]
- 33.Pallitto, M. M., and R. M. Murphy. 2001. A mathematical model of the kinetics of beta-amyloid fibril growth from the denatured state. Biophys. J. 81:1805–1822. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Chi, E. Y., B. S. Kendrick, J. F. Carpenter, and T. W. Randolph. 2005. Population balance modeling of aggregation kinetics of recombinant human interleukin-1 receptor antagonist. J. Pharm. Sci. 94:2735–2748. [DOI] [PubMed] [Google Scholar]
- 35.Burchard, W. 1999. Solution properties of branched macromolecules. In Branched Polymers II. J. Roovers, editor. Springer, New York.
- 36.Bartkowski, R. E., R. Kitchel, N. R. Peckham, and L. Margulis. 2002. Aggregation of recombinant bovine granulocyte colony stimulating factor in solution. J. Protein Chem. 21:137–143. [DOI] [PubMed] [Google Scholar]
- 37.Kueltzo, L. A., and C. R. Middaugh. 2003. Structural characterization of bovine granulocyte colony stimulating factor: Effect of temperature and pH. J. Pharm. Sci. 92:1793–1804. [DOI] [PubMed] [Google Scholar]
- 38.Roberts, C. J., R. T. Darrington, and M. B. Whitley. 2003. Irreversible aggregation of recombinant bovine Granulocyte-Colony Stimulating Factor (bG-CSF) and implications for predicting protein shelf life. J. Pharm. Sci. 92:1095–1111. [DOI] [PubMed] [Google Scholar]
- 39.Kasraian, K., A. Kuzniar, D. Earley, B. J. Kamicker, G. Wilson, T. Manion, J. Y. Hong, C. Reiber, and P. Canning. 2001. Sustained in vivo activity of recombinant bovine granulocyte colony stimulating factor (rbG-CSF) using HEPES buffer. Pharma. Dev. Tech. 6:441–447. [DOI] [PubMed] [Google Scholar]
- 40.Andrews, J. M., and C. J. Roberts. 2007. Non-native aggregation of alpha-chymotrypsinogen occurs through nucleation and growth with competing nucleus sizes and negative activation energies. Biochemistry. 46:7558–7571. [DOI] [PubMed] [Google Scholar]
- 41.Hartley, B. S. 1964. Amino-acid sequence of bovine chymotrypsinogen-A. Nature. 201:1284–1287. [DOI] [PubMed] [Google Scholar]
- 42.Duhrsen, U., J. L. Villeval, J. Boyd, G. Kannourakis, G. Morstyn, and D. Metcalf. 1988. Effects of recombinant human granulocyte colony stimulating factor on hematopoietic progenitor cells in cancer-patients. Blood. 72:2074–2081. [PubMed] [Google Scholar]
- 43.Levine, H. 1993. Thioflavine T interaction with synthetic Alzheimer's disease beta-amyloid peptides: detection of amyloid aggregation in solution. Protein Sci. 2:404–410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Stathopulos, P. B., G. A. Scholz, Y. M. Hwang, J. A. O. Rumfeldt, J. R. Lepock, and E. M. Meiering. 2004. Sonication of proteins causes formation of aggregates that resemble amyloid. Protein Sci. 13:3017–3027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Sunde, M., and C. C. F. Blake. 1998. From the globular to the fibrous state: protein structure and structural conversion in amyloid formation. Q. Rev. Biophys. 31:1–39. [DOI] [PubMed] [Google Scholar]
- 46.Stromer, T., and L. C. Serpell. 2005. Structure and morphology of the Alzheimer's amyloid fibril. Microsc. Res. Tech. 67:210–217. [DOI] [PubMed] [Google Scholar]
- 47.Rousseau, F., J. Schymkowitz, and L. Serrano. 2006. Protein aggregation and amyloidosis: confusion of the kinds? Curr. Opin. Struct. Biol. 16:118–126. [DOI] [PubMed] [Google Scholar]
- 48.O'Nuallain, B., A. D. Williams, P. Westermark, and R. Wetzel. 2004. Seeding specificity in amyloid growth induced by heterologous fibrils. J. Biol. Chem. 279:17490–17499. [DOI] [PubMed] [Google Scholar]
- 49.Bhattacharyya, A. M., A. K. Thakur, and R. Wetzel. 2005. Polyglutamine aggregation nucleation: thermodynamics of a highly unfavorable protein folding reaction. Proc. Natl. Acad. Sci. USA. 102:15400–15405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Bender, T. M., R. J. Lewis, and R. Pecora. 1986. Absolute Rayleigh ratios of four solvents at 488 nm. Macromolecules. 19:244–245. [Google Scholar]
- 51.Hiemenz, P. C., and R. Rajagopalan. 1997. Principles of Colloid and Surface Chemistry. Marcel Dekker, New York.
- 52.Huglin, M. B. 1972. Specific refractive index increments. In Light Scattering from Polymer Solutions. Academic Press, New York.
- 53.Huber, P. 1981. Robust Statistics. Wiley, New York.
- 54.Lawson, J., and J. Erjavec. 2001. Modern Statistics for Engineering and Quality Improvement. Duxbury Press, Pacific Grove, CA.
- 55.Koppel, D. E. 1972. Analysis of macromolecular polydispersity in intensity correlation spectroscopy: the method of cumulants. J. Chem. Phys. 57:4814–4820. [Google Scholar]
- 56.Frisken, B. J. 2001. Revisiting the method of cumulants for the analysis of dynamic light-scattering data. Appl. Opt. 40:4087–4091. [DOI] [PubMed] [Google Scholar]
- 57.Selser, J. C. 1979. A determination of polymer number-averaged and weight-averaged molecular-weight using photon correlation spectroscopy. Macromolecules. 12:909–916. [Google Scholar]
- 58.Burchard, W., M. Schmidt, and W. H. Stockmayer. 1980. Information on polydispersity and branching from combined quasi-elastic and integrated scattering. Macromolecules. 13:1265–1272. [Google Scholar]
- 59.Burchard, W., M. Schmidt, and W. H. Stockmayer. 1980. Influence of hydrodynamic pre-averaging on quasi-elastic scattering from flexible linear and star-branched macromolecules. Macromolecules. 13:580–587. [Google Scholar]
- 60.Hiemenz, P. C. 1984. Polymer Chemistry: The Basic Concepts. Marcel Dekker, New York.
- 61.Schmidt, M., and W. H. Stockmayer. 1984. Quasi-elastic light scattering by semiflexible chains. Macromolecules. 17:509–514. [Google Scholar]
- 62.Chu, B., and J. Liu. 2000. Characterization of nanoparticles by scattering techniques. J. Nanopart. Res. 2:29–41. [Google Scholar]
- 63.Harding, S. E. 1995. On the hydrodynamic analysis of macromolecular conformation. Biophys. Chem. 55:69–93. [DOI] [PubMed] [Google Scholar]
- 64.Pjura, P. E., A. M. Lenhoff, S. A. Leonard, and A.G. Gittis. 2000. Protein crystallization by design: chymotrypsinogen without precipitants. J. Mol. Biol. 300:235–239. [DOI] [PubMed] [Google Scholar]
- 65.Lovejoy, B., D. Cascio, and D. Eisenberg. 1993. Crystal structure of canine and bovine granulocyte-colony stimulating factor (G-CSF). J. Mol. Biol. 234:640–653. [DOI] [PubMed] [Google Scholar]
- 66.Eisert, R., L. Felau, and L. R. Brown. 2006. Methods for enhancing the accuracy and reproducibility of Congo red and thioflavin T assays. Anal. Biochem. 353:144–146. [DOI] [PubMed] [Google Scholar]
- 67.Kratochvil, P. 1972. Particle scattering functions. In Light Scattering from Polymer Solutions. M. B. Huglin, editor. Academic Press, New York.
- 68.Balbirnie, M., R. Grothe, and D. S. Eisenberg. 2001. An amyloid-forming peptide from the yeast prion Sup35 reveals a dehydrated beta-sheet structure for amyloid. Proc. Natl. Acad. Sci. USA. 98:2375–2380. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Sambashivan, S., Y. S. Liu, M. R. Sawaya, M. Gingery, and D. Eisenberg. 2005. Amyloid-like fibrils of ribonuclease A with three-dimensional domain-swapped and native-like structure. Nature. 437:266–269. [DOI] [PubMed] [Google Scholar]
- 70.Cooper, J. 1969. An evaluation of current methods for the diagnostic histochemistry of amyloid. J. Clin. Pathol. 22:410–413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Gibson, T. J., and R. M. Murphy. 2005. Design of peptidyl compounds that affect beta-amyloid aggregation: Importance of surface tension and context. Biochemistry. 44:8898–8907. [DOI] [PubMed] [Google Scholar]
- 72.Ghanta, J., C. L. Shen, L. L. Kiessling, and R. M. Murphy. 1996. A strategy for designing inhibitors of beta-amyloid toxicity. J. Biol. Chem. 271:29525–29528. [DOI] [PubMed] [Google Scholar]
- 73.Speed, M. A., J. King, and D. I. C. Wang. 1997. Polymerization mechanism of polypeptide chain aggregation. Biotechnol. Bioeng. 54:333–343. [DOI] [PubMed] [Google Scholar]
- 74.Gast, K., A. J. Modler, H. Damaschun, R. Krober, G. Lutsch, D. Zirwer, R. Golbik, and G. Damaschun. 2003. Effect of environmental conditions on aggregation and fibril formation of barstar. Eur. Biophys. J. 32:710–723. [DOI] [PubMed] [Google Scholar]
- 75.Wetzel, R. 2006. Kinetics and thermodynamics of amyloid fibril assembly. Acc. Chem. Res. 39:671–679. [DOI] [PubMed] [Google Scholar]