Two Gears of Pumping by the Sodium Pump

Abstract

The kinetics of the phosphorylation and subsequent conformational change of Na⁺,K⁺-ATPase was investigated via the stopped-flow technique using the fluorescent label RH421 (pH 7.4, 24°C). The enzyme was preequilibrated in buffer containing 130 mM NaCl to stabilize the E1(Na⁺)₃ state. On mixing with ATP in the presence of Mg²⁺, a fluorescence increase occurred, due to enzyme conversion into the E2P state. The fluorescence change accelerated with increasing ATP concentration until a saturating limit in the hundreds of micromolar range. The amplitude of the fluorescence change (ΔF/F₀) increased to 0.98 at 50 μM ATP. ΔF/F₀ then decreased to 0.82 at 500 μM. The decrease was attributed to an ATP-induced allosteric acceleration of the dephosphorylation reaction. The ATP concentration dependence of the time course and the amplitude of the fluorescence change could not be explained by either a one-site monomeric enzyme model or by a two-pool model. All of the data could be explained by an (αβ)₂ dimeric model, in which the enzyme cycles at a low rate with ATP hydrolysis by one α-subunit or at a high rate with ATP hydrolysis by both α-subunits. Thus, we propose a two-gear bicyclic model to replace the classical monomeric Albers-Post model for kidney Na⁺,K⁺-ATPase.

INTRODUCTION

The Na⁺,K⁺-ATPase (or sodium pump) was the first ion pump to be discovered (1) and it is one of the most fundamentally important enzymes of animal physiology. The electrochemical potential gradient for Na⁺ ions, which the enzyme maintains, is used as the driving force for numerous secondary transport systems. Examples include the Na⁺ channels in nerve, which allow the action potential to be produced, the Na⁺-glucose cotransporter, which is responsible for glucose uptake in intestinal cells, and the Na⁺/Ca²⁺ exchanger in heart, which plays an important role in muscle relaxation. The Na⁺,K⁺-ATPase, furthermore, contributes to the osmotic regulation of cell volume and is a major determinant of body temperature. For all of these functions the enzyme derives its energy from the hydrolysis of ATP, which is coupled to Na⁺ transport.

It has been known for over 30 years that if one measures the ATP dissociation constant of the enzyme in the E1 conformation in isolation from the rest of the pump cycle, i.e., under conditions where phosphorylation does not occur, then the value obtained is generally below 1 μM. In the absence of Mg²⁺ ions, the values reported include: 0.12 μM (2), 0.22 μM (3), 0.24 μM (4), and 0.63 μM (5). However, if pre-steady-state kinetic measurements of enzyme phosphorylation via ATP are carried out, it is found that much higher concentrations of ATP are required to achieve a half-maximal rate of phosphorylation. ATP dissociation constants reported from such studies include: 3.5 μM (6), 10 μM (7), 14 μM (8), 5 μM (9), 7 μM (10), and 8 μM (11). Averaging these values indicates that the ATP dissociation constant from phosphorylation studies is ∼40 times greater than that measured in the absence of phosphorylation.

One possibility to explain this apparent discrepancy is via a Mg²⁺-induced change in ATP affinity, since Mg²⁺ is required as a cofactor of ATP for phosphorylation to occur but it is absent in binding studies on the E1 conformation alone. Such an explanation appears unlikely, however, because Campos and Beaugé (12) found that Mg²⁺ had no effect on the rate constant for ATP association and that it decreased the dissociation rate constant only by a factor of 4.

Another possibility is that the E1 conformation of the enzyme has two distinct ATP affinities. From stopped-flow kinetic studies of ATP phosphorylation of shark rectal gland Na⁺,K⁺-ATPase using the voltage-sensitive probe RH421, Cornelius (13) did in fact find evidence for two apparent ATP dissociation constants, one of 5.4 (±0.3) μM and another of 32 (±11) nM. He suggested that the two binding affinities could indicate that the E2 → E1 transition without and with ATP bound proceeds with different rate constants in the absence of K⁺. However, he presented no data supporting this interpretation and no explanation of how a difference in E2 → E1 kinetics might affect his results. Furthermore, under the experimental conditions which he used, i.e., preequilibration of the enzyme in 130 mM NaCl and in the absence of K⁺, virtually all of the enzyme would be expected to be in the E1(Na⁺)₃ state. Therefore, no E2 → E1 transition would be expected before enzyme phosphorylation (14). The explanation offered by Cornelius (13) for two apparent ATP affinities would, thus, seem to be very unlikely. Tsuda et al. (15) also found evidence for at least two different ATP binding affinities based on stopped-flow studies using pig kidney Na⁺,K⁺-ATPase covalently labeled with the fluorescent probe BIPM. They, however, attributed this behavior to the presence of the enzyme in an oligomeric state.

Recently, in the course of studying the kinetics of the E2 → E1 conformational transition as a function of the ATP concentration, we found evidence supporting the idea that the Na⁺,K⁺-ATPase actually occurs in the membrane as a diprotomer (16). After the conformational transition, however, it appeared that the diprotomer only had a single bound ATP, i.e., it was in the state E1(Na⁺)₃ATP:E1(Na⁺)₃. In principle this, therefore, leaves one protein monomer within the diprotomer available for binding a second ATP molecule. If a cooperative interaction between the two monomers occurs within a diprotomer, then this could easily explain two distinctly different ATP binding affinities for the E1 conformation.

The purpose of this article is, therefore, to reinvestigate the kinetics of the phosphorylation of the Na⁺,K⁺-ATPase over a wide range of ATP concentrations. The experimental technique we use is the same as that employed by Cornelius (13), i.e., the stopped-flow method in combination with the voltage-sensitive dye RH421, which is known to detect the formation of the E2P state (13,17,18). Using this technique it is possible to accurately observe the entire time course of the fluorescence change associated with the formation of the E2P state from E1(Na⁺)₃. Via comparisons of the predictions of theoretical simulations of both the time course and the amplitude of the fluorescence change for different model mechanisms with those determined experimentally, we propose significant modifications to the classical Albers-Post mechanism of Na⁺,K⁺-ATPase function.

Based on these studies, the major new finding which we will present is that the Na⁺,K⁺-ATPase possesses two gears of ion pumping, i.e., ion pumping can proceed at two different speeds depending on the number of ATP molecules bound.

MATERIALS AND METHODS

Enzyme

Na⁺,K⁺-ATPase-containing membrane fragments were prepared and purified from the red outer medulla of pig kidney according to a modification (19) of procedure C of Jørgensen (20,21). Further details of the enzyme purification procedure can be found elsewhere (10). The specific ATPase activity of the preparation at 37°C was ∼1800 μmol of Pi/h per mg of protein in 30 mM histidine (Microselect, Fluka, Buchs, Switzerland)/HCl containing 130 mM NaCl, 20 mM KCl, 3 mM MgCl₂, and 3 mM ATP (Boehringer Mannheim, Mannheim, Germany), and its protein concentration was typically 2 mg/ml. The enzymatic activity in the presence of 1 mM ouabain was <1%. The protein concentration was determined by the Lowry method (22).

Materials

N-(4-Sulfobutyl)-4-(4-(p-(dipentylamino)phenyl)butadienyl)-pyridinium inner salt (RH421) was obtained from Molecular Probes (Eugene, OR) and was used without further purification. RH421 was added to Na⁺,K⁺-ATPase-containing membrane fragments from an ethanolic stock solution. The dye is spontaneously incorporated into the membrane fragments.

The origins of the various reagents used were as follows: imidazole (99%+, Sigma, Taufkirchen, Germany; or ≥99.5%, Fluka), EDTA (99%, Sigma), NaCl (Suprapur, Merck, Darmstadt, Germany), MgCl₂·6H₂O (analytical grade, Merck), HCl (0.1 N Titrisol solution, Merck), ATP disodium·3H₂O (special quality, Boehringer Mannheim), and ethanol (analytical grade, Merck).

Stopped-flow measurements

Stopped-flow experiments were carried out using an SF-61 stopped-flow spectrofluorimeter from Hi-Tech Scientific (Salisbury, UK). The solution in the observation chamber was excited using a 100 W short-arc mercury lamp (Osram, Munich, Germany) and the fluorescence was detected at right angles to the incident light beam using an R928 multialkali side-on photomultiplier. The exciting light was passed through a grating monochromator with a blaze wavelength of 500 nm. The mercury line at 577 nm was used for excitation and the fluorescence was collected at wavelengths ≥665 nm by using an RG665 glass cutoff filter (Schott, Mainz, Germany) in front of the photomultiplier. The kinetic data were collected via a high-speed 12-bit analog-to-digital data acquisition board and were analyzed using software developed by Hi-Tech Scientific. Each individual trace consisted of 1024 data points. To improve the signal/noise ratio, typically between 6 and 14 experimental traces were averaged before the reciprocal relaxation time was evaluated. This was done by fitting a sum (either one or two) of exponential functions to the averaged experimental trace. The choice between a single or a double exponential fit was made based on the presence or absence of any observed deviation from random fluctuation in residual plots and the values of the chi-squared parameter. The relaxation time is here defined as the time necessary for the difference in fluorescence intensity from its final steady-state value to decay to 1/e of its value at any point in time. This is based on the standard definition for all relaxation kinetic methods. It should be noted that the stopped-flow method employed here is not strictly a relaxation method, but, because most experiments were carried out under pseudo-first-order conditions, exponential decay behavior is to be expected, and for simplicity the term “relaxation time” is therefore used throughout.

The kinetics of the Na⁺,K⁺-ATPase conformational changes and ion translocation reactions were investigated in the stopped-flow apparatus by mixing Na⁺,K⁺-ATPase labeled with RH421 in one of the drive syringes with an equal volume of an ATP solution from the other drive syringe. Both solutions were prepared in a buffer containing 30 mM imidazole, 130 mM NaCl, 5 mM MgCl₂, and 1 mM EDTA, so that no change in the Na⁺ concentration occurred on mixing. The solutions in the drive syringes were equilibrated to a temperature of 24°C before each experiment. The drive syringes were driven by compressed air. The dead-time of the stopped-flow mixing cell was determined to be 1.7 (±0.2) ms. The electrical time constant of the fluorescence detection system was set to a value of not greater than one tenth of the relaxation time of the fastest enzyme-related transient, i.e., from 0.33 ms for measurements at saturating ATP concentrations down to 10 ms at the lowest ATP concentrations. Interference of photochemical reactions of RH421 with the kinetics of the Na⁺,K⁺-ATPase-related fluorescence transients was avoided by inserting neutral density filters in the light beam in front of the monochromator to ensure that the kinetics of dye photochemical reactions occurred on a timescale significantly longer than enzyme-related processes. The timescale and amplitude of the dye photochemical reactions were determined in separate control experiments in the stopped-flow apparatus. In this case, RH421 was added to Na⁺,K⁺-ATPase membrane fragments and the photochemical reactions were initiated by synchronously opening a shutter to expose the sample to illumination and starting data collection.

Simulations

Computer simulations of the time course of fluorescence changes experimentally observed via stopped-flow were performed using the commercially available program Berkeley Madonna 8.0 (University of California, Berkeley) via the variable step-size Rosenbrock integration method for stiff systems of differential equations. The simulations yield the time course of the concentration of each enzyme intermediate involved as well as the total fluorescence. For the purposes of the simulations, each enzyme intermediate was normalized to a unitary enzyme concentration.

RESULTS

ATP-induced stopped-flow fluorescence traces

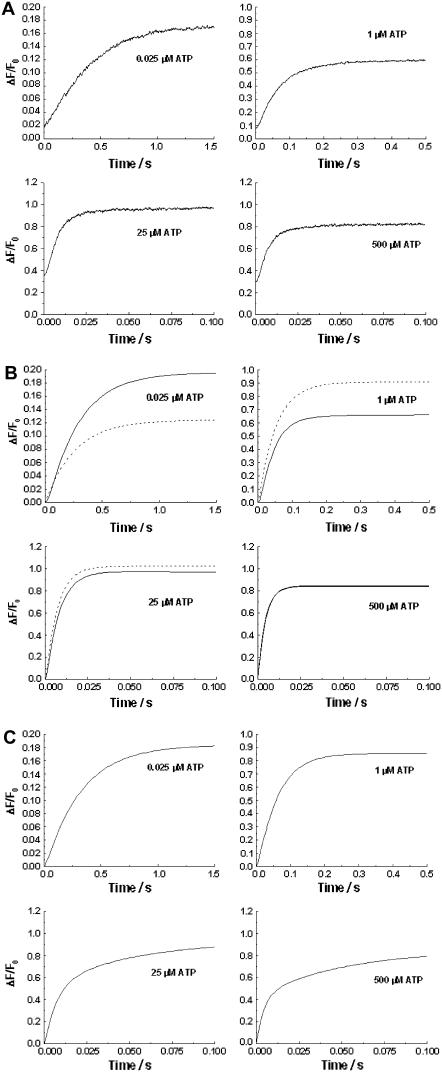
On mixing pig kidney Na⁺,K⁺-ATPase-containing membrane fragments labeled with RH421 with Na₂ATP (as described under Materials and Methods), an increase in fluorescence occurred (see Fig. 1 A). As the Na₂ATP concentration was increased, the overall kinetics of the fluorescence change became faster until a saturating limit was reached, which was characterized by a reciprocal relaxation time of ∼180 s⁻¹ (10). The fact that the kinetics saturate at a constant value implies that the overall rate-determining step in the system being observed is a first-order reaction (i.e., phosphorylation). The slower kinetics observed under nonsaturating ATP concentrations implies that the first-order reaction is preceded by ATP binding, i.e., the first-order reaction is induced by ATP binding (10). Therefore, any reaction scheme in which ATP binding occurs subsequent to a slow conformational change can be excluded as a possible mechanism.

FIGURE 1.

(A) Stopped-flow fluorescence transients of Na⁺,K⁺-ATPase from pig kidney noncovalently labeled with RH421 (75 nM, after mixing). Na⁺,K⁺-ATPase (10 μg/ml or 68 nM, after mixing) was rapidly mixed with an equal volume of a solution containing varying concentrations of Na₂ATP. Both the enzyme suspension and the Na₂ATP solutions were prepared in a buffer containing 130 mM NaCl, 30 mM imidazole, 5 mM MgCl₂, and 1 mM EDTA (pH 7.4, 24°C). The fluorescence of membrane-bound RH421 was measured at an excitation wavelength of 577 nm at emission wavelengths of ≥665 nm (RG665 glass cutoff filter). The calculated reciprocal relaxation times were: 0.025 μM ATP, 2.57 (±0.03) s⁻¹; 1 μM ATP, 6.51 (±0.04) s⁻¹; 25 μM ATP, 138 (±2) s⁻¹ (96% of the total amplitude) and 12 (±3) s⁻¹ (4%); and 500 μM ATP, 179 (±6) s⁻¹ (89%), and 41 (±6) s⁻¹ (11%). (B) Kinetic simulations of the experimental fluorescence transients based on a single-site monomer model (dashed line, see Fig. 3 a) and a dimer model (solid line, see Fig. 4). The values of the rate constants, equilibrium constants, and fluorescence levels for the dimer model are given in Table 1. (C) Kinetic simulations of the experimental transients based on a two-pool enzyme model (see Fig. 3 b).

Control experiments in which 30 mM sodium orthovanadate was added to the drive syringe containing the Na⁺,K⁺-ATPase membrane fragments resulted in the complete disappearance of the fluorescence change (10). The signal was also abolished if Mg²⁺ ions were omitted from the buffer medium (10). On mixing with ATP a small increase in ionic strength occurs due to the Na₂ATP itself (maximum concentration 1 mM, in comparison to a constant background of 130 mM NaCl, 5 mM MgCl₂, and 1 mM EDTA). Control experiments showed, however, that as long as the preequilibration buffer has a sufficiently high ionic strength to stabilize the enzyme totally in the E1 state, any further increase in ionic strength causes a negligible fluorescence change (16). An ionic strength of ∼50 mM was found to be sufficient for this purpose (14,16). In the experiments reported here, the ionic strength of the buffer solution was 160 mM (excluding contributions from imidazole and EDTA). These control experiments indicate that the observed fluorescence changes are in fact due to the ATP hydrolytic action of the Na⁺,K⁺-ATPase.

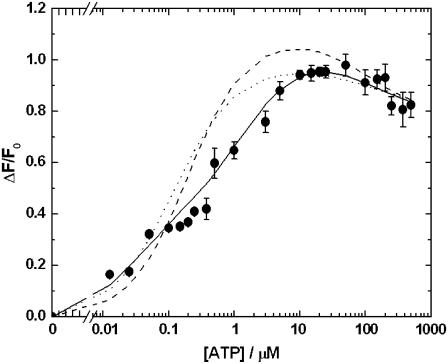
The total amplitudes of the fluorescence change, ΔF/F₀, are shown in Fig. 2. ΔF/F₀ increased with increasing ATP concentration until it reached a maximum value of ∼0.98 at ∼50 μM ATP. At higher ATP concentrations (>50 μM), a slight drop in ΔF/F₀ occurred.

FIGURE 2.

Amplitudes (ΔF/F₀) of the observed fluorescence change under the conditions described in Fig. 1 A as a function of the ATP concentration. ΔF is the total fluorescence change (i.e., of both phases if a two-phase signal was observed) and F₀ is the initial fluorescence level before mixing with ATP. The dashed line represents the prediction of simulations based on a single-site monomer model (see Fig. 3 a). The dotted line represents the prediction of simulations based on a two-pool enzyme model (see Fig. 3 b). The solid line represents the prediction of simulations based on a dimer model (see Fig. 4). Below ATP concentrations of 0.3 μM, the error bars of the experimental points cannot be seen because they are so small that they are obscured by the symbols used for the points.

Based on previous studies (13,17,18), it is known that, under the conditions used in these experiments, RH421 responds to the formation of the E2P state with an increase in fluorescence. An increase in fluorescence amplitude, therefore, implies an increase in the rate of E2P formation relative to the rate of E2P breakdown.

Theoretical simulations

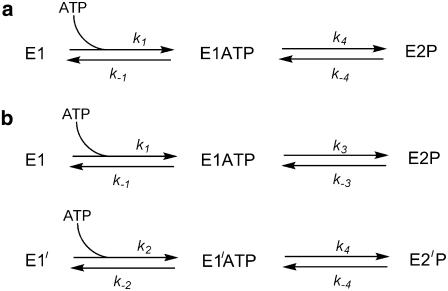
Based on the experimental observations we first considered a kinetic model (see Fig. 3 a) in which the E1 state of the enzyme only binds a single ATP molecule. After binding ATP, the enzyme is assumed to undergo a reversible formation of the E2P state. In a previous publication (10), we treated the E1ATP → E2P transition as irreversible. However, in the light of the amplitude data presented here (see Fig. 2), this cannot be the case, because if that were so the enzyme would all be converted to the E2P state regardless of how much ATP was present and the fluorescence change would always be constant. Experimentally, however, significant changes in the amplitude occur with changes in the ATP concentration (see Fig. 2). For the purposes of the simulations, we have chosen an ATP dissociation constant of 7.0 μM for consistency with previous experimental measurements of its value (10). The results of these simulations are shown in Figs. 1 B and 2. The equations used in carrying out the simulations are presented in the Appendix.

FIGURE 3.

One-site monomer model (a) and two-pool model (b) of Na⁺,K⁺-ATPase phosphorylation by ATP.

Although simulations based on this simple one-site monomer model reproduce relatively well the time course of the fluorescence change and its acceleration with increasing ATP concentration, the amplitudes of the fluorescence change are not well described. For example, at the lowest ATP concentration used of 0.0125 μM, experimentally the measured relative fluorescence change (ΔF/F₀) was 0.164 (±0.002). However, the simulations predict a ΔF/F₀ value of only 0.067, i.e., only 41% of the experimental value. Furthermore, at ATP concentrations above 0.1 μM, the one site monomer model predicts significantly higher amplitudes than those observed experimentally. Therefore, we conclude that this model must be discarded as a description of the experimental behavior.

We next considered a model in which two independent pools of enzyme exist (see Fig. 3 b). In this model, we assume that before mixing with ATP there are two enzyme populations in conformations designated as E1 and E1′. Each conformation is capable of binding ATP, but with different affinities (K_d = 0.25 μM for E1 and 7.0 μM for E1′). The value of K_d of 0.25 μM for E1 was based on ATP binding data in the literature (2–5). After ATP binding, both the E1ATP and E1′ATP conformations were assumed to undergo phosphorylation but with different rate constants. The equations necessary for carrying out simulations based on this model are also given in the Appendix.

It was found that the two-pool model provided a slightly better description of the total amplitude data (see Fig. 2) than the one-site monomer model. However, in the ATP concentration range 0.1–10 μM, ΔF/F₀ was still significantly higher than that observed experimentally. Furthermore, the time course predicted by the two-pool model deviates significantly from experimental behavior (see Fig. 1 C). This is particularly the case at high ATP concentrations, e.g., 25 and 500 μM. Under these conditions, the two-pool model predicts distinctly double-exponential kinetics, because of the independent phosphorylation reactions of the two pools of enzyme. The experimentally observed traces (see Fig. 1 A) are, in contrast, almost single exponential. We are also not aware of any experimental data in the literature which would support the existence of two independent E1-like pools of enzyme. Therefore, we consider that the two-pool enzyme model can also be discarded.

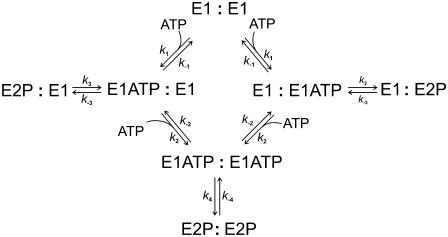
As a final model to describe the data we propose a dimer model of the enzyme (see Fig. 4). Here we consider only a single conformation of the enzyme, E1. However, each E1 monomer within a dimer can separately bind an ATP molecule and undergo phosphorylation. The first ATP molecule which binds is assumed to bind with high affinity (K_A1 = 0.25 μM). The second ATP molecule which binds is assumed to bind with much lower affinity (K_A2 = 7.0 μM). Phosphorylation is assumed to occur after the binding of either one or two ATP molecules but with different rate constants. The equations necessary to simulate this model are again given in the Appendix.

FIGURE 4.

Dimer model of Na⁺,K⁺-ATPase phosphorylation by ATP.

In contrast to the single-site monomer model and the two-pool model, the dimer model of the enzyme reproduces very well both the experimental amplitude data (see Fig. 2) and the experimental time courses (see Fig. 1 B). The dimer model is also consistent with recent kinetic data on the E2 → E1 conformational change of the enzyme (16), which could also only be explained by the enzyme existing in dimeric form. Therefore, we conclude that the dimer model provides the best description of the enzyme's kinetic behavior presented here.

DISCUSSION

The analysis of the time course and amplitudes of the stopped-flow kinetic measurements we have presented here support the conclusion that the Na⁺,K⁺-ATPase of pig kidney functions as a dimer, in which each monomer of the enzyme can be phosphorylated independently leading to two different rates of its conversion from E1 into E2P depending on the number of ATP molecules bound.

Before discussing further the dimeric nature of the enzyme we would first like to consider the reversibility of the reactions investigated. In a previous stopped-flow study the formation of E2P from E1ATP was treated as an irreversible process (10). Here it was shown that the amplitude change was dependent on the ATP concentration (see Fig. 2), which indicates that this cannot be the case. E2P must be capable of being converted back to E1ATP, otherwise a constant amplitude change would be expected. The question remains, however, as to the mechanism of the reverse reaction. A direct dephosphorylation of E2P to E1ATP via reaction with ADP would seem to be unlikely, since ADP is thought to react with the E1P state of the enzyme (13). Furthermore, the amount of ADP present in solution is very small because it is only that which is produced over the timescale of an experiment. For an enzyme concentration of 68 nM and assuming that the enzyme is hydrolyzing ATP at a rate of ∼5 s⁻¹ (12,23–25), it can be shown that, after 0.1 s (the time range of the experiments at 10 μM ATP and above), only 34 nM of ADP would be produced.

A more likely mechanism by which E1ATP could be obtained from E2P is by continuing around the enzymatic cycle following the physiological route, i.e., dephosphorylation of E2P to E2, conversion of E2 into E1, followed by rebinding of ATP. Since ATP is, in most cases, far in excess of the enzyme, the enzyme could continue cycling for some time until all the ATP is exhausted. If one accepts this mechanism of conversion of E2P to E1ATP, the observation that ΔF/F₀ decreases at ATP concentrations >50 μM (see Fig. 2) can be rationalized. This is the concentration range in which one normally expects low affinity allosteric binding of ATP to the E2 state of the enzyme (10,11,16,26–29). From these studies it is well established that ATP concentrations in the range of 100 μM stimulate the kinetics of the E2 → E1 transition. Previous studies on pig kidney enzyme have indicated that, in the absence of ATP and Mg²⁺ ions but in the presence of 65 mM NaCl, this reaction proceeds with a rate constant of not more than 4 s⁻¹ (10). However, if saturating concentrations of ATP, Mg²⁺, and Na⁺ are all present, the rate constant increases to a value of ∼65 s⁻¹ (14). Therefore, in the simulations the rate constant, k₋₄, has been chosen to vary between minimum and maximum values depending on the ATP concentration according to Eq. 5 in the Appendix.

In the case of the experiments reported here it was found that a rate constant of 75 s⁻¹ for the conversion of (E2P)₂ATP to (E1ATP)₂ was required to reproduce the observed drop in ΔF/F₀. If the pathway being followed is via the physiological route via E2, then this drop can be explained in part by an acceleration of the E2 → E1 transition by ATP. However, before the enzyme can undergo the E2 → E1 transition, it must first be dephosphorylated, i.e., E2P → E2. Therefore, these results imply that the rate constant of the E2P → E2 reaction must also be at least 75 s⁻¹ at high saturating ATP concentrations. This is in contrast to the rate constant of only ∼5 s⁻¹ on preequilibration of the enzyme with either zero or much lower ATP concentrations (12,23,24). Our results suggest, therefore, that ATP has an allosteric role, not only in accelerating the E2 → E1 transition, but also in accelerating the dephosphorylation of the enzyme by binding to E2P. In fact, in a previous study (25), we observed a relaxation of the dephosphorylation reaction in the absence of K⁺ and the presence of 1 mM ATP with a reciprocal relaxation time of ∼50 s⁻¹. There it was suggested that this high value might be due to a contribution from rephosphorylation via ATP. However, in light of the findings presented here, a direct acceleration of the dephosphorylation reaction itself by ATP is more likely. Whether one or two molecules of ATP bind to an (E2P)₂ dimer we cannot be certain. However, since we have previously only found evidence for a single bound ATP acting to accelerate the E2 → E1 transition within a protein dimer (16), we suggest that it is also most likely that here only a single ATP binds. If two ATP molecules were to bind to (E2P)₂ then one ATP molecule would have to immediately dissociate again after dephosphorylation for the E2 → E1 transition to proceed with a single bound ATP.

Now let us return to the dimer model (see Fig. 4). The essential points of our new proposed mechanism can be summarized as follows:

1. The enzyme exists in the membrane as an (αβ)₂ diprotomer.

2. Each α-subunit can independently bind ATP, undergo phosphorylation, and conversion into the E2P state.

3. The binding of the first ATP molecule to the diprotomer occurs with high affinity (K_A1 = 0.25 μM) regardless of the α-subunit to which it binds.

4. The binding of the second ATP molecule to the diprotomer occurs with a much lower affinity (K_A2 = 7.0 μM) regardless of the α-subunit to which it binds.

5. When only a single ATP molecule is bound to the diprotomer, phosphorylation and conversion to E2P occur with a relatively low rate constant (k₃ ≈ 15 s⁻¹).

6. When two ATP molecules are bound to the diprotomer, phosphorylation and conversion to E2P occur with a much higher rate constant (k₄ ≈ 173 s⁻¹).

Apart from explaining all of the data presented here, this model has a further appeal in that it explains a long-standing apparent discrepancy in the literature. As mentioned in the Introduction, it has been known for over 30 years that the ATP dissociation constant for the E1 conformation in the absence of Mg²⁺ ions is in the submicromolar range. However, from pre-steady-state kinetic measurements, half-saturation in the rate of phosphorylation is not achieved until ∼10 μM ATP. Within the dimer model, both of these findings are perfectly compatible and the apparent discrepancy disappears. The dimer model possesses a high affinity submicromolar binding of the first ATP molecule, but the maximal rate of phosphorylation is not achieved until much higher ATP concentrations after binding of the second ATP molecule.

One might wonder why the lower affinity (K_A2 = 7.0 μM) ATP binding has never been detected in binding studies. A possible explanation is that after the binding of one ATP molecule to E1, the ATP binding site of the neighboring α-subunit in the diprotomer becomes inaccessible to ATP unless Mg²⁺ ions are present. Such an explanation is supported by our recent results on the kinetics of the E2 → E1 transition in the absence of Mg²⁺ ions (16). In that study it was also concluded based on independent data that the enzyme existed as a dimer, but even up to an ATP concentration of 1 mM, evidence could only be found for an occupation of one of the α-subunits within the diprotomer by ATP.

The dimer model assumes that both α-subunits within a diprotomer are initially identical, i.e., both have the same affinity for ATP. The affinity for an unoccupied α-subunit only decreases once its neighboring α-subunit has bound an ATP molecule. This implies a negative cooperativity in ATP binding due to interaction between the two α-subunits within a diprotomer. Negative cooperativity of ATP binding within a dimer was first proposed many years ago by Ottolenghi and Jensen (30), who found that in the presence of K⁺ ions their Scatchard plots did not show the linear behavior expected for ATP binding to a site with a single affinity, rather they displayed significant curvature. Their results could, however, alternatively be explained by a K⁺-induced shift in the E2 ↔ E1 equilibrium of the enzyme and it is well known that the E2 and E1 conformations have very different affinities for ATP (16). Probably for this reason the hypothesis of negative cooperativity in ATP binding by Ottolenghi and Jensen (30) did not receive wide acceptance (31). In contrast to their experiments, however, the results which we have presented here have been obtained in the complete absence of K⁺ ions and in the presence of 130 mM Na⁺, conditions which would be expected to completely stabilize the E1 state of the enzyme. Therefore, it is not possible to attribute the two different ATP binding affinities to the E1 and E2 states. Both ATP molecules must be binding to the E1 state. Although the experimental justification for dimeric behavior and negative cooperativity in ATP binding put forward by Ottolenghi and Jensen (30) thus appears to have been flawed, nevertheless their hypothesis does seem to have been correct.

Based on our results we would like to suggest that in the absence of Mg²⁺ ions the negative cooperativity is so strong as to totally inhibit the binding of a second ATP molecule to a diprotomer. The presence of Mg²⁺ ions as an ATP cofactor within its binding site appears to weaken the negative cooperativity so that a second ATP can bind to a diprotomer, although with significantly lower affinity than the first.

It is important to point out that the idea that the Na⁺,K⁺-ATPase exists as an (αβ)₂ diprotomer is not new. This was first proposed by Stein et al. (32) and Repke and Schon (33) in 1973, and has been a subject of debate ever since. The evidence for a diprotomer was nicely reviewed by Askari (31) in 1987. In the abstract of this article, Askari expressed the opinion that “… any realistic approach to the resolution of the kinetic mechanism of the sodium pump should include the consideration of the established site-site interactions of the oligomer.” A further review of the topic was published by Taniguchi et al. (34) in 2001. Apart from multiple ATP binding affinities, two further important points described there that indicate the inadequacy of a monomeric Albers-Post cycle are: 1), phosphorylation of half of the ATP binding sites relative to the ouabain binding sites; and 2), the simultaneous presence of two different intermediates of the Albers-Post cycle, e.g. E1(Na⁺)₃ occurring simultaneously with E2(K⁺)₂ or simultaneous occurrence of ATP-bound and phosphorylated forms of the enzyme. Both of these observations are consistent with an oligomeric reaction scheme containing at least an enzyme diprotomer and can be explained by the reaction scheme we will now present.

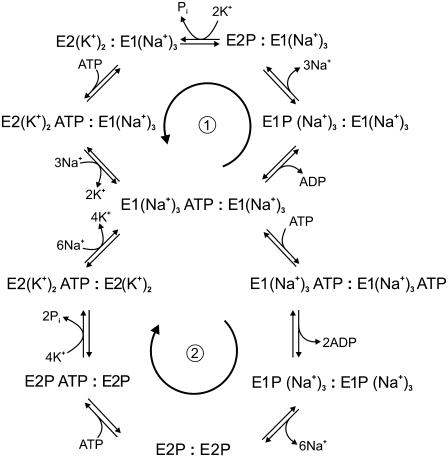
Based on the results presented here and those of our recent work on the kinetics of the E2 → E1 transition (16), it is possible to summarize the findings of both articles in a modified version of the Albers-Post cycle which incorporates the dimeric nature of the Na⁺,K⁺-ATPase and its effect on ATP binding. This is shown in Fig. 5. Our proposed modified cycle is now, in fact, a bi-cycle model. The upper slower cycle would be expected to function at low ATP concentrations. At higher ATP concentrations, when both α-subunits are occupied by ATP, the lower faster cycle would become active. This is probably the most important difference between our model and the classical Albers-Post model, i.e., the enzyme has two gears or speeds of pumping; a low gear with one ATP bound and a high gear with two ATP molecules bound per diprotomer. From a consideration of the physiological substrate conditions (i.e., cytoplasmic and extracellular Na⁺ and K⁺ concentrations and cytoplasmic ATP concentration) we were previously able to conclude that the ATP phosphorylation of the enzyme is a major rate-determining step of the entire enzyme cycle (35). Therefore, a higher gear of phosphorylation kinetics would certainly increase the overall steady-state turnover of the enzyme. The higher pumping rate made possible by Na⁺,K⁺-ATPase dimerization would then more efficiently counter the passive diffusion of Na⁺ ions into the cell and K⁺ ions out, so that less Na⁺,K⁺-ATPase molecules would be required within the plasma membrane to maintain the ion concentration gradients necessary to drive secondary transport processes. In excitable cells, such as nerve and muscle cells, in which a transient action potential is produced, a faster ion pumping rate by the Na⁺,K⁺-ATPase would also allow the cell to return to its resting condition after excitation in a shorter period of time. As a consequence of this, fewer ions would leak through the membrane in this time and therefore less ATP would be consumed by the Na⁺,K⁺-ATPase in counteracting the passive ion leakage. If less ATP is required for ion pumping this would have the beneficial effect for the cell of making more ATP available for other functions, e.g., muscle contraction by the myosin ATPase in muscle fibers.

FIGURE 5.

Two-gear dimeric model of Na⁺,K⁺-ATPase function. The upper cycle (1) represents the pathway followed at low concentrations of ATP, when only one of the ATP binding sites of an α-subunit is occupied. The lower cycle (2) represents the pathway followed at high concentrations of ATP, when both of the ATP binding sites of the (αβ)₂ dimer are occupied. The arrows indicate the physiological direction of cycling by the enzyme.

Within the top cycle of the reaction scheme shown in Fig. 5 the possibility of phosphorylation of half of the ATP binding sites at any point in the enzyme's steady state is allowed for, as required to explain the results reported by Taniguchi et al. (34). The upper cycle also contains dimeric species which combine two different monomeric reaction intermediates of the Albers-Post cycle, a necessary criterion also described by Taniguchi et al. (34). It must be pointed out that this is not the first time that a bicyclic model of the Na⁺,K⁺-ATPase mechanism has been proposed. A bicyclic model was suggested by Plesner et al. (36) in 1981. However, the model which they presented consisted of two separate cycles depending on the ionic conditions. They proposed an “Na⁺-enzyme cycle” for conditions with no K⁺ ions in the medium and an “(Na⁺ + K⁺)-enzyme cycle” for conditions when both Na⁺ and K⁺ ions are present in millimolar concentrations. In contrast, in the bicyclic model which we present here the cycle followed by the enzyme does not depend on the Na⁺ or K⁺ concentrations but on the ATP concentration. In fact, in our model, both cycles can be seen as classical Albers-Post cycles with the difference that, in the upper cycle (see Fig. 5), only one of the α-subunits binds ATP and undergoes phosphorylation, whereas in the lower cycle both α-subunits bind ATP and undergo phosphorylation.

Finally, it is important to point out that it cannot be concluded from this study that Na⁺,K⁺-ATPase dimerization is a completely general phenomenon occurring in all tissues. The work performed here and in our previous article (16) was carried out using Na⁺,K⁺-ATPase from kidney, which is known to have a very high density of the protein and which requires a high density to maintain the efficiency of nutrient reabsorption via the driving force of the Na⁺ gradient across the membrane produced by the Na⁺,K⁺-ATPase. Therefore, it is possible that Na⁺,K⁺-ATPase dimerization is a mechanism employed specifically in cells with a high demand for ion transport (e.g., kidney, nerves, and muscle) to enhance their rate of Na⁺ pumping and minimize ATP consumption.

APPENDIX: SIMULATION OF FLUORESCENCE TRANSIENTS

One-site monomer model

Based on the simple one-site monomer model (see Fig. 3 a), the differential rate equations describing the changes in the concentrations of all the enzyme intermediates are

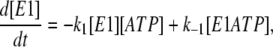(1)

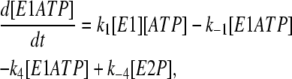(2)

(3)

The total fluorescence, F, is due to contributions from fluorescence levels, f, of the probe associated with each of the enzyme conformational states. Because the addition to the enzyme of ATP alone in the absence of Mg²⁺ ions was found to cause no fluorescence change in the stopped-flow apparatus, we assume that the fluorescence levels of an enzyme state are independent of whether or not it has ATP bound. The total fluorescence is then given by

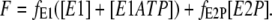(4)

Arbitrarily we define the fluorescence level of the E1 state to be 1.0, i.e., f_E1 = 1.0. The fluorescence level of the E2P state was chosen to give agreement with the fluorescence change observed experimentally at the highest ATP concentration of 500 μM.

Experimentally it was found that the fluorescence change observed on mixing with ATP decreased with increasing ATP concentration in the range 50–500 μM ATP. This implies a decrease in the conversion of enzyme from E1 to E2P in this concentration range. To take this behavior into account within the model we assume that the observed backward rate constant for the phosphorylation reaction, k₋₄, is ATP-dependent. This assumption is explained further in the Discussion. Mathematically this is done by including the equation

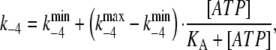(5)

where 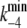and 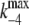represent the values of k₋₄ at zero and saturating concentrations of ATP, respectively, and K_A represents an ATP dissociation constant for allosteric binding of ATP to the E2P state.

Two-pool enzyme model

Based on the two-pool enzyme model (see Fig. 3 b), the differential rate Eqs. 1 and 5 for k₋₄ are still valid. The additional differential rate equations required to carry out simulations based on this model are

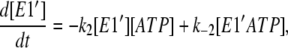(6)

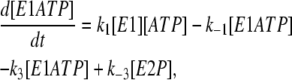(7)

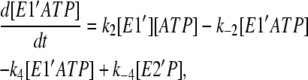(8)

(9)

(10)

Similar to the one-site model, in this case it was also assumed that the fluorescence levels of enzyme with and without bound ATP are identical and both phosphorylated forms of the enzyme were assumed to have identical fluorescence levels. The total fluorescence level is then given by

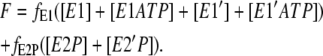(11)

To create the greatest possible difference between simulations based on this model and those of the one-site model, we assumed that the enzyme was initially equally distributed between the two pools, i.e., the initial populations of E1 and E1′ were both 50%.

Dimer model

In the case of the dimer model (see Fig. 4), the differential rate Eq. 5 from the previous model for k₋₄ is still valid. The new differential equations required to carry out simulations are

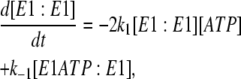(12)

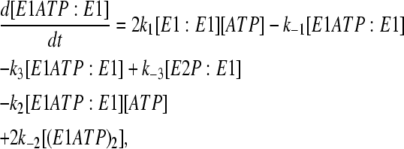(13)

(14)

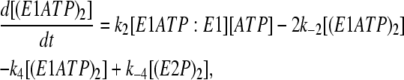(15)

(16)

In the scheme shown in Fig. 4, E1ATP:E1 and E1:E1ATP are equivalent species; the same is true for E2P:E1 and E1:E2P. Therefore, in Eqs. 12–17, for simplicity, we have used the concentrations [E1ATP:E1] and [E2P:E1] to signify the sum of the concentrations of each of the two equivalent species. (E1ATP)₂ represents an E1 dimer in which both monomers have bound ATP and (E2P)₂ represents the dimer E2P:E2P. The rate constants k₁, k₋₁, k₂, and k₋₂ in this set of differential rate equations represent the rate constants for ATP binding to or dissociation from a binding site (not an enzyme dimer as a whole). This accounts for the factors of 2 in Eqs. 12, 13, and 15, because each dimer has two ATP sites available for binding.

For the dimer model the total fluorescence is given by

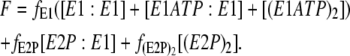(17)

In this case we assume that the maximum fluorescence change on ATP mixing is produced by phosphorylation of both monomers within a dimer. Therefore, as in the case of the monomer model, the value of f_(E2P)2 was chosen to give agreement with the experimentally observed fluorescence change at 500 μM ATP. The value of f_E2P was chosen to be exactly midway between the values of f_E1 (0) and f_(E2P)2. The values of all the parameters used in simulations based on the dimer model are given in Table 1. Wherever possible, the values used were based on previous literature measurements.

TABLE 1.

Values of the rate constants, equilibrium constants, and fluorescence parameters of the dimer model used for the simulations shown in Figs. 1 B and 2

Parameter	Reaction*	Value	Reference
k1	E1 + ATP → E1ATP	52 μM−1 s−1	(4,37,38)†
k−1	E1ATP → E1 + ATP	13 s−1	(38)
k2	E1ATP + ATP → (E1ATP)2	52 μM−1 s−1	this work‡
k−2	(E1ATP)2 → E1ATP + ATP	364 s−1	this work§
k3	E1ATP → E2P	15 s−1	this work¶
k−3	E2P → E1ATP	5 s−1	(11)‖
k4	(E1ATP)2 → (E2P)2	173 s−1	(10)**
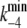	(E2P)2 → (E1ATP)2	5 s−1	(11)‖
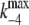	(E2P)2ATP → (E1ATP)2	75 s−1	this work††
KA1	E1ATP ↔ E1 + ATP	0.25 μM	(4,37,38)
KA2	(E1ATP)2 ↔ E1ATP + ATP	7.0 μM	(10)‡‡
KA	(E2P)2ATP ↔ (E2P)2 + ATP	143 μM	(10)§§
fE1	Fluorescence level of E1, E1ATP, and (E1ATP)2	1.0	this work¶¶
fE2P	Fluorescence level of E2P	1.57	this work‖‖
f(E2P)2	Fluorescence level of (E2P)2	2.14	this work***

^*For each reaction, Na⁺ ions have been omitted for simplicity, but in each case the rate constant refers to the value in the presence of 130 mM NaCl. Under such conditions all of the E1 states, with or without ATP, would be completely saturated with Na⁺ ions and would, thus, all have three bound Na⁺ ions. Also for simplicity, the dimeric nature of each enzyme species has been omitted. Thus, E1 actually represents a dimer E1:E1, where each E1 monomer can only bind a single ATP molecule.

^†The rate constant for ATP binding to the E1 state has been estimated by dividing the dissociation rate constant by the ATP dissociation constant, i.e., k₁ = k₋₁/K_A1.

^‡The rate constants for ATP binding to the E1ATP state has been taken to be equal that of binding to the E1 state. The differences in their ATP affinities are assumed to be due to different dissociation rate constants alone.

^§The rate constant for ATP dissociation from (E₁ATP)₂ has been estimated by multiplying the ATP dissociation constant by its ATP binding rate constant, i.e., k₋₂ = K_A2 × k₂.

^¶This value has been chosen so as to reproduce closely the observed experimental ATP dependence of the time course and the amplitudes of the fluorescence transients and to satisfy the condition (k₃ + k₋₃) = 20 s⁻¹, which is approximately the experimentally determined reciprocal relaxation time at an ATP concentration of 1 μM, which would be reasonably expected to saturate the first ATP binding site.

^‖The reverse reactions E2P → E1ATP and (E2P)₂ → (E1ATP)₂ are assumed to occur indirectly via the pathways E2P → E2 → E1 + ATP → E1ATP and (E2P)₂ → E2 → E1 + ATP → E1ATP + ATP → (E1ATP)₂ (see the Discussion for further explanation). In the absence of K⁺ ions the rate-determining step in these pathways would be expected to be the dephosphorylation, which has been experimentally determined to have a rate constant of ∼5 s⁻¹ under these conditions ((11); and references cited therein).

^**This value has been chosen to satisfy the condition (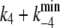) = 178 s⁻¹, the experimentally determined reciprocal relaxation time at saturating concentrations of ATP (10).

^††This value has been chosen to reproduce the experimentally determined drop in ΔF/F₀ at ATP concentrations >50 μM (see Fig. 2).

^‡‡This value has been derived from the concentration of ATP necessary to achieve half-saturation of the reciprocal relaxation time for the RH421 fluorescence change on mixing with ATP in the presence of Mg²⁺ ions.

^§§This value has been taken to equal the experimentally determined low affinity allosteric ATP dissociation constant of the E2 conformation of pig kidney enzyme (10).

^¶¶f_E1 has been arbitrarily been defined as 1.0 as a reference point for the fluorescence changes.

^‖‖This value has been chosen to be exactly midway between the values of f_E1 and f_(E2P)2.

^***This value has been chosen to give agreement with the experimentally observed ΔF/F₀ value at 500 μM ATP.