Abstract
All eukaryotic cells rely on the active self-organization of protein filaments to form a responsive intracellular cytoskeleton. The necessity of motility and reaction to stimuli additionally requires pathways that quickly and reversibly change cytoskeletal organization. While thermally driven order-disorder transitions are, from the viewpoint of physics, the most obvious method for controlling states of organization, the timescales necessary for effective cellular dynamics would require temperatures exceeding the physiologically viable temperature range. We report a mechanism whereby the molecular motor myosin II can cause near-instantaneous order-disorder transitions in reconstituted cytoskeletal actin solutions. When motor-induced filament sliding diminishes, the actin network structure rapidly and reversibly self-organizes into various assemblies. Addition of stable cross linkers was found to alter the architectures of ordered assemblies. These isothermal transitions between dynamic disorder and self-assembled ordered states illustrate that the interplay between passive crosslinking and molecular motor activity plays a substantial role in dynamic cellular organization.
INTRODUCTION
Filaments and molecular motors such as actin and myosin II are key elements of the cytoskeleton, which actively and passively supports and organizes the cell, thus providing a framework for its active processes (1–5). Certain specialized functions of intracellular polymer-motor systems such as contractility in both muscle and nonmuscle cells and chromosome division in mitosis have been extensively studied (6). Beyond these specific tasks, the fundamental role of polymer-molecular motor systems in controlling dynamic cellular organization is far more complex and essential to vital cell functions such as motility, mechanotransduction, and elasticity-based lineage specification (7). It has previously been shown that active artificial motor constructs organize microtubules into spindlelike structures similar to those found during mitosis (8). In contrast, we have found that biologically occurring multiheaded constructs of the actin-specific motor myosin II maintain disorder in solutions of the semiflexible polymer actin when active, while inducing spontaneous organization when the activity of the motors approaches a minimum.
In solution, individual myosin II motors associate in their tail regions to form bipolar myosin minifilaments, averaging 8–13 proteins in size (9,10). The statistical average of several motors on each end of the minifilament leads to an increased collective duty cycle, allowing the motor construct to stay attached to actin filaments for a sufficient time to cause filament sliding (9), despite their individual nonprocessive nature. These minifilaments form the structural basis for the ability of myosin II to act both as a stable cross linker (in near-chemical-rest conditions) and a kinetic device which drives actin filament sliding (in the active, nonequilibrium state). Filament sliding induced by active myosin has been recently implicated in the control of the viscoelasticity of the cytoskeleton (9,11–13); however, its more general role in the spatiotemporal organization of the actin cytoskeleton has not been investigated. Given its importance in rapid functions such as cell motility, it is a foremost requirement that the pathways of actin cytoskeletal reorganization act quasi-instantaneously. Since the cytoskeleton exists in a persistent, far from equilibrium state, the rapid response of these pathways could be achieved by “switching” via instabilities occurring naturally within the cell. By instabilities, as suggested by Turing in 1952, we mean the spontaneous transitions between different kinds of order, e.g., from an isotropic and homogeneous state to one which displays clustering or an aster pattern (14,15). Moreover, these instabilities would allow that minute molecular signals would have the ability to induce such transitions in cytoskeletal organization. The extent to which molecular motors contribute to this reorganization of the actin cytoskeleton is yet unknown.
Due to a cell's molecular complexity, the identification and characterization of its specific intracellular self-organization mechanisms are impractical and lead to ambivalent results. Nevertheless, the actin cytoskeleton often acts as an independent, functional unit, as can be seen in the autonomous motion of lamella fragments (16). Thus, different cytoskeletal processes can be well studied in vitro in reconstituted systems (17) containing a minimal molecular ensemble, as has been demonstrated for actin polymerization-driven motility (18). Consequentially, we studied the interactions between actin filaments and myosin II minifilaments as a function of motor activity and density by fluorescently visualizing actin filament aggregation (19).
MATERIALS AND METHODS
Actomyosin self-assembly
Actin and myosin II were purified according to the protocols recently established by Humphrey et al. (9), which pay specific attention to the removal of inactive myosin. Labeled and unlabeled filaments were polymerized separately at 24 μM with a 60-min polymerization time sufficient for each. Labeled and unlabeled filaments were diluted together in F-Buffer (10 mM Tris, 0.5 mM ATP, 0.15 M KCl, 2 mM MgCl2, 0.2 mM CaCl2) to attain the overall actin concentration of 2.4 μM. In all experiments, polymerized labeled actin filaments were mixed with polymerized unlabeled actin filaments at a ratio of 1:3. The filaments were gently mixed with cut pipette tips to avoid filament breakage. All experiments were performed with 0.5 mM ATP present. Myosin was added to the mixed solution to attain the desired myosin minifilaments per actin filament ratio. Based on average filament length of 10 μm (∼4000 monomers), the number ratio of myosin minifilaments to actin filaments n was calculated as n = (cmyosinNfil)/(Nminicactin), where cactin is the molar actin concentration, cmyosin is the molar myosin concentration, Nfil is the average number of monomers per filament, and Nmini is the average number of individual myosin molecules per minifilament. Nmini has been previously determined to be ∼13 (9,10) and is the natural state of the myosin minifilaments resulting from our preparations methods. Forty microliters of the mixture was sealed in a slide for observation and analysis through fluorescence microscopy (19) with a 32× objective on an Axiovert 100 (Zeiss, Stuttgart, Germany). Images were captured with a digital charge-coupled device camera (model No. C4792-95-12; Hamamatsu, Iwata City, Japan) using KS400 software (Zeiss).
Streptavidin crosslinking of filaments
For streptavidin crosslinking experiments, actin was additionally gel-filtered with a HiLoad Superdex 200 column. Crosslink points were added during polymerization (in the methods described above) by the addition of a specific amount of biotinylated actin monomers (Molecular Probes/Invitrogen, Carlsbad, CA) to the unmodified actin solution. Crosslink points are assumed to occur in equally probable random placements along the filaments, with no positional preference. Excess streptavidin (Sigma Aldrich, Milwaukee, WI) was added to the final solution to form crosslinks between incorporated biotinylated actin monomers. In crosslinking/bundling experiments, myosin II minifilaments were first treated with 3 mM N-ethylmaleimide (NEM) for 1 h at room temperature. The reaction was stopped with 4 mM DTT (20).
Fluorescent labeling of myosin II minifilaments
Myosin II minifilaments which had been purified according to Humphrey et al. (9) were labeled with the fluorescent thiol-reactive BODIPY-FL (Molecular Probes, Eugene, OR) marker. The myosin was first diluted to a concentration of 2 μM and deoxygenated for ∼15 min. The myosin was incubated for 1 h with a 15-fold molar excess of a reducing agent (TCEP) subsequently followed by the addition of a 25-fold excess of the fluorescent dye. The dye was left to conjugate with the minifilaments for 2 h before an excess of TRIS buffer was added to the solution to consume free BODIPY molecules. The myosin was dialyzed in the dark for two days against an appropriate buffer (0.6 M KCl, 1 mM EDTA, 2 mM MgCl2, 10 mM imidazole) to remove excess TRIS-BODIPY conjugates.
Luciferase assays
The presence of ATP in the actomyosin solutions was monitored through a luciferase assay (21). Luciferase-luciferin in glycine buffer (Sigma Aldrich) was used in a 5 mg/ml concentration. For ATP content measurement at a given time point, 100 μl of luciferase solution was added to 20 μl of the desired actin solution. Luminescence was measured on a Quanta Master model-C cuvette-based scanning spectrofluorometer and visualized using the Felix software package (PTI, Birmingham, AL). Correlation of ATP content to filament assembly was examined by making simultaneous visual observations as described above.
Use of caged-ATP
Chemical energy to reactivate the myosin motors was reintroduced into the actomyosin system through caged-ATP (Sigma Aldrich) (22). In addition to the normal F-Buffer with ATP, caged-ATP with a concentration of 0.5 mM was present. Quartz slides were used to allow passage of ultraviolet (UV) light. ATP was released by exposing the samples to UV light emitted from the microscope's mercury lamp for a time of 90 s. Release of caged-ATP was verified through a luciferase assay as described above.
Modeling growth of clusters and immobilization
So far, modeling efforts on filament-motor systems have concentrated on the dissipative case, as occurring in microtubule-motor mixtures, where the ATP supply in the system is considered to be a constant in space and time (23,24,25) and one is beyond an instability if the driving is sufficiently high. The arguments given above and in the main body of the text that, upon ATP depletion, an interplay of filament bundling and immobilization gives rise to a crossing of an instability border with time, can be exemplified within the existing models as shown in this section. However, as a quantitative analysis even for the stationary dissipative case is still lacking, for the more subtle case discussed here, where an instability is crossed and a transient pattern is then frozen-in, only qualitative insight about the suggested mechanisms can be expected from the present mean-field approaches.
The temporary clustering and the immobilization leading to ultimate freezing of the actomyosin structures can be implemented in the previously-established model for interactions between filaments and active cross linkers (23,26). In the case addressed here, the probability distribution function (pdf) 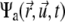 must be related to actively transported, growing clusters (at position
must be related to actively transported, growing clusters (at position 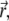 in orientation
in orientation 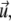 at time t) rather than to single filaments. This pdf for the active clusters is coupled to an equation for a second pdf of immobilized clusters
at time t) rather than to single filaments. This pdf for the active clusters is coupled to an equation for a second pdf of immobilized clusters 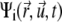 as follows:
as follows:
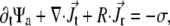 |
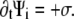 |
Here 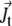 is the translational current and
is the translational current and 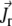 the rotational current. Both currents have active contributions due to the motor-induced transport (23). If the pdf for the total (active + immobilized) cluster is written as
the rotational current. Both currents have active contributions due to the motor-induced transport (23). If the pdf for the total (active + immobilized) cluster is written as 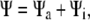 both currents depend locally on
both currents depend locally on 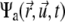 and nonlocally on
and nonlocally on 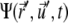 of the other clusters within the region where overlap is possible. The value σ describes transitions from the active to the immobilized cluster state and reads
of the other clusters within the region where overlap is possible. The value σ describes transitions from the active to the immobilized cluster state and reads
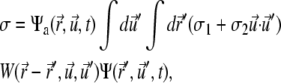 |
where W is the overlap function and σ1 and σ2 are two phenomenological parameters, the latter favoring parallel alignment upon inclusion into the immobile cluster. For more details on the single-pdf model, we refer to the literature (23,26).
The growth of the actively transported clusters of size S can be accounted for by assuming simple scaling behaviors for the model parameters: the diffusion coefficient should scale with cluster size like D → D/S due to growing mass, the cluster density should scale like ρ → ρ/S due to the overall conservation of filaments, and the phenomenological parameter of motor transport introduced in Eq. 1 should vary like α → αS due to the increasing cross section of growing clusters as discussed above.
Implementing a coarse-grained version of this model that extracts equations for the cluster density and the cluster orientation field, one gets frozen-in structures reminiscent of those seen in the experiments shown in Fig. 4.
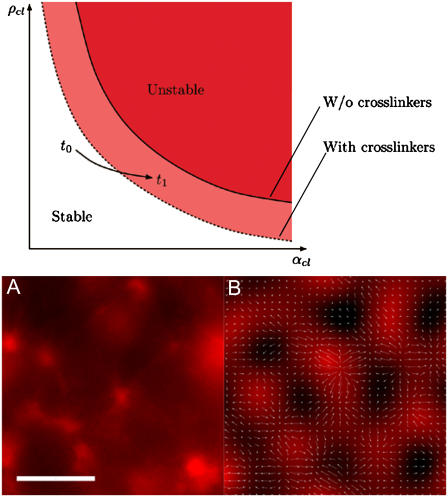
FIGURE 4.
Phase diagram from mean-field models for instability-driven ordering in actomyosin solutions. (Diagram) As the ATP available to be hydrolyzed by the motors is depleted, the clustering process enhances the cross section and thus the effective cluster activity αcl, causing an approach toward the instability threshold (solid line). Addition of static cross linkers such as streptavidin to the system shifts the instability threshold (as indicated by the dashed line) to smaller values of αcl, thus enhancing the tendency of ordered clustering. (A and B) Experimentally observed and theoretically reproduced aster architectures demonstrating similarity between final assembly properties. In the simulation of the mean-field model on the right-hand side, the filament cluster density ρcl is color-coded in red while arrows show the orientation field. (Scale bar is 20 μm.)
Influence of disorder
The dynamics of spatial patterns near an instability can be described in terms of envelope equations (15,24,26) for the envelope of the spatially varying fields. Starting from the basis model (23) and considering, as discussed above, that the motor activity parameter has a small random contribution due to crosslinker-induced randomly varying cluster density (α(x) = α0 + ɛα1(x) + …), in the case of the orientational instability we are led to the modified Ginzburg-Landau equation for the envelope A(x,t) (we restrict ourselves to the one-dimensional case):
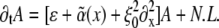 |
Here N.L. denotes nonlinear terms which are not of importance for the instability threshold. The value ɛ is the relative distance of the control parameter, here chosen as α, from its threshold value α0, and 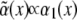 is the disorder contribution. Assuming for the random contribution a vanishing mean value,
is the disorder contribution. Assuming for the random contribution a vanishing mean value, 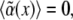 and a correlation
and a correlation 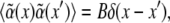 one gets a shift of the average threshold 〈ɛc〉 ∝ − B, making pattern formation more likely (27) in the presence of disorder, i.e., cross linkers. In case of the density-demixing instability present in both models (23,24), the threshold lowering can be caught similarly in the framework of the Cahn-Hilliard equation (28).
one gets a shift of the average threshold 〈ɛc〉 ∝ − B, making pattern formation more likely (27) in the presence of disorder, i.e., cross linkers. In case of the density-demixing instability present in both models (23,24), the threshold lowering can be caught similarly in the framework of the Cahn-Hilliard equation (28).
RESULTS AND DISCUSSION
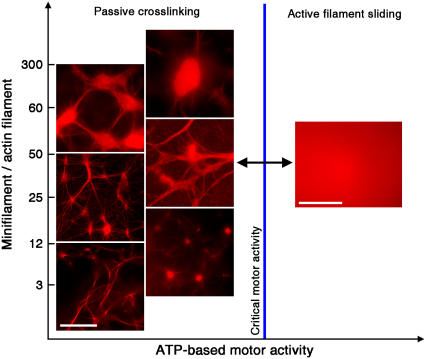
The overall self-organization of actomyosin solutions depends on the two key interactions of actin and myosin: temporary crosslinking of actin filaments by myosin in non-ATP conditions and myosin-induced sliding of actin filaments in the presence of excess ATP. With an actin concentration of 2.4 μM, we first examined the effect of varying the ratio between myosin minifilaments and actin filaments from 3 to 300 minifilaments per actin filament. We observed a rich phase space of self-organized structures, including networks of thick filament bundles, asters (ranging over a large size scale and connectivity), networks reminiscent of neuronal geometries, and dense, irregularly shaped condensates of filaments reminiscent of structures commonly referred to in literature as super-precipitates (29,30), as indicated in the left-hand side of the phase diagram (Fig. 1). The asters in vitro resemble previously observed cytoskeletal structures found in the lamellipodium of fish epidermal keratocyte cells (16,31). The observed self-assembled structures formed after time intervals ranging from 45 to 90 min, after which they persisted in a stable state.
FIGURE 1.
Phases of actin and myosin II self-organization. In all figures, the actin concentration is 2.4 μM. The different types of assembly architecture are shown as a function of the ratio of myosin II minifilaments to actin filaments and the ATP-dependent activity of the motors (active sliding or passive crosslinking). When the motors are active, a state of dynamic disorder persists. When the ATP is diminished to a point where the activity of the motors is below a critical threshold, passive crosslinking dominates, triggering a spontaneous transition to different types of ordered actomyosin aggregates, as indicated. (Scale bar is 20 μm.)
To further investigate the dynamics of these self-assembly processes, we studied actomyosin solutions in relation to both time and presence of chemical fuel. In all cases, the initial ATP concentration was 500 μM, which was subsequently hydrolyzed by the molecular motors. Even though the typical time required for the formation of the observed ordered structures after the addition of motors ranged from 45 to 90 min, the actual assembly process was seen to occur during a period of 1–2 min near the end of the observation time, after an initial lag phase (Fig. 2). Therefore, the transition from the dynamically disordered state to one displaying a high degree of order is not a linear process beginning from the time of the introduction of active motors into the system; instead it is sudden and quick, which is a rather common signature of exponentially growing structures beyond an instability (15).
FIGURE 2.
Temporal dynamics of aster formation in an actin/myosin system. Actin concentration is 2.4 μM with an average of 40 myosin minifilaments per actin filament. (A–F) 6 min, 16 min, 31 min, 41 min, 45 min, and 48 min. After an initial lag phase where the system stays disordered, aster formation starts at 41 min with permanent structures observed at 45 min. (Scale bar is 20 μm.)
To determine the correlation between filament assembly and ATP-dependent motor activity, we performed a luciferase assay to evaluate myosin ATPase activity. This assay served as a measure for the amount of chemical fuel available to power filament-sliding at specific time points after motors have been added to the system. While a consistent decline in ATP concentration was always observed with active motors present, the sudden transition to the self-assembled state did not typically begin until the remaining ATP concentration dropped below ∼10% of the initial content (see Supplementary Material Fig. 1). At this point, roughly one-third of the minifilaments became transiently inactive due to insufficient fuel. All subsequent observations showed no further structural change since the ATP-deficient myosin froze the assemblies by permanent crosslinking. By this, it is clear that spontaneous self-assembly occurs only as the filament-sliding behavior of the motors diminishes below a certain critical threshold, triggering the sudden transition to crosslink-dominated ordering of actomyosin structures (Fig. 1).
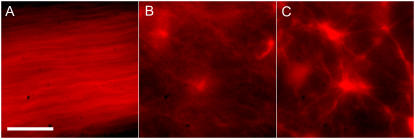
The self-assembled architectures additionally displayed a variance relative to the concentration of an external static cross linker inserted into the solution, such as a biotin-streptavidin-based crosslinking system. We inserted a controlled number of crosslink points into actin filaments by way of commercially obtained biotinylated actin monomers, which were subsequently linked via addition of streptavidin to the solution. In a pure system of actin and myosin devoid of any exterior crosslinking, the stable final state consisted of an aligned nematiclike gel of actin filaments (Fig. 3 A) similar to architectures predicted to arise due to nonequilibrium phase transitions in filament-gliding assays (32). The inclusion of trace amounts of crosslink points induced asterlike clustering of filaments (Fig. 3, B and C). With an increasing number of cross linkers, the structures were observed to be both larger and denser in nature, with a greater number of actin filaments from the surrounding solution incorporated into the compacted asters. The various structures appeared invariable in relation to conditions such as sample thickness (in a range of ∼5–50 μm) and temperature (within the viable range for such proteins) while only showing a significant alteration depending on the specific biochemical conditions such as relative actin, myosin, and crosslink concentrations.
FIGURE 3.
Dependence of actomyosin architectures on external cross linkers. In all figures, the actin concentration is 2.4 μM and the ratio of myosin minifilaments to actin filaments is 50. (A) Aligned nematiclike phase in the absence of any external cross linkers. (B and C) Aster formations at 0.1 and 0.5 crosslink points per filament, respectively. (Scale bar is 10 μm.)
Motivated by experiments on microtubules interacting with oligomeric motor complexes (8), there have been recent efforts to model such interactions occurring between filaments and mobile cross linkers, i.e., motors. This work has established that patterns such as asters and bundles can arise from the instabilities induced by motor transport (23–26), triggered either by an increase in filament or motor density, or by an increase in the activity of the motors (Fig. 4). In the case of the structures observed in microtubule systems, the patterns are dissipative, meaning that they require a constant energy supply by means of ATP hydrolysis. By contrast, in the experiments reported here, the clustering effect occurs as the supply of ATP is approaching depletion. Here we give two arguments about how these observations in actomyosin can also be traced back to instabilities. In Materials and Methods, we exemplify these mechanisms in terms of a specific model.
In the initial stages of ATP depletion, local and temporary crosslinking of inactive motors causes the formation of small actomyosin clusters through enhancement of local actin filament concentration via a bundling process. This bundling is similar to the local “zipping mechanism” in gel-sol transitions as observed by Uhde et al. (33) and has additionally been observed in actomyosin solutions containing NEM-modified myosin II minifilaments displaying purely crosslinking activity (see Supplementary Material Fig. 2). In addition, it is known from single-motor experiments that active motors can easily overcome the few stationary rigor bonds in the tangential direction relative to filament sliding (34,35). Given the propensity of temporarily inactive motors to form filament clusters, we consider the density and motor activity of actomyosin clusters rather than of single filaments and motors as considered in microtubule systems.
It has been estimated by Liverpool et al. (23) that the motor activity for a single filament (α) should behave as
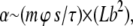 |
(1) |
where m is the motor density, ϕ the duty ratio, s the step size, and τ the time of a single cycle for a single motor. The filament properties are summed up in the second term, which can be considered as the total collision cross section for the filament, where L is the length of the filament and b its diameter. The net effect of an increasing degree of temporary crosslinking during ATP depletion is an overall increase in the cluster-related motor activity αcl, leading to a crossing of the instability border (Fig. 4). The increase in αcl comes as a result of an enlarged cross section from bundling, while the myosin motor activity is not strongly impeded due to the temporary nature of the motor cross linkers and the relatively weak strength of the rigor states in the tangential direction as mentioned above. This effect is further enhanced by the decrease in diffusion resulting from the increasing mass of the clusters. Since the total number of filaments is conserved, there is a decrease in the overall density of clusters ρcl within the system as the clusters grow larger. In tandem with the increasing αcl, this leads, upon ATP depletion, to a shift in parameter space as indicated by the arrow in Fig. 4. Upon further depletion approaching the equilibrium state for myosin hydrolysis of ATP (36), the strong decrease in the motor part of αcl due to rapidly vanishing motor activity m leads to the freezing of the system.
We implemented these effects in the model of Liverpool et al. (23,26), obtaining simulated architectures reminiscent of those seen in the experimental system (Fig. 4). While not demonstrating any quantitative comparison between the specific structures seen, the results of this implementation do offer preliminary evidence of why the ordering of motor-filament systems can occur as a function of rapidly-decreasing motor activity. Motor-filament systems previously examined both experimentally and theoretically have only displayed active, motor-driven assembly whereas the seemingly contrary observations here indicate a very different mechanism. By showing how the rapid cessation of motor activity can also trigger an instability-driven aggregation and ordering process, this modeling effort alleviates the seeming paradox between previous observations, and those shown here with the actin-myosin II system.
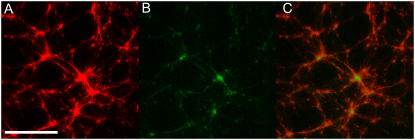
In systems showing an assembly of filament structures such as asters driven by active motors, both an accumulation of motors in the centers of the asters as well as an aligned polarity of the filaments incorporated within the asters has been observed (8). On the contrary, the mechanism of bundling by inactive motors leading to the instability-driven aggregation hypothesized here should yield a distribution of motors that is more proportional to the local actin concentration. In an effort to visualize the location of motors within self-assembled actomyosin structures, myosin minifilaments were labeled with a BODIPY-FL fluorescent marker to allow colocalization of both protein species. As evidenced by observation with a laser-scanning microscope to avoid cross-excitation of the two types of fluorophores, the motors were distributed throughout the asters in an evenly-distributed manner in relation to the actin (Fig. 5). While the signal from the myosin is substantially weaker due to less overall myosin (∼10% by number compared to rhodamine phalloidin-labeled actin monomers), it is clear that myosin is still present in all parts of contracted actomyosin structures, with no clear proclivity for the center regions of asters, as previously seen for motor-driven assembly of microtubule aster (8). Such a relative distribution distinctly favors the bundling and “freezing” process described above.
FIGURE 5.
Colocalization of actin and myosin within self-assembled structures. Actin concentration is 2.4 μM with an average of 35 myosin minifilaments and an average of 0.5 biotin-streptavidin crosslink points per actin filament. Visualization of (A) actin structures via rhodamine-phalloidin antibody labeling and (B) myosin II minifilaments via BODIPY-FL covalent labeling. (C) Overlay of actin and myosin images, indicating colocalization of actin and myosin. (Scale bar is 50 μm.)
As indicated by our experimental observations, the addition of permanent cross linkers, e.g., streptavidin, further enhances the propensity for dense structure formation. Streptavidin is assumed to form small, permanent, randomly distributed filament clusters which change the local filament density and motor activity. Due to their random distribution and decreased mobility compared to single filaments, these clusters effectively represent a time-independent spatial disorder. From other pattern-forming systems (15,37,38), it is known that disorder decreases the instability threshold. In the framework of the existing motor-filament models, this can be incorporated by allowing (the motor activity) α to have a small spatially varying random contribution, as detailed in Materials and Methods. Similar to the approach used in Ziebert et al. (26), one can describe the dynamics near the instability border by reduced equations. One resulting equation has been recently investigated and indeed the analysis yielded a lowering of the instability threshold proportional to the noise amplitude (27). In relation to the actomyosin system, the consequently reduced threshold resulting from the addition of permanent streptavidin cross linkers proved crucial for the occurrence of clusters (Fig. 3).
The dynamic behavior of a motor-driven instability is determined by the time required for the filament to undergo directed sliding of a distance equal to its length (5 s for a 10 μm filament) (9), which is much faster than Brownian-driven motion, having a characteristic timescale several times that of the reptation time of an individual filament in an inactive, non-crosslinked gel (which is ∼10 min for a 10-μm filament) (9). Therefore, if the above-described actomyosin structures are formed due to an instability, quick and reversible switching should be observable.
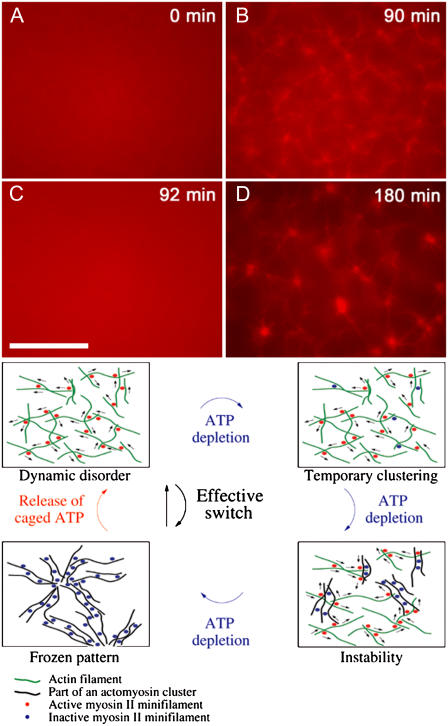
To examine reversibility with respect to myosin activity, we used caged-ATP molecules to facilitate controlled reintroduction of chemical fuel into a system which has already attained its stable, self-organized rest state (Fig. 6). An actomyosin system initially containing equal amounts of ATP and caged-ATP (500 μM) was allowed to organize into a state displaying asters, with ATP maximally depleted (and all caged-ATP still inactivated). We then flashed the system with UV light to release ATP from its cage, providing a sudden restoration of myosin II motor activity. This triggered, within 1–2 min, a complete return to the initial dynamically disordered state, with no discernible structure or clustering remaining. After an additional time to allow for the reintroduced ATP to be depleted by the active motors as before, the system returned to a near-chemical-rest state, and asters were once again seen to form by a sudden transition. This demonstrated the ability of myosin minifilaments to repeatedly switch actin networks between states of fixed filament order and dynamic disorder. By this process, one may envision a cycle whereby ordered, stable actomyosin structures form as a result of ATP depletion instigating an instability-induced growth of actomyosin clusters, while a reactivation of the motors triggers a rapid return to the state of dynamically disordered filaments and motors (Fig. 6). This is in contrast to the microtubule-kinesin system, where active motor constructs caused ordering but the complimentary disordering transition required for a reversible switch was not observed (8).
FIGURE 6.
Reversibility of disorder-order transitions in the actin myosin system. Actin concentration is 2.4 μM with an average of 50 myosin minifilaments per actin filament. (A) In the presence of ATP, i.e., motor activity, the system stays disordered. (B) Self-assembly is observed when initial ATP is exhausted (90 min). (C) ATP is reintroduced through UV-activated caged-ATP molecules. Self-assembled structures are disrupted in 2–3 min and the system returns to a disordered state. (D) Self-assembly is again observed when reintroduced ATP is subsequently exhausted (180 min). (Diagram) Illustrated schematic for instability-driven switch between dynamic disorder and ordered actomyosin architectures. Free actin filaments are indicated in green, actin filaments incorporated into a cluster in black, active myosin II minifilaments in red, and inactive myosin II minifilament in blue. (Scale bar is 20 μm.)
CONCLUSION
An isothermic (39) rapid switching of different intracellular architectures controlled by motor activity exceeds transition rates possible through thermal (i.e., Brownian) pathways while exploiting a cell's nonequilibrium state. The resulting instabilities are particularly well-suited to induce sudden and drastic transitions in cellular organization triggered by small molecular signals. Such mechanisms have already been implicated as key in crucial cell functions such as DNA replication, and cell division. In the case of DNA replication, motors—instead of a thermally driven helix-coil transition—are used to unwind the two strands. In cell division, the motors do not only generate the forces to separate the chromosomes via the spindle apparatus but are also instrumental in the self-organization of the spindle itself (8). In addition, the myosin II-directed actin assembly can potentially play a quintessential role in actin-driven morphological changes of the cell such as the organization of the contractile ring in dividing cells (T. Kamasaki, M. Osumi, and I. Mabuchi. 2005. Paper presented at the 45th Annual Meeting of the American Society for Cell Biology, Abstract #149). While DNA replication, the spindle apparatus, and the actomyosin system may at first seem unconnected, the molecular motors involved in each share a common specific role in the control of order and self-organization. The synonymous functions in three widely dissimilar systems suggest a reevaluation in the consideration of the cellular functions of molecular motors from that of being simply machines in specific molecular processes, to the more general role of controlling and causing rapid switching of intracellular order. Future studies involving other species of myosin motors displaying varying properties (e.g., processive myosin V or single-headed heavy meromyosin) or alteration and tight control of myosin II minifilament composition could further elucidate the full scope of this mechanism. While order-disorder transitions in actin solutions can also be mediated by temperature (40) or confinement effects (41), thermal or steric-based polymer dynamics are inherently slower than motor-based switching. Consequently, it becomes evident that motor activity is a powerful tool to control and switch the state of order in polymer systems.
SUPPLEMENTARY MATERIAL
To view all of the supplemental files associated with this article, visit www.biophysj.org.
Supplementary Material
Acknowledgments
We acknowledge usage of the Integrative Graduate Education and Research Traineeship center in the University of Texas at Austin and the help of J. Wright, and also acknowledge the Paul Flechsig Institute in the University of Leipzig and Dr. Jens Grosche for their assistance with laser-scanning microscope measurements. We thank the following for discussions: V. Bell, T. Liverpool, K. Kruse, F. Jülicher, U. Schwarz, H. Carl, R. Everaers, R. Lipowsky, B. Gentry, B. Stuhrmann, and A. Ehrlicher.
We acknowledge funding by the Alexander von Humboldt Foundation through the Wolfgang Paul Preis and the Deutsche Forschungsgemeinschaft via Research Group 608.
Editor: Shin'ichi Ishiwata.
References
- 1.Borisy, G. G., and T. M. Svitkina. 2000. Actin machinery: pushing the envelope. Curr. Opin. Cell Biol. 12:104–112. [DOI] [PubMed] [Google Scholar]
- 2.Pollard, T. D. 2001. Genomics, the cytoskeleton and motility. Nature. 409:842–843. [DOI] [PubMed] [Google Scholar]
- 3.Pantaloni, D., C. Le Clainche, and M. F. Carlier. 2001. Mechanism of actin-based motility. Science. 292:1502–1506. [DOI] [PubMed] [Google Scholar]
- 4.Bershadsky, A. D., N. Q. Balaban, and B. Geiger. 2003. Adhesion-dependent cell mechanosensitivity. Annu. Rev. Cell Dev. Biol. 19:677–695. [DOI] [PubMed] [Google Scholar]
- 5.Ingber, D. E. 2002. Mechanical signaling. Ann. N. Y. Acad. Sci. 961:162–163. [DOI] [PubMed] [Google Scholar]
- 6.Lodish, H., A. Berk, S. L. Zipursky, P. Matsudaira, D. Baltimore, and J. Darnell. 2000. Molecular Cell Biology. W. H. Freeman and Company, New York.
- 7.Engler, A. J., S. Sen, H. L. Sweeney, and D. E. Discher. 2006. Matrix elasticity directs stem cell lineage specification. Cell. 126:677–689. [DOI] [PubMed] [Google Scholar]
- 8.Nedelec, F. J., T. Surrey, A. C. Maggs, and S. Leibler. 1997. Self-organization of microtubules and motors. Nature. 389:305–308. [DOI] [PubMed] [Google Scholar]
- 9.Humphrey, D., C. Duggan, D. Saha, D. Smith, and J. Käs. 2002. Active fluidization of polymer networks through molecular motors. Nature. 416:413–416. [DOI] [PubMed] [Google Scholar]
- 10.Verkhovsky, A. B., T. M. Svitkina, and G. G. Borisy. 1999. Cell behavior: control and mechanism of motility. In Biochemical Society Symposium 65. J. M. Lackie, G. A. Dunn, and G. E. Jones, editors. Portland Press, London.
- 11.Keller, M., R. Tharmann, M. A. Dichtl, A. R. Bausch, and E. Sackmann. 2003. Slow filament dynamics and viscoelasticity in entangled and active actin networks. Philos. Trans. R. Soc. Lond. B Biol. Sci. 361:699–712. [DOI] [PubMed] [Google Scholar]
- 12.Le Goff, L., F. Amblard, and E. M. Furst. 2001. Motor-driven dynamics in actin-myosin networks. Phys. Rev. Lett. 88:018101. [DOI] [PubMed] [Google Scholar]
- 13.Girard, K. D., S. C. Kuo, and D. N. Robinson. 2006. Dictyostelium myosin II mechanochemistry promotes active behavior of the cortex on long time scales. Proc. Natl. Acad. Sci. USA. 103:2103–2108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Turing, A. M. 1952. The chemical basis of morphogenesis. Phil. Trans. R. Soc. London B. 237:37–72. [Google Scholar]
- 15.Cross, M. C., and P. C. Hohenberg. 1993. Pattern formation outside of equilibrium. Rev. Mod. Phys. 65:851–1112. [Google Scholar]
- 16.Verkhovsky, A. B., T. M. Svitkina, and G. G. Borisy. 1999. Self-polarization and directional motility of cytoplasm. Curr. Biol. 9:11–20. [DOI] [PubMed] [Google Scholar]
- 17.Bausch, A. R., and K. Kroy. 2006. A bottom-up approach to cell mechanics. Nat. Phys. 2:231–238. [Google Scholar]
- 18.Loisel, T. P., R. Boujemaa, D. Pantaloni, and M. F. Carlier. 1999. Reconstitution of actin-based motility of Listeria and Shigella using pure proteins. Nature. 401:613–616. [DOI] [PubMed] [Google Scholar]
- 19.Käs, J., H. Strey, and E. Sackmann. 1994. Direct visualization of reptation for semiflexible actin filaments. Nature. 368:226–229. [DOI] [PubMed] [Google Scholar]
- 20.Sheetz, M. P., R. Chasan, and J. A. Spudich. 1984. ATP-dependent movement of myosin in vitro: characterization of a quantitative assay. J. Cell Biol. 99:1867–1871. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Gould, S. J., and S. Subramani. 1988. Firefly luciferase as a tool in molecular and cell biology. Anal. Biochem. 175:5–13. [DOI] [PubMed] [Google Scholar]
- 22.McCray, J. A., and D. R. Trentham. 1989. Properties and uses of photoreactive caged compounds. Annu. Rev. Biophys. Chem. 18:239–270. [DOI] [PubMed] [Google Scholar]
- 23.Liverpool, T. B., and M. C. Marchetti. 2003. Instabilities of isotropic solutions of active polar filaments. Phys. Rev. Lett. 90:138102. [DOI] [PubMed] [Google Scholar]
- 24.Aranson, I. S., and L. S. Tsimring. 2005. Pattern formation of microtubules and motors: inelastic interaction of polar rods. Phys. Rev. E. 71:050901. [DOI] [PubMed] [Google Scholar]
- 25.Kruse, K., J. F. Joanny, F. Jülicher, J. Prost, and K. Sekimoto. 2005. Generic theory of active polar gels: a paradigm for cytoskeletal dynamics. Eur. Phys. J. E. 16:5–16. [DOI] [PubMed] [Google Scholar]
- 26.Ziebert, F., and W. Zimmermann. 2005. Nonlinear competition between asters and stripes in filament-motor systems. Eur. Phys. J. E. 18:41–54. [DOI] [PubMed] [Google Scholar]
- 27.Hammele, M., S. Schuler, and W. Zimmermann. 2006. Effects of parametric disorder on a stationary bifurcation. Physica D. 218:139–157. [Google Scholar]
- 28.Cahn, J. W., and J. E. Hilliard. 1958. Free energy of a nonuniform system. I. Interfacial free energy. J. Chem. Phys. 28:258–267. [Google Scholar]
- 29.Sekine, T., and M. Yamaguchi. 1966. Superprecipitation of actomyosin reconstructed with F-actin and NEM-modified myosin. J. Biochem. (Tokyo). 59:195–196. [DOI] [PubMed] [Google Scholar]
- 30.Nonomura, Y., and S. J. Ebashi. 1974. Electron microscopic studies of superprecipitation with special reference to its optical properties. Mechanochem. Cell Motil. 3:1–8. [PubMed] [Google Scholar]
- 31.Takiguchi, K. 1991. Heavy meromyosin induces sliding movements between antiparallel actin filaments. J. Biochem. (Tokyo). 109:520–527. [DOI] [PubMed] [Google Scholar]
- 32.Kraikivski, P., R. Lipowsky, and J. Kierfeld. 2006. Enhanced ordering of interacting filaments by molecular motors. Phys. Rev. Lett. 96:258103. [DOI] [PubMed] [Google Scholar]
- 33.Uhde, J., M. Keller, and E. Sackmann. 2004. Internal motility in stiffening actin-myosin networks. Phys. Rev. Lett. 93:268101. [DOI] [PubMed] [Google Scholar]
- 34.Nishizaka, T., R. Seo, H. Tadakuma, K. Sinosita, Jr., and S. Ishiwata. 2000. Characterization of single actomyosin rigor bonds: load dependence of lifetime and mechanical properties. Biophys. J. 79:962–974. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Parmeggiani, A., F. Jülicher, L. Peliti, and J. Prost. 2001. Detachment of molecular motors under tangential loading. Europhys. Lett. 56:603–609. [Google Scholar]
- 36.Bagshaw, C. R., and D. R. Trentham. 1973. The reversibility of adenosine triphosphate cleavage by myosin. Biochem. J. 133:323–328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Zimmermann, W., M. Sesselberg, and F. Petruccione. 1993. Effects of disorder in pattern formation. Phys. Rev. E. 48:2699–2703. [DOI] [PubMed] [Google Scholar]
- 38.Zimmermann, W., B. Painter, and R. Behringer. 1998. Pattern formation in an inhomogeneous environment. Eur. Phys. J. B. 5:757–770. [Google Scholar]
- 39.Jülicher, F., A. Ajdari, and J. Prost. 1997. Modeling molecular motors. Rev. Mod. Phys. 69:1269–1281. [Google Scholar]
- 40.Limozin, L., and E. Sackmann. 2002. Polymorphism of cross-linked actin networks in giant vesicles. Phys. Rev. Lett. 89:168103. [DOI] [PubMed] [Google Scholar]
- 41.Claessens, M. M., R. Tharmann, K. Kroy, and A. R. Bausch. 2006. Microstructure and viscoelasticity of confined semiflexible polymer networks. Nat. Phys. 2:186–189. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.