Nonlinear Force-Length Relationship in the ADP-Induced Contraction of Skeletal Myofibrils

Abstract

The regulatory mechanism of sarcomeric activity has not been fully clarified yet because of its complex and cooperative nature, which involves both Ca²⁺ and cross-bridge binding to the thin filament. To reveal the mechanism of regulation mediated by the cross-bridges, separately from the effect of Ca²⁺, we investigated the force-sarcomere length (SL) relationship in rabbit skeletal myofibrils (a single myofibril or a thin bundle) at SL > 2.2 μm in the absence of Ca²⁺ at various levels of activation by exogenous MgADP (4–20 mM) in the presence of 1 mM MgATP. The individual SLs were measured by phase-contrast microscopy to confirm the homogeneity of the striation pattern of sarcomeres during activation. We found that at partial activation with 4–8 mM MgADP, the developed force nonlinearly depended on the length of overlap between the thick and the thin filaments; that is, contrary to the maximal activation, the maximal active force was generated at shorter overlap. Besides, the active force became larger, whereas this nonlinearity tended to weaken, with either an increase in [MgADP] or the lateral osmotic compression of the myofilament lattice induced by the addition of a macromolecular compound, dextran T-500. The model analysis, which takes into account the [MgADP]- and the lattice-spacing-dependent probability of cross-bridge formation, was successfully applied to account for the force-SL relationship observed at partial activation. These results strongly suggest that the cross-bridge works as a cooperative activator, the function of which is highly sensitive to as little as ≤1 nm changes in the lattice spacing.

INTRODUCTION

In striated muscle, the regulation of contraction is mediated through troponin/tropomyosin bound to the thin filament, which regulates cyclic interactions between the myosin (thick) and the actin (thin) filaments (1). The regulation of the thin filament activity is a cooperative process involving both Ca²⁺ binding and cross-bridge formation (2,3). Ca²⁺ binding to troponin induces the structural change in tropomyosin, such that myosin can strongly interact with actin and generate force. On the other hand, the myosin heads in the nucleotide-free or the ADP-bound state, which strongly bind to the thin filament regardless of the presence of Ca²⁺, also contribute to the thin filament activation as reported by solution (4,5), in vitro (6), and fiber studies (7–9). That is, the formation of the cross-bridges shifts the thin filament toward the “ON” state, which facilitates further formation of the cross-bridges in the vicinity of the previously formed cross-bridges and potentiates the sarcomeric activity. Therefore, it is expected that there exists a positive cooperative mechanism where the sarcomeric activity is autonomously regulated by the cross-bridges themselves.

The relationship between SL and generated force provides important information revealing the molecular events that underlie the force regulation in sarcomeres. It has been established that at maximal activation the active isometric force of skeletal muscle is proportional to the length of overlap between the thick and the thin filaments, in other words, to the number of myosin heads that are able to interact with the thin filament (10,11). This is considered to be the foundation of the molecular mechanism of muscle contraction, implying that the cross-bridge is an independent force generator (12). In contrast, it is also known that, at partial activation by Ca²⁺, the generated force is not proportional to the length of overlap, but reaches maximum at longer SL (13,14). Besides, it has been reported that in skeletal muscle the Ca²⁺ sensitivity of force increases with increasing SL (15,16), whereas the affinity of troponin for Ca²⁺ is SL independent (17,18). These facts suggest that the cross-bridges work as a cooperative activator, and that the cooperativity becomes especially prominent at partial activation. So far, however, it has been difficult to fully comprehend the mechanism of activation mediated by the cross-bridges in a sarcomere, mainly for the following reasons. First, the thin filament activation is a complex process involving both Ca²⁺ binding to troponin and the cross-bridge formation, as described above. Second, the solution composition, such as the concentration of Ca²⁺ and the nucleotides, cannot be precisely controlled in skinned muscle fibers due to its considerable (∼50 μm) thickness (19). Third, the nonuniform length distribution of sarcomeres associated with inhomogeneous contraction may cause overestimation of the active force production (10,13).

To overcome these difficulties and reveal the mechanism of cooperative activation in sarcomeres mediated exclusively by the cross-bridges, we examined the force-SL relationship in skeletal myofibrils (with a thickness of only a few micrometers) in the absence of Ca²⁺ at various levels of activation induced by exogenous MgADP in the presence of MgATP. The experiments were carried out under the inverted phase-contrast microscope equipped with the dual laminar flow system (20), followed by the image analysis of individual sarcomeres. The advantages of using a myofibril over the fiber are its small diameter allowing the solution to be exchanged rapidly and remain uniform, and that the quantitative measurement of the dynamics in each sarcomere is possible (21). Thus, the measurements of the length-dependent properties and their dependence on [MgADP] in a myofibril are more informative and reliable than in muscle fibers.

In this study, we found that at low levels of activation, the larger active force was generated at longer SL, which clearly indicates that the ADP-bound cross-bridge itself is the source of cooperativity without the involvement of Ca²⁺. Besides, such length dependence was weakened either by increasing [MgADP] or by osmotically compressing the interfilament spacing between the thick and the thin filaments with the macromolecular compound, dextran T-500. Based on the experimental results and the model analysis, we discuss the mechanism of cooperative activation by the ADP-bound cross-bridges in sarcomeres.

MATERIALS AND METHODS

Preparation of myofibrils

Myofibrils were obtained from psoas muscle of white rabbits (2–3 kg), which were decapitated after anesthesia by injection of 25 mg/kg sodium pentobarbital into an ear vein. All procedures were performed according to the Regulations for Animal Experimentation at Waseda University. Single myofibrils or thin bundles of myofibrils were prepared by homogenization of the fiber bundles as previously described (22) except that the fibers stored in 51% (v/v) glycerol solution at −20°C were used within 10 days. The prepared myofibrils were stored in rigor solution at 2°C and used within 12 h. Chemical skinning with 0.1% (v/v) Triton X-100 (28314, Pierce Biotechnology, Rockford, IL) was performed for 10 min in the experimental chamber immediately before the force measurements.

Solutions

The pH of all solutions was adjusted to 7.0 at room temperature, and the ionic strength was adjusted by KCl to 150 mM (rigor solution) or 180 mM (activating and relaxing solutions). The rigor solution also contained 2 mM free Mg²⁺, 20 mM MOPS, and 4 mM EGTA. The relaxing solution contained 2 mM free Mg²⁺, 20 mM MOPS, 4 mM EGTA, 1 mM DTT, and 1 mM MgATP. The ADP-activating solutions contained 2 mM free Mg²⁺, 20 mM MOPS, 4 mM EGTA, 1 mM DTT, 1 mM MgATP, and 4–20 mM MgADP. The Ca²⁺-activating solution contained 2 mM free Mg²⁺, 20 mM MOPS, 4 mM EGTA, 1 mM DTT, 1 mM MgATP, and 4 mM CaCl₂ (pCa 4.5). The composition was calculated based on the equilibrium constants described by Fabiato (23). Some experiments were performed with dextran T-500 (average mol wt 400–500 kDa, D1037, Sigma Aldrich, St. Louis, MO) in the activating solution. ATP and ADP were purchased from Roche Applied Science (Indianapolis, IN).

Experimental setup

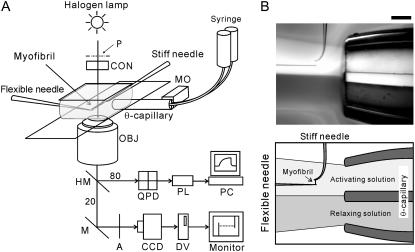
The experimental setup is schematically illustrated in Fig. 1. A single myofibril or a thin bundle composed of two to three myofibrils floating in the experimental chamber was captured and held with a pair of glass microneedles without glue in the rigor condition as described previously (24). The needles were manipulated with the micromanipulators (MHW-3, Narishige, Tokyo, Japan) mounted on the inverted microscope (TE2000, Nikon, Tokyo, Japan). One of the microneedles was >50-fold stiffer than the other. Myofibrils containing 10–30 sarcomeres were used in the experiments. The solution exchange was performed by a dual laminar flow system where the two solutions, i.e., the relaxing and the activating solutions, were infused continuously through the θ-capillary in the direction perpendicular to the long axis of the myofibril (Fig. 1 B) (20). The tip of the θ-capillary was fabricated by pulling the capillary (the inner diameter 1 mm, TGC-150-15, Harvard Apparatus, Holliston, MA) with a pipette puller (PB-7, Narishige), and after breaking the stretched part the exposed tip was polished with the sandpaper, which yielded the tip with the inner diameter of ∼700 μm. The flow rate of each solution was ∼3 μl/s, corresponding to the speed of flow passage through the myofibril being ∼15 μm/ms. The deflection of the flexible needle due to the laminar flow during the force measurements was negligibly small, as the viscous drag applied perpendicular to the myofibrils due to the flow is estimated to be in the order of 10⁻⁹ N. The solution around the myofibril was exchanged within 30 ms by moving the capillary with a stepping motor (SGSP20-35, Sigma Koki, Tokyo, Japan). All experiments were carried out at 23 ± 1°C.

FIGURE 1.

Experimental setup. (A) Schematic diagram of the experimental setup. Abbreviations are: P, phase plate with polarizer; A, analyzer; MO, stepping motor; CON, condenser lens; OBJ, objective lens; QPD, quadrant photodiode; PL, PowerLab; PC, personal computer; CCD, CCD camera; DV, digital video recorder; M, mirror. The light was split into beams (80% and 20%) by the half-mirror (HM). For more details, see Materials and Methods. (B) A bright-field image showing a configuration of the dual laminar flow and the myofibril. The dual laminar flow was infused from the right-hand side through the θ-capillary. The dye was included in the bottom flow to visualize the laminar flow. The needles on the upper side (having a perpendicularly bent tip) and on the left side of the micrograph are the stiff and the flexible, respectively. The myofibrils are held between the microneedles. Scale bar, 200 μm.

Apparatus for data acquisition

The schematic diagram of the setup for force and SL measurements is shown in Fig. 1 A. Phase-contrast image of a myofibril was obtained with the 40× objective (ELWD ADL 40×C, Nikon), projected onto a charge-coupled device (CCD) camera (CCD-300, DAGE-MTI, Michigan, IN), and recorded with a digital video recorder (WV-DR9, Sony, Tokyo, Japan). The magnification was 0.25 μm/pixel. The transmission image of the flexible needle was projected onto a quadrant photodiode (S4349, Hamamatsu Photonics, Shizuoka, Japan), and the output signal was collected by the data acquisition system (PowerLab, ADInstruments, Colorado Springs, CO) to measure the developed force. The center of the phase plate was replaced with the polarizer, and the analyzer was placed in front of the CCD camera with the cross-Nicol configuration to combine the sensitivity of a photodiode with the ability to acquire a clear phase image (25).

Force measurement

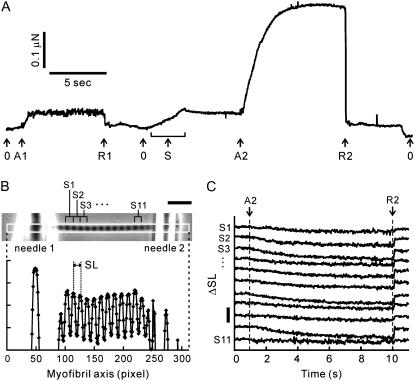
Each set of force measurements included two activation-relaxation cycles (Fig. 2 A). The first activation was performed near slack SL (2.3–2.5 μm) as a reference to check the deterioration of a myofibril, whereas during the second the active force was measured at the SL of interest. Both activations were performed at the same activating conditions. Such set of measurements was repeated typically 2–4 times, changing SL at the second activation until the reference active force decreased to <80% of that at the initial activation. When the active force oscillated spontaneously as described below, the value of the average force during steady oscillation was used in the subsequent analysis.

FIGURE 2.

Measurement of the force-SL relationship in myofibrils. (A) The time course of force development obtained from a single myofibril. The myofibril was activated by 6 mM MgADP at A1 and A2, and relaxed at R1 and R2, at average SL 2.35 μm and 2.67 μm, respectively. Arrows with index 0 indicate the zero level of force. The myofibril was stretched under relaxing conditions to adjust SL (arrow S). The large fluctuation of force shown at the first activation (between the arrows A1 and R1) indicates spontaneous oscillation (for details, see text). (B) Phase-contrast image of a single myofibril suspended between a pair of glass microneedles (top) and the corresponding intensity profile along the myofibril axis within the region of interest (white rectangle in the micrograph) (bottom). In this image the solution flow was directed downwards, perpendicular to the long axis of the myofibril. (C) Change in SL (ΔSL) of 11 consecutive sarcomeres during activation. The sarcomere number shown at the left side of each trace corresponds to that in panel B. The time moments indicated as A2 (activation) and R2 (relaxation) correspond to those in panel A. The horizontal scale bar in panel B is 10 μm. The vertical scale bar in panel C is 0.5 μm.

The generated force was determined from the deflection of the flexible needle. The stiffness of the flexible needle was 0.1–1.0 μN/μm (resonant frequency 3.0–10.0 kHz in solution, depending on the needle stiffness), which was determined by the cross-calibration method (24). A needle of the appropriate stiffness was used at various levels of activation, so that the shortening of a myofibril during activation was confined within at most 10% (typically 3–5%) of the initial SL. The active force was determined by subtracting the average resting force (measured before and after activation) from the total force, observed as a force plateau at each activation. The resting force measured before and after the activation did not significantly differ, although in some cases it slightly decreased due to a slippage of the ends of the myofibril on the microneedles upon activation. The cross-sectional area of a myofibril was estimated from the width of the myofibril in the phase-contrast image, assuming that a myofibril is a uniform cylinder.

The force-[MgADP] relationship (Fig. 5) was fitted by a nonlinear curve using KaleidaGraph Version 3.5 (Synergy Software, Reading, PA) to the Hill equation, 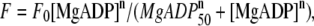where F₀ is the average active force obtained at pCa 4.5, n is the Hill coefficient, and MgADP₅₀ is [MgADP] at the half-maximal force.

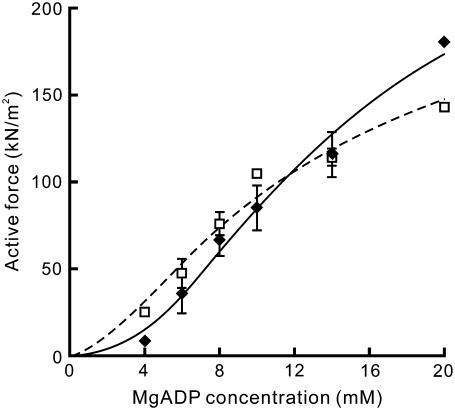
FIGURE 5.

Force-[MgADP] relationship at two different SLs. The active force was replotted against [MgADP] in two regions of SLs, 2.3–2.6 μm (♦, solid line) and 2.7–3.0 μm (□, dashed line). The active force was averaged within each range of SL; the data points at which the spontaneous oscillation occurred (Fig. 4) are not included. Solid and dashed lines were drawn according to the fitted Hill equation. Data points are the mean ± SD (n = 2–5 at each point, except for n = 1 at 20 mM MgADP at SL 2.3–2.6 μm and at 10 mM and 20 mM MgADP at SL 2.7–3.0 μm).

SL measurement

The phase-contrast image of myofibrils was recorded on the digital videotape and then stored in a personal computer (Power Macintosh G4, Apple Japan, Tokyo, Japan) with a frame grabber board (LG3, Scion Corporation, Frederick, MD). The intensity profile along the myofibril was obtained using Scion Image (Scion Corporation). The average SL and the standard deviation of SL distributions were determined by measuring individual SLs as the distance between the centers of mass of the adjacent A-bands in the intensity profile using self-compiled macros in Microsoft Excel. The centroid of the A-band was determined with the accuracy of ±40 nm.

Measurement of the width of a myofibril

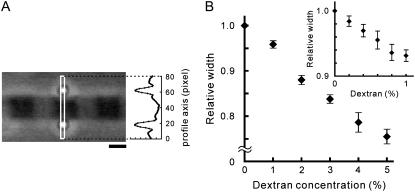
To examine the effect of dextran on the width of a single myofibril, the two polystyrene beads (07307, Polysciences, Warrington, PA) were attached to both lateral sides of an A-band of a sarcomere (Fig. 6 A). First, a suspension of myofibrils in the relaxing solution was infused into a chamber made by two coverslips, followed by a suspension of beads in the relaxing solution. Next, the two beads (0.535 ± 0.01 μm in diameter) were attached to both lateral sides of an A-band using optical tweezers. Finally, the solution was replaced with the relaxing solution containing 1–5% (w/v) or 0.2–1% (w/v) dextran with the stepwise (1% or 0.2%, respectively) change in the dextran concentration, increasing it from the lowest to the highest value and then decreasing it to zero in the similar stepwise manner. The distance between the centers of mass of the two beads was analyzed with the Scion Image and Microsoft Excel macros. The lateral width of an A-band was determined by subtracting 0.535 μm (corresponding to the bead diameter) from the distance between the two beads with the accuracy of ±5 nm.

FIGURE 6.

Effect of dextran on the width of the relaxed single myofibrils. (A) Phase-contrast image showing how the width of myofibrils was measured. Two polystyrene beads were attached to both lateral sides of an A-band of the myofibril for the width measurement (see Materials and Methods). The intensity profile of the phase-contrast image was obtained within the region of interest, indicated by the white rectangle in the micrograph. Scale bar, 1 μm. (B) The change in width of myofibrils at SL around 2.5 μm under relaxing conditions with the stepwise increase in dextran concentration from 0 to 5% with 1% intervals. Data points are the mean ± SE (n = 4 from four myofibrils at each point). (Inset) The change in width induced by the stepwise increase in dextran concentration from 0 to 1% with 0.2% intervals (n = 4 from four myofibrils).

RESULTS

Activation of the relaxed myofibrils by the externally applied MgADP

A single myofibril or a thin bundle composed of two to three myofibrils was activated in the absence of Ca²⁺ by adding various concentrations of MgADP in the presence of MgATP to investigate the activation exclusively by strongly bound cross-bridges. Fig. 2 A shows a typical force record of a single myofibril activated by 6 mM MgADP. [MgADP] in the vicinity of a myofibril was abruptly increased (i.e., myofibril was activated) and then decreased (i.e., myofibril was relaxed), whereas [MgATP] was fixed at 1 mM. Active force was developed after an abrupt increase in [MgADP]. The active force increased with increasing the [MgADP]/[MgATP] ratio, not only by increasing [MgADP] (from 4 to 20 mM), but by decreasing [MgATP] (from 2.0 to 0.2 mM) as well (data not shown), indicating that MgADP competitively binds to the MgATP-binding site of myosin, so that the ADP-bound cross-bridges function as the activator for the thin filament in the absence of Ca²⁺.

At short SLs around 2.5 μm, spontaneous oscillations of force and SL, accompanying the propagation of SL oscillation along the myofibril, were frequently observed at 4–8 mM MgADP (Supplementary Fig. S1 and Movie S1, Supplementary Material). These oscillations looked similar to the phenomenon called spontaneous oscillatory contraction (SPOC) that we reported previously (24,26). During the oscillation, the active force largely fluctuated, whereas the length of individual sarcomeres oscillated in a saw-tooth waveform with the peak-to-peak amplitudes exceeding 300 nm (Supplementary Fig. S1). The force oscillation ranged from 67 ± 8% to 125 ± 12% of the average force (mean ± SD, n = 9 from six myofibrils). The oscillation continued over minutes, maintaining the level of average force nearly constant, and was well reproduced during the repeated activations.

SL-dependent activation by the ADP-bound cross-bridges

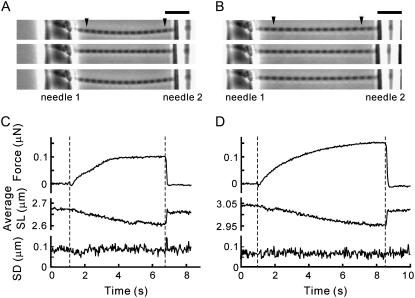
To examine the SL dependence of activation by the ADP-bound cross-bridges, we compared the active force induced by the exogenous MgADP at different SLs. A set of force measurements, which consisted of two sequential activation-relaxation cycles at different SLs (Fig. 2 A), was repeated several times with examining the deterioration of the myofibril during every measurement (for details, see Materials and Methods). The striation pattern of sarcomeres was observed from the phase-contrast image (Fig. 2 B) throughout the force measurement, and the individual SLs between the inner edges of the needles were analyzed (Fig. 2 C). Fig. 3 shows typical time courses of force development, average SLs, and variation of SLs (SD of SL) in a single myofibril activated by 6 mM MgADP in the presence of 1 mM MgATP at two different SLs. Note that the active force at average SL 2.95 μm was larger by a factor of 1.5 than at average SL 2.61 μm (top traces in Fig. 3, C and D; see also arrows in Fig. 4), though the length of overlap between the thick and the thin filaments was smaller by 30%.

FIGURE 3.

Force and SL behavior at two different SLs under a low level of activation by MgADP. Activations were performed at short (A and C) and medium (B and D) SLs with 1 mM MgATP and 6 mM MgADP in the absence of Ca²⁺. (A and B) The phase-contrast images of a myofibril from top to bottom were taken during relaxation, at the plateau of force development, and during subsequent relaxation. The individual SLs in the region between the arrowheads were analyzed. Needles 1 and 2 are the stiff and the flexible, respectively. The bowed shape of the myofibril is due to the solution flow. (C and D) The active force (top), the average SL (middle), and the standard deviation of SL distribution (bottom). The period between the two vertical dashed lines indicates the activation. The maximum active force recorded was 30.3 kN/m² at SL 2.61 μm (A) and 44.1 kN/m² at SL 2.95 μm (B). The cross-sectional area of the myofibril was 3.02 μm². Scale bar, 10 μm.

FIGURE 4.

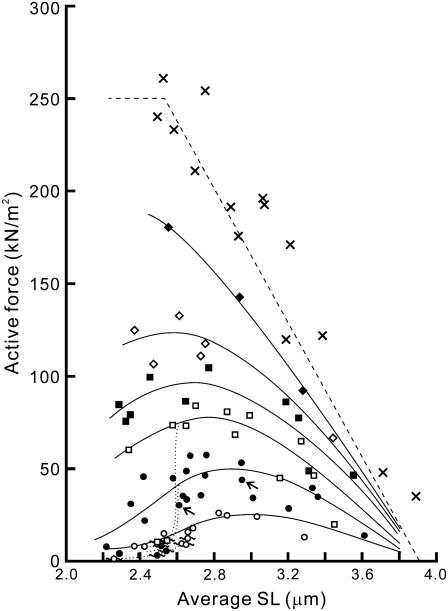
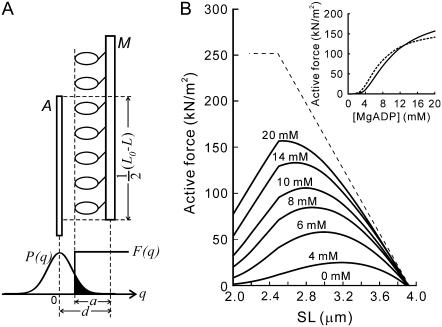
Force-SL relationship at various MgADP concentrations. The active force at the plateau of force development in 4 mM (two myofibrils; ○), 6 mM (four myofibrils; •), 8 mM (three myofibrils; □), 10 mM (three myofibrils; ▪), 14 mM (two myofibrils; ⋄), and 20 mM (one myofibril; ♦) MgADP with 1 mM MgATP in the absence of Ca²⁺ was plotted against SL. Here, only the average SL is plotted for clarity (for standard deviation showing the homogeneity of SL, see Supplementary Fig. S3 A, Supplementary Material). Spontaneous oscillation of force and SL was sometimes observed at 4, 6, and 8 mM MgADP as shown by symbols with wavy lines. The active force declined when the oscillation occurred, as shown by the dotted lines. Both solid and dotted lines were drawn by eye. The relationship obtained at pCa = 4.5 in the absence of MgADP (three myofibrils) is shown by crosses. The linear dashed line was obtained by assuming that the active force is proportional to the length of overlap between the thick and the thin filaments (the parameters were determined from the electron micrographs (31)). The data are plotted without correction for the rundown of the active force during repeated activations. The data indicated by small arrows correspond to those shown in Fig. 3.

Inhomogeneous distribution of SLs in a myofibril may cause artificial larger force production at longer SL due to the stretch of the elastic component, connectin/titin (27). We therefore constantly monitored the SL and its distribution during both relaxation and activation, and only the records where the striation was clearly observed throughout the measurements were used in the subsequent analysis (Fig. 3, A and B; Supplementary Movies S2 and S3, Supplementary Material). Upon successful activations as shown in Fig. 3, all the sarcomeres within the observed region (between the arrowheads in the micrographs in Fig. 3) shortened by ∼100 nm on average (middle traces in Fig. 3, C and D), while maintaining the variation of SL at the same level (SD ≤ 100 nm) as during relaxation (bottom traces in Fig. 3, C and D). Within this range of standard deviation, the distributions of SLs with average SL 2.95 μm (n = 12 sarcomeres distributed between SL 2.85–3.01 μm) and 2.61 μm (n = 12 sarcomeres distributed between SL 2.47–2.70 μm) did not overlap with each other.

The sarcomeres sometimes showed a slow continuous shortening with the average shortening velocity of up to 5 nm/s/sarcomere (∼0.2% SL/s) at a plateau of activation whereas the standard deviation of SL did not change. This implies that there exists some end compliance outside the observed region, e.g., underneath the microneedles. This shortening possibly causes underestimation of active isometric force according to the force-velocity relationship. The shortening velocity was, however, more than two orders of magnitude slower than the maximal shortening velocity of rabbit skeletal myofibrils (28). Therefore, we conclude that in the measurements of the active isometric force, the estimation error due to the slow shortening of SL is negligibly small, and the larger force production at longer SL is therefore the inherent property of sarcomeres.

We also confirmed that the SL-dependent activation is not affected by the deterioration of myofilaments. The reference active and resting forces (see Materials and Methods) did not increase after repeated activations, and the resting force measured at the SL of interest was consistent with that without activation (Supplementary Fig. S2, Supplementary Material). Note that the value of the resting force was consistent with that previously reported (29). These confirm that the regulatory function of the thin filaments is kept intact throughout the measurements.

Dependence of the active force on [MgADP]

Next, we examined the force-SL relationship at various concentrations of MgADP (4–20 mM). The results are summarized in Fig. 4. The active force and its SL dependence changed depending on [MgADP]. At 4 mM MgADP, the active force substantially increased with increasing SL from 2.2 to ∼3.0 μm and monotonically decreased with a further increase in SL, reaching the maximum at SL 2.8–3.0 μm. As [MgADP] increased, the SL at which the maximal force was observed gradually shifted leftward (to SL 2.4–2.6 μm at 14 mM MgADP), accompanied by an increase in the magnitude of force. Concomitantly, the region of SLs where the active force monotonically decreased with increasing SL became broader, approaching the well-established linear force-SL relationship. These results show that the length-dependent thin filament activation depends on the population of the ADP-bound cross-bridges. Furthermore, at each SL the active force increased with increasing [MgADP] in a sigmoidal manner (Fig. 5), suggesting that the ADP-bound cross-bridges cooperatively activate the thin filaments. Such cooperativity in force enhancement is similar to that observed in muscle fibers (8). The Hill coefficient n was determined as 2.20 and 1.60, whereas the MgADP₅₀ was 13.6 mM and 11.9 mM at SL 2.3–2.6 μm and SL 2.7–3.0 μm, respectively.

At a full activation by Ca²⁺ (pCa 4.5) in the absence of MgADP, the active force monotonically decreased with an increase in SL, which is consistent with the previous results obtained in muscle fibers (10,11) and myofibrils (30). However, the force-SL relationship we obtained is shifted rightward by ∼100 nm compared to that predicted from the length of overlap between the thick and the thin filaments (the dashed line in Fig. 4; see Sosa et al. (31)). This shift is attributable to the broad distribution of SLs (SD = 200–300 nm) at full activation by Ca²⁺. At low levels of activation by MgADP, where the standard deviation of SL was typically confined within ±100 nm (Supplementary Fig. S3 A, Supplementary Material), the effect of the variation of SL on the force-SL relationship must be smaller; therefore, the peak position is determined with the accuracy of ≤100 nm.

On the other hand, the shortening of SL upon activation results in the underestimation of the active force, because the actual resting force, where the active force was measured, must be smaller than that measured at relaxation. Typically, the extent of shortening of sarcomeres was 1–3% at low levels of activation (4–8 mM MgADP) and at most 10% at a high level of activation (20 mM MgADP), which corresponds to the reduction of resting force by ∼5 kN/m² and 15 kN/m², respectively. This error gives at most 10% underestimation of the active force, which becomes especially significant at longer SL. Hence, the actual peak position of each force-SL relationship may in fact be located by up to 50 nm to the right from those shown in Fig. 4.

Effect of interfilament spacing

It has been reported that an increase in SL causes a reduction of the interfilament spacing between the thick and the thin filaments (16,32,33), which may possibly cause the larger force production at longer SL due to an increase in the effective concentration of myosin heads in the vicinity of the thin filaments (13,34,35). Hence, we examined the effect of dextran T-500, which compresses the lattice spacing of a muscle, on the force-SL relationship at 6 mM MgADP. The effect of dextran on the lattice spacing has been extensively studied in skinned muscle fibers (36,37), but almost never in myofibrils. Thus, we first examined the extent to which dextran perturbs the interfilament spacing in skeletal myofibrils. Due to low spatial resolution, the width change in myofibrils could not be measured with nanometer-order accuracy directly from the phase-contrast images during the active force measurements; therefore, it was examined separately using micrometer-sized beads attached to the lateral sides of a myofibril (Fig. 6 A; for details, see Materials and Methods). The width of a myofibril at SL around 2.5 μm, which was 1.42 ± 0.26 μm (mean ± SD, n = 8 myofibrils), decreased by 4–6% with the addition of 1% (w/v) dextran under relaxing conditions (Fig. 6 B and inset). During stepwise increase and decrease in the dextran concentration, the difference in width at each point was within 2% of the initial width (in the absence of dextran) (data not shown). Considering that the width of the fiber correlates with the lattice spacing (36), we conclude that the interfilament spacing in myofibrils is effectively compressed by dextran T-500.

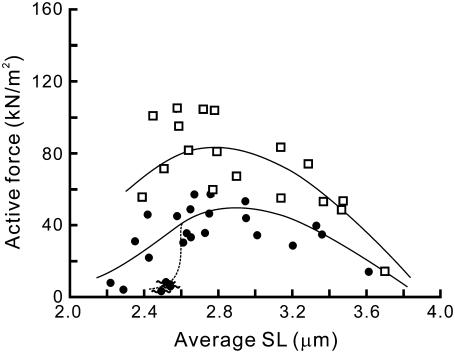
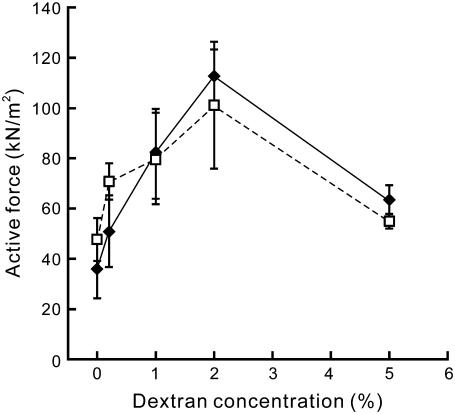
We found that with the addition of 1% dextran the active force increased twofold at SL 2.3–2.6 μm, i.e., from 36.0 ± 11.6 kN/m² in the absence of dextran (mean ± SD, n = 6 from four myofibrils) to 81.8 ± 17.8 kN/m² (n = 7 from four myofibrils). The shape of the force-SL relationship drastically changed involving force enhancement and the leftward shift of the peak (Fig. 7). Moreover, the SPOC (see Supplementary Fig. S1) observed at short SLs disappeared. The active force increased with an increase in the dextran concentration within the range between 0.2% and 2%, whereas further addition of dextran up to 5% caused force reduction to a half of the maximal force obtained at 2% dextran (Fig. 8).

FIGURE 7.

Effect of dextran on the force-SL relationship. The force-SL relationships obtained at activations with 6 mM MgADP and 1 mM MgATP in the absence of Ca²⁺, with 1% (w/v) dextran T-500 (four myofibrils; □) and without dextran (four myofibrils; •), are shown. The data at 6 mM MgADP without dextran are replotted from Fig. 4 (the data with standard deviation are shown in Supplementary Fig. S3 B, Supplementary Material). The lines were drawn by eye.

FIGURE 8.

Active force depending on the dextran concentration. The active force was measured at various concentrations of dextran within two regions of SLs, 2.3–2.6 μm (♦, solid line) and 2.7–3.0 μm (□, dashed line), in the presence of 6 mM MgADP and 1 mM MgATP in the absence of Ca²⁺ (cf. Fig. 7). The active force was averaged within each range of SL, except for the data at which spontaneous oscillation was observed (symbols with wavy lines in Fig. 7). Data points are the mean ± SD (n = 2–8 for each point).

DISCUSSION

In this study, the use of a single myofibril or a small bundle of myofibrils, together with a rapid solution exchange system equipped in the optical microscopy system, allowed us to obtain reliable force-SL relationship through the quantitative analysis of individual SLs simultaneously with the active force measurement. Furthermore, we could focus on the role of cross-bridges on the mechanism of force regulation by activating the contractile system with MgADP instead of Ca²⁺. As a result, our mechanical measurements revealed that the ADP-bound cross-bridges are essential for the length-dependent regulation of the thin filament activity independently of the regulation by Ca²⁺ (Figs. 3 and 4). We demonstrated that the activation by the ADP-bound cross-bridges is a positive cooperative process (Fig. 5), and that the interfilament spacing between the thick and the thin filaments is critical for such activation (Fig. 7). These observations suggest that both the cooperative binding and the interfilament spacing underlie the mechanism of the cross-bridge mediated force regulation in sarcomeres. This mechanism may also be important at partial activation by Ca²⁺ (13,14), where the cross-bridges also function as an activator for the thin filament.

Considering that the stretch of sarcomeres induces a reduction in interfilament spacing, it is inferred that the length-dependent activation, that is, the larger force production at longer SL, is caused primarily by the increase in the effective concentration and/or the increase in the affinity of the ADP-bound cross-bridges for the thin filament (13,34,35). However, the effect of lattice spacing responding to changes in SL alone is not sufficient to completely explain the mechanism of activation by the cross-bridges, because the active force cooperatively increases with increasing [MgADP], and both the cooperativity (n) and the sensitivity (MgADP₅₀) are SL dependent (Fig. 5). We discuss below the possible mechanisms of cooperative activation in sarcomeres based on the interfilament spacing and its modulation by the strongly bound cross-bridges.

Model analysis

We discuss these results based on a simple model previously proposed by Ishiwata and Oosawa (38). The model takes into account the interaction probability between the thick and the thin filaments, which depends on the interfilament spacing, d (Fig. 9 A). The active force is assumed to be proportional to the interaction probability between a myosin head, which protrudes away from the thick filament according to a step function, F(q), and the thin filament, which is thermally fluctuating in the lateral direction according to a Gaussian distribution, P(q), with a variance σ_A. Here we make a critical assumption that the average extent of protrusion of myosin heads from the thick filament, a, increases with [MgADP] according to a = a₀[MgADP]/(K_D + [MgADP]), so that the level of activation increases with [MgADP]. The parameter K_D is considered to be the apparent affinity of cross-bridges for MgADP, and a₀ is a constant. The active isometric force (F) is then expressed as the following equation (for details see Appendix):

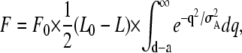(1)

where F₀ and L₀ (= 3.9 μm) are constants, and L is SL. Here, the length of overlap, L₀ − L, is kept constant at 1.4 (= 3.9–2.5) μm for L shorter than 2.5 μm, below which the number of myosin heads is constant. The value of K_D was chosen as 2 mM to fit the data, which is an order of magnitude weaker than those previously reported for normal activating condition (39,40). Nevertheless, such a low affinity of ADP is realistic in the absence of Ca²⁺. Actually, the increase in [Ca²⁺] decreases the apparent K_D to ∼1/10 of that at activation by MgADP (41). In addition, the apparent K_D is affected by MgATP, because it binds to the myosin heads competitively with exogenous MgADP. Hence, the value of K_D we adopted is appropriate for the conditions we examined.

FIGURE 9.

Model analysis. (A) The interaction of myosin heads with the thin filament is assumed to occur when the thin filament fluctuates over the distance > (d − a), therefore, the probability of the cross-bridge formation is proportional to the solid area. M, the thick filament; A, the thin filament. F(q) and P(q) are the existence probabilities of the myosin heads and the thin filaments, respectively. Here it is assumed that the value of a depends on [MgADP]. For further details, see text. (B) The force-SL relationship obtained from the model in panel A. The MgADP concentration is shown above each trace. The trace at 0 mM MgADP, corresponding to the relaxing state, almost coincides with the abscissa. (Inset) The force-[MgADP] relationship at SL 2.5 μm (solid line) and SL 2.9 μm (dashed line) corresponding to Fig. 5. It is to be noted that the effect of lattice compression induced by dextran was also explained by this model (Supplementary Fig. S4, Supplementary Material). For the values of parameters used in the model analysis, see Appendix.

The force-SL relationship thus obtained is shown in Fig. 9 B. We assumed the sarcomere structure to be isovolumic (d²L = V, where V is the sarcomeric volume) to simplify the model analysis, although the volume is not strictly maintained constant in skinned fibers (33,42). In this analysis, therefore, the lattice spacing d decreases in reciprocal proportion to L^1/2, resulting in a steep increase in the probability of the cross-bridge formation with stretching a sarcomere. The perturbation of the optimal interfilament spacing by dextran (Fig. 7) experimentally supports the validity of this model (Supplementary Fig. S4, Supplementary Material). There is therefore no need in postulating the existence of the cooperativity to account for the nonlinear relationship between active force and the length of overlap. Thus, one of the characteristics of the observed force-SL relationship, namely the increase of force with increasing SL at low [MgADP] (Fig. 3), can be explained by the lattice spacing-dependent interaction probability between the thick and the thin filaments.

To explain the peak-shift with increasing [MgADP] (Fig. 4) and the SL dependence of cooperativity (Fig. 5), the relative distance between the myosin heads and the thin filament, d − a, should be [MgADP] dependent. If we assume that the cross-bridge formation occurs according to the cooperative Hill equation, 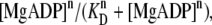while keeping the value of a constant, a sigmoidal increase in force with increasing [MgADP] can be obtained. However, the peak-shift with increasing [MgADP] and the SL dependence of cooperativity cannot be explained with any n (see Appendix and Supplementary Fig. S5). This suggests that the cooperative behavior, which is derived from the steric effect involving relative distance between the myosin heads and the thin filament, underlies the mechanism of the cross-bridge mediated activation.

Implications for the mechanism of the cross-bridge mediated force regulation

These findings and the model analysis suggest that the following dual mechanism underlies the cross-bridge mediated activation in sarcomeres. First, the interfilament spacing between the thick and the thin filaments affects the effective concentration of myosin heads within the overlap, as demonstrated by our model. Assuming that the changes in the width of a myofibril are solely attributable to the changes in the lattice spacing, the distance between the thick and the thin filaments shortens by ≤1 nm with the addition of 1% dextran. It should be stressed that such a small perturbation of a subnanometer order enhances the active force twofold near slack SL (Fig. 7). Moreover, the active force reached the maximum with 2% dextran, and was reduced by further compression of the lattice spacing with 5% dextran (Fig. 8), implying that there exists the optimal distance between the thick and the thin filaments where the probability of the cross-bridge formation is maximal and the cross-bridges work most efficiently (43,44). Such high sensitivity to the geometric arrangement of the filament lattice must be playing an important role in the mechanism of autonomous force regulation in sarcomeres, especially at both transient phase and intermediate levels of activation.

Second, activation of the thin filament by the ADP-bound cross-bridges is a positive cooperative process, as shown in Fig. 5. The model analysis predicts that the cooperativity is derived from the increase in the average protrusion of myosin heads from the thick filament, a, with an increase in the number of ADP-bound cross-bridges. What does this assumption imply in terms of the molecular events in sarcomeres? As mentioned above, the binding of myosin heads to the reconstituted thin filaments shows positive cooperativity in the solution experiments (4,5,45), which may contribute to cooperative activation. In addition, it is quite reasonable that this cooperativity is enhanced by a steric effect, leading to the reduction of the relative distance, d − a, in the above model, being equivalent to the increase in the value of a at constant d (Fig. 9 A). It has been reported that the myofilament lattice is compressed as the number of working cross-bridges increases upon activation (44,46). If this is also true for the conditions we examined here, the interfilament spacing, d, must be reduced by the formation of the cross-bridges so that the equilibrium position of the thin filament shifts closer to the thick filament. The other property to be considered is the flexural rigidity of the thin filament, which is likely to be reduced upon binding of myosin heads (47,48). If we take into account this property, the variance of the lateral bending fluctuation of the thin filaments, σ_A, must increase with an increase in the number of cross-bridges. The broadening of the variance may also occur simply due to the pulling force generated by cross-bridges. Although there exist several possible molecular mechanisms of cooperativity, we emphasize that the steric cooperativity is characteristic for the crystalline lattice structure of sarcomere, where the myosin heads are arranged periodically at fixed positions. This situation is quite different from that in solution where the molecules are distributed randomly.

From the implications we have described so far, the weakening of the length dependence of activation with increasing the level of activation (Fig. 4) is explained as follows. At low levels of activation, the effect of the interfilament spacing is predominant since the number of the ADP-bound cross-bridges is small; however, as the level of activation increases, the value of d − a becomes smaller such that the effect of the interfilament spacing tends to be reduced, because the interaction probability, which is proportional to the solid area of Fig. 9 A, tends to be saturated; in this model, the value of a most sensitive to d is near the inflection point of the distribution function P(q) (see the solid area of Fig. 9 A). To sum up, these analyses strongly suggest that the optimal interfilament spacing under relaxing conditions and its modulation due to strongly bound cross-bridges are the important factors determining the characteristics of force regulation in sarcomeres.

The filament lattice of skinned fibers, especially myofibrils, may be swollen to some extent compared with the intact muscle (33,42). If the lattice structure is optimized for force generation in intact fiber, the fact that the maximum force enhancement was induced by the addition of 2% dextran (Fig. 8), which compresses the lattice spacing by 15% (Fig. 6 B), implies that the lattice spacing of myofibrils may have been expanded by ∼15%. Nevertheless, the characteristics of the force generation in myofibrils described above have to be important in the intact muscle as well, because the lattice spacing does change with SL due to the isovolumic behavior in the intact fibers. Recently, Konhilas et al. suggested that the length-dependent properties do not correlate simply with the lattice spacing measured under relaxing conditions (16). The resting lattice structure is likely to change upon activation in skeletal muscle (49), whereas it remains constant in cardiac muscle (50), implying that the difference in the responsiveness of the interfilament spacing upon activation, which corresponds to the degree of change in (d − a) in our model, at least partly, accounts for the quantitative differences in the apparent Ca²⁺ sensitivity and cooperativity between various types of striated muscle.

Implications for the mechanism of SPOC

We found that the steady spontaneous oscillation of force and SL, i.e., SPOC (24,26), occurs at low levels of activation with MgADP in the absence of Ca²⁺ (Figs. 4 and Supplementary S1; see also Supplementary Movie S1). The fact that weakening of the length-dependent activation either by increasing [MgADP] (Fig. 4) or by the addition of dextran (Fig. 7) eliminated SPOC, together with the model analysis, suggests that SPOC is driven by shortening deactivation and lengthening activation of sarcomeres coupled with the length-dependent changes in the lattice spacing. Therefore, it is possible that the lattice structure of sarcomeres dynamically changes with SL oscillation. The propagation of the lengthening phase along the myofibrils (the SPOC wave, Supplementary Fig. S1 and Movie S1) may be explained by the propagation of transient change in the lattice spacing via the Z- and M-lines. This hypothesis on the mechanism of SPOC should be experimentally examined in future.

CONCLUSIONS

In summary, the force-SL relationship obtained here provides important insights into the mechanism of the thin filament regulation by the cross-bridges in sarcomeres. We found that the cross-bridge mediated activation is strongly affected by ≤1 nm changes in the lattice spacing between the thick and the thin filaments. Hence, the active force development in muscle is not determined simply by the length of overlap, but is a highly cooperative process involving the changes in interfilament spacing. The studies focusing not only on the static properties, such as the force-SL relationship, but also on the dynamic properties based on the crystalline lattice structure of sarcomeres will be indispensable for the complete understanding of the molecular mechanism of force development and its regulation in striated muscle.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.

APPENDIX

Model analysis of the force-SL relationship

The model analysis performed here is based on the simple model previously proposed by Ishiwata and Oosawa (38). In this study, we assumed that the lateral position of myosin heads, extending up to a, depends on [MgADP] as described below.

The location probability during the lateral fluctuation of the thin filament is assumed to follow Gaussian distribution:

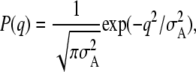(A1)

where q is a lateral coordinate from an equilibrium position of the thin filament as shown in Fig. 9 A, and σ_A is a variance of its lateral fluctuation.

The thin filament is assumed to interact with myosin heads only when the deviation, q, exceeds the intermolecular distance, d − a:

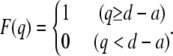(A2)

The interaction probability is then given by:

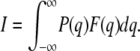(A3)

Here, the parameter a, which is considered to hold the key to this model analysis (for the meaning of this parameter in the contractile system of muscle, see Discussion), is assumed to be expressed as follows:

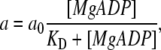(A4)

where a₀ is a constant, and K_D is the apparent affinity of MgADP for myosin (to be precise, for actomyosin complex in the absence of Ca²⁺). The best-fit values for a₀ and K_D were 29 nm and 2 mM, respectively.

The volume of myofilament lattice is assumed to be constant according to the Eq. A5. The interfilament spacing between the thick and the thin filaments is estimated from the value of d₁₀ = 40 nm (51), which corresponds to the interfilament spacing of 26.7 nm, at SL 2.2 μm.

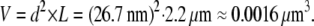(A5)

Although those values slightly differ between the reports (36,46,51), the difference does not affect our conclusions. When the effect of 1% (w/v) dextran was examined (Supplementary Fig. S4, Supplementary Material), the sarcomeric volume of 1.41–1.47 × 10⁻³ μm³ was taken instead of 1.6 × 10⁻³ μm³ with the assumption that the osmotic compression by the addition of 1% dextran reduces the sarcomeric volume by 8–12% according to the reduction of myofibrils width, 4–6% (Fig. 6 B). It is to be noted here that the essential point of this model is not the constant volume, but the reduction of the interfilament spacing accompanied by the increase in SL, which has been experimentally confirmed; when the volume does not remain constant, the best-fit values for the parameters may become different, but the essential features of these experimental results still can be explained by the same model.

Finally, the active isometric force is determined by the following equation:

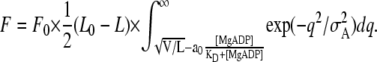(A6)

The values of the other parameters used for the model analysis were determined as follows: L₀ = 3.9 μm, which was determined from the observation of the electron micrographs (31); σ_A = 5 nm, which was determined based on the flexural rigidity of the regulated thin filament (1 μm long) in a sarcomere in the absence of Ca²⁺ (38); and F₀ = 8, which is a parameter chosen so as to make the absolute values of active force fit to the experimental data. It is to be noted that the value of (L₀ − L) is kept constant at (3.9 − 2.5) μm for L shorter than 2.5 μm, because we assume that the full overlap between the thick and the thin filaments is achieved at L = 2.5 μm.

Thus, the model analysis well reproduced not only the larger force production at longer SL (Fig. 9 B), but also the SL-dependent force enhancement with the increase in [MgADP] (Fig. 9 B, inset).

Finally, we present a result of the model analysis obtained by assuming that the interaction probability of the force-generating cross-bridges depends on [MgADP] according to the Hill equation (the Hill coefficient larger than unity) whereas the interaction probability determined by the value of a is unchanged (also see Discussion). This means that the active force F depends on [MgADP] according to 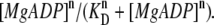Thus, the isometric force is determined by the following equation:

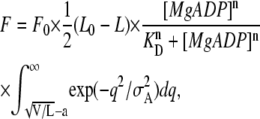(A7)

where a = 29 nm, K_D = 10 mM, and F₀ = 9 were chosen to fit the range of the active force. The Hill coefficient, n, was chosen as 2. The other parameters are the same as used in Eq. A6. According to this equation, the force-SL relationship is simply extended in vertical direction without peak shift with increasing [MgADP], although the sigmoidal increase in force with increasing [MgADP] was reproduced (Supplementary Fig. S5, Supplementary Material).